Nickel phlorin intermediate formed by proton-coupled electron transfer in hydrogen evolution mechanism

Significance

Global energy sustainability requires the development of effective energy conversion processes. In the hydrogen evolution reaction, electrons and protons are combined to generate molecular hydrogen, which stores energy in its chemical bond. Molecular electrocatalysts have been designed to facilitate this reaction by making it occur faster with lower energy input, often utilizing proton-coupled electron transfer (PCET), which couples the motions of electrons and protons to avoid high-energy intermediates. Examination of a nickel porphyrin electrocatalyst indicates that the active intermediate stores electrons in the C–H bond of the modified porphyrin generated by PCET, rather than in the traditional metal-hydride bond. The ability to store electrons in the ligand rather than in the metal has significant implications for the design of electrocatalysts.

Abstract

The development of more effective energy conversion processes is critical for global energy sustainability. The design of molecular electrocatalysts for the hydrogen evolution reaction is an important component of these efforts. Proton-coupled electron transfer (PCET) reactions, in which electron transfer is coupled to proton transfer, play an important role in these processes and can be enhanced by incorporating proton relays into the molecular electrocatalysts. Herein nickel porphyrin electrocatalysts with and without an internal proton relay are investigated to elucidate the hydrogen evolution mechanisms and thereby enable the design of more effective catalysts. Density functional theory calculations indicate that electrochemical reduction leads to dearomatization of the porphyrin conjugated system, thereby favoring protonation at the meso carbon of the porphyrin ring to produce a phlorin intermediate. A key step in the proposed mechanisms is a thermodynamically favorable PCET reaction composed of intramolecular electron transfer from the nickel to the porphyrin and proton transfer from a carboxylic acid hanging group or an external acid to the meso carbon of the porphyrin. The C–H bond of the active phlorin acts similarly to the more traditional metal-hydride by reacting with acid to produce H₂. Support for the theoretically predicted mechanism is provided by the agreement between simulated and experimental cyclic voltammograms in weak and strong acid and by the detection of a phlorin intermediate through spectroelectrochemical measurements. These results suggest that phlorin species have the potential to perform unique chemistry that could prove useful in designing more effective electrocatalysts.

Direct solar-to-fuel processes are important components of global energy sustainability efforts (1, 2). Such processes include the hydrogen evolution reaction (HER), oxidation of water to oxygen, and reduction of CO₂ to hydrocarbons (3, 4). Proton-coupled electron transfer (PCET), which is generally defined in terms of coupling between electron transfer (ET) and proton transfer (PT) reactions, is essential to all of these processes. PCET can be classified as occurring via either a sequential or a concerted mechanism (5, 6). The mechanism is determined to be sequential rather than concerted if a stable intermediate associated with initial ET or PT can be identified. This distinction is not rigorous, however, because the identification of a stable intermediate may depend on the experimental approach or the level of theory, as well as the lifetime of the intermediate. Regardless of the specific mechanism, the coupling of ET and PT plays a significant role in a wide range of energy conversion processes (7–11). Moreover, the coupling of ET and PT can be enhanced by incorporating proton relays into molecular catalysts, exploiting the proximal positioning of the proton donor and acceptor (12–16). Recognition and characterization of successful PCET motifs within molecular electrocatalysts provides insight into the design of efficient catalytic processes (17–19).

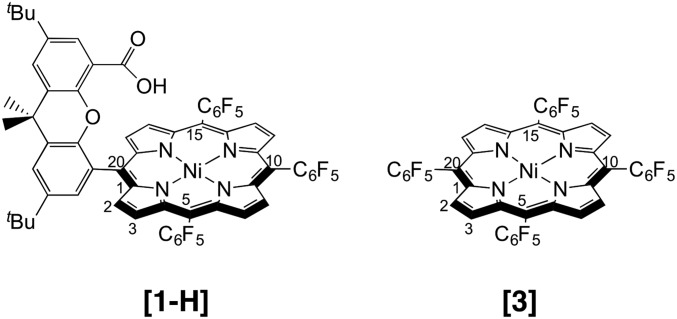
Cobalt and nickel metalloporphyrins, depicted in Fig. 1, have been investigated as HER electrocatalysts (20, 21). Experimental (22) and theoretical (23) examination of the key PCET step within the HER mechanism of the cobalt “hangman” complex (the cobalt analog of [1-H] in Fig. 1) revealed a sequential ET–PT mechanism, with an experimentally measured PT rate constant k_PT = 8.5 × 10⁶ s⁻¹ (22). In the proposed mechanism, the formally Co(I) is reduced to a Co(“0.5”) complex in which the unpaired electron is shared between the metal and the ligands, breaking the aromaticity of the porphyrin ring. Subsequent PT from the carboxylic acid proton of the hangman moiety to the porphyrin meso carbon, forming a cobalt phlorin intermediate, was hypothesized on the basis of a theoretical study (23). In particular, the calculations indicated that this PT to the porphyrin is structurally and thermodynamically favored over PT to the metal center, and the calculated PT rate constant k_PT = 1.4 × 10⁶ s⁻¹ is consistent with the experimental value. Upon protonation of the hangman carboxylate by benzoic acid and additional electrochemical reduction, H₂ is thermodynamically favored to self-eliminate from the complex (23). With strong acid, H₂ is evolved through the more traditional protonation of the metal to generate a metal-hydride, which is more thermodynamically favorable than phlorin formation. For the nickel hangman complex ([1-H] in Fig. 1), previous computational results suggested that the PT step involves a proton acceptor other than the nickel center (21), as was the case for the cobalt analog (23), but the specific mechanism was not determined.

Fig. 1.

Structures of nickel porphyrins [1-H] and [3]. Select carbon atoms of the porphyrin ring are labeled according to position, including meso carbons 5, 10, 15, and 20. Complex [2] is the analog of [1-H], where a bromine atom replaces the carboxylic acid substituent.

In this paper, we use computational and experimental methods to elucidate the full catalytic cycle for the electrochemical HER catalyzed by the nickel metalloporphyrins [1-H] and [3]. On the basis of density functional theory (DFT) calculations, referenced to values from experimental cyclic voltammetry to enhance the quantitative accuracy, we propose mechanisms for the HER in the presence of weak or strong acid. Our calculations indicate that [1-H] and [3] evolve H₂ through key phlorin intermediates, in which the meso carbon of the porphyrin is protonated, and that no nickel-hydride complexes are formed. Spectroelectrochemical experiments provide evidence of the phlorin intermediate formed via protonation of the dianionic species [3]^2–. Moreover, simulated cyclic voltammograms (CVs) based on the proposed mechanism, in conjunction with the calculated reduction potentials, pK_a’s, and free energy barriers, provide further support of this mechanism through agreement with experimental CVs.

Results and Discussion

Electronic Structure of [3].

The relative free energies for various charge, spin, and structural states of [3] were calculated using DFT. The most stable form of [3]⁰ contains a puckered porphyrin ring (denoted bent hereafter) as a closed-shell singlet. A structure in which the pyrrolic nitrogens are coplanar with the nickel center (denoted flat hereafter) is the most stable form of [3]^–. The single unpaired electron in the doublet [3]^– is localized on the nickel in the more stable flat geometry, generating a formally Ni(I) species upon reduction with a Mulliken spin density on the nickel center of ρ_Ni ≈ 1. The less-stable bent porphyrin geometry is a Ni(II) porphyrin radical species with the unpaired electron localized on the porphyrin and ρ_Ni ≈ 0. The most stable form of [3]^2– is the flat triplet, in which one reducing electron is localized on the nickel center (ρ_Ni ≈ 1) and the other reducing electron is localized on the porphyrin, consistent with our previous work (21). The more-stable flat triplet can be described as a Ni(I) porphyrin radical, whereas the less-stable bent triplet, which corresponds to ρ_Ni ≈ 0, is a Ni(II) porphyrin diradical, in which both unpaired electrons are localized on the porphyrin.

We considered four protonation sites for protonated [3], denoted [3-H]: the nickel center, producing [3-H_Ni]; a pyrrolic nitrogen, producing [3-H_N]; a meso carbon, producing [3-H_C]; and the π-electrons of a pyrrole, producing [3-H_pyr]. Note that [3-H_pyr] is analogous to an intermediate proposed recently for HER catalysis by Pd and Cu tetraferrocenylporphyrin complexes (24); however, our calculations indicate that protonation occurs at the C2 carbon rather than at the face of the pyrrole. For the three relevant charge states of [3], the thermodynamically favored protonation site is at the meso carbon position, forming a phlorin complex that is 5.5, 15.6, and 15.7 kcal/mol lower in free energy than the next most stable species for the neutral, monoanionic, and dianionic species, respectively (SI Appendix, Table S4). This result differs from our previous finding for the cobalt analog of [3], where the cobalt-hydride was the thermodynamically preferred protonated complex in the neutral form (23). As with deprotonated [3], the Ni(II) species have bent structures but the Ni(I) species have flat structures for protonated [3]. The neutral phlorin [3-H_C]⁰ is calculated to be a bent doublet with the spin density of the unpaired electron localized on the ligand rather than the metal center, indicating a Ni(II) phlorin radical, where the phlorin ring has an effective charge of −2. Thus, protonation of flat [3]^–, a Ni(I) complex, at the meso carbon position is accompanied by an additional intramolecular ET from the metal to the porphyrin, oxidizing Ni(I) to Ni(II), as well as a structural change in the porphyrin ring from flat to bent.

Similarly, protonation of flat [3]^2– at the meso carbon position is also accompanied by intramolecular ET from the metal to the porphyrin and the associated structural change in the porphyrin ring. The anionic phlorin [3-H_C]^– is calculated to be a bent singlet, with a Ni(II) center and an effective charge of −3 on the phlorin ring. For protonation of the flat triplet [3]^2– species to result in the closed-shell phlorin [3-H_C]^–, in which all electrons are paired, one unpaired electron in the flat triplet [3]^2– must undergo a spin flip to produce the flat open-shell singlet [3]^2–, which is only slightly higher in free energy. Owing to the greater spin-orbit coupling between spin states on the metal center than on the organic ligands, this spin flip is most likely to occur for the unpaired electron localized on nickel (25). Intramolecular ET within the flat open-shell singlet oxidizes Ni(I) to Ni(II) and is accompanied by the structural change within the porphyrin ring from flat to bent, producing a bent closed-shell singlet.

This analysis of [3]^– and [3]^2– indicates that PT reactions to the meso carbon in flat Ni(I) species are effectively PCET reactions. The intramolecular ET can occur first, forming the bent geometries in a sequential ET–PT reaction, or the ET and PT can occur concertedly. We were unable to model the sequential PT–ET reaction because we could not identify minimum-energy flat phlorin complexes. Similar behavior was found for [1-H], as discussed below.

Electronic Structure of [1-H].

The electronic, geometric, and thermodynamic properties of the various charge and spin states of [1-H] are similar to those of [3]. The neutral [1-H]⁰ is a closed-shell singlet Ni(II) in the bent structure. Upon reduction to [1-H]^–, the most stable structure is a doublet with a flat geometry and ρ_Ni = 0.98, indicating a Ni(I) species. Further reduction to [1-H]^2– preferentially yields a flat triplet Ni(I) porphyrin radical structure (ρ_Ni = 1.02). These results are consistent with the results for [3] in that the first reducing electron is localized on the metal center and the second reducing electron is localized on the ligand. The calculations imply that the meso carbon (position 20 in Fig. 1) is the most likely proton acceptor for intramolecular PT from the carboxylic acid of both [1-H]^– and [1-H]^2– and is particularly thermodynamically favorable for the dianionic species, with a reaction free energy of −18.4 kcal/mol (SI Appendix, Tables S5 and S6). The inclusion of a water bridge between the carboxylic acid and the metal center does not significantly alter the thermodynamic favorability of PT to the meso carbon. Thus, the present calculations indicate that a phlorin intermediate is required for H₂ evolution and that formation of a nickel-hydride is not thermodynamically favorable.

Analogous to the above analysis for [3], PT reactions to the meso carbon in the flat Ni(I) anionic and dianionic [1-H] species are effectively intramolecular PCET reactions because they involve intramolecular ET from the nickel center to the ligand, forming a Ni(II) phlorin species. Again the intramolecular ET can occur first, forming the bent geometries, denoted [1′-H]^– and [1′-H]^2–, in a sequential ET–PT reaction, or the ET and PT can occur concertedly. Formation of the bent singlet [1′-H]^2– also requires a spin flip, analogous to [3]. Assuming the sequential ET–PT mechanism, we calculated the transition states associated with intramolecular PT from the hangman moiety to the closest meso carbon after intramolecular ET for both the anionic and dianionic complexes, producing [1-H_C]^– and [1-H_C]^2–, respectively. Starting with the bent structures [1′-H]^– and [1′-H]^2–, we calculated intramolecular PT free energy barriers of $\mathrm{\Delta }{G}_{\text{PT}}^{‡}$ = 16.3 kcal/mol and $\mathrm{\Delta }{G}_{\text{PT}}^{‡}$ = 6.1 kcal/mol, respectively. Using transition state theory, the corresponding PT rate constants are k_PT = 7.1 s⁻¹ and k_PT = 2.1 × 10⁸ s⁻¹, respectively, at 298.15 K. On the basis of the relative free energy barriers to PT, the second reduction to produce the dianion is presumably necessary to enable intramolecular PT to form the phlorin. The PCET reaction for the dianion is depicted in Fig. 2.

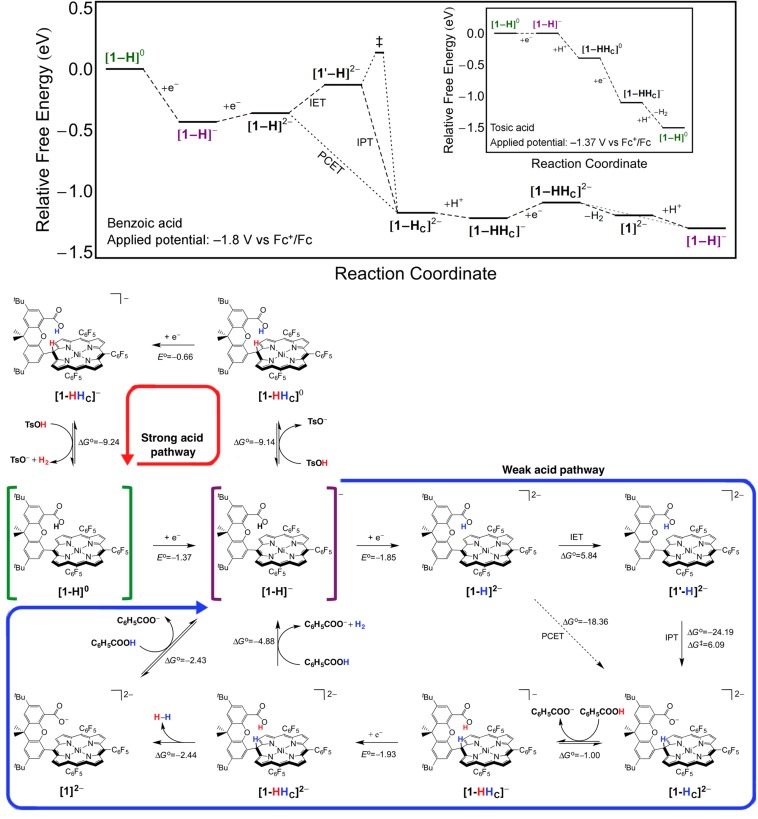
Fig. 2.

Depiction of the structures for the intramolecular PCET reaction for [1-H]. The labels show the formal oxidation state of the nickel center and the porphyrin (Por) or phlorin (Phl-H), as well as the protonation state of the hanging carboxylic acid (COOH). The IET arrow includes a spin flip of the unpaired electron on the nickel of the flat triplet to generate the flat open-shell singlet [1-H]^2–, followed by IET from the nickel to the porphyrin ring to produce the bent closed-shell singlet [1′-H]^2–. The IPT arrow includes proton transfer from the carboxylic acid to the meso carbon to produce the bent closed-shell singlet [1-H_C]^2–. The net PCET reaction is thermodynamically downhill by 18.4 kcal/mol.

In addition to the intramolecular PT that can occur within [1-H], external acid can also be used to form a doubly protonated complex, denoted [1-HH]. For all charge states considered, protonation at the metal center forming a nickel-hydride is thermodynamically unfavorable compared with protonation at the meso carbon and carboxylate positions (SI Appendix, Table S10). This result suggests that regardless of acid strength, phlorin complexes will always be preferred over metal-hydrides, in contrast to the analogous cobalt complex that was hypothesized to evolve H₂ via a phlorin with weak acid and via a metal-hydride with strong acid (23).

Cyclic Voltammetry, Reduction Potentials, and pK_a Determinations.

CVs recorded in acetonitrile for [1-H] and [3], referenced to the standard reduction potential ferrocenium/ferrocene (Fc⁺/Fc), are depicted in Fig. 3. As shown previously (21), CVs of [3] exhibit two reversible waves with midpoint potentials E_1/2 = –1.27 V and E_1/2 = –1.83 V, assigned to the reduction of [3]⁰ and [3]^–, respectively. The CVs of [1-H] also exhibit two reversible waves with E_1/2 = –1.37 V and E_1/2 = –1.99 V, assigned to the reduction of [1-H]⁰ and [1]^2–, respectively, as well as a central irreversible couple with peak potential E_p = –1.8 V. In the presence of benzoic acid (pK_a = 20.7) (26), the central irreversible wave of [1-H] and the second reversible wave of [3] become catalytic (Fig. 3 A and C). When titrated with tosic acid (pK_a = 8.0) (27), the first reversible waves of [1-H] and [3] become catalytic (Fig. 3 B and D). Bulk electrolysis of [3] with tosic acid at –1.2 V generated H₂ at 85% faradaic efficiency, similar to previous experiments of [3] with benzoic acid (21). These experiments suggest that H₂ evolution is catalyzed by [1-H] and [3] in benzoic acid and tosic acid, although H₂ could also be formed by other reduced macrocycles, such as Ni chlorin, Ni bacteriochlorin, or Ni isobacteriochlorin species. Using the initial [1-H]⁰/[1-H]^– reduction as a reference, reduction potentials calculated with DFT are given in Table 1 and SI Appendix, Table S11. Comparison with available experimental values for [1-H] and [3] lead to an average error of only 13 mV. This high level of agreement with experiment provides validation for the chosen computational methods.

Fig. 3.

Cyclic voltammetry of [1-H] and [3] in benzoic and tosic acids in 0.1 M TBAPF₆/acetonitrile electrolyte at a glassy carbon electrode with a scan rate of 0.1 V/s. (A) CVs of 0.3 mM [1-H] in the presence of 0 (black), 0.16 (red), 0.40 (green), 0.80 (dark blue), and 2.0 (light blue) mM benzoic acid. (B) CVs of 0.4 mM [1-H] in the presence of 0 (black), 0.40 (red), 1.0 (green), 2.0 (dark blue), 5.0 (light blue), and 10.0 (magenta) mM tosic acid. (C) CVs of 0.4 mM [3] in the presence of 0 (black), 0.20 (red), 0.40 (green), 0.80 (dark blue), and 2.0 (light blue) mM benzoic acid. (D) CVs of 0.4 mM [3] in the presence of 0 (black), 1.0 (green), 2.0 (dark blue), 5.0 (light blue), and 10.0 (magenta) mM tosic acid. Note that some CVs of [1-H] with benzoic acid (A) exhibit minor curve crossing, which is thought to be an artifact of background subtraction. No crossing is observed for the uncorrected CVs.

Table 1.

Calculated reduction potentials

Oxidized species	Reduced species	E°
[1-H]0	[1-H]–	–1.37 (–1.37)*
[1-H]–	[1-H]2–	−1.85
[1′-H]–	[1-H]2–	−1.78
[1-H]–	[1-HC]2–	−1.05
[1-HC]–	[1-HC]2–	−0.81
[1-HC]2–	[1-HC]3–	−1.96
[1]–	[1]2–	−1.40 (–1.42)†
[1]2–	[1]3–	−2.01 (–1.99)
[3]0	[3]–	−1.26 (–1.27)‡
[3]–	[3]2–	−1.83 (–1.83)‡
[3]2–	[3]3–	−2.61
[1-HHC]0	[1-HHC]–	−0.66
[1-HHC]–	[1-HHC]2–	−1.93
[3-HC]0	[3-HC]–	−0.59
[3-HC]–	[3-HC]2–	−1.86

Values given in volts vs. Fc⁺/Fc in acetonitrile. Experimental values of E_1/2 are given in parentheses, as obtained from ref. 21. See SI Appendix, Table S11 for additional calculated values.

^*E_1/2([1-H]⁰/[1-H]^–) was used as the reference and agrees by construction.

^†Complex [1]^– is in the bent-down geometry, ∼2 kcal/mol lower in free energy than the corresponding bent-up structure.

^‡Calculated values corrected from ref. 21.

Calculated pK_a’s are required to complete the analysis of the HER mechanisms by [1-H] and [3]. Analysis of the experimental CVs generated in tosic acid and benzoic acid provides information about the pK_a’s of certain protonated forms of [3] and [1-H] (see SI Appendix for details). On the basis of this analysis and calculations of absolute pK_a’s, the pK_a of [3-H_C]⁰ is estimated to be 15.0, where the italicized proton is removed. Using this value as a reference for additional calculations, the calculated pK_a’s of [3-H_C]^–, [1-HH_C]⁰, and [1-HH_C]^– are 35.9, 14.7, and 21.4, respectively. These computed values are consistent with the experimental values (SI Appendix, Table S12).

To provide more reliable pK_a’s of [1-H]⁰ and [1-H]^–, a second reference was used. To obtain this experimental value, we recorded CVs of [1]^– (generated by treatment with K₂CO₃) in acetonitrile with varying concentrations of benzoic acid. The CVs (SI Appendix, Fig. S1A) show that as the benzoic acid concentration is increased, the midpoint potential for the reversible first reduction wave shifts anodically from that of [1]^– (–1.42 V) to that of [1-H]⁰ (–1.37 V). Simulated fits of the experimental CVs yield an equilibrium constant of 17 ± 3 for protonation of the carboxylate group of [1]^– by benzoic acid, which corresponds to a pK_a of 21.9 ± 0.1 for [1-H]⁰. The pK_a’s of other [1-H] species with various charges and with the removed proton at various sites were calculated using this pK_a for [1-H]⁰ as a reference. The pK_a’s of [1-H]⁰ and [1-H]^– were subsequently used in the calculation of the free energy of H₂ self-elimination from [1-HH_C]^– and [1-HH_C]^2– with thermodynamic cycles. See SI Appendix for further details.

Hydrogen Evolution Mechanisms.

The HER mechanisms for [3] can be deduced from the calculated reduction potentials, pK_a’s, and relative free energies. For H₂ production with tosic acid and benzoic acid, the CVs show catalysis occurring at the [3]⁰/[3]^– couple (–1.27 V) and the [3]^–/[3]^2– couple (–1.83 V), respectively (Fig. 3 D and C). Protonation of [3]^– by tosic acid is thermodynamically downhill by 9.5 kcal/mol. The resulting phlorin product, [3-H_C]⁰, is easily reduced to [3-H_C]^– at the [3]⁰/[3]^– potential. Reaction of [3-H_C]^– with tosic acid to eliminate H₂ is thermodynamically downhill by 4.8 kcal/mol, regenerating the neutral [3]⁰ catalyst. Unlike tosic acid, benzoic acid is unlikely to protonate [3]^– because it is thermodynamically uphill by 7.8 kcal/mol. Therefore, reduction to [3]^2– is required, consistent with the experimental CVs. Protonation of [3]^2– by benzoic acid to form [3-H_C]^– is thermodynamically downhill by 20.8 kcal/mol. Although H₂ production from [3-H_C]^– reacting with tosic acid is thermodynamically favorable, such a reaction is 12.5 kcal/mol uphill in free energy with benzoic acid. Therefore, an additional reduction from [3-H_C]^– to [3-H_C]^2– is necessary. The calculated reduction potential for this process, –1.86 V, is only slightly negative of the calculated [3]^–/[3]^2– potential, indicating that such a mechanism is plausible. H₂ production from reaction of [3-H_C]^2– with benzoic acid is thermodynamically downhill by 1.3 kcal/mol, regenerating the monoanion [3]^–. Thus, the HER mechanism for [3] is proposed to involve a phlorin intermediate for both weak and strong acids (SI Appendix, Fig. S2).

The proposed HER mechanisms for [1-H] are depicted in Fig. 4. First we focus on the mechanism with a weak acid, specifically benzoic acid. According to experiment, solutions of [1-H] and benzoic acid evolve H₂ at –1.8 V (Fig. 3A). After initial reduction to [1-H]^– (shown in purple brackets in Fig. 4), the following possible steps were determined to be unlikely on the basis of thermodynamics: an intramolecular PCET reaction to [1-H_C]^–, which is thermodynamically unfavorable by 5.7 kcal/mol, and direct protonation to form [1-HH_C]⁰, which is thermodynamically unfavorable by 8.2 kcal/mol. The proposed mechanism in Fig. 4 indicates that [1-H]^– is electrochemically reduced to [1-H]^2–, with a calculated E^o = –1.85 V, which is consistent with the experimentally measured E_p = –1.8 V. Note that we cannot rule out the possibility that [1-H]^– is reduced directly to [1-H_C]^2– in a concerted electrochemical PCET reaction, with a calculated standard reduction potential of E^o = –1.05 V; as discussed below, however, the simulated CVs support the [1-H]^–/[1-H]^2– reduction step.

Fig. 4.

Free energy diagrams (Top) for H₂ production catalyzed by [1-H] with benzoic acid (C₆H₅COOH, pK_a = 20.7) and an applied potential of –1.8 V vs. Fc⁺/Fc and tosic acid (TsOH, pK_a = 8.0) with an applied potential of –1.37 V vs. Fc⁺/Fc (Inset). The chosen applied potentials, which define the zero for the free energy changes associated with reduction steps, correspond to the peaks of the catalytic waves in the CVs. Complete mechanistic cycle of proposed mechanisms (Bottom), starting from [1-H]⁰ (shown in green brackets). Reduction potentials are listed in volts vs. Fc⁺/Fc, and free energies are listed in kcal/mol. Proposed cycles in strong (red arrow) and weak (blue arrow) acid regimes begin with reduction to [1-H]^– (shown in purple brackets). With benzoic (weak) acid, additional reduction is required to form [1-H]^2–. The subsequent intramolecular PCET step is thermodynamically favorable and can occur either concertedly (dotted line) or sequentially via intramolecular ET from the nickel to the porphyrin to form the bent structure [1′-H]^2– followed by intramolecular PT to produce the phlorin [1-H_C]^2–. Protonation from benzoic acid at the carboxylate forms [1-HH_C]^–, which is subsequently reduced. H₂ is evolved from [1-HH_C]^2–, either via self-elimination to the deprotonated [1]^2– or by reaction with benzoic acid, forming [1-H]^–. With tosic (strong) acid, protonation of [1-H]^– yields the phlorin [1-HH_C]⁰, which is rapidly reduced at the operating potential. The phlorin formation involves an analogous PCET step as shown for the weak acid pathway, but it is not shown explicitly for the strong acid pathway. H₂ is evolved by reaction of [1-HH_C]^– with tosic acid, forming the neutral [1-H]⁰. Note that other branches leading to Ni chlorin, Ni bacteriochlorin, and Ni isobacteriochlorin species are not shown but may be thermodynamically favorable and possibly nonproductive toward H₂ catalysis.

The subsequent intramolecular PCET reaction from [1-H]^2– to [1-H_C]^2– could occur concertedly (dotted diagonal line in Figs. 2 and 4), which is thermodynamically downhill by 18.4 kcal/mol, or sequentially via an ET–PT mechanism. The ET–PT mechanism starts with intramolecular ET, accompanied by a structural change in the porphyrin ring from flat to bent, with a reaction free energy $\mathrm{\Delta }{G}_{\text{ET}}^{\text{o}}$ = 5.8 kcal/mol, followed by intramolecular PT with a reaction free energy $\mathrm{\Delta }{G}_{\text{PT}}^{\text{o}}$ = –24.2 kcal/mol and a free energy barrier $\mathrm{\Delta }{G}_{\text{PT}}^{‡}$= 6.1 kcal/mol. The initial intramolecular ET reaction could be viewed as the electronic charge redistribution resulting from a thermal fluctuation that leads to the bent conformation of the porphyrin ring. These PCET steps could be explored further with theoretical methods that examine the relative rate constants for the sequential and concerted mechanisms (6).

Electrochemical reduction of [1-H_C]^2– to [1-H_C]^3– requires additional potential slightly beyond E_p = –1.8 V; however, protonation of the carboxylate group in [1-H_C]^2– by benzoic acid to form [1-HH_C]^– is thermodynamically favorable by 1.0 kcal/mol. H₂ production by reaction of [1-HH_C]^– with benzoic acid is thermodynamically unfavorable by 8.1 kcal/mol, and H₂ self-elimination is thermodynamically unfavorable by 9.7 kcal/mol. Reduction to [1-HH_C]^2–, which occurs at a calculated standard potential of –1.93 V, is therefore likely to occur before H₂ production. Reduction of [1-HH_C]^– is compatible with the experimentally measured E_p = –1.8 V because of the anodic shifting that can occur as a result of subsequent catalytic steps, as supported by simulated CVs (discussed below). H₂ production by reaction of [1-HH_C]^2– with benzoic acid is thermodynamically favorable by 4.9 kcal/mol, and self-elimination of H₂ is thermodynamically favorable by 2.4 kcal/mol. Self-elimination may be favored by the structural proximity of the two hydrogen nuclei, which are separated by 1.89 Å. For the self-elimination mechanism, the cycle is completed by reprotonation of the carboxylate of [1]^2–, reforming [1-H]^– (shown in purple brackets in Fig. 4).

Next we explore the HER mechanism in strong acid. Solutions of [1-H] and tosic acid catalyze H₂ production at the [1-H]⁰/[1-H]^– potential of –1.37 V (Fig. 3B). Protonation of [1-H]^– with tosic acid directly yields [1-HH_C]⁰ with $\mathrm{\Delta }{G}_{\text{PT}}^{\text{o}}$ = –9.1 kcal/mol. As discussed above, the DFT calculations indicate that [1-H]^– is flat and [1-HH_C]⁰ is bent, implying that such protonation also requires a structural change of the porphyrin ring from flat to bent and the accompanying intramolecular ET from the Ni center to the porphyrin ring. At the catalytic potential of –1.37 V, [1-HH_C]⁰ is easily reduced to [1-HH_C]^–. H₂ production by reaction of [1-HH_C]^– with tosic acid is thermodynamically favorable by 9.2 kcal/mol, forming the original [1-H]⁰ complex (shown in green brackets in Fig. 4). Flowcharts depicting all of the possible elementary steps toward H₂ evolution are shown in SI Appendix, Figs. S3 and S4.

We emphasize that the quantitative free energy differences are expected to exhibit errors on the order of ∼3 kcal/mol from a combination of factors such as the puckering of the porphyrin, the side for protonation by external acid, the DFT functional and basis set, the pK_a references, and the replacement of the tert-butyl and pentafluorophenyl groups, which could lead to minor structural differences. For example, calculation of the relative free energies of the species depicted in Fig. 2 with the pentafluorophenyl groups indicates that the free energies differences are the same to within 2.4 kcal/mol. The qualitative mechanistic insights, however, are expected to be insensitive to these factors, as shown by the agreement of the CV simulations with the experimental data and the experimental detection of the theoretically predicted phlorin intermediate discussed below.

Cyclic Voltammetry Simulations.

To support the validity of the computed HER mechanisms proposed above, CV simulations were performed for [1-H] and [3] in the absence of acid and in the presence of tosic and benzoic acids (Fig. 5). Reduction potentials for all electrochemical ET steps in the simulations were fixed at the values computed using DFT, and the equilibrium constants for all homogeneous chemical steps were based on differences in calculated reduction potentials, pK_a’s, and thermodynamic cycles for H₂ generation (SI Appendix, Tables S13 and S14). These parameters were not fit to the experimental data, although slight refinement would improve the agreement between the simulated and experimental CVs. The simulated CV of [1-H] in the absence of external acid (red dotted curve in Fig. 5A) shows reasonable agreement with the experimental CV (solid black curve), because it reproduces most of the CV features at appropriate peak potentials. The simulated mechanism assumed two consecutive reductions to [1-H]^2–, followed by sequential intramolecular ET–PT to the phlorin [1-H_C]^2–. Reprotonation of the carboxylate is assumed to occur by neutral [1-H]⁰ in solution in the absence of external acid. Note that the large shoulder on the return scan for the Ni(II/I) couple is not reproduced in the simulated CV. This discrepancy is likely due to the use of the calculated –1.40 V value for the [1]^–/[1]^2– reduction potential, which is too close to the [1-H]⁰/[1-H]^– potential of –1.37 V to be properly resolved in the simulation. Previous simulations that did capture the shoulder did so by leaving the [1]^–/[1]^2– potential as a free parameter, resulting in a value of –1.45 V for the couple (21). A difference of 0.05 V is within the accuracy of the DFT calculations, and all other CV features are well reproduced using the DFT results.

Fig. 5.

Experimental (black curve) and simulated (dotted curves) CVs of (A) 0.34 mM [1-H] and (B) 0.30 mM [3]. The simulated curves correspond to the reaction in the absence of external acid (red curve), in the presence of 1 mM tosic acid (blue curve), or in the presence of 1 mM benzoic acid (green curve). The vertical lines correspond to the experimentally measured catalytic peak positions for tosic acid (blue line) or benzoic acid (green line). Parameters used for simulations are tabulated in SI Appendix, Tables S13 and S14.

The CV simulations of [1-H] in the presence of tosic acid or benzoic acid assumed the mechanisms depicted in Fig. 4. The blue dotted curve in Fig. 5A shows the simulation when the concentration of tosic acid is set to 1 mM, corresponding to the proposed mechanism for strong acid in Fig. 4 (red arrow). The large increase in current at the [1-H]⁰/[1-H]^– reduction potential is consistent with the experimental observation of catalytic H₂ generation at that potential (Fig. 3B). The green dotted curve in Fig. 5A shows the simulation when the concentration of benzoic acid is set to 1 mM, corresponding to the proposed mechanism for weak acid in Fig. 4 (blue arrow). H₂ is evolved via protonation of [1-HH_C]^2– or by self-elimination, necessitating reduction of [1-HH_C]^– at a calculated standard reduction potential of E^o = –1.93 V. The simulated CV exhibits a large increase in current near the central irreversible peak (E_p = –1.8 V), which again is consistent with experimental results (Fig. 3A) despite the more negative calculated reduction potential for the [1-HH_C]^–/[1-HH_C]^2– couple. A similar level of agreement between the CV simulations and the experimentally generated CVs was found for [3] in the presence of tosic acid or benzoic acid (Fig. 5B). All of the CV simulations presented in Fig. 5 neglected the possibility of concerted intramolecular PCET; however, alternative simulations that included this possibility both exclusively as well as in addition to the stepwise pathway all agreed with the experimental data to the same extent. Thus, the CV simulations were not able to distinguish between the concerted and sequential intramolecular PCET mechanisms.

We emphasize that the CV simulations for [1-H] required a total of 38 parameters: 20 were fixed to the DFT results without any adjustment, 4 were assumed to be diffusion limited, 4 were obtained from experimental trumpet plots, and the remaining 10 corresponded to rate constants that were not available via DFT and therefore were adjusted to fit the experimental CVs. Upon simulation of the CVs, the rate constants used as free parameters were confirmed to correspond to physically reasonable values, and those that did not depend on the external acid were constrained to be the same for all acids studied. Although these CV simulations do not definitively prove the validity of the mechanistic cycles proposed in this study, they do demonstrate their plausibility compared with experimental results.

Spectroelectrochemical Observation of Nickel Phlorin Anion.

To experimentally observe phlorin formation from a nickel porphyrin, thin-layer UV-visible spectroelectrochemical experiments were carried out using complex [3] in acetonitrile. When no potential is applied, the absorption spectrum of the neutral Ni(II) porphyrin [3]⁰ is observed (black curve in Fig. 6A), with the most notable features being two well-resolved Q bands at 520 and 555 nm. When a potential at –1.3 V is applied, the spectrum of [3]^– (red curve) is observed, featuring a lower intensity of the Q bands and the appearance of new peaks at 608 and 841 nm, which are typical for one-electron reduced nickel porphyrins (28–30). The spectrum observed when a potential of ca. –1.9 V is applied in the absence of acid is characterized by the appearance of a broader, slightly more intense band at 613 nm (green curve), with no absorption bands observed in the near-infrared, and it is therefore assigned to the doubly reduced Ni porphyrin [3]^2–. However, when phenol (pK_a = 29.1) (31) is added and a potential of ca. –1.9 V is applied, a very broad peak centered at 769 nm is observed (blue curve). This peak is consistent with the spectral features reported for metallophlorins (32, 33), including those of nickel phlorins (30).

Fig. 6.

(A) Absorption spectra of [3] acquired using thin-layer spectroelectrochemistry in 0.1 M TBAPF₆/acetonitrile electrolyte. Spectra taken before electrolysis (black), after electrolysis at –1.3 V vs. Fc⁺/Fc (red), after electrolysis at –1.9 V vs. Fc⁺/Fc in the absence of external acid (green), and after electrolysis at –1.9 V vs. Fc⁺/Fc in the presence of 10 mM phenol (blue). (B) CVs of 0.4 mM of [3] without acid (black curve) and in the presence of 1 mM phenol (red curve).

Phenol is strong enough to protonate [3]^2– with $\mathrm{\Delta }{G}_{\text{PT}}^{\text{o}}$ = –9.3 kcal/mol; however, the generation of H₂ from [3-H_C]^2– with phenol is calculated to be thermodynamically uphill by 10.2 kcal/mol. These calculations suggest that a buildup of a phlorin intermediate should occur under these conditions and therefore be detectable via spectroelectrochemical methods. This buildup of phlorin intermediate is confirmed by the CV of [3] and phenol (Fig. 6B), in which a peak tentatively assigned to the phlorin reduction [3-H_C]^–/ [3-H_C]^2– is observed at E_1/2 = –1.92 V (calculated to be E^o = –1.86 V) without H₂ evolution. The UV-visible spectrum provides strong evidence for the phlorin intermediate predicted by our previous computational study of the analogous cobalt hangman porphyrins, as well as the current computational results for the nickel porphyrins.

Conclusions

In this paper, DFT calculations were used to propose mechanisms for H₂ evolution by molecular electrocatalysts [3] and [1-H] in the presence of weak or strong acid. For [1-H] in weak acid, the catalytic pathway begins with two electrochemical reduction steps: First the nickel center is reduced and then the porphyrin ring is reduced. The next step is a PCET reaction that could occur either concertedly or via a sequential ET–PT mechanism, in which intramolecular ET from the nickel to the porphyrin ring is accompanied by a structural change in the porphyrin ring from flat to bent, followed by intramolecular PT from the carboxylic acid to the meso carbon of the porphyrin. The net PCET reaction, which results in a phlorin dianion, is thermodynamically favorable, as is the subsequent reprotonation of the carboxylate by the acid. Following another electrochemical reduction, which further reduces the phlorin ring, H₂ evolution via either self-elimination or reaction with the acid is thermodynamically favorable. For [1-H] in strong acid, the catalytic pathway begins with only a single electrochemical reduction step, which reduces the nickel, followed by a PCET reaction composed of intramolecular ET from the nickel to the porphyrin ring and protonation of the meso carbon by the acid, resulting in a neutral phlorin. Following another electrochemical reduction, which produces a phlorin anion, H₂ evolution via reaction with the acid is thermodynamically favorable. The HER mechanisms for [3], which lacks the carboxylic acid hanging group, are analogous in weak and strong acid except that the meso carbon is protonated by external acid rather than by the carboxylic acid hanging group in weak acid.

Further support for the proposed mechanisms is provided by a comparison of CV simulations to experimentally generated CVs. For the CV simulations, 20 out of the 38 parameters (SI Appendix, Table S13) were fixed to values obtained from DFT calculations of reduction potentials and pK_a’s, as well as reaction free energies and free energy barriers for intramolecular PT. Eight of the remaining parameters were fixed on other grounds, and only the remaining 10 parameters were adjusted. The resulting CV simulations are in good agreement with the experimentally generated CVs for [1-H] and [3] in the absence of acid and in the presence of benzoic acid or tosic acid. In particular, the catalytic peaks are all found to be within 0.03 V of the experimental peaks. This level of agreement provides compelling support for the proposed mechanisms.

These proposed mechanisms are unusual in that the active species for H₂ evolution is a phlorin instead of a metal-hydride, which has been presumed to be the active species for most other H₂-evolving molecular electrocatalysts. According to the proposed mechanisms, the C–H bond in the phlorin behaves similarly to the more traditional metal-hydride, and H^– can react with acid or with the carboxylic acid of the hanging group to produce H₂. The possibility of an active phlorin intermediate was first proposed for the analogous cobalt hangman H₂ evolution catalysts (23). More recently, metallophlorin species have been suggested as intermediates in the electocatalytic generation of H₂ by copper and palladium porphyrins (24). The present work indicates that phlorin formation is also structurally and thermodynamically favored over metal-hydride formation for the nickel hangman catalysts. Specifically, considering PT from the carboxylic acid group of [1-H]^2–, the PT donor–acceptor distance is shorter by 0.78 Å for PT to the meso carbon of the porphyrin than to the nickel center, and the reaction free energy is −18.4 kcal/mol for PT to the meso carbon and 5.4 kcal/mol for PT to the nickel center. Note that storing formal hydride equivalents at carbon centers is also used in other chemical and biological processes, such as reactions involving the reduction of NAD⁺ (nicotinamide adenine dinucleotide) to generate NADH (34, 35), and it has been demonstrated that the heterolytic bond dissociation energy of the C4–H bond in NADH derivatives is considerably smaller than those of typical sp³ C–H bonds (36). However, the nickel hangman porphyrin catalysts are uncommon in exhibiting an implied preference for protonating a carbon over a metal center, suggesting that the metal’s role is to influence the energetics and conformation of the porphyrin rather than serving as a site of protonation. This lack of metal protonation also raises the possibility of H₂ electrocatalysis from free-base porphyrins that contain no coordinated metal.

In addition, the present work provides experimental evidence for a phlorin intermediate through spectroelectrochemical measurements of [3] in the presence of phenol, which according to our calculations can protonate the meso carbon of [3]^2– without evolving H₂. The spectroelectrochemical measurements at an applied potential expected to produce the dianion [3]^2– show the buildup up of a species with spectroscopic features that are in agreement with those reported by Kadish and coworkers (30) for nickel phlorin anions produced via the protonation of electrogenerated Ni(II) porphyrin dianions. This spectral observation provides strong experimental evidence for the feasibility of stable phlorin formation from the nickel complexes studied in this work. Although a phlorin intermediate has been detected experimentally for [3], it has not yet been shown experimentally to produce H₂ under acidic conditions. Production of H₂ could require additional protonation and reduction steps, and other possibly nonproductive pathways leading to Ni chlorin, Ni bacteriochlorin, and Ni isobacteriochlorin species could occur. Future experimental and theoretical work will be needed to fully characterize the phlorin intermediate and investigate additional potential mechanisms, as well as explore the possibility of catalysis from free-base porphyrins. The ability to store reducing equivalents within porphyrins through phlorin intermediates holds the potential for unique chemistry and has significant implications for the design of effective catalysts for other energy conversion processes.

Computational and Experimental Methods

DFT calculations were performed with the Gaussian 09 program and a double-ζ basis set with polarization and diffuse functions (37). Geometry optimizations were performed with implicit acetonitrile solvent using the conductor-like polarizable continuum method. The tert-butyl and pentafluorophenyl groups were truncated to methyl and chlorine groups, respectively, for computational tractability. After benchmarking with seven different functionals (SI Appendix, Tables S1–S3), B3P86 (38, 39) was used for the full analysis for consistency with our previous work (21). Long-range corrected functionals may be more accurate for determining electron localization upon reduction but gave similar results in the benchmarking. Note that the open-shell singlet states contain significant spin contamination and therefore are not considered reliable (SI Appendix, Table S3), but spin contamination in the calculated triplet states was found to be negligible. Restricted open-shell DFT or other higher-level ab initio calculations could be used to explore the relative energies among different spin states more accurately.

Reduction potentials and pK_a’s were calculated in acetonitrile with respect to experimental references. All reduction potentials were calculated relative to the experimentally determined half-wave potential (E_1/2) for the reversible [1-H]⁰/[1-H]^– couple vs. Fc⁺/Fc in acetonitrile and are considered to be standard reduction potentials E^o. Comparison with peak potentials is therefore approximate due to experimental conditions that affect peak position. See SI Appendix for additional computational details and benchmarking.

Electrochemical measurements were performed in a nitrogen-atmosphere glovebox. All CVs were background-corrected, recorded at room temperature with iR compensation, and referenced the Fc⁺/Fc couple using an internal standard. Bulk electrolysis was performed in a gas-tight electrochemical cell; the amount of H₂ gas produced in the headspace was analyzed by gas chromatography. Thin-layer spectroelectrochemistry experiments were performed as above in a 0.5-mm path length quartz cuvette. CVs were simulated with the DigiElch 7 software (40). The parameters used in data fitting were set to experimental and theoretical values. See SI Appendix for additional experimental details.