Nonequivalent release sites govern synaptic depression

Significance

Activity-dependent depression is a common aspect of synaptic plasticity resulting from an inability to recover full-release competency during bouts of high-frequency stimulation. At the zebrafish neuromuscular synapse, frequencies between 1 and 10 Hz lead to 50% depression, but paradoxically, this synapse can still follow frequencies approaching the refractory period of the action potential without failure. Capitalizing on the advantages offered by this synapse, we report a new mechanism causal to nonlinear dependence of steady-state depression on frequency involving two types of release sites differing in vesicle reloading rates. The slow sites cannot sustain vesicle release at high frequencies, and therefore, it is the number of fast reloading sites that determines the steady-state level of transmission associated with depression.

Abstract

Synaptic depression is prominent among synapses, but the underlying mechanisms remain uncertain. Here, we use paired patch clamp recording to study neuromuscular transmission between the caudal primary motor neuron and target skeletal muscle in zebrafish. This synapse has an unusually low number of release sites, all with high probabilities of release in response to low-frequency stimulation. During high-frequency stimulation, the synapse undergoes short-term depression and reaches steady-state levels of transmission that sustain the swimming behavior. To determine the release parameters underlying this steady state, we applied variance analysis. Our analysis revealed two functionally distinct subclasses of release sites differing by over 60-fold in rates of vesicle reloading. A slow reloading class requires seconds to recover and contributes to depression onset but not the steady-state transmission. By contrast, a fast reloading class recovers within tens of milliseconds and is solely responsible for steady-state transmission. Thus, in contrast to most current models that assign levels of steady-state depression to vesicle availability, our findings instead assign this function to nonuniform release site kinetics. The duality of active-site properties accounts for the highly nonlinear dependence of steady-state depression levels on frequency.

Synaptic depression is a functional hallmark of many central synapses, particularly those characterized by a high release probability (1). Most studies, this one included, attribute the onset of depression to rapid depletion of a limited pool of vesicles that are poised for release (1–4). However, the mechanisms governing the levels of steady-state depression that occur in response to maintained stimulation are less well-studied. Of particular interest is the observation that depression, at certain synapses, shows a dependence on stimulus frequency that is highly nonlinear. This nonlinearity is reflected in depression levels associated with high-frequency stimulation that fall short of levels predicted on the basis of low-frequency measurements. Indeed, at zebrafish neuromuscular junction, depression is seen at frequencies as low as 1 Hz but can still follow frequencies approaching the refractory limit of the action potential without failures. This nonlinear dependence on frequency enables synaptic strength to be either increased or decreased through a variety of reported means of synaptic modulation (5, 6).

One mechanism that contributes to the nonlinearity at some synapses is a dependence of vesicle recruitment and release on stimulus frequency that is reflected as augmented transmitter release (7–10). Augmentation has been linked to elevations in intracellular calcium and counters the expected drop in steady-state depression levels based on lower-frequency stimulation (10). In this manner, the synaptic responses are resistant to failure at high-frequency stimulation. Because of its potential importance in regulating synaptic strength, we have explored in greater depth, using zebrafish neuromuscular junction, the processes governing nonlinearity of depression. Paired patch clamp recordings between the motor neuron and target muscle offer unique advantages over most synapses that include an unusually low quantal content and the ability to fully resolve all unitary events because of a very large quantal size (11, 12). As such, this synapse further provides an ideal platform for investigation of frequency-dependent depression using multinomial variance analysis. Our findings reveal an altogether new mechanism causal to the nonlinear dependence of steady-state depression on frequency: specifically, the existence of two classes of release sites, slow and fast, that exhibit over 60-fold difference in their rate of reloading. At frequencies corresponding to 0.2 Hz or less, both classes of release sites are operative, but as the frequency of stimulation exceeds 1 Hz, only the fast class is operative. The relative proportion of fast vs. slow release sites is a major determinant of steady-state depression levels.

Results

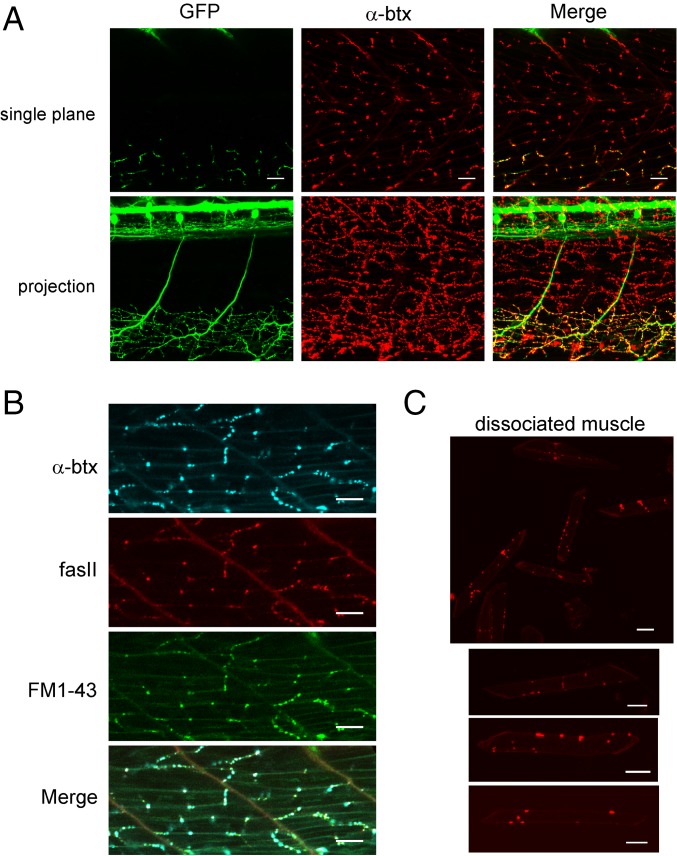
Imaging of the SAIGFF213A/UAS:GFP transgenic line (13) revealed the stereotypic innervation pattern of the caudal primary (CaP) motor neuron (Fig. 1A). Within each segment, a CaP motorneuron, located on each side of the fish, branched to innervate two-thirds of ventral muscle field. The location of synapses was determined on the basis of labeling by either fasciculin II (fasII), which binds to the hydrolyzing enzyme acetylcholinesterase, or α-bungarotoxin (α-btx), which binds to acetylcholine receptors (Fig. 1 A and B). The two labels colocalize to individual synapses that form in en passant fashion along each muscle. Because α-btx binds irreversibly, it was possible to dissociate muscle and determine the number of individual clusters formed on each cell (12.8 ± 5.4; n = 60 cells) (Fig. 1C). Each cluster likely represents a functional synapse based on in situ colocalization with FM1-43–labeled presynaptic vesicles (Fig. 1B).

Fig. 1.

En passant neuromuscular synapses between the CaP motor neuron and target fast muscle. (A) Sample images of two segments of an SAIGFF213A/UAS:GFP transgenic fish with labeled CaP motor neurons and α-btx–labeled acetylcholine receptors. A single image plane is shown in Upper, and a projection through the fish is shown in Lower. The merge is shown in Right. (B) Distribution of α-btx, fasII, and FM1-43 labels in ventral muscle. (C) Dissociated muscle cells labeled with α-btx. Upper shows a field with multiple muscle cells, and three examples of individual cells are shown in Lower. (Scale bars: 20 μm.)

We turned to quantal analysis to determine the parameters underlying transmission at the CaP–fast muscle synapse and how they change during depression. Quantal analysis treats vesicle release as a binomial process according to Eq. 1, wherein the end plate current (EPC) amplitude depends on quantal size (Q), release site number (N), and the release probability at each release site (P_r):

$$I=Q\times N\times P_r.$$ [1]

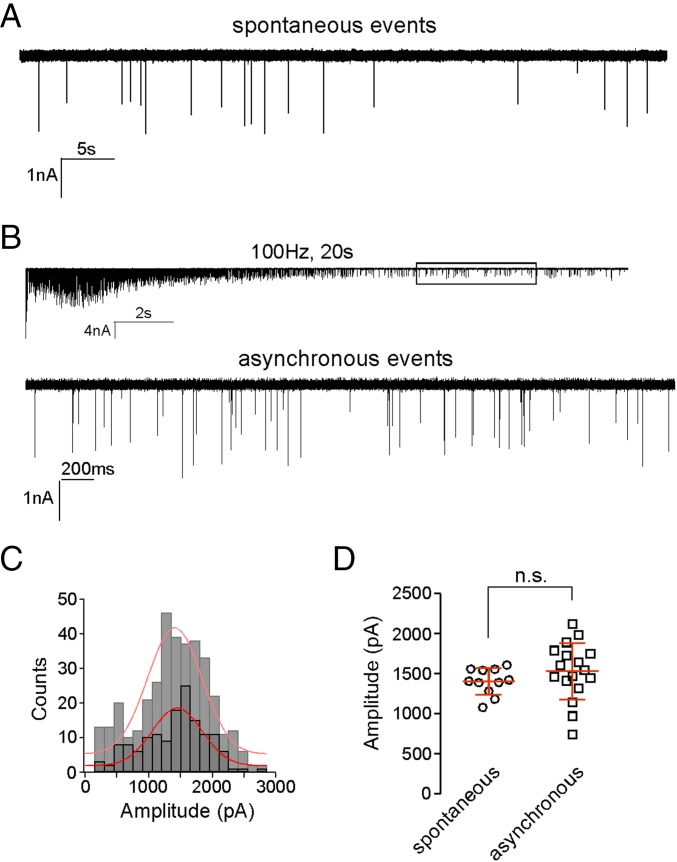
Quantal size was first determined by generating amplitude distributions for the unitary miniature endplate current (mEPC). The mean mEPC was determined on the basis of either spontaneously occurring (Fig. 2A) or asynchronous unitary events that occurred after 100-Hz stimulation lasting 10 s (Fig. 2B). In this condition, the synaptic responses were no longer synchronized to the presynaptic action potential, and the stochastic release reflected principally unitary events caused by vesicle depletion (12). The mEPC distributions obtained by either method were well-fit by a Gaussian curve, supporting the assertion that all or nearly all of the unitary events were resolved (Fig. 2C). The fact that the amplitude distributions were not skewed and lacked multiple peaks was consistent with each mEPC representing release of a single vesicle with uniform transmitter content. The overall mean values obtained for spontaneous events (1,406 ± 166 pA; n = 11) and asynchronous events (1,543 ± 351 pA; n = 17) were not significantly different (Fig. 2D). The high frequency of asynchronous events offered the additional advantage of generating a high-confidence amplitude distribution for each recording. Thus, we routinely measured asynchronous events in each recording and determined both mean quantal size and variance from the Gaussian fit to the amplitude distribution.

Fig. 2.

Measurement of unitary mEPC event amplitude. (A) Sample recording of spontaneous mEPC events. Spontaneous events averaged 17.8 ± 8.4 per min (n = 11). (B) A 100-Hz stimulation for 20 s depletes transmitter over time, leaving asynchronous unitary events. The boxed region is expanded to show the unitary asynchronous events in Lower. (C) Amplitude distributions comparing spontaneous (light gray) and asynchronous (dark gray) unitary events. To obtain sufficient numbers of events for generating the distribution of spontaneous unitary event amplitude, data were pooled from 11 cells. Sample distribution of asynchronous unitary events shown for the example recording in B. Each distribution was fit with a Gaussian function (red lines). (D) Scatterplot of the mean values for spontaneous and asynchronous unitary event amplitudes shown for individual recordings. The overall means obtained for spontaneous and asynchronous events are not significantly different (n.s.; P = 0.29).

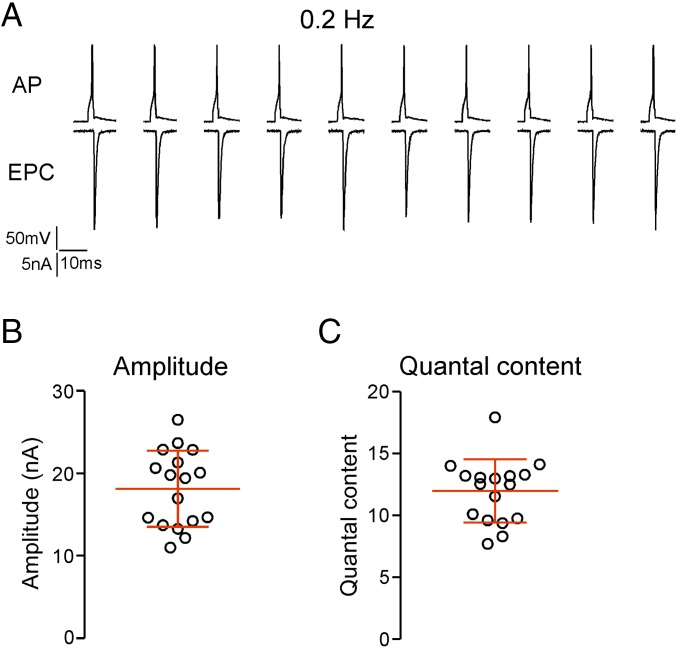
The mean mEPC amplitude determined for each recording was used to estimate quantal content using the direct method (mean EPC/mean mEPC). For this purpose, the EPCs were measured using 0.2-Hz stimulation to avoid synaptic depression (Fig. 3A). The mean overall amplitude from 17 individual recordings was 18.1 ± 4.6 nA (Fig. 3B), resulting in an estimated quantal content that ranged from 7.7 to 17.9 and averaged 12.0 ± 2.6 (Fig. 3C).

Fig. 3.

Estimating quantal content during 0.2-Hz stimulation. (A) Sample recordings showing the motor neuron action potential (AP) and associated muscle EPC. The traces are discontinuous because of the long interstimulus interval. (B) The mean EPC amplitude for individual recordings with associated overall mean and SD (n = 17). (C) The estimated quantal content for each of the recordings shown in B.

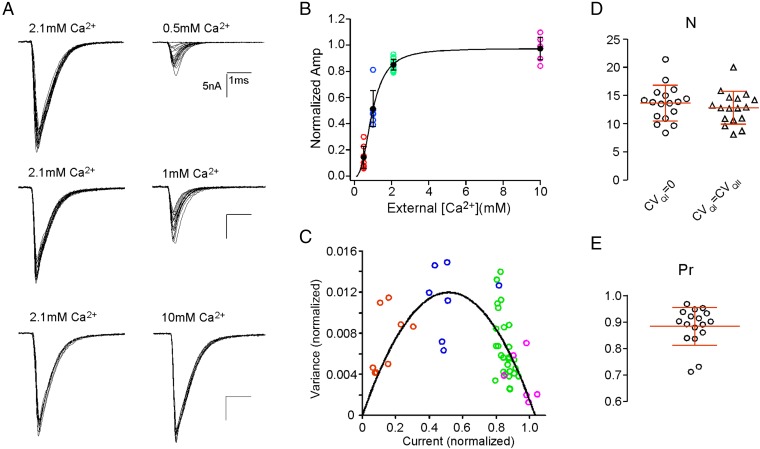
Because quantal content is calcium-dependent, it was necessary to elevate external Ca²⁺ levels to obtain estimates for maximal values. To determine the calcium dependence of release, EPCs were measured using low-frequency stimulation at 0.2 Hz to avoid synaptic depression. EPCs were recorded at 0.5, 1.0, 2.1, and 10 mM external Ca²⁺ concentrations (Fig. 4A). Owing to the time involved in accumulating sufficient numbers of EPCs at this low rate of acquisition, only a subset of calcium concentrations could be tested for each cell. Thus, each recording used 2.1 mM Ca²⁺ and one other test [Ca²⁺], which permitted all amplitude measurements to be normalized to the maximal current for 2.1 mM Ca²⁺ in the same cell. The overall relationship between normalized mean amplitude and calcium concentration was fit by the Hill equation, yielding a slope of 2.6 (Fig. 4B). The plateau of the EPC amplitude reflected saturating calcium at a limited number of release sites and not saturation of postsynaptic receptors. Treatment with either methanesulphonic acid (MSF) or fasII, both inhibitors of acetylcholinesterase, increased peak synaptic current amplitude by 38% and 37%, respectively, pointing to the existence of spare receptors. This increase is in good agreement with published studies on frog (14), chick (15), and mouse (15, 16) neuromuscular junctions. Thus, the average 85% of release measured at 2.1 mM Ca²⁺ is interpreted as near saturation of release probability for all of the release sites. Accordingly, the low quantal content at this synapse results from a small number of release sites, each with a high release probability.

Fig. 4.

Calcium dependence of EPC amplitude and fluctuation analysis to estimate N. (A) Shown are 15–20 superimposed sample EPCs recorded at 2.1 mM Ca²⁺ (Left) compared with 15–20 superimposed traces recorded at the indicated concentration (Right) in the same muscle cell. (B) The scatterplot for each experimental calcium concentration after normalizing to the maximal amplitude measured at 2.1 mM Ca²⁺. The maximal amplitude at 2.1 mM Ca²⁺ was not significantly different from the mean amplitude measured at 10 mM Ca²⁺ (P = 0.73; n = 7), suggesting that it represents release at P_r near one. The overall mean amplitudes at each concentration (black circles) were fit to the Hill equation, yielding a slope value of 2.6. (C) The normalized EPC variance vs. normalized mean amplitude and fit with a multinomial model of release (Eq. 2). The different symbol colors indicate data acquired at individual [Ca²⁺] shown in B. (D) Scatterplot of estimates of N from the fluctuation analysis using two sets of CV_Q. (E) Scatterplot of estimated P_r assuming CV_QI = 0.

As an independent estimate of the number of functionally competent release sites, we applied fluctuation analysis (17–19) to the mean and variance associated with EPCs generated at each calcium concentration. As expected, the variance bore a dependence on EPC amplitude, with the peak variance associated with 1 mM Ca²⁺ (Fig. 4C). The relationship was well-fit with a simple multinomial model that takes into account of quantal size variability (Eq. 2 and Fig. 4C). Quantal variability (CV_Q), including intrasite (CV_QI) and intersite (CV_QII) variabilities, was estimated for each cell using our ability to fully resolve quantal events (details in Methods and SI Text). Assuming equal intra- and intersite variabilities, CV_QI = CV_QII, the number of functional release sites (N) was estimated at 12.8 ± 2.9 (n = 17) (Fig. 4D). If CV_QI only contributed to a small amount of the total (CV_QI = 0) as suggested by the low variance of EPCs measured in 10 mM Ca²⁺, N is estimated at a similar value of 13.6 ± 3.2 (n = 17) (Fig. 4D), which is not significantly different from the estimates based on the assumption CV_QI = CV_QII. With these estimates of N in hand, the release probability (P_r) for each release site could be estimated. At physiological Ca²⁺, P_r averaged 0.88 ± 0.07 (n = 17) (Fig. 4E) at low-frequency stimulation.

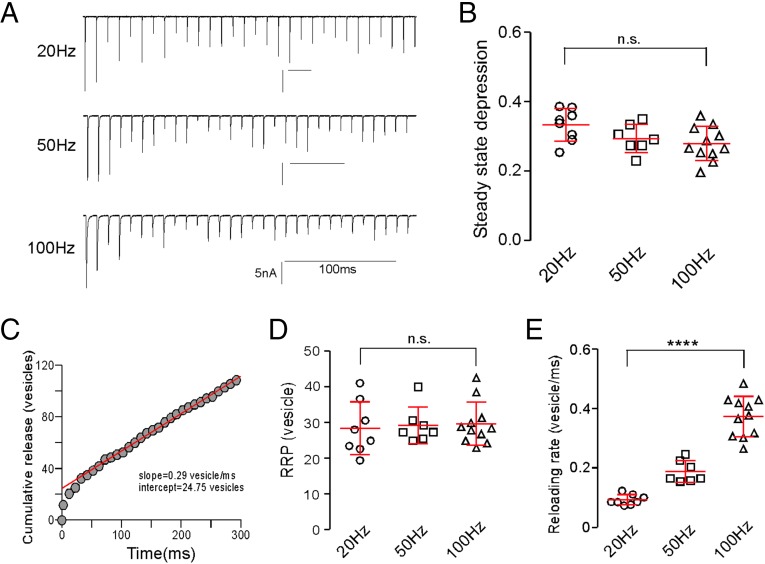
Next, we turned to analysis of the processes governing synaptic depression. Stimulus frequencies of 1 Hz or greater showed pronounced early depression that was reflected in reduced EPC amplitudes, beginning with the second response. The depression reached a steady state within the five EPCs at frequencies exceeding 20 Hz (Fig. 5A). Steady-state depression was quantified on the basis of the last 25 EPCs in a train of 30 stimuli. Depression levels, expressed as the ratio of steady-state amplitude to the first EPC, showed only a modest frequency dependence between 20 and 100 Hz (Fig. 5B).

Fig. 5.

Frequency-dependent synaptic depression. (A) Sample EPC recordings in response to 30 stimuli delivered at three different frequencies. (B) Scatterplot of steady-state depression levels for individual recordings at each frequency. The steady-state depression was based on the ratio of average steady-state EPC amplitude to the first EPC. The overall mean ± SD values are shown. n.s., P = 0.056 (one-way ANOVA). (C) A representative cumulative release time course for the 100-Hz recording shown in A. Each circle represents a 10-ms epoch. The release was converted from amplitude to vesicle number on the basis of quantal size. The red line represents the best linear fit for data points between the 60- and 300-ms regions backextrapolated to time zero. The indicated y intercept and slope provided estimates for the RRP size and the reloading rate for the cell, respectively. (D) Estimates of the size of the RRP pool for individual recordings and overall mean ± SD at each frequency. n.s., P = 0.9 (one-way ANOVA). (E) Estimates of the reloading rates for individual recordings at different stimulus frequencies. ****P < 0.0001 (one-way ANOVA).

The most commonly held explanation for the rapid synaptic depression onset centers on depletion of a readily releasable pool (RRP) of vesicles (1–4), and release eventually reaches a level of steady-state depression that reflects the balance between the rates of release and vesicle reloading. As a first step toward testing the idea of RRP depletion as causal to depression, we adopted an approach originally developed for the neuromuscular junction and subsequently applied to central neurons using patch clamp (3, 20, 21). Peak EPC amplitudes were first converted to quantal content, and the accumulated quantal content was plotted against time during the stimulus train (Fig. 5C). Data points corresponding to steady-state responses (stimuli 6–30) were fitted using linear regression and backextrapolated to time zero. The reloading rate was estimated from the slope of the fit, and the RRP available at the beginning of stimulation was estimated from the y intercept.

The estimated size of the RRP was similar at 20-, 50-, and 100-Hz stimulation (Fig. 5D). Estimation from 100 Hz showed that RRP size for a single muscle cell ranged from 23 to 43 and averaged at 30 ± 6 vesicles (n = 11). Divided by the total number of release sites, estimated on the basis of low-frequency stimulation, each functional release site would contain one to three vesicles, a value consistent with those obtained from mammalian calyx of Held and neuromuscular junction (20, 22). Therefore, depletion at release sites would be expected to occur within the first few EPCs.

In contrast to RRP estimates, the overall reloading rate, measured by the slope of the linear part of cumulative release vs. time plot, was frequency-dependent. Faster reloading rates were associated with increases in stimulus frequency (Fig. 5E). The rate increased from a mean of 0.09 ± 0.02 vesicles per millisecond at 20 Hz (n = 8) to 0.37 ± 0.07 vesicles per millisecond at 100 Hz (n = 11) (Fig. 5E). This rate translated to a time constant of 2.7 ms for reloading a single vesicle at 100 Hz. The frequency-dependent augmentation in reloading rate has been attributed to reflecting calcium-dependent vesicle recruitment, which was greater at shorter interval action potentials (7–10).

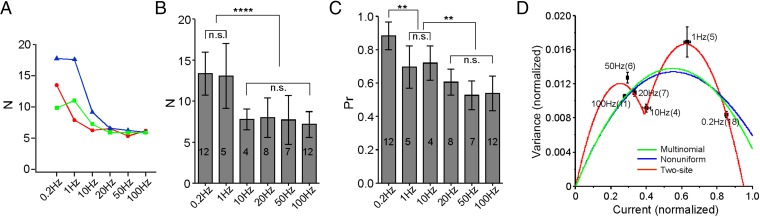
We next applied multinomial variance analysis to identify changes in release parameters during frequency-dependent depression. Direct comparison of quantal event amplitudes measured for spontaneously occurring mEPCs and asynchronous mEPCs elicited by high-frequency stimulation (Fig. 2D) indicated that quantal size stayed constant during activity, leaving release site number and release probability as the variables potentially accounting for frequency-dependent depression. Estimates of both parameters were made for the steady-state level of transmission and compared with those obtained at low frequency. Surprisingly, the estimated number of release sites consistently dropped with increased stimulus frequency (Fig. 6 A and B). The frequency at which the transition occurred varied between recordings but fell somewhere between 1 and 10 Hz (Fig. 6A). On average, the functional release site number dropped to 58 ± 12% as the frequency was increased from 0.2 to 10 Hz, staying relatively constant with additional increases in frequency (55 ± 15% at 100 Hz) (Fig. 6B). Estimates of average release probability corresponded to 0.88 ± 0.08 at 0.2 Hz and 0.54 ± 0.10 at 100 Hz (Fig. 6C). These data suggested that the frequency-dependent depression observed at zebrafish neuromuscular junction does not arise exclusively from a uniform reduction of release probability across all of the release sites. Instead, depression reflected the collective dropout of approximately one-half of the functional release sites along with a frequency-dependent drop in release probability for the remaining sites.

Fig. 6.

Decrease in N contributes to the steady-state depression. (A) Three colored examples of frequency-dependent N change. N was estimated for each cell at different frequencies using the multinomial model (Eq. 2). (B) Overall estimates of N for steady-state levels at different frequencies. The number of experiments is indicated for each condition. n.s., P > 0.8. ****P < 0.0001. (C) Overall estimates of P_r for steady-state levels at different frequencies. Sample size is indicated for each condition. n.s., P > 0.2. **P < 0.01. (D) Variance vs. mean plot for different frequencies. Fitting of the plot assuming a single class of release sites with uniform P_r (multinomial; green), a single class with nonuniform P_r (blue), and a two-site model with two parabolic functions (red). Both variance and mean amplitude were normalized to the maximal current of the cell. Data are shown as means ± SEMs, and the numbers of experiments are indicated in the parentheses.

To further investigate the contribution of a decrease in release site number to depression, data were pooled across cells by normalizing both the mean amplitude of EPC and mEPC and the EPC variance to the maximal release for individual cells. It is clear from the pooled variance–mean plot that variances associated with higher- and lower-stimulation frequencies do not fall on a single parabola that would result from a uniform change in release probability across a constant number of release sites (Eq. 2 and Fig. 6D, green line: simple multinomial model). In light of the evidence supporting heterogeneous release probability across release sites at central neurons (23, 24), we used a second model that took into account nonuniformly distributed release probabilities among a fixed number of release sites. This nonuniformity can be represented by a single parameter, α, from a β-distribution in the multinomial fit (Eq. 3) (17, 19). As with the simple multinomial model that assumed a uniform release probability distribution, this second model also failed to account for data points for both the low and high frequencies (Fig. 6D, blue line). We, therefore, developed a novel model (termed two-site model) composed of two distinct groups of functional release sites that differ in their ability to follow high-frequency activities (Methods and SI Text). Both groups are active (high release probability) at low frequencies, but only one group could sustain release as stimulus frequencies exceed 10 Hz (Eq. 4 and Eq. S6). This model predicted a two-parabola curve of variance vs. mean, which fit the experimental data (Fig. 6D, red line). The two-site model further accounted for the dropout (reduction of release probability to zero) of about one-half of the sites, which was causal to depression.

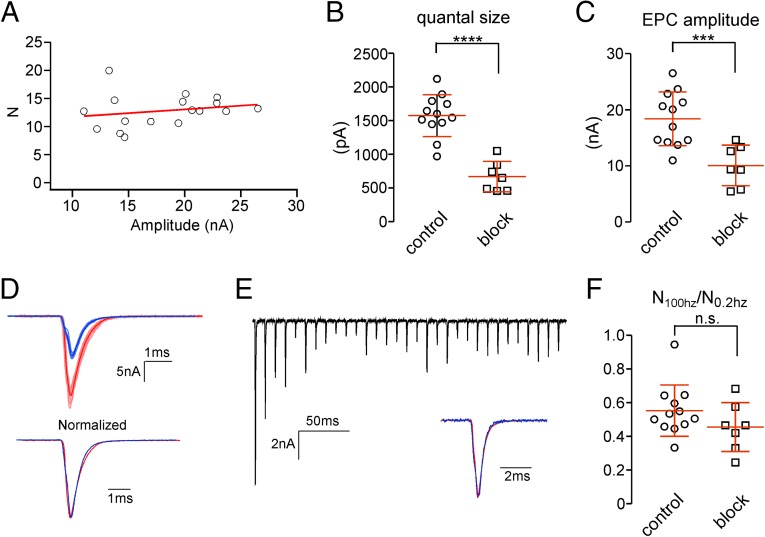
These estimates of functional release sites are critically dependent on accurate measurements of EPC amplitude and associated variance. The large current size raised concern that our estimates of release site number and its frequency-dependent reduction were prone to errors associated with inadequate series resistance (Rs) correction. Two independent sources of evidence argued against this possibility. First, plotting release site number estimates vs. mean EPC amplitude showed no correlation across a range of ∼2.5-fold scatter of EPC amplitudes (Fig. 7A). Second, we reduced the synaptic conductance by decreasing the number of functional postsynaptic receptors through application of either 100 nM α-btx or 30–200 nM d-tubocurare. Curare is an active-site antagonist, and α-btx binds irreversibly to block acetylcholine-mediated activation. It was difficult to obtain a reliable level of inhibition by either agent, calling for many recordings. With both agents, a deep block (>70%) usually resulted in non-Gaussian–distributed quantal events because of an inability to resolve the smallest mEPCs. Therefore, only recordings with intermediate block where both mEPC and EPC amplitudes were reduced to about 50% of the control level were used (Fig. 7 B and C). Neither means of reduction led to alterations in the EPC waveform (Fig. 7D). The reduction in EPC amplitude also had no effect on either the onset or fractional steady-state levels of depression associated with high-frequency stimulation (Fig. 7E). Estimation of release site numbers was then determined for 0.2- and 100-Hz protocol using the multinomial model for individual cells. The ratio of estimated release site number during steady-state depression at 100 Hz to that at 0.2 Hz averaged at 46 ± 15%, not significantly different from the control condition (Fig. 7F). Thus, frequency-dependent decreases in release site number were also observed under conditions of reduced quantal size, ruling out errors associated with the large amplitude of the EPCs.

Fig. 7.

Estimating N under conditions of partial postsynaptic conductance block. (A) Scatterplot of N estimates vs. mean EPC amplitude at 0.2 Hz for control condition. Each symbol represents an individual recording with a trend line shown in red. (B) Scatterplot of quantal size determined from Gaussian fit to asynchronous event amplitude distributions for both control and partial blocked conditions. ****P < 0.0001. (C) Scatterplot of EPC amplitudes at 0.2 Hz for both control and partial blocked conditions. ***P < 0.001. (D) Sample recordings of control (red) and blocked (blue) EPCs obtained in response to a 0.2-Hz stimulation. (Upper) Ten individual EPCs (light red and light blue) were used to generate the average EPCs (dark red and dark blue). (Lower) The averages were normalized for comparison of waveform. (E) Sample recording of partially blocked EPCs at 100-Hz stimulation. Inset compares the average postdepression EPC (blue; averaged from the 10th, 15th, 20th, 25th, and 30th EPCs in the train) normalized to the first EPC in the train (red). (F) The extent of drop in N is represented as the ratio of N at 100 to 0.2 Hz; 12 recordings are shown for the control, and 7 recordings are shown (2 α-btx and 5 d-tubocurare) for the partial blocked condition. n.s., P = 0.7.

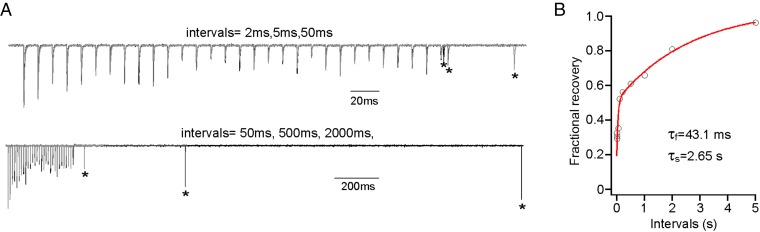
Finally, the two-site model for frequency-dependent depression predicted that the two groups of release sites were kinetically distinct in the ability to reload. This prediction was tested by measuring the time dependence of recovery of EPC amplitude after establishment of steady-state depression. A 100-Hz train of stimuli was delivered for 300 ms, after which a test EPC was elicited at a varying interval (Fig. 8A). Recovery was assayed as the ratio of test EPC to that of the first EPC in the train. Because the first EPC has a release probability close to unity, this ratio provides a measure of recovery of all release sites. The pooled data were fitted with the sum of two exponentials (τ_f = 43.1 ms and τ_s = 2.65 s), with the slow component accounting for 53% (Fig. 8B).

Fig. 8.

Recovery time course from 100 Hz induced steady-state depression. (A) Example traces showing the protocol to measure the recovery time course. Test pulses (indicated by asterisks) were given at different time intervals after 30 stimuli at 100 Hz. Stimulus trains were separated by at least 30-s resting time to allow full recovery between tests. All traces are normalized to the first EPC of each train. Examples for intervals of 2 (black), 5 (dark gray), and 50 ms (light gray) are overlaid and shown in Upper. Examples for intervals of 2 s (black), 500 ms (dark gray), and 50 ms (light gray) are overlaid and shown in Lower. (B) Biexponential fit to the fractional recovery vs. time interval plot. Each data point represents the average from 8 to 20 cells. Error bars are excluded for clarity.

The slow component of recovery accounts well for the dropout of one-half of the sites that are associated with stimulus frequencies as low as 1–10 Hz.

Discussion

Our interest in understanding the processes governing steady-state levels of depression was prompted by the observation that the steady-state levels are not linearly dependent on stimulus frequency at the zebrafish neuromuscular junction. In this study, we investigated how the determinants of synaptic response change during activity, including the quantal size, the number of the release sites, and the release probability at each site. Our analysis led to the surprising finding that only a subset of release sites was used at steady state under high-frequency stimulation. Thus, the transition into steady-state depression involves a newly identified process that centers on a decrease in the number of active sites.

The CaP–fast skeletal muscle synapse features an unusually low number of functional release sites. This feature is reflected in the low quantal content of ∼12 measured for 0.2 Hz at physiological concentrations of external calcium, where the release probability is near one. EPC amplitudes increased less than 15% when the external calcium was further elevated to 10 mM. The possibility that this represents saturation of postsynaptic receptors was ruled out by means of acetylcholinesterase inhibitors. Should receptor saturation occur, the inhibition would not have resulted in the observed ∼40% further increase in instantaneous peak EPC amplitude. Instead, the saturation reflects involvement of nearly all release sites at physiological calcium levels. A high release probability was also reflected in the low variance associated with EPC amplitudes at 0.2 Hz (CV = 0.10 ± 0.03; n = 17). Direct estimates for the number of release sites derived from mean vs. variance analysis confirmed the low quantal content and the ability of the multinomial model to adequately describe the release behavior at our synapse.

The onset of synaptic depression is widely ascribed to depletion of RRP vesicles, although postsynaptic receptor desensitization (25–27) and calcium channel inactivation (28, 29) have also been proposed. In our case, inactivation of the CaV2.1 calcium channels and desensitization of the nicotinic muscle receptor are too slow to account for the rapid onset of depression (30–32). Instead, our findings lend support to the idea that depletion of a small RRP is the contributing factor to onset of depression. Our estimates of RRP, placing one to three vesicles per site, would be predicted to sustain release for only the first few EPCs.

Recovery from the steady-state depression followed a time course that was best described by the sum of two exponential processes with time constants differing by over 60-fold. This finding suggests that either recovery at each release site has two kinetic steps or alternatively, two subtypes of release sites are present, each with distinct recovery kinetics. The first interpretation was promoted in a number of studies, wherein the two components of the recovery were assigned to heterogeneity of vesicle properties (10, 33). For example, recovery in the calyx of Held is interpreted in the context of fast-releasing vesicles that recover slowly and slowly releasing vesicles that recover rapidly (10, 33). Because each release site has both populations of vesicles, the recovery shows a fast step followed by a slow one. Our analysis of release parameters for the steady state, however, provides direct evidence for the second interpretation, which assigns the two recovery components to kinetically distinct release sites rather than vesicles.

Multinomial analysis, applied to the mean and variance of steady-state amplitudes, led to the unexpected finding that the number of active release sites associated with steady state were about one-half the predepression levels. Moreover, this estimate remained nearly constant as frequency was further increased. Consequently, the variance vs. mean plot could not be described by a single parabolic function as expected for a simple drop in release probability across a fixed number of release sites. Instead, we observed a more complex distribution with two maxima in variance centered around 1 and 50 Hz. Fitting the overall relationship required two separate parabolas, each with a different value for active-site numbers, with the smaller value representing the high-frequency component. The trough in variance, occurring around 10 Hz, corresponded to the midpoint of depression after dropout of a class of slow release sites.

Based on the frequency-dependent reduction in active-site numbers and the biexponential recovery from depression, we propose a two-site model, wherein roughly equivalent numbers of slow and fast release sites exhibit 60-fold differences in reloading. According to this model, reloading rates of these sites and their relative abundance will be major determinants of steady-state levels of depression. At stimulus frequencies low enough to avoid depression, both slow and fast sites will contribute to the high release probability. However, as the frequency is raised above 1 Hz, the slow sites will drop out because of slow reloading. The fast release sites alone will sustain the steady-state level of release.

The 60-fold difference in reloading rates for slow vs. fast sites accounted well for the ability to depress over a wide range of frequencies. However, estimates of reloading rates by these fast sites over the range of frequencies between 20 and 100 Hz pointed to an additional contribution by a second well-recognized process. Specifically, repetitive stimulation led to a potent acceleration in vesicle reloading that was highly frequency-dependent. The augmentation in reloading rate has been shown to reflect a calcium-dependent process (7–10). Thus, the collective actions of slow sites dropping out of action and augmentation for the remaining fast reloading sites set a midpoint of steady-state depression that could be modulated in either direction over a broad dynamic range.

The multiple mechanisms governing the levels of steady-state depression provide an efficient means to modulate transmitter release over a range of physiologically important frequencies. In the case of zebrafish neuromuscular junction, an initial large synaptic response would be expected to assist the initiation of escape through generation of a single powerful startle response (34). This response would require involvement of both fast and slow reloading sites. However, during subsequent rhythmic swimming, a powerful startle response would compromise or potentially abort swimming. The slow recovery associated with slow reloading sites reduces likelihood of this happening and places temporal limits on the startle response. Of more general importance, the ability to express release sites tuned to different frequencies could serve a multitude of functions at CNS synapses, a possibility that merits additional exploration.

What might distinguish fast sites from slow sites? At first glance, heterogeneous vesicle populations seem a likely source for the distinction, because both morphological and functional measurements have pointed to their existence (35–38). For it to be vesicle pools, however, would require precise sorting of slow vs. fast vesicle types or pools among selective release sites within each postsynaptic cell contacted by the motor neuron. Roughly one-half of the presynaptic release sites would be armed with fast release vesicles, and the other one-half would be armed with slow release vesicles. Because there is no simple mechanism to account for such precise sorting of kinetically distinct vesicle pools among active release sites, we favor the two-site model. Another possibility that we considered was differences in the distances between the CaV2.1 calcium channel and release site as causal to the kinetic distinctions. This idea builds on the accumulating evidence for the spatial coupling between calcium signal and release kinetics (39). However, the variance–mean relationship acquired by varying external Ca²⁺ was equally well-fit by a simple parabola and a two-site model, indicating similar sensitivity to calcium for all sites at low frequencies. This observation along with the high release probability measured at low frequencies where calcium might be expected to be limiting are at odds with differences in calcium dependence as the source of distinction. It seems more likely that the difference resides in the ability of certain active sites to arm vesicles for release. A complex array of active-site proteins has been shown to be involved in the docking/priming of vesicles and regulation of release kinetics (40–44). Their distribution and modulation at individual release sites could all potentially contribute to the distinction.

A means to potentially identify the features responsible for distinguishing fast and slow reloading sites is in unique physical distribution of synapses at the zebrafish neuromuscular junction. Unlike frog and mammalian neuromuscular junctions, zebrafish motor neurons form tractable numbers of individual, distinct synapses on a single muscle cell. The two-site model predicts that release sites are distinct fixed entities, which also suggests spatial segregation. Moreover, a general agreement between the number of individual postsynaptic receptor clusters and the number of functionally determined release sites on each muscle cell raises the possibility that each en passant bouton corresponds to a single release site. Should individual synapses represent a single release site, their physical separation might open a door to functional and ultrastructure identification of the molecular distinctions causal to slow vs. fast release sites.

Methods

Electrophysiology.

All experiments were performed on zebrafish larva at 72–96 h postfertilization. All animal procedures performed were approved by the Oregon Health and Sciences Institutional Animal Care and Use Committee. Animal care was conducted in accordance with institutional guidelines. Paired in vivo electrophysiological recordings between CaP motor neuron and fast skeletal muscle were performed as described previously (11, 45). The bath solution contained 134 mM NaCl, 2.9 mM KCl, 1.2 mM MgCl₂, 2.1 mM CaCl₂, 10 mM glucose, and 10 mM Na-Hepes, pH 7.8. The intracellular solution for both CaP and muscle contained 115 mM K-gluconate, 15 mM KCl, 2 mM MgCl₂, 10 mM K-Hepes, 4 mM Mg-ATP, and 5 mM K-EGTA, pH 7.2. The CaP neuron was held at −80 mV, and action potentials were elicited with either 1 or 2 ms current injection. The muscle cells were held at −50 mV to prevent contraction, and EPCs were recorded with a sampling frequency of 100 kHz under whole-cell voltage clamp. Data were acquired with an EPC10/2 Dual Patch Clamp Amplifier with HEKA PatchMaster software (List Electronics).

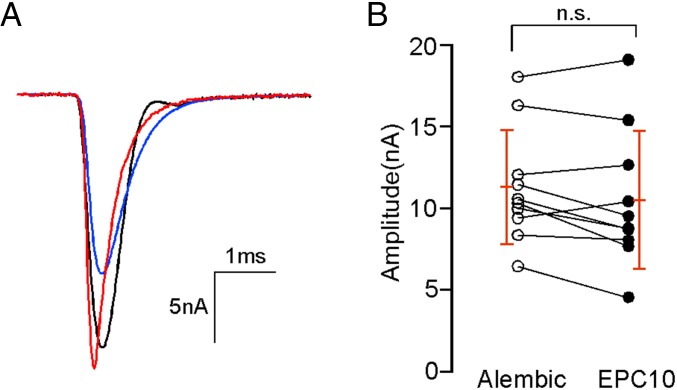
Because of the large amplitude of the synaptic currents, it was necessary to minimize the voltage error associated with Rs. Electrodes with a low resistance of 2–3 MΩ were fabricated with a steep taper and large bore. Rs was estimated from the current response to a 10-mV step depolarization and monitored throughout the experiment. Experiments were terminated when Rs exceeded 8 MΩ. Rs was routinely 60% compensated online using the EPC10/2 Dual Patch Clamp Amplifier, with the remaining 40% correction performed offline (60:40 correction). The offline correction was performed using a custom Igor procedure assuming a linear voltage–current relationship over the voltage range used for our data acquisition, similar to that described previously (46). The effectiveness of the 60:40 method of correction was validated experimentally by comparison with 100% online Rs compensation provided by an Alembic Amplifier (Alembic Instruments). Comparisons were made from the same muscle cell by sequential EPC10/2 Dual Patch Clamp Amplifier and Alembic Amplifier recordings (Fig. 9). This specific experiment used a transgenic fish line expressing channelrhodopsin in the spinal motor neurons (Gal4^s1020t/UAS:ChR-YFP; gift from Claire Wyart, University Pierre et Marie Curie, Paris). The channelrhodopsin was activated using a triggered mercury arc lamp. Between 5 and 10 EPCs were recorded first using the List EPC10/2 Dual Patch Clamp Amplifier with 60% compensation (Fig. 9A, blue trace) followed by recordings from the same cell using the Alembic Amplifier (Fig. 9A, black trace). Each measurement was preceded with a live Rs estimate. EPCs recorded using the EPC10/2 Dual Patch Clamp Amplifier were further corrected using 40% offline correction (Fig. 9A, red trace), and the peak amplitudes were compared with those obtained with the Alembic Amplifier (Fig. 9B). The peak EPC amplitudes determined for individual cells were not significantly different (Fig. 9B). All data in this study used the 60:40 method, because the Alembic Amplifier was prone to overcompensation and ringing over the course of the experiment.

Fig. 9.

Validation of Rs corrections. (A) Sample EPCs with 60% correction (blue trace) and 60:40 (red trace) correction for EPC10/2 Dual Patch Clamp Amplifier recordings and 100% correction provided by Alembic Amplifier recordings (black) in the same cell. Motor neurons were stimulated with channelrhodopsin 2. Average traces from 5–10 EPCs were shown. The EPC shown by the black trace has an irregular decay phase caused by the instability of the compensation circuit. (B) Scatterplot of peak EPC amplitudes recorded using the 100% (Alembic Amplifier; white circles) method or the 60:40 correction (EPC10/2 Dual Patch Clamp Amplifier; black circles) method. Each line connects measurements from an individual muscle. Overall means and SDs are indicated in red. n.s., P = 0.09 (paired t test).

The effects of acetylcholinesterase inhibition on synaptic current amplitude were tested using either MSF (Sigma-Aldrich) or fasII (Alomone Labs). Recordings of synaptic currents were made after a 20-min exposure to 1 mM MSF or 330 µM fasII. For acetylcholine receptor block experiments, recordings were obtained either in the presence of 30–200 nM d-tubocurare or after a 3- to 5-min pretreatment with 100 nM α-btx. Calcium dependence experiments were performed at two external Ca²⁺ concentrations for each cell, one being 2.1 mM Ca²⁺ for standardization; 15–40 EPCs were measured in response to 0.2-Hz stimulation at each concentration. For bath recording solutions with different Ca²⁺ concentrations, [Ca²⁺] and [Mg²⁺] were varied as follows: 1.5 mM Ca²⁺, 2.8 mM Mg²⁺, and 1 mM EGTA (to yield a free Ca²⁺ concentration of 0.5 mM); 1 mM Ca²⁺ and 2.3 mM Mg²⁺; 2.1 mM Ca²⁺ and 1.2 mM Mg²⁺; 4 mM Ca²⁺ and 0 mM Mg²⁺; and 10 mM Ca²⁺ and 0 mM Mg²⁺.

Data were analyzed using Igor Pro (WaveMetrics) and MiniAnalysis (SynaptoSoft Inc.) and are presented as means ± SDs unless otherwise indicated in the figures. Statistical comparisons were made with t tests or one-way ANOVA in Prism (Graphpad Software, Inc.).

Variance vs. Mean Analysis.

Three models of the relationship between the mean and the variance of EPCs were considered.

Model 1 assumes multinomial release with uniform release probability across synapses and intrasite (type I) and intersite (type II) quantal variability. Following equation 11 in the work by Silver (19), the variance and mean of quantal and evoked currents were normalized to the maximum current in each muscle cell to facilitate analysis across muscle recordings, yielding the following equation:

$${\overline{\sigma }}_I^2=\left[{\overline{Q}}_P\times \overline{I}-\frac{{\overline{I}}^2}{N}\right]\times \left(1+C{V}_{QII}^2\right)+{\overline{Q}}_P\times \overline{I}\times C{V}_{QI}^2.$$ [2]

The relationship between ${\overline{\sigma }}_I^2$ (the EPC variance divided by the square of the maximum observed EPC amplitude, I_max) and $\overline{I}$ (the mean EPC divided by I_max) in a given condition (extracellular [Ca²⁺] or stimulation rate) is a function of four parameters: ${\overline{Q}}_P$, the mean quantal amplitude divided by I_max; N, the number of release sites; and $C{V}_{QI}$ and $C{V}_{QII}$, the coefficients of variation of type 1 and type 2 quantal variability, respectively. The $C{V}_Q$ values were constrained by the equation $C{V}_{Qtotal}^2=C{V}_{QI}^2+C{V}_{QII}^2$, where $C{V}_{Qtotal}$ is the total measured CV for quantal events in asynchronous release conditions. Two sets of values for the $C{V}_Q$ values were used. For condition 1, it was assumed that $C{V}_{QI}^2=0$ based on the extremely low variability in EPC amplitude (0.07 ± 0.03; n = 7) observed in 10 mM [Ca²⁺], where release probability is ∼1. Condition 2 assumed that $C{V}_{QI}^2=C{V}_{QII}^2$, allowing for the possibility that type I variance contributes to the overall CV_QI. Both conditions of model 1 have two free parameters, N and ${\overline{Q}}_P$, which were constrained by least-squared fitting to the normalized population data.

Model 2 assumes a distribution of release probability across release sites that is nonuniform following a β-distribution; it is based on equation 19 in the work by Silver (19) and normalized as in model 1 to yield

$${\overline{\sigma }}_I^2=\left[{\overline{Q}}_P\times \overline{I}-\frac{{\overline{Q}}_P\times {\overline{I}}^2\times (1+\alpha )}{\overline{I}+N\times {\overline{Q}}_P\times \alpha }\right]\times \left(1+C{V}_{QII}^2\right)+{\overline{Q}}_P\times \overline{I}\times C{V}_{QI}^2.$$ [3]

$${\sigma }_I^2=\{\begin{array}{r}\hfill \left[{\overline{Q}}_P\times \overline{I}-\frac{{\overline{I}}^2}{\frac{\widehat{p}\times {\widehat{N}}^2}{\left({\widehat{p}}^2\times N_1+N_2\right)}}\right]\times \left(1+C{V}_{QII}^2\right)+{\overline{Q}}_P\times \overline{I}\times C{V}_{QI}^2,\hspace{0.17em}\hspace{1em}I<{\overline{Q}}_P\times \widehat{N}\\ \hfill \left[{\overline{Q}}_P\times \left(\overline{I}-{\overline{Q}}_P\times N_2\right)-\frac{{\left(\overline{I}-{\overline{Q}}_P\times N_2\right)}^2}{N_1}\right]\times \left(1+C{V}_{QII}^2\right)+{\overline{Q}}_P\times \overline{I}\times C{V}_{QI}^2,\hspace{1em}I\ge {\overline{Q}}_P\times \widehat{N}\end{array}.$$ [4]

Model 2 has one additional free parameter over model 1: α from the β-distribution; the same two conditions of quantal variance were considered.

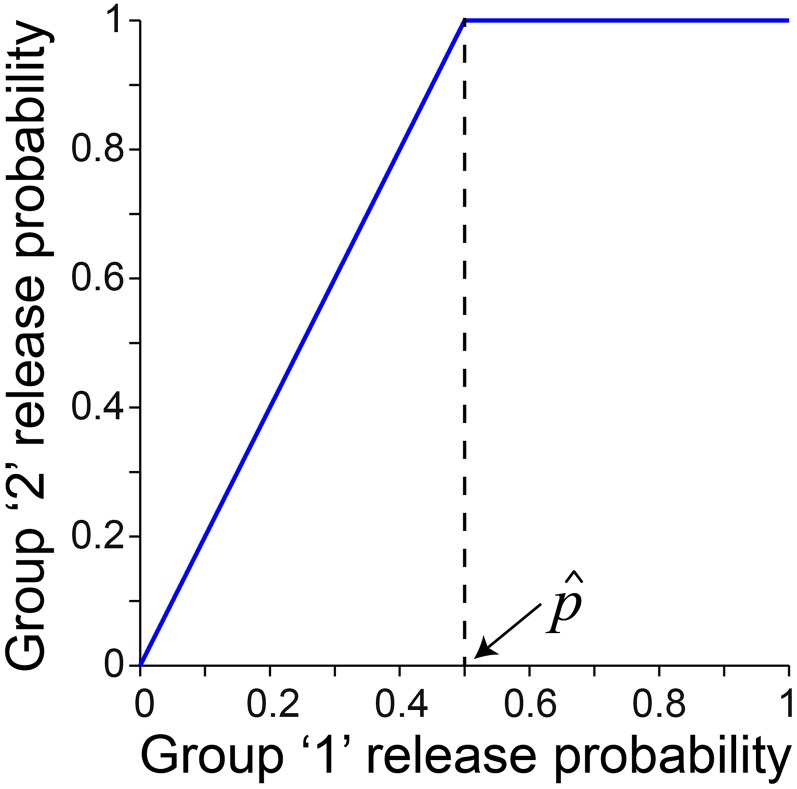
Model 3 assumes two groups of release sites under conditions of steady-state depression: group 1 has comparatively low release probability, and group 2 has high release probability. Each group of sites follows a multinomial model of release with uniform release probability. The release probabilities for the two groups are linearly related. The high-release probability synapses achieve a release probability of one under those conditions (external [Ca²⁺] or rate of stimulation in a train) in which the low-release probability synapses have a release probability of $\widehat{p}$, referred to as the transition probability (Fig. S1). The relationship between normalized variance and mean EPC amplitude was derived for this model and found to be Eq. 4.

Fig. S1.

A linear relationship between the release probability for group 1 and group 2 release sites is assumed in the two-site model (model 3). The release probably for group 2 release sites saturates at one (100%) at a transition probability $\widehat{p}$ for the group 1 sites. $\widehat{p}$ is 0.5 (50%) in this illustration.

Model 3 has four free parameters (one more parameter than model 2): N₁, the number of low-release probability synapses; N₂, the number of high-release probability synapses; $\widehat{p}$, the transition probability; and ${\overline{Q}}_P$, the mean quantal size (as above). The same two conditions of quantal variance as used for models 1 and 2 were considered. Note that $\widehat{N}=\hspace{0.17em}{N}_1\times \widehat{p}+N_2$ is substituted for notational simplicity, which can be interpreted at the apparent N under the experimental conditions for which $p=\widehat{p}$ for the low-release probability synapses (transition probability conditions).

Estimates of N were computed using Eq. 2. Estimates of P_r for each cell were computed from the binominal model using Eq. 1. Models were fit using nonlinear least squares curve fitting in Matlab with a trust region-reflective optimization algorithm and multiple random seed parameters to avoid local minima.

Fluorescence Imaging.

Live imaging of the zebrafish neuromuscular junction was performed with a Zeiss 710 Confocal Microscope equipped with an LD C-Apochromat 40× objective. Acetylcholine receptors were labeled with Alexa Fluor 555-conjugated α-btx (Life Technologies), and acetylcholinesterase was labeled with fasII that was conjugated with Alexa Fluor 633 in the laboratory using an Alexa Fluor Protein Labeling Kit (Life Technologies). Both α-btx and fasII were microinjected into the circulatory system or yolk sac of the larva and allowed 20 min before observation in the whole-mount configuration. Presynaptic terminals were identified by loading of vesicles with FM1-43 (Life Technologies) as previously described for zebrafish motor neurons (47). For quantitation of synaptic number, larva were injected with Alexa Fluor 555-conjugated α-btx, skinned, and incubated in 20 mg/mL collagenase (Life Technologies) at 28 °C for ∼2 h. When the muscle segments began to lift away, the larva were gently triturated to dissociate muscle. Single muscle cells were plated in recording solution on coverslips and examined by confocal microscopy.

SI Text

Existing models of the relationship between the mean postsynaptic response and its variance have assumed either uniform or continuously distributed vesicle release statistics across the population of release sites (19). Here, we derive a model of the situation, in which the postsynaptic response is triggered by a population of release sites with two distinct subgroups. In a given experimental condition (e.g., external calcium concentration or stimulation rate), group 1 has comparatively low release probability, and group 2 has high release probability. Specifically, we assume that the release probabilities are linearly related up to a point of saturation of the high-release probability synapses, which occurs at a release probability, $\widehat{p}$, referred to as the transition probability (illustrated in Fig. S1 for the case $\widehat{p}=0.5$):

$$p_2=\{\begin{array}{rr}\hfill \frac{p_1}{\widehat{p}},& \hfill p_1<\widehat{p}\\ \hfill 1,& \hfill p_1\ge \widehat{p}\end{array}.$$ [S1]

We then assume a simple multinomial model of release with mean quantal size, ${\overline{Q}}_P$; intrasite variability, CV_QI; and intersite variability, CV_QII. Assuming that there are N₁ release sites in group 1 and N₂ release sites in group 2, the mean synaptic response can be decomposed into the components contributed by the two subgroups of release sites:

$$\overline{I}=\overline{I_1}+\overline{I_2}=N_1{p}_1{\overline{Q}}_P+N_2{p}_2{\overline{Q}}_P.$$ [S2]

Substituting Eq. S1 for p₂ in Eq. S2 yields the following equation for the mean postsynaptic mean current:

$$\overline{I}=\{\begin{array}{rr}\hfill \left[N_1{p}_1+N_2\left(\hspace{0.17em}\frac{p_1}{\widehat{p}}\right)\right]{\overline{Q}}_P,& \hfill p_1<\widehat{p}\\ \hfill \left[N_1{p}_1+N_2\right]{\overline{Q}}_P,& \hfill p_1\ge \widehat{p}\end{array}.$$ [S3]

The variance of the synaptic response can similarly be decomposed into the components contributed by the two subgroups of release sites:

$${\sigma }_I^2={\sigma }_{I,1}^2+{\sigma }_{I,2}^2=[N_1{p}_1\left(1-p_1\right)+N_2{p}_2\left(1-p_2\right)]{\overline{Q}}_P\left(1+C{V}_{QII}^2\right)+[N_1{p}_1+N_2{p}_2]{\overline{Q}}_p^{2}C{V}_{QI}^2.$$ [S4]

Substituting Eq. S1 for p₂ yields the following equation for the postsynaptic variance:

$${\sigma }_I^2=\{\begin{array}{rr}\hfill \left[N_1{p}_1\left(1-p_1\right)+N_2\frac{p_1}{\widehat{p}}\left(1-\frac{p_1}{\widehat{p}}\right)\right]{\overline{Q}}_P\left(1+C{V}_{QII}^2\right)+\left[N_1{p}_1+N_2\frac{p_1}{\widehat{p}}\right]{\overline{Q}}_p^{2}C{V}_{QI}^2,& \hfill p_1<\widehat{p}\\ \hfill \left[N_1{p}_1\left(1-p_1\right)\right]{\overline{Q}}_P\left(1+C{V}_{QII}^2\right)+\left[N_1{p}_1+N_2\right]{\overline{Q}}_p^{2}C{V}_{QI}^2,& \hfill p_1\ge \widehat{p}\end{array}.$$ [S5]

Solving for p₁ in Eq. S3 and substituting into Eq. S5 yields the following relationship between the variance and mean of the postsynaptic response:

$${\sigma }_I^2=\{\begin{array}{rr}\hfill \left[{\overline{Q}}_P\times \overline{I}-\frac{{\overline{I}}^2}{\widehat{p}\times {\widehat{N}}^2/\left({\widehat{p}}^2\times N_1+N_2\right)}\right]\times \left(1+C{V}_{QII}^2\right)+{\overline{Q}}_P\times \overline{I}\times C{V}_{QI}^2,& \hfill I<{\overline{Q}}_P\times \widehat{N}\\ \hfill \left[{\overline{Q}}_P\times \left(\overline{I}-{\overline{Q}}_P\times N_2\right)-\frac{{\left(\overline{I}-{\overline{Q}}_P\times N_2\right)}^2}{N_1}\right]\times \left(1+C{V}_{QII}^2\right)+{\overline{Q}}_P\times \overline{I}\times C{V}_{QI}^2,& \hfill I\ge {\overline{Q}}_P\times \widehat{N}\end{array}.$$ [S6]

$\widehat{N}=\hspace{0.17em}{N}_1\times \widehat{p}+N_2$ has been substituted for notational simplicity.