Wetting hysteresis induced by nanodefects

Significance

Drops may fail to slide even on extremely smooth surfaces. This fact is due to the ubiquitous imperfections of surfaces: defects of molecular size—here too small to be noticed and experimentally characterizable—can hinder a macroscopic drop. To understand these far-reaching nanoscale phenomena, we combine a molecular description of the liquid with advanced techniques for the study of rare events. This approach allows us to bridge the diverse scales involved, demonstrating that even weak nanometer-sized surface defects can give rise to measurable differences between advancing and receding liquid fronts, i.e., contact angle hysteresis. The present results also shed new light on the unexpectedly long life of surface nanobubbles.

Abstract

Wetting of actual surfaces involves diverse hysteretic phenomena stemming from ever-present imperfections. Here, we clarify the origin of wetting hysteresis for a liquid front advancing or receding across an isolated defect of nanometric size. Various kinds of chemical and topographical nanodefects, which represent salient features of actual heterogeneous surfaces, are investigated. The most probable wetting path across surface heterogeneities is identified by combining, within an innovative approach, microscopic classical density functional theory and the string method devised for the study of rare events. The computed rugged free-energy landscape demonstrates that hysteresis emerges as a consequence of metastable pinning of the liquid front at the defects; the barriers for thermally activated defect crossing, the pinning force, and hysteresis are quantified and related to the geometry and chemistry of the defects allowing for the occurrence of nanoscopic effects. The main result of our calculations is that even weak nanoscale defects, which are difficult to characterize in generic microfluidic experiments, can be the source of a plethora of hysteretical phenomena, including the pinning of nanobubbles.

Within the burgeoning field of wetting (1, 2), the behavior of droplets on heterogeneous surfaces is one of the most active subjects of research (3–8). Indeed, the interaction of a liquid front with surface heterogeneities poses challenges concerning even the static behavior that are still open nowadays (1). Here, we take a fresh look at this subject using microscopic density functional theory (DFT) in conjunction with the string method for the study of rare events.

More specifically, the present study deals with a liquid front that advances or recedes over a surface with isolated nanometer-sized heterogeneities. All surfaces of practical use do feature heterogeneities at this scale, forming either chemical blemishes or topographical defects such as bumps or cavities; even advanced fabrication techniques cannot completely prevent them to occur. Although tiny and thus difficult to control and to characterize, these nanoscale defects have remarkable macroscopic consequences, such as generating measurable differences between advancing and receding liquid fronts, i.e., the contact angle hysteresis investigated here.

The phenomena that originate from the interaction between surface heterogeneities and liquids are diverse, and various names are used to underscore different aspects. For instance, “pinning” refers to hindrance of the motion of the contact line, “wetting hysteresis” is here defined as the qualitative difference between advancing and receding processes, whereas “contact angle hysteresis” indicates the difference observed between the apparent contact angle of advancing and receding drops. Understanding and relating all these different aspects of the problem requires a thorough theoretical investigation about the origin of hysteresis in wetting: many years after the first systematic studies (9, 10), contact angle hysteresis continues to be a very active research topic in physics, physical chemistry, and materials science (1).

The issue of surface nanobubbles (11, 12) is a contemporary example of the debate on wetting hysteresis. The pinning of their contact line seems to be the crucial element for explaining the unexpectedly long lifetime of nanobubbles. Recent findings have shown that nanobubbles can survive for hours due to a combination of contact line pinning and retarded one-dimensional diffusion (13–15). Zhang et al. (16) experimentally verified that nanobubbles are indeed pinned at the surface and that their apparent shape is that of a spherical cap. The size of surface nanobubbles, with a typical base radius <1 μm, and the regularity of their shape suggest that the pinning originates from much smaller surface defects, i.e., in the nanometer range. However, it is still an open question whether defects below 100 nm can pin a liquid–gas interface at all (9, 17) and thus whether they can be the cause of the stability of nanobubbles.

Recent experiments, using atomic force microscopy (AFM), reported the pinning force exerted by nanoscale defects (18, 19): Ondarçuhu et al. were able to identify single pinning or depinning events. However, to the best of our knowledge, there are no wetting experiments, involving a single well-characterized nanoscale defect, that are capable to relate the characteristics of the defect with the pinning force. Therefore, it is crucial to resolve how the chemical and topographical nanofeatures of surfaces determine contact angle hysteresis. Another intriguing and still open question is how a liquid front advances or recedes across such features.

Pinning of the contact line is important not only for static contact angle hysteresis but also for contact line motion (see, e.g., ref. 20). In the case of nanoscale defects, experiments suggest that the mechanism of contact line motion is governed by thermally activated pinning and depinning events (21, 22). Indeed, the “pinning energy” (i.e., the free-energy barrier) related to nanodefects may be of the order of $k_{\text{B}}T$ (19); thus, depending on the physical and chemical properties of the nanodefects, the migration across a defect may be a deterministic process driven by an external force or a stochastic one induced by thermal fluctuation. Recent experiments on colloids at the air–water interface suggest that thermal activation of local deformations of the triple line, possibly induced by pinning at nanodefects, can explain their anomalous diffusion coefficient (23). This experimental evidence also call for a better characterization of the advance and the retreat of liquids over nanodefects in terms of free-energy barriers, revealing the type of mechanism at work and the associated rate of the process.

Contact angle hysteresis was studied theoretically in the seminal paper by Joanny and de Gennes (JdG) (24) alluding to strong, isolated defects with characteristic size larger than ∼30 nm. Therein the macroscopic deformation of the liquid–vapor interface was worked out by assigning a given defect “force” both to smooth and to mesa defects having sharp discontinuities. Robbins and Joanny (25) focused on weak, macroscopic heterogeneities that individually are incapable to pin the interface but that induce contact angle hysteresis via collective pinning by many defects. Yeomans and coworkers (3, 26) performed mesoscale (>50 nm) lattice Boltzmann simulations for drops and liquid slabs in channels to calculate contact angle hysteresis on superhydrophobic surfaces and dense chemical patterns. This way, a quasistatic numerical experiment was performed, which determines the (meta)stable configurations at given drop radii (3) or at prescribed apparent contact angles (26). A similar approach was followed by Semprebon et al. (27) who used Surface Evolver (28) to compute the modes of advance of the liquid on macroscopically structured surfaces. The string method was used in connection with Ginzburg–Landau models to explore the Cassie–Wenzel transition for droplets on superhydrophobic surfaces (29, 30). To date, only a few studies investigated how the “pinning force” or the corresponding free-energy barriers are related to the geometrical and chemical characteristics of defects (3, 14). Furthermore, at the nanoscale, at which the typical dimensions of the roughness are comparable to the size of the liquid particles and where van der Waals forces come into play, wetting hysteresis as well as advancing and receding mechanisms remain still unexplored.

The present study aims at a microscopic understanding of the mechanism of hysteresis induced by chemical or topographical defects at the nanoscale. Contact line motion at that scale might also be a thermally assisted process (21, 22). We therefore discuss, within the same framework, both macroscopic deterministic pinning or depinning, as has been done in many previous analyses, as well as thermally activated depinning. Predicting thermally activated pinning or depinning rates requires inter alia the knowledge of the corresponding activation barriers. Thus, to understand hysteresis, one has to go beyond the equilibrium picture and investigate how the free-energy landscape, including features such as metastable minima and activation barriers, is influenced by deterministic forces driving the liquid. Here, we have combined a microscopic description of the fluid in terms of the classical DFT due to Rosenfeld, which is reliable on molecular scales (31–33), with the string method (34), a state-of-the-art tool for the study of rare events. This facilitates to accurately characterize the mechanism and the free-energy barriers associated with a liquid wedge advancing or receding over a single chemical or topographical nanodefect. The string method allowed us to overcome the limitations of brute-force calculations in the presence of metastabilities, to identify the transition path (shown in Movies S1–S4), and to provide accurate estimates for free-energy barriers for wetting or drying across a single heterogeneity. (Here, we use the notion “most probable path” or, more concisely, “transition path” to denote the most probable succession of configurations that the liquid assumes while it advances or recedes past a heterogeneity.) Because we are including microscopic details of the fluid, our approach can capture the diverse effects related to nanodefects. As demonstrated by our results, for such defects predictions based on macroscopic concepts like surface energies and contact angle become unreliable and incomplete. Given the experimental difficulty to access simultaneously the geometry and the chemistry of a nanodefect and the force exerted by it on advancing or receding liquid fronts, the present calculations are the first attempt (to our knowledge) to fully characterize nanoscale wetting hysteresis.

The paper is organized such that the first section is devoted to the description of the computational methods, with particular emphasis on novel aspects. The second section is concerned with the results on wetting hysteresis on single defects and the discussion of them. The third section investigates the role of dilute distributions of nanodefects on the macroscopic advancing and receding contact angles (i.e., contact angle hysteresis).

Combined DFT and String Calculations

Fundamental Measure Theory.

Classical DFT allows one to determine the equilibrium number density of a fluid by minimizing the grand potential functional $\mathrm{\Omega }$ of the system under investigation:

$$\mathrm{\Omega }\left[\rho \right]=F\left[\rho \right]+{\displaystyle \int {\text{d}}^{3}r\hspace{0.17em}\rho \left(\mathit{r}\right)\left[V\left(\mathit{r}\right)-\mu \right]},$$ [1]

where $F\left[\rho \right]$ is the intrinsic Helmholtz free-energy functional encompassing the fluid–fluid interactions, $\rho \left(\mathit{r}\right)$ is the fluid number density at position $\mathit{r}$, $V\left(\mathit{r}\right)$ is the substrate potential, and μ is the chemical potential.

For $F\left[\rho \right]$, we have chosen the fundamental measure theory of Rosenfeld (31–33), which accurately accounts for the repulsive part of the interaction between the fluid particles. For the attractive part of the fluid–fluid and fluid–solid interaction, we have adopted forces of the van der Waals type. Their length and energy scales are set by the particle diameter σ and by the interaction strength ε. The attractive part of the wall–fluid interaction is expressed in terms of the wall energy $u_{\text{w}}$, which determines the attractive potential $V_{\text{att}}\left(d\right)=-u_{\text{w}}/d^3$ acting on a fluid particle at a distance d from the planar surface of a half-space filled continuously and homogeneously by the same particles as the wall. To mimic chemical or topographical surface heterogeneities the wall energy $u_{\text{w}}\left(\mathit{r}\right)$ can vary spatially. Concerning the detailed forms of $F\left[\rho \right]$ and $V\left(\mathit{r}\right)$ as well as the calculation details, see refs. 33 and 35 and Supporting Information.

Model System.

We consider a liquid wedge defined as a semiinfinite liquid domain bounded by a planar liquid–vapor interface that forms an angle θ with the substrate (Fig. 1A). In a macroscopic description of the liquid wedge, this angle coincides with the equilibrium Young contact angle $\cos {\theta }_{\text{Y}}\equiv \left({\gamma }_{\text{sv}}-{\gamma }_{\text{sl}}\right)/{\gamma }_{\text{lv}}$, where ${\gamma }_{\text{sv}}$, ${\gamma }_{\text{sl}}$, and ${\gamma }_{\text{lv}}$ denote the surface tensions of the solid–vapor, solid–liquid, and liquid–vapor interfaces, respectively.

Fig. 1.

(A) Macroscopic model of a liquid wedge meeting the solid wall with an angle $\theta ={\theta }_{\text{Y}}\equiv {\theta }_{\text{Y}}^{\text{low}}$. (B) Actual liquid “wedge” used in DFT calculations. The color code indicates $\rho \left(\mathit{r}\right){\sigma }^3$. The position $x_{\text{tl}}$ of the triple line in x direction is marked by the white dot, typically close to the middle of the liquid–vapor interface. The defects introduced in the next section (not present here) will be placed at the center of the lower wall at position $x_{\text{d}}$ along the x axis (black dot) to ensure that the boundary conditions on the left and right do not interfere with the migration of the liquid wedge across the defects.

The system used in our DFT calculations for producing the liquid wedge in a finite computational box consists of two planar, parallel walls with the wall energies $u_{\text{w}}^{\text{up}}$ and $u_{\text{w}}^{\text{low}}$ tuned such that the liquid–vapor interface meets the two walls with complementary macroscopic angles ${\theta }_{\text{Y}}^{\text{low}}$ and ${\theta }_{\text{Y}}^{\text{up}}=180°-{\theta }_{\text{Y}}^{\text{low}}$ (Fig. 1B). Specifically, the lower wall is slightly lyophilic with $u_{\text{w}}^{\text{low}}=3\epsilon$ corresponding to ${\theta }_{\text{Y}}^{\text{low}}=80°$, whereas the upper wall exhibits $u_{\text{w}}^{\text{up}}=2.6\epsilon$ corresponding to ${\theta }_{\text{Y}}^{\text{up}}=100°$. The angles correspond to our choice $k_{\text{B}}T=\epsilon$ for the temperature T; the chemical potential is that for liquid–vapor coexistence in the bulk, $\mu ={\mu }_0\left(T\right)$, so that ${\rho }_{\text{l}}{\sigma }^3=0.658$ and ${\rho }_{\text{v}}{\sigma }^3=0.0199$ where ${\rho }_{\text{l}}\hspace{0.17em}\text{and}\hspace{0.17em}{\rho }_{\text{v}}$ denote the bulk liquid and vapor number density, respectively. The computational box size is $L_{\text{x}}\times L_{\text{y}}\times L_{\text{z}}=32.5\sigma \times 17.5\sigma \times 16\sigma$.

In Fig. 1B, we show the equilibrium profile for the fluid number density in the presence of defect-free, planar walls. It reproduces the salient features of a liquid wedge including, near the wall, the layering on the liquid side and the wetting film formation on the vapor side (see also ref. 36). This defect-free system is also used as a reference system to subtract small background variations of the free energy due to translations of the liquid wedge that result from the shift of the capillary liquid–vapor coexistence (37) relative to bulk coexistence due to various finite size effects (see Free-Energy Profiles).

The system used to study wetting hysteresis in the next section differs from the system in Fig. 1 in that the lower wall features a single defect. We consider the following defects (for details, see Supporting Information):

• •chemical defects: lyophobic ($u_{\text{w}}=2\epsilon$), partially wet ($u_{\text{w}}=3.5\epsilon$), and completely wet ($u_{\text{w}}=4\epsilon$) $\mathrm{\Delta }x\times \mathrm{\Delta }y=2.5\sigma \times 2.5\sigma$ patches on the lower wall (with $u_{\text{w}}=3\epsilon$); the contrast in $u_{\text{w}}$ intrudes into the wall up to a depth of $3\sigma$.
• •a combined topographical and chemical defect (hereafter called “post”): $\mathrm{\Delta }x\times \mathrm{\Delta }y\times \mathrm{\Delta }z=2.5\sigma \times 2.5\sigma \times 2.5\sigma$ cube protruding from the bottom planar wall with an effectively lyophobic chemistry (see Supporting Information and Fig. S1 and S2 for a precise characterization of this defect).

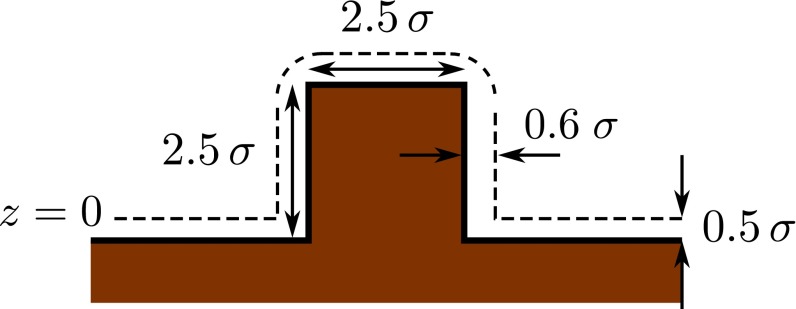
Fig. S1.

Schematic drawing of the wall with a post defect, here a cube. The wall is defined as the semiinfinite region in brown occupied by the centers of the wall particles. The dashed lines correspond to the distance of closest approach to the wall for the centers of the fluid particles; beneath these lines $V\left(\mathit{r}\right)=100\epsilon$, and the number density of the fluid is de facto zero. The plane $z=0$ is located at the lower horizontal dashed line as indicated.

Fig. S2.

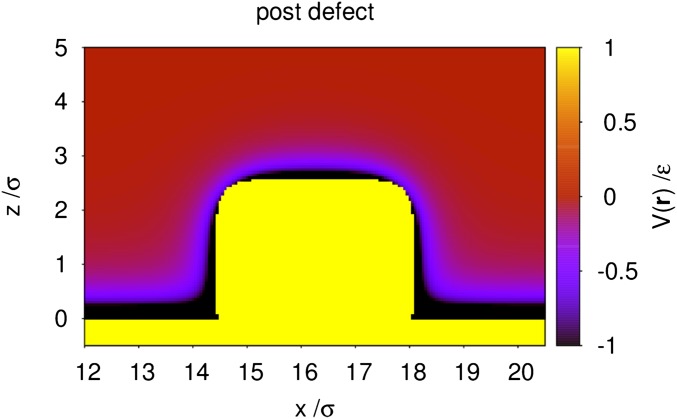
Wall potential $V\left(\mathit{r}\right)$ in units of ε in the vicinity of the post defect within a vertical cut $y=8.75\sigma$ through its center at $\left(x,y,z\right)=\left(x=16.25\sigma ,y=8.75\sigma ,z=1.25\sigma \right)$. The post is a cube of size $\mathrm{\Delta }x\times \mathrm{\Delta }y\times \mathrm{\Delta }z=2.5\sigma \times 2.5\sigma \times 2.5\sigma$, and the computational box has the size $\mathrm{\Delta }x\times \mathrm{\Delta }y\times \mathrm{\Delta }z=32.5\sigma \times 17.5\sigma \times 16\sigma$. The yellow domain, where $V\left(\mathit{r}\right)$ is positive, represents the region inaccessible to the fluid due to harshly repulsive interactions.

This setup allows the liquid front to advance or to recede over the defect, while recovering the undisturbed wedge shape far from it. Actual defects are certainly more complex; however, already the above model defects have allowed us to identify the various distinct aspects of hysteresis.

Although devised to produce a liquid wedge, the system adopted in our calculations and shown in Fig. 1B is in the first instance a narrow channel confined by walls having suitably different wall–fluid interactions. In this sense, it is possible to conceive an equivalent experiment in which a liquid is actually confined between two chemically distinct solid walls. While working in the grand canonical ensemble is appropriate for DFT calculation, the chemical potential can be easily converted into experimentally relevant observables via $\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)\left(\mu -{\mu }_0\left(T\right)\right)=p_{\text{l}}-p_{\text{v}}$, where $p_{\text{l}}$ and $p_{\text{v}}$ are the liquid and the vapor pressure, respectively.

String Method.

The string method is used in the context of rare events to determine the path of maximum probability connecting two metastable states (34). Although on its own DFT is capable of capturing only the stable and metastable states by minimizing the relevant free energy (Eq. 1), by combining DFT with the string method it is possible to access also the intermediate configurations of the system along the activated process—in this case, a liquid wedge advancing or receding across a surface defect. The probabilistic meaning of the transition path identified by the string method is that of the most probable path followed by the activated process under investigation at fixed thermodynamic conditions (μ and T) (34). Here, the space in which the string is computed is the same (discretized) density field $\rho \left(\mathit{r}\right)$ as used in the DFT calculations. Thus, by combining DFT calculations and the string method, we identify the most probable path for an advancing or receding liquid wedge in terms of the natural descriptor of a capillary system, i.e., the local number density.

The string $\rho \left(\mathit{r},\tau \right)$ can be thought of as an abstract curve such that, for each real number ${\tau }_0\in \left[\alpha ,\beta \right]$, there is a corresponding 3D number density distribution $\rho \left(\mathit{r},\tau ={\tau }_0\right)$. This curve connects the initial and final states A and B, respectively, of the activated process of advance and retreat, which are defined as $\rho \left(\mathit{r},\tau =\alpha \right)$ and $\rho \left(\mathit{r},\tau =\beta \right)$. In the case of a liquid wedge, the states A and B physically correspond to the liquid wedge far from the defect on the left and right, respectively; being (metastable) minima of the free energy, these states can be computed by standard DFT calculations (Fig. 1). The intermediate configurations forming the transition path are found, instead, by imposing the constrained free-energy minimization:

$${{\left(\frac{\delta \mathrm{\Omega }\left[\rho \right]}{\delta \rho \left(\mathit{r}\right)}\right)}_{\perp }|}_{\rho =\rho \left(\mathbf{r},\tau \right)}=0,$$ [2]

for all points $\rho \left(\mathit{r},\tau \right)$ along the string (34). Eq. 2 states that the components of the functional derivative of the grand potential with respect to the density perpendicular to the string (denoted as $\perp$) have to be zero. In the direction tangential ($\parallel$) to the string, the driving force ${\left(\delta \mathrm{\Omega }\left[\rho \right]/\delta \rho \left(\mathit{r}\right)\right)}_{\parallel }$ can be nonzero. (This driving force arises from the fact that, away from A and B, the system is not at equilibrium; therefore, this force is of “intrinsic” character and thus should be distinguished from the external driving force, which will be discussed in the next sections.) In short, condition [2] requires the transition path to lay at the bottom of a “valley” in the free-energy landscape, so that the only intrinsic driving force for the process is the one acting along that valley. The initial and final states A and B, instead, are (local) minima of the free-energy landscape where all components of the functional derivative vanish, $\delta \mathrm{\Omega }\left[\rho \right]/\delta \rho \left(\mathit{r}\right)=0$, and there is no intrinsic driving force.

The string is discretized in terms of so-called images, which de facto are number density configurations at distinct stages of the advancement of the wetting process. The initial and final images, corresponding to the (meta)stable states A and B, are kept fixed. We use the improved string method due to E et al. (38), which converges to Eq. 2 upon iterating the following algorithm:

• 1.Evolution of the images for a few minimization steps (here 5–20) of the grand potential [1]. Here, we use the standard Piccard iteration technique frequently used within classical DFT (33).
• 2.Reparametrization of the string to enforce an equal, generalized “distance” (in the abstract function space) $d=\sqrt{{\displaystyle \int {\text{d}}^{3}r\hspace{0.17em}{\left(\rho \left(\mathit{r},{\tau }_{\text{i}}\right)-\rho \left(\mathit{r},{\tau }_{\text{i}+1}\right)\right)}^2}}$ between contiguous images numbered by i (corresponding to an equal arc length parametrization).

The first step, amounting to a standard minimization procedure, ensures that the images evolve toward the bottom of the valleys of the free-energy landscape. The second step is implemented via the method of Lagrange multipliers, which enforces a uniform parametrization of the images along the string by constraining d. In other words, the second step prevents the images to converge toward the closest minimum (states A or B) as it would happen in a standard DFT calculation consisting solely of the first step. Further details of the combined DFT and string method are given in Supporting Information (see also Fig. S3).

Fig. S3.

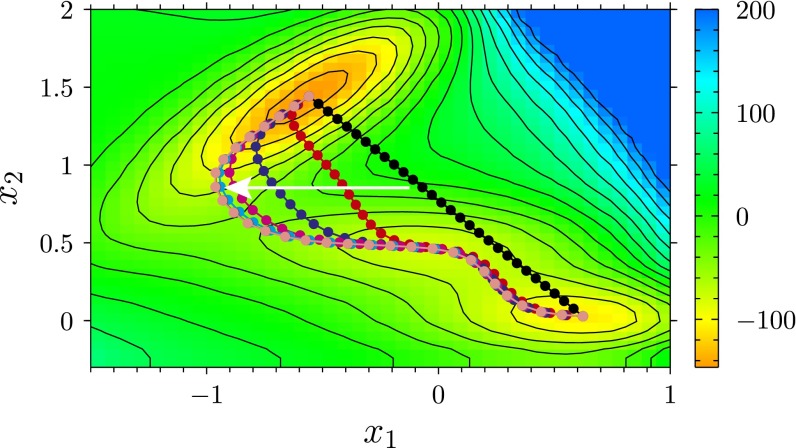
Illustration of the string method on a 2D model energy landscape, generated by the so-called Müller potential used in ref. 38, which depends on two dimensionless parameters $x_1$ and $x_2$. Color code and contour lines provide the value of the potential in dimensionless units. The dots denote the images in which the string is discretized. The white arrow indicates the direction in which the images evolve according to Eq. S5, starting from their initial position (black) and ending at the converged one (pink). The two ends of the string are initialized at the two minima of interest.

Liquid Wedge Migrating Across a Nanodefect

Transition Path.

In Fig. 2, we show the transition paths for the completely wet chemical defect and for the post defect. To visualize the 3D deformation of the interface as it crosses a defect, we use the isodensity surface ${\rho }^{\ast }=\left({\rho }_{\text{l}}+{\rho }_{\text{v}}\right)/2$; this surface (in gray) reveals that, upon retreat, the lower wall is covered by the expected liquid-like wetting film (39, 40). The post, instead, dries upon retreat (in brown), behaving as an effectively lyophobic chemical defect.

Fig. 2.

Transition path at bulk coexistence $\mu ={\mu }_0\left(T\right)$ for both the advance and the retreat across the completely wet patch with $u_{\text{w}}=4\epsilon$ (A) and the cubic post (B). In the top and bottom rows, the gray isodensity surface ${\rho }^{*}$ locates the liquid–vapor interface; the liquid domain lies on the right of these surfaces and the vapor on the left. In the top row, the position of the wet patch is indicated by the blue square. In the bottom row, the brown color corresponds to the post, uncovered by liquid. In the middle row, the number density $\rho \left(\mathit{r}\right){\sigma }^3$ is shown for a single image of the string corresponding to the third picture, both for the chemical patch (top row) and for the post defect (bottom row); the section is taken in the center of the channel. The bars in the middle row denote the lateral position and the size of the defects.

Based on macroscopic arguments, it is expected that the interface deformations decay exponentially away from the defect (24). Fig. 2 shows that the decay is indeed rapid even on the nanoscale and thus explains the difficulty to experimentally resolve the deformations induced by a single nanodefect. This result also suggests that, although the periodic boundary conditions in principle mimic an array of defects, the effect of having a periodic arrangement is limited and does not hinder the global advancement or retreat of the liquid–vapor interface.

The two defects have a qualitatively different effect on the liquid wedge: in the case of the wet patch, the receding liquid domain is held back by the defect, whereas in the post case it is locally pushed toward further retreat. On the other hand, the advancing liquid domain is pulled forward by the wet patch and is held back by the post. Accordingly, the deformations of the liquid–vapor interface along the transition paths suggest that the completely wet patch (post) hinders the receding (advancing) motion of a liquid front. This will be clarified in terms of free-energy barriers in the next subsection.

It is important to note that the transition paths shown in Fig. 2 do not have a directionality: they are the same for advancing and receding liquid wedges at fixed external conditions μ and T. As will be shown in the following, hysteresis arises because along a given transition path the system might be trapped in a metastable minimum. Whether this minimum occurs or not depends on the forces driving the system; e.g., tuning the chemical potential μ off coexistence drives the liquid wedge externally.

A representative density field is shown in the middle row of Fig. 2 for configurations for which the liquid front is just about to cross the defect. The liquid layering induced by the walls is apparent, with more pronounced effects at the lower lyophilic wall. The patch, which is more lyophilic than the rest of that wall, further enhances the density oscillations at the wall and shifts their maxima toward the wall (see, e.g., ref. 36). Close to the post, instead, the layering is slightly reduced due to its lyophobic nature, which is reflected by the local contact angle ${\theta }_{\text{Y}}\approx 125°$ on the top of the defect. At the lower corners of the cube, the interference of packing effects on the horizontal surface and on the side walls induces regions where the density is alternatingly increased and reduced.

Free-Energy Profiles.

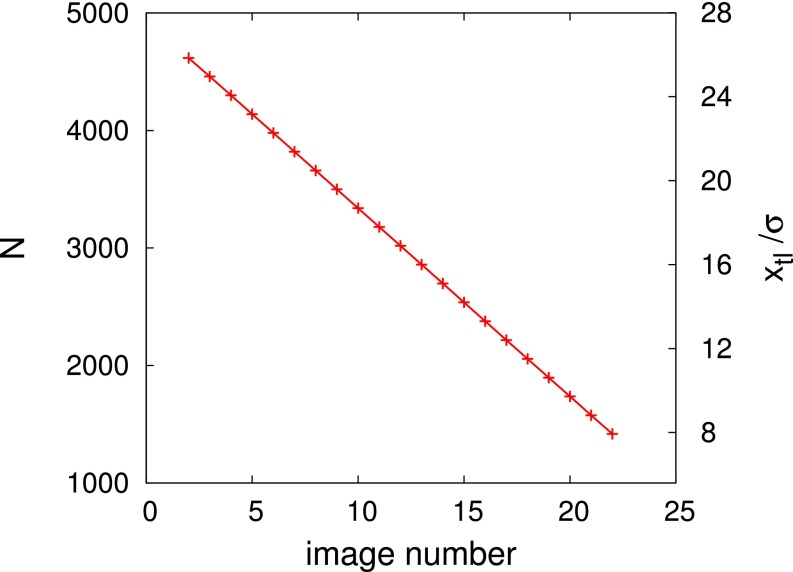
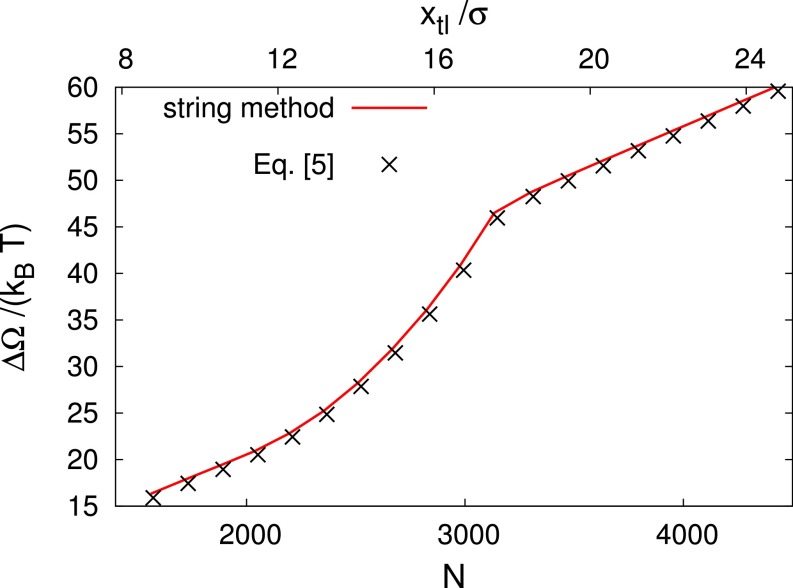
From the density fields constituting the transition path (Fig. 2) and from Eq. 1, we compute the free-energy profiles for the advance or retreat of the liquid wedge along the string. In Fig. S4, we demonstrate that there is a one-to-one correspondence between the image number along the string and the amount of fluid in the channel, i.e., the number of particles $N={\displaystyle \int {\text{d}}^{3}r\rho \left(\mathit{r}\right)}$ as obtained along the transition path. An even more instructive parametrization of the string is the quantity $x_{\text{tl}}=N/\left(L_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)\right)$, where $L_{\text{y}}$ and $L_{\text{z}}$ are the dimensions of the computational box in the y and z direction, respectively; it serves as a measure of the position of the triple line (Fig. 1).

Fig. S4.

Number of particles N in the computational box of size $\mathrm{\Delta }x\times \mathrm{\Delta }y\times \mathrm{\Delta }z=32.5\sigma \times 17.5\sigma \times 16\sigma$ for the images of the string in the case of the defect-free channel. The position $x_{\mathrm{tl}}=N/\left(L_y{L}_z\left({\rho }_l-{\rho }_v\right)\right)$ of the triple line is shown, too, on the right vertical axis. The cases with defects also exhibit linear relationships between the image number and N or $x_{\mathrm{tl}}$.

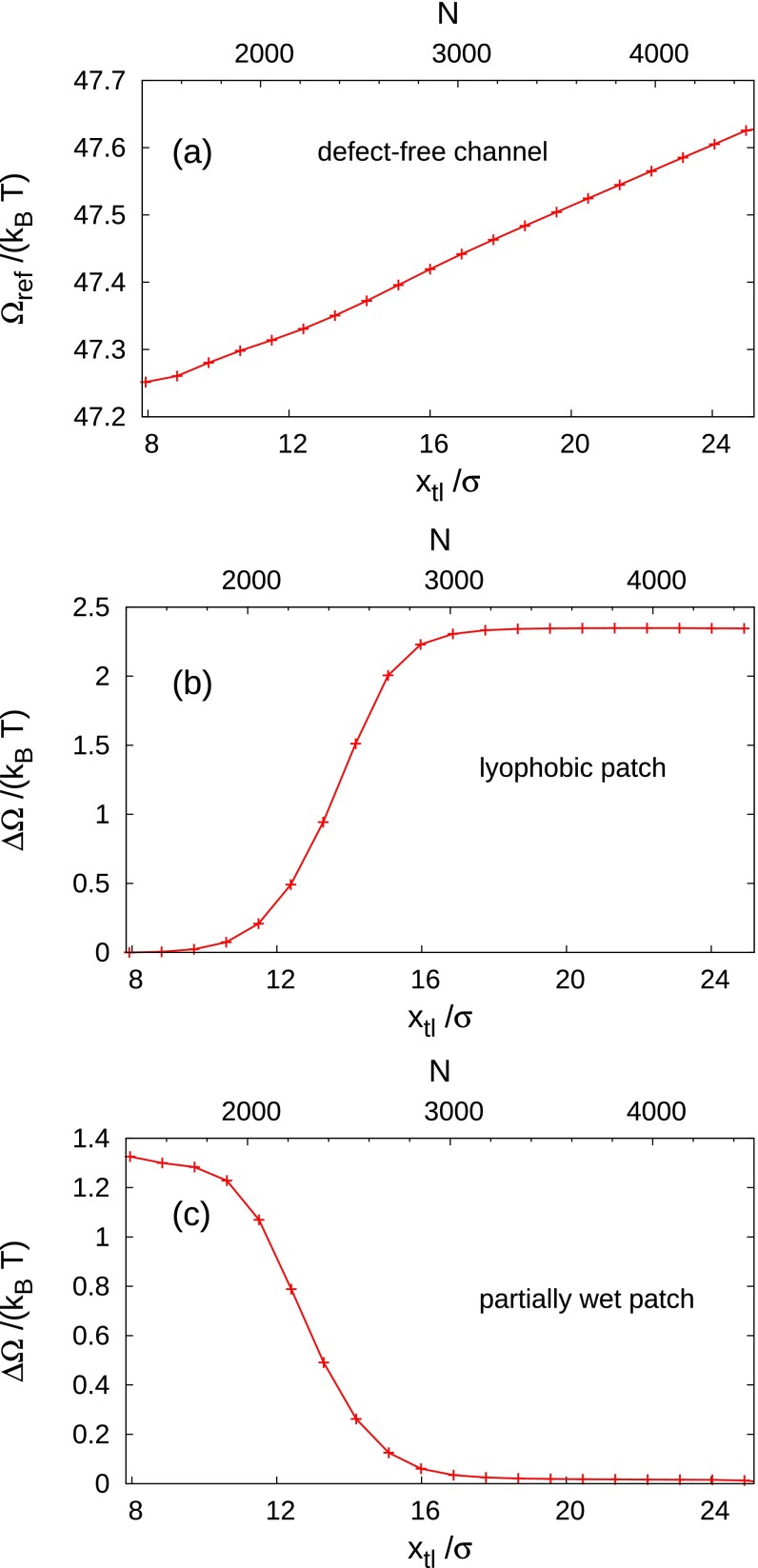
From the free-energy profiles for the advance or retreat of the liquid wedge over a defect, we subtract the free-energy profile obtained for the filling of the corresponding defect-free channel (Fig. 1B and Fig. S5). This results in the excess free-energy profile $\mathrm{\Delta }\mathrm{\Omega }\left(x_{\text{tl}}\right)$ for a system with zero external driving forces, which is plotted in Fig. 3. The data show a monotonic trend of the free-energy profile connecting the stable and metastable states corresponding to the lower and upper plateau branches, respectively. The occurrence of these essentially horizontal plateaus shows that the interaction of the liquid wedge with a defect decays rapidly upon increasing the distance between them.

Fig. S5.

(A) Reference free energy, taken to be that of a liquid wedge advancing or receding in a defect-free channel at bulk two-phase coexistence $\mu ={\mu }_0\left(T\right)$. The excess free energy $\mathrm{\Delta }\mathrm{\Omega }$ at two-phase coexistence is shown for a lyophobic patch (B) ($u_{\mathrm{w}}/\epsilon =2$) and for a partially wet patch (C) ($u_{\mathrm{w}}/\epsilon =3.5$).

Fig. 3.

Excess free-energy profiles $\mathrm{\Delta }\mathrm{\Omega }\left(x_{\text{tl}}\right)$ at two-phase coexistence [$\mu ={\mu }_0\left(T\right)$] computed from the transition paths shown in Fig. 2; $x_{\text{tl}}$ is a measure of the position of the triple line defined as $x_{\text{tl}}=N/\left(L_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)\right)$, where N is the number of fluid particles in the computational box. Receding (advancing) corresponds to a decrease (an increase) of $x_{\text{tl}}$ or N (Fig. 1B). The defects considered here are a completely wet chemical patch (red solid line; $u_{\text{w}}=4\epsilon$) and a cubic post (black dashed line) placed at the horizontal position $x_{\text{d}}=16.25\sigma$. After subtracting the defect-free free-energy profile, in both cases the resulting free-energy difference $\mathrm{\Delta }\mathrm{\Omega }\left(x_{\text{tl}}\right)$ exhibits an upper and a lower plateau. $\mathrm{\Delta }\mathrm{\Omega }\left(x_{\text{tl}}\right)$ is shifted such that the latter one is zero. For the wet chemical patch, the thermodynamically stable state (absolute minimum) is outside of the considered range of $x_{\text{tl}}$. For the post, a very shallow minimum is attained at $x_{\text{tl}}\approx 11\sigma$; because, within our computational precision, this minimum cannot be distinguished from the plateau, we regard the lower part of the post profile as a plateau with $\mathrm{\Delta }\mathrm{\Omega }=0$.

In the case of a wet (chemical) patch, the stable state corresponds to a configuration in which the liquid completely covers the defect and the liquid–vapor interface is undeformed and far to the left of the patch ($x_{\text{tl}}$ large); the metastable state corresponds to the patch being exposed to the vapor and the planar liquid–vapor interface far to the right of the patch ($x_{\text{tl}}$ small). The intermediate configurations are characterized by a progressive increase of the free energy, due to the wetting of the defect and the deformation of the liquid–vapor interface. Thus, the wet patch constitutes an obstacle to the retreat of the liquid wedge, characterized by a free-energy barrier of 2.5 $k_{\text{B}}T$ (Table 1). Viewing the free-energy profile in the opposite direction, the wet patch favors the advancing motion of the liquid front.

Table 1.

Summary of the results for the advance and retreat of a liquid wedge across defects

Defect type	$u_{\text{w}}/\epsilon$	${\theta }_{\text{Y}}$	$\delta \mathrm{\Omega }/k_{\text{B}}T$	$\delta {\mathrm{\Omega }}^{\text{macro}}/k_{\text{B}}T$	$\mathrm{\Delta }{\mu }_{\text{sp}}/k_{\text{B}}T$	$\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)/k_{\text{B}}T$
Defect-free channel (up)	2.6	99.67°	—	—	—	—
Defect-free channel (low)	3.0	80.51°	—	—	—	—
Lyophobic patch	2.0	124.85°	2.4	1.87	0.0035	1.1
Partially wet patch	3.5	51.13°	−1.3	−1.17	−0.00186	0.61
Completely wet patch	4.0	0.0°	−2.5	−2.22	−0.0034	1.2
Cubic post	3.0	126.81°	15.2	8.02	0.027	10.5

$u_{\text{w}}$ is the wall energy for the upper and lower walls and the defects, ${\theta }_{\text{Y}}$ is the Young contact angle, $\delta \mathrm{\Omega }\equiv {\mathrm{\Omega }}_{\text{wet}}-{\mathrm{\Omega }}_{\text{dry}}$ is the free-energy difference at two-phase coexistence, $\delta {\mathrm{\Omega }}^{\text{macro}}$ is the corresponding macroscopic estimate, $\mathrm{\Delta }{\mu }_{\text{sp}}$ is the excess chemical potential at the spinodal, and $\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)\equiv \mathrm{\Delta }\mathrm{\Omega }\left(\mathrm{\Delta }\mu =\mu -{\mu }_0\left(T\right)=0,V,T;x_{\text{tl},\text{sp}}\right)$ is the excess free energy at the spinodal (see Forcing the System: The Origin of Hysteresis and Contact Angle Hysteresis Induced by a Random Distribution of Defects). A positive sign of $\delta \mathrm{\Omega }$ implies a barrier ${\mathrm{\Omega }}_{\text{barrier}}=\delta \mathrm{\Omega }$ for an advancing liquid front; a negative sign implies a barrier ${\mathrm{\Omega }}_{\text{barrier}}=\left|\delta \mathrm{\Omega }\right|$ for a receding liquid front. ${\theta }_{\text{Y}}$ is determined independently via the interfacial tensions using Young’s formula, $\cos {\theta }_{\text{Y}}=\left({\gamma }_{\text{sv}}-{\gamma }_{\text{sl}}\right)/{\gamma }_{\text{lv}}$; because of an imperfect choice of the wall potentials, ${\theta }_{\text{Y}}^{\text{up}}+{\theta }_{\text{Y}}^{\text{low}}=180.18°>180°$.

The post represents, instead, a hindrance to the advance of the liquid wedge with a free-energy barrier of 15 $k_{\text{B}}T$. Because according to transition state theory the typical time $t_{\text{cr}}$ for crossing a free-energy barrier ${\mathrm{\Omega }}_{\text{barrier}}>0$ scales exponentially with its height, $t_{\text{cr}}=t_0\exp \left({\mathrm{\Omega }}_{\text{barrier}}/\left(k_{\text{B}}T\right)\right)$, a single post may block the advance of a liquid front on a timescale $t_{\text{cr}}\approx 0.5$ μs, which is relevant for experimental observations [at least at $\mu ={\mu }_0\left(T\right)$; for μ being off coexistence, see below]. For this estimate, we have adopted conservatively a microscopic attempt frequency $1/t_0=k_{\text{B}}T/h\approx {10}^{13}$ ${\text{s}}^{-1}$, where h is Planck’s constant (41).

Given the sigmoidal shape of the free-energy profiles in Fig. 3 and Fig. S5, the quantity characterizing thermally activated (de)pinning by (from) various types of defects is the free-energy difference $\delta \mathrm{\Omega }\equiv {\mathrm{\Omega }}_{\text{wet}}-{\mathrm{\Omega }}_{\text{dry}}$ between the two plateau values, where ${\mathrm{\Omega }}_{\text{wet}}$ and ${\mathrm{\Omega }}_{\text{dry}}$ are the free energy of the state in which the liquid–vapor interface is sufficiently far from the defect to the left and to the right (Fig. 1), respectively. The free-energy differences $\delta \mathrm{\Omega }$ are reported in Table 1. A positive sign of $\delta \mathrm{\Omega }$ implies that an advancing liquid front has to climb up a barrier and is hindered in its motion, whereas for $\delta \mathrm{\Omega }$ negative a receding liquid front has to climb up a barrier and is hindered. The data in Table 1 tell that, if at all, single nanometer-sized chemical blemishes are only weak obstacles to the motion of a liquid front: thermal fluctuations can be sufficient to facilitate the crossing of a single chemical defect. On the other hand, nanodefects that are both topographical and chemical such as the post strongly hinder the motion of liquid fronts.

The ratio between the free-energy barrier ${\mathrm{\Omega }}_{\text{barrier}}\equiv \left|\delta \mathrm{\Omega }\right|$ and the thermal energy $k_{\text{B}}T$ discriminates between deterministic pinning and reversible thermally activated motion of the triple line: for ${\mathrm{\Omega }}_{\text{barrier}}/\left(k_{\text{B}}T\right)\sim 1$ the defect is weak and thermal fluctuations are able to reversibly switch between the two plateaus, whereas for ${\mathrm{\Omega }}_{\text{barrier}}/\left(k_{\text{B}}T\right)\gg 1$ the liquid front is blocked by the strong defect. This measure of the defect strength is an alternative to the classical distinction of weak and strong defects based on the “spring constant” and the wetting force of the defects (24). Our findings seem to be in accordance with the experiments of Delmas et al. (19), who find that the crossing of nanodefects is reversible if the defect “energy” is comparable with $k_{\text{B}}T$. For high barriers, external forces have to be applied to drive the liquid front across the defects. As discussed in the next section, this requires knowledge of the full free-energy profile. The same is true for intermediate barriers in which case force-assisted, thermally activated (de)pinning may also become relevant.

Within a macroscopic theory, the free-energy differences $\delta \mathrm{\Omega }\equiv {\mathrm{\Omega }}_{\text{wet}}-{\mathrm{\Omega }}_{\text{dry}}$ can be easily estimated a priori from the surface free energy associated with the defect: for macroscopic chemical blemishes, for which the relevant quantities (the solid–liquid and the solid–vapor interfacial tensions) are well defined and line contributions do not matter, the free-energy difference is $\delta {\mathrm{\Omega }}^{\text{macro}}={\gamma }_{\text{lv}}\left(\cos {\theta }_{\text{Y}}^{\text{sub}}-\cos {\theta }_{\text{Y}}^{\text{def}}\right)A$, where ${\theta }_{\text{Y}}^{\text{sub}}$ and ${\theta }_{\text{Y}}^{\text{def}}$ is Young contact angle related to the defect-free substrate and to the one on the defect, respectively, and A is the area of the defect. In the case of a topographical defect, one has $\delta {\mathrm{\Omega }}^{\text{macro}}=-{\gamma }_{\text{lv}}\cos {\theta }_{\text{Y}}{A}_{\text{lat}}$, where $A_{\text{lat}}$ is the area of the side walls of the protrusion; ${\theta }_{\text{Y}}$ is Young’s angle, which, for a purely topographical defect and on a macroscopic level, is the same for the substrate and the defect. For a topographical and chemical defect, such as the post, the macroscopic expression is a combination of the previous two: $\delta {\mathrm{\Omega }}^{\text{macro}}={\gamma }_{\text{lv}}\left(\cos {\theta }_{\text{Y}}^{\text{sub}}-\cos {\theta }_{\text{Y}}^{\text{def}}\right)A-{\gamma }_{\text{lv}}\cos {\theta }_{\text{Y}}^{\text{def}}{A}_{\text{lat}}$. The macroscopic estimates $\delta {\mathrm{\Omega }}^{\text{macro}}$ are reported in Table 1. For the chemical patches, these agree surprisingly well with the results from the corresponding microscopic calculations. For the post defect, however, the macroscopic estimate is about one-half of that obtained from the microscopic theory. One reason for the inaccuracy of the macroscopic estimate is the particular liquid structure near the nanosized post, which is not captured by a macroscopic description. The other reason seems to be related to the weaker attraction of the walls of nanosized posts in comparison with the walls of macroscopic bodies composed of the same material.

Forcing the System: The Origin of Hysteresis.

Free-energy profiles at two-phase coexistence per se do not explain the emergence of wetting hysteresis. Hysteresis is due to the occurrence of a free-energy barrier between a metastable “pinned” state and the thermodynamically stable state. The pinned state is present only within a certain range of external forcing, here realized via the chemical potential μ. Experimentally, the same forcing can be obtained by small temperature differences between the sample and the liquid reservoir, which controls $\mathrm{\Delta }\mu$ for volatile liquids (42), or by changing the pressure (for nonvolatile liquids). Body forces like gravity, electrical fields, etc., act in a similar way. Depending on the history of the forcing—i.e., the actual experimental procedure—the system can either get trapped or not in metastable states and thus can evolve through different sequences of configurations while advancing or receding.

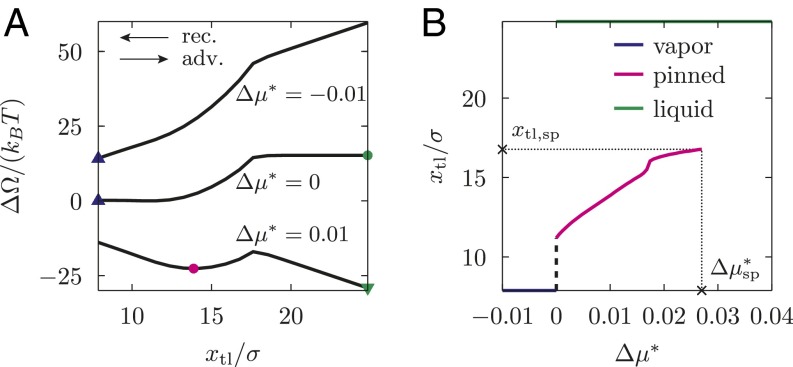
To reveal this mechanism for hysteresis, for the defects introduced above we compute the transition path and the free-energy profiles for several values of μ off coexistence, as done in Fig. 3 for $\mu ={\mu }_0\left(t\right)$. For the post defect, Fig. 4A shows the excess free-energy profiles as a function of the position $x_{\text{tl}}$ of the triple line. As expected, positive reduced chemical potentials $\mathrm{\Delta }{\mu }^{\ast }\equiv \left(\mu -{\mu }_0\left(T\right)\right)/\epsilon$ tilt the whole free-energy profile toward the fully wet state, so that at $x_{\text{tl}}=x_{\text{tl},\text{l}}\left(\mu \right)$ the liquid phase fills the whole space of the channel (green triangle). (In the case of an unbounded liquid wedge, one has $x_{\text{tl},\text{l}}\to \mathrm{\infty }$. However, for the computational box shown in Fig. 1, $x_{\text{tl},\text{l}}$ is finite and corresponds to the position of the triple line at the left end of the computational box.) For $\mathrm{\Delta }{\mu }^{\ast }>0$, the sigmoidal free-energy profile observed for $\mathrm{\Delta }{\mu }^{\ast }=0$ (the same as the dashed black line in Fig. 3) turns into one featuring a metastable state (magenta circle, emerging from the blue triangle), separated from the stable one (green triangle) by a barrier. The metastable state (magenta circle) corresponds to one with the meniscus in the channel pinned at the defect; it exhibits a deformation of the liquid–vapor interface and a perturbation of the density distribution compared with the defect-free configuration (Fig. 2). This metastable state occurs within the range $0<\mathrm{\Delta }{\mu }^{\ast }<\mathrm{\Delta }{\mu }_{\text{sp}}^{\ast }$, with $\mathrm{\Delta }{\mu }_{\text{sp}}^{\ast }$ as the spinodal value. In this range, the thermodynamically stable equilibrium (i.e., the global minimum of the free-energy profile) corresponds to the liquid phase (green triangle); however, free-energy barriers of ∼10 k_BT may effectively trap the system in the metastable pinned state, thus giving rise to hysteresis (see ref. 43 for a similar situation on superhydrophobic surfaces). For $\mathrm{\Delta }{\mu }^{\ast }<0$, instead, the only stable state is the one filling the computational box with vapor (blue triangle). In Fig. 4B, we show the loci of the free-energy minima (stable or metastable ones) in the $\mathrm{\Delta }{\mu }^{\ast }$ – $x_{\text{tl}}$ plane.

Fig. 4.

(A) Excess free-energy profiles $\mathrm{\Delta }\mathrm{\Omega }$ for selected reduced chemical potentials $\mathrm{\Delta }{\mu }^{*}=\left(\mu -{\mu }_0\left(T\right)\right)/\epsilon$ for the cubic post as a function of the position $x_{\text{tl}}$ of the triple line. Symbols identify the local (circle) and global minima (triangles) for a given μ. The global minima are outside of the plotted range at $x_{\text{tl},\text{v}}$ and $x_{\text{tl},\text{l}}$ (see main text); here, the corresponding symbols are drawn at the edge of the computational box. (B) Position $x_{\text{tl}}$ of the triple line at the minima of the free-energy profiles in A as a function of $\mathrm{\Delta }{\mu }^{*}$: metastable pinned state (magenta), stable vapor phase (blue), and stable liquid phase (green). The pinned minimum disappears at the spinodal $\mathrm{\Delta }{\mu }_{\text{sp}}^{*}$. The black dashed line indicates that, for $\mathrm{\Delta }{\mu }^{*}=0^{+}$, the pinned minimum is likely to shift continuously toward the vapor phase. However, the very steep slope of this black line prevents to verify this behavior in the actual calculations.

The calculations off coexistence also show that the transition paths (e.g., the sequence of number densities shown in Fig. 2) are not changed by the external “force” μ (for an extended discussion, see refs. 44 and 45). Thus, given the weak dependence of $\rho \left(\mathit{r},\tau \right)$ on μ for fixed $x_{\text{tl}}$, it follows from Eq. 1 that the free-energy profiles (i.e., the sequence of constrained free energies along the most probable path, which is parametrized, e.g., by the position $x_{\text{tl}}$ of the triple line) $\mathrm{\Omega }\left(\mu ,V,T;x_{\text{tl}}\right)$ off coexistence can be computed within good approximation from that at coexistence:

$$\mathrm{\Omega }\left(\mu ,V,T;x_{\text{tl}}\right)=\mathrm{\Omega }\left({\mu }_0\left(T\right),V,T;x_{\text{tl}}\right)-\left(\mu -{\mu }_0\left(T\right)\right)N\left(x_{\text{tl}}\right),$$ [3]

where the relation between the number of particles and the position of the triple line is $N\left(x_{\text{tl}}\right)=x_{\text{tl}}{L}_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)$. Eq. 3 states that the only relevant effect of tuning the chemical potential off coexistence is to tilt the free-energy profile obtained at $\mathrm{\Delta }{\mu }^{\ast }=0$. In that way, metastable minima separated by barriers from the stable ones may be created along the transition paths. In Fig. S6, it is demonstrated that free-energy profiles off coexistence obtained via a direct calculation or from Eq. 3 actually coincide.

Fig. S6.

Excess free-energy profile $\mathrm{\Delta }\mathrm{\Omega }$ at $\mathrm{\Delta }{\mu }^{*}=-0.01$ for the post defect as computed directly via the string method (black crosses) and via Eq. 3 in the main text. N is the number of particles in the computational box of size $\mathrm{\Delta }x\times \mathrm{\Delta }y\times \mathrm{\Delta }z=32.5\sigma \times 17.5\sigma \times 16\sigma$. As reference, $x_{\mathrm{tl}}=N/\left(L_y{L}_z\left({\rho }_l-{\rho }_v\right)\right)$ is reported, too, on the upper horizontal axis. This curve is the same as the upper one in Fig. 4A of the main text. Calculations for different μ render similar agreements.

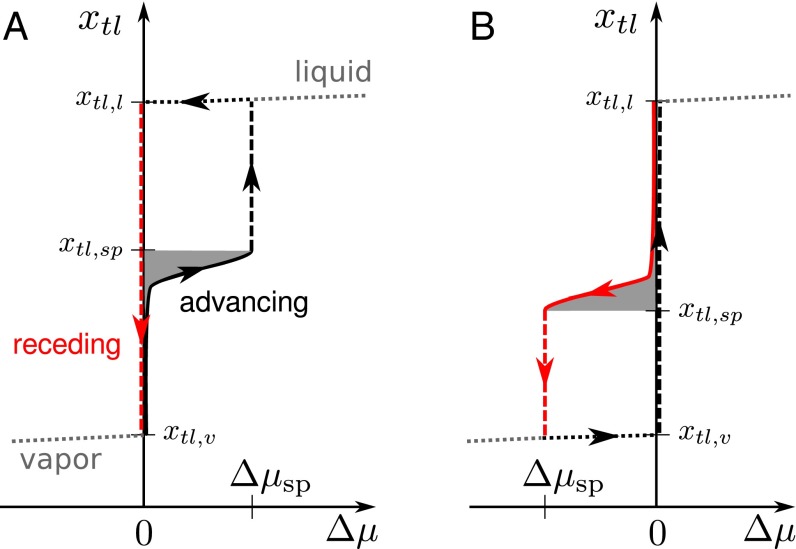
The overall mechanism of hysteresis during the advance or retreat of a liquid wedge is summarized in Fig. 5. To this end, we consider an experimental procedure according to which the system is initially in the vapor phase (lower left corner of Fig. 5A) and the chemical potential—or, alternatively, the pressure—is gradually increased (black line); the experiment is assumed to be carried out adiabatically to allow the system to relax to the local minimum of the free energy. At coexistence $\mathrm{\Delta }\mu =0$, a liquid–vapor interface is formed, such that it is assumed to be formed on the right of the post defect (Fig. 2B) and moves to the left along the wall up to the post, where it is stopped by the free-energy barrier. Upon increasing μ the interface remains pinned at the defect until the free-energy barrier has decreased to a value comparable with $k_{\text{B}}T$, which occurs near the spinodal $\mu ={\mu }_{\text{sp}}$. For $\mu >{\mu }_{\text{sp}}$, the channel is completely filled by liquid. The retreat of the wedge (red line) follows a different sequence of states, because the system remains trapped in the global minimum (liquid state). The liquid–vapor interface is formed only at coexistence $\mathrm{\Delta }\mu =0$, at which the wedge moves unhindered along the wall to the other minimum, i.e., the vapor state. The two qualitatively different advancing and receding branches in Fig. 5 explain wetting hysteresis induced by surface defects.

Fig. 5.

Sketch of the behavior of an advancing or receding liquid wedge across defects of the post type (A) (compare with Figs. 3 and 4B: advance barrier, spinodal $\mathrm{\Delta }{\mu }_{\text{sp}}>0$) and of the wet chemical patch type (B) (retreat barrier, Fig. 3, $\mathrm{\Delta }{\mu }_{\text{sp}}<0$). The sequence of (meta)stable states constituting the advancing (receding) process is plotted with a solid black (solid red) line. The loci of the minima of the free energy related to the pure-liquid or pure-vapor phases are shown as dotted lines. Dashed lines are used for irreversible processes, i.e., the “snapping” of the contact line at $\mathrm{\Delta }{\mu }_{\text{sp}}$ and the sliding of the liquid wedge downhill the free-energy profiles at $\mathrm{\Delta }\mu =0$. The area shaded in gray, ${\displaystyle {\int }_{x_{\text{tl},\text{v}}}^{x_{\text{tl},\text{sp}}}\mathrm{\Delta }\mu \hspace{0.17em}\text{d}{x}_{\text{tl}}}$ in A, ${\displaystyle {\int }_{x_{\text{tl},\text{l}}}^{x_{\text{tl},\text{sp}}}\mathrm{\Delta }\mu \hspace{0.17em}\text{d}{x}_{\text{tl}}}$ in B, corresponds to $\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)/\left(L_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)\right)$; this can be obtained using Eq. 4 in the above expressions for the areas.

The range of chemical potentials $\mathrm{\Delta }\mu$, for which the metastable pinned state occurs, is for the post case $0\le \mathrm{\Delta }{\mu }^{\ast }\le \mathrm{\Delta }{\mu }_{\text{sp}}^{\ast }=0.027$ in units of ε (for the other defects, see Table 1). However, $\mathrm{\Delta }{\mu }_{\text{sp}}^{\ast }$ is not an intrinsic quantity as it depends on the individual system under consideration and, in particular, on the box dimensions. For a given value of $\mathrm{\Delta }\mu$, the total force exerted on the liquid–vapor interface increases proportionally to the cross-section of the channel. This force has to be balanced by the single defect in the box. However, the maximum force the individual defect can withstand is given and independent of the computational box size. Thus, upon doubling the height of the computational box, $\mathrm{\Delta }{\mu }_{\text{sp}}^{\ast }$ is halved. In the following section, defect-specific quantities independent of incidental computational details are introduced, which allow us to relate the characteristics of a specific defect to its macroscopic effect on contact angles.

We are now in a position to compare in more detail the present approach with the seminal paper of JdG (24). This comparison is beneficial to understand the differences between wetting hysteresis on the macroscale and on the nanoscale. First, JdG consider a special case of wetting hysteresis, i.e., one which arises from macroscale (>30 nm), strong defects, where strong means that the defect is capable of inducing two distinct configurations of the liquid–vapor interface—a weakly and a strongly deformed one—at the same nominal position of the unperturbed contact line. Depending on the history of contact line motion (i.e., advance or retreat), one of these two configurations is selected, giving rise to wetting hysteresis. However, the nanodefects considered here are weak in the JdG sense, and there is only a single configuration of the liquid–vapor interface for a given position of the triple line, as demonstrated by the free-energy profiles in Figs. 3 and 4A. In fact, wetting hysteresis for these nanodefects emerges if the quasistatic procedure in Fig. 5 requires different forcing for advance and retreat. Alternatively, it can be regarded as a hysteresis in the contact line position upon cycling the driving force. In our approach, we explicitly refer to the driving force $\mathrm{\Delta }\mu$ (or $\mathrm{\Delta }p$); this suggests an experimental realization of our thought experiment in which a liquid front is quasistatically driven through a narrow channel with suitably prepared walls by stepwise changing the pressure in an attached fluid reservoir and simultaneously measuring the position of the liquid front. Alternatively, the AFM technique with special carbon tips used in ref. 19 is capable to determine both the force and the position of the contact line for a single nanodefect; a comparison with Fig. 5 appears to be possible. [For a direct comparison, an experimental characterization of the nanodefect is needed. In addition, the comparison should be done not directly with $\mathrm{\Delta }\mu$, but with the (intrinsic) defect force $\partial \mathrm{\Omega }/\partial x_{\text{tl}}$ introduced in the next section.] Another experimental technique is the noncontact AFM for nanoscale wetting used by Checco et al. (46). On a larger scale, also the Wilhelmy plate technique (47) could be used, while macroscopic contact angle hysteresis arising from dilute distributions of nanodefects can be measured and related to the defect characteristics via Eq. 7 (see next section). Another peculiarity of nanodefects are thermally activated crossings, the description of which requires specialized rare-events techniques to reveal the transition path and thus the (unexpected) sigmoidal free-energy profile. In a certain sense, the findings of the present nanoscale analysis are complementary to the macroscopic picture of JdG for strong defects, revealing that wetting hysteresis induced by nanodefects proceeds via a different mechanism; hysteresis disappears if thermal fluctuations become dominant.

A major difference between the two approaches is our capability to achieve a microscopic description that can cope with the problem that for nanodefects there is no clear scale separation between the linear extensions of the defects and the length scales characterizing the fluid inhomogeneities at the solid–fluid and at the liquid–vapor interfaces, the deformations of the latter, and the range of the force fields. Indeed, we have found that incorporating such details can be important for obtaining a quantitative prediction of the pinning characteristics of nanodefects. Furthermore, to fully exploit the potential of our microscopic approach, we are searching for the transition path in the infinite dimensional configuration space spanned by all possible density distributions. This way, we also avoid the problem of “hidden” variables, which may arise if one uses only a reduced set of variables (actually two in the treatment of JdG); the actual path may be even completely concealed within a reduced description (see, e.g., refs. 45 and 48). This latter problem affects the estimates of, e.g., the free-energy barriers involved and, with exponential sensitivity, those of the kinetics.

Advancing and Receding Contact Angles

In the discussion above, we have referred to wetting hysteresis as the qualitative differences in the advancing and receding processes, occurring in nanochannels and for a single defect—thereby avoiding the notion of contact angle hysteresis. The latter requires scale separation between the characteristic size of the defects and that of the macroscopic liquid body (e.g., the drop), which for nanodefects is typically the case, and a definition of the macroscopic apparent contact angle ${\theta }^{\text{macro}}$. In the following, we provide such a definition and we express ${\theta }^{\text{macro}}$ in terms of the microscopic quantities given in Table 1, which, rigorously speaking, were computed for nanodefects in nanochannels. We first derive these relations for a straight row of nanoscale defects parallel to the liquid front. Subsequently, we generalize these results to a random, dilute distribution of defects, which is closer to actual surfaces studied experimentally.

Before discussing the two special arrangements of nanodefects, we introduce a general definition of the macroscopic apparent contact angle. We first observe that the deformations of the liquid–vapor interface induced by the wall and by the defects vanish at sufficiently large distances from the walls and from the defects and that the interface assumes one of the simple macroscopic shapes compatible with the macroscopic Laplace equation (spherical cap, cylindrical cap, plane, etc.). This macroscopic interface can be extrapolated up to the wall surface and the intersection of these two surfaces defines the apparent contact angle ${\theta }^{\text{macro}}$ and the macroscopic geometrical position of the three-phase-contact or triple line. In the cases discussed here, the macroscopic triple line is a straight line in the x–y plane parallel to the y axis, characterized by the coordinate $x=x_{\text{tl}}$.

Contact Angle Hysteresis Induced by a Row of Defects.

To characterize static contact angle hysteresis, we seek for mechanically (meta)stable configurations of the contact line. For the system studied in the previous sections—a liquid wedge migrating across a periodic arrangement (row) of defects aligned along the y direction—metastable states correspond to the minima of Eq. 3. Differentiating that equation with respect to $x_{\text{tl}}$ and recalling the relation $\text{d}N/\text{d}{x}_{\text{tl}}=L_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)$ leads to the following:

$${-\frac{\partial {\mathrm{\Omega }}_0}{\partial x_{\text{tl}}}|}_{x_{\text{tl}}=x_{\text{tl},\mathrm{st}}}+L_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)\mathrm{\Delta }\mu =0\hspace{0.17em},$$ [4]

where we introduced the more compact notation ${\mathrm{\Omega }}_0\equiv \mathrm{\Omega }\left(\mathrm{\Delta }\mu =0,V,T;x_{\text{tl}}\right)$. The first term is the microscopic force $-\partial {\mathrm{\Omega }}_0/\partial x_{\text{tl}}$ exerted on the contact line by the single defect present in the computational box. The second term is the total macroscopic force, which has to be balanced by the microscopic defect force. Using the relation $\mathrm{\Delta }\mu \left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)=\mathrm{\Delta }p$, the macroscopic force can be also expressed in terms of the pressure difference across the liquid–vapor interface as $L_{\text{y}}{L}_{\text{z}}\mathrm{\Delta }p$. As indicated by the acronym “st,” Eq. 4 has stable solutions $x_{\text{tl}}=x_{\text{tl},\text{st}}\left(\mathrm{\Delta }\mu \right)$ only within a certain range of macroscopic forces along the advancing or receding processes, which correspond to the black or red solid lines in Fig. 5, respectively. The quantity $\partial {\mathrm{\Omega }}_0/\partial x_{\text{tl}}$ is defect specific and independent of $L_{\text{y}}$ and $L_{\text{z}}$, because it is determined by the local wetting properties of the defect and by the local deformations of the liquid–vapor interface. According to Eq. 4, to render also $\mathrm{\Delta }\mu$ and $\mathrm{\Delta }p$ defect specific, one has to multiply them by $L_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)$. For instance, by multiplying $\mathrm{\Delta }{\mu }_{\text{sp}}$ in Table 1 by our system specific quantity $L_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)\approx 179{\sigma }^{-1}$, one obtains an intrinsic quantity that can be related to the maximum force a defect can exert on the triple line (19, 47).

To connect with macroscopic contact angles and contact angle hysteresis, we proceed as follows. First, we observe that, in Eq. 4, the total macroscopic driving force $L_{\text{y}}{L}_{\text{z}}\left({\rho }_{\text{l}}-{\rho }_{\text{v}}\right)\mathrm{\Delta }\mu =L_{\text{y}}{L}_{\text{z}}\mathrm{\Delta }p$ must act also on the contact line. On the other hand, within a macroscopic description, the force on the triple line is determined by the action of the interfacial tensions. Its relevant lateral component is Young’s unbalanced force $-L_{\text{y}}{\gamma }_{\text{lv}}\left(\cos {\theta }^{\text{macro}}-\cos {\theta }_{\text{Y}}\right)$, with the macroscopic apparent contact angle ${\theta }^{\text{macro}}$. Replacing in Eq. 4 the total macroscopic driving force by the unbalanced Young’s force, we obtain the following:

$${\gamma }_{\text{lv}}\left(\cos {\theta }^{\text{macro}}-\cos {\theta }_{\text{Y}}\right)=-\frac{1}{L_{\text{y}}}{\frac{\partial {\mathrm{\Omega }}_0}{\partial x_{\text{tl}}}|}_{x_{\text{tl}}=x_{\text{tl},\text{st}}}.$$ [5]

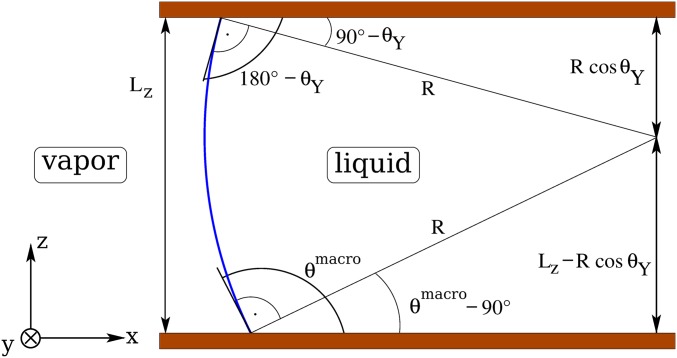
Eq. 5 links the macroscopic contact angle at a given driving force $\mathrm{\Delta }\mu$ to the microscopic defect force acting effectively on the triple line in correspondence to its stable configurations identified by $x_{\text{tl},\text{st}}\left(\mathrm{\Delta }\mu \right)$. Supporting Information provides an alternative route to Eq. 5 based on Laplace’s law (Fig. S7).

Fig. S7.

Macroscopic description of a driven liquid front in a slit pore of width $L_z$. The cut is perpendicular to the y direction defined by the lined-up defects. The liquid–vapor interface is indicated by the blue portion of a circle with radius R. The prescribed contact angle at the upper wall is $180°-{\theta }_{\mathrm{Y}}$. The macroscopic contact angle ${\theta }^{\text{macro}}$ follows from geometry.

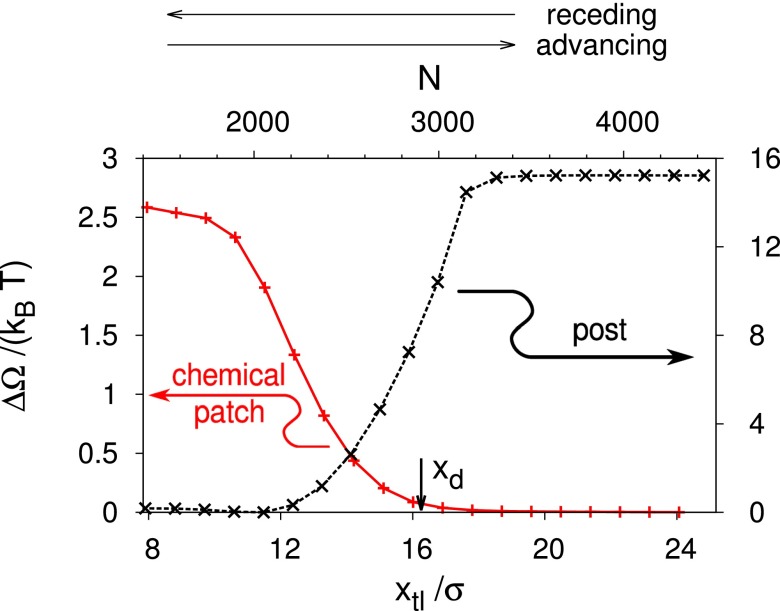
A quantity of particular interest is the so-called advancing contact angle ${\theta }_{\text{a}}$, which is the maximum apparent contact angle compatible with a static configuration during the advancing process. It is obtained by evaluating Eq. 5 at the maximum force the defects can exert upon opposing the advancing process, yielding ${\theta }_{\text{advancing}}^{\text{macro}}\equiv {\theta }_{\text{a}}$. For an advancing barrier, the maximum force is reached at $x_{\text{tl},\text{st}}\left(\mathrm{\Delta }{\mu }_{\text{sp}}\right)$. Similarly, the receding contact angle ${\theta }_{\text{r}}$ corresponds to the maximum force (with opposite direction) the defects can exert upon opposing the receding process. To obtain ${\theta }_{\text{r}}$ for a receding barrier, we likewise evaluate Eq. 5 at $x_{\text{tl},\text{st}}\left(\mathrm{\Delta }{\mu }_{\text{sp}}\right)$, but now $\mathrm{\Delta }{\mu }_{\text{sp}}$ has a negative sign. For a pure advance barrier, the maximum force opposing the receding process is zero. Therefore, the right-hand side of Eq. 5 is zero so that $\cos {\theta }_{\text{r}}\equiv \cos {\theta }_{\text{Y}}$ for this type of barrier. The above definitions of ${\theta }_{\text{a}}$ and ${\theta }_{\text{r}}$ coincide with the usual experimental notion of static contact angle hysteresis, which is measured just before the macroscopically defined contact line starts moving. For the posts discussed in the previous section (advance barrier; Fig. 5A), the definitions of ${\theta }_{\text{a}}$ and ${\theta }_{\text{r}}$, together with Eq. 5, yield a very strong contact angle hysteresis: $\cos {\theta }_{\text{r}}-\cos {\theta }_{\text{a}}=\cos {\theta }_{\text{Y}}-\cos {\theta }_{\text{a}}=0.68$, corresponding to ${\theta }_{\text{a}}=121°$ and ${\theta }_{\text{r}}=81°$. These two angles refer to a defect line density of $L_{\text{y}}^{-1}=0.057\hspace{0.17em}{\sigma }^{-1}$ corresponding to $L_{\text{y}}=17.5\hspace{0.17em}\sigma$ and to the liquid–vapor interface advancing simultaneously across all lined-up defects.

Contact Angle Hysteresis Induced by a Random Distribution of Defects.

We now consider a random, dilute distribution of identical nanodefects. As discussed in the previous subsection, even in this case, away from the walls the liquid–vapor interface attains its macroscopic shape characterized by the apparent contact angle ${\theta }^{\text{macro}}$ and the position $x_{\text{tl}}$ of the macroscopic triple line. Therefore, it is possible to establish a force balance between the unbalanced Young’s force on the macroscopic triple line and the forces provided by the distribution of defects, analogous to Eq. 5. To provide an explicit equation, we first assume that the combined effect of the defects on a liquid front follows from linear superposition of the individual effects (24). This additivity hypothesis, which is expected to be valid for dilute defect distributions, neglects the fact that also the presence of a neighboring defect can alter the local shape of the triple line, thus affecting the metastable configurations. Therefore, within this assumption, the free-energy profiles and the metastable configurations are the same for the quite distinct two cases of randomly distributed and aligned defects. Actually, this is the content of a second hypothesis according to which the force on the macroscopic straight triple line exerted by a single defect at a distance $\mathrm{\Delta }{x}_{\text{d}}\equiv x_{\text{d}}-x_{\text{tl}}$ from the triple line is the same as the one (for the same $\mathrm{\Delta }{x}_{\text{d}}$) computed per defect for a periodic row of defects sufficiently apart from each other. However, in contrast to the above case of aligned defects, the force each defect exerts on the triple line depends on its distance $\mathrm{\Delta }{x}_{\text{d}}$ from the macroscopic triple line, which is random. We therefore have to average the right-hand side of Eq. 5 over the contribution of all defects adding to the force on a (straight) segment of the macroscopic triple line of length $L_{\text{y}}$.

However, before performing this average in mathematical terms, some further remarks are needed, and we have to introduce a third hypothesis, which actually is related to the other two. We first remark that, in the absence of an external driving force, the (mesoscopic) triple line avoids crossing those regions where the forces are not negligible; these regions do not extend much beyond the defects (i.e., less than an order of magnitude of the defect size). Without this wiggling, the two hypotheses above would lead to a nonzero mean defect force, which is not balanced by an external driving force. These wiggles typically have a long wavelength, given by the average distance between the defects along the triple line, and an amplitude that is small and of the order of the linear extension of the defects, i.e., of nanometric size for the nanodefects discussed here. To calculate the mean force on the macroscopic triple line, we do not explicitly consider the aforementioned wiggles of the (mesoscopic) triple line. Instead, we average over the forces computed for various distances from the straight triple line, but we exclude from the average those relative distances $\mathrm{\Delta }{x}_{\text{d}}$ that would lead to locally unstable configurations. This is the content of our third hypothesis, which by now is formulated, taking into account an external driving force acting on the liquid–vapor interface.

We are interested in the maximum absolute value of the total defect force on a triple line segment, which can be provided by a random distribution of defects in an advance or a retreat experiment. We first focus on the advancing process across postlike defects (exhibiting a barrier in advancing direction). For a row of defects, our calculations have shown that the defect force steadily increases if the liquid–vapor interface is pushed against it until it reaches a maximum at a driving force $\mathrm{\Delta }\mu =\mathrm{\Delta }{\mu }_{\text{sp}}$. In the case shown in Fig. 5B, for $x_{\text{tl}}>x_{\text{tl},\text{st}}\left(\mathrm{\Delta }{\mu }_{\text{sp}}\right)$ the position of the triple line becomes unstable and snaps over those parts of each defect in the straight row that are not covered by liquid. We now assume that locally a similar behavior occurs for randomly distributed defects. Once $\mathrm{\Delta }{x}_{\text{d}}$ is larger than the critical distance corresponding to the maximum force that can be mustered by an individual defect, the triple line becomes locally unstable and slides over the still dry part of that specific defect. Accordingly, the defect forces corresponding to these unstable positions do not contribute to the overall force average. The average is performed only over forces corresponding to (meta)stable positions, which are characterized by $\mathrm{\Delta }{x}_{\text{d}}=x_{\text{d}}-x_{\text{tl},\text{st}}$. A relation to a driving force $\mathrm{\Delta }\mu$ is not given, because only the total driving force on the liquid front can be controlled, but not the force of a specific defect acting on a segment of the macroscopic triple line. For an advancing process over defects exhibiting a barrier in advance direction, $x_{\text{tl},\text{st}}$ ranges from a value $x_{\text{tl}}$ on the lower plateau in Fig. 3 to $x_{\text{tl},\text{st}}=x_{\text{tl},\text{sp}}$, characterizing the distance corresponding to the maximum defect force. $x_{\text{tl},\text{sp}}$ is identified with $x_{\text{tl},\text{st}}\left(\mathrm{\Delta }{\mu }_{\text{sp}}\right)$ as determined from the computations for a row of defects. For a receding process over postlike defects, the defect forces are zero for all (meta)stable triple line positions. For analyzing the case of defects providing a receding barrier, one has to interchange the role of advancing and receding processes in the discussion above.

To provide quantitative results, we first introduce a length $l_{\text{d}}$ characterizing the range of distances from the triple line within which the defect forces are nonnegligible. The total number M of defects interacting with the segment $L_{\text{y}}$ of the triple line is $M=n{L}_{\text{y}}{l}_{\text{d}}$ with n the areal number density of the defects. The averaging is carried out by integrating over all possible defect distances $\mathrm{\Delta }{x}_{\text{d}}\equiv x_{\text{d}}-x_{\text{tl}}$ with equal weight $\text{d}\mathrm{\Delta }{x}_{\text{d}}/l_{\text{d}}$ (so that ${\displaystyle {\int }_{-l_{\text{d}}/2}^{l_{\text{d}}/2}{l}_{\text{d}}^{-1}\text{d}\mathrm{\Delta }{x}_{\text{d}}}=1$) or, equivalently, by integrating over the relative triple-line position $\mathrm{\Delta }{x}_{\text{tl}}\equiv x_{\text{tl}}-x_{\text{d}}=-\mathrm{\Delta }{x}_{\text{d}}$ :

$$\begin{array}{c}{\gamma }_{\text{lv}}\left(\cos {\theta }^{\text{macro}}-\cos {\theta }_{\text{Y}}\right)=-\frac{M}{l_{\text{d}}{L}_{\text{y}}}{\displaystyle \underset{-{\mathrm{l}}_{\text{d}}/2}{\overset{{\mathrm{l}}_{\text{d}}/2}{\int }}\hspace{0.17em}{\frac{\partial {\mathrm{\Omega }}_0}{\partial x_{\text{tl}}}|}_{x_{\text{tl},\text{st}}}\text{d}\mathrm{\Delta }{x}_{\text{tl}}}\\ =-n\left({\mathrm{\Omega }}_0\left(x_{\text{tl},\text{max}}\right)-{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{min}}\right)\right).\end{array}$$ [6]

Without randomness, Eq. 6 reduces to Eq. 5 with $M=1$. In Eq. 6, the notation should be interpreted such that integrands are equal to zero for positions $\mathrm{\Delta }{x}_{\text{tl}}$ that do not belong to metastable positions $x_{\text{tl},\text{st}}$ of the triple line along the advancing or the receding processes. This also applies to the last equation, in which we evaluate ${\mathrm{\Omega }}_0$ at the maximum and the minimum values of $x_{\text{tl},\text{st}}$ ($x_{\text{tl},\text{max}}$ and $x_{\text{tl},\text{min}}$, respectively). For instance, the advancing process over postlike defects is characterized by $x_{\text{tl},\text{max}}^{\text{a}}=x_{\text{tl},\text{sp}}$, whereas $x_{\text{tl},\text{min}}^{\text{a}}$ corresponds to some position $x_{\text{tl}}$ along the lower plateau in the free-energy profile, e.g., $x_{\text{tl},\text{v}}$ (Fig. 5A). Evaluating Eq. 6 over the whole metastable interval $x_{\text{tl},\text{min}}^{\text{a}}<x_{\text{tl},\text{st}}<x_{\text{tl},\text{max}}^{\text{a}}$ of the advancing process yields the advancing contact angle ${\theta }_{\text{advancing}}^{\text{macro}}$. For the receding process across the same kind of defects, there are no metastable configurations of the system ($x_{\text{tl},\text{st}}\in \mathrm{Ø}$), and therefore the integral in Eq. 6 vanishes, yielding $\cos {\theta }_{\text{receding}}^{\text{macro}}-\cos {\theta }_{\text{Y}}=0$.

As shown in Fig. 5A, for postlike defects $x_{\text{tl},\text{max}}^{\text{a}}\left(\mathrm{\Delta }{\mu }_{\text{sp}}\right)\equiv x_{\text{tl},\text{sp}}$ and $x_{\text{tl},\text{min}}^{\text{a}}\left(0\right)\equiv x_{\text{tl},\text{v}}$, yielding ${\gamma }_{\text{lv}}\left(\cos {\theta }_{\text{a}}-\cos {\theta }_{\text{Y}}\right)=-n\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)$, where the maximum contact angle compatible with Eq. 6 coincides with the notion of the advancing contact angle introduced before, ${\theta }_{\text{advancing}}^{\text{macro}}\equiv {\theta }_{\text{a}}$, and $\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)={\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)-{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{v}}\right)$; for the receding process, instead, ${\theta }_{\text{receding}}^{\text{macro}}\equiv {\theta }_{\text{r}}$ and $\cos {\theta }_{\text{r}}-\cos {\theta }_{\text{Y}}=0$. Combining the previous two expressions, we obtain an estimate for the contact angle hysteresis:

$$\cos {\theta }_{\text{r}}-\cos {\theta }_{\text{a}}=n\frac{\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)}{{\gamma }_{\text{lv}}}.$$ [7]

Eq. 7 is valid also for retreat barriers (Fig. 5B) for which, however, $\cos {\theta }_{\text{a}}-\cos {\theta }_{\text{Y}}=0$ and ${\gamma }_{\text{lv}}\left(\cos {\theta }_{\text{r}}-\cos {\theta }_{\text{Y}}\right)=n\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)$.

The values of $\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)$ in Table 1 together with Eq. 7 allow us to determine which density of nanodefects of the post kind, with the characteristics chosen in the present investigations, is needed to induce macroscopically relevant pinning. As a typical measurable difference in cosines, we adopt $\cos {\theta }_{\text{r}}-\cos {\theta }_{\text{a}}=0.25$, use the surface tension of our simple liquid ${\gamma }_{\text{lv}}=0.406\hspace{0.17em}\epsilon {\sigma }^{-2}$, and assume $\sigma =0.3$ nm, which yields for the post defect a projected area $A_{\text{d}}=0.56$ nm². Because $\mathrm{\Delta }{\mathrm{\Omega }}_0\left(x_{\text{tl},\text{sp}}\right)\approx 10$ ε for a single post defect, from Eq. 7 we obtain $n=0.11$ ${\text{nm}}^{-2}$, corresponding to a surface coverage $n\hspace{0.17em}{A}_{\text{d}}$ of ∼6%. This simple calculation for a post of size 0.75 × 0.75 × 0.75 nm and Young contact angle ${\theta }_{\text{Y}}\approx 125°$ suggests that even dilute chemical and topographical defects of subnanometer scale can be responsible for the pinning phenomena associated with nanobubble stability (12, 13). For comparison, the contact angle hysteresis of the substrate used in recent experiments on nanobubbles (16) was $\cos {\theta }_{\text{r}}-\cos {\theta }_{\text{a}}=0.25$ for a slightly larger roughness.

Conclusions

We have studied a liquid wedge advancing or receding across a single chemical or topographical heterogeneity of nanometric size. We have devised a method that combines string calculations with microscopic classical DFT to determine free-energy profiles for overcoming such obstacles. This approach has allowed us to take into account specific microscopic effects, which have turned out to be significant on the nanoscale. At liquid–vapor coexistence, the free-energy profiles exhibit as function of the position of the triple line a sigmoidal shape with two plateaus that correspond to the heterogeneity being exposed solely to vapor or completely covered with liquid, respectively. For the topographical and chemical protrusion studied, the macroscopic estimate for the difference of these plateau values is one-half of the actual microscopic result. Based on the computed free-energy profiles we have discussed thermally activated depinning of the three-phase contact line in the absence of driving forces. We have shown that wetting hysteresis originates from the occurrence of a metastable pinned state within a certain range of chemical potentials. Forcing the system toward and off two-phase coexistence leads to qualitatively distinct advance and retreat branches. The defects considered here are weak in terms of the classification of JdG; nonetheless, some of them give rise to wetting hysteresis. Our estimates of the macroscopic effects of a distribution of nanoscale defects indicate that a $6\text{\%}$ surface coverage of lyophobic topographical defects with a lateral extension smaller than 1 nm is sufficient to induce a measurably large contact angle hysteresis, i.e., $\cos {\theta }_{\text{r}}-\cos {\theta }_{\text{a}}=0.25$. These figures match well with those obtained from recent nanobubbles experiments. Our results suggest that this provides a mechanism for contact line pinning that is needed to explain the unexpected long lifetime of the nanobubbles. Finally, the techniques introduced here and the proposed framework for discussing wetting hysteresis have laid a common probabilistic ground for understanding deterministic and thermally activated pinning of three-phase contact lines. Accordingly, this analysis is expected to clear the way for future detailed microscopic studies of activated processes in fluids at small scales.

Density Functional Theory

Fluid–Fluid and Fluid–Wall Interactions.

In the present study, we use the fundamental measure theory (FMT) due to Rosenfeld to determine the molecular details of the fluid. This classical density functional theory (DFT) provides a nonlocal functional $F_{\mathrm{FMT}}\left[\rho \right]$, which accounts for the repulsive part of the interaction between the fluid particles, taken to be a hard-sphere pair potential: ${\mathrm{\Phi }}_{\mathrm{HS}}=\infty$ if the distance between the centers of two fluid particles is smaller than the particle diameter σ, and zero otherwise. The attractive part ${\mathrm{\Phi }}_{\mathrm{att}}$ of the interaction between the fluid particles is included perturbatively by applying the spirit of the Weeks–Chandler–Andersen theory (49) to the Lennard–Jones potential:

$${\mathrm{\Phi }}_{\text{att}}\left(r\right)=-\epsilon \mathrm{\Theta }\left(2^{1/6}\sigma -r\right)+4\epsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]\mathrm{\Theta }\left(r-2^{1/6}\sigma \right),$$ [S1]

where r is the distance between the centers of a pair of particles, ε is the interaction strength, σ corresponds to the particle diameter, and $\mathrm{\Theta }$ is the Heaviside function. In the following, ε sets the energy scale. In the calculations, a cutoff of $2.5\hspace{0.17em}\sigma$ is used for ${\mathrm{\Phi }}_{\mathrm{att}}\left(\mathit{r}\right)$. Concerning the detailed form of $F_{\mathrm{FMT}}\left[\rho \right]$ and the calculation details, see refs. 33 and 35.

The external substrate potential $V\left(\mathit{r}\right)$ in Eq. 1 of the main text is expressed as the sum of a repulsive contribution $V_{\text{rep}}\left(\mathit{r}\right)$ and an attractive one $V_{\text{att}}\left(\mathit{r}\right)$: $V\left(\mathit{r}\right)=V_{\text{rep}}\left(\mathit{r}\right)+V_{\text{att}}\left(\mathit{r}\right)$. We account for $V_{\text{rep}}\left(\mathit{r}\right)$ in terms of a hard-sphere repulsion, chosen such that the distance of closest approach of the centers of a fluid particle and a wall particle with diameter ${\sigma }_{\mathrm{w}}$ is ${\sigma }_{\mathrm{wall}}=\left(\sigma +{\sigma }_{\mathrm{w}}\right)/2$. $V_{\text{rep}}\left(\mathit{r}\right)=\infty$ if the distance between the center of a fluid particle and a wall particle is smaller than ${\sigma }_{\mathrm{wall}}$ (the region beneath the dashed lines in Fig. S1), $V_{\text{rep}}\left(\mathit{r}\right)=0$ otherwise. For the bottom part of the wall, we have used the limit ${\sigma }_{\mathrm{w}}/\sigma \to 0$, i.e., ${\sigma }_{\mathrm{wall}}=\sigma /2$. Around the post, instead, ${\sigma }_{\mathrm{wall}}=0.6\hspace{0.17em}\sigma$ has been chosen. In the presence of a nonzero and fixed $V_{\text{att}}\left(\mathit{r}\right)$, a larger value of ${\sigma }_{\mathrm{wall}}$ around the post corresponds to a more lyophobic behavior; this is due to the fact that repulsive interactions overrule attractive ones in a more extended region close to the defect (Fig. S1). $V_{\text{att}}\left(\mathit{r}\right)$ is taken as the linear superposition of the attractive part ${\mathrm{\Phi }}_{\mathrm{w}}$ of the Lennard–Jones potential between the fluid particles and the particles forming the wall with a number density ${\rho }_{\mathrm{w}}$:

$$V_{\text{att}}\left(\mathit{r}\right)={\displaystyle \underset{D_{\mathrm{w}}}{\int }{\text{d}}^{3}r\prime \hspace{0.17em}{\rho }_{\mathrm{w}}(\mathit{r}\prime )\hspace{0.17em}{\mathrm{\Phi }}_{\mathrm{w}}\left(\mathit{r}-\mathit{r}\prime \right)}.$$ [S2]

Here the fluid–wall pair potential ${\mathrm{\Phi }}_{\mathrm{w}}\left(\mathit{r}-\mathit{r}\prime \right)$, which depends on the distance between the positions $\mathit{r}$ and $\mathit{r}\prime$ of the fluid and wall particles, respectively, is integrated over the domain $D_{\mathrm{w}}$ occupied by the wall; as stated above, ${\mathrm{\Phi }}_{\mathrm{w}}\left(\mathit{r}-\mathit{r}\prime \right)=-4\hspace{0.17em}{\epsilon }_{\mathrm{w}}(\mathit{r}\prime ){\left({\sigma }_{\mathrm{w}}/\left|\mathit{r}-\mathit{r}\prime \right|\right)}^6$. The strength of the wall potential is determined by the parameter combination $u_{\mathrm{w}}(\mathit{r}\prime )\equiv \left(2\pi /3\right)\hspace{0.17em}{n}_{\mathrm{w}}(\mathit{r}\prime )\hspace{0.17em}{\epsilon }_{\mathrm{w}}(\mathit{r}\prime )$, where $n_{\mathrm{w}}={\rho }_{\mathrm{w}}{\sigma }_{\mathrm{w}}^3$ is the number of wall particles in the volume ${\sigma }_{\mathrm{w}}^3$. The specific parameter $u_{\mathrm{w}}$, subsequently called wall energy, has been introduced because it characterizes the attractive potential $V_{\text{att}}\left(d\right)=-u_{\mathrm{w}}/d^3$ acting on a fluid particle with its center at a distance d from the planar surface of a half-space of continuously and homogeneously distributed wall particles of a certain kind. More details can be found in ref. 35. To model a wetting contrast between the wall and a chemical blemish, the wall material underneath the corresponding surface area is replaced, up to a certain depth, by material characterized by a wall energy $u_{\mathrm{w}}\left(\mathit{r}\right)$, which is distinct from the wall energy $u_{\mathrm{w}}$ characterizing the bulk of the wall. Unlike in macroscopic models, such as the “mesa” defects considered by Joanny and de Gennes (24) for which the wetting properties of the substrate vary step-like, here the wall potential $V\left(\mathit{r}\right)$ varies smoothly even where $u_{\mathrm{w}}$ varies discontinuously in the lateral spatial directions.

The chemical defects are obtained by starting from a homogeneous wall occupying the lower half-space with $u_{\mathrm{w}}=3\epsilon$ (see above). Then a parallelepiped of size $\mathrm{\Delta }x\times \mathrm{\Delta }y\times \mathrm{\Delta }z=2.5\sigma \times 2.5\sigma \times 3\sigma$ is carved out at the surface of the semiinfinite wall and replaced by one with a different value of $u_{\mathrm{w}}$. The resulting heterogeneous wall is still planar (${\sigma }_{\mathrm{wall}}$ is constant and equal to $\sigma /2$ over the entire wall) but with an inclusion of a different material and of depth $3\sigma$. We classify these chemical defects based on the contact angles measured for homogeneous semiinfinite walls having the same $u_{\mathrm{w}}$ as the inclusion: $u_{\mathrm{w}}=2\epsilon$ corresponds to a lyophobic substrate with ${\theta }_{\mathrm{Y}}=124.85°$, $u_{\mathrm{w}}=3.5\epsilon$ corresponds to a substrate that is partially wet with ${\theta }_{\mathrm{Y}}=51.13°$, and $u_{\mathrm{w}}=4.0\epsilon$ corresponds to a substrate that is completely wet.

The system used in the present analysis is shown in Fig. 1B of the main text. The density is initialized with the bulk liquid and vapor densities at two-phase coexistence at the right and the left side of the computational box, respectively. At the right and left ends of the computational box we have chosen reflecting boundary conditions (the y–z planes at both ends are mirror symmetry planes); this is virtually equivalent to having capillary liquid boundary conditions on the right and capillary vapor boundary conditions on the left, as long as the liquid–vapor interface and the surface defects introduced in the next section are sufficiently far away from the box boundaries. The remaining two boundaries at the front and at the rear exhibit periodic boundary conditions. The domain is discretized with 20 points per particle diameter σ, such that the actual computational domain consists of 650 × 350 × 300 = 68,250,000 points.

Wall Potential for the Post Defect.

In Fig. S2, we show the wall potential $V\left(\mathit{r}\right)$ for the post defect introduced in the main text. Within the yellow domain, one has repulsive interactions between the fluid and the wall consisting of a hard core with $V\left(\mathit{r}\right)=\infty$. In practice, the potential has been set to the large but finite value $V\left(\mathit{r}\right)=100\epsilon$. The hard core of the lower wall is located at $z/\sigma =0$. The top corners of the post are not perfectly smooth because for numerical reasons the potential is defined on a discrete lattice and due to the way we test the overlap between the hard wall and the hard core of the fluid particles. Fig. S2 demonstrates that, although the bottom wall and the post share the same attractive interaction strength $u_{\text{w}}$, the potential next to the spatial regions dominated by strongly repulsive interactions (defining depletion zones within which the liquid densities are zero) is very different at the bottom wall (where it reaches $-4\epsilon$) or near the post (where it reaches $-2\epsilon$). This difference is partially due to the attractive part of the interaction being reduced by the enlarged depletion zone (${\sigma }_{\mathrm{wall}}=0.6\sigma$) introduced in our model of the post compared with the planar bottom part of the wall (${\sigma }_{\mathrm{wall}}=0.5\sigma$). A second reason is the fact that the wall particles at the top of the post have fewer close neighbors than the particles at the bottom surface of the wall. The combination of these two effects leads to an effectively lyophobic behavior of the post (see $\delta {\mathrm{\Omega }}_{\mathrm{post}}>0$ in Table 1 and Fig. 2B in the main text).

Combining Microscopic DFT with the String Method

Our calculations combine classical DFT with the string method as follows.

The DFT code we are using implements the FMT functional for the repulsive part of the pair interaction between the fluid particles. The same code also computes, via a separate algorithm, the wall potentials (as the one shown, e.g., in Fig. S2). The free minimization (without string) of the grand potential defined in Eq. 1 of the main text is performed via the Piccard iteration technique.

The string $\rho \left(\mathit{r},\tau \right)$ is defined as a sequence of number density configurations spanning the entire activated process—in the present case, the advance or retreat of a liquid wedge across a defect—from an initial state A to a final one B. The variable τ is the arc “length” computed along the string:

$$\tau ={\displaystyle \underset{s_A}{\overset{s_L}{\int }}\text{d}s\hspace{0.17em}\sqrt{{\displaystyle \underset{D_c}{\int }{\text{d}}^{3}r\hspace{0.17em}{\left(\frac{\partial \rho \left(\mathit{r},s\right)}{\partial s}\right)}^2}}},$$ [S3]

where A is the initial state, $D_c$ is the computational domain, L is a generic point of the string with $s_A<s_L<s_B$, and s is an arbitrary parametrization of the string.

We construct the initial string by a rough free minimization ($\approx 300$ iteration steps) of 20–22 suitably selected independent fluid configurations—the so-called images. These initial images are computed starting from distinct initial conditions that consist of a vertical liquid–vapor interface separating the liquid domain to the right and the vapor one to the left. Each configuration corresponds to a different filling level of the channel, spanning it from the far left of the defect to its far right. After the preequilibration, the initial string consists of liquid wedges like the one in Fig. 1B of the main text translated along the horizontal x axis.

The most probable path defined in Eq. 2 of the main text can be computed via the following pseudodynamics for the images:

$$\frac{\partial \rho \left(\mathit{r},\tau ,t\right)}{\partial t}=-{\left(\frac{\delta \mathrm{\Omega }\left[\rho \right]}{\delta \rho \left(\mathit{r},\tau ,t\right)}\right)}_{\perp },$$ [S4]

which at stationarity reduces to Eq. 2 of the main text.

One way to compute the functional derivative perpendicular to the string (denoted as $\perp$ in Eq. S4) is to subtract from $\delta \mathrm{\Omega }\left[\rho \right]/\delta \rho \left(\mathit{r},\tau ,t\right)$ the component tangential to the string:

$$\frac{\partial \rho \left(\mathit{r},\tau ,t\right)}{\partial t}=-\frac{\delta \mathrm{\Omega }\left[\rho \right]}{\delta \rho \left(\mathit{r},\tau ,t\right)}+\lambda \hspace{0.17em}\widehat{T}\left(\mathit{r},\tau ,t\right),$$ [S5]

where, using the ${\mathrm{ℒ}}^2$-norm, the tangent $\widehat{T}\left(\mathit{r},\tau ,t\right)$ to the string is defined as $\widehat{T}\left(\mathit{r},\tau ,t\right)\equiv \left(\partial \rho \left(\mathit{r},\tau ,t\right)/\partial \tau \right)/\Vert \partial \rho \left(\mathit{r},\tau ,t\right)/\partial \tau \Vert$ and $\lambda \equiv \langle \delta \mathrm{\Omega }\left[\rho \right]/\delta \rho \left(\mathit{r},\tau ,t\right),\widehat{T}\left(\mathit{r},\tau ,t\right)\rangle$, with $\langle ,\rangle$ indicating the inner product defined as $\langle f,g\rangle \equiv {\displaystyle {\int }_{D_c}{\text{d}}^{3}r\hspace{0.17em}f\left(\mathit{r}\right)g\left(\mathit{r}\right)}$ within the computational domain $D_c$ (see, e.g., Fig. 2 of the main text). In the dynamics for the string described by Eq. S5, the tangential component of $\delta \mathrm{\Omega }\left[\rho \right]/\delta \rho \left(\mathit{r},\tau ,t\right)$ does not change the string itself but it affects its parametrization τ, displacing the images along it [which is a general result for curve dynamics (38)]. In other words, the term $\lambda \widehat{T}\left(\mathit{r},\tau ,t\right)$ prevents the images along the string from collapsing into the closest minima.

To ensure that the images maintain a particular parametrization during the evolution, in Eq. S5 we consider explicitly an additional term. Here, we use the equal arc length parametrization, which guarantees that two contiguous images remain at the same normalized distance along the string during the evolution. For the continuous string, this constraint reads $\Vert \partial \rho \left(\mathit{r},\tau ,t\right)/\partial \tau \Vert =\text{const}$, which can be enforced by Lagrange multipliers. In practice, the procedure consists in adding the term $\overline{\lambda }\hspace{0.17em}\left(\partial \rho \left(\mathit{r},\tau ,t\right)/\partial \tau \right)/\Vert \partial \rho \left(\mathit{r},\tau ,t\right)/\partial \tau \Vert \equiv \overline{\lambda }\hspace{0.17em}\widehat{T}\left(\mathit{r},\tau ,t\right)$ to Eq. S5 (38). This additional term does not change the functional form of Eq. S5 provided that $\lambda +\overline{\lambda }$ is substituted for λ. This additional Lagrange multiplier enforces a particular parametrization of the string, and thus Eq. S5 can be solved via the two-step procedure described in the following (38). The string algorithm just described is illustrated in Fig. S3 for the so-called Müller potential, which depends on two dimensionless parameters $x_1$ and $x_2$ (38). For the discretized string actually used in the present calculations, the normalized distance d between two generic images i and $i+1$ is considered, i.e., $d=\sqrt{{\displaystyle \int {\text{d}}^{3}r{\left(\rho \left(\mathit{r},{\tau }_i\right)-\rho \left(\mathit{r},{\tau }_{i+1}\right)\right)}^2}}/{\tau }_{\mathrm{tot}}$, where ${\tau }_{\mathrm{tot}}$ is the total length of the string computed from Eq. S3 taking $s_L\equiv s_B$.

Following again ref. 38, we use a time splitting procedure for the two terms on the right-hand side of Eq. S5. First, the unrestrained dynamics,

$$\frac{\partial \rho \left(\mathit{r},\tau ,t\right)}{\partial t}=-\frac{\delta \mathrm{\Omega }\left[\rho \right]}{\delta \rho \left(\mathit{r},\tau ,t\right)},$$ [S6]

is solved for each image. Second, the equal arc length parametrization is enforced, not by computing explicitly $\lambda +\overline{\lambda }$ and $\widehat{T}\left(\mathit{r},\tau ,t\right)$, but by a simpler interpolation step, in which the images are redistributed along the interpolated string so that $d=1/\left(\mathrm{ℳ}-1\right)$ where d is the normalized distance between any two contiguous images and $\mathrm{ℳ}$ is the total number of images. The significant advantage of this two-step algorithm is that, for the first step (Eq. S6), the standard free-energy minimization procedure of DFT can be used, such as the Piccard iteration implemented in our code. For the second step, with cubic splines we interpolate the values of the number densities $\rho \left(\mathit{r},{\tau }_i,t\right)$ along the string using as independent variable the arc length ${\tau }_i$ of the string up to the ith image; ${\tau }_i$ is computed from Eq. S3 taking $s_L=s_i$ with the image index taking the values $i=0,\dots ,\mathrm{ℳ}-1$. The new, interpolated string is constructed by computing the number densities ${\rho }^{\mathrm{new}}\left(\mathit{r},{\tau }_i^{\mathrm{new}},t\right)$ at the points ${\tau }_i^{\mathrm{new}}$, which are uniformly distributed along the string: ${\tau }_i^{\mathrm{new}}\equiv {\tau }_{\mathrm{tot}}\hspace{0.17em}i/\left(\mathrm{ℳ}-1\right)$, where the total length of the string is ${\tau }_{\mathrm{tot}}\equiv {\tau }_{\mathrm{ℳ}-1}$. In sum, the hybrid string–DFT algorithm consists of $\mathrm{ℳ}$ short, independent free minimizations of the grand potential (one for each image) alternated with an interpolation step.

Evidently, the string method seeks the most probable path in a space with the same dimensionality as the discretized number density, i.e., ∼10⁸. In this scheme, no a priori assumption is made on what are the relevant parameters to describe the activated process (the so-called collective variables in the language of studies of rare events).

Parametrization of the String

Based on the discussion in Combining Microscopic DFT with the String Method, the natural parametrization of the string is the arc length τ defined in Eq. S3. Because, however, the images are equally spaced along the string, τ and the image number are both valid parametrizations of the string.

As shown in Fig. S4, it is also possible to verify a posteriori that the most probable path can be parametrized by the total number $N\equiv {\displaystyle \int {\text{d}}^{3}r\hspace{0.17em}\rho \left(\mathit{r}\right)}$ of particles in the computational box. The dependence of N on the image number is apparently linear. This parameter is easy to compute and has a direct physical meaning, related to the progressive filling of the channel during the advance of the liquid wedge. Furthermore, the parameter N is also useful for directly applying Eq. 3 of the main text as has been done, e.g., in Fig. S6.

The variable N can also be related to the position $x_{\mathrm{tl}}$ of the triple line via $x_{\mathrm{tl}}=N/\left(L_y{L}_z\left({\rho }_l-{\rho }_v\right)\right)$ (see Fig. 1B and the main text). Clearly, $x_{\mathrm{tl}}$ maintains a linear dependence on the image number (Fig. S4). The position of the triple line can be monitored experimentally (see, e.g., ref. 19); accordingly, $x_{\mathrm{tl}}$ is used throughout the main text as well as for the free-energy profiles presented in the following section.

Lyophobic and Partially Wet Patches

In this section and in Fig. S5, we report the free-energy profiles for the defect-free channel and for the kind of defects not discussed explicitly in the main text, i.e., the lyophobic and partially wet patches. Concerning the related transition paths, see Movies S1 and S2.

Fig. S5A shows the free-energy profile related to the filling of the defect-free channel. The profile is not constant, but it exhibits to a large extent a linear dependence on $x_{\mathrm{tl}}$. This tells that, despite the judicious choice of the substrate strengths $u_{\mathrm{w}}$, for the channel under study bulk coexistence $\mathrm{\Delta }\mu =0$ does not exactly correspond to coexistence between capillary liquid and capillary vapor. This discrepancy is due to the imperfect matching of the lower and upper contact angles ${\theta }_{\mathrm{Y}}^{\mathrm{low}}+{\theta }_{\mathrm{Y}}^{\mathrm{up}}=180.18°$ and possibly also due to microscopic effects such as liquid layering. The thermodynamic force resulting from the small slope of the free-energy profile for the defect-free channel is in practice very small. After relaxing to the configuration shown in Fig. 1B of the main text, the system indeed moves toward the global free-energy minimum but extremely slowly: even after iterating several hundreds of times the unrestrained minimization algorithm, the change in the number density is negligible.

The images for small and large $x_{\mathrm{tl}}$ do not lie on a perfect straight line; it can be verified from the corresponding number density configurations that this deviation is due to the interaction of the liquid–vapor interface with the reflecting boundaries. Accordingly, these images have not been used for computing the free-energy barriers, the locations of the minima, etc.

The defect-free free-energy profile ${\mathrm{\Omega }}_{\text{ref}}\left(x_{\mathrm{tl}}\right)$ in Fig. S5A is used as a reference for computing the profiles in cases in which a defect is present; from the free-energy profiles $\mathrm{\Omega }\left(x_{\mathrm{tl}}\right)$ computed by the string method, we subtract ${\mathrm{\Omega }}_{\text{ref}}\left(x_{\mathrm{tl}}\right)$ at the corresponding values of $x_{\mathrm{tl}}$ yielding the excess free-energy profiles $\mathrm{\Delta }\mathrm{\Omega }\left(x_{\mathrm{tl}}\right)\equiv \mathrm{\Omega }\left(x_{\mathrm{tl}}\right)-{\mathrm{\Omega }}_{\text{ref}}\left(x_{\mathrm{tl}}\right)$ reported in Fig. S5 B and C as well as in Fig. 3 of the main text. With this definition, the excess free-energy profiles indeed correspond to those of an unbounded liquid wedge advancing or receding across a defect.

Fig. S5 B and C shows the excess free-energy profiles for a chemical defect of lyophobic character ($u_{\mathrm{w}}/\epsilon =2$) and for one being partially wet ($u_{\mathrm{w}}/\epsilon =3.5$), respectively. A summary of the characteristics of these defects is given in Table 1 in the main text.

Free-Energy Profiles Off Coexistence

Eq. 3 of the main text provides a convenient yet approximate route to compute a free-energy profile off coexistence from that at bulk coexistence. To ensure that this is a reliable approximation within the range of chemical potentials explored here, we have performed direct string calculations off coexistence and have compared the resulting free-energy profile with that computed via Eq. S5. Fig. S6 demonstrates that this approximation is indeed reliable.

Macroscopic Description of the Liquid Front

To illustrate explicitly the construction of defining the macroscopic contact angle, here we provide in addition an alternative route to Eq. 5 of the main text. To this end, we analyze the same setup as used in our microscopic computations with the only difference that we now consider a macroscopically large width $L_z$ of the channel, which de facto cannot be realized within an entirely microscopic calculation. In a sufficiently wide channel, large portions of the liquid–vapor interface are not directly influenced by the walls and by the surface defects; these portions can be described in macroscopic terms. On the other hand, we may use information from our microscopic computations. We know that for driven systems there are (meta)stable configurations of the contact line, and we know within which limited range of $\mathrm{\Delta }\mu$ or $\mathrm{\Delta }p$ they occur. The portions of the liquid–vapor interface away from the walls attain the macroscopic shape that is cylindrical for the chosen channel geometry. The radius of curvature $R={\gamma }_{\mathrm{lv}}/\mathrm{\Delta }p$ (Laplace’s law) follows from the pressure difference $\mathrm{\Delta }p$ compatible with the occurrence of (meta)stable configurations, which is known from the microscopic computations for any value of $L_z$ via the extrapolation scheme discussed in Contact Angle Hysteresis Induced by a Row of Defects. (In narrow channels, as used in our microscopic computations, the liquid–vapor interfaces are intrinsically curved as well, but it is difficult to distinguish wall and defect-induced curvatures from the one induced by a pressure difference, because there is no scale separation.) Furthermore, we have prescribed a contact angle close to $180°-{\theta }_{\mathrm{Y}}$ on the upper wall, which is complementary to Young’s angle ${\theta }_{\mathrm{Y}}$ on the defect-free part of the lower wall; this specific choice was made to ensure that the liquid–vapor interface is planar in the absence of a driving pressure difference and in the absence of defects. With the knowledge of the curvature radius R and the prescribed contact angle on the upper wall, the macroscopic contact angle ${\theta }^{\text{macro}}$ on the lower wall, featuring the pinning defect, follows from purely geometrical considerations.

Fig. S7 illustrates this geometrical construction. The macroscopic cylindrical liquid–vapor interface is seen as the portion of a circle with radius R intersecting the upper wall at the prescribed contact angle $180°-{\theta }_{\mathrm{Y}}$ and the lower wall at the macroscopic contact angle ${\theta }^{\text{macro}}$ given by the following geometrical relation:

$$\text{sin}\left({\theta }^{\text{macro}}-90°\right)=-\cos {\theta }^{\text{macro}}=\frac{L_z-R\cos {\theta }_{\mathrm{Y}}}{R},$$ [S7]

as can be read off from Fig. S7. Eq. S7 can be rewritten as follows:

$$\cos {\theta }^{\text{macro}}-\cos {\theta }_{\mathrm{Y}}=-\frac{L_z}{R}.$$ [S8]

Using Laplace’s law ($\mathrm{\Delta }p={\gamma }_{\mathrm{lv}}/R$), one eventually obtains the following:

$${\gamma }_{\mathrm{lv}}\left(\cos {\theta }^{\text{macro}}-\cos {\theta }_{\mathrm{Y}}\right)=-L_z\mathrm{\Delta }p.$$ [S9]

By expressing $L_z\mathrm{\Delta }p$ in terms of the chemical potential via $\mathrm{\Delta }p=\left({\rho }_l-{\rho }_v\right)\mathrm{\Delta }\mu$ and by using Eq. 4 of the main text, extrapolated to macroscopic values of $L_z$ to relate $\mathrm{\Delta }\mu$ with the computed microscopic defect force $\partial {\mathrm{\Omega }}_0/\partial x_{\mathrm{tl}}$, one recovers Eq. 5 in the main text.