Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Jan 18;6:19407. doi: 10.1038/srep19407

Evidencing the existence of exciting half-metallicity in two-dimensional TiCl3 and VCl3 sheets

Yungang Zhou 1,a, Haifeng Lu 1,b, Xiaotao Zu 1,2, Fei Gao 3,c
PMCID: PMC4726018  PMID: 26776358

Abstract

Half-metallicity combined with wide half-metallic gap, unique ferromagnetic character and high Curie temperature has become a key driving force to develop next-generation spintronic devices. In previous studies, such half-metallicity always occurred under certain manipulation. Here, we, via examining a series of two-dimensional transition-metal trichlorides, evidenced that TiCl3 and VCl3 sheets could display exciting half-metallicity without involving any external modification. Calculated half-metallic band-gaps for TiCl3 and VCl3 sheets are about 0.60 and 1.10 eV, respectively. Magnetic coupled calculation shows that both sheets favor the ferromagnetic order with a substantial collective character. Estimated Curie temperatures can be up to 376 and 425 K for TiCl3 and VCl3 sheets, respectively. All of these results successfully disclose two new promising two-dimensional half-metallic materials toward the application of next-generation paper-like spintronic devices.

Two-dimensional (2D) nanomaterial, proposed as the versatile material, recently attracts significant interest in the scientific community1,2,3,4,5,6. Ultrathin, transparent and flexible properties render 2D nanomaterials promising and noteworthy candidates for the application of next-generation paper-like spintronic devices7,8,9. However, towards such an application, a key issue is to require 2D nanomaterials having the ability of completely spin-resolved electric current10,11. Half-metallicity, which has a metallic nature for one spin and a semiconducting nature for the opposite spin, can fully meet this demand12,13,14,15,16,17,18. As a result, a achievement of half-metallicity charmed materials scientists.

Up to now, tremendous effort has been devoted to realize the novel half-metallicity on 2D nanostructures. When graphene, BN and MoS2 sheets were doped by transition-metal (TM) atoms, half-metallicity could be successfully achieved19,20,21. It may open an effective pathway to next-generation paper-like spintronics. However, TM atoms on 2D structures are like to form the clusters, leading to the degeneration of material’s half-metallicity. To avoid this difficulty, via the introduction of zigzag edges in vacancy, Du et al. and Wang et al. successfully predicated half-metallicity in BN and MnO2 sheets, respectively22,23. Theoretical method seems successful in showing half-metallicity while it is still experimentally impractical because the zigzag edges of the vacancy are easy to be saturated by foreign atoms or molecules resulting the deterioration of material’s half-metallicity. The achievement of half-metallicity in h-BN and ZnO sheets by functionalizations, such as hydrogenation and fluoridation, recently also has been reported24,25, while functionalized atoms are liable to form in a random way on a host surface but not the precise arrangement leading to the decadence of material’s half-metallicity. Another effective approach to obtain the half-metallicity is to apply an external strain or voltage gate. The novel half-metallicity has been successfully predicated theoretically in strain-interacted NbS2 and NbSe2 sheets26, and voltage gate-interacted MnPSe3 sheet27. Nevertheless, the experimental achievement also represents a difficulty because the electronic properties of materials are extremely sensitive to the strain or voltage gate that requires a fine control of strain or voltage gate on 2D structures. Consequently, based on these analyses, an effective acquisition of half-metallic 2D materials without external conditions becomes the big challenge facing now.

Layered transition-metal trichlorides of MCl3 type (M = Ti, V, Cr, Fe, Mo, Ru, Rh, Ir) have been achieved for many years28,29,30,31,32,33. These crystals are stacked in an AB sequence with interlayer distances of 3.16, 3.15, 3.48, 3.17, 3.32, 3.12, 3.44, 3.30 Å for TiCl3, VCl3, CrCl3, FeCl3, MoCl3, RuCl3, RhCl3, IrCl3 structures, respectively. Relatively weak van der Waals interaction between the interlayers allows their exfoliation down to sheets by applying different technologies, as reported in graphene, phosphorene, BN sheet and MoS2 sheet34,35,36,37. Experimental feasibility of the exfoliation may open a new door for achieving the long-standing dream of intrinsic half-metallic sheet, since, depending on the variety of TM atoms, such MCl3 sheets can possess very rich electronic phases. Nevertheless, all of previous studies mainly focused on 2D carbon-group materials38,39,40,41,42, nitrogen-group materials43,44,45, transition-metal dichalcogenides46,47 and other related hybridized structures48,49,50,51, while the study for such transition-metal trichlorides was totally neglected.

In this article, two exciting two-dimensional half-metallic materials, i.e. TiCl3 and VCl3 sheets, were confirmed for the first time. Cleavage energy calculation shows that such 2D structures can be effectively obtained by exfoliating their bulk structures with the cleavage energy comparable to that of graphite. Interestingly, TiCl3 and VCl3 sheets can possess bellow these advanced properties: (1) the spin band-gaps for TiCl3 and VCl3 sheets can be arrived at 0.60 and 1.10 eV for TiCl3 and VCl3 sheets, respectively; (2) the induced half-metallicity for both structures presents substantial ferromagnetic character through long-rang magnetic coupling; (3) estimated Curie temperatures for TiCl3 and VCl3 sheets can be up to 376 and 425 K, respectively. These advantages render TiCl3 and VCl3 sheets with great potential for the application of next-generation paper-like spintronics.

Results

Exfoliated capabilities

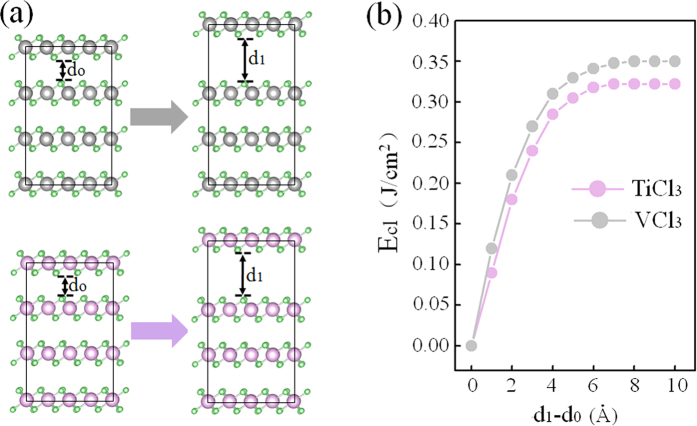
Before studying the properties of TiCl3 and VCl3 sheets, we first tested their exfoliated capabilities. In generally, relatively small van der Waals interaction between the interlayers in TiCl3 and VCl3 sheets implies a possibility of successful exfoliations of TiCl3 and VCl3 sheets experimentally. To verity this guess, we applied an effective exfoliation method, implemented by introducing a fracture in the bulk and then calculating the corresponding exfoliated energy52. The reliability of this method has been widely confirmed27,53. In this method, for the exfoliation of 2D sheets from their bulk crystals, so-called cleavage decohesion energies have to be overcome52. As depicted in Fig. 1, such decohesion energies can be obtained by determining the asymptotic limits of exfoliated energies, which are 0.33 and 0.35 J/m2 for TiCl3 and VCl3 sheets, respectively. These values are quite comparable with the experimentally estimated cleavage energy of 0.36 J/m2 in graphite54, implying a possible achievement of TiCl3 and VCl3 sheets from their bulk structures experimentally. Thus, similar as for other 2D sheets, scotch tape and liquid exfoliations might be two effective methods for the production of TiCl3 and VCl3 sheets.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic illustration of the exfoliation procedure. (b) Cleavage energy, Ecl, as a function of the separation between fractured parts.

Geometrical structures

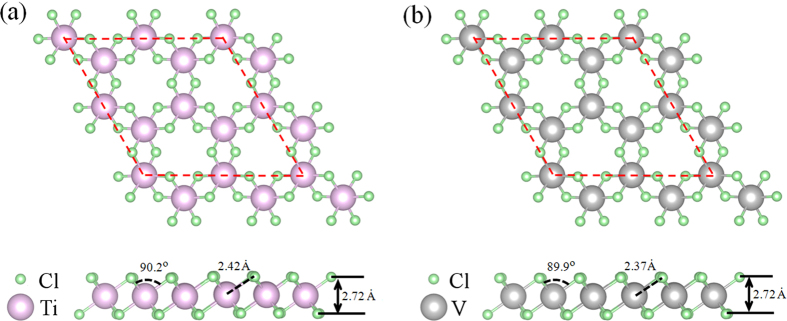
We then studied the geometrical structures of TiCl3 and VCl3 sheets. Optimized geometries of TiCl3 and VCl3 sheets are shown in Fig. 2. Clearly, TiCl3 and VCl3 sheets are trilayered with a metallic atom in the middle that is covalently bonded to six Cl atoms located in the top and bottom layers forming Cl-Ti-Cl and Cl-V-Cl arrangements, respectively. Calculated lattice constant of 6.09 Å, Cl-Ti bond length of 2.42 Å, Cl-Cl distance of 2.72 Å and Cl-Ti-Cl angle of 90.2° in TiCl3 sheet are quite comparable with those found in TiCl3 crystal28, and calculated lattice constant of 6.01 Å, Cl-V bond length of 2.37 Å, Cl-Cl distance of 2.72 Å and Cl-V-Cl angle of 89.9° in VCl3 sheet are quite comparable with those found in VCl3 crystal29. As a result, TiCl3 and VCl3 sheets remain the geometries as those found in TiCl3 and VCl3 crystals very well, implying an structural rigidity of such sheets after exfoliation.

Figure 2. Top and side views of the optimized geometric structures of (a).

Figure 2

Open in a new tab

TiCl3 and (b) VCl3 sheets.

Half-metallicity

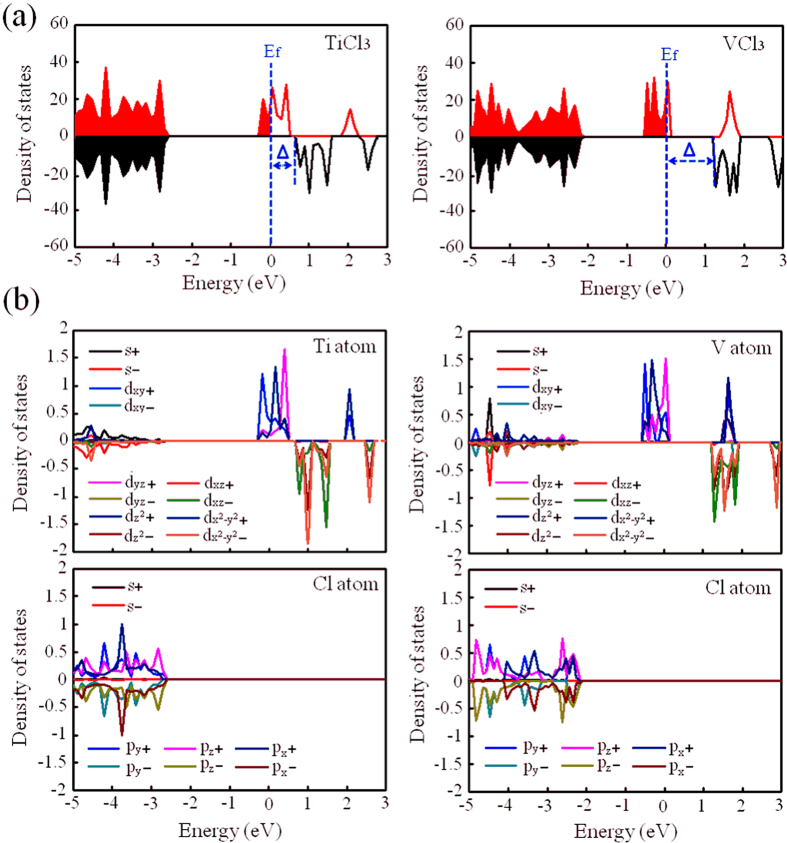
In order to explore if TiCl3 and VCl3 sheets can possess the half-metallic character, we plotted their spin-polarized total density of states (TDOS), as listed in Fig. 3a. Luckily, the novel half-metallicity was observed for both structures. The spin-up electrons are metallic around the Fermi level while the spin-down electrons are semiconducting. Such a polarized character opens a transport channel for spin-up electrons and blocks the channel for spin-down electrons, ensuring a 100% passage of preferred spin. Note that, comparing with previous studies where half-metallicity occurred under certain external constraints, the half-metallicity found here is totally intrinsic without any external constraints, meaning that TiCl3 and VCl3 sheets should be more suitable for actual spin applications. In order to understand the half-metallic character in more detail, we investigated the atomic projected density of states (PDOS), as listed in Fig. 3b. As demonstrated by the states of entire energy regions for TM atom and Cl atom in both sheets, the states of TM atom and Cl atom can be divided into two parts: one part related with the energies from −2.0 to −5.0 eV (identified as part 1) and the other part related with the energies around the Fermi level (identified as part 2). For part 1, a strong hybridization was found in both sheets, mainly contributed by Ti’s s, dxz, dx2−y2 states and Cl’s px, py and pz states. It has been revealed in our previous studies that strong hybridized interaction can certainly reduce or quench magnetism of TM atom26. Thus, these states don’t contribute spin-polarization, in which spin-up states match spin-down states very well. For part 2, the situation is quite different. Because of the deficiency of states at Cl atom, states of TM atom in both sheets, contributed by Ti’s dxy, dyz, dz2 states, are not hybridized. Consequently, these states present a spin-polarization, in which spin-up states don’t match spin-down states. Based on these results, we can conclude that half-metallicity in TiCl3 and VCl3 sheets mainly comes from the non-hybridized TM’s 3d states while the contribution from hybridized TM’s 3d states can be neglected.

Figure 3.

Figure 3

Open in a new tab

(a) Spin-polarized total density of states of TiCl3 and VCl3 sheets. (b) Spin-polarized projected density of states of Cl and TM atoms in TiCl3 and VCl3 sheets.

Half-metallic gap

To achieve the great promise for the use of half-metallicity in spintronic devices, wide half-metallic gap is extremely important55,56. Thus, we valuated the values of half-metallic gap for TiCl3 and VCl3 sheets. Calculated half-metallic gaps, labeled as Δ in Fig. 3a, are about 0.60 and 1.10 eV for TiCl3 and VCl3 sheets, respectively. In order to conveniently compare with previous works, we also used density functional theory (DFT) method to estimate the half-metallic gap. Values, employed by DFT, for TiCl3 and VCl3 sheets are about 0.42 and 0.64 eV, respectively, which are comparable with the values of 0.46 eV in half-metallic LaMn0.5Zn0.5AsO0.5H0.5 alloy and 0.50 eV in half-metallic Sr2FeMoO6 and Sr2FeReO6 alloys57,58,59. Note that, the bandgaps are also dependent on the choice of parameters. Thus, wide half-metallic gaps here seems survived to the choice of functional, which provides a great capability for the prevention of spin flip transition, a tremendous challenge, that might occur at a low temperature.

Ferromagnetic coupling

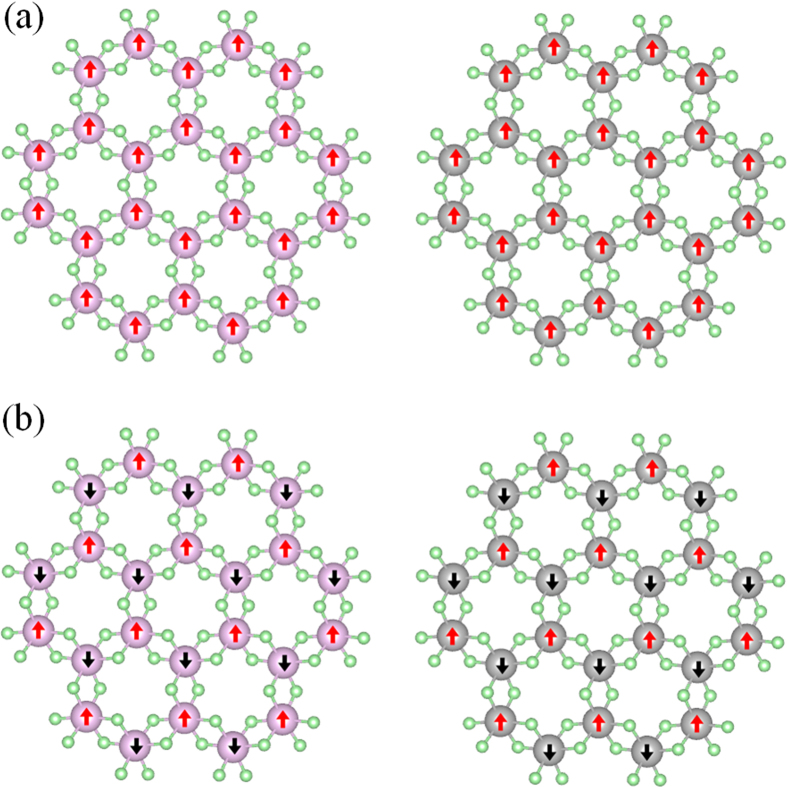
Ferromagnetic coupling is another vital property for the application of half-metallic materials in spintronic devices60,61,62. Bearing this in mind, we considered two different coupling configurations, namely, ferromagnetic (FM) coupling and antiferromagnetic (AFM) coupling, as listed in Fig. 4. After optimization, we found that the energy of FM state in TiCl3 sheet lies 780 eV lower than that of AFM state, and the energy of FM state in VCl3 sheet lies 880 eV lower than that of AFM state. Since our calculations are based on a supercell that consists of four unit cells, the energy of FM state for one unit cell composed of two TM atoms and six Cl atoms is lower than that of AFM state by 195 and 220 meV for TiCl3 and VCl3 sheets, respectively, clearly showing that the FM coupling is favored for both sheets. In order to understand the strength of ferromagnetism with the distance, we calculated strain-dependent energy difference between AFM coupling and FM coupling in Figure 1S. It shows that the difference of energy between AFM coupling and FM coupling increases with the tensile strain for both cases. This finding is in agreement with the result found in strain-interacted VS2 and VSe2 sheets and can be attributed to the competitive effect between the change of through-bond interaction and the change of through-space interaction with the tensile strain63. To visualize the spin distribution of FM coupling on TiCl3 and VCl3 sheets, we plot their spin densities, i.e. the charge density difference between spin-up and spin-down channels, as listed in Fig. 5. Agreeing with the magnetic moment analysis, the induced spin polarization is mainly contributed by TM atoms while the contribution from Cl atoms can be neglected for both sheets. Note that, the unpaired spin electrons in TiCl3 and VCl3 sheets exhibit a substantial collective character, which is crucially important for the applications of system in spintronic devices but is often overlooked in the previous studies. Thus, the finding of unique FM coupling here might render TiCl3 and VCl3 sheets more practical applications to spintronic devices.

Figure 4. Schematic illustrations of (a) ferromagnetic and (b) antiferromagnetic couplings in TiCl3 and VCl3 sheets.

Figure 4

Open in a new tab

Figure 5. Spin densities of (a) two-dimensional plot and (b) isosurface in TiCl3 and VCl3 sheets (isovalue 0.02 e/Å3).

Figure 5

Open in a new tab

Curie temperature

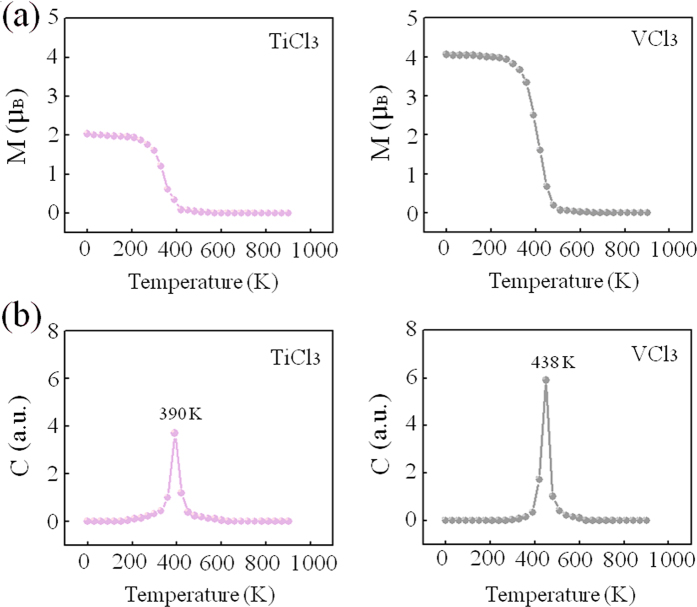
Considering the practical application of half-metallicity in spintronic devices, Curie temperature of materials is the other important property that should be comparable to or higher than room temperature64. To this end, we finally estimate the Curie temperature TC, based on the Heisenberg model with the expression of kBTC = (2/3)ΔE, where kB is the bolzmann constant, Tc is the Curie temperature and ΔE is the energy difference between FM state and AFM state65. According to this model, we found the values of 376 and 425 K for TiCl3 and VCl3 sheets, respectively. Obviously, half-metallic TiCl3 and VCl3 sheets can be utilized at room temperature. In order to directly verify such an exciting result, Monte Carlo simulation was also carried out. Before the Monte Carlo simulation, the exchange coupling constant, J, was firstly considered according to the Ising theory, H = −J∑mimj, where mi and mj are the magnetic moments at sites i and j, and H is the Hamiltoninan. For TiCl3 and VCl3 structures here, this formula can be written as J = ΔE/64m2, where ΔE is the energy difference between FM state and AFM state and m = |m|. Calculated exchange coupling constants are about 12.2 and 3.4 meV for TiCl3 and VCl3 sheets, respectively. Then the Monte Carlo simulation was lasted for 5 × 105 loops with a 100 × 100 supercell. Temperature-dependent magnetic moment curve and heat capacity curve are listed in Fig. 6a,b, respectively. As shown in Fig. 6a, Curie temperature of TiCl3 sheet can be evaluated to the value between 300 K at which the magnetic moment of TiCl3 sheet starts dropping gradually and 400 K at which the paramagnetic state of TiCl3 sheet is achieved, and Curie temperatures of VCl3 sheet can be evaluated to the value between 350 K at which the magnetic moment of VCl3 sheet starts dropping gradually and 450 K at which the paramagnetic state of VCl3 sheet is achieved. As shown in Fig. 6b, via locating the peak position of the heat capacity curve, Curie temperatures of TiCl3 and VCl3 sheets were precisely determined to be 390 and 438 K, respectively. In generally, Monte Carlo simulation is easy to give a Curie temperature of 0 K for 2D system. However, considering that the interlayer magnetic couplings through the van der Waals gap in bulk TiCl3 and VCl3 crystals are vanishingly small, the Curie temperatures of bulk TiCl3 and VCl3 crystals are dominated by nearest-neighbor exchange interactions. Thus, Curie temperatures of TiCl3 and VCl3 sheets seem equal to those of bulk TiCl3 and VCl3 crystals. This may explain why TiCl3 and VCl3 sheets can present certain Curie temperatures. As a result, Heisenberg model and Monte Carlo simulation give the similar results, confirming the validity of our estimated Curie temperature. Based on the result of such high curie temperatures found in TiCl3 and VCl3 sheets, explaining the origin of this property is important. According to the Heisenberg model, ΔE, the energy difference between FM state and AFM state, plays a key role for the magnitude of Curie temperature. Previous studies have shown that the FM state of TM atoms in such system was caused by the through-bond coupling interaction via which an atom with spin-up (spin-down) density would induce a spin-down (spin-up) density on the adjacent atom bonded to it by the expression of “…MTM → -MCl → MTM…” and the AFM coupling of TM atoms in such system was caused by the through-space coupling via which an atom with spin-up (spin-down) density would induce a spin-down (spin-up) density on the nearest-neighboring atom directly without mediation atom by the expression of “…MTM → -MTM…”63. Here MTM and MCl denote the magnetic moment of TM and Cl atoms, respectively. Thus, based on such an analysis, the value of ΔE in both structures can be recognized as a competitive effect of through-bond coupling interaction and through-space coupling interaction. When the difference between through-bond interaction and through-space interaction is distinct, the value of ΔE is large, otherwise small. Note that, for both structures, spin electrons contributed by TM’s 3d states are rather localized which leads to a very slight through-space coupling interaction while the bond between TM and Cl atoms is rather strong which induces a very strong through-bond coupling interaction. Naturally, distinct difference between through-bond coupling interaction and through-space coupling interaction gives a large value of ΔE, resulting in the high Curie temperature.

Figure 6. Variations of (a) the magnetic moment per cell, M, and (b) heat capacity, C, as a function of temperature in TiCl3 and VCl3 sheets.

Figure 6

Open in a new tab

Discussion

In this work, we, via examining a series of transition-metal trichlorides, identified two intrinsic two-dimensional half-metallic materials: TiCl3 and VCl3 sheets. Cleavage energy calculation shown such 2D structures can be effectively obtained by exfoliating their bulk structures. In contrast to previous studies, the half-metallicity found in TiCl3 and VCl3 structures has the following advantages: (1) it is not necessary to substitutionally or adsorptionly dope 2D structure by TM atoms; (2) it is not necessary to induce zigzag edges in 2D structure by fabricating vacancy; (3) it is not necessary to functionalize the 2D structure, such as hydrogenation and fluoridation; (4) it is not necessary to apply an external strain or voltage gate to the 2D structure. Although all these methods can make 2D structures successfully obtain half-metallicity, experimental effective manipulations are still difficult. Further studies show that (1) the spin band-gaps for TiCl3 and VCl3 sheets can be arrived at 0.60 and 1.10 eV for TiCl3 and VCl3 sheets, respectively; (2) the induced half-metallicity for both structures favors ferromagnetic coupling; (3) the estimated Curie temperatures for TiCl3 and VCl3 sheets can be up to 376 and 425 K, respectively. Therefore, based on these analyses, the intrinsic half-metallicity combined with wide half-metallic gap, unique ferromagnetic character and high Curie temperature render TiCl3 and VCl3 sheets with great potential for the application of next-generation paper-like spintronics.

Methods

DFT calculations

The first-principle calculations are performed using the Vienna ab initio simulation package (VASP). Note that, in order to count the electron correlation effects of Ti’s and V’s 3d orbitals and obtain precise electronic and magnetic properties of TiCl3 and VCl3 sheets, we employ the screened hybrid HSE06 functional, which includes the accurate Fock exchange and thus performs much better than the DFT method. In our calculations, a 2 × 2 supercell was used for both TiCl3 and VCl3 structures. The electronic wave functions were expanded using a plane-wave basis set with a cutoff energy of 500 eV. The pseudopotentials with 3d24s2, 3d34s2 and 3s23p5 valence electron configurations were used for Ti, V and Cl atoms, respectively. For bulk TiCl3 and VCl3 crystals, van der Waals interaction was considered, and the corresponding brillouin zone integration was performed with a 6 × 6 × 2 k-point grid. For TiCl3 and VCl3 sheets, a vacuum space of 15 Å was used to avoid the interaction between images, and the corresponding brillouin zone integration was performed with a 10 × 10 × 1 k-point grid. All the calculations were carried out with spin-polarization. The atomic positions and lattice constants of the structures were relaxed until all the force components were smaller than 0.01 eV/Å. Here the spin-orbital coupling correcting was not considered, since our test shown that it had little influence on our results.

Additional Information

How to cite this article: Zhou, Y. et al. Evidencing the existence of exciting half-metallicity in two-dimensional TiCl3 and VCl3 sheets. Sci. Rep. 6, 19407; doi: 10.1038/srep19407 (2016).

Supplementary Material

Supplementary Information
srep19407-s1.doc (172.5KB, doc)

Acknowledgments

This project was supported by the National Natural Science Foundation of China (Nos 11504044 and 61474018) and the Fundamental Research Funds for the Central Universities (No. ZYGX2015KYQD012).

Footnotes

Author Contributions Y.G.Z. performed calculations and wrote the manuscript. H.F.L. discussed the results. X.T.Z. and F.G. revised the paper.

References

  1. Novoselov K. S., Jiang D., Schedin F., Booth T. J., Khotkevich V. V., Morozov S. V. & Geim A. K. Two-dimensional Atomic Crystals. P. Natl. Acad. Sci. USA . 102, 10451–10453 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Miro P., Audiffred M. & Heine T. An Atlas of Two-dimensional Materials. Chem. Soc. Rev. 43, 6537–6554 (2014). [DOI] [PubMed] [Google Scholar]
  3. Huang X., Tan C. L., Yin Z. Y. & Zhang H. 25th Anniversary Article: Hybrid Nanostructures Based on Two-dimensional Nanomaterials. Adv. Mater. 26, 2185–2204 (2014). [DOI] [PubMed] [Google Scholar]
  4. Zhuang X. D., Mai Y. Y., Wu D. Q., Zhang F. & Feng X. L. Two-dimensional Soft Nanomaterials: A Fascinating World of Materials. Adv. Mater. 27, 403–427 (2015). [DOI] [PubMed] [Google Scholar]
  5. Zhang S. L., Yan Z., Li Y. F., Chen Z. F. & Zeng H. B. Atomically Thin Arsenene and Antimonene: Semimetal-semiconductor and Indirect-direct Band-gap Transitions. Angew. Chem. Int. Edit . 54, 3112–3115 (2015). [DOI] [PubMed] [Google Scholar]
  6. Zhao H. J., Song J. Z., Song X. F., Yan Z. & Zeng H. B. Ag/white Graphene Foam for Catalytic Oxidation of Methanol with High Efficiency and Stability. J. Mater. Chem. A 3, 6679–6684 (2015). [Google Scholar]
  7. Song X. F., Hu J. L. & Zeng H. B. Two-dimensional Semiconductors: Recent Progress and Future Perspectives. J. Mater. Chem. C 1, 2952–2969 (2013). [Google Scholar]
  8. Kheirabadi N., Shafiekhani A. & Fathipour M. Review on Graphene Spintronic, New Land for Discovery. Superlattice. Microst. 74, 123–145 (2014). [Google Scholar]
  9. Han W., Kawakami R. K., Gmitra M. & Fabian J. Graphene Spintronics. Nat. Nanotechnol . 9, 794–807 (2014). [DOI] [PubMed] [Google Scholar]
  10. Prinz G. A. Magnetoelectronics. Science 282, 1660–1663 (1998). [DOI] [PubMed] [Google Scholar]
  11. Wolf S. A., Awschalom D. D., Buhrman R. A., Daughton J. M., von Molnar S., Roukes M. L., Chtchelkanova A. Y. & Treger D. M. Spintronics: A Spin-based Electronics Vision for the Future. Science 294, 1488–1495 (2001). [DOI] [PubMed] [Google Scholar]
  12. Park J. H., Vescovo E., Kim H. J., Kwon C., Ramesh R. & Venkatesan T. Direct Evidence for A Half-metallic Ferromagnet. Nature 392, 794–796 (1998). [Google Scholar]
  13. Zhang X. D., Zhang J. J., Zhao J. Y., Pan B. C., Kong M. G., Chen J. & Xie Y. Half-metallic Ferromagnetism in Synthetic Co9Se8 Nanosheets with Atomic Thickness. J. Am. Chem. Soc. 134, 11908–11911 (2012). [DOI] [PubMed] [Google Scholar]
  14. Ishizuka H. & Motome Y. Dirac Half-metal in A Triangular Ferrimagnet. Phys. Rev. Lett. 109, 237207 (2012). [DOI] [PubMed] [Google Scholar]
  15. Du A. J., Sanvito S. & Smith S. C. First-principles Prediction of Metal-free Magnetism and Intrinsic Half-metallicity in Graphitic Carbon Nitride. Phys. Rev. Lett. 108, 197207 (2012). [DOI] [PubMed] [Google Scholar]
  16. Kan E. J., Hu W., Xiao C. Y., Lu R. F., Deng K. M., Yang J. L. & Su H. B. Half-metallicity in Organic Single Porous Sheets. J. Am. Chem. Soc. 134, 5718–5721 (2012). [DOI] [PubMed] [Google Scholar]
  17. Kan E., Li M., Hu S., Xiao C., Xiang H. & Deng K. Two-dimensional Hexagonal Transition-metal Oxide for Spintronics. J. Phys. Chem. Lett. 4, 1120–1125 (2013). [DOI] [PubMed] [Google Scholar]
  18. Hashmi A. & Hong J. Metal Free Half Metallicity in 2D System: Structural and Magnetic Properties of g-C4N3 on BN. Sci. Rep . 4, 4374 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Zhou Y. G., Yang P., Wang Z. G., Zu X. T., Xiao H. Y., Sun X., Khaleel M. A. & Gao F. Electronic and Magnetic Properties of Substituted BN sheets: A Density Functional Theory Study. Phys. Chem. Chem. Phys. 13, 7378–7383 (2011). [DOI] [PubMed] [Google Scholar]
  20. Zhou Y. G., Su Q. L., Wang Z. G., Deng H. Q. & Zu X. T. Controlling Magnetism of MoS2 Sheets by Embedding Transition-metal Atoms and Applying Strain. Phys. Chem. Chem. Phys. 15, 18464–18470 (2013). [DOI] [PubMed] [Google Scholar]
  21. Li Z. Y., Xie W. Z., Liu X. G. & Wu Y. Magnetic Property and Possible Half-metal Behavior in Co-doped Graphene. J. Appl. Phys. 117, 084311 (2015). [Google Scholar]
  22. Du A. J., Chen Y., Zhu Z. H., Amal R., Lu G. Q. & Smith S. C. Dots versus Antidots: Computational Exploration of Structure, Magnetism, and Half-metallicity in Boron-nitride Nanostructures. J. Am. Chem. Soc. 131, 17354–17359 (2009). [DOI] [PubMed] [Google Scholar]
  23. Wang H., Zhang J. J., Hang X. D., Zhang X. D., Xie J. F., Pan B. C. & Xie Y. Half-metallicity in Single-layered Manganese Dioxide Nanosheets by Defect Engineering. Angew. Chem. Int. Edit . 54, 1195–1199 (2015). [DOI] [PubMed] [Google Scholar]
  24. Chen W., Li Y. F., Yu G. T., Li C. Z., Zhang S. B., Zhou Z. & Chen Z. F. Hydrogenation: A Simple Approach To Realize Semiconductor–half-metal–metal Transition in Boron Nitride Nanoribbons. J. Am. Chem. Soc. 132, 1699–1705 (2010). [DOI] [PubMed] [Google Scholar]
  25. Kan E. J., Xiang H. J., Wu F., Tian C., Lee C., Yang J. L. & Whangbo M. H. Prediction for Room-temperature Half-metallic Ferromagnetism in the Half-fluorinated Single Layers of BN and ZnO. Appl. Phys. Lett. 97, 122503 (2010). [Google Scholar]
  26. Zhou Y. G., Wang Z. G., Yang P., Zu X. T., Yang L., Sun X. & Gao F. Tensile Strain Switched Ferromagnetism in Layered NbS2 and NbSe2. Acs Nano 6, 9727–9736 (2012). [DOI] [PubMed] [Google Scholar]
  27. Li X. X., Wu X. J. & Yang J. L. Half-metallicity in MnPSe3 Exfoliated Nanosheet with Carrier Doping. J. Am. Chem. Soc. 136, 11065–11069 (2014). [DOI] [PubMed] [Google Scholar]
  28. Troyanov S. I. & Snigireva E. M. X-ray-diffraction Study of Phase-transition in Alpha-TiCl3. Zh. Neorg. Khim. 36, 1117–1123 (1991). [Google Scholar]
  29. Klemm W. & Krose E. Z. Die Kristallstrukturen von ScCl3, TiCl3 und VCl3. Anorg. Allg. Chem . 253, 218–225 (1947). [Google Scholar]
  30. Morosin B. & Narath A. Magnetic Materials Analyses by Nuclear Spectrometry: A Joint Approach to Mössbauer Effect and Nuclear Magnetic Resonance. J. Chem. Phys. 40, 1958–1967 (1964). [Google Scholar]
  31. Troyanov S. I. Crystal Structure of FeCl3 Polytyped Modifications. Zh. Neorg. Khim. 38, 1946–1949 (1993). [Google Scholar]
  32. Hillebrecht H. & Schmidt P. J., Rotter, H. W., Thiele, G., Zönnchen, P., Bengel, H., Cantow. H. J., Magonov S. N. & Whangbo M. H. Structural and Scanning Microscopy Studies of Layered Compounds MCl3 (M = Mo, Ru, Cr) and MOCl2 (M = V, Nb, Mo, Ru, Os). J. Alloy. Compd. 246, 70–79 (1997). [Google Scholar]
  33. Bengel H., Cantow H. J., Magonov S. N., Hillebrechtb H., Thieleb G., Liangc W. & Whangbo M. H. Tip-force Induced Surface Corrugation in Layered Transition-metal Trichlorides MCl(3) (M = Ru, Mo, Rh, Ir). Sur. Sci . 343, 95–103 (1995). [Google Scholar]
  34. Coleman J. N., Lotya M., O’Neill A., Bergin S. D., King P. J., Khan U., Young K., Gaucher A., De S. & Smith R. J. Two-dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 331, 568–571 (2011). [DOI] [PubMed] [Google Scholar]
  35. Yasaei P., Kumar B., Foroozan T., Wang C. H., Asadi M., Tuschel D., Indacochea J. E., Klie R. F. & Salehi-Khojin A. High-quality Black Phosphorus Atomic Layers by Liquid-phase Exfoliation. Adv. Mater. 27, 1887–1888 (2015). [DOI] [PubMed] [Google Scholar]
  36. Warner J. H., Rummeli M. H., Bachmatiuk A. & Buchner B. Atomic Resolution Imaging and Topography of Boron Nitride Sheets Produced by Chemical Exfoliation. Acs Nano 4, 1299–1304 (2010). [DOI] [PubMed] [Google Scholar]
  37. Bang G. S., Nam K. W., Kim J. Y., Shin J., Choi J. W. & Choi S. Y. Effective Liquid-phase Exfoliation and Sodium Ion Battery Application of MoS2 Nanosheets. Acs Appl. Mater. Inter . 6, 7084–7089 (2014). [DOI] [PubMed] [Google Scholar]
  38. Li X. M., Yin J., Zhou J. X., Wang Q. & Guo W. L. Exceptional High Seebeck Coefficient and Gas-flow-induced Voltage in Multilayer Graphene. Appl. Phys. Lett. 100, 183108 (2012). [Google Scholar]
  39. Si C., Liu Z., Duan W. H. & Liu F. First-principles Calculations on the Effect of Doping and Biaxial Tensile Strain on Electron-phonon Coupling in Graphene. Phys. Rev. Lett. 111, 196802 (2013). [DOI] [PubMed] [Google Scholar]
  40. Yin K., Zhang Z. H., Li. X. M., Yu J., Zhou J. X., Chen Y. Q. & Guo W. L. Waving Potential in Graphene. Nat. Commun. 5, 3582 (2014). [DOI] [PubMed] [Google Scholar]
  41. Yin J., Li X. M., Yu J., Zhang Z. H., Zhou J. X. & Guo W. L. Generating Electricity by Moving a Droplet of Ionic Liquid along Graphene. Nat. Nanotechnol . 9, 378–383 (2014). [DOI] [PubMed] [Google Scholar]
  42. Xu Y., Zi Z. Y. & Duan W. H. Thermal and Thermoelectric Properties of Graphene. Small 10, 2182–2199 (2014). [DOI] [PubMed] [Google Scholar]
  43. Cai Y. Q., Zhang G. & Zhang Y. W. Layer-dependent Band Alignment and Work Function of Few-layer Phosphorene. Sci. Rep. 4, 6677 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Liu H., Neal A. T., Zhu Z., Luo Z., Xu X. F., Tomanek D. & Ye P. D. Phosphorene: An Unexplored 2D Semiconductor with a High Hole Mobility. Acs Nano 8, 4033–4041 (2014). [DOI] [PubMed] [Google Scholar]
  45. Dai J. & Zeng X. C. Bilayer Phosphorene: Effect of Stacking Order on Bandgap and Its Potential Applications in Thin-film Solar Cells. J. Phys. Chem. Lett. 5, 1289–1293 (2014). [DOI] [PubMed] [Google Scholar]
  46. Hu Z. Y., Zhang S. L., Zhang Y. N., Wang D., Zeng H. B. & Liu L. M. Modulating the Phase Transition between Metallic and Semiconducting Single-layer MoS2 and WS2 through Size Effects. Phys. Chem. Chem. Phys. 17, 1099–1105 (2015). [DOI] [PubMed] [Google Scholar]
  47. Jiang L. F. & Zeng H. B. Comment on “Strongly Luminescent Monolayered MoS2 Prepared by Effective Ultrasound Exfoliation”. Nanoscale 7, 4580–4583 (2015). [DOI] [PubMed] [Google Scholar]
  48. Zou X. L., Zhou G., Duan W. H., Choi K. & Ihm J. Chemical Modification Strategy for Hydrogen Storage in Covalent Organic Frameworks. J. Phys. Chem. C 114, 13402–13407 (2010). [Google Scholar]
  49. Li X. X., Zhao J. & Yang J. L. Semihydrogenated BN Sheet: A Promising Visible-light Driven Photocatalyst for Water Splitting. Sci. Rep. 3, 1858 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Dai J., Wu X. J., Yang. J. L. & Zeng X. C. Porous Boron Nitride with Tunable Pore Size. J. Phys. Chem. Lett. 5, 393–398 (2014). [DOI] [PubMed] [Google Scholar]
  51. Yu J. & Guo W. L. Strain Tunable Electronic and Magnetic Properties of Pristine and Semihydrogenated Hexagonal Boron Phosphide. Appl. Phys. Lett. 106, 043107 (2015). [Google Scholar]
  52. Medvedeva N. I., Mryasov O. N., Gornostyrev Y. N., Novikov D. L. & Freeman A. J. First-principles Total-energy Calculations for Planar Shear and Cleavage Decohesion Processes in B2-ordered NiAl and FeAl. Phys. Rev. B 54, 13506–13514 (1996). [DOI] [PubMed] [Google Scholar]
  53. Sachs B., Wehling T. O., Novoselov K. S., Lichtenstein A. I. & Katsnelson M. I. Ferromagnetic Two-dimensional Crystals: Single Layers of K2CuF4. Phys. Rev. B 88, 201402 (2013). [Google Scholar]
  54. Zacharia R., Ulbricht H. & Hertel T. Interlayer Cohesive Energy of Graphite from Thermal Desorption of Polyaromatic Hydrocarbons. Phys. Rev. B 69, 155406 (2004). [Google Scholar]
  55. Yao Z. Y., Zhang Y. S. & Yao K. L. Large Half-metallic Gap in Ferromagnetic Semi-Heusler Alloys CoCrP and CoCrAs. Appl. Phys. Lett. 101, 062402 (2012). [Google Scholar]
  56. Gao G. Y., Hu L., Yao K. L., Luo B. & Liu N. Large Half-metallic Gaps in the Quaternary Heusler Alloys CoFeCrZ (Z = Al, Si, Ga, Ge): A First-principles Study. J. Alloy. Compd. 551, 539–543 (2013). [Google Scholar]
  57. Kobayashi K. L., Kimura T., Sawada H., Terakura K. & Tokura Y. Room-temperature Magnetoresistance in An Oxide Material with an Ordered Double-perovskite Structure. Nature 395, 677–680 (1998). [Google Scholar]
  58. Kobayashi K. I., Kimura T., Tomioka Y., Sawada H., Terakura K. & Tokura Y. Intergrain Tunneling Magnetoresistance in Polycrystals of the Ordered Double Perovskite Sr2FeReO6. Phys. Rev. B 59, 11159–11162 (1999). [Google Scholar]
  59. Li X. X., Wu X. J. & Yang J. L. Room-temperature Half-metallicity in La(Mn,Zn)AsO Alloy via Element Substitutions. J. Am. Chem. Soc. 136, 5664–5669 (2014). [DOI] [PubMed] [Google Scholar]
  60. Zhang S. H., Li Y. W. & Zhao T. S. Robust Ferromagnetism in Monolayer Chromium Nitride. Sci. rep . 4, 5241 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Kan M., Zhou J., Sun Q., Kawazoe Y. & Jena P. The Intrinsic Ferromagnetism in A MnO2 Monolayer. J. Phys. Chem. Lett. 4, 3382–3386 (2013). [DOI] [PubMed] [Google Scholar]
  62. Zhou J., Wang Q., Sun Q., Chen X. S., Kawazoe Y. & Jena P. Ferromagnetism in Semihydrogenated Graphene Sheet. Nano Lett. 9, 3867–3870 (2009). [DOI] [PubMed] [Google Scholar]
  63. Ma Y. D., Dai Y., Guo M., Niu C. W., Zhu Y. T. & Huang B. B. Evidence of the Existence of Magnetism in Pristine VX2 Monolayers (X = S, Se) and Their Strain-induced Tunable Magnetic Properties. Acs Nano 6, 1695–1701 (2012). [DOI] [PubMed] [Google Scholar]
  64. Ma Y. W., Lu Y. H., Yi J. B., Feng Y. P., Herng T. S., Liu X., Gao D. Q., Xue D. S., Xue J. M., Ouyang J. Y. & Ding J. Room Temperature Ferromagnetism in Teflon due to Carbon Dangling Bonds. Nat. Commun. 3, 727 (2012). [DOI] [PubMed] [Google Scholar]
  65. Jin H., Dai Y., Huang B. & Whangbo M. H. Ferromagnetism of Undoped GaN Mediated by Through-bond Spin Polarization between Nitrogen Dangling Bonds. Appl. Phys. Lett. 94, 162505 (2009). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep19407-s1.doc (172.5KB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES