Orbital Delocalization and Enhancement of Magnetic Interactions in Perovskite Oxyhydrides

Abstract

Recent experiments showed that some perovskite oxyhydrides have surprisingly high magnetic-transition temperature. In order to unveil the origin of this interesting phenomenon, we investigate the magnetism in SrCrO₂H and SrVO₂H on the basis of first-principles calculations and Monte Carlo simulations. Our work indicates that the Cr-O-Cr superexchange interaction in SrCrO₂H is unexpectedly strong. Different from the previous explanation in terms of the H⁻ ion substitution induced increase of the Cr-O-Cr bond angle, we reveal instead that this is mainly because the 3d orbitals in perovskite oxyhydrides becomes more delocalized since H⁻ ions have weaker electronegativity and less electrons than O²⁻ ions. The delocalized 3d orbitals result in stronger Cr-O interactions and enhance the magnetic-transition temperature. This novel mechanism is also applicable to the case of SrVO₂H. Furthermore, we predict that SrFeO₂H will have unprecedented high Neel temperature because of the extraordinarily strong Fe-H-Fe σ-type interactions. Our work suggests the anion substitution can be used to effectively manipulate the magnetic properties of perovskite compounds.

Complex transition metal oxides have been the subject of enduring interest due to the wide variety of physical properties they exhibit, to name a few, high-T_c superconductivity, magnetoresistance, multiferroicity, thermoelectric response, and so on¹,²,³,⁴,⁵,⁶,⁷. For the past few years, scientists have found that replacing segmental O²⁻ ions in transition metal oxides by N³⁻, F⁻ or S²⁻ can result in novel materials such as pigments, water-splitting photocatalysis, dielectric and cathode material⁸,⁹,¹⁰,¹¹,¹². Different from N³⁻, F⁻ or S²⁻ which has p valence electrons, the H⁻ anion has a filled 1 s² electronic configuration that is fundamentally different from the O²⁻ ion case. Therefore, it is expected that the H⁻ ion substitution might leads to exotic behaviors in perovskite. In pioneering works, a large amount of hydrogen species were incorporated into ATiO₃ (A = Ba, Sr, Ca) and Sr₂VO₄ lattice through the use of CaH₂ reductant¹³,¹⁴,¹⁵,¹⁶. The resulting oxyhydride ATiO_3−xH_x exhibits high electronic conductivity and its hydride ions are exchangeable with gaseous hydrogen at elevated temperature, indicating that it can be an ideal mixed electron/hydride proton conductor for electrochemical applications¹³,¹⁴,¹⁵. In oxyhydride Sr₂VO_4−xH_x, the hydride ion could act as an effective carrier dopant because the hydrogen and oxygen concentrations can be controlled¹⁶.

Interestingly, it was experimentally found that the magnetic properties of transition metal oxides may change dramatically if some oxygen anions are replaced by hydrogen anions. An antiferromagnetic-to-ferromagnetic transition in EuTiO_3–xH_x induced by hydride substitution was reported, where the ferromagnetism was caused by the Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction between the Eu²⁺ spins mediated by the itinerant Ti 3d electrons¹⁷. LaSrCoO₃H_0.7¹⁸,¹⁹,²⁰ and Sr₃Co₂O_4.33H_0.84²¹ were found to display high magnetic transition temperatures. Recently, the stoichiometric perovskite oxyhydrides SrCrO₂H and SrVO₂H have been synthesized²²,²³. The average structure of SrCrO₂H is the cubic perovskite where the hydride ions are randomly distributed. In SrVO₂H, the planar VO₂ layers are connected by hydride ions. The experimentally observed antiferromagnetic (AFM) Neel temperature (T_N) of SrCrO₂H and SrVO₂H are around 380 K and higher than 300 K²²,²³, respectively. It is puzzling that the Neel temperature T_N of SrCrO₂H is higher than that (290 K)²⁴,²⁵ of LaCrO₃. In both SrCrO₂H and LaCrO₃, the valence of Cr element is 3+ with the three 3d electrons occupying the t_2g orbitals, that is, the electron configuration is (d_xy)¹(d_yz)¹(d_xz)¹. In average, each Cr³⁺ ion in SrCrO₂H has two Cr-H-Cr superexchange paths and four Cr-O-Cr superexchange paths. Since the t_2g orbitals of the Cr³⁺ ion could not interact with the 1s orbitals of H⁻ ions by symmetry, the Cr-H-Cr superexchange interaction is negligible. In LaCrO₃, there are six Cr-O-Cr superexchange paths for each Cr³⁺ ion. So the fact that the Neel temperature T_N of SrCrO₂H is higher than that of LaCrO₃ is rather unexpected.

To probe the origin of the high T_N in SrCrO₂H and SrVO₂H, we studied the magnetic properties of SrCrO₂H, SrVO₂H, and LaCrO₃ based on the density functional theory (DFT). We show that due to weaker electronegativity and less electrons of H⁻ ions than those of O²⁻ ions, the substitution of H⁻ ions with O²⁻ ions lead to more delocalized 3d orbitals of Cr³⁺ ions which make Cr-O-Cr superexchange in SrCrO₂H much stronger and leads to a high T_N. This new mechanism is also applicable to the case of SrVO₂H.

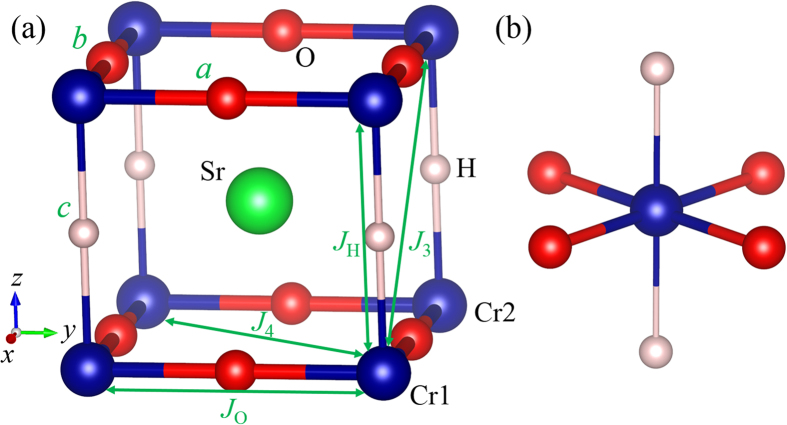
Although the H⁻ ion was experimentally reported to be randomly distributed in SrCrO₂H, we will adopt an ordered structure (see Fig. 1a) to investigate the magnetism in SrCrO₂H for the following reasons. First, by using the cluster expansion approach, we find the ground state structure of SrCrO₂H is similar to the experimentally observed structure of SrVO₂H. Second, we find that the magnetic properties of another SrCrO₂H structure with a more random H⁻ ion distribution are similar to those of the ordered structure (see Supplementary Material). The ground state structure (tetragonal P4/mmm symmetry) of SrCrO₂H has one H⁻ ion and two O²⁻ ions in the primitive cell. The Cr³⁺ cations are located within square planes of oxide ions and form CrO₂ sheets. The CrO₂ sheets are connected by hydride ions, which occupy the remaining two coordination sites around each Cr³⁺ center. Thus the ground state structure of SrCrO₂H can be described by a CrO₂-SrH-CrO₂-SrH stacking sequence. The computed phonon frequencies²⁶ (see Supplementary Figure S3) indicate that the ground state structure of SrCrO₂H is dynamically stable. 

Figure 1.

(a) Perspective view of the ground state structure of SrCrO₂H. The green, blue, red, and greyish spheres represent the Sr²⁺, Cr³⁺, O²⁻, and H⁻ ions, respectively. The spin exchange paths J_O, J_H, J₃, and J₄ are also indicated. (b) The local structure of the CrO₄H₂ octahedron.

Figure 2.

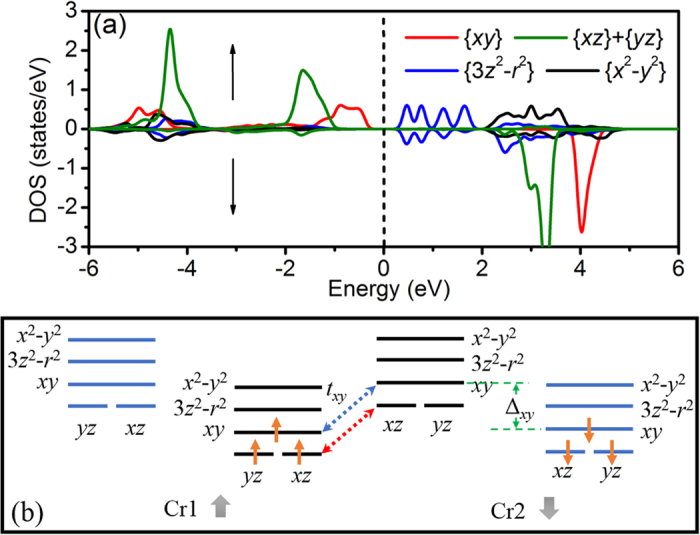
(a) PDOS of the spin-up Cr³⁺ ion in SrCrO₂H with the G-type AFM order. (b) Energy level and electron occupation for the spin-up Cr1 ion and spin-down Cr2 ion. The positions of Cr1 and Cr2 are shown in Fig. 1a. The spin-up and spin-down levels are denoted by black and blue colors, respectively. The effective orbitals hoppings responsible for the Cr1-Cr2 superexchange interaction are illustrated.

To examine the magnetic properties of SrCrO₂H, we considered four ordered spin states, namely, the ferromagnetic (FM), A-type AFM, C-type AFM and G-type AFM states. The experimentally observed AFM structure is the G-type. Our GGA + U calculations show that all the AFM states have lower energy than the FM state, and the G-type AFM is indeed the ground state, in consistent with experimental observations²². To extract the values of the spin exchange parameters, we adopt the four-state mapping approach²⁷,²⁸. There are four relevant Cr-Cr spin exchange interactions (see Fig. 1a): (1) J_O is the nearest neighbor (NN) superexchange interaction for the Cr-O-Cr path; (2) J_H is the NN spin exchange interaction for the Cr-H-Cr path; (3) J₃ is next nearest neighbor (NNN) super-superexchange interaction in the plane; (4) J₄ is the NNN out of plane super-superexchange interaction. The calculated exchange parameters in the tetragonal structure of SrCrO₂H are summarized in Table 1. As expected, the NN Cr-O-Cr path has the strongest spin exchange interaction (J_O) since it is mediated by the strong π-π hybridization between 3d and 2p orbitals. The NN spin exchange interaction J_H is weakly AFM due to the direct through-space overlap between the t_2g orbitals of Cr³⁺ ions. The NNN exchange interactions (J₃ and J₄) are negligible. The AFM nature of the NN interactions can result in the G-type AFM order. Based on the calculated spin exchange parameters, our Monte Carlo (MC) simulations indicate that the T_N is around 285 K. If a smaller Hubbard U is adopted, we can get higher T_N according to the theory of superexchange, in better agreement with the experimentally observed T_N²².

Table 1. Spin exchange parameters and Neel temperature of perovskite systems considered in this work.

	JO (meV)	JH (meV)	J3 (meV)	J4 (meV)	TN (K)
SrCrO2H (opt.)	23.95	3.26	−0.96	0.34	285
SrCrO2H (cubic)	29.69	1.27	−1.26	0.69	325
LaCrO3 (opt.)	8.88	–	–	0.38	137
LaCrO3 (cubic)	14.25	–	–	0.73	204
SrVO2H (opt.)	23.54	1.88	−0.71	0.17	255
SrFeO2H (opt.)	39.63	89.26	−4.42	4.22	950
SrFeO2H (cubic)	42.89	70.41	−3.89	−0.91	922

In SrCrO₂H, SrVO₂H, and SrFeO₂H, the spin exchange paths J_O, J_H, J₃, and J₄ are defined in Fig. 1a. Positive (negative) values indicate that the spin exchange interactions are AFM (FM). The exchange parameters are effective by setting the spin magnitude to 1. In LaCrO₃, J_O is the average NN spin exchange parameter and J₄ is the average NNN spin exchange parameter. “opt.” refers to the structure optimized by GGA + U calculations, while “cubic” refers to the cubic perovskite structure.

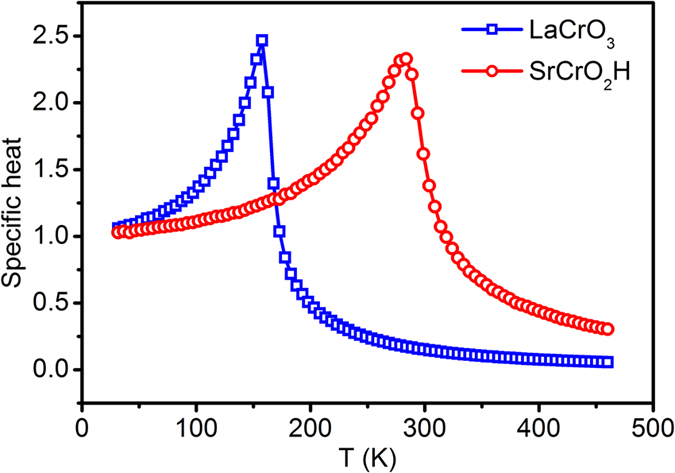
For comparison, we also studied the magnetism in LaCrO₃. Experiments show the ground state structure of LaCrO₃ is the GdFeO₃–type distorted perovskite with Pbnm space group and its lattice constants are a = 5.478, b = 7.759, and c = 5.516²⁹. The lattice constants of our optimized Pbnm structure are a = 5.468 Å, b = 7.758 Å, and c = 5.497 Å, in good agreement with experiment. The obtained spin exchange parameters of the optimized LaCrO₃ are summarized in Table 1. The NN interaction J_O is AFM and the NNN interactions are negligible. This is in accord with the experimentally observed G-type AFM ground state in LaCrO₃. Compared with SrCrO₂H, it is clear that J_O in LaCrO₃ is much weaker. Based on the calculated spin exchange parameters, our MC simulations indicate that the T_N for LaCrO₃ is around 133 K. Therefore, our theoretical calculations confirm the experimental observation that SrCrO₂H has a higher T_N than LaCrO₃, as shown in Fig. 3.

Figure 3. Specific heat of SrCrO₂H and LaCrO₃ calculated as a function of temperature from the MC simulations of the classical spin Hamiltonian.

Now we begin to understand the difference in the magnetic properties between SrCrO₂H and LaCrO₃. There are two significant differences between SrCrO₂H and LaCrO₃. First, there is a structural difference. The CrO₆ octahedron in LaCrO₃ is tilted due to a small tolerance factor, while there is no octahedron tilt in SrCrO₂H. As a result, the Cr-O-Cr angle in SrCrO₂H is 180° while the average Cr-O-Cr angle in LaCrO₃ is 167°. Second, a chemical difference exists since one third of the O²⁻ ions are replaced by H⁻ ions.

To make clear whether the structural difference or the chemical difference is responsible for the stronger Cr-O-Cr exchange in SrCrO₂H, we investigate the magnetic properties of SrCrO₂H and LaCrO₃ with the same cubic perovskite crystal structure. The lattice constant is set to be the average lattice constant (3.85 Å) of experimental SrCrO₂H structure²². Note that the hypothetic cubic LaCrO₃ phase can be regarded as a result of substituting Sr²⁺ and H⁻ in cubic SrCrO₂H with La³⁺ and O²⁻, respectively. The computed spin exchange parameters of these two cubic structures are summarized in Table 1. Surprisingly and interestingly, the Cr-O-Cr superexchange (29.69 meV) in SrCrO₂H is almost as twice as that (14.25 meV) in LaCrO₃ despite of the fact that the Cr-O bond length and the Cr-O-Cr bond angle are identical in cubic SrCrO₂H and LaCrO₃. As expected, the Cr-O-Cr exchange in cubic LaCrO₃ is stronger than that (8.88 meV) in Pbnm LaCrO₃ according to the Goodenough-Kanamori rule³⁰,³¹,³². Previously, it was suggested that the structural difference is solely responsible for the high T_N in SrCrO₂H²². However, our calculations show that the structure difference and chemical difference enhance the Cr-O-Cr exchange interaction by 5.37 meV and 15.44 meV, respectively. Therefore, the effect of chemical difference on the Cr-Cr exchange interaction is much more important than that of the structural difference.

To account for why J_O in the cubic SrCrO₂H is as twice as that in the cubic LaCrO₃, we examine their electronic structures in details. Figure 2a shows the partial density of states (PDOS) of the spin-up Cr³⁺ ion in SrCrO₂H with the G-type AFM order. We can see that, for SrCrO₂H, the majority-spin t_2g (d_xy, d_xz, and d_yz) orbitals are occupied by three electrons but the majority-spin e_g orbitals are unoccupied, which is similar to the orbital occupation in LaCrO₃. The energy level and occupancy of the 3d orbitals of the tetragonal SrCrO₂H are shown in Fig. 2b. Note that the t_2g orbitals split into the low-lying two-fold degenerate d_xz/d_yz level and a higher d_xy level as a result of the tetragonal symmetry.

Without loss of generality, we consider the spin exchange J_O for the Cr1-O-Cr2 path along the x axis, as shown in Fig. 1a. According to Anderson’s superexchange theory³³, the magnitude of the spin exchange can be estimated by 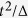, where t is the effective hopping between the d orbitals and Δ is the energy difference between majority-spin and minority-spin orbitals. In the cubic SrCrO₂H or LaCrO₃, the d_xz orbital can only interact with the neighboring d_xz orbital, and so do d_xy, d_yz. The magnitude of J_O for the Cr1-O-Cr2 path can be estimated as 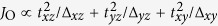, where t_m (m=xz, yz, xy) is effective hopping between the m orbitals of Cr1 and Cr2, and Δ_m is the energy difference between the majority-spin m orbital and minority-spin m orbital of the Cr³⁺ ion (see Fig. 2b). The Δ_m parameters are estimated by constructing the maximally localized Wannier functions (MLWFs) based on the ferromagnetic electronic structure. It turns out that Δ_m (about 5.3 eV) in SrCrO₂H is rather close to that (about 5.5 eV) in LaCrO₃. Therefore, we can regard Δ_m as a constant. The effective hopping paramters t_m between the Cr 3d orbitals is obtained by constructing the MLWFs using the spin-unpolarized Bloch wavefunctions. These hopping parameters are listed in Table 2. We can see that the hopping parameter t_yz between the d_yz orbitals of Cr1 and Cr2 is negligible since these two orbitals are almost parallel to each other. The π-π hopping parameter t_xy in the cubic SrCrO₂H are the same as that in the cubic LaCrO₃. The striking result is that the π-π hopping parameter t_xz between the d_xz orbitals of Cr1 and Cr2 in the cubic SrCrO₂H is almost 50% stronger than that in LaCrO₃. Using these hopping parameters, we can estimate the ratio between J_O in cubic SrCrO₂H and that in LaCrO₃ as:

Table 2. Effective hopping between the d _xz , d _yz , d _xy orbitals of nearest neighboring Cr ions in cubic SrCrO₂H and LaCrO₃ through the MLWF technique.

	txz(eV)	tyz(eV)	txy(eV)
SrCrO2H (cubic)	−0.385	0.002	−0.213
LaCrO3 (cubic)	−0.217	−0.017	−0.217

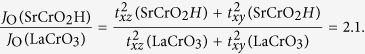Thus, our first-principles result can be well accounted for by this simple model. This analysis clearly shows that the stronger t_xz hopping in SrCrO₂H is responsible for its high T_N.

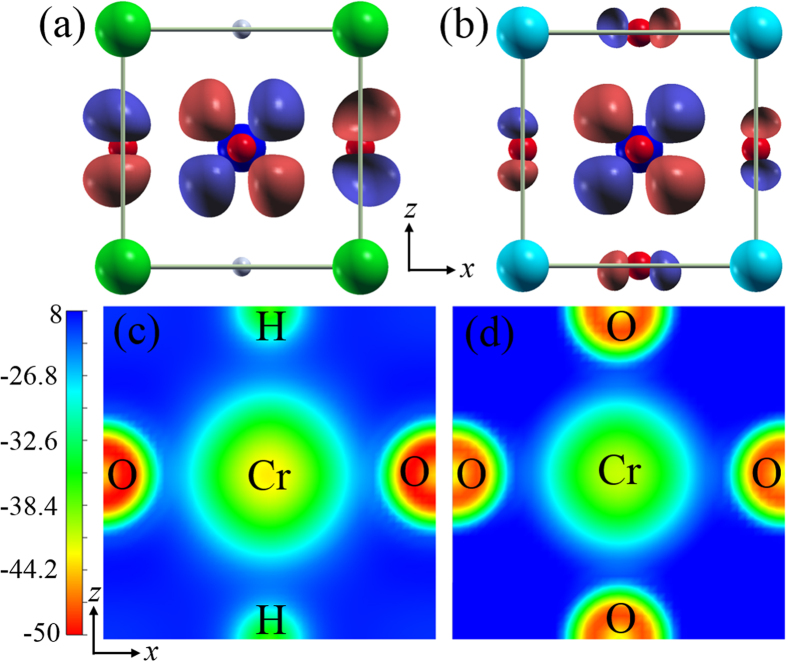
Figure 4a,b shows the real-space distribution of the d_xz-like MLWFs in the cubic SrCrO₂H and LaCrO₃. It is clear that the effective d_xz-like MLWF not only distributes around the Cr ion, but also has tails on the neighboring O²⁻ ions due to the anti-bonding π^* hybridization between Cr-d_xz and O-2p orbitals. It is the tails on the O²⁻ ions that mediate the effective hopping between the Cr-d_xz orbitals. An interesting observation is that the lobes on the O²⁻ ion in the MLWF of SrCrO₂H are bigger than those in LaCrO₃. This suggests that the interaction between Cr-d_xz orbital and O-p_z orbital in SrCrO₂H is stronger than that in LaCrO₃, in agreement with our previous result that the effective hopping between the d_xz orbitals of Cr1 and Cr2 in SrCrO₂H is larger than that in LaCrO₃.

Figure 4. Isosurface plots of the Cr-d_xz like MLWFs for (a) cubic SrCrO₂H and (b) cubic LaCrO₃.

The lobes on the O²⁻ ion in the MLWF of SrCrO₂H are bigger than those of LaCrO₃, indicating that the hybridization between Cr-d_xz orbital and O-p_z is stronger in SrCrO₂H. Contour plots of the electrostatic potential in (c) cubic SrCrO₂H and (d) cubic LaCrO₃, projected on the xz-plane passing through Cr, H, and O sites. The electrostatic potential along the Cr-H direction is much weaker than that along the Cr-O direction in SrCrO₂H.

We propose that the stronger interaction between Cr-d_xz orbital and O-p_z orbital in SrCrO₂H results from the more delocalized Cr-d_xz orbital in SrCrO₂H (see Supplementary Figure S5). This is supported by a separate MLWF analysis which indicates that the spread of the atomic Cr-d_xz orbital in the cubic SrCrO₂H is larger than that in the cubic LaCrO₃. The more delocalized Cr-d_xz orbital in SrCrO₂H can be reasoned by considering the electrostatic potential exerted on the Cr 3d electrons. The contour plots of the electrostatic potential on the x-z plane are displayed in the Fig. 4c,d. We can see that the electrostatic potential along the Cr-H direction is much weaker than that along the Cr-O direction. Thus, the d_xz orbital in SrCrO₂H is more delocalized along the z-axis, as can also be seen from Fig. 4a. It is the weaker repulsion between the H⁻ ion and the 3d electrons that makes the d_xz orbital in SrCrO₂H more delocalized. The weaker electrostatic potential along the Cr-H direction results from the fact that H⁻ ions have the weaker electronegativity and less charge than O²⁻ ions. Therefore, the replacement of O²⁻ ions by H⁻ ions will not only change the hybridization type between the transition metal and the anions, but also affect the wavefunction distribution of d orbitals. Such novel mechanism revealed here for SrCrO₂H can be also applied to SrVO₂H. The only difference is that there is one d electron less than that in SrCrO₂H, which makes the T_N slightly lower (see Supplementary Material). We note that first-principles calculations³⁴ were recently carried out to study the electronic and magnetic properties of SrVO₂H. However, the mechanism for the high Neel temperature in SrVO₂H was not discovered.

The mechanism that the H⁻ ion induced delocalization of the d orbitals is general and may have profound effect on the electronic and magnetic properties of other perovskite oxyhydrides. Below we will predict that SrFeO₂H has an extremely high T_N. With the cluster expansion approach, we predict that SrFeO₂H takes the same ground state structure as that of SrCrO₂H. This is reasonable since the ionic radius of the Fe³⁺ ion is close to that of the Cr³⁺ ion. The optimized lattice constants a and c for SrFeO₂H are 3.997 Å and 3.645 Å, respectively. The computed phonon dispersion²⁶ (see Supplementary Figure S4) indicates that SrFeO₂H is dynamically stable. The spin exchange parameters calculated for the optimized SrFeO₂H structures are listed in Table 1. SrFeO₂H takes the G-type AFM order as the magnetic ground state since the NN AFM spin exchanges J_O (Fe-O-Fe) and J_H (Fe-H-Fe) are dominant. To our surprise, the spin exchange J_H (89.26 meV) in SrFeO₂H is much stronger than J_O (39.63 meV) in SrFeO₂H. Note that the much stronger Fe-H-Fe interaction is not mainly caused by the shorter Fe-H distance than the Fe-O distance, because similar results are also obtained in the cubic perovskite SrFeO₂H structure. In fact, the much stronger Fe-H-Fe interaction is mainly because the out-of-plane Fe-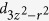 orbital is more delocalized than the in-plane Fe- 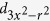and 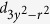orbitals. Therefore, the σ bond between the H 1s orbital and Fe- 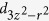orbital is much stronger than the σ bond between the O-2p orbitals and the in-plane Fe 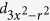/ 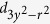orbitals (see Supplementary Figure S6). Similar to the cases of SrCrO₂H and SrVO₂H, the weaker electrostatic potential of H⁻ ions exerting on the d electrons of Fe³⁺ ions leads to more delocalized Fe- 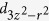orbitals, which results in an anomalously strong spin exchange J_H. Our MC simulations indicate that the T_N of SrFeO₂H is around 826 K, which is even higher than that of BiFeO₃ (T_N = 643 K)³⁵ and SrFeO₂ with a quasi-two-dimensional structure (T_N = 473 K)³⁶,³⁷. Our result suggests that the replacement of O²⁻ ions by H⁻ ions can enhance the magnetic interactions not only in t_2g d² and d³ systems, but also in d⁵ systems. Our work suggests that the high magnetic transition temperature in LaSrCoO₃H_0.7¹⁸,¹⁹,²⁰ and Sr₃Co₂O_4.33H_0.84²¹ should be also due to the H⁻ ion induced delocalization of the 3d e_g orbitals.

In summary, we perform a systematic theoretical study on the magnetic properties of perovskite oxyhydrides. The high magnetic transition temperature in SrCrO₂H is revealed to be due to the delocalization of 3d orbitals in perovskite oxyhydrides. This is because H⁻ ions have weaker electronegativity and fewer electrons than O²⁻ ions. The more delocalized 3d orbitals in SrCrO₂H make Cr-O-Cr superexchange strong and T_N high. This novel mechanism also applies to the case of SrVO₂H. We predict that the σ-type Fe-H-Fe interactions in SrFeO₂H are extraordinarily strong which also result from the delocalization of the 3d orbitals. The delocalization of d orbitals in oxyhydrides discovered in this work is universal and may also have profound effects on properties other than the magnetic properties.

Methods

Our DFT calculations are performed on the basis of the projector augmented wave method³⁸,³⁹ encoded in the Vienna ab initio simulation package⁴⁰,⁴¹ (VASP) using the generalized-gradient approximation (GGA) of Perdew, Burke, and Ernzerhof⁴². The plane-wave cutoff energy is set to be 450 eV. To properly describe the strong electron correlation in the 3d transition-metal oxide, the GGA plus on-site repulsion U method (GGA + U) is employed⁴³. U = 4 eV and J = 1eV are applied to the 3d electron of Cr³⁺ ions. The maximally localized Wannier functions (MLWFs) are constructed with the Wannier90 program⁴⁴,⁴⁵. The spread functional is considered to be converged if the corresponding fractional change because two successive iterations is smaller than 10⁻¹⁰. To find the ground state structures of SrCrO₂H, SrVO₂H, and SrFeO₂H, we adopt the cluster expansion approach⁴⁶ by using the alloy theoretic automation toolkit (ATAT)⁴⁷.

We perform parallel tempering Monte Carlo (PTMC) simulations⁴⁸,⁴⁹ to estimate the magnetic transition temperature. In PTMC simulations, many replicas with different temperature are simultaneously simulated and a virtual process exchanging configuration of these replicas is introduced. PTMC simulations can avoid a local minimum at low temperatures and can reduce relaxation time. We adopt a 10 × 10 × 10 supercell to perform PTMC simulations. Our test shows that the results obtained with a 12 × 12 × 12 supercell are almost the same as those with the 10 × 10 × 10 supercell. The number of replicas is set to 120.

Additional Information

How to cite this article: Liu, K. et al. Orbital Delocalization and Enhancement of Magnetic Interactions in Perovskite Oxyhydrides. Sci. Rep. 6, 19653; doi: 10.1038/srep19653 (2016).