Abstract
As a fundamental primitive, Secure Multiparty Summation and Multiplication can be used to build complex secure protocols for other multiparty computations, specially, numerical computations. However, there is still lack of systematical and efficient quantum methods to compute Secure Multiparty Summation and Multiplication. In this paper, we present a novel and efficient quantum approach to securely compute the summation and multiplication of multiparty private inputs, respectively. Compared to classical solutions, our proposed approach can ensure the unconditional security and the perfect privacy protection based on the physical principle of quantum mechanics.
Secure Multiparty Computation (SMC)1 is an important branch in modern cryptography. Secure Multiparty Summation or Multiplication is a fundamental primitive of SMC that enables multiple parties to jointly compute the summation or multiplication of their respective private inputs without revealing any private input. As we know, Secure Multiparty Summation and Multiplication can be used to build complex secure protocols for other multiparty computations, specially, numerical computations. In addition, there are also lots of other important applications of Secure Multiparty Summation and Multiplication in distributed networks, such as secret sharing, electronic voting, secure sorting, data mining and so on.
On the one hand, there existed some classical protocols for Secure Multiparty Summation2,3,4 and Multiplication5,6,7, which were based on classical cryptography. However, classical cryptography cannot provide the unconditionally secure communications and cannot resist the attack of the quantum computer especially.
On the other hand, quantum cryptography can provide the unconditional security, which is guaranteed by physical principles of quantum mechanics. Since Bennett and Brassard8 presented the first quantum key distribution protocol (BB84 protocol), quantum cryptography has been widely studied and rapidly developed. Compared to classical cryptography, the most important advantage is that an eavesdropper can easily be detected by using the characteristics of quantum mechanics. Therefore, a lot of results have been gained, such as quantum key distribution, quantum teleportation, quantum secret sharing, quantum secure direct communication, quantum key agreement, quantum signature and so on. Furthermore, SMC is also studied extensively in quantum cryptography9,10,11,12,13,14.
However, there are only a few quantum protocols for Secure Multiparty Summation. In 2007, Du et al.15 presented a secure quantum addition module n + 1 based on non-orthogonal states, where n denoted the number of all parties. In 2010, Chen et al.16 proposed another secure quantum addition module 2 based on multi-particle entangled states with the trusted third party. However, the module of the two protocols is too small, so that it limits their more extensive applications. Furthermore, the two protocols lack high communication efficiencies due to their bit-by-bit computation and communication. In addition, to the best of our knowledge, there is no any quantum protocol for Secure Multiparty Multiplication.
In this paper, we present a novel quantum approach to systematically and efficiently compute Secure Multiparty Summation and Multiplication, in which the computations of Secure Multiparty Summation and Multiplication are securely translated into the computations of the corresponding phase information by the quantum Fourier transform, and later the phase information is extracted out after performing an inverse quantum Fourier transform.
Here, we first introduce the quantum Fourier transform, which will be used later in proposed protocols. The quantum Fourier transform is a linear transformation on qubits, and is the quantum version of the standard discrete Fourier transform. For  , the quantum Fourier transform and the inverse quantum Fourier transform are defined as follows17:
, the quantum Fourier transform and the inverse quantum Fourier transform are defined as follows17:
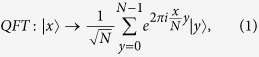 |
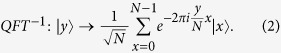 |
Furthermore,
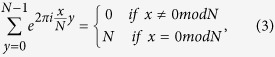 |
so,
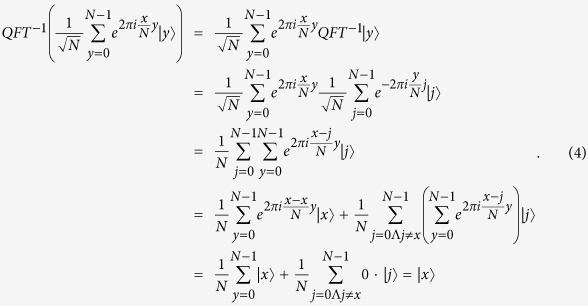 |
That is,
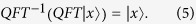 |
In addition, another multi-qubit quantum logic gate, which will be used later in proposed protocols, is the controlled-NOT or CNOT gate: 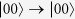 ,
, 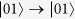 ,
, 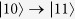 and
and 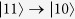 , where the first qubit is the control qubit, and the second qubit is the target qubit. That is, if the control qubit is set to 0, then the target qubit is left alone. If the control qubit is set to 1, then the target qubit is flipped.
, where the first qubit is the control qubit, and the second qubit is the target qubit. That is, if the control qubit is set to 0, then the target qubit is left alone. If the control qubit is set to 1, then the target qubit is flipped.
Results
Proposed protocols
Secure multiparty quantum summation
Assume that there are n parties: P1, P2, …, Pn (n > 2), where each party Pk (1 ≤ k ≤ n) has a secret integer 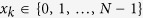
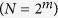 , and further all n parties want to jointly compute the summation
, and further all n parties want to jointly compute the summation 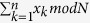 without revealing their respective secret xks. In the following Protocol I, we suppose that P1 is the initiator party.
without revealing their respective secret xks. In the following Protocol I, we suppose that P1 is the initiator party.
Protocol I (Secure multiparty quantum summation)
Step 1. The initiator 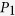 first prepares an m-qubit basis state
first prepares an m-qubit basis state 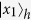 , where
, where 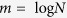 and
and 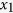 is his private secret. Then
is his private secret. Then 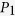 applies a quantum Fourier transform to the state
applies a quantum Fourier transform to the state 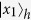 and gets the resultant state
and gets the resultant state 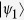 . That is,
. That is,
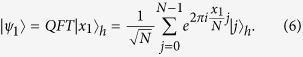 |
Step 2.
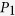 prepares another m-qubit ancillary state
prepares another m-qubit ancillary state 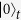 and further performs m CNOT gate operators on the product state
and further performs m CNOT gate operators on the product state 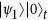 , where each qubit of the first m qubits is the control qubit and the corresponding qubit of the second m qubits is the target qubit. Here we call the resultant state
, where each qubit of the first m qubits is the control qubit and the corresponding qubit of the second m qubits is the target qubit. Here we call the resultant state 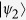 , which is written as
, which is written as
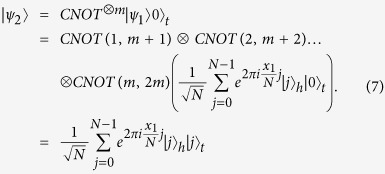 |
Clearly, 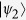 is an entangled state, where the subscript h or t denotes that the qubits will stay at home or be transmitted through the quantum channel.
is an entangled state, where the subscript h or t denotes that the qubits will stay at home or be transmitted through the quantum channel.
Step 3.
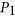 sends the second m qubits (i.e., the ancillary state
sends the second m qubits (i.e., the ancillary state 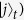 to
to 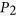 through the authenticated quantum channel.
through the authenticated quantum channel.
Step 4. After receiving the ancillary state 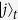 ,
, 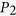 first prepares his secret state
first prepares his secret state 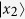 . Then he applies an oracle operator
. Then he applies an oracle operator 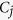 on
on 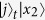 , where
, where 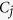 is defined by
is defined by
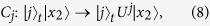 |
with
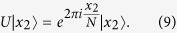 |
That is, 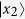 is an eigenvector of U with the eigenvalue
is an eigenvector of U with the eigenvalue 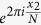 . After applying the oracle operator
. After applying the oracle operator 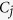 , the whole composite quantum systems of
, the whole composite quantum systems of 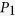 and
and 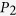 are in the following state
are in the following state
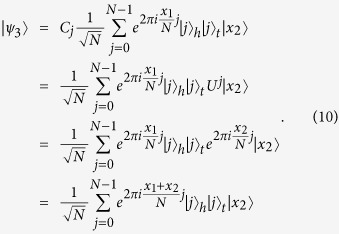 |
Step 5. Furthermore, 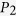 passes the ancillary state
passes the ancillary state 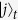 to
to 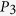 through the authenticated quantum channel and keeps
through the authenticated quantum channel and keeps 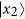 in secret. Afterward,
in secret. Afterward, 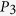 executes the similar process of
executes the similar process of 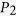 , and so on. This process is repeated
, and so on. This process is repeated 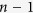 times, so that, if everyone honestly executes the protocol, the composite quantum systems of all n parties are in the following state
times, so that, if everyone honestly executes the protocol, the composite quantum systems of all n parties are in the following state
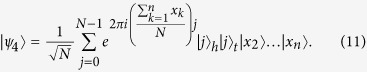 |
Step 6. Finally, 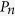 sends the ancillary state
sends the ancillary state 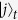 back to
back to 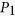 . After receiving the ancillary state
. After receiving the ancillary state 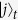 ,
, 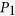 again applies
again applies 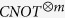 on his
on his 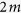 qubits, where each qubit of the first m qubits is the control qubit and the corresponding qubit of the second m qubits is the target qubit. Call the resultant state
qubits, where each qubit of the first m qubits is the control qubit and the corresponding qubit of the second m qubits is the target qubit. Call the resultant state 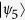 . That is,
. That is,
 |
Step 7. Furthermore, 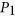 measures the second m qubits (i.e.,
measures the second m qubits (i.e., 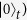 in the computational basis. If the measured result is
in the computational basis. If the measured result is 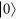 , then he continues to execute the next step; otherwise he believes that there is at least one dishonest party and ends this protocol.
, then he continues to execute the next step; otherwise he believes that there is at least one dishonest party and ends this protocol.
Step 8. Finally, 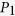 applies
applies 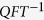 to the first m qubits and further measures it to obtain
to the first m qubits and further measures it to obtain 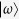 , where
, where 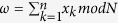 .
.
The correctness proof.
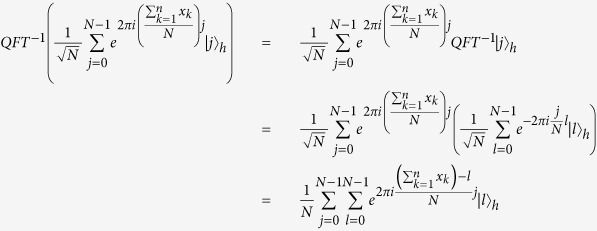 |
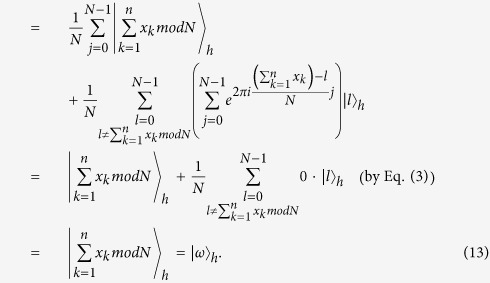 |
Therefore, if all parties honestly execute this protocol, 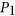 will rightly get
will rightly get 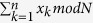 .
.
Secure multiparty quantum multiplication
Assume that there are n parties 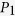 ,
, 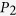 , …,
, …, 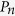
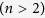 , each party with a private secret
, each party with a private secret 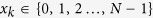
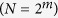 , and all n parties want to jointly compute the multiplication of their respective private secret, i.e.,
, and all n parties want to jointly compute the multiplication of their respective private secret, i.e., 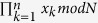 . Since each secret
. Since each secret 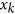 can be split and expressed as
can be split and expressed as 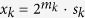 , where
, where 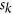 is an odd integer, then we can get
is an odd integer, then we can get
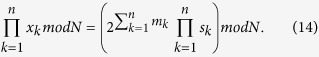 |
By Eq. (14), if we get the results of 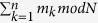 and
and 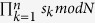 , then we can easily compute
, then we can easily compute 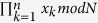 . Accordingly, the computation of
. Accordingly, the computation of 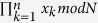 can be translated into the computations of
can be translated into the computations of 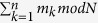 and
and 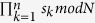 , respectively. We have proposed Protocol I to compute
, respectively. We have proposed Protocol I to compute 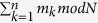 . Furthermore, we present Protocol II to compute
. Furthermore, we present Protocol II to compute 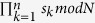 , where all
, where all 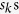 are odd integers. Similarly, in the following Protocol II, we suppose that
are odd integers. Similarly, in the following Protocol II, we suppose that 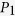 is the initiator.
is the initiator.
Protocol II (Secure multiparty quantum multiplication)
Step 1. The initiator 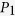 randomly chooses an odd integer
randomly chooses an odd integer 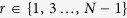 and further prepares two m qubits in the original state
and further prepares two m qubits in the original state 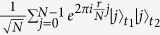 , where the preparation process is the same as that of Step 1 and 2 in Protocol I. Then
, where the preparation process is the same as that of Step 1 and 2 in Protocol I. Then  sends
sends  to
to 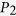 through the authenticated quantum channel and keeps
through the authenticated quantum channel and keeps 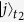 in hand.
in hand.
Step 2. After receiving 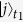 ,
, 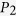 applies an oracle operator
applies an oracle operator 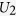 on
on 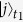 by his private secret
by his private secret 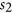 , where
, where 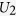 is defined by,
is defined by,
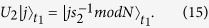 |
Please note that 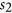 is an odd integer and
is an odd integer and 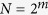 , thus there exists its modulo-N multiplicative inverse
, thus there exists its modulo-N multiplicative inverse 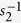 , which implies that
, which implies that 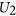 is inverse. Furthermore,
is inverse. Furthermore, 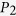 sends
sends 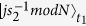 to
to 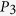 through the authenticated quantum channel. Afterward,
through the authenticated quantum channel. Afterward, 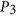 executes the similar process of
executes the similar process of 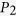 (i.e.,
(i.e., 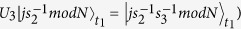 , and so on. This process is repeated
, and so on. This process is repeated 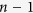 times, so that, if everyone honestly executes the protocol, the final quantum states of the qubits of the subscripts
times, so that, if everyone honestly executes the protocol, the final quantum states of the qubits of the subscripts 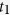 and
and 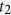 are in,
are in,
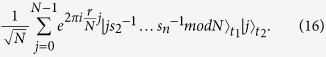 |
Finally, 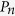 sends
sends 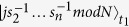 back to
back to 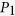 .
.
Step 3. After receiving the returned state 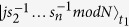 ,
, 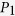 continues to send
continues to send 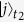 to
to 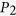 through the authenticated quantum channel.
through the authenticated quantum channel.
Step 4. After receiving the state 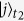 ,
, 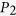 again applies the oracle operator
again applies the oracle operator 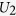 on
on 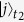 by his private input
by his private input 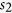 , i.e.,
, i.e., 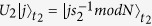 . Furthermore he sends it to
. Furthermore he sends it to 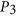 through the authenticated quantum channel, and so on. This process is repeated
through the authenticated quantum channel, and so on. This process is repeated 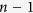 times, so that, if everyone honestly executes the protocol, the final quantum states of the 2 m qubits are in,
times, so that, if everyone honestly executes the protocol, the final quantum states of the 2 m qubits are in,
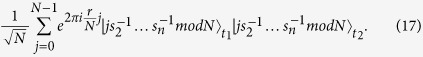 |
Finally, 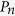 again sends
again sends 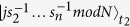 back to
back to 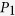 .
.
Step 5. After receiving the state 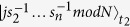 ,
, 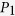 performs m CNOT gate operators on the two returned states, such that the quantum systems of the subscripts
performs m CNOT gate operators on the two returned states, such that the quantum systems of the subscripts 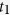 and
and 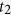 will be disentangled. That is,
will be disentangled. That is,
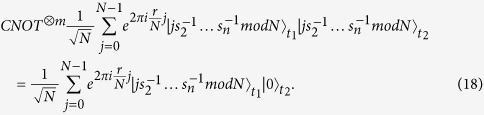 |
Furthermore, 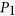 measures the qubits of the subscript
measures the qubits of the subscript 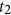 in the computation basis. If the measured result is
in the computation basis. If the measured result is 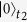 , then he continues to execute the next step. Otherwise, he believes that there is at least one dishonest party and ends this protocol.
, then he continues to execute the next step. Otherwise, he believes that there is at least one dishonest party and ends this protocol.
Step 6. Finally 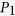 applies an inverse quantum Fourier transform
applies an inverse quantum Fourier transform 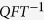 on the remaining qubits and further measures it to obtain
on the remaining qubits and further measures it to obtain 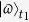 in the computation basis, where
in the computation basis, where  . Then
. Then 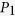 outputs
outputs  . That is,
. That is, 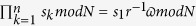 .
.
The correctness proof.
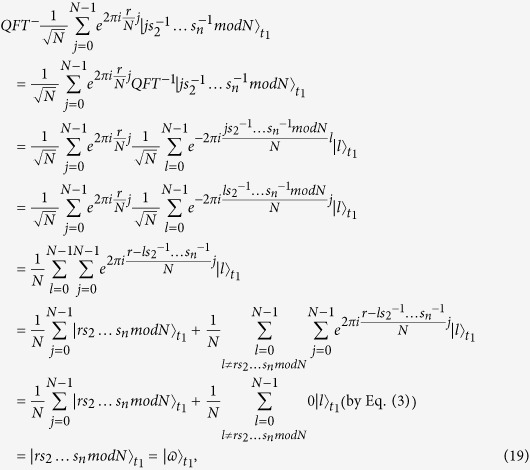 |
since
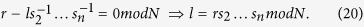 |
Obviously, 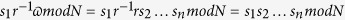 , where r is an odd integer. Therefore, Protocol II can rightly output
, where r is an odd integer. Therefore, Protocol II can rightly output 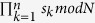 . Furthermore, in order to perfectly compute
. Furthermore, in order to perfectly compute 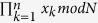 , the initiator first calls Protocol I to securely compute
, the initiator first calls Protocol I to securely compute 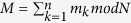 and then calls Protocol II to securely compute
and then calls Protocol II to securely compute 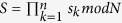 . Finally, the initiator computes
. Finally, the initiator computes 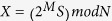 . Obviously,
. Obviously, 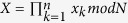 .
.
Security Analysis
We have analyzed the correctness of Protocol I and II, and further analyze their securities. In order to save space, please note that we mainly analyze the security of Protocol I, because the security of Protocol II is the same as that of Protocol I.
We first analyze that 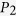 does not get any secret information about the initiator
does not get any secret information about the initiator 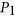 ’s input
’s input 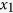 . In Protocol I,
. In Protocol I, 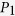 only sends the ancillary state
only sends the ancillary state  to
to  without any classical information. So, for a dishonest
without any classical information. So, for a dishonest  , if he wants to eavesdrop
, if he wants to eavesdrop  ’s secret, all possible attacks he can perform with the present technology are as follows:
’s secret, all possible attacks he can perform with the present technology are as follows:
(1)  directly measures the ancillary state
directly measures the ancillary state 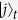 in the computational basis. Obviously, he will get
in the computational basis. Obviously, he will get 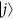
 with the equal probability of
with the equal probability of  , but the measured result j is independent of
, but the measured result j is independent of 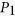 ’s secret
’s secret 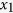 . That is, this attack is infeasible.
. That is, this attack is infeasible.
(2) After applying a unitary operator on the ancillary state  ,
,  again measures it. Especially,
again measures it. Especially,  has a knowledge that
has a knowledge that  ’s secret state
’s secret state 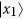 has evolved into the same state (i.e.,
has evolved into the same state (i.e., 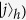 as the ancillary state
as the ancillary state 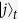 based on the quantum Fourier transform, so he may perform an inverse quantum Fourier transform
based on the quantum Fourier transform, so he may perform an inverse quantum Fourier transform 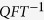 on the ancillary state
on the ancillary state 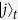 to expect to extract out
to expect to extract out 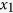 . That is, this attack can be described as follows:
. That is, this attack can be described as follows:
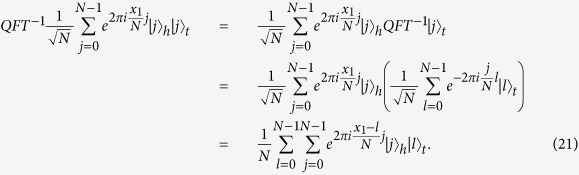 |
By the above equation, if 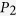 measures the ancillary state, he will get
measures the ancillary state, he will get 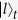
 with the equal probability of
with the equal probability of  . It implies that
. It implies that 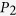 cannot get any secret information about
cannot get any secret information about 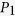 ’s private input, because he cannot extract out the global phase information from the partial qubits of the entangled quantum systems with the subscripts h and t. In fact, any local unitary operator on the partial qubits cannot fully disentangle the entanglement of the composite system unless directly measured. Therefore, even if
’s private input, because he cannot extract out the global phase information from the partial qubits of the entangled quantum systems with the subscripts h and t. In fact, any local unitary operator on the partial qubits cannot fully disentangle the entanglement of the composite system unless directly measured. Therefore, even if 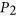 performs this attack, he still cannot get any private information about
performs this attack, he still cannot get any private information about 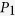 ’s secret
’s secret 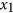 .
.
(3) 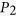 performs a more complicated entangle-measure attack that he is able to prepare another ancillary system
performs a more complicated entangle-measure attack that he is able to prepare another ancillary system 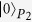 and entangle the two ancillary systems by his local unitary operations, where one is transmitted from
and entangle the two ancillary systems by his local unitary operations, where one is transmitted from  , and afterward he can measure the ancillary system prepared by himself to get the partial information about
, and afterward he can measure the ancillary system prepared by himself to get the partial information about  ’s private inputs.
’s private inputs.  ’s dishonest action when he receives
’s dishonest action when he receives  ’s ancillary
’s ancillary 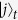 can be described by a unitary operator
can be described by a unitary operator 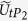 , which acts on
, which acts on 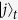 and
and 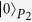 . We can describe it as follows:
. We can describe it as follows:
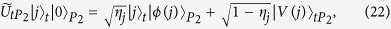 |
where 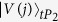 is a vector orthogonal to
is a vector orthogonal to 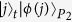 , i.e.,
, i.e.,
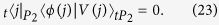 |
In order to completely pass the honest test (see Step 7), it can easily deduce that 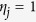 . That is, the whole quantum systems of
. That is, the whole quantum systems of 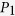 and
and 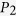 should be in the following state after performing
should be in the following state after performing 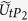 :
:
 |
Then  sends
sends  back to
back to  . After
. After  performing
performing 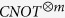 and further measuring the ancillary system t, the state of the remaining quantum system becomes
and further measuring the ancillary system t, the state of the remaining quantum system becomes
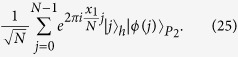 |
Now if  measures his ancillary state
measures his ancillary state  , as the above analysis in the case of (2), he still cannot get any secret information about
, as the above analysis in the case of (2), he still cannot get any secret information about 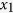 because of the entanglement of
because of the entanglement of 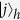 and
and 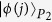 . If
. If 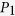 further applies
further applies 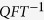 to the first m qubits, the state of the remaining quantum system will be updated into
to the first m qubits, the state of the remaining quantum system will be updated into
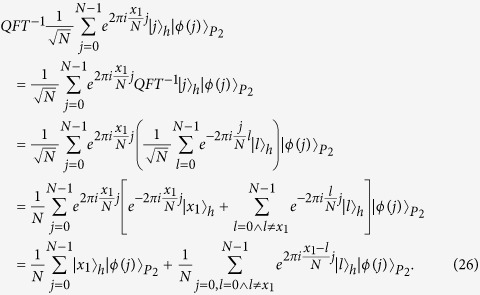 |
This equation shows that if 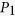 measures his remaining m qubits, he will get
measures his remaining m qubits, he will get 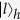
 with the equal probability of
with the equal probability of  , which implies that the probability of getting
, which implies that the probability of getting 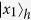 is also
is also  , unless
, unless 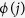 is independent of j. Similarly,
is independent of j. Similarly, 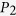 cannot get the secret
cannot get the secret 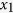 with the probability of more than
with the probability of more than  due to their entanglement yet. It implies that
due to their entanglement yet. It implies that  cannot get any secret information about
cannot get any secret information about  ’s private input
’s private input 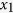 . Therefore, the entangle-measure attack is infeasible.
. Therefore, the entangle-measure attack is infeasible.
From what we have analyzed above, we can see clearly that  cannot get any secret information about
cannot get any secret information about 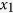 . Furthermore, we can easily and naturally generalize that any party
. Furthermore, we can easily and naturally generalize that any party 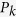
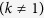 cannot obtain any secret information about
cannot obtain any secret information about 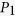 ’s private input. Therefore, the initiator’s private input is unconditionally secure against other dishonest parties. In turn, if all party honesty execute this protocol,
’s private input. Therefore, the initiator’s private input is unconditionally secure against other dishonest parties. In turn, if all party honesty execute this protocol, 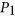 only gets the final summation
only gets the final summation 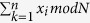
 , instead of single party’s private secret
, instead of single party’s private secret 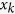 . However, if the parties
. However, if the parties 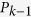 and
and 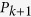 are dishonest, they can collude to get
are dishonest, they can collude to get 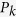 ’s private input
’s private input 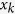 . In order to overcome this weakness, we can use the communication model in a random order instead of the fixed order, that is, how to choose the next party is randomly determined by the party himself, not pre-determined by a designated party.
. In order to overcome this weakness, we can use the communication model in a random order instead of the fixed order, that is, how to choose the next party is randomly determined by the party himself, not pre-determined by a designated party.
In addition, in order to full resist the collusion attack of any less 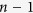 parties, we can design the following Protocol III, in which all parties are full parity.
parties, we can design the following Protocol III, in which all parties are full parity.
Protocol III (to compute 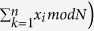
Round 1
Step 1. Each party 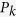
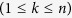 randomly generates
randomly generates 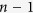 integers
integers 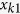 ,
, 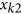 , …,
, …, 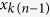 in
in  , and then computes
, and then computes 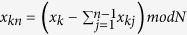 . That is,
. That is,
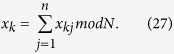 |
Step 2. Each party 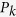
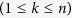 as the initiator calls Protocol I to compute
as the initiator calls Protocol I to compute
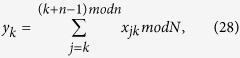 |
where 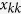 is
is 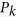 ’s the initial input.
’s the initial input.
Round 2
Finally, all parties designate an agent who could be one of them to again call Protocol I to compute and announce
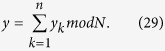 |
Obviously,
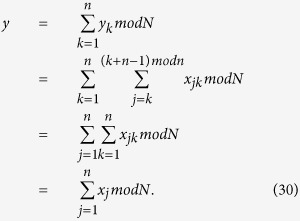 |
Because Protocol I can ensure the unconditional security of the private input of the initiator, every sub-secret 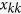 of
of 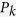
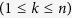 in Round 1 of Protocol III is unconditionally secure against any less
in Round 1 of Protocol III is unconditionally secure against any less 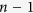 parties. Therefore, Protocol III is unconditional secure against any collusion attack, unless there are
parties. Therefore, Protocol III is unconditional secure against any collusion attack, unless there are 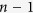 cheating parties.
cheating parties.
As for Protocol II, obviously 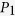 ’s secret
’s secret 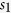 is unconditionally secure because the transmitted quantum messages don’t include any private information about
is unconditionally secure because the transmitted quantum messages don’t include any private information about 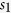 . Conversely, if all parties honestly execute Protocol II,
. Conversely, if all parties honestly execute Protocol II, 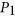 only gets the final multiplication
only gets the final multiplication 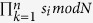
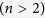 , instead of certain party’s secret
, instead of certain party’s secret 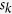 . In addition, the n-th party
. In addition, the n-th party 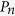 can easily perform an intercept-resend attack. That is, he intercepts all qubits passing through his hands, and then sends fake qubits back to
can easily perform an intercept-resend attack. That is, he intercepts all qubits passing through his hands, and then sends fake qubits back to 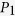 . Accordingly,
. Accordingly, 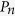 may finally obtain
may finally obtain 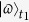 after applying m CNOT gate operators and an inverse quantum Fourier transform
after applying m CNOT gate operators and an inverse quantum Fourier transform 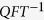 to his intercepted qubits, where
to his intercepted qubits, where  . However,
. However, 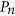 does not know r, so he still cannot get any secret information about other parties’ private inputs. Therefore, this attack is infeasible. Furthermore, in order to resist the collusion attack, we can also use the communication model in a random order instead of the fixed order. Similarly, we can also design the unconditionally secure quantum protocol for Secure Multiparty Multiplication.
does not know r, so he still cannot get any secret information about other parties’ private inputs. Therefore, this attack is infeasible. Furthermore, in order to resist the collusion attack, we can also use the communication model in a random order instead of the fixed order. Similarly, we can also design the unconditionally secure quantum protocol for Secure Multiparty Multiplication.
Protocol IV (to compute 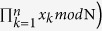
Round 1
Step 1. Each party 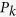
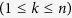 splits his secret
splits his secret 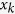 into n random integers
into n random integers 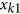 ,
, 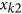 , …,
, …, 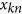 in
in  , such that
, such that
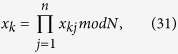 |
where 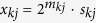 . That is,
. That is, 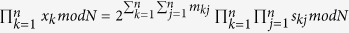 .
.
Step 2. Each party 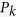
 as the initiator calls Protocol III to compute
as the initiator calls Protocol III to compute
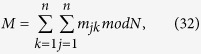 |
where 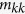 is
is 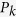 ’s the initial input.
’s the initial input.
Step 3. At the same time, each party 
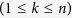 as the initiator calls Protocol II to compute
as the initiator calls Protocol II to compute
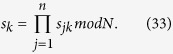 |
where 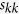 is
is 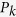 ’s the initial input.
’s the initial input.
Round 2
Finally, all parties designate an agent who could be one of them to again call Protocol II to compute 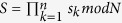 and to further announce
and to further announce
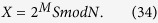 |
As for the security of the quantum channel, we can use the decoy technology to check eavesdropping in all proposed protocols. That is, the initiator randomly inserts enough decoy particles into the qubit sequence to be transmitted, where every decoy particle is prepared randomly with either Z-basis (i.e. 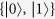 or X-basis (i.e.
or X-basis (i.e. 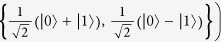 . After confirming that the receiver has received the transmitted sequence, the initiator announces the positions of partial decoy particles and the corresponding measurement basis. The receiver measures these decoy particles according to the initiator’s announcements and tells the initiator his measurement results. Then the initiator compares the measurement results of the receiver with the initial states of these corresponding decoy particles in the transmitted sequence and analyzes the security of the transmissions. If the error rate is higher than the threshold determined by the channel noise, they cancel this protocol and restarts; or else they continue to the next step.
. After confirming that the receiver has received the transmitted sequence, the initiator announces the positions of partial decoy particles and the corresponding measurement basis. The receiver measures these decoy particles according to the initiator’s announcements and tells the initiator his measurement results. Then the initiator compares the measurement results of the receiver with the initial states of these corresponding decoy particles in the transmitted sequence and analyzes the security of the transmissions. If the error rate is higher than the threshold determined by the channel noise, they cancel this protocol and restarts; or else they continue to the next step.
In addition, the authenticated quantum channel can further ensure the security of quantum communications. Like most existing secure multiparty quantum computations, our protocols need there is an authenticated quantum channel. This is the only assumption we need to have for proposed protocols to work. In principle, we may use a quantum authentication scheme (QAS)18 based on Clifford operators introduced in19 to implement it. We may also use quantum encryptions combined with classical authenticated keys20,21. In addition, we may still ensure the authentication by sharing the entangled quantum resources in advance22 or using the detecting (or decoy) particle technologies23.
Discussion
In this paper, we presented a novel and efficient quantum approach to systematically compute secure multiparty summation and multiplication. In our approach, there is an initiator who prepares an entangled state and further transmits the partial qubits of the entangled state to every party in turn through the quantum channel. According to the different computations, there are two specific processing ways: the receiver in computing the summation adds his secret into the global phase of the entangled state by an oracle operator, while the receiver in computing the multiplication embeds his secret into the received basis state by another oracle operator. Finally, the initiator takes the transmitted qubits back and subtly extracts out the corresponding summation and multiplication from the phase information by an inverse quantum Fourier transform. More specifically, we proposed several quantum protocols for secure multiparty summation and multiplication, where Protocol I and II have higher efficiency due to the linear communication complexity, and Protocol III and IV provide the unconditional security and the perfect privacy protection with 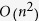 communication complexity.
communication complexity.
In conclusion, our approach securely implements the fundamental arithmetic operations (i.e., summation and multiplication) in secret-by-secret way instead of bit-by-bit way, which may give some good references for solving other SMC problems. In theory, it can be generalized to compute lots of secure multiparty numerical computations.
Additional Information
How to cite this article: Shi, R.- et al. Secure Multiparty Quantum Computation for Summation and Multiplication. Sci. Rep. 6, 19655; doi: 10.1038/srep19655 (2016).
Acknowledgments
This work was supported by National Natural Science Foundation of China (Nos 61173187, 61173188 and 11301002), the Ministry of Education institution of higher learning doctor discipline and scientific research fund aids a project financially (No. 20133401110004), Natural Science Foundation of Anhui Province (No. 1408085QF107), and the 211 Project of Anhui University (Nos 33190187 and 17110099).
Footnotes
Author Contributions Study conception, design, and writing of the manuscript: R.-H.S. and Y.M. Analysis and discussion: H.Z., J.C. and S.Z. All authors reviewed the manuscript.
References
- Yao A. C. Protocols for secure computations. In Proc. 23rd IEEE Symposium on Foundations of Computer Science (FOCS’ 82), 160 (1982).
- Clifton C., Kantarcioglu M., Vaidya J., Lin X. & Zhu M. Y. Tools for Privacy-Preserving Distributed Data Mining. ACM SIGKDD Explorations Newsletter 4, 28–34 (2002). [Google Scholar]
- Sanil A. P., Karr A. F., Lin X. & Reiter J. P. Privacy preserving regression modeling via distributed computation. In Proc. the 2004 ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 677-682 (2004).
- Atallah M., Bykova M., Li J., Frikken K. & Tophara M. Private collaborative forecasting and benchmarking. In Proc. the 2004 ACM Workshop on Privacy in the Electronic Society, 103-114 (2004).
- Masayuki A. Non-interactive and optimally resilient distributed multiplication (Special Section on Discrete Mathematics and Its Applications). IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E83A, 598–605 (2000). [Google Scholar]
- Ronald C., Ivan D. & Robbert D. H. Atomic Secure Multi-party Multiplication with Low Communication. In Proc. Advances in Cryptology-EUROCRYPT 2007. LNCS 4515, 329-346 (2007).
- Peter L. Secure Distributed Multiplication of Two Polynomially Shared Values: Enhancing the Efficiency of the Protocol. In Proc. 3rd International Conference on Emerging Security Information, Systems and Technologies, 286-291 (2009).
- Bennett C. H. & Brassard G. Quantum Cryptography: Public Key Distribution and Coin Tossing. In Proc. IEEE International Conference on Computers, Systems, and Signal Processing, 175-179 (1984).
- Lo H. K. Insecurity of quantum secure computations. Phys. Rev. A 56, 1154–1162 (1997). [Google Scholar]
- Colbeck R. The impossibility of secure two-party classical computation. Phys. Rev. A 76, 062308 (2007). [Google Scholar]
- Buhrman H., Christandl M. & Schaffner C. Complete Insecurity of Quantum Protocols for Classical Two-Party Computation. Phys. Rev. Lett. 109, 160501 (2012). [DOI] [PubMed] [Google Scholar]
- Crépeau C., Gottesman D. & Smith A. Secure multi-party quantum computation. In Proc. STOC’02 Proceedings of the thirty-fourth annual ACM symposium on Theory of Computing, 643-652 (2002).
- Ben-or M., Crépeau C., Gottesman, D., Hassidim, A. & Smith A. Secure Multiparty Quantum Computation with (Only) a Strict Honest Majority. In Proc. FOCS’06, 47th Annual IEEE Symposium on Foundations of Computer Science, 249-260 (2006).
- Unruh D. Universally Composable Quantum Multi-party Computation. In Proc. Advances in Cryptology - EUROCRYPT 2010, LNCS 6110, 486-505 (2010).
- Du J. Z., Chen X. B., Wen Q. X. & Zhu F. C. Secure multiparty quantum summation. Acta Phys Sin-Ch Ed 56, 6214–6219 (2007). [Google Scholar]
- Chen X. B., Xu G., Yang Y. X. & Wen Q. Y. An Efficient Protocol for the Secure Multi-party Quantum Summation. Int J Theor Phys. 49, 2793–2804 (2010). [Google Scholar]
- Diao Z. J., Huang C. F. & Wang K. Quantum Counting: Algorithm and Error Distribution. Acta Appl Math. 118, 147–159 (2012). [Google Scholar]
- Barnum H., Crépeau C., Gottesman, D., Smith A. & Tapp A. Authentication of quantum messages. In Proc. 43rd Annual IEEE Symposium on Foundations of Computer Science (FOCS), 449–458 (2002).
- Aharonov D., Ben-Or M. & Eban E. Interactive proofs for quantum computations. In Proc. Innovations in Computer Science, arxiv.org/abs/0810.5375 (2008).
- Yu K. F., Yang C. W., Liao C. H. & Hwang T. Authenticated semi-quantum key distribution protocol using Bell states. Quantum Inf. Process. 13, 1457–1465 (2014). [Google Scholar]
- Guan D. J., Wang Y. J. & Zhuang E. S. A practical protocol for three-party authenticated quantum key distribution. Quantum Inf. Process. 13, 2355–2374 (2014). [Google Scholar]
- Farouk A., Zakaria M., Megahed A. & Omara F.A. A generalized architecture of quantum secure direct communication for N disjointed users with authentication. Sci. Rep 5, 16080 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi R. H., Mu Y., Zhong H., Cui J. & Zhang S. Two Quantum Protocols for Oblivious Set-member Decision Problem. Sci. Rep 5, 15914 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]


