Abstract
Tungsten ditelluride (WTe2), a layered transition-metal dichalcogenide (TMD), has recently demonstrated an extremely large magnetoresistance effect, which is unique among TMDs. This fascinating feature seems to be correlated with its special electronic structure. Here, we report the observation of 6 Raman peaks corresponding to the  ,
,  ,
, 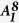 ,
, 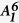 ,
, 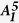 and
and 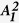 phonons, from the 33 Raman-active modes predicted for WTe2. This provides direct evidence to distinguish the space group of WTe2 from those of other TMDs. Moreover, the Raman evolution of WTe2 from bulk to monolayer is clearly revealed. It is interesting to find that the
phonons, from the 33 Raman-active modes predicted for WTe2. This provides direct evidence to distinguish the space group of WTe2 from those of other TMDs. Moreover, the Raman evolution of WTe2 from bulk to monolayer is clearly revealed. It is interesting to find that the 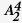 mode, centered at ~109.8 cm−1, is forbidden in a monolayer, which may be attributable to the transition of the point group from C2v (bulk) to C2h (monolayer). Our work characterizes all observed Raman peaks in the bulk and few-layer samples and provides a route to study the physical properties of two-dimensional WTe2.
mode, centered at ~109.8 cm−1, is forbidden in a monolayer, which may be attributable to the transition of the point group from C2v (bulk) to C2h (monolayer). Our work characterizes all observed Raman peaks in the bulk and few-layer samples and provides a route to study the physical properties of two-dimensional WTe2.
Transition-metal dichalcogenides (TMDs) of the MX2 type, where M refers to Mo and W, and X refers to S, Se and Te, have attracted much attention as graphene-like semiconductors with remarkable electric, spintronic and optical properties1,2,3,4,5,6,7. The basic structure of bulk MX2 comprises two-dimensional (2D) X-M-X layers stacked through Van der Waals forces. Mono- and few-layer MX2 can be fabricated by the mechanical exfoliation method8. The physical properties of MX2 are greatly dependent on the number of layers9,10,11. Weak Van der Waals forces play a very important role in the interlayer bands and atomic vibration. As the thickness decreases, MX2 exhibits a transition from indirect to direct gaps, while the frequency of the Raman peaks shift away from those of the bulk sample12,13.
Tungsten ditelluride (WTe2) is a unique TMD as it has the large interlayer spacing, an orthorhombic lattice structure and a semi-metal electronic structure1,14,15,16. This material has drawn extensive interest since the recent discovery of an extremely large magnetoresistance (XMR) effect in diamagnetic WTe2 single crystal, which has not been observed in other TMDs1. Such a fascinating feature implies potential spintronic applications for mono- and few-layer WTe2. However, to date no study has examined the physical properties of the 2D WTe2 system. Raman spectroscopy is a powerful tool for investigating the symmetries of 2D semiconductors; it is necessary, therefore, to characterize the Raman fingerprint of WTe2 as it evolves from a 3D to a 2D system.
This article reports the observation of Raman scattering in bulk and few-layer WTe2 samples. Six optical vibrational modes, 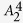 ,
, 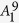 ,
,  ,
, 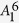 ,
, 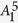 and
and 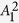 , were observed at room temperature. Density functional perturbation theory (DFPT) was used to calculate phonon branches, simulate Raman spectra and verify their corresponding optical phonons. Group analysis demonstrated that the lattice symmetry differentiated WTe2 from other TMDs17,18. In our experiments, WTe2 flakes, exfoliated from a piece of bulk, showed strong thickness-dependent Raman spectra. As the number of layers increased, the
, were observed at room temperature. Density functional perturbation theory (DFPT) was used to calculate phonon branches, simulate Raman spectra and verify their corresponding optical phonons. Group analysis demonstrated that the lattice symmetry differentiated WTe2 from other TMDs17,18. In our experiments, WTe2 flakes, exfoliated from a piece of bulk, showed strong thickness-dependent Raman spectra. As the number of layers increased, the 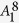 , and
, and 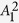 modes softened (red-shift) and the
modes softened (red-shift) and the 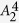 and
and 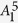 mode stiffened (blue-shift). It was also interesting to find that the
mode stiffened (blue-shift). It was also interesting to find that the 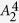 mode was absent in the monolayer. This phenomenon may be attributable to the transition of the point group from C2v to C2h. Our results provide a well-defined and reliable method for determining the number of layers using Raman spectroscopy.
mode was absent in the monolayer. This phenomenon may be attributable to the transition of the point group from C2v to C2h. Our results provide a well-defined and reliable method for determining the number of layers using Raman spectroscopy.
Results and Discussions
Figure 1a shows the layered crystal structure of WTe2, in which tungsten layers are sandwiched between two neighboring tellurium sheets. The distance (0.703 nm) between two adjacent sandwich layers is the largest of all known TMDs. Most TMDs exhibit a hexagonal structure with the space group D46h. However, naturally formed WTe2 reveals an orthorhombic unit cell with the space group C72v (Pmn21), which may be derived from a distorted hexagonal net1,15. The unit cell contains two tungsten atoms and four tellurium atoms. The two tungsten atoms (distinguished by W1 and W2) are not equivalent to each other and the W-Te bond length ranges from 2.7 to 2.8 Å. WTe2 bulk exhibits the Td stacking order, in which the atoms in the upper layer are rotated by 180 degrees with respect to those in the lower layer17. And the tungsten atoms shift away from the center of the octahedron formed by the tellurium atoms. Therefore, the vibrational modes of Td-WTe2 are very different from those of 2H-MX2, and the previous calculation of vibrational modes, based on 2H-WTe2, is inapplicable to our experimental Raman results19.
Figure 1. Lattice structure.
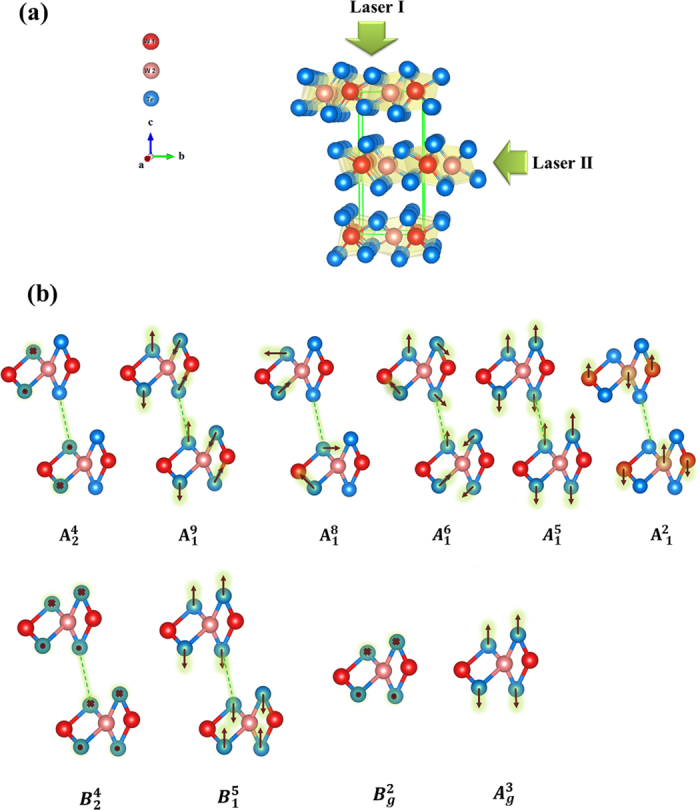
(a) Crystal structure of WTe2 along the a-axis direction, showing the orthorhombic unit cell. (b) Atomic displacements of Raman active modes in WTe2 bulk and monolayer. Here, “×” and “·” indicate that the Te atoms move into and out of the bc plane, respectively.
Due to the C72v symmetry group, the irreducible representations of the optical phonons in the bulk WTe2 at the center of the Brillouin zone (Γ point) are
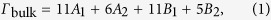 |
where all of the vibrational modes are Raman active, and the 11A1, 11B1 and 5B2 modes are infrared active. Here, the Raman tensors corresponding to different symmetries can be written as
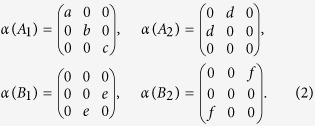 |
Although 33 Raman vibrations are predicted by group theory, only 6 Raman peaks were observed in our experiments. To distinguish these vibrational modes, we use 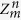 (Z = A or B; m = 1 or 2; n = integer) to represent them. The frequency of
(Z = A or B; m = 1 or 2; n = integer) to represent them. The frequency of 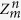 mode is smaller than that of
mode is smaller than that of 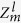 mode if n is larger than l. This method allows us to name all appropriate vibrational modes.
mode if n is larger than l. This method allows us to name all appropriate vibrational modes.
DFPT has been used to calculate all 33 Raman vibrational modes. Among them, the atomic displacements of the six Raman active modes that could potentially explain our Raman results are shown in Fig. 1b. The Raman spectra of WTe2 bulk at room temperature are presented in Fig. 2a. Raman peaks centered at ~109.8 cm−1, ~130.4 cm−1 ~162.5 cm−1 and 208.4 cm−1 were observed with Laser I applied in the z(xx)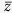 geometry. Another two Raman peaks, centered at ~119.6 cm−1 and ~139.1 cm−1, were observed with Laser II applied in the y(zz)
geometry. Another two Raman peaks, centered at ~119.6 cm−1 and ~139.1 cm−1, were observed with Laser II applied in the y(zz)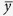 geometry. Due to the non-polarized Raman measurement, the
geometry. Due to the non-polarized Raman measurement, the 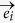 and
and 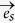 vectors are not along a- or c- axis in the either geometry. Thus, a total of six Raman peaks were identified in our experiments. Due to the non-polarized Raman measurements, the assignment of these Raman peaks could not be performed through symmetry analysis. Instead, we calculated the Raman intensities and spectrum (green curve in Fig. 2a) to verify the phonon modes corresponding to the observed Raman peaks. Only 6 Raman peaks were observed in comparison with 33 Raman modes in theory, which suggests that only those modes with high Raman intensities might appear experimentally. For example, Table 1 shows that for the first Raman peak (centered at ~109.8 cm−1), the
vectors are not along a- or c- axis in the either geometry. Thus, a total of six Raman peaks were identified in our experiments. Due to the non-polarized Raman measurements, the assignment of these Raman peaks could not be performed through symmetry analysis. Instead, we calculated the Raman intensities and spectrum (green curve in Fig. 2a) to verify the phonon modes corresponding to the observed Raman peaks. Only 6 Raman peaks were observed in comparison with 33 Raman modes in theory, which suggests that only those modes with high Raman intensities might appear experimentally. For example, Table 1 shows that for the first Raman peak (centered at ~109.8 cm−1), the 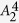 ,
, 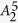 and
and 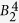 modes were all candidates, with frequencies close to ~110 cm−1. Only the
modes were all candidates, with frequencies close to ~110 cm−1. Only the 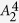 mode exhibited a sufficiently strong Raman intensity, whereas the intensities of the others were very weak. Therefore, the
mode exhibited a sufficiently strong Raman intensity, whereas the intensities of the others were very weak. Therefore, the 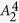 mode should be assigned to the first peak. Similarly, the
mode should be assigned to the first peak. Similarly, the 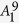 (~119.6 cm−1),
(~119.6 cm−1),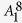 (~130.4 cm−1),
(~130.4 cm−1), 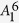 (~139.1 cm−1),
(~139.1 cm−1), 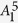 (~162.5 cm−1) and
(~162.5 cm−1) and 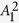 (~208.4 cm−1) modes were assigned frequencies from low to high, which agrees with the results in ref. 20. It should be noted that although the
(~208.4 cm−1) modes were assigned frequencies from low to high, which agrees with the results in ref. 20. It should be noted that although the 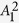 mode was associated with the peak centered at ~208.4 cm−1, the
mode was associated with the peak centered at ~208.4 cm−1, the 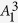 mode still exhibited a strong Raman intensity theoretically and could not be neglected. It is very possible that the
mode still exhibited a strong Raman intensity theoretically and could not be neglected. It is very possible that the 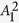 and
and 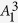 modes both exist, but the difference between their frequencies is so small that they cannot be distinguished in the Raman spectra.
modes both exist, but the difference between their frequencies is so small that they cannot be distinguished in the Raman spectra.
Figure 2. Experimental and calculated phonons.
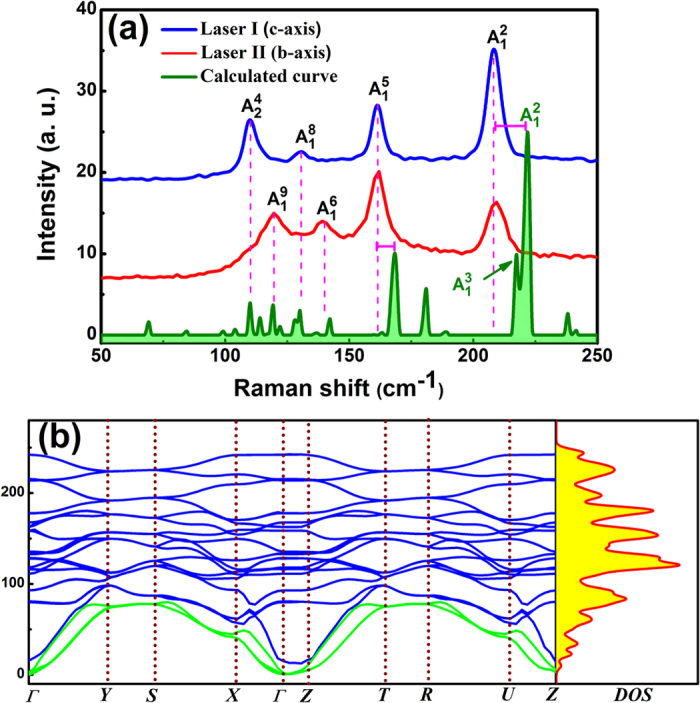
(a) Raman spectra of the bulk sample with incident Laser I and Laser II along the c- and b-axes at room temperature, respectively. The calculated Raman spectrum is plotted for comparison. (b) Calculated phonon dispersion curve along the Γ-Y-X-Γ-Z direction in the orthorhombic Brillouin zone (BZ), and the vibrational density of states (DOS) for WTe2 bulk at the equilibrium volume. The blue and green curves are the optical and acoustic vibrational branches, respectively.
Table 1. All of the possible optical phonons investigated through calculations and experiments.
| Symmetry | Raman Activity | Infrared Activity | Experimental Frequency (cm−1) | Calculated Frequency (cm−1) |
|---|---|---|---|---|
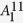 |
Y | Y | 10.9 | |
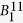 |
Y | Y | 23.9 | |
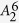 |
Y | N | 29.7 | |
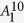 |
Y | Y | 69.3 | |
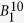 |
Y | Y | 84.8 | |
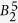 |
Y | Y | 99.3 | |
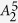 |
Y | N | 103.9 | |
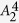 |
Y | N | 109.8 | 110.0 |
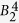 |
Y | Y | 112.5 | |
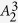 |
Y | N | 114.0 | |
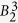 |
Y | Y | 117.4 | |
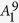 |
Y | Y | 119.6 | 119.4 |
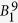 |
Y | Y | 122.1 | |
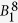 |
Y | Y | 127.9 | |
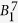 |
Y | Y | 129.5 | |
 |
Y | Y | 130.4 | 130.0 |
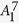 |
Y | Y | 136.0 | |
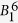 |
Y | Y | 137.3 | |
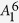 |
Y | Y | 139.1 | 142.3 |
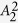 |
Y | N | 160.0 | |
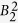 |
Y | Y | 160.1 | |
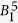 |
Y | Y | 163.3 | |
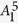 |
Y | Y | 162.5 | 168.5 |
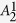 |
Y | N | 180.1 | |
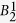 |
Y | Y | 181.2 | |
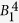 |
Y | Y | 188.6 | |
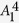 |
Y | Y | 189.7 | |
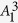 |
Y | Y | 217.3 | |
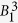 |
Y | Y | 218.1 | |
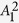 |
Y | Y | 208.4 | 222.2 |
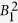 |
Y | Y | 223.1 | |
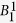 |
Y | Y | 238.1 | |
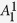 |
Y | Y | 241.7 |
“Y” or “N” indicates that the chosen mode is allowed or forbidden.
As shown in Fig. 1b, the first five modes originate from the relative movements of Te atoms, while the 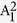 mode is due to the displacement between adjacent W1 and W2 atoms.
mode is due to the displacement between adjacent W1 and W2 atoms. 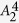 and
and 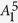 are pure longitudinal and transverse optical modes, respectively. For the in-plane configuration [z(xx)
are pure longitudinal and transverse optical modes, respectively. For the in-plane configuration [z(xx) , the B1 and B2 modes are forbidden due to the forms of their Raman tensors. In the case of the out-of-plane configuration [y(zz)
, the B1 and B2 modes are forbidden due to the forms of their Raman tensors. In the case of the out-of-plane configuration [y(zz)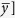 , the
, the 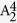 mode may be forbidden and the
mode may be forbidden and the 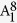 Raman intensity vanishes. Instead, the
Raman intensity vanishes. Instead, the 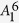 and
and 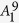 modes reveal significant Raman intensities. Here when we state that one mode is “forbidden”, it means that this Raman mode is prevented from observing by group theory or unable to exist on account of the DFPT calculation, while “vanish” means a Raman mode is active in theory, but in a certain configuration its intensity is too weak to observe due to the specific parameters in its Raman tensor. To clarify this phenomenon, the relationship between Raman intensity and Raman tensor can be written as21
modes reveal significant Raman intensities. Here when we state that one mode is “forbidden”, it means that this Raman mode is prevented from observing by group theory or unable to exist on account of the DFPT calculation, while “vanish” means a Raman mode is active in theory, but in a certain configuration its intensity is too weak to observe due to the specific parameters in its Raman tensor. To clarify this phenomenon, the relationship between Raman intensity and Raman tensor can be written as21
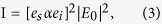 |
where es and ei are the scattered light and incident light vectors, respectively. This equation makes it easy to understand the anisotropy of the 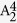 mode. The specific values of a, b and c in the Raman tensors of the
mode. The specific values of a, b and c in the Raman tensors of the 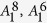 and
and 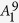 modes determine the dependence on the laser configuration. In the case of Laser I, the
modes determine the dependence on the laser configuration. In the case of Laser I, the 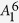 and
and 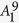 modes with very small values of a and b vanish, while the
modes with very small values of a and b vanish, while the 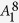 mode appears due to its large value of b. There is a similar effect for Laser II: the
mode appears due to its large value of b. There is a similar effect for Laser II: the 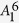 and
and 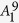 modes appear due to their large c values and the
modes appear due to their large c values and the 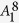 mode vanishes due to its very small a and c values. The a, b and c values of the
mode vanishes due to its very small a and c values. The a, b and c values of the 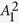 and
and 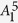 modes are large enough for them to be observed in both configurations.
modes are large enough for them to be observed in both configurations.
Figure 2b shows the calculated phonon dispersion curve in the Brillouin zone and the density of states for the WTe2 bulk. There are 3 acoustic (green curves) and 33 optical (blue curves) phonon branches. Table 1 shows all of the calculated and experimental vibrational modes. The calculated Raman intensities of the 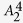 ,
, 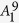 ,
, 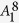 ,
, 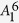 ,
, 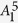 and
and 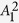 modes are strong at frequencies of ~110.0 cm−1, ~119.4 cm−1, ~130.0 cm−1, ~142.3 cm−1, ~168.5 cm−1 and 222.2 cm−1, respectively. The good agreement between the experimental and theoretical results supports our assignment of the Raman vibrational modes. It should be noted that all calculations were performed at zero temperature, while the Raman spectra were investigated at room temperature. Although frequencies of phonon modes depend on the temperature, it is unable to influence the assignment of the Raman modes. The frequency displacements between 5 K and 294 K were less than 4 cm−1 for all of the observed Raman peaks20. Such small displacements would not affect the association with specific phonon modes. In addition, the frequencies of all Raman peaks increase as the temperature increases, which may explain why most of the calculated frequencies were higher than those measured in the experiments.
modes are strong at frequencies of ~110.0 cm−1, ~119.4 cm−1, ~130.0 cm−1, ~142.3 cm−1, ~168.5 cm−1 and 222.2 cm−1, respectively. The good agreement between the experimental and theoretical results supports our assignment of the Raman vibrational modes. It should be noted that all calculations were performed at zero temperature, while the Raman spectra were investigated at room temperature. Although frequencies of phonon modes depend on the temperature, it is unable to influence the assignment of the Raman modes. The frequency displacements between 5 K and 294 K were less than 4 cm−1 for all of the observed Raman peaks20. Such small displacements would not affect the association with specific phonon modes. In addition, the frequencies of all Raman peaks increase as the temperature increases, which may explain why most of the calculated frequencies were higher than those measured in the experiments.
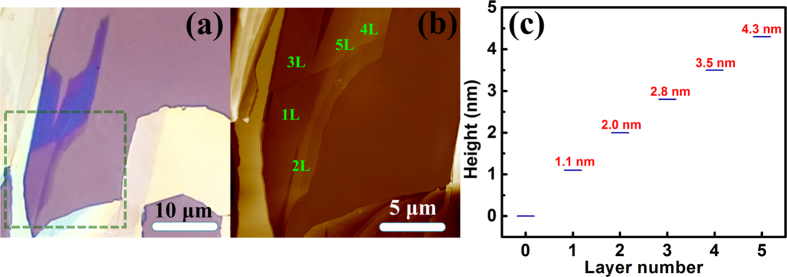
WTe2 flakes were fabricated on a Si substrate with a 300 nm SiO2 layer using the mechanical exfoliation method. As shown in Fig. 3a,b, an ultrathin WTe2 flakes was first identified by optical microscopy, and then imaged by atomic force microscopy (AFM) to determine its thickness. Figure 3c shows that the height of a monolayer WTe2 on the SiO2 layer is about 1.1 nm, while the height of the monolayer on the WTe2 flake is 0.7~0.9 nm and close to the interlayer spacing (about 0.703 nm) of the bulk.
Figure 3. Microscopic Imaging.
(a) Optical microscopic images of mono- to multilayer WTe2 on a Si substrate with a 300 nm SiO2 layer. (b) AFM image of the area (20 × 20 μm2) surrounded by a green dashed line in (a). (c) Height of the flake as a function of the layer number.
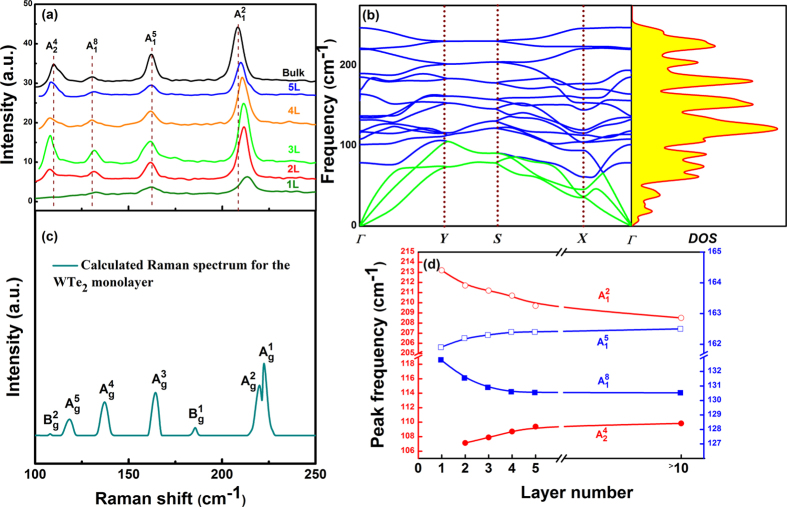
Figure 4a illustrates the Raman spectra of WTe2 as it evolved from bulk to monolayer. The four Raman active modes can be observed in the 2L, 3L, 4L and 5L samples. It is interesting to note that the 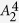 mode is absent in the 1L sample, which may make it convenient to use the Raman spectra to identify the WTe2 monolayer. The frequency difference between the
mode is absent in the 1L sample, which may make it convenient to use the Raman spectra to identify the WTe2 monolayer. The frequency difference between the 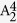 modes of the 2L sample and the bulk is about 2.7 cm−1. The
modes of the 2L sample and the bulk is about 2.7 cm−1. The 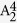 and
and 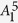 modes stiffen (blue-shift) in frequency as the number of layers increases, while the
modes stiffen (blue-shift) in frequency as the number of layers increases, while the 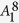 and
and 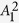 modes soften (red-shift). The
modes soften (red-shift). The 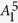 mode is the most stable and the displacement of its Raman shift, caused by the change in thickness, is less than 1 cm−1. In contrast, the
mode is the most stable and the displacement of its Raman shift, caused by the change in thickness, is less than 1 cm−1. In contrast, the 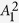 mode is found to be the most sensitive to the number of layers, and shifts up by about 4.8 cm−1 when the number of layers decreases to one.
mode is found to be the most sensitive to the number of layers, and shifts up by about 4.8 cm−1 when the number of layers decreases to one.
Figure 4. Raman evolution.
(a) Raman spectra of bulk and few-layer WTe2. (b) Calculated phonon dispersion curve along the Γ-Y-X-Γ direction in the orthorhombic BZ, and DOS for the WTe2 monolayer. Blue and green curves are optical and acoustic vibrational branches, respectively. (c) Calculated Raman spectrum for the WTe2 monolayer. (d) Frequencies of the 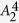 ,
, 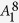 ,
, 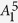 and
and 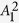 modes as functions of the layer number.
modes as functions of the layer number.
With WTe2 evolving from bulk to monolayer, its point group changes from C2v to C2h. The irreducible representation of the optical phonons in a WTe2 monolayer at the Brillion zone center (Γ point) is expressed as:
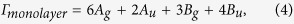 |
where 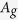 and
and 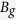 are Raman active;
are Raman active; 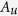 and
and 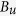 are infrared active. Only nine Raman-active modes are allowed in the WTe2 monolayer. This implies that some Raman peaks, observed in bulk, may be forbidden in the monolayer. Based on the group analysis, we calculated phonon dispersion curve in BZ, and DOS for WTe2 monolayer as shown in Fig. 4b. There are three acoustic (green curves) and fifteen optical (blue curves) phonon branches.
are infrared active. Only nine Raman-active modes are allowed in the WTe2 monolayer. This implies that some Raman peaks, observed in bulk, may be forbidden in the monolayer. Based on the group analysis, we calculated phonon dispersion curve in BZ, and DOS for WTe2 monolayer as shown in Fig. 4b. There are three acoustic (green curves) and fifteen optical (blue curves) phonon branches.
The vibrational modes of the WTe2 monolayer are exhibited in Table 2. To compare the vibrational modes of the bulk with those of the monolayer, we used the symmetry symbols of the C2v and C2h groups to name the corresponding modes, respectively. The atomic displacements of the Raman active modes were used to build a bridge between Raman modes of monolayer and bulk WTe2 as shown in Fig. 1b. Two of the vibrational modes in the bulk may correspond to the same modes in the monolayer. For example, the 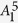 and
and 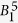 modes correspond to the
modes correspond to the 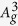 mode in Table 2, indicating that the
mode in Table 2, indicating that the 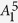 and
and 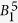 modes have the same atomic displacement as that of the
modes have the same atomic displacement as that of the 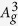 mode. For the
mode. For the 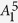 mode, the upper and lower atom layers exhibit the same phase of the atomic oscillations. But for the
mode, the upper and lower atom layers exhibit the same phase of the atomic oscillations. But for the 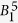 mode, the upper atom layer has an anti-phase with respect to the lower atom layer. Both of the modes can be distinguished in the multilayer samples (layer number ≥ 2), but turn into the
mode, the upper atom layer has an anti-phase with respect to the lower atom layer. Both of the modes can be distinguished in the multilayer samples (layer number ≥ 2), but turn into the 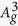 mode in the monolayer.
mode in the monolayer.
Table 2. The calculated vibrational modes of the WTe2 monolayer.
| Symmetry | Symmetry (bulk) | Experimental Frequency (cm−1) | Calculated Frequency (cm−1) |
|---|---|---|---|
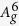 |
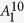 or or 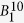
|
81.4 | |
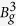 |
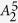 or or 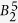
|
93.2 | |
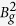 |
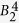 |
108.5 | |
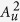 |
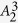 or or 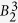
|
114.3 | |
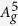 |
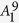 |
118.5 | |
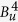 |
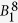 |
132.2 | |
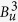 |
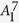 or or 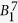
|
135.1 | |
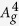 |
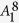 or or 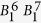
|
132.8 | 137.2 |
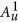 |
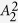 or or 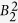
|
156.6 | |
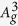 |
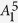 or or 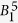
|
161.9 | 164.5 |
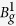 |
 or or 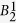
|
185.7 | |
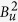 |
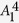 or or 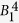
|
190.2 | |
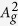 |
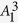 |
220.3 | |
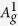 |
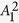 |
213.2 | 222.6 |
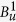 |
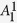 or or 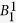
|
247.2 |
Our calculations show the 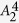 mode is forbidden in the monolayer, which consists with the experiments. Figure 4c shows the calculated Raman spectrum of the WTe2 monolayer. Only the
mode is forbidden in the monolayer, which consists with the experiments. Figure 4c shows the calculated Raman spectrum of the WTe2 monolayer. Only the 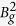 mode is a candidate to correspond to the
mode is a candidate to correspond to the 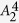 mode. However, Fig. 1b demonstrates that the atomic displacement of the
mode. However, Fig. 1b demonstrates that the atomic displacement of the 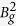 mode is different from that of the
mode is different from that of the 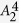 mode, but the same as that of the
mode, but the same as that of the 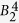 mode. Therefore, the
mode. Therefore, the 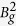 mode corresponds to the
mode corresponds to the 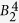 mode instead of the
mode instead of the 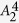 mode. On the basis of the theoretical analysis, the transition of point group from C2v (bulk) to C2h (monolayer) may be responsible for the absence of the
mode. On the basis of the theoretical analysis, the transition of point group from C2v (bulk) to C2h (monolayer) may be responsible for the absence of the 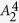 mode. In addition, the atomic displacement of the
mode. In addition, the atomic displacement of the 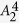 mode shows that only the half of tellurium atoms participate in oscillation, while the other half remains still (see Fig. 1b). In contrast to WTe2 bulk, all of the tellurium atoms participated in oscillation in the monolayer. This phenomenon may be attributed to the interlayer Van der Waals forces which are a dominant interaction between the adjacent atom layers. The loss of Van der Waals forces in the monolayer caused its atomic displacements to differ from those of bulk.
mode shows that only the half of tellurium atoms participate in oscillation, while the other half remains still (see Fig. 1b). In contrast to WTe2 bulk, all of the tellurium atoms participated in oscillation in the monolayer. This phenomenon may be attributed to the interlayer Van der Waals forces which are a dominant interaction between the adjacent atom layers. The loss of Van der Waals forces in the monolayer caused its atomic displacements to differ from those of bulk.
The frequencies of the four modes as a function of the number of layers are shown in Fig. 4d. The 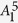 and
and 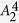 modes stiffen and the
modes stiffen and the 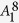 , and
, and 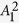 modes soften as the WTe2 monolayer evolves into a bulk. This implies that not only the interlayer Van der Waals coupling, but also stacking-induced structural changes or long-ranged Coulombic interlayer interaction may affect the atomic vibration9,22. If only Van der Waals coupling influenced the atomic vibrations, the
modes soften as the WTe2 monolayer evolves into a bulk. This implies that not only the interlayer Van der Waals coupling, but also stacking-induced structural changes or long-ranged Coulombic interlayer interaction may affect the atomic vibration9,22. If only Van der Waals coupling influenced the atomic vibrations, the  ,
, 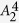 ,
, 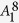 and
and 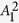 modes should all stiffen with layer number increasing10,23. The softening of the
modes should all stiffen with layer number increasing10,23. The softening of the 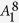 , and
, and 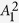 modes indicates that stacking-induced structural changes or long-ranged Coulombic interlayer interaction also plays an important role in the atomic vibration9,10,22. Our calculated results for the WTe2 monolayer confirm the shift directions of these vibrational modes.
modes indicates that stacking-induced structural changes or long-ranged Coulombic interlayer interaction also plays an important role in the atomic vibration9,10,22. Our calculated results for the WTe2 monolayer confirm the shift directions of these vibrational modes.
In summary, we studied bulk and few-layer WTe2 using Raman spectroscopy. The six first-order Raman-active modes observed at room temperature differed from those of all other TMDs. DFPT and group theory were used to analyze the frequencies of the Raman peaks and their corresponding vibration modes. The Raman peaks were found to correlate with the optical phonons of 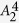 ,
, 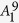 ,
, 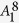 ,
, 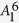 ,
, 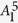 and
and 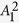 . The
. The 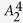 mode was forbidden in the monolayer due to the transition of the point group from C2v (bulk) to C2h (monolayer). As the number of layers increased, the
mode was forbidden in the monolayer due to the transition of the point group from C2v (bulk) to C2h (monolayer). As the number of layers increased, the 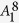 , and
, and 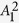 modes softened and the
modes softened and the 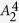 and
and 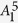 modes stiffened. Our study characterized all of the Raman peaks observed in bulk and few-layer WTe2 and provides a route to study the physical properties of 2D WTe2.
modes stiffened. Our study characterized all of the Raman peaks observed in bulk and few-layer WTe2 and provides a route to study the physical properties of 2D WTe2.
Methods
The WTe2 single crystals were prepared using a chemical vapor transport method described by ref. 1. WTe2 flakes were mechanically exfoliated from a piece of bulk single crystal onto Si wafers covered with a 300-nm-thick SiO2 layer. The few-layer samples were first identified by optical microscopy, and then measured by atomic-force microscopy (AFM) to determine the thickness. Micro-Raman spectroscopy was used to analyze the WTe2 under ambient conditions. Non-polarized and off-resonance Raman measurements were performed with a 514.5-nm excitation laser. When the WTe2 flakes were investigated, the power of the excitation laser was reduced to 0.5 mW to obtain reliable Raman spectra against the oxidation. Our calculation and analysis were performed on basis of DFPT and group theory, using the experimental lattice parameters a = 3.496 Å, b = 6.282 Å and c = 14.07 Å and the same wavelength of the incident light as that in experiments14. The exchange correlation potential was represented by the local density approximation (LDA). The Brillouin zone integrations were performed with a 16×8×4 Monkhorst-Pack k-point mesh by using a plane-wave energy cutoff of 500 eV. All DFPT calculations model was appropriate for explaining the Raman spectrum using the CASTEP code24.
Additional Information
How to cite this article: Jiang, Y. C. et al. Raman fingerprint for semi-metal WTe2 evolving from bulk to monolayer. Sci. Rep. 6, 19624; doi: 10.1038/srep19624 (2016).
Acknowledgments
The authors thank Dr. An Zhao, Dr. Bairen Zhu and Dr. Xiangbo Liu for their fruitful discussions, and Miss Manxiu Feng for her technique support. This work has been supported by the National Key Project for Basic Research (No. 2014CB921002), the National Natural Science Foundation of China (Grant No. 11504254, 11374225, 11574227, 11304193), and the Research Grant Council of Hong Kong (Project code: 701813). This work is also supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions and the USTS Cooperative Innovation Center for Functional Oxide Films and Optical Information.
Footnotes
Author Contributions J.G. proposed and led the project. Y.C.J. designed and did all the experiments. Y.C.J. and L.W. performed the DFPT calculations. Y.C.J. and J.G. wrote the manuscript and prepared all figures together.
References
- Ali M. N. et al. Large, non-saturating magnetoresistance in WTe2. Nature 514, 205–208 (2014). [DOI] [PubMed] [Google Scholar]
- Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A. Single-layer MoS2 transistors. Nat. Nano. 6, 147–150 (2011). [DOI] [PubMed] [Google Scholar]
- Coleman J. N. et al. Two-dimensional nanosheets produced by liquid exfoliation of layered materials. Science 331, 568–571 (2011). [DOI] [PubMed] [Google Scholar]
- Geim A. K. & Grigorieva I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013). [DOI] [PubMed] [Google Scholar]
- Gong Y. et al. Vertical and in-plane heterostructures from WS2/MoS2 monolayers. Nat. Mater. 13, 1135–1142 (2014). [DOI] [PubMed] [Google Scholar]
- Zeng H., Dai J., Yao W., Xiao D. & Cui X. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nano. 7, 490–493 (2012). [DOI] [PubMed] [Google Scholar]
- Zeng H. et al. Optical signature of symmetry variations and spin-valley coupling in atomically thin tungsten dichalcogenides. Sci. Rep. 3, 1608 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novoselov K. S. et al. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 102, 10451–10453 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C. et al. Anomalous Lattice Vibrations of Single- and Few-Layer MoS2. ACS Nano 4, 2695–2700 (2010). [DOI] [PubMed] [Google Scholar]
- Li H. et al. From Bulk to Monolayer MoS2: Evolution of Raman Scattering. Adv. Funct. Mater. 22, 1385–1390 (2012). [Google Scholar]
- Yamamoto M. et al. Strong Enhancement of Raman Scattering from a Bulk-Inactive Vibrational Mode in Few-Layer MoTe2. ACS Nano 8, 3895–3903 (2014). [DOI] [PubMed] [Google Scholar]
- Mak K. F., Lee C., Hone J., Shan J. & Heinz T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 105, 136805 (2010). [DOI] [PubMed] [Google Scholar]
- Splendiani A. et al. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 10, 1271–1275 (2010). [DOI] [PubMed] [Google Scholar]
- Brown B. The crystal structures of WTe2 and high-temperature MoTe2. Acta Crysta. 20, 268–274 (1966). [Google Scholar]
- Mar A., Jobic S. & Ibers J. A. Metal-metal vs tellurium-tellurium bonding in WTe2 and its ternary variants TaIrTe4 and NbIrTe4. J. Am. Chem. Soc. 114, 8963–8971 (1992). [Google Scholar]
- Kabashima S. Electrical Properties of Tungsten-Ditelluride WTe2. J. Phys. Soc. Jpn. 21, 945–948 (1966). [Google Scholar]
- Augustin J. et al. Electronic band structure of the layered compound Td-WTe2. Phys. Rev. B 62, 10812–10823 (2000). [Google Scholar]
- Rousseau D. L., Bauman R. P. & Porto S. P. S. Normal mode determination in crystals. J. Raman Spectrosc. 10, 253–290 (1981). [Google Scholar]
- Ataca C., Şahin H. & Ciraci S. Stable, Single-Layer MX2 Transition-Metal Oxides and Dichalcogenides in a Honeycomb-Like Structure. J. Phys. Chem. C 116, 8983–8999 (2012). [Google Scholar]
- Kong W.-D. et al. Raman scattering investigation of large positive magnetoresistance material WTe2. Appl. Phy. Lett. 106, 081906 (2015). [Google Scholar]
- Bower D. I. Investigation of Molecular Orientation Distributions by Polarized Raman Scattering and Polarized Fluorescence. J. Polym. Sci. Polym. Phys. Ed. 10, 2135–2153 (1972). [Google Scholar]
- Wieting T. J. & Verble J. L. Interlayer Bonding and the Lattice Vibrations of β-GaSe. Phys. Rev. B 5, 1473–1479 (1972). [Google Scholar]
- Bagnall A. G., Liang W. Y., Marseglia E. A. & Welber B. Raman studies of MoS2 at high pressure. Physica 99B, 343 (1980). [Google Scholar]
- Clark S. J. et al. First principles methods using CASTEP. Z. Kristallogr 220, 567 (2005). [Google Scholar]