Optimal acquisition and modeling parameters for accurate assessment of low K_trans blood-brain barrier permeability using dynamic contrast-enhanced MRI

Abstract

Purpose

To determine optimal parameters for acquisition and processing of dynamic contrast-enhanced (DCE) MRI to detect small changes in near normal low blood-brain barrier (BBB) permeability.

Methods

Using a contrast-to-noise ratio metric (K-CNR) for K_trans precision and accuracy, the effects of kinetic model selection, scan duration, temporal resolution, signal drift and length of baseline on the estimation of low permeability values was evaluated with simulations.

Results

The Patlak model was shown to give the highest K-CNR at low K_trans. The K_trans transition point, above which other models gave superior results, was highly dependent on scan duration and tissue extravascular extracellular volume fraction (v_e). The highest K-CNR for low K_trans was obtained when Patlak model analysis was combined with long scan times (10-30 minutes), modest temporal resolution (<60 seconds/image), and long baseline scans (1-4 minute). Signal drift as low as 3% was shown to affect the accuracy of K_trans estimation with Patlak analysis.

Conclusion

DCE acquisition and modeling parameters are interdependent and should be optimized together for the tissue being imaged. Appropriately optimized protocols can detect even the subtlest changes in BBB integrity and may be used to probe the earliest changes in neurodegenerative diseases such as Alzheimer’s disease and Multiple Sclerosis.

Introduction

Dynamic contrast-enhanced (DCE) MRI gives quantitative and semi-quantitative information about the integrity of the vascular system (1). It is commonly used to study a number of diseases such as cancer, stroke and multiple sclerosis (MS) (2-6). While originally developed to assess blood-brain barrier (BBB) integrity (7-10), it has also found many applications outside of the brain (3,11-14). The parameter of interest in BBB integrity is the transfer constant K_trans (15), which describes the transfer rate of molecules from plasma space into interstitial space. Since the BBB permeability to molecules is size and transporter dependent (16-18), interpretation of K_trans requires consideration of structural and physiological changes at play at the BBB as well as contrast agent (CA) being used to infer K_trans. Most applications of DCE in the brain have focused on imaging relatively high BBB breakdown (such as observed in malignant tumors or stroke), rather than on subtle changes in the BBB, using small molecule CA. This is in part driven by the fact that CA extravasation in the highly compromised BBB is high, resulting in easier detection of the CA signal. K_trans values in the intact or subtly damaged BBB are at least one to two orders of magnitude lower than those found when the BBB is highly compromised (8,19,20). Thus, it is much more difficult to measure.

Recent studies indicate a pathophysiological role for the BBB in diabetes (21), cognitive disorders such as mild cognitive impairment (MCI) (20,22), Alzheimer’s disease (AD) (23,24), MS (6,25-28) and chronic traumatic encephalopathy (CTE) (29-31). Although dysfunctional, changes in BBB integrity for these conditions are thought to be subtle and close to intact values (32). Early attempts to measure K_trans in the normal appearing brain for MCI and AD failed to detect significant changes (33,34). These studies may have been hampered by their relatively long sampling interval and the semi-quantitative nature of their analyses. More recent studies acquired at higher field strengths and using more sophisticated kinetic modeling have determined that the K_trans of healthy BBB is low but not zero and detected differences in MS patients compared to controls (19,26,28) as well as increases during normal aging and in MCI patients(20). K_trans from these studies are within a range of previously reported BBB K_trans values using small inert polar molecules in mammals (32,35,36).

Despite these developments and recent successes (19,20,26,28), optimal methods to collect and analyze DCE data in order to detect subtle changes to BBB integrity remain unclear (1,37,38). This imaging effort poses a distinct set of challenges because the contrast changes are much lower and it can take much longer for detectable leakage to occur. This places considerable demands on the imaging sequence and post-processing used to minimize noise and maximize contrast to detect these subtle changes (25,37).

The few studies that have applied DCE in the low permeability regime have used a wide range of different techniques. Taheri et al introduced a serial T₁ mapping technique with low CA concentration (0.025 mmol/kg) injection, finding differences in white matter permeability between controls (K_i ≈ 3 ∗ 10⁻⁴ mL·g⁻¹·min⁻¹, K_i = K_trans/[1-hematocrit]) and MS patients (28). Using a multiple dose injection protocol and a data-driven post-processing, Ingrisch et al reported differences between normal appearing white matter and MS lesions (6). They noted that a two compartment uptake model (8) was appropriate at the low permeability regime. Larsson and colleagues reported that the Patlak model can estimate low vascular permeability well (K_i ≈ 0.1 mL/100mL/min for normal brain tissue) (25,26). They also proposed that the combination of model-free estimation of perfusion (using the Tikhonov’s method, Tik) and the two-compartment exchange model (2CXM) can estimate BBB permeability across a wider range of K_trans (19). In a subsequent study, Cramer et al compared the ability of Patlak, extended-Tofts and Tik-2CXM to estimate K_trans, reporting the threshold for accurate Patlak estimation to be K_i ≈ 0.3 mL/100g/min (25). Accuracy of the extended Tofts model was shown to be very sensitive to blood volume and perfusion compared to the other two models. The authors also examined the effects of sampling interval and acquisition duration on K_trans estimation, finding that the use of short sampling intervals and long acquisition times to be the most accurate. Recent work using the Patlak model with high spatial resolution and short sampling intervals clearly shows that low K_trans determinations are possible and provide crucial information about BBB dysfunction (20).

While these findings provide some guidelines on acquisition parameters and post-processing methodology, it remains unclear from the published studies under what circumstances these recommendations hold. Most notably, the two parameters that dramatically affect the appropriateness of the Patlak model, imaging time and v_e (extravascular extracellular volume fraction), have not been examined. It therefore remains difficult to currently draw specific, quantitative recommendations for ongoing studies. Thus, quantitative analytical methods that simplify the evaluation of how the different experimental factors combine to influence the accuracy, reliability, and ability to resolve changes in the measured K_trans will greatly facilitate future study design.

Here, we introduce a metric, the contrast-to-noise ratio for K_trans (subsequently referred to as K-CNR), which enables quantitative comparison of different models to estimate DCE vascular permeability. We demonstrate how K-CNR simplifies model selection analysis at low K_trans given specific acquisition parameters. Conversely, using the Patlak model as an example, we show how K-CNR can guide the selection of optimized image acquisition parameters to maximize the model’s ability to resolve differences at low K_trans. The impact of temporal resolution, acquisition time, signal drift and the number of baseline images on K-CNR are examined for a variety of physiological conditions.

Methods

DCE Simulations

A population averaged curve published by Parker et al (39) was modified for use as the simulated arterial input function (AIF). Briefly, the AIF curve is a mixture of two Gaussians plus two exponentials modulated with a sigmoid function:

$$C_a\left(t\right)=\sum _{n=1}^2\frac{A_n}{{\sigma }_n\sqrt{2\pi }}{e}^{-{(t-T_n)}^2∕2{\sigma }_n^2}+{\alpha }_n{e}^{-{\beta }_{n}t}∕(1+e^{-s(t-\tau )})$$ (1)

where C_a is the arterial plasma concentration, A_n, T_n, and σ_n are the scaling constants, centers and widths of the n^th Gaussian; α and β are the amplitude and decay constant of the exponential; s and τ are the width and center of the sigmoid, respectively. To provide an AIF curve mimicking the behavior in our clinical datasets, different input parameters for Equation 1 were used for our simulations compared to those defined by Parker et al. The amplitude of the first pass bolus was lowered, and the bi-exponential decay constant was altered to accommodate the longer blood half-life of the MultiHance^® (Bracco, Milan, Italy) CA used at our site. The parameters were manually adjusted to fit our population-averaged AIF.

Simulated tissue curves were generated by a convolution of the impulse response for a 2CXM with the AIF (40). The 2CXM is described by:

$$C\left(t\right)=({\mathrm{F}}_{+}{e}^{-t{K}_{+}}+\mathrm{F}\_e^{-t{K}_{-}})\otimes C_a\left(t\right)$$ (2)

where “⊗” is convolution and F_± and K_± are defined elsewhere (40). The free parameters used to define the 2CXM are K_trans, v_e, v_p and F_p; where K_trans is the blood-tissue transfer constant, v_e is the extravascular extracellular volume fraction, F_p is plasma flow and v_p is plasma volume fraction. Unless stated otherwise these parameters were set to v_e = 0.05, v_p = 0.025, and F_p = 0.130 ml/min/ml assuming 1g = 1ml. These values are within expected physiological ranges (41-45), and similar to average 2CXM values measured in our healthy controls.

The AIF curve and tissue curves were generated at sampling intervals of 100 ms and 1 second respectively. These intervals are significantly faster than the rate of change of the curves and capture all features of the curves; a longer interval was used for the tissue curve to take advantage of its slower rate of change to reduce computation time. The temporal resolution of DCE-MRI studies is known to influence the accuracy of parameter estimation (11,25,46-50). Thus, the generated tissue curves and the AIF were down-sampled to study the effect of temporal resolution on K_trans analysis. This was done using a Gaussian filter with the standard deviation equal to a third of the sampling window of the desired temporal resolution. This incorporates all the information in the sampling window and simulates the center weighting imposed by k-space sampling.

To evaluate the effect of signal-to-noise ratio (SNR) on DCE analysis, MR-realistic noise was added to achieve the stated SNR levels by adding Gaussian noise to the real and imaginary channels (the MR signal was assumed to be real) and then taking the modulus. The AIF and tissue concentration curves were converted to MRI signal intensity curves using the standard spoiled gradient echo (SPGR) equation at steady state (51), with TR=8.3 ms, FA=15°, blood pre T₁=1200 ms, and tissue pre T₁=1800 ms. The stated SNR values are the SNR in the tissue prior to CA injection. Unless otherwise stated we defined SNR=30 as this reflects the SNR observed in our clinical datasets. These noise-added signal intensity curves were then converted back into concentration curves and used to calculate the DCE parameters.

Timing alignments between the AIF and sampling window may also affect the accuracy and precision of K_trans measurement (50), AIF and tissue curve simulation studies were also performed with jitter offsets at 2 second interval increments within each sampling interval. This was only done for datasets with sampling intervals greater than 2 seconds.

Accuracy and precision of K_trans estimation using different models and acquisition variables for different tissue parameters were assessed using the K-CNR (see below) by adding noise (as described above) and fitting 1000 times per parameter combination. The effect of the number of baseline images was evaluated by generating and fitting curves with baselines ranging from 15 to 240 s prior to CA injection.

To explore the effect of signal drift, a constant ranging from −10% to +10% of the baseline signal was added to the generated AIF and tissue curves prior to noise addition and K_trans estimation. To simulate drift correction, a noise-added phantom (to serve as an intensity standard) with signal intensity equivalent to half the maximal AIF intensity was used to derive correctional scaling factors across the time series. Robust fitting of the scaling factor versus time curve to a fourth-order polynomial was performed to minimize the noise amplification of using the scaling factor directly. K_trans was estimated using scale factor-corrected AIF and tissue curves and compared to their uncorrected counterparts.

Clinical studies

Subjects

Participants with no significant history of neurological disease were recruited through the University of Southern California (USC) from May 2013 to May 2014. The study was approved by the USC Institutional Review Board. All participants signed informed consent. We enrolled six participants of both genders with ages 23-47. All procedures were performed at the Keck Medical Center of USC. All participants underwent a medical examination as well as blood draw to ensure appropriate kidney function for CA administration. MRI scans were screened and no subcortical white matter lesions were found on any subjects. MRI scans of the brain were performed on a total of six participants.

Magnetic resonance imaging

All images were obtained on a GE 3T HDXT MR scanner with a standard eight-channel array head coil. Anatomical coronal spin echo T2-weighted scan were first obtained through the hippocampi (TR/TE 1550/97.15 ms, NEX = 1, slice thickness 5 mm with no gap, FOV = 188 × 180 mm, matrix size = 384 × 384). Baseline coronal T1-weighted maps were then acquired using a T1-weighted 3D SPGR pulse sequence and variable flip angle method using flip angles of 2°, 5° and 10°. (TR/TE = 8.29/3.08 ms, NEX = 1, slice thickness 5 mm with no gap, FOV 188 × 180 mm, matrix size 160 × 160). Coronal DCE MRI covering the hippocampi and temporal lobes were acquired using a T1-weighted 3D SPGR pulse sequence (FA = 15°, TR/TE = 8.29/3.09 ms, NEX = 1, FOV 180 × 135 × 60 mm, matrix size 160 × 120 × 12, voxel size was 1.125 × 1.125 × 5 mm³). This sequence was repeated for a total of 16 minutes with an approximate temporal resolution of 15.4 seconds. Multihance (0.05 mmol/kg) was administered intravenously into the antecubital vein using a power injector, at a rate of 3mL/sec followed by a 25mL saline flush, 30 seconds into the DCE scan.

DCE data analysis

Post-processing of the collected MRI data and simulated data was done using in-house DCE processing software implemented in Matlab (The MathWorks Inc., Natick, MA). Plasma concentrations were assumed with Hct=0.45 for all cases. For the acquired data the AIF was obtained from the common carotid artery.

Three different kinetic models were examined: Patlak, extended Tofts, and the 2CXM.

The 2CXM, introduced above, is the most general model considered in this analysis with four free variables. The 2CXM assumes two well-mixed compartments (blood plasma and extracellular extravascular tissue) and allows for general transport back and forth between these compartments. Blood flow is considered finite, so mixing in the capillaries is assumed.

The extended Tofts model is a simplification of the 2CXM, with three free variables it assumes minimal mixing occurs in the capillaries (F_p=∞), and is defined by:

$$C\left(t\right)=v_p{C}_a\left(t\right)+{\mathrm{K}}_{trans\cdot }{e}^{-t\cdot Ktrans{∕}_{Ve}}\otimes C_a\left(t\right)$$ (3)

The Patlak model is a simplification of the extended Tofts, with two free variables it assumes minimal back-flux from the tissue back to the arteries, or equivalently that C_a(t)>>C(t). It is defined by:

$$C\left(t\right)=v_p{C}_a\left(t\right)+{\mathrm{K}}_{trans}\otimes C_a\left(t\right)$$ (4)

All these models assume well mixed compartments; a thorough analysis of the mathematics and assumptions has been examined in a recent review (15).

The experimental data were converted to concentration curves using the acquired T₁ maps and the standard steady state incoherent equation.

$$SI=\frac{\rho \sin \theta (1-e^{-TR∕T1})}{(1-e^{-TR∕T1}\cos \theta )}$$ (5)

The concentration curves were fitted to equations (2)-(4) using non-linear fitting routines with the trust-region-reflective algorithm in Matlab. To ensure that the fitting converges on a global minimum, tolerances were set to 10⁻¹², 10⁻, 50, and 50 for the function tolerance, parameter tolerance, maximum iterations, and maximum function evaluations respectively. Multiple starting locations of K_trans were used during the fit convergence process with the minimal residual used as the final value. Other kinetic parameters were less sensitive to initial starting values; thus, this strategy was not used in those cases.

To assess the impact of different imaging parameters to accurately measure and detect group changes in K_trans during simulations, we define a K-CNR metric, which estimates the CNR that would be observed for a 10% change in K_trans:

$$K-CNR=\frac{\partial K_{trans\left(fitted\right)}}{\partial K_{trans}\left(true\right)}\cdot 0.1\cdot K_{trans\left(true\right)}∕\sigma$$ (6)

where K_trans(true) is the defined K_trans value used to generate the simulated curve, K_{trans(fitted)} is the median of the output K_trans values obtained by fitting the simulated curve with software. The derivative is the slope of the K_{trans(fitted)} versus K_trans(true), this is multiplied by 0.1·K_trans(true) to estimate the contrast observed for a 10% change in K_trans(true). σ is the standard deviation of the 1000 repetitions at that specific K_trans. The slope was estimated using a Savitzky-Golay filter (52) with a seven point quadratic polynomial kernel to suppress noise in the derivative calculation, and a three point moving average was applied to the K-CNR to reduce noise from the standard deviation term. This metric can be interpreted the same as CNR is normally interpreted, it is a respected measure of precision and contrast, and not directly sensitive to the accuracy of the model.

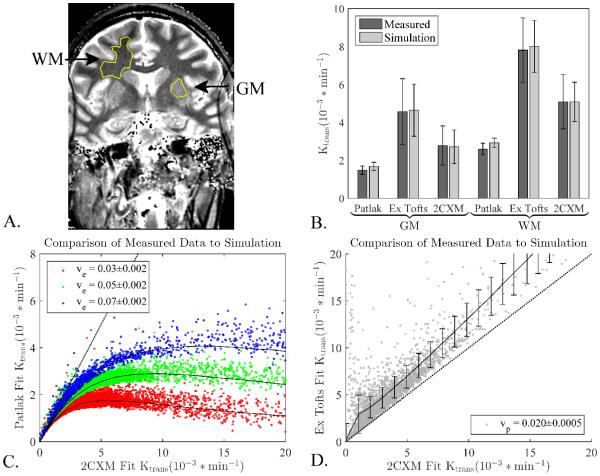
To ensure that the above simulation strategy was capable of generating realistic DCE curves that had the same characteristics of the measured clinical data, a number of steps were taken. First, the simulated curves were visually compared to the measured curves to ensure that no significant features of the curves were different and that the noise levels were similar. Once we had established that the curves were qualitatively the same a quantitative comparison was performed. Regions of interest (ROI) were drawn in normal appearing grey matter (GM) and white matter (WM) regions in control datasets (Figure 1A). The median values for all four parameters in the 2CXM derived from these ROIs were recorded. Simulated DCE curves were then generated using these values and the population AIF as described above. Curve fitting was performed using the three different models on the simulated curves and the fit values from the simulations were compared to the measured values in the subjects for all three different models. This ensured that the population AIF and noise addition used to generate the simulated curves did not significantly alter the characteristics of the curves. It also ensures that the simulated curves reflect the behavior of the measured curves for all three models (2CXM, extended Tofts, and Patlak). The 2CXM was used as it is the most general model; thus provides the best estimate of the true tissue values. Although the plasma flow values derived from this model might not be completely accurate due to the temporal resolution (15.4 seconds) of the DCE MRI data, the calculated median value of 0.13 ml/min/ml (or a blood flow of 0.29 ml/min/ml) is within the expected range (43) and so was considered sufficient for the simulations.

Figure 1.

Simulation results compared to collected data in healthy controls. A) Typical ROIs for a single subject. B) Mean values and standard deviations of measured K_trans values from GM and WM regions defined in the subjects correspond well to simulated results. Simulated curves were generated and all three models were fit to the simulated data to ensure that the population AIF and generating procedures would give values and noise characteristics similar to the measured data. The similar results for each model show that the simulated curves are representative of the real data. C) Each dot represents a voxel from a healthy control and the black lines are simulation results using the central v_e value measured from the clinical data, error bars on simulation results excluded for clarity. D) Same as C, but comparing extended Tofts to 2XCM and using the central v_p value measured from the clinical data. Error bars are the standard deviation. The measured voxels follow the simulation results extremely well showing the simulations captures the different behavior of each model. Dotted line indicates slope of unity, i.e. where Patlak or extended Tofts fit is identical to 2CXM fit.

Results

Simulation curve fits with 2CXM and Patlak are consistent with clinical data fits

Comparisons between measured data fits and simulated data fits are shown in Figure 1. For the various models, simulated and measured curves were not significantly different; with Patlak giving values lower than 2CXM, and extended Tofts higher than 2CXM (Figure 1B). The noise characteristics of the models were also accurately reproduced with the simulation matching very close to the measured data, again with extended Tofts showing the highest standard deviation, and Patlak the lowest.

The measured data were also compared against the simulations in a voxel-wise comparison. All brain voxels from the healthy controls were initially considered, then voxels were removed that had poor fits (approximately the top 8% of residuals) or v_p > 10% (to eliminate blood vessels). The fitted 2CXM values were compared to the fitted Patlak values for various v_e values. Simulation curves comparing 2CXM and Patlak values generated at the corresponding v_e were overlaid for comparison (Figure 1C). Simulations corresponded very well to the collected data for the majority of voxels, with the Patlak model showing the expected underestimation at higher K_trans values for both measured and simulated data. Comparison of 2CXM versus extended Tofts fitted values with their simulated counterparts showed a similar pattern at fixed v_p (Figure 1D), further supporting applicability of our simulations to reflect clinically measured data.

Patlak model provides good estimation of true values in low K_trans regimes

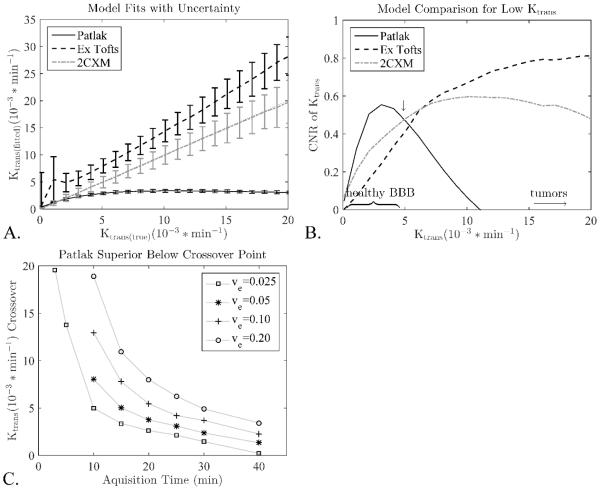
Different models were directly compared by fitting to the same simulated curves and examining their K-CNR (Figure 2A). The Patlak model had the highest K-CNR for low K_trans values, while extended Tofts and 2CXM had higher K-CNR at higher K_trans (Figure 2B). The exact crossover point between these two regimes depended on the acquisition time and the v_e value (Figure 2C).

Figure 2.

The much lower variance in the Patlak model leads to significantly better K-CNR values compared to the extended Tofts and 2CXM models at low K_trans. At higher K_trans significant backflux starts to flatten the Patlak response leading to a loss of contrast and lower CNR values. A) Median fits and standard deviations for the different models, This plot was used to calculate the K-CNR values. B) For a scan time of 15 minutes and a v_e=0.05 this crossover occurs around K_trans=5*10⁻³/min (arrow). C) Different scans times and v_e values lead to different cross over points, below which Patlak outperforms 2CXM model. For clarity only the crossover points for the 2CXM model are shown, the extended Tofts are almost identical.

Effects of acquisition time on K_trans estimation

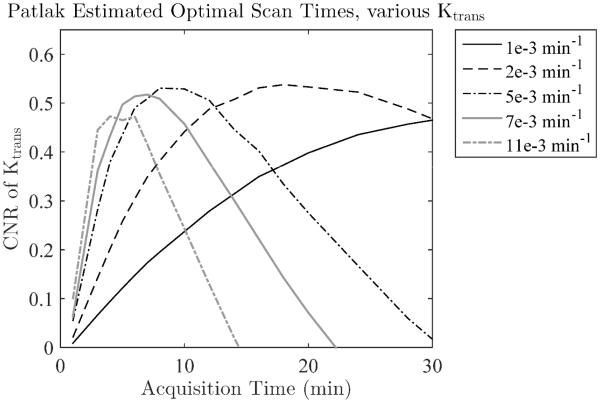
Since the Patlak model had the highest K-CNR in the range of K_trans values found in intact BBB, the Patlak model was further evaluated to determine the optimal acquisition time. As expected, the optimal acquisition time was found to depend on the K_trans value: shorter scan times give better K-CNR for higher K_trans values as this limits the amount of CA backflux that is captured during imaging, which confounds the Patlak K_trans estimation (Figure 3).

Figure 3.

The optimal scan time depends on the K_trans value for the Patlak model, as long scan times and high K_trans will lead to significant backflux and poor results. Scanning longer than 15 minutes is only beneficial for the very lowest K_trans values, and longer than 5 minutes leads to sharp drops in the K-CNR of K_trans > 10*10⁻³/min.

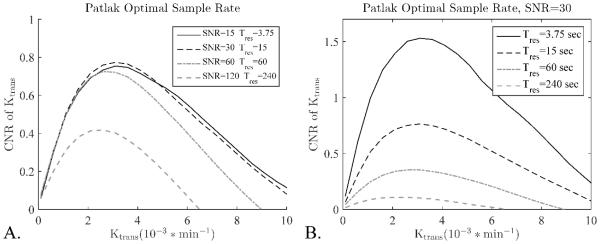
Effects of sampling rate on K_trans estimation

The effect of sampling rate on K-CNR was evaluated for the Patlak model in two different scenarios. First, the sampling interval was lengthened by a factor and the SNR was increased by the square root of the factor (Figure 4A). This simulates the scenario whereby additional averages were collected or if additional partitions were collected in a 3D scan to increase the field of view. Second, the sampling interval was lengthened with no change to the SNR (Figure 4B). This simulates the scenario whereby more slices were collected in a 2D scan to increase the FOV. When longer sampling intervals lead to increases in SNR, the K-CNR held mostly constant up to a sampling interval of 60 seconds, longer than that it fell significantly (Figure 4A). When changes in sampling interval had no effect on the SNR (SNR held constant), each lengthening in sampling interval caused a steady and significant reduction in the K-CNR (Figure 4B).

Figure 4.

The effect of sampling rate on K-CNR for the Patlak model depends on the effect adjusting the sampling interval has on the SNR of the scan, two different scenarios are considered. A) Lengthened sampling interval increases the SNR, as would happen by adding averages or increasing the matrix size and field of view together. Only small differences are seen between sampling intervals shorter than 60 seconds, while sampling intervals longer than 60 seconds lead to significant K-CNR loss. B) Changing the sampling interval has no effect on SNR (SNR is held constant), as would happen by adding or removing slices in a 2D scan. In this case longer sampling intervals lead to a consistent and significant decrease in the K-CNR.

Effects of baseline acquisition duration on K_trans estimation

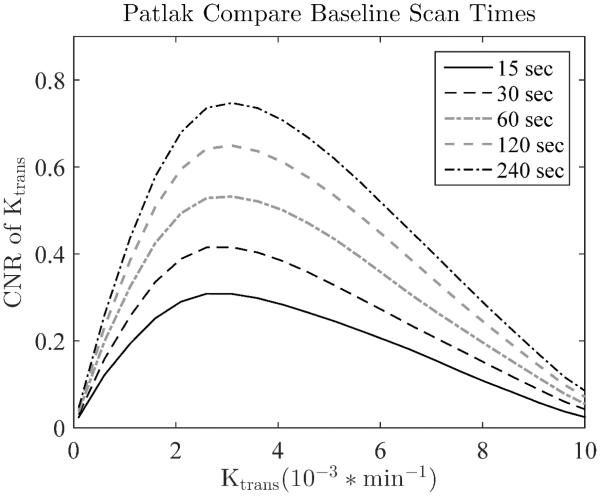
The length of the baseline scan was evaluated for its effect on the K-CNR values. From Figure 5, it can be seen that acquiring a longer baseline scan significantly increases the K-CNR of the calculated DCE parameters by reducing the variance of the fit values. Adding as little as 30 seconds to the baseline can increase the K-CNR by approximately 30% (moving from a 30 second to a 60 second baseline).

Figure 5.

The concentration curves for both the AIF and tissue are calculated relative to the baseline images collected before CA injection. Thus increasing the number of baseline images, and therefore baseline SNR, increases the SNR of all calculated values. This is probably the most efficient way to increase the SNR and CNR of the entire DCE study. Temporal resolutions was 15 sec.

Effects of signal drift on K_trans estimation

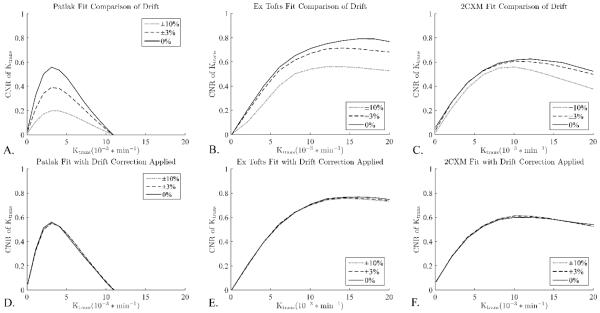
A constant linear drift up or down causes an under or over estimation of K_trans, respectively. This effect will be consistent in a single study, but across multiple studies variation in the drift will cause variations in the bias it introduces. This will show up as an additional source of variance and uncertainty for inter-study comparisons. To model this, a range of drifts were combined together for analysis. Figures 6 shows the effect of this increased variance on the K-CNR values, the drift causes decreases of K-CNR in all models, especially in the Patlak model (Figure 6A-C). Drift correction using an external intensity standard largely eliminated these discrepancies (Figures 6D-F).

Figure 6.

Drift correction improves precision for inter-study comparison. Patlak is especially sensitive to drift as its lower contrast makes it more sensitive to any increase in variance. Unlike the other variables considered here, signal drift is not a parameter than can be easily controlled or defined a priori. However, it can be largely corrected for using an intensity standard, a small tube of water placed in the FOV whose signal can be used to estimate and remove the drift.

Discussion

The comparison of the measured data to simulations showed excellent correspondence (Figure 1). This shows that the method of simulation curve generation provides realistic DCE curves that are nearly identical to real measured curves in both fitted values and noise characteristics. The fitted K_trans values from the 2CXM are reflective of more accurate values across the entire K_trans range; the extended Tofts generally overestimates K_trans; and Patlak does well at low permeability values (≤5 × 10⁻³ min⁻¹ ), but underestimates K_trans at larger values. These findings validate previous studies (6,25).

While this may suggest that one should apply the 2CXM across all K_trans, it is limited by several factors. The accuracy of the K_trans values in the extended Tofts and the 2CXM models are strongly affected by the temporal resolution used, likely due to their dependency on accurate perfusion and blood volume estimation (25). Given that 2CXM requires the fitting of four parameters, the potential for curve fitting error is high (25). Past studies examining how other models perform in K_trans estimation demonstrated that the Patlak model accurately estimates low K_trans values, consistent with the fact that the model neglects backflux (19,25). To date however, these studies have focused on the accuracy of K_trans estimations for the respective models. From Figure 2A, we see that K_trans precision is also important for model selection. Figure 2A shows that, while both 2CXM and Patlak may estimate low K_trans accurately, the error bounds are much smaller for Patlak. This has practical implications, especially when we wish to differentiate small differences in permeability. In these scenarios we show that Patlak will give a higher K-CNR due to its superior precision, and are able to predict the cross over point where 2CXM or Extended Tofts will start outperforming Patlak. The exact value of the crossover points, and its strong dependence on v_e and the acquisition time, has not been shown before. This superior sensitivity has enabled Patlak to detect small regional differences between grey and white matter due to its high precision (20).

The K-CNR metric captures both K_trans contrast and precision for each model in a single value. This enables facile evaluation of the suitability of different models in estimating K_trans as a functional of multiple imaging variables. Using the K-CNR metric, we show that the Patlak model clearly outperformed the other two models in the low K_trans regime due to its high precision (Figure 2). The precision is a direct result of the simplicity of the model, with only two free parameters it is less likely to fit the noise and is therefore very stable. Eventually the high precision is overwhelmed by its K_trans underestimation at higher K_trans values, resulting in a sharp drop in K-CNR. While K-CNR offers the ability to easily compare various models, it does not capture all aspects of image quality. In particular it is not the best measure of model accuracy. Despite this shortcoming it is a valuable tool to make clear comparisons across models for a wide variety of parameters.

The sensitivity of the Patlak model to backflux places direct limits on acquisition time, and is dependent on the K_trans and v_e of the tissue being measured. Higher K_trans values using the Patlak model can be accurately estimated if the acquisition time is kept sufficiently short (Figure 2C). This is generally an acceptable trade off; higher K_trans does not need long scan times to achieve sufficient K-CNR. However, at higher K_trans values the other models generally outperform Patlak even if the Patlak acquisition time is sufficiently short. Thus, if the tissue of interest is expected to have high K_trans then analysis with a different model will generally be more appropriate.

Acquisition times longer than 15 minutes can lead to significant improvement in the K-CNR using the Patlak model, but only for low K_trans values (K_trans < 2 * 10⁻³/min, Figure 3). Long scan times may be beneficial in normal healthy mice where very low K_trans values have been measured with DCE-MRI using Gd-DTPA (K_i = 0.6±1.9 * 10⁻³ mL/g/min (53)). However, they should not be necessary in humans, which show higher values in healthy brain ranging from 0.5 – 4.5 * 10⁻³/min as reported here and elsewhere (19,20,25-28). That scan times of 15 minutes are sufficient is of particular importance in large multicenter trials where extending scan time is extremely difficult.

Generally, the Patlak model shows almost no loss of K-CNR up to a sampling interval of about sixty seconds (Figure 4A). Anything longer leads to a sharp increase in the variance of the fit parameters and a corresponding decrease in K-CNR. However, this K-CNR stability only occurs when the longer sampling interval leads to higher SNR, e.g. if extra partitions are collected to increase the FOV in a 3D scan. If the longer sampling interval does not lead to gains in SNR, e.g. adding more slices to a 2D scan, then K-CNR steadily drops with each decrease in sampling interval (Figure 4B). The use of 3D scans, therefore, gives extra flexibility to increase the FOV and gain more coverage without sacrificing much K-CNR - up to a point. Any increase in FOV in a 2D scan leads to a direct reduction of the K-CNR of the study. It is therefore advisable to use 3D scans whenever possible.

Figure 4A also shows that there is no benefit from running averages during a DCE experiment. The gain in SNR is canceled by the lower sampling interval leading to a net decrease in K-CNR. The extra time points in the short sampling interval scans have a noise reducing effect on fit parameters by adding additional constraints to the fit. Averaging removes these extra constraints and reduces the amount of information extracted from the data curve.

The number of baseline images collected is an acquisition parameter often neglected and rarely optimized in DCE protocols. The number of pre-injection images acquired vary greatly in the literature, from no baseline at all (54), one pre-contrast time point (28), more than 30 seconds (55,56) and a wide time range in between (6,39,57). Too short of a baseline is suboptimal as the concentration curves are calculated partially as the ratio of the pre-injection and post-injection signal intensities. The variance of the ratio will be approximately proportional to the sum of the individual variances, so reducing the variance of the pre-injection scans directly reduces the variance of the concentration curve. This can be a very time efficient way to increase the sensitivity of a study, as adding an extra two minutes to the baseline measurement could potentially double the K-CNR of the study (Figure 5) depending on the initial SNR and acquisition time. Table 1 outlines some typical examples; in some cases it is optimal to spend up to 1/3 of the imaging time collecting the baseline images.

Table 1.

Optimal Baseline Scan Times Differ for High and Low K_trans

Total Available Scan Time	Optimal Baseline Time Ktrans=1e−3/min	Optimal Baseline Time Ktrans=5e−3/min
10 min	1 min	2 min
15 min	3 min	5 min
30 min	4 min	>15 min
45 min	8 min	>30 min

For a given total scan time, the optimal division of time between pre-contrast (baseline) and post-contrast depends on the tissue K_trans and the scan duration. Calculated using the Patlak model with v_e=0.05. The baseline times are very long for 30-45 minutes and K_trans=5e−3/min as these scan times extend well beyond the no backflux assumption for the Patlak model, in this situation a different model would give superior results.

Previously, the effects of scanner drift on DCE results were reported to be negligible, due to either ROI averaging of time intensity curves cancelling out those effects, or that the magnitude of the drift is within the uncertainty of K_trans estimation (25,37). Our results suggest that the effects of signal drift on DCE parameter estimation are significant especially when comparing studies from different scanners or subjects. This is most prominent with Patlak fitting, but is present for all the models examined. Comparing K_trans derived from curves with different drifts can drastically increase the uncertainty of the K_trans comparisons (Figure 6), effectively reducing one’s ability to resolve small K_trans changes. Patlak is especially vulnerable to these types of inter-study errors as its lower contrast is sensitive to increases in variance. Drift correction can essentially eliminate this error. We assume here that the magnitude of the drift across the phantom, tissue and AIF ROIs are the same. In practice, this is likely not the case (58). How this impacts DCE parameter estimation needs to be explored in future studies.

When performing non-linear curve fitting, convergence to a local rather than global minimum is always a concern. This is a significant issue in DCE fitting. In Patlak, which can be linearized, we achieve good results by using the output from a linear fit as the starting location for a non-linear fit. This causes the non-linear fit to converge quickly and reliably giving more accurate values. To avoid local minimum in the other models we use multiple different starting locations, which improves the chances of finding the global minimum. In this regard, the starting value of K_trans had the largest effect on the final value and it was necessary to try multiple different K_trans starting values to reliably find the global minimum. It was also quite effective to constrain all the parameters to physiologically realistic values. Specifically, it was helpful to put a lower limit on v_e of 1-2%. Without this constraint there was instability at very low K_trans values; the v_e fit tends to fall to zero and the fit K_trans to rise to relatively high values. This instability at low K_trans is easily fixed by constraining v_e. Other groups have reported difficulty in getting 2CXM to properly converge to accurate values (19). We did not find this to be the case, as our 2CXM and extended Tofts models both converged with both simulated and measured data. Poor convergence has been a criticism of the 2CXM (59), but with proper selection of convergence tolerances, constraints on parameter ranges, and multiple starting locations we have not found this to be an issue.

The values that the 2CXM generates for our measured data in healthy controls largely fell within expected physiological ranges, with the exception of v_e. The measured values of v_e (3.3% and 5.1% median GM and WM, respectively and 7.4% and 6.4% mean GM and WM, respectively) are significantly lower than the expected value of approximately 15-30% (45) as measured with diffusion techniques. There could be a number of explanations for this difference. First, the measured v_e in this study will be lower than the true v_e due to the partial albumin binding of the Multihance used in this study. The partial binding to albumin extends the blood half-life of the CA and will cause an underestimation of v_e directly proportional to the extent of binding. Unfortunately, it is difficult to estimate the degree that it will be underestimated as the published binding affinities have huge uncertainties so the amount of bound CA could be anywhere from 2%-30% (60,61). Due to the significantly extended blood half-life the binding is probably closer to 30% than 2% and is likely a source of significant underestimation of v_e. Second, the extravascular extracellular space sampled by the CA may be different than the diffusion space mentioned above. Restrictions in the diffusion of the CA away from the blood vessels could cause the effective space they inhabit to be smaller than the actual space and give lower v_e values. Third, of all four parameters in the 2CXM the curves contain the least amount of information about v_e as the low leakage rates do not allow enough time for the extravascular extracellular compartment to fill with CA. Therefore the v_e values have a much lower precision than the other parameters, this low precision likely contributes to the low measured values. Finally, deficiencies in measurements techniques, insufficient temporal resolution, or poor curve fitting all are known to bias the DCE values, and it could be that these biases combined with the previously mentioned reasons could cause low v_e values to be measured. An accurate measurement of K_trans should not be taken as an indication that the other fit parameters (v_e, v_p, and f_p) will also be accurate.

The partial albumin binding of Multihance mentioned above could also affect the measured K_trans values. The magnitude of the change will depend on the binding affinity of Multihance, but as stated above this value is quite ill determined (60,61). Without a reasonable value it is hard to predict if this will be a significant effect. To our knowledge no study has yet examined the differences between different Gd based contrast agents, this could be an important question for future studies.

In conclusion, we have examined the effects of multiple scan parameters and modeling options on the ability to detect small changes in low K_trans values that can be used to detect subtle changes in BBB permeability. We have defined a K-CNR metric that highlights differences between models. Just as improving image CNR increases our ability to differentiate between regions of interest, improving K-CNR leads to better defined K_trans values. Using this K-CNR metric, we found that the Patlak model gives the best results in these circumstances when combined with fairly long scan times (10-30 minutes), modest temporal resolution (<60 seconds/image), and long baseline scans (1-4 minutes). These parameters can be used to detect even the subtlest changes in the integrity of the BBB and may be used to probe the earliest changes in neurodegenerative diseases.