Fast two-dimensional super-resolution image reconstruction algorithm for ultra-high emitter density

Abstract

Single-molecule localization microscopy achieves subdiffraction-limit resolution by localizing a sparse subset of stochastically activated emitters in each frame. Its temporal resolution is limited by the maximal emitter density that can be handled by the image reconstruction algorithms. Multiple algorithms have been developed to accurately locate the emitters even when they have significant overlaps. Currently, compressive-sensing-based algorithm (CSSTORM) achieves the highest emitter density. However, CSSTORM is extremely computationally expensive, which limits its practical application. Here, we develop a new algorithm (MempSTORM) based on two-dimensional spectrum analysis. With the same localization accuracy and recall rate, MempSTORM is 100 times faster than CSSTORM with ℓ₁-homotopy. In addition, Memp-STORM can be implemented on a GPU for parallelism, which can further increase its computational speed and make it possible for online super-resolution reconstruction of high-density emitters.

Single molecule localization based super-resolution microscopy techniques [1–3] achieve sub-diffraction-limit resolution by stochastically activating and localizing a sparse subset of emitters with nanometer resolution. The final super-resolution image is reconstructed from thousands of frames, which generally takes tens of minutes. This greatly limits its application from live cell imaging.

One way to improve the temporal resolution is to increase the number of emitters localized at each frame. Multiple algorithms have been developed to locate emitters even when they significantly overlap with each other [4–7]. Among these algorithms, compressive-sensing-based method (CSSTORM) [4] utilizes the sparsity of the signal in each frame and achieves the state-of-the-art recall rate and localization accuracy when the density is as high as 10 emitters/µm². However, CSSTORM solves a large-scale convex problem and suffers from high computation complexity. In addition, it experiences the intrinsic bias due to the discretization of the two-dimensional (2D) parameter space [8].

By transforming the super-resolution imaging model to the frequency domain, the problem of emitter localization becomes 2D spectrum estimation, a problem often encountered in signal processing. We developed an algorithm (MempSTORM) based on a 2D spectrum-estimation method called matrix enhancement and matrix pencil (MEMP) [9] to extract the number of emitters and their positions by determining the 2D frequencies.

We have extensively tested the method by both simulation and experimentation. MempSTORM achieves the same localization accuracy and recall rate as the CSSTORM, but is 100 times faster in computation. The most time-consuming steps of MempSTORM are a truncated singular-value decomposition (SVD) and two generalized eigenvalue decomposition. MempSTORM can be further speeded up by implementing on a GPU.

The 2D point spread function (PSF) of a microscope can be approximated by a Gaussian function [10]:

$$f(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{(x^2+y^2)}{2{\sigma }^2}},$$ (1)

where σ is the standard deviation of the Gaussian function, and (x, y) ∈ ℝ² is the 2D spatial coordinate. The signal s(x, y) received at the camera can be represented as a weighted summation of the shifted PSFs from all the I emitters:

$$s(x,y)=\sum _{i=1}^I{c}_{i}f(x-x_i,y-y_i),$$ (2)

where c_i is the intensity of the emitter i, and (x_i, y_i) ∈ ℝ² represents its location. The 2D continuous-time Fourier transform (CTFT) of the image can be written as

$$𝒮(u,v)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }s(x,y)e^{-j2\pi (xu+yv)}\mathrm{d}x\mathrm{d}y,$$ (3)

$$=ℱ(u,v)\sum _{i=1}^I{c}_i{e}^{-j2\pi (x_{i}u+y_{i}v)},$$ (4)

where ℱ(u, v) is the CTFT of f(x, y).

The image s = {s[m, n]} acquired by the camera is a matrix of size M × N, where s[m, n] represents the intensity value of the pixel at (m, n) obtained by integrating s(x, y) over the pixel area, approximated as

$$s[m,n]={\int }_{m-0.5}^{m+0.5}{\int }_{n-0.5}^{n+0.5}s(x,y)\mathrm{d}x\mathrm{d}y\approx A·s(m,n),$$ (5)

where 1 ≤ m ≤ M, 1 ≤ n ≤ N, and A is the area of a pixel. The discrete Fourier transform (DFT) S {S[k, l]} of s can be approximated as

$$S[k,l]\approx F[k,l]\sum _{i=1}^I{c}_i{e}^{-j2\pi (\frac{k{x}_i}{M}+\frac{l{y}_i}{N})},$$ (6)

where F[k, l] = ℱ(k/M, l/N), for 1 ≤ k ≤ M and 1 ≤ l ≤ N. Denote $f_{1i}=\frac{x_i}{M},f_{2i}=\frac{y_i}{N}$, and divide both sides of Eq. (6) by F[k, l], we obtain

$$R[k,l]=\frac{S[k,l]}{F[k,l]}\approx \sum _{i=1}^I{c}_i{e}^{-j2\pi (k{f}_{1i}+l{f}_{2i})}.$$ (7)

After these transformations, the problem of emitter localization becomes a 2D frequency-estimation problem in Eq. (7). We apply the MEMP method [9] for the frequency estimation step, considering its low computational cost and capability to resolve high-density signals.

We further rewrite Eq. (7) into

$$R[k,l]=\sum _{i=1}^I{c}_i{p}_i^k{q}_i^l,$$ (8)

where p_i = e^−j2πf_1i, q_i = e^−j2πf_2i are called the 2D poles. With this notation, we can write R = {R[k, l]} as an M × N matrix with the following factorization:

$$\mathit{R}=\mathit{P}\mathit{C}\mathit{Q},$$ (9)

where

$$\mathit{P}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill \\ \hfill p_1\hfill & \hfill p_2\hfill & \hfill \cdots \hfill & \hfill p_I\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill p_1^{M-1}\hfill & \hfill p_2^{M-1}\hfill & \hfill \cdots \hfill & \hfill p_1^{M-1}\hfill \end{array}\right]\in {ℂ}^{M\times I},$$ (10)

$$\mathit{C}=\left[\begin{array}{cccc}\hfill c_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill c_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill c_I\hfill \end{array}\right]\in {ℝ}^{I\times I},$$ (11)

$$\mathit{Q}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill q_1\hfill & \hfill \cdots \hfill & \hfill q_1^{N-1}\hfill \\ \hfill 1\hfill & \hfill q_2\hfill & \hfill \cdots \hfill & \hfill q_2^{N-1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill q_I\hfill & \hfill \cdots \hfill & \hfill q_I^{N-1}\hfill \end{array}\right]\in {ℂ}^{I\times N}.$$ (12)

From Eqs. (9)–(12), in principle one can obtain {p_i; i = 1, …, I} and {q_i; i = 1, …, I} from the left and right principal singular vectors of R. However, p_i and q_i cannot be obtained from the SVD when either set of {p_i; i = 1, …, I} or {q_i; i = 1, …, I} does not contain distinct elements, due to the rank deficiency of R, i.e., rank(R) < I.

To solve this problem, a partition-and-stacking process, referred to as matrix enhancement [9], is applied before SVD. The enhanced matrix R_e is defined as a block Hankel matrix of size K × (M − K + 1):

$${\mathit{R}}_e=\left[\begin{array}{cccc}\hfill {\mathit{R}}_0\hfill & \hfill {\mathit{R}}_1\hfill & \hfill \cdots \hfill & \hfill {\mathit{R}}_{M-K}\hfill \\ \hfill {\mathit{R}}_1\hfill & \hfill {\mathit{R}}_2\hfill & \hfill \cdots \hfill & \hfill {\mathit{R}}_{M-K+1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathit{R}}_{K-1}\hfill & \hfill {\mathit{R}}_K\hfill & \hfill \cdots \hfill & \hfill {\mathit{R}}_{M-1}\hfill \end{array}\right],$$ (13)

where each block R_m, 0 ≤ m ≤ M − 1, is a Hankel matrix of size L × (N − L + 1) defined as

$${\mathit{R}}_m=\left[\begin{array}{cccc}\hfill R[m,0]\hfill & \hfill R[m,1]\hfill & \hfill \cdots \hfill & \hfill R[m,N-L]\hfill \\ \hfill R[m,1]\hfill & \hfill R[m,2]\hfill & \hfill \cdots \hfill & \hfill R[m,N-L+1]\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill R[m,L-1]\hfill & \hfill R[m,L]\hfill & \hfill \cdots \hfill & \hfill R[m,N-1]\hfill \end{array}\right].$$

It is shown in [9] that rank(R_e) = I as long as the two pencil parameters K and L

$$M-I+1\ge K\ge I,\text{ and }N-I+1\ge L\ge I,$$ (14)

eliminating the earlier described rank deficiency issue.

In the noise-free case, the SVD of R_e can be given as

$${\mathit{R}}_e=\sum _{i=1}^I{\sigma }_i{\mathit{u}}_i{\mathit{v}}_i^H=\mathit{U}\mathbf{\Sigma }{\mathit{V}}^H,$$ (15)

where U = [u₁, …, u_I] ∈ ℂ^KL×I, Σ = diag(σ₁, …, σ_I) ∈ ℝ^I×I, V = [v₁, …, v_I] ∈ ℂ^{(M−K+1)(N−L+1)×I}, respectively.

In the case when R_e is noisy, we can similarly define U, Σ, and V as the top I left singular vectors, singular values, and right singular vectors of R_e.

Denote the ith column of U^H as w_i, then U^H = [w₁, w₂, …, w_KL]. Further define U_p ∈ ℂ^KL×I by permuting the rows of U as

$${\mathit{U}}_p^H=[{\mathit{w}}_1,{\mathit{w}}_{L+1},\dots ,{\mathit{w}}_{(K-1)L+1},{\mathit{w}}_2,{\mathit{w}}_{L+2},\dots ,{\mathit{w}}_{(K-1)L+2},\dots ,{\mathit{w}}_L,{\mathit{w}}_{2L},\dots ,{\mathit{w}}_{KL}].$$ (16)

Define U₁ ∈ ℂ^{(K −1)L×I} as the submatrix of U by deleting its last L rows, ${\mathit{U}}_1^H=[{\mathit{w}}_1,\dots ,{\mathit{w}}_{(K-1)L}]$ and U₂ ∈ ℂ^{(K −1)L×I} as the submatrix of U by deleting its first L rows, U₂ = [w_L+1, …, w_KL], then the matrix pencil U₂ − λU₁ can be written as [9]

$${\mathit{U}}_2-\lambda {\mathit{U}}_1=\mathit{E}({\mathit{Y}}_d-\lambda \mathit{I})\mathit{T},$$ (17)

where Y_d = diag(p₁, …, p_I) is a diagonal matrix of the poles {p_i; i = 1, …, I}, E and T are full-rank matrices. Thus the poles {p_i; i = 1, …, I} can be found as the rank-reducing numbers λ such that the matrix pencil U₂ − λU₁ is rank-deficient. This can be achieved by solving a generalized eigenvalue decomposition.

Similarly, {q_i; i = 1, …, I} can be found as the rank-reducing numbers of the matrix pencil U₄ − λU₃, where U₃ ∈ ℂ^{K (L−1)×I} as the submatrix of U_p by deleting its last K rows, ${\mathit{U}}_3^H=[{\mathit{w}}_1,{\mathit{w}}_{L+1},\dots ,{\mathit{w}}_{KL-1}]$, and U₄ ∈ ℂ^{K (L−1)×I} as the submatrix of U_p by deleting its first K rows, ${\mathit{U}}_4^H=[{\mathit{w}}_2,{\mathit{w}}_{L+2},\dots ,{\mathit{w}}_{KL}]$, which again can be done by solving a generalized eigenvalue decomposition.

After extracting {p_i; i = 1, …, I} and {q_i; i = 1, …, I} separately, we need to further determine the one-to-one (or one-to-more, if there are multiplicity in the retrieved poles) correspondence between the poles to fully determine the set of 2D poles. First, we consider all the possible pairings between {p_i; i = 1, …, I} and {q_i; i = 1, …, I}, with a total of no more than I² pairs. We then pose a non-negative least-squares problem, by minimizing the quadratic loss between the data matrix R and the fitting using all possible pairs, given in Eq. (9), under the constraint that the coefficient of each pair is non-negative. We then select I pairs corresponding to the highest coefficients. From the paired 2D poles {(p_i, q_i); i = 1, …, I}, the set of 2D frequencies (f_1i, f_2i) as well as the positions (x_i, y_i) of the I emitters can be calculated.

In implementing the above MempSTORM method, a pair of pencil parameters K and L needs to be chosen for matrix enhancement. Equation (14) is a sufficient condition for the rank of enhanced matrix R_e to be I. Under this condition, the rule of thumb is to choose K and L such that the enhanced matrix R_e is as square as possible, i.e., choose K to be close to (M + 1)/2 and L to be close to (N + 1)/2. Moreover, since the number of emitters I is not known a priori, we choose a threshold value and determine the number of emitters as the number of singular values of R_e that is larger than the threshold. The threshold value is chosen such that the sum energy of the selected singular vectors is 80%–90% of the total.

For super-resolution image reconstruction, the noise in the frequency domain has similar energy across different frequencies due to the Poisson noise in the spatial domain. However, the energy of the signal is not uniformly distributed in the frequency domain due to the shape of the PSF. Instead, most of the energy is concentrated in the low frequency with the high-frequency components dominated by noise. In practice, we only use entries that correspond to the low-frequency region of R and apply MEMP on a truncated data matrix. For an image of size 30 × 30, we only use the submatrix of size 11 × 11 of Eq. (7) that corresponds to the low-frequency region of the image to generate the matrix enhancement.

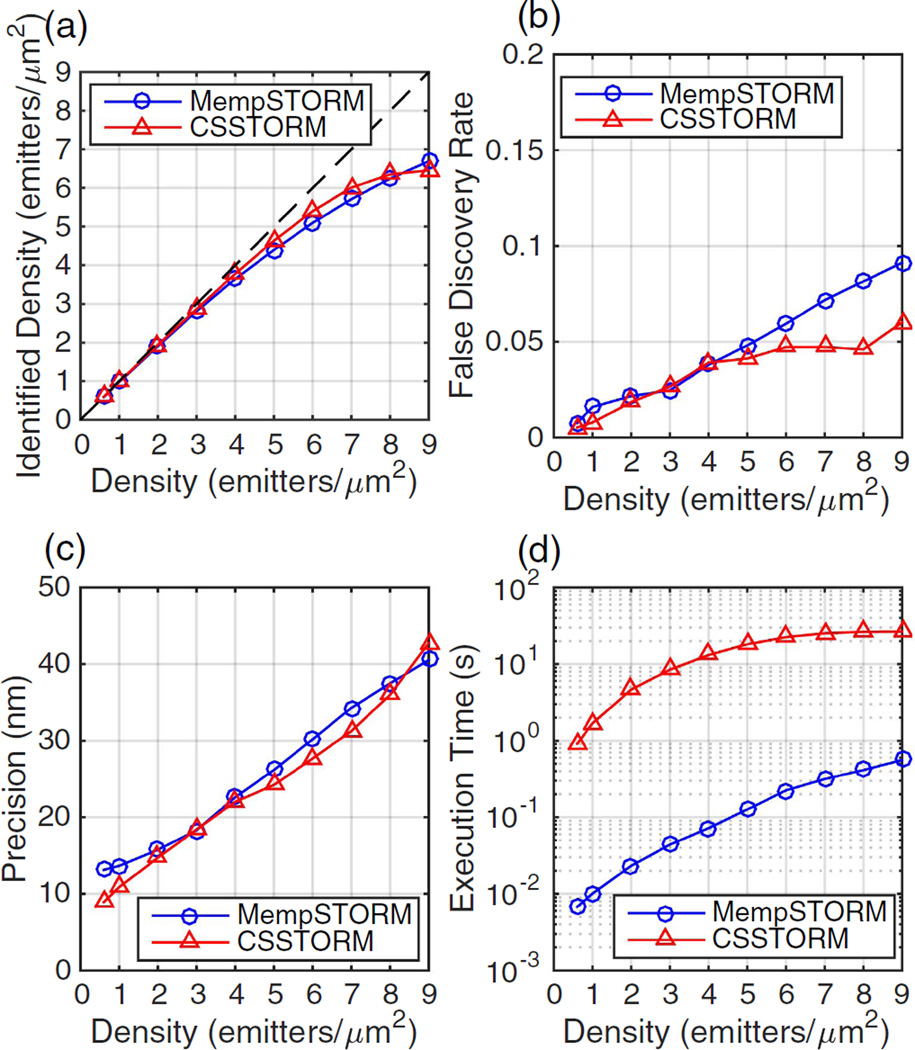
To evaluate the performance of MempSTORM, we generate a series of simulated STORM movies of size 30 × 30 across a range of emitter densities (0.5 emitter/µm² to 9 emitters/µm²). An average photon number of 1500 per emitter is used in the simulation. The movies are comparatively analyzed using MempSTORM and CSSTORM [4]. We implement CSSTORM using ℓ₁-homotopy, which has been proven to be two orders of magnitude faster than CVX implementation [11]. An up-sampling factor of 8 is used in CSSTORM. As shown in Fig. 1, MempSTORM achieves the same level of identified density and false discovery rate as CSSTORM, and maintains similar precision with CSSTORM. The false discovery rate is defined as the percentage of incorrectly detected emitters in all detected emitters. Most importantly, MempSTORM is more than 100 times faster than CSSTORM in most densities [Fig. 1(d)].

Fig. 1.

Comparison of (a) the identified density, (b) false discovery rate, (c) precision, and (d) execution time between MempSTORM and CSSTORM.

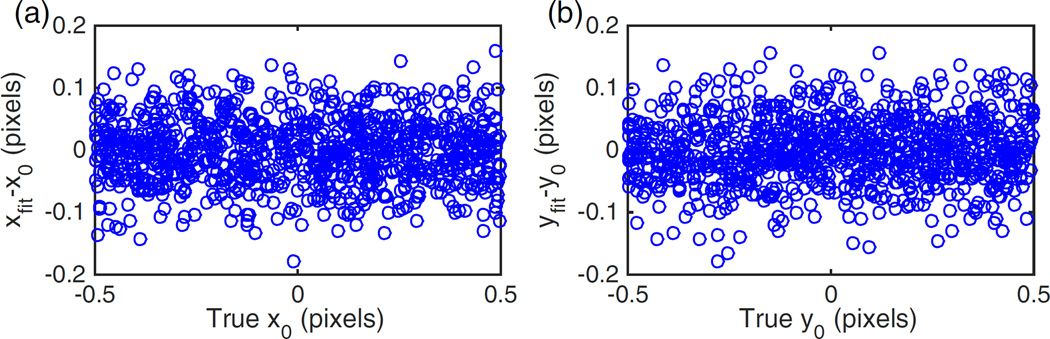
To examine the bias of MempSTORM, we simulate a stack of images of size 30 × 30 with a single emitter positioned randomly. The photon number of the emitter is set to 1500. The localization bias is plotted as a function of the emitter location in both the x and y direction. As shown in Fig. 2, there is no bias associated with the MempSTORM method.

Fig. 2.

Bias of single-emitter localization using MempSTORM in (a) x direction and (b) y direction.

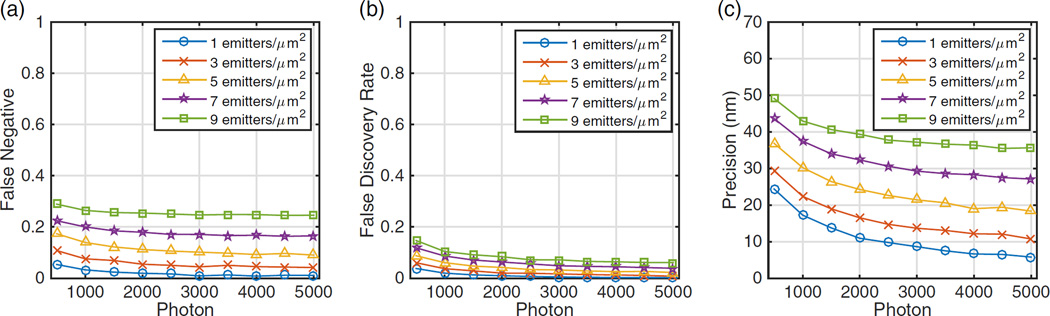
We then evaluated the performance of MempSTORM when the number of photons varies. A series of STORM images with different emitter photon numbers are generated and analyzed. The performance of MempSTORM deteriorates when the number of photons decreases, but within a tolerable range (Fig. 3). Even when the photon number is as low as 500, MempSTORM can still detect a reasonable amount of emitters with high precision (<50 nm).

Fig. 3.

Comparison of (a) false-negative, (b) false discovery rate, and (c) precision when the emitter photon varies under different densities.

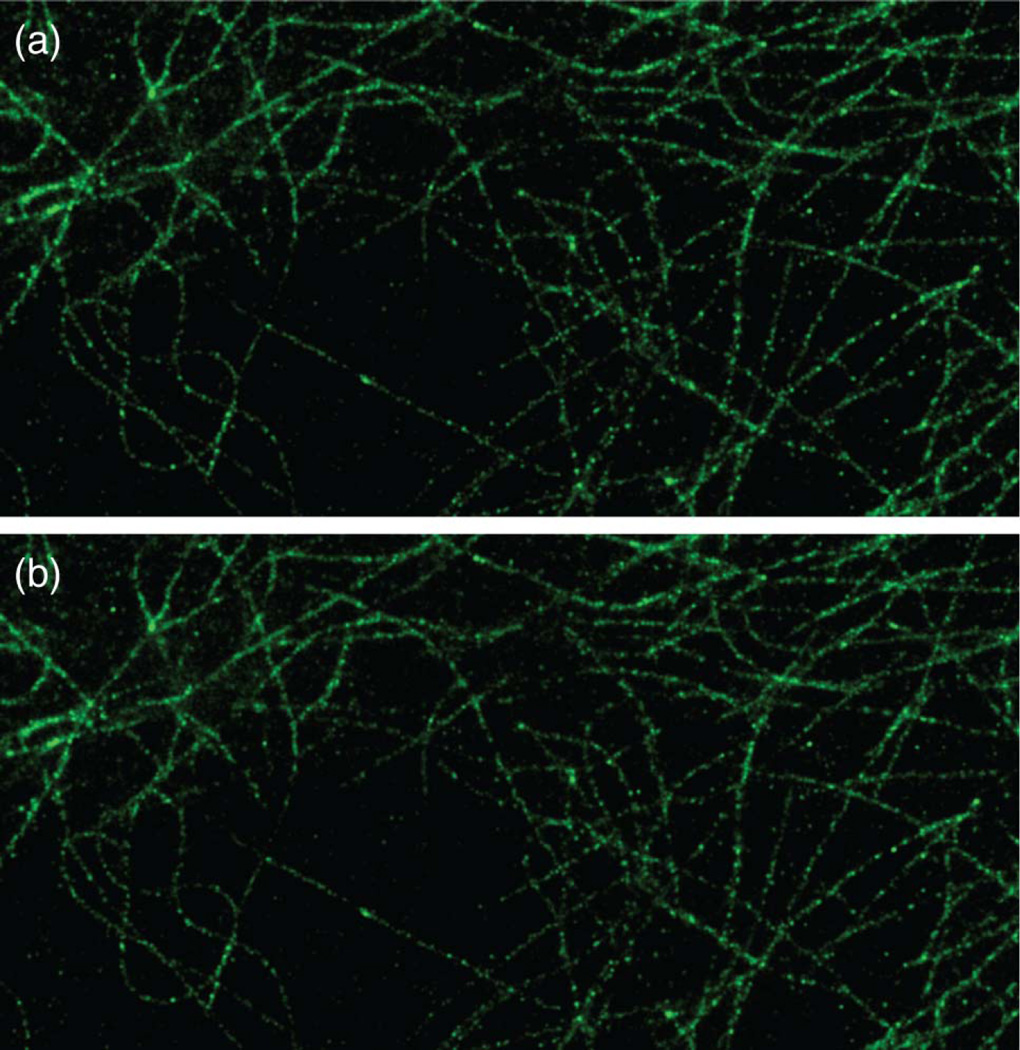
To further test the practical applicability of MempSTORM, we analyze STORM images of microtubules stained with Alexa 647 in HeLa cells. In total, 5000 frames were acquired at 56 frames per second. Figure 4 shows the comparison of reconstructed microtubule images using the MempSTORM and CSSTORM methods, where MempSTORM achieves similar performance with CSSTORM. However, the reconstruction time using MempSTORM is only 20 min, while with the same computational configurations, CSSTORM requires more than 100 h.

Fig. 4.

Reconstructed microtubule image using 5000 raw frames with (a) MempSTORM and (b) CSSTORM.

In conclusion, we have developed the MempSTORM method for super-resolution imaging with high emitter densities, which significantly improves the temporal resolution of STORM. MempSTORM achieves the same performance as the current state-of-the-art method, CSSTORM, but is more than 100 times faster.

The experiments in this Letter were performed on the compute nodes of the Ohio Supercomputing Center Oakley cluster. Each node has one Intel Xeon X5650 CPU clocked at 2.66 GHz and 48 GB of memory. Currently, the algorithm is implemented in MATLAB. By porting the algorithm to C/C++ and using GPU parallelism, we expect to further accelerate the analysis and make online reconstruction of dense emitter images practical.