Abstract
Muscle myosin cyclically hydrolyzes ATP to translate actin. Ventricular cardiac myosin (βmys) moves actin with three distinct unitary step-sizes resulting from its lever-arm rotation and with step-frequencies that are modulated in a myosin regulation mechanism. The lever-arm associated essential light chain (vELC) binds actin by its 43 residue N-terminal extension. Unitary steps were proposed to involve the vELC N-terminal extension with the 8 nm step engaging the vELC/actin bond facilitating an extra ~19 degrees of lever-arm rotation while the predominant 5 nm step forgoes vELC/actin binding. A minor 3 nm step is the unlikely conversion of the completed 5 to the 8 nm step. This hypothesis was tested using a 17 residue N-terminal truncated vELC in porcine βmys (Δ17βmys) and a 43 residue N-terminal truncated human vELC expressed in transgenic mouse heart (Δ43αmys). Step-size and step-frequency were measured using the Qdot motility assay. Both Δ17βmys and Δ43αmys had significantly increased 5 nm step-frequency and coincident loss in the 8 nm step-frequency compared to native proteins suggesting the vELC/actin interaction drives step-size preference. Step-size and step-frequency probability densities depend on the relative fraction of truncated vELC and relate linearly to pure myosin species concentrations in a mixture containing native vELC homodimer, two truncated vELCs in the modified homodimer, and one native and one truncated vELC in the heterodimer. Step-size and step-frequency, measured for native homodimer and at two or more known relative fractions of truncated vELC, are surmised for each pure species by using a new analytical method.
INTRODUCTION
Myosin in cardiac muscle transduces ATP chemical energy into mechanical work. It is the molecular mover comprised of a motor domain containing ATP and actin binding sites, and, mechanical elements coupling motor impulsive force to the myosin filament backbone in a combined function called transduction/mechanical-coupling. Myosin mechanical coupling is through the heavy chain α-helical lever-arm domain that has two bound light chains essential (ELC) and regulatory (RLC). The lever-arm/light-chain complex undergoes cyclical rotary movement to impel a bound actin filament. Linear actin displacement due to one lever-arm rotation is the unitary myosin step-size. Skeletal myosin has a dominant unitary step-size of ~5 nm (1). Cardiac myosin has three distinct unitary step-sizes (nominally 3, 5, and 8 nm) that move actin with varying relative step-frequencies to adapt contractile force and power to demand (2). Relative step-frequency modulation is an activation mechanism increasing the dynamic range for myosin produced power. It is coupled to RLC phosphorylation (3) implicating it in normal heart function and in heart failure disease compensation mechanisms (4–6).
Ventricular cardiac myosin essential light chain (vELC) has a 43 residue N-terminus extension compared to its skeletal short ELC counterpart ELC(A2) (Figure 1). The vELC extension binds actin and affects the actomyosin interaction in cardiac muscle (7–10). We observed relative step-frequencies for the 3, 5, and 8 nm steps under unloaded conditions and proposed that the major 5 nm step is identical to the dominant unitary step in skeletal myosin, that the less likely 8 nm step is different from the 5 nm step by involving the vELC N-terminus actin binding facilitating additional actin translation, and that the minor 3 nm step is the unlikely conversion of the 5 nm step to the full vELC bound 8 nm step. The infrequent 3 nm step-size is isolated in time from the 5 nm step by slow ADP dissociation so that we observe it occasionally as a separate step (11). These ideas are summarized in Figure 2 where actin binding of the vELC extension facilitates an extra ~19 degrees of lever-arm rotation adding 3 nm to the nominal 5 nm step-size (2).
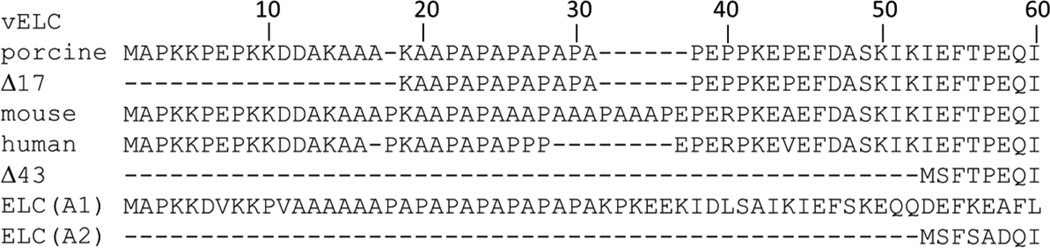
Figure 1.
Sequences of vELC isoforms: porcine (NP_001265702, 197 residues) and its 17 amino acid N-terminal truncation, Δ17; mouse (P09542, 204 residues); human (P08590, 195 residues) expressed in mice in this study (WT) and its 43 amino acid N-terminal truncation mutant, Δ43. Sequences of human skeletal muscle ELC isoforms: A1 (NP_524144.1, 194 residues) and A2 (P06741, 150 residues). ELC(A2) is the model for Δ43. Following I60 are 144 residues not shown.
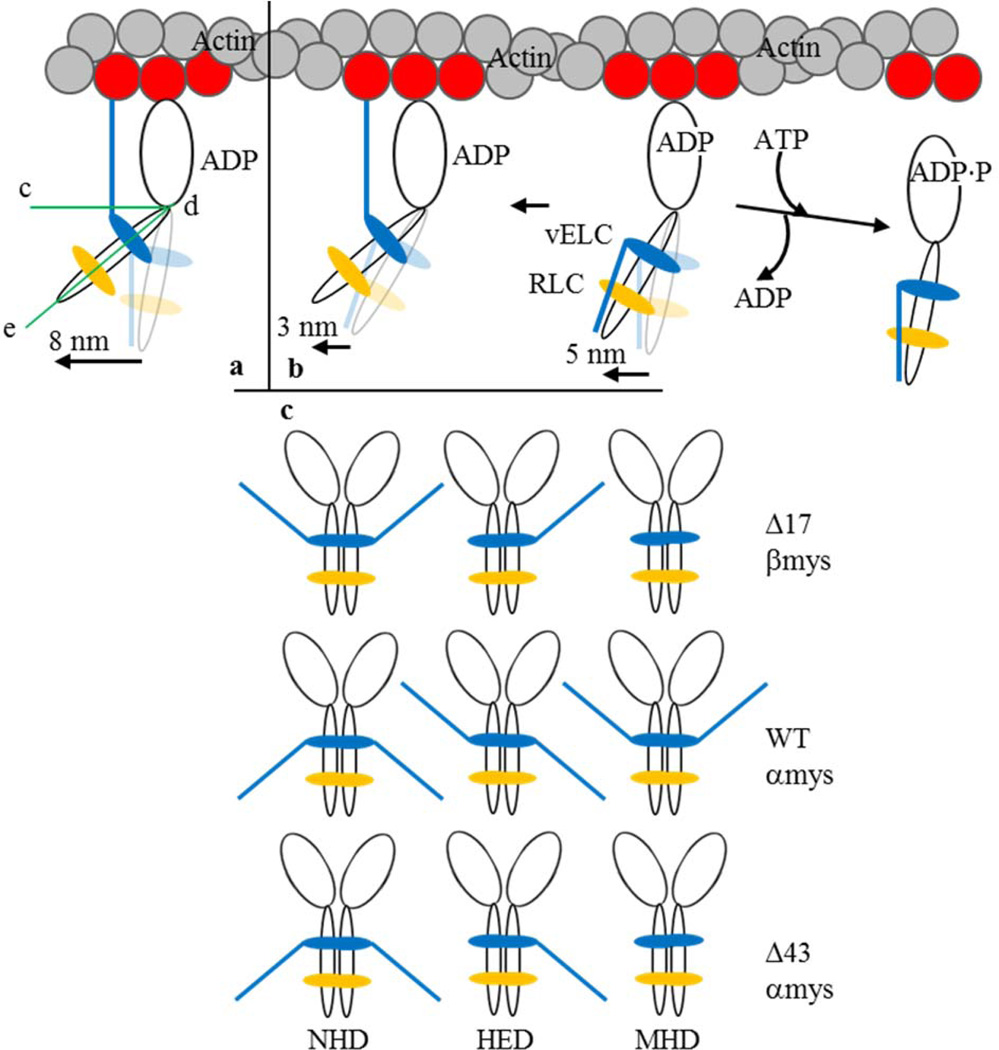
Figure 2.
The proposed 3 step-size mechanism for cardiac myosin moving actin in vitro and the myosin dimers participating in motility. Panel a is the full lever-arm swing step of 8 nm with actin binding of the vELC N-terminus. Panel b shows the 5 nm step followed by detachment from actin (towards right) or an unlikely event when lingering ADP causes a subsequent 3 nm step (towards left). The full 8 nm step facilitated by the vELC/actin link corresponds to a lever-arm rotation ~19° larger than that for a 5 nm step. Angle, ∠cde in panel a, indicates the acute angle specifying lever-arm orientation relative to the actin filament. Panel c shows the myosin dimers participating in motility and notation representing the native homodimers (NHD) containing intact vELC, the heterodimer (HED) with one modified and one native vELC, and the modified homodimer (MHD) with two modified vELC’s. Mouse vELC is distinguished from human vELC by the tip-down (mouse) or tip-up (human) ELC N-terminus.
In this report we tested the model using several cardiac myosin isoforms based on slow porcine ventricular myosin with the β heavy chain (βmys) and mouse cardiac myosin with the α heavy chain (αmys) including: a 17 residue N-terminal truncated vELC in porcine ventricular myosin (Δ17βmys) made by papain digestion (12) and a 43 residue N-terminal truncated human vELC expressed in a transgenic mouse heart (Δ43αmys) (13). Control porcine and mouse cardiac myosin isoforms have wild type porcine vELC on porcine myosin (βmys or Δ0βmys), expressed native human vELC on mouse cardiac myosin (WTαmys), and the nontransgenic mouse vELC on mouse cardiac myosin (NTg). We measured cardiac myosin step-size, step-frequency, motility velocity, and actin-activated myosin ATPase from dimerized molecules containing two motor (head) domains each with an associated vELC. High-throughput step-size and step-frequency measurements used a new, more efficient, version of the Qdot super-resolution in vitro motility assay (2, 3).
The native porcine βmys behaved as previously described with 5, 8 and 3 nm steps in relative frequency ratios of 0.5, and 0.37, and 0.13. Δ17βmys contained both cleaved and native species with truncated vELC fractional concentrations of 0.3 and 0.6 in two experimental trials. Changing step-frequency compared to native control in these samples confirms that the vELC N-terminal extension modulates probabilities for the 5 and 8 nm step-sizes as suggested by the model in Figure 2. Step-frequency variability vs the truncated βmys fractional concentration was analyzed using a novel method to ascertain step-size, step-frequency, and duty-ratio distributions for pure species of modified myosin homodimer (MHD with two truncated vELCs) and heterodimer (HED with one copy each of native and truncated vELCs). The MHD & HED species move actin similarly with increased 5 nm and decreased 8 nm step-frequencies, however, MHD maintains a reduced but significant probability for making an 8 nm step. We can similarly resolve step-frequency distributions for the pure MHD and HED species of αmys. Truncation of the vELC N-terminus in mouse αmys has effects broadly following those in βmys.
The vELC N-terminus facilitates the additional lever-arm rotation needed for the 8 nm step-size of the cardiac motor in a new mechanism for modulating contractile power. It presents a novel target for cardiac myosin specific therapeutics.
MATERIALS and METHODS
Methods summarized in Sections A-C are: Protein Preparations, In Vitro Biochemical Assays, and Estimating Step-Frequency for Pure MHD and HED Species. Section A and parts of Section B summarize previously published or standardized methods. Section C on measuring pure MHD and HED characteristics is a new approach developed for this application.
A. Protein Preparations
Porcine βmys and mouse αmys preparations are described in Supplementary Information.
B. In Vitro Biochemical Assays
Actin-activated myosin ATPase, in vitro motility, and Qdot assay event-velocity histogram simulation are described in Supplementary Information. All assays were conducted at room temperature (20–22 °C).
High-throughput super-resolution measurements in the Qdot assay
Qdot assays for β and αmys were performed as described (2). The total events acquired in the velocity unit range typically sampled have increased by an order of magnitude or more over previous applications using the semi-automated approach introduced here and described below.
The QuickPALM software (14) identified and localized point objects that qualified for super-resolution fitting according to user specifications including minimum SNR (> 25 isolating Qdots) and maximum full width at half maximum (FWHM) of 5 pixels (107 nm/pixel in object space for the 150X objective). QuickPALM analysis produced a table (SRTable) listing each qualifying particle, particle position in pixels, position standard deviation, and frame identifier. Using the SRTable, QuickPALM rendered the super-resolved particle data as single pixels per particle in the frame sequence of the original data. Rendered frames were analyzed in a semi-automated process in three steps. First, MTrackJ (15) in ImageJ was used to identify the region containing a super-resolved Qdot track in the acquired frames. Second, a new routine written in Matlab, QPTracklinker, linked the super-resolved Qdot positions from one track in a time ordered sequence. Third, SRTrack written in Mathematica, updated the SRTable with the frame-to-frame tracking linked list. SRTrack eliminated any incorrectly identified particles that did not have a super-resolved equivalent. The latter removed the effect of Qdot blinking.
In any motility assay a few Qdots did not visibly move due to apparent immobilization on the glass surface. These particles were tracked at super-resolution to quantitate thermal/mechanical fluctuations.
Qdot assay calibration and compliance
Qdots fixed by adsorption on a glass slide were observed in the aqueous medium and under conditions imitating the Qdot motility assay except that a nanopositioning stage (NanoBioS100, MCL, Madison, WI) translated the glass slide. The stage was controlled using Labview (National Instruments, Austin, TX) with step-size randomly selected from the sets {3,5,8} nm or {6,10,16} nm with step-frequencies {0.125, 0.5, 0.375}. The step-probabilities and the {3,5,8} nm size-size set imitated values observed for βmys. Calibration data had a single selected step-size translation occurring during the camera frame capture interval Δt=200 or 500 ms and with stepping along one axis (x- or y-axis). Data from x-or y-axis translations were pooled. Control velocity data originates from a position sensor in the stage controller called the stage readout. The change in stage readout position between frame captures divided by the frame capture interval gives the known velocity. Qdot assay velocity data analysis for the calibrated movement of the Qdots is the same as that used when quantitating myosin in vitro motility.
Compliance in the Qdot assay implies that the myosin unitary working stroke displacement will not fully transfer to a resistive Qdot labeled actin filament in the single actomyosin interaction leading to an underestimate of the myosin step-size. We compared myosin step-sizes measured in the absence and presence of an external load to detect the presence of system compliance. A frictional loading assay was performed as described (16) but using Qdot labeled actin. The labeled actin moved over surface adsorbed myosin from 0.16 µM myosin in bulk solution and in the presence of 3 µg/mL α-actinin (Cytoskeleton, Denver, CO). The flow cell was infused at the start with the mixture of myosin and α-actinin. The presence of 3 µg/mL α-actinin lowered average motility velocity compared to control by a factor of ~2.
C. Estimating Step-Frequency for Pure MHD and HED Species
Step-frequency, step-size, or duty-ratio expectations for pure species of myosin
Native and papain digested βmys or native and transgenic αmys have vELC occupying two binding sites on the myosin dimer. Truncated or otherwise modified vELC partially and randomly replaces the native species. Each myosin dimer falls into one of three categories containing 2 native (native homodimer or NHD), 1 native and 1 modified (heterodimer or HED), and 2 modified vELC species (modified homodimer or MHD). For n0 myosin monomers containing either a native or modified vELC, and if fc is the fraction of modified vELC’s, then probabilities for the NHD (p0), HED (p1), and MHD (p2) species for random pairwise associations are,
| (1) |
where p0+p1+p2 = 1. For large n0, p0 = (1-fc)2, p1 = 2fc(1-fc), and p2 = fc2. We assume this fc-dependent distribution of modified vELC in the αmys and βmys samples. In one Δ17βmys sample studied, we altered the random distribution of native and truncated vELCs by addition of NHD to the digested protein and assumed there was no subsequent redistribution of the native and truncated vELCs. The expressed native human vELC (this is a modified vELC in the mouse isoform) distributes in WTαmys just like the truncated species.
A Qdot assay data set consists of 10–12 acquisitions (one acquisition is one in vitro motility movie and corresponding event-velocity histogram) from preparations of one unknown and one control protein. Total events acquired in the velocity unit range typically sampled have increased by an order of magnitude or more over previous applications by using the automated data analysis described in Section B. Simulation of the pooled data set requires a similar increase in computing cost. We have changed to a fixed computing cost basis by simulating a standard event total in the event-velocity histogram that is renormalized to match event total in each acquisition. Event-velocity histogram simulation is described in Section B of Supplementary Information. Comparison to data minimizes the χ2 goodness-of-fit test that is weighted by event total then summed over all the acquisitions for evaluating global goodness-of-fit.
Simulated event-velocity histogram ensembles were created by using the 10–12 minimum global goodness-of-fit simulations generated for the full Qdot assay data set. These simulations are combined linearly, with coefficients ≥0 that minimize the χ2 goodness-of-fit test with all points equally weighted, to approximate the measured event-velocity histogram from the pooled Qdot assay data set. The respective step-frequencies (one set of 3 frequencies for each simulation) were also combined linearly with identical coefficients into a histogram indicating the discrete step-frequency probability densities with superscript j = S, I, and L for the short, intermediate, and long step-sizes and subscript i indicating histogram bin. The bin width is 1/N covering 0 to 1 probability on the abscissa in N bins. We will sometimes use vector notation,
| (2) |
to indicate probability density (ξ = ρ) in each bin or bin coordinate (ξ = x). Similarly ρ can represent: the step-size probability densities for each of the three categorical step-sizes (S, I, or L) on an abscissa covering step-size distance in nm in N bins, and, the duty-ratio probability densities for each of the three categorical step-sizes (S, I, or L) on an abscissa covering dimensionless duty-ratio in N bins.
Step-frequency, expectation eji, characterizes step-frequency for given step-size j and protein species where,
| (3) |
for xi the ith bin coordinate. The step-frequency expectation value,
| (4) |
or in vector notation,
| (5) |
The step-frequency probability densities for the three step-sizes and for sample m are collected into matrix vm with,
| (6) |
Control protein contains only intact vELC (in Δ0βmys or NTg) providing vNHD. Modified protein has step-frequencies from the linear combination of the NHD, HED, and MHD species with coefficients that depend on the fraction of modified vELC’s, fc, such that,
| (7) |
where fc dependence is in the p-coefficients from eq. 1. Known quantities are on the left and unknowns (except for p1 and p2) on the right side of eq. 7. Two or more measurements of vm for modified vELC myosin species at different but known fractional content (0< fc≤1) provides a system of equations with information sufficient to estimate vHED and vMHD using linear optimization with constraints such that ρji ≥ 0 and for each step-size j . Identical constraints apply when ρ represents step-size or duty-cycle probability densities. Equation 7 also relates the linear scalar quantity Vmax for the pure species (unknowns) to the measured quantities from control and modified myosin. The analysis outlined above was applied to data from βmys by combining measurements for fc = 0.3, and 0.6 (the fc = 0 case is explicit in eq. 7 within the term proportional to p0 on the left side). Additional measurements at other fc values increase constraints but not unknowns.
Alternatively, for 1 measurement of vm at 1 value of fc as in the case of the αmys isoforms, we must introduce an a priori model for vHED to solve eq. 7. The models, vHED = vNHD, vMHD, or ½(vNHD + vMHD), allow an estimate for vMHD using linear optimization of eq. 7. A good model minimizes the normalized residual,
| (8) |
Motility velocity of a binary mixture of skeletal myosin with another slower myosin isoform was non-linear in the skeletal myosin fractional concentration (17). The slower myosin strong binding dwell time, ton (~d/sm, eq. S3 Supplementary Information), sufficiently exceeded its skeletal myosin counterpart to disproportionally inhibit the faster skeletal myosin motility thus producing the non-linearity. Equation 7 indicates a mixture of the NHD, HED, and MHD pure myosin species moving an actin filament has ensemble characteristics related to pure species characteristics by coefficients linear in their relative concentration. We implicitly assume with eq. 7 that the closely related NHD, HED, and MHD myosins isoforms have similar ton’s such that their characteristics are sampled proportionally to their abundance. We test sliding velocity of the mixture vs MHD or NHD+HED relative concentration to evaluate validity of eq. 7 and show that MHD and the combined NHD+HED isoforms play the roles of fast and slow myosins in the mixture.
Statistics
Statistical analysis tested whether data is distributed normally at the significance level of 0.05 and using several methods including Cramer-von Mises, Pearson chi-squared, and others. All tests found normally distributed sampling unless specified otherwise.
Three independent data sets were acquired for each of the porcine βmys isoforms (Δ0βmys, Δ17βmys @ 60%, and Δ17βmys @ 30%) and one data set was acquired for the mouse αmys isoforms (NTg, WTαmys, and Δ43αmys). Each data set corresponded to 10–12 independent event-velocity histogram measurements. We simulated each data set independently to estimate single myosin mechanical characteristics consisting of 3 step-sizes and 3 step-frequencies. We compared 3 step-sizes or 3 step-frequencies as categorical variables in factor 1 and the 3 independent data sets acquired for βmys in factor 2 using two-way ANOVA with Bonferroni or Tukey post-tests for significance at the 0.05 level. No significant difference in the independent data sets was indicated for the βmys isoforms hence the data sets were pooled.
Step-size and step-frequency parameters were compared among the βmys isoforms or among the αmys isoforms using one-way ANOVA with Bonferroni or Tukey post-tests for significance at the 0.05 level. Outcomes of statistical testing is described in RESULTS.
RESULTS
Standard assay characterization of β and αmys isoforms include: verification of the native and modified vELC content using SDS-PAGE in Figure S1, actin-activated myosin ATPase results in Figure S2 giving Michaelis-Menten constants Vmax and KM summarized in Table 1, and standard in vitro motility assay results in Figure S3 all in Supplementary Information.
Table 1.
1: Cardiac myosin actin-activated ATPase and in vitro motility
| βmys | |||||||
|---|---|---|---|---|---|---|---|
| Δ0 NHD | Δ17 @ 20% | Δ17 @ 30% | Δ17 @ 60% | Δ17 MHD | Δ17 HED | ||
| Vmax (s−1) | 1.51±0.08 | 1.59±0.05 | 1.63±0.06 | 2.29±0.24 | 3.09±0.84 | 1.88±0.59 | |
| KM (µM) | 9.33 ± 1.66 | 18.6±1.8 | 37.8±3.5 | 114.4± 20.6 | - | - | |
| sm (µm/s) Qdot | 0.27±0.02 | - | 0.29±0.02 | 0.32±0.03 | 0.40±0.04 | 0.25±0.04 | |
| sm (µm/s) standard | 0.26±0.02 | - | 0.31±0.02 | 0.31±0.01 | - | - | |
| <d> (nm) | 6.0±0.3 | - | 6.2±0.4 | 5.7±0.5 | 6.1±0.5 | 5.5±0.5 | |
| <F> (uf) | 14.4±1.2 | - | 16.8±1.6 | 19.6±2.3 | 24.1±2.0 | 21.7±2.6 | |
| <P> (µm/s) (uf) | 3.9±0.3 | - | 4.4±0.4 | 6.3±0.7 | 9.7±0.5 | 5.5±0.3 | |
| αmys | |||||||
| NTg NHD | WT @ 30% | WT MHD | Δ43 @ 60% | Δ43 MHD | |||
| Vmax (s−1) | 2.67±0.24 | 2.60±0.19 | 2.53±0.44 | 1.50±0.09 | 1.28±0.09 | ||
| KM (µM) | 3.55±1.08 | 3.18±0.80 | - | 4.35±0.85 | - | ||
| sm (µm/s) Qdot | 1.21±0.07 | 1.24±0.06 | 1.31±0.38 | 1.14±0.04 | 1.00±0.14 | ||
| sm (µm/s) standard | 1.02±0.06 | 0.97±0.08 | - | 0.82±0.04 | - | ||
| <d> (nm) | 6.9±0.4 | 6.0±0.3 | 6.0±2.4 | 6.2±0.4 | 6.2±0.4 | ||
| <F> (uf) | 6.6±0.7 | 5.5±0.7 | 4.9±1.4 | 3.8±0.3 | 3.6±0.5 | ||
| <P> (µm/s) (uf) | 8.0±0.9 | 6.8±0.9 | 6.5±2.0 | 4.4±0.4 | 3.7±0.2 | ||
Vmax and KM are defined in eq. S1 from SI. Motility velocity sm from standard and Qdot motility assays occasionally differ for the higher velocity αmys because subtraction of thermal/mechanical fluctuations, possible only with Qdot data, removes some of the lowest velocities in the velocity histogram that are not due to myosin activity. This effect is negligible for βmys. Quantities denoted by <q> are ensemble averages defined in System (ensemble) analytics (Section B. SI) for step-size, d, force F, and power, P. Average force <F> is in arbitrary units of force (uf). All experimental errors indicated are standard deviation. Quantities for the MHD and HED pure species are calculated using eqs. 1 & 7 as explained in Methods with standard deviation estimated by random variate generation from their probability distribution as described (45).
Figure S4 in Supplementary Information compares motility velocity with MHD fractional concentration to validate the linearity of eq. 7.
Qdot assay calibration and compliance
We imitate in vitro motility conditions with mechanical translation of Qdots adsorbed to a glass slide. Qdot mechanical movement is precisely controlled using a nanopositioning stage imitating the myosin powered Qdot movement. Figures S5–S8 in the Supplementary Information (SI) indicates the measured Qdot event-velocity histograms for the calibration data. The final result summarized in Figure S8 indicates Qdot assay step-size estimates are equivalent to peaks in the stage readout. Both are systematically higher than the input values of 3, 5, and 8 nm due apparently to actual stage translation overshoot. The curves in Figure S8 show that the Qdot assay has lower dispersion for quantitating position than the stage sensor. Step-frequency in the Qdot assay likewise accurately represents input frequencies. These results are from direct quantitation of the Qdot assay event-velocity histogram and do not involve simulation. They demonstrate the robust reliability of the Qdot assay for measuring nanometer size steps.
Data not shown here involves input step-sizes of 6, 10, and 16 nm and step-frequencies identical to those for the shorter 3, 5, and 8 nm step-sizes. We find equivalently accurate estimates for step-size and step-frequency from the Qdot assay for these parameters.
The fraction of moving actin filaments versus α-actinin concentration in a motility assay for βmys indicates an approximately linear decline for increasing α-actinin except at the highest α-actinin concentrations where linearity fails because α-actinin is unable to fully inhibit actin filament sliding. The latter implies the α-actinin is a viscoelastic inhibitor of the βmys induced actin displacement (18) and that the force developed by βmys during a single α-actinin/actin bound kinetic lifetime is less than the rupture force for the bond (16). Hence compliance in the system (due to intrinsic myosin elasticity (19) and myosin linkage to the nitrocellulose coated substrate) manifests as a difference in measured step-size between unloaded and α-actinin loaded actin. No change in measured step-size implies compliance in the myosin linkage is negligible while compliance due to intrinsic myosin elasticity is undetectable because the α-actinin generally kinetically detaches from actin during the course of the myosin power stroke.
The Qdot assay indicates native βmys step-size and step-frequency in the presence of the external load exerted by the actin binding α-actinin. Figure S9 in SI shows the event-velocity histogram and step-frequency expectation for the system under loaded conditions where motility velocity is reduced to approximately half that of the unloaded protein. We find no significant change in the step-sizes or step-frequency expectations due to the loading of βmys implying negligible assay compliance. However, duty-cycle rises with the increasing load as the βmys develops force as expected (19).
Cardiac myosin step-size and step-frequency
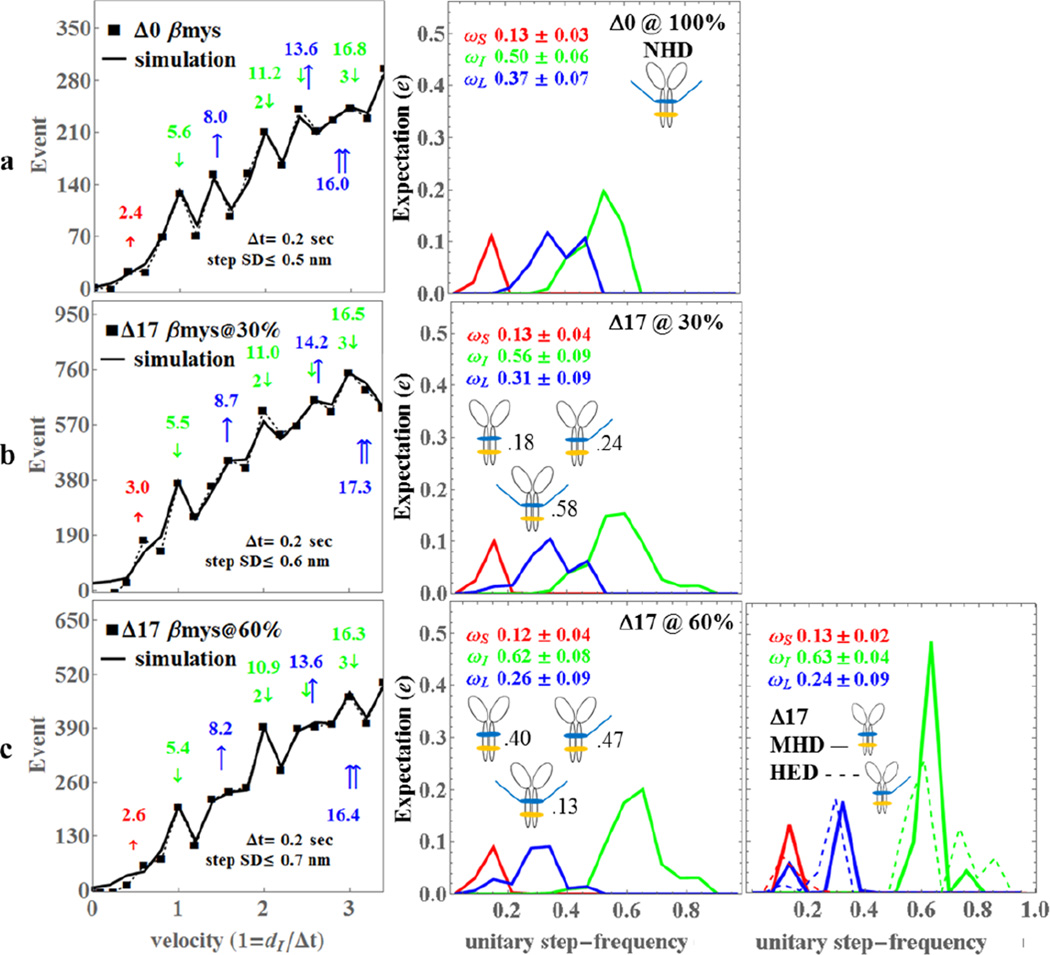
The Qdot assay has labeled actin filaments 1–2 µm long translating over surface bound cardiac myosin. Figure 3 panels in rows a-c show the Qdot assay event-velocity histogram (left most column) and the step-frequency expectation (right two columns) for the control Δ0βmys pure species (row a) and truncated Δ17βmys mixed isoforms (rows b & c).
Figure 3.
The Qdot assay event-velocity histogram (left most column) and the unitary step-frequency expectations (middle and right columns) for porcine Δ0 (row a), Δ17βmy@30% with 30% of the vELC’s truncated at residue 17 (row b), and Δ17βmy@60% with 60% of the vELC’s truncated at residue 17 (row c). Left column rows a-c: The event-velocity histogram for unitary step-size data (■ and dashed line) and simulation (solid line) at the low velocity end. Step-sizes correspond to the short (↑red), intermediate (↓green), and long, (↑blue) steps with associated numeric values in nm. Middle column rows a-c: Step-frequency expectation corresponds to the short (red), intermediate (green), and long (blue) step-sizes with numeric mean values ωS, ωI, and ωL ± standard deviation. Step-frequency expectations are derived from simulation of event-velocity histogram data as described in METHODS. Relative fractions of NHD, HED, and MHD are indicated next to their icon. Right column row c: Step-frequency expectations for pure species MHD (truncated vELC homodimer, solid lines) and HED (1 truncated and 1 native vELC heterodimer, dashed lines) are derived as explained in METHODS. Numeric mean values ωS, ωI, and ωL ± standard deviation represent the pure MHD species only. An independent experimental event-velocity histogram was obtained from each of 10–12 acquisitions × 3 separate protein preparations or 30–36 acquisitions for each isoform (Δ0, Δ17@30%, and Δ17@60%). The 30–36 best fitting independent simulations of these data were the basis for the standard deviation estimates indicated in the figure.
Measured data in the left column of rows a-c (■ connected with dashed line) is pooled from 10–12 acquisitions × 3 independent protein preparations and after linear transformation of the independent coordinate for data in individual slides to the natural velocity units (vu) where (dI/Δt) = 1 for dI the intermediate step-size (~5 nm) and uniform frame capture interval Δt = 0.2 sec. Event-velocity histogram baselines due to thermal/mechanical fluctuations were subtracted as described (2). Simulated velocity-event curves are shown as a solid line in the left column. Peaks or inflection points appearing below 2 vu are short (↑red or S), intermediate (↓green or I), and long (↑blue or L) step-sizes in nm. Intermediate and long steps in combination are also shown. The principal basis for accurate simulation is identifying positions and probabilities for the 5 dominant step-types (↑red, ↓green, ↑blue, ↓↓, ↓↑blue). Step-sizes and step-frequency estimates and standard deviations are indicated in the figures. Figure 4, rows a-c show identical quantitation as in Figure 3 but for the mouse constructs with Δt = 0.06 sec.
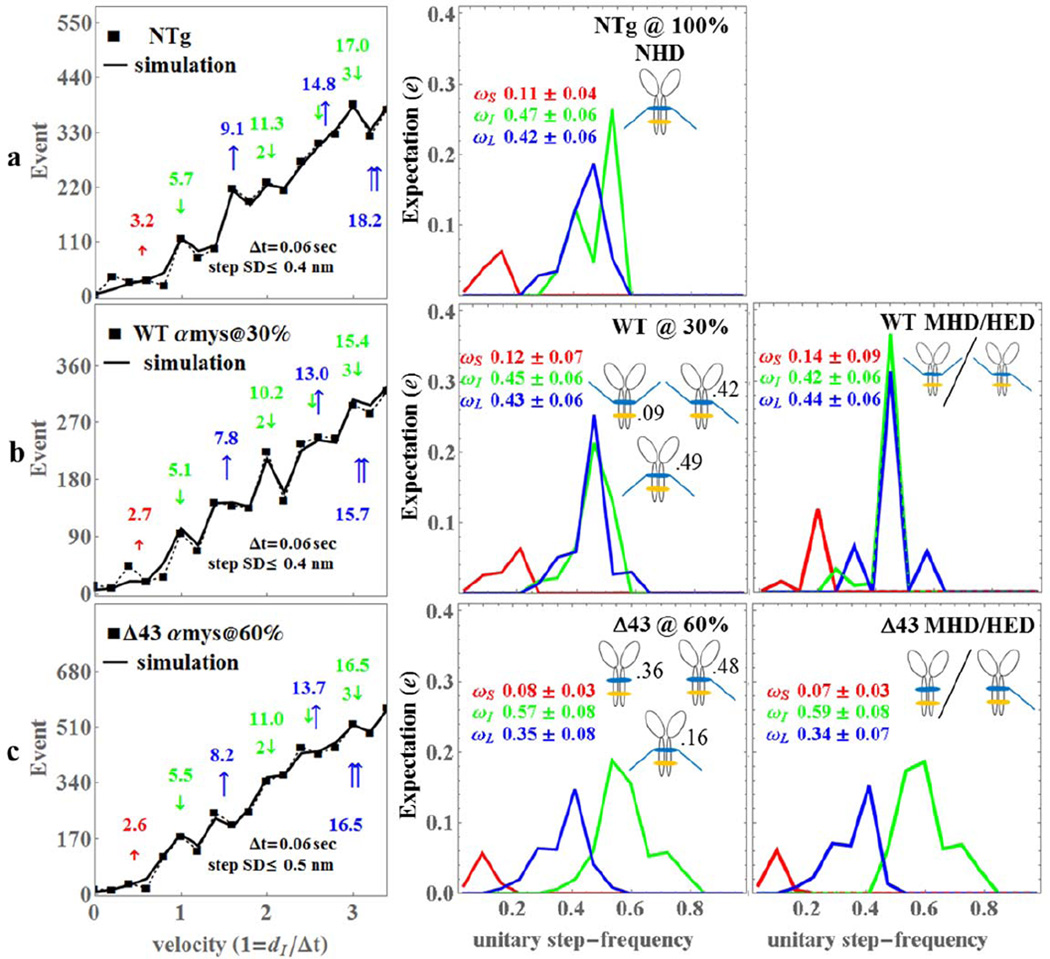
Figure 4.
The Qdot assay event-velocity histogram (left most column) and the unitary step-frequency expectations (middle and right columns) for mouse NTg (row a), WTαmys@30% with 30% of the native mouse vELC replaced with intact human vELC (row b), and Δ43αmys@60% with 60% of the native mouse vELC replaced with human vELC truncated at residue 43 (row c). Left column rows a-c: The event-velocity histogram for unitary step-size data (■ and dashed line) and simulation (solid line) at the low velocity end. Step-sizes correspond to the short (↑red), intermediate (↓green), and long, (↑blue) steps with associated numeric values in nm. Middle column rows a-c: Step-frequency expectations correspond to the short (red), intermediate (green), and long (blue) step-sizes with numeric mean values ωS, ωI, and ωL ± standard deviation. Step-frequency expectations are derived from simulation of event-velocity histogram data as described in METHODS. Relative fractions of NHD, HED, and MHD are indicated next to their icon. Right column row b: Step-frequency expectations for pure species MHD (human vELC homodimer) and HED (1 human and 1 native vELC heterodimer) assuming Model 2 where MHD and HED are identical. Right column row c: Step-frequency expectations for pure species MHD (Δ43 human vELC homodimer) and HED (1 Δ43 human and 1 native vELC heterodimer) assuming Model 2 where MHD and HED are identical. An independent experimental event-velocity histogram was obtained from each of 10–12 acquisitions × 1 protein preparation or 10–12 acquisitions for each isoform (NTg, WT@30%, and Δ43@60%). The 10–12 best fitting independent simulations of these data were the basis for the standard deviation estimates indicated in the figure.
The Qdot labeled single actin filaments translate in steps ranging from 3 to ~250 nm in the order caused by the actin filament microenvironment providing multiplexed time-distance data. The data is decoded in a velocity histogram with the low velocity end readily interpretable as single molecule step-sizes and step-frequencies. The raw data depicted in Figure S10 of SI shows histogrammed data obtained from one in vitro motility movie with the independent variable transformed linearly to natural velocity units. Subsequently, data undergoes baseline subtraction (also shown in Figure S10) and (when appropriate) combination with similarly constructed data from parallel experiments. Figure S10 shows representative raw data sets from individual slides before linear transformation and baseline subtraction for all measured samples in Figures 3 & 4.
Step-size values for Δ0βmys are statistically equivalent to previous results (2, 3). We compared 3 step-sizes for the pooled βmys data from Δ0 and Δ17βmys @ 60% (60% truncated) using one-way ANOVA. Step-sizes, dS, dI, and dL were not significantly different between the Δ0 and Δ17βmys @ 60% isoforms (Figure 3). We compared 3 step-sizes for the αmys data from NTg, WTαmys, and Δ43αmys isoforms using one-way ANOVA. Step-sizes, dS, dI, and dL were all significantly different comparing NTg to WTαmys or NTg to Δ43αmys isoforms. Step-size differences between WT and Δ43αmys isoforms were insignificant (Figure 4). Previously measured average step-size for β or αmys is 5–9 nm (2, 20–23).
Figures 3 & 4 show step-frequency expectation (e), expectation values (ω), and standard deviations for the S, I, and L unitary steps. The expectation curves (Methods eq. 3) indicate the relative probability for step-frequency values along the abscissa. The area under the color coded curves for the S, I, and L steps equal expectation values ωS, ωI, and ωL, respectively. The sum ωS+ ωI + ωL for a given sample or pure species is 1. Middle columns in Figures 3 & 4 correspond to step-frequencies determined by simulation of the event-velocity histogram in the left adjacent panel. Native isoforms, Δ0βmys and NTg, have homogeneous vELC’s hence they are also pure NHD species. Modified isoforms (Δ17βmys, WTαmys, and Δ43αmys) combine native vELC with truncated (Δ17 vs Δ43) or alternative sequence (WT) vELC. The right most columns in Figures 3 & 4, corresponding to the step-frequency expectation for the homogeneous modified vELC species are discussed in the Results section following this one.
Step-frequency expectation values for Δ0βmys are statistically equivalent to previous results where the 5 nm step predominates (2, 3). Probability for the 5 nm step increased while probabilities for the 3 and 8 nm steps declined in Δ17βmys compared to Δ0βmys as the fractional contribution from the truncated vELC increased (Figure 3 middle column). Changes to intermediate and long step frequencies, ωI and ωL, between Δ0βmys and the Δ17βmys @ 60% βmys are statistically significant (ωS is a dependent variable). These changes to step-frequency expectation are evident from inspection of the event-velocity histograms for the samples depicted in the left column of Figure 3. Thus the increasing fraction of truncated vELC enhances the 5 nm step signature and its harmonics (indicated with 2 or 3 down pointing arrows) at the expense of the 8 nm step-size such that when 60% of the vELC is cleaved the 8 nm step disappears into the broad baseline of events. vELC N-terminus truncation in βmys apparently down regulates vELC/actin binding resulting in changes to step-frequency consistent with the Figure 2 model.
There are no previous measurements of step-frequency expectation for αmys. The NTg αmys step-frequency expectation broadly follows that of the βmys due to dominance of the intermediate 5 nm step. Statistical comparison of NTg and WTαmys step-frequency expectation values show they are not significantly different. In contrast, step-frequencies ωI and ωL were significantly different between the NTg/Δαmys or WTαmys/Δαmys isoforms. Probability for the 5 nm step increased while probabilities for the 3 and 8 nm steps decreased in Δ43αmys compared to NTg or WTαmys. These changes to step-frequency expectation are evident from inspection of the event-velocity histograms for the samples depicted in the left column of Figure 4. Truncated vELC in Δ43αmys visibly diminishes the presence of the long (~8 nm) compared to intermediate (~5 nm) step-size in the event-velocity histogram, however, enhancement of the intermediate step-size harmonics (at ~11 & ~16.5 nm) is not as evident as it is for βmys. This could be due to many factors including the counting statistics and the additional heterogeneity in step-size caused by combination of Δ43 and mouse vELC in the Δ43αmys HED (Figure 2).
vELC N-terminus truncation in αmys apparently down regulates vELC/actin binding resulting in these changes in relative step-frequency consistent with the Figure 2 model.
Step-frequency expectation for the pure MHD and HED species
The right columns in Figures 3 & 4 show MHD and HED expectation. The Δ17βmys has 57%, 58%, and 63% (nominally 60%) truncated vELC (Δ17βmys @ 60%) generated by proteolysis and a 30% truncated vELC sample (Δ17βmys @ 30%) obtained by diluting the 63% sample with 1.05× volume of equimolar Δ0βmys (Figure 3). These samples provide sufficient information to calculate pure MHD and HED step-frequency expectations. We find that MHD and HED step-frequency expectations differ substantially (Figure 3, row c, right column) reflecting the heterogeneity of the actomyosin interaction for the native or truncated vELC isoforms. The MHD moves actin predominantly by the 5 nm step-size in a narrow step-frequency range with average ωI ≈ 0.63. We also find that the MHD maintains a reduced but significant probability for making an 8 nm step. The HED likewise moves actin predominantly by the 5 nm step but in a broadened step-frequency range with average ωI ≈ 0.64. Heterogeneity in the actomyosin interaction for the HED is likely due to the asymmetric vELCs in the dimer.
The sole WTαmys sample has 30% intact human vELC. We assume a model for the HED expectation (vHED) to solve for MHD expectation as explained in Methods (see text just above eq. 8) such that, vHED = vNHD (Model 1), vHED = vMHD (Model 2), or vHED = ½(vNHD + vMHD) (Model 3). We find that Model 2 best fits the data. MHD expectation using Model 2 is shown in (Figure 4, row b, right column). Human vELC appears to reverse the predominance of the intermediate step-frequency in NTg by making the long step-frequency predominant in MHD. However, ANOVA statistics comparing the NTg and WTαmys step-frequencies indicates their difference could be accidental. In contrast, ANOVA statistics indicate the step-size of the long step decreases significantly for both the WTαmys @ 30% sample and the MHD species where the long step-size changes 1.3–1.4 nm from 9.1 (NTg) to 7.8 (WTαmys @ 30%) or 7.7 (MHD) nm. The mouse to human vELC replacement causes fundamental alteration to the myosin motor lowering ensemble step-size, force, and power (Table 1).
The sole Δ43αmys sample has 60% truncated human vELC. We find that Model 2 with vHED = vMHD again best fits the data and the MHD expectation is shown in (Figure 4, row c, right column). The data favoring equality of HED and MHD step-frequency expectations implies that vELC truncation in one of the myosin heads removes the modulatory effect of the second intact vELC in αmys. This is unlike the βmys HED. Additional experiments with higher or lower expressions levels for the Δ43αmys vELC could confirm whether the native vELC contributes to the motility of the HED.
The intact vELC N-terminus up-regulates ωL from 0.24 to 0.37 for βmys and from 0.34 to 0.42 for αmys. Step-frequency expectations show that for both αmys and βmys there is reduced but significant probability for the 8 nm step-size in the MHD. This property was not anticipated by the model in Figure 2.
Systemic performance
Table 1 summarizes systemic data. Average step-size, <d> for the βmys and αmys isoforms are equivalent at ~6 nm except for the NTg that is longer at ~7 nm. Average force, <F>, is ~2 fold higher for native βmys compared to native αmys but the higher motility velocity for αmys compensates its lower force to give ~2 fold higher average power, <P>. This is true for both intact αmys proteins, NTg and WTαmys. Most systematic quantities are also estimated for the MHD and HED species of βmys. The MHD and HED species are identical for αmys in Model 2 hence only the quantities for the MHD species are listed.
The N-terminal vELC truncation has effects on myosin function that depend on the βmys and αmys heavy chain. Vmax in actin-activated myosin ATPase rises modestly in Δ17 compared to A0βmys but decreases more substantially in Δ43αmys compared to NTg or WTαmys. The latter agrees with previously reported results for these myosins (13). The divergent ATPase results between the porcine and mouse isoforms might be due to the different truncation lengths of the Δ17βmys vs Δ43αmys forms but implies in both cases that modifying vELC impacts myosin energy transduction kinetics. Similarly, average force and power decline in Δ43αmys but increase in Δ17βmys paralleling the effect of vELC truncation on actin-activated ATPase and probably reflecting the same phenomena.
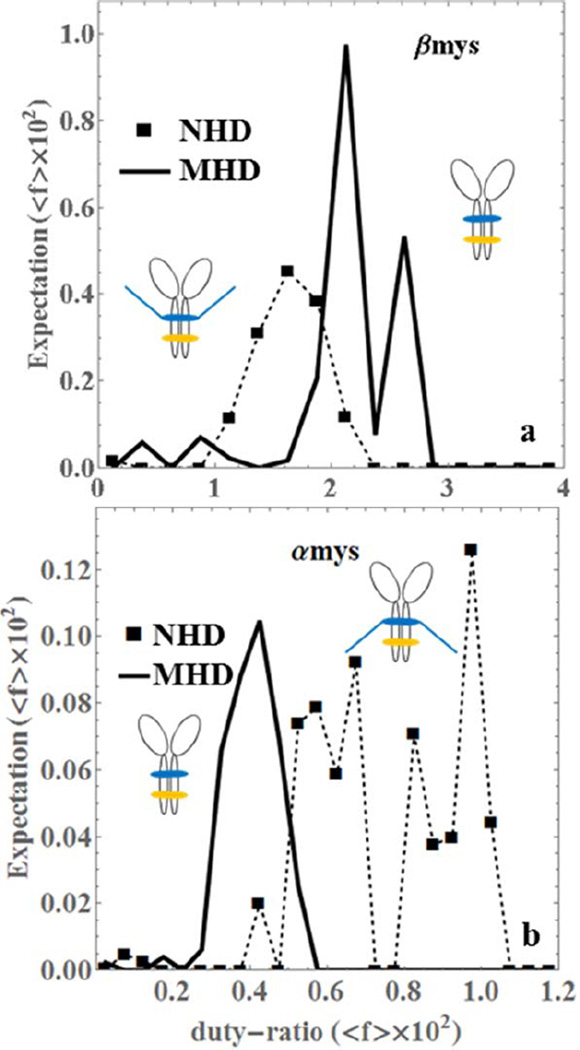
Figure 5 compares the ensemble average duty-ratio (eq. S4 in SI) for the NHD and MHD species. It shows that truncation advances average duty-ratio in βmys and retards duty-ratio in αmys indicating an interesting functional dichotomy between the pure species. The duty-ratio in αmys distributes into two broad peaks corresponding to short and intermediate (lower duty-ratio range) and long (higher duty-ratio range) step-sizes indicating an extensive force-velocity tuning capacity in αmys that is absent from βmys.
Figure 5.
The ensemble averaged duty-ratio (<f> × 102) expectation for pure native vELC homodimers (NHD, dashed line with squares) and truncated vELC homodimers (MHD, thick line) of βmys (panel a) and αmys (panel b).
Single myosins propel actin
Spatially super-resolved Qdot labeled actin tracking measures the event-velocity histogram over the entire velocity domain for βmys adsorbed to nitrocellulose coated coverslips at 0.16 µM bulk concentration as shown in Figure S11 panel a (solid squares) where the abscissa is in natural units <d>/Δt for average step-size <d> = 6 nm and Δt = 200 ms. Mean velocity is 9.1 natural units (nu) corresponding to an apparent <n> = 9.1 for n the number of cross-bridge cycles per Δt. The best fitted Normal distribution approximation to a Binomial distribution for an actin filament 1.3 µm long with available binding sites every 37 nm (35 sites) is indicated by the blue curve.
Myosins strongly bind actin for time ton while impelling the actin filament. Motility buffer has saturating MgATP (2 mM) where ton is 11 or 19 ms for α or βmys (21). We simulated actin-filament translation due to actomyosin cyclical interactions with the random binding of myosins to sites on an actin filament. Myosins simultaneously occupying sites on the actin filament count as one binding event. The simulation provides actual <n> vs apparent <n> relationship shown in panel b indicating that an apparent <n> = 9.1 implies an actual <n> = 11.2. Softening the assumption that “simultaneous myosins binding one actin filament count like one event” to “simultaneous myosins binding one actin filament causes elastic distortion in the myosins to shorten the apparent myosin step-size” would move apparent <n> closer to the actual <n> = 11.2 but has no other implications for what follows. Simulation indicates βmys heads overlap during strong binding ~19% of the total time for the surface density from 0.16 µM βmys bulk concentration. Qdot tracking of actin for the 0.16 µM bulk [αmys] gives apparent <n> = 11.9 implying actual <n> = 13.8 with ~14% predicted strong binding time overlap (data and simulation not shown).
Apparent vs actual <n> in Figure S11 panel b increasingly deviates from approximate equality for n > 10 indicating the impact of ensemble behavior. It limits filament velocity to < 20 nu that is close to the limiting velocity observed in Figure S11 panel a. Observation indicates the maximum apparent <n> is somewhat larger than 20 nu suggesting that: ton < 19 ms, our assumption that “simultaneous myosins binding one actin filament count like one event” is too strict, or both. Each possibility implies that in the real system apparent <n> more closely approximates the actual <n> over a larger domain than that indicated in Figure S11 panel b.
When negligible mutual myosin motor inhibition of actin translation holds, the natural unit on the abscissa in Figure S11 panel a directly indicates the number of myosin interactions with the actin filament during Δt. This situation applies to myosin translation of actin at an apparent 2 nu’s where actual translation is also 2 nu’s because myosins overlap in <4% of their actin bound time. Velocity histograms in Figures 3 & 4 show the discretized velocities indicative of truly single molecule events < 2 nu and the occasional contribution from the small percentage of overlapping myosin impulses to actin that fall between discrete values giving the rising baseline. Closer inspection also show multiples of discrete peak translations that appear at velocities >2 nu indicating when two or three single myosin events with no overlapping actin bound time occur during Δt. A “dead-head” scenario where myosin heads strongly bind actin but do not cycle thus influencing the step-size of a single cycling head does not contribute to the event-velocity histograms in Figures 3 & 4. Dead-head inhibited filaments do not translate and are eliminated from consideration except for estimating baseline contributed by thermal/mechanical fluctuation. We find that the data in Figures 3 & 4 display the unambiguous signature of single myosin translations of actin because the discretized translations occur independently without overlap and beyond any influence from the myosin ensemble.
Event-velocity distribution shape in the Qdot assay
While the existence of single myosin interactions with actin is not in question, the Binomial distribution is expected to describe random binding of myosins to sites on an actin filament. The actual event-velocity distribution (Figure S11 panel a) is much broader hence we considered two hypotheses to explain the discrepancy. The two variables in a Binomial distribution suggest that heterogeneity in either myosin binding probability for actin (Model A) or the number of myosin binding sites for inhomogeneous actin filaments lengths (Model B) could broaden the distribution. Combined Models A & B (Model C) could work while introducing twice the free parameters and we do not consider it further.
We find that Models A and B both adequately fit the experimental data by using a sum of >3 distributions so we chose 3. Actin is constant in the assay so binding probability in Model A is proportional to myosin surface density implying that the moving actin filament encounters areas of lower and higher myosin density than average causing the widely varying motility. Single myosin events selectively occur when actin filaments encounter the lower myosin density as suggested previously (2). Additional experiments are underway to explore the implications of Model B.
Figure S12 in SI compares the three components for actin binding probability in Model A at two surface densities. The faster motility component (blue) grows with surface density (compare panels a with b) mostly at the expense of the intermediate motility component (green) as could be anticipated. Most single myosin events occur due to the slowest motility component (red) with some contribution from the intermediate component. The fractional contribution of single myosin events compared to total is 0.034 and 0.037 for 0.08 and 0.16 µM bulk [βmys], respectively. These data confirm that either bulk concentration for β and αmys is suitable for detecting single myosin interactions with actin in the Qdot assay.
DISCUSSION
In vitro motility assays measure actin gliding velocity over myosin immobilized on a surface (24). Myosin translates actin when the two molecules are strongly bound. The duty-ratio is the time fraction spent strongly actin bound during an ATPase cycle. Muscle myosin has low duty-ratio to enable rapid actin translation in the presence of many actomyosin interactions (25). Low duty-ratio cardiac myosins elude conventional single molecule assays because actomyosin dissociates quickly and the freely moving element diffuses away prohibiting further interaction. Laser trapping solved the problem by confining the relevant molecules to a region small enough to ensure their interaction with high probability (26). We solved this problem by using super-resolution particle tracking of Qdot labeled actin in the standard in vitro motility assay (2, 3, 27). The Qdot in vitro motility assay (Qdot assay) has modestly more actomyosin interactions than a single molecule encounter while actin diffusion is inhibited by methylcellulose in the motility buffer. The net effect sustains the actomyosin complex while preserving a subset of encounters that do not overlap in time on a single actin filament. While the traditional in vitro motility assay measures myosin ensemble characteristics, the Qdot assay uses super-resolution to characterize the lowest finite actin sliding velocities where impulses from single myosin steps are isolated in time and space. In this low velocity domain, discrete actin translations occur independently without overlapping in time (see Results sections Single myosins propel actin and Event-velocity distribution shape in the Qdot assay). Consequently, Qdot assay results from the low velocity domain are practically uninfluenced by ensemble properties of myosin heads including the effect of elastic coupling. Our Qdot assay is an investigative tool providing new insight into the structural basis for: sub-steps in the βmys power-stroke (2, 28), natural βmys activation by RLC phosphorylation (3, 5, 29), and pharmaceutical βmys activation by omecamtive mecarbil (27, 30, 31).
The Qdot assay performed on rabbit skeletal heavy meromyosin (sHMM) indicated a dominant ~5 nm step-size expected for this isoform (1). Porcine βmys indicated three unitary steps-sizes of ~3, ~5, and ~8 nm with 5 nm the major contributor, 8 nm slightly less, and 3 nm a low probability step (2). We proposed the model in Figure 2 for the basis of the three unitary steps-sizes where the major 5 nm step is the default step identical to the dominant unitary step in sHMM, the less likely 8 nm step involves additional lever-arm rotation due to an extra interaction with actin via the unique N-terminus of vELC (32–34), and the minor 3 nm step is the unlikely conversion of the 5 nm step to the full vELC bound 8 nm step.
In the present work we tested the Figure 2 model using porcine and mouse cardiac myosin isoforms and measured the effect of vELC N-terminal truncation on Vmax, KM, and single myosin mechanical characteristics. Characteristics were measured in low ionic strength conditions suitable for both motility and ATPase measurements. Vmax and KM values for porcine βmys are equivalent to our previous measurements and similar but lower than sHMM in low ionic strength conditions and where a truncated long skeletal ELC(A1) had slightly increased Vmax compared to control (35). Previously measured Vmax and KM values from porcine βmys at higher ionic strength differ due to the incompatibility of the ionic strength conditions (12). Our Vmax and KM, measured from the mouse αmys, are likewise larger than when measured at high ionic strength although trends due to vELC truncation are parallel with the Vmax decreasing and KM unchanged (13).
Vmax from β and αmys isoforms responded differently to vELC truncation with an increased rate for Δ17βmys and decreased rate for Δ43αmys. The difference might be due to the different truncation lengths where Δ17 retains some, while Δ43 retains none, of the residues thought to interact with the myosin heavy chain SH3 domain (36). The Vmax changes indicate vELC truncation affects heavy chain active site kinetics by a mechanism not indicated in the model.
Low-angle X-ray diffraction studies on Δ43αmys papillary muscle fibers in rigor revealed a shift of cross-bridge mass away from the thick filament backbone while center-to-center distance between thick filaments was statistically unchanged (8). A schematic representation of these observations suggests the acute actin-filament/lever-arm angle, ∠cde in Figure 2 panel a, is smaller for WTαmys compared to the Δ43αmys species. The model in Figure 2 implies that actin binding of the vELC extension facilitates an extra ~19 degrees of lever-arm rotation adding 3 nm to the nominal 5 nm step-size. The extra rotation lowers ∠cde in agreement with the X-ray diffraction results. In closely related work on skeletal myosin, an extra ~18 degree lever-arm rotation was attributed to the actin binding of the N-terminus of skeletal ELC(A1) (37).
The unitary step-size in the myosin motor has been recognized for a long time as its principal structural characteristic relating to mechanical function. Unitary step-size is modified in nature to adapt the highly conserved myosin motor domain to its various tasks in muscle contractility and cell motility (25). For cardiac myosin, step-frequency varies among the myosin step-sizes and the continuity of actin motility with multiple actomyosin interactions implies that each step-size has a unique duty-ratio and characteristic time strongly actin bound (27). Step-frequency is a second fundamental motor characteristic likely involved in adapting myosin work production to the changing power demands in a normal heart (3).
vELC N-terminus truncation caused significant redistribution in the step-frequencies among the unitary steps. An ensemble containing a large fraction of myosin with bound vELC missing its N-terminus had significantly lower probability for making the 8 nm step that was offset by higher probability for the 5 nm step as expected from the model. The effect was observed in both the porcine βmys and mouse αmys. vELC N-terminus truncation had little effect on the myosin step-sizes. Combining finding for step-frequency, step-size, motility velocity (sm), and Vmax we surmise that the ensemble average duty-ratio and force <F> for Δ43 is significantly lower than the other αmys isoforms (Table 1) in agreement with force measurements in skinned mouse cardiac muscle (34, 38). In contrast, duty-ratio and force <F> for Δ17 is significantly higher than the Δ0βmys isoform. These distinctions are even sharper considering the MHD species for the βmys and αmys.
In adult chicken skeletal muscle myosin where ensemble averages of ELC(A1) and ELC(A2) content are equal, the A1 and A2 light chains are randomly distributed and the heterodimer is half of the total myosin (39). The chicken skeletal A2 homodimer (equivalent to our MHD) has 1.5× larger in vitro motility velocity than the A1 homodimer (equivalent to our NHD). Velocity up-regulation was attributed to the absence of drag caused by the ELC(A1)/actin interaction that did not apparently inhibit the A1/A2 heterodimer (equivalent to our HED) (40). That the A1 head in the A1/A2 heterodimer rarely or never interacts with actin predicts that sHMM, with A2/A2 and A1/A2 dimer species accounting for 75% of all dimers, will overwhelmingly move actin with an intermediate (~5 nm) step-size in agreement with experiments (1, 2). The A1 and A2 ELC distribution in skeletal myosin resembles best that of the intact and truncated vELC distribution in the Δ17βmys @ 60% sample. The latter has the event-velocity histogram in Figure 3 (row c, left column) where the 5.4 nm step-size dominates with event peaks at 5.4, 10.9, and 16.3 nm (the latter two corresponding to 2 and 3 distinct cross-bridge 5.4 nm impulsions of actin during Δt).
Like the chicken skeletal A1 homodimer, we surmised a 1.5× larger in vitro motility velocity for MHD compared to the NHD βmys (Table 1). Unlike the skeletal myosin A1/A2 heterodimer, our HED βmys retains characteristics from both the native and truncated vELC. The latter is most likely due to the Δ17 truncation that retains a Pro/Ala sequence missing from Δ43 (36). The Δ43 αmys construct does not up-regulate motility velocity but does have an HED that imitates its own MHD like the skeletal A1/A2 heterodimer. The apparent functional dichotomy between βmys and αmys isoforms suggests two functions for the intact vELC N-terminus related to the 5 nm step-frequency down regulation in both βmys and αmys (possibly related to residues 1–17) and force up-regulation in βmys and down-regulation in αmys (possibly related to residues 18–43).
Potential differences in specific nitrocellulose-coated-substrate/myosin interactions among the various isoforms tested could impact motility or Qdot assay results just as functionalized surfaces were shown to alter adsorbed myosin motor function (41). These concerns appear unlikely based on the in vitro force measurements (Figure S9 in SI) where βmys on an α-actinin coated nitrocellulose surface has statistically identical myosin dimer step-sizes and step-frequencies as the plain nitrocellulose only surface.
Myosin power stroke sub-steps were reported for skeletal (42) and cardiac myosin (28) using the laser trap. Our distances appropriately match with the latter work where the cardiac myosin has a long 6.6 nm step-size (compared to our 8 nm) with 4.7 and 1.9 nm sub-steps (compared to our 5 and 3 nm steps) exactly as indicated in Figure 2 except that the 3+5 nm steps are always coupled (as expected, see below). Another laser trapping experiment reported 2 myosin step-sizes of 5 and 9 nm from native mouse cardiac ventricular myosin with step-frequency in approximate agreement with our values (43). Tyska et al. propose it is the effect of two heads in a myosin dimer while we favor our model in Figure 2. The laser trap measuring displacement fluctuations would not separate the 5+3 nm sub-steps belonging to one 8 nm step because there is no actin dissociation between the sub-steps explaining why the 3 nm step is missing from their data. We can now elaborate slightly on our model to propose that a slow ADP release in cardiac myosin provides opportunity for the vELC N-terminus to bind actin. The vELC actin binding inhibits ADP release either sterically or by creating strain (44) until completion of the full 8 nm step. Failure of a timely cELC actin binding event allows early ADP release with the step-size terminating at 5 nm, or, for the 5+3 step sequence to be detected in the Qdot assay as separate 3 and 5 nm steps.
Truncated or otherwise modified vELC isoforms were incorporated into porcine or mouse cardiac myosin with various efficiencies <100% potentially complicating interpretation of the single myosin mechanical data since actin displacement due to a single myosin impulse cannot be traced to the participating isoform in the mixture a priori. These experimental challenges emulate real biological systems where protein isoform mixtures are the norm due to distinctive properties or advantages that the heterogeneous system provides. We surmised the single molecule characteristics of the mixed isoforms as probability densities for step-size, step-frequency, and duty-ratio that equal a linear combination of the pure species probability densities weighted by their known concentration. Experiments at two or more different values of the modified vELC content provide sufficient information to extract the probability densities for step-size, step-frequency, and duty-ratio for each pure species. Averages, standard deviation (Table 1) and other modes of the distributions are calculable from the probability densities themselves while representative individual data points are re-constructed statistically using random variate generation (45). Pure species probability densities are indicated in Figures 3–5. We find that the MHD retains a modest ability to translate actin with 8 nm steps suggesting that myosin is built to step with variable step-sizes probably related structurally to how ADP release occurs and that vELC modifies this pre-existing condition.
The converse problem, constructing a motor ensemble to certain chemomechanical specifications by designing the appropriate mixture of various pure myosin isoforms with known mechanical and enzymatic characteristics, is a design challenge apparently solved in natural systems. For instance, human skeletal muscle has a mixture of several myosin isoforms with relative abundance affected by use (46). Porcine and human ventriculum contain minor populations of αmys and skeletal actin that decrease in abundance with advancing disease 47–50). Both circumstances suggest isoform diversity fulfills a specific chemomechanical specification that, in the case of ventriculum, is driven beyond design limits by disease onset. Likewise normal myosin light chain heterogeneity fulfills roles in muscle regulation and performance adaptation that has been recognized for decades (51, 52). The problem is formally posed as reversing the roles of knowns and unknowns in eq. 7 and would also involve “cost” expressed as Vmax from actin-activated myosin ATPase (SI eq. S1). This problem is an important one for in vitro ensemble motor engineering and in vivo if correcting a disease defect will one day involve gene therapy or cell reprogramming.
We have verified, using truncated and native versions of vELC in cardiac myosins, our earlier hypothesis that the vELC N-terminal extension uses the novel mechanism of step-frequency modulation to affect power output. This is an unexplored basis for modulating cardiac myosin power generation in vivo.
Supplementary Material
Acknowledgments
Funding Source Statement: Supported by NIH grants R01AR049277, R01HL095572 (to TPB), and R01HL108343 (to DSC).
ABBREVIATIONS
- Δ0
intact vELC
- Δ17
17 residue N-terminal truncated vELC
- Δ43
43 residue N-terminal truncated human vELC
- αmys
α heavy chain (MYH6) ventricular cardiac myosin
- βmys
β heavy chain (MYH7) ventricular cardiac myosin
- ELC(A1)
long skeletal myosin essential light chain
- ELC(A2)
short skeletal myosin essential light chain
- HED
heterodimeric vELC myosin
- MHD
modified homodimeric vELC myosin
- NHD
native homodimeric vELC myosin
- NTg
nontransgenic mouse αmys
- RLC
cardiac regulatory light chain
- sHMM
skeletal heavy meromyosin
- vELC
ventricular cardiac myosin essential light chain (MYL3)
- WT
human vELC expressed in mouse
Footnotes
Supplementary information includes: Materials and Methods Sections A and B, Results Figures S1-S10, and related references. This material is available free of charge via the Internet at http://pubs.acs.org.
REFERENCES
- 1.Steffen W, Smith D, Simmons R, Sleep J. Mapping the actin filament with myosin. Proc. Natl. Acad. Sci. USA. 2001;98:14949–14954. doi: 10.1073/pnas.261560698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang Y, Ajtai K, Burghardt TP. Qdot labeled actin super-resolution motility assay measures low duty cycle muscle myosin step-size. Biochemistry. 2013;52:1611–1621. doi: 10.1021/bi301702p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang Y, Ajtai K, Burghardt TP. Ventricular myosin modifies In vitro step-size when phosphorylated. J. Mol. Cell. Cardiol. 2014;72:231–237. doi: 10.1016/j.yjmcc.2014.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Toepfer C, Caorsi V, Kampourakis T, Sikkel MB, West TG, Leung M-C, Al-Saud SA, MacLeod KT, Lyon AR, Marston SB, Sellers JR, Ferenczi MA. Myosin Regulatory Light Chain (RLC) Phosphorylation Change as a Modulator of Cardiac Muscle Contraction in Disease. J. Biol. Chem. 2013;288:13446–13454. doi: 10.1074/jbc.M113.455444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yuan C-C, Muthu P, Kazmierczak K, Liang J, Huang W, Irving TC, Kanashiro-Takeuchi RM, Hare JM, Szczesna-Cordary D. Constitutive phosphorylation of cardiac myosin regulatory light chain prevents development of hypertrophic cardiomyopathy in mice. Proc. Natl. Acad. Sci. USA. 2015;112 doi: 10.1073/pnas.1505819112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Karabina A, Kazmierczak K, Szczesna-Cordary D, Moore JR. Myosin regulatory light chain phosphorylation enhances cardiac β-myosin in vitro motility under load. Arch. Biochem. Biophys. 2015;580:14–21. doi: 10.1016/j.abb.2015.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Timson DJ, Trayer HR, Trayer IP. The N-terminus of A1-type myosin essential light chains binds actin and modulates myosin motor function. Eur. J. Biochem. 1998;255:654–662. doi: 10.1046/j.1432-1327.1998.2550654.x. [DOI] [PubMed] [Google Scholar]
- 8.Muthu P, Wang L, Yuan C-C, Kazmierczak K, Huang W, Hernandez OM, Kawai M, Irving TC, Szczesna-Cordary D. Structural and functional aspects of the myosin essential light chain in cardiac muscle contraction. FASEB J. 2011;25:4394–4405. doi: 10.1096/fj.11-191973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lossie J, Köhncke C, Mahmoodzadeh S, Steffen W, Canepari M, Maffei M, Taube M, Larchevêque O, Baumert P, Haase H, Bottinelli R, Regitz-Zagrosek V, Morano I. Molecular mechanism regulating myosin and cardiac functions by ELC. Biochem. Biophys. Res. Commun. 2014;450:464–469. doi: 10.1016/j.bbrc.2014.05.142. [DOI] [PubMed] [Google Scholar]
- 10.Petzhold D, Simsek B, Meißner R, Mahmoodzadeh S, Morano I. Distinct interactions between actin and essential myosin light chain isoforms. Biochem. Biophys. Res. Commun. 2014;449:284–288. doi: 10.1016/j.bbrc.2014.05.040. [DOI] [PubMed] [Google Scholar]
- 11.Siemankowski RF, White HD. Kinetics of the interaction between actin, ADP, and cardiac myosin-S1. J. Biol. Chem. 1984;259:5045–5053. [PubMed] [Google Scholar]
- 12.Moczarska A, Kakol I. The influence of regulatory light chains on structural organization of cardiac myosin heads interacting with actin and ATP. Biochem.Mol.Biol.Int. 1995;37:765–772. [PubMed] [Google Scholar]
- 13.Kazmierczak K, Xu YY, Jones M, Guzman G, Hernandez OM, Kerrick WGL, Szczesna-Cordary D. The role of the N-terminus of the myosin essential light chain in cardiac muscle contraction. J. Mol. Biol. 2009;387:706–725. doi: 10.1016/j.jmb.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Henriques R, Lelek M, Fornasiero EF, Valtorta F, Zimmer C, Mhlanga MM. QuickPALM: 3D real-time photoactivation nanoscopy image processing in ImageJ. Nature Methods. 2010;7:339–340. doi: 10.1038/nmeth0510-339. [DOI] [PubMed] [Google Scholar]
- 15.Meijering E, Dzyubachyk O, Smal I. Chapter nine - Methods for Cell and Particle Tracking. In: Conn PM, editor. Methods Enzymol. Academic Press; 2012. pp. 183–200. [DOI] [PubMed] [Google Scholar]
- 16.Greenberg MJ, Moore JR. Cytoskeleton. Vol. 67. Hoboken, N.J.: 2010. The molecular basis of frictional loads in the in vitro motility assay with applications to the study of the loaded mechanochemistry of molecular motors; pp. 273–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cuda G, Pate E, Cooke R, Sellers JR. In vitro actin filament sliding velocities produced by mixtures of different types of myosin. Biophys. J. 1997;72:1767–1779. doi: 10.1016/S0006-3495(97)78823-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Greenberg MJ, Kazimierczak K, Szczesna-Cordary D, Moore JR. Cardiomyopathy-linked myosin regulatory light chain mutations disrupt myosin strain-dependent biochemistry. Proc. Natl. Acad. Sci. USA. 2010;107:17403–17408. doi: 10.1073/pnas.1009619107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kaya M, Higuchi H. Nonlinear elasticity and an 8-nm working stroke of single myosin molecules in myofilaments. Science. 2010;329:686–689. doi: 10.1126/science.1191484. [DOI] [PubMed] [Google Scholar]
- 20.Sugiura S, Kobayakawa N, Fujita H, Yamashita H, Momomura S-i, Chaen S, Omata M, Sugi H. Comparison of Unitary Displacements and Forces Between 2 Cardiac Myosin Isoforms by the Optical Trap Technique: Molecular Basis for Cardiac Adaptation. Circ. Res. 1998;82:1029–1034. doi: 10.1161/01.res.82.10.1029. [DOI] [PubMed] [Google Scholar]
- 21.Palmiter KA, Tyska MJ, Dupuis DE, Alpert NR, Warshaw DM. Kinetic differences at the single molecule level account for the functional diversity of rabbit cardiac myosin isoforms. J. Physiol. 1999;519:669–678. doi: 10.1111/j.1469-7793.1999.0669n.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Debold EP, Saber W, Cheema Y, Bookwalter CS, Trybus KM, Warshaw DM, VanBuren P. Human actin mutations associated with hypertrophic and dilated cardiomyopathies demonstrate distinct thin filament regulatory properties in vitro. J. Mol. Cell. Cardiol. 2010;48:286–292. doi: 10.1016/j.yjmcc.2009.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schmitt JP, Debold EP, Ahmad F, Armstrong A, Frederico A, Conner DA, Mende U, Lohse MJ, Warshaw D, Seidman CE, Seidman JG. Cardiac myosin missense mutations cause dilated cardiomyopathy in mouse models and depress molecular motor function. Proc. Nat. Acad. Sci. USA. 2006;103:14525–14530. doi: 10.1073/pnas.0606383103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Uyeda TQP, Warrick HM, Kron SJ, Spudich JA. Quantized velocities at low myosin densities in an in vitro motility assay. Nature. 1991;352:307–311. doi: 10.1038/352307a0. [DOI] [PubMed] [Google Scholar]
- 25.O’Connell CB, Tyska MJ, Mooseker MS. Myosin at work: Motor adaptations for a variety of cellular functions. Biochim. Biophys. Acta. 2007;1773:615–630. doi: 10.1016/j.bbamcr.2006.06.012. [DOI] [PubMed] [Google Scholar]
- 26.Finer JT, Simmons RM, Spudich JA. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature. 1994;368:113–119. doi: 10.1038/368113a0. [DOI] [PubMed] [Google Scholar]
- 27.Wang Y, Ajtai K, Burghardt TP. Analytical comparison of natural and pharmaceutical ventricular myosin activators. Biochemistry. 2014;53:5298–5306. doi: 10.1021/bi500730t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Greenberg Michael J, Shuman H, Ostap EM. Inherent Force-Dependent Properties of β-Cardiac Myosin Contribute to the Force-Velocity Relationship of Cardiac Muscle. Biophys. J. 2014;107:L41–L44. doi: 10.1016/j.bpj.2014.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Granzier HL, de Tombe PP. Myosin light chain phosphorylation to the rescue. Proc. Natl. Acad. Sci. USA. 2015;112 doi: 10.1073/pnas.1511455112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liu Y, White HD, Belknap B, Winkelmann DA, Forgacs E. Omecamtiv Mecarbil Modulates the Kinetic and Motile Properties of Porcine β-Cardiac Myosin. Biochemistry. 2015;54:1963–1975. doi: 10.1021/bi5015166. [DOI] [PubMed] [Google Scholar]
- 31.Mamidi R, Gresham KS, Li A, dos Remedios CG, Stelzer JE. Molecular effects of the myosin activator omecamtiv mecarbil on contractile properties of skinned myocardium lacking cardiac myosin binding protein-C. J. Mol. Cell. Cardiol. 2015;85:262–272. doi: 10.1016/j.yjmcc.2015.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Miyanishi T, Ishikawa T, Hayashibara T, Maita T, Wakabayashi T. The two actin-binding regions on the myosin heads of cardiac muscle. Biochemistry. 2002;41:5429–5438. doi: 10.1021/bi0118355. [DOI] [PubMed] [Google Scholar]
- 33.Schaub MC, Hefti MA, Zuellig RA, Morano I. Modulation of contractility in human cardiac hypertrophy by myosin essential light chain isoforms. Cardiovasc. Res. 1998;37:381–404. doi: 10.1016/s0008-6363(97)00258-7. [DOI] [PubMed] [Google Scholar]
- 34.Miller MS, Palmer BM, Ruch S, Martin LA, Farman GP, Wang Y, Robbins J, Irving TC, Maughan DW. The essential light chain N-terminal extension alters force and fiber kinetics in mouse cardiac muscle. J. Biol. Chem. 2005;280:34427–34434. doi: 10.1074/jbc.M508430200. [DOI] [PubMed] [Google Scholar]
- 35.Stepkowski D, Efimova N, Paczynska A, Moczarska A, Nieznanska H, Kakol I. The possible role of myosin A1 light chain in the weaking of actin-myosin interaction. Biochim. Biophys. Acta. 1997;1340:105–114. doi: 10.1016/s0167-4838(97)00031-9. [DOI] [PubMed] [Google Scholar]
- 36.Lowey S, Saraswat LD, Liu H, Volkmann N, Hanein D. Evidence for an interaction between SH3 domain and the N-terminal extension of the essential light chain in class II myosins. J. Mol. Biol. 2007;371:902–913. doi: 10.1016/j.jmb.2007.05.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Guhathakurta P, Prochniewicz E, Thomas DD. Amplitude of the actomyosin power stroke depends strongly on the isoform of the myosin essential light chain. Proc Natl Acad Sci USA. 2015;112:4660–4665. doi: 10.1073/pnas.1420101112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Michael JJ, Gollapudi SK, Ford SJ, Kazmierczak K, Szczesna-Cordary D, Chandra M. Deletion of 1–43 amino acids in cardiac myosin essential light chain blunts length dependency of Ca2+ sensitivity and cross-bridge detachment kinetics. Am. J. Physiol. Heart Circ. Physiol. 2013;304:H253–H259. doi: 10.1152/ajpheart.00572.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lowey S, Benfield PA, Silberstein L, Lang LM. Distribution of light chains in fast skeletal myosin. Nature. 1979;282:522–524. doi: 10.1038/282522a0. [DOI] [PubMed] [Google Scholar]
- 40.Lowey S, Waller GS, Trybus KM. Function of skeletal muscle myosin heavy and light chain isoforms by an in vitro motility assay. J. Biol. Chem. 1993;268:20414–20418. [PubMed] [Google Scholar]
- 41.Balaz M, Sundberg M, Persson M, Kvassman J, Månsson A. Effects of Surface Adsorption on Catalytic Activity of Heavy Meromyosin Studied Using a Fluorescent ATP Analogue. Biochemistry. 2007;46:7233–7251. doi: 10.1021/bi700211u. [DOI] [PubMed] [Google Scholar]
- 42.Capitanio M, Canepari M, Cacciafesta P, Lombardi V, Cicchi R, Maffei M, Pavone FS, Bottinelli R. Two independent mechanical events in the interaction cycle of skeletal muscle myosin with actin. Proc. Natl. Acad. Sci. U. S. A. 2006;103:87–92. doi: 10.1073/pnas.0506830102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tyska MJ, Hayes E, Giewat M, Seidman CE, Seidman JG, Warshaw DM. Single-Molecule Mechanics of R403Q Cardiac Myosin Isolated From the Mouse Model of Familial Hypertrophic Cardiomyopathy. Circ. Res. 2000;86:737–744. doi: 10.1161/01.res.86.7.737. [DOI] [PubMed] [Google Scholar]
- 44.Nyitrai M, Rossi R, Adamek N, Pellegrino MA, Bottinelli R, Geeves MA. What limits the velocity of fast-skeletal muscle contraction in mammals? J. Mol. Biol. 2006;355:432–442. doi: 10.1016/j.jmb.2005.10.063. [DOI] [PubMed] [Google Scholar]
- 45.Mitchell RL, Stone CR. Table-Lookup Methods for Generating Arbitrary Random Numbers. IEEE Transactions on Computers. 1977;c-26:1006–1008. [Google Scholar]
- 46.Harridge SDR. Plasticity of human skeletal muscle: gene expression to in vivo function. Exp. Physiol. 2007;92:783–797. doi: 10.1113/expphysiol.2006.036525. [DOI] [PubMed] [Google Scholar]
- 47.Vandekerckhove J, Bugaisky G, Buckingham M. Simultaneous expression of skeletal muscle and heart actin proteins in various striated muscle tissues and cells. J. Biol. Chem. 1986;261:1838–1843. [PubMed] [Google Scholar]
- 48.Lim D-S, Roberts R, Marian AJ. Expression Profiling of Cardiac Genes in Human Hypertrophic Cardiomyopathy: Insight Into the Pathogenesis of Phenotypes. J. Am. Coll. Card. 2001;38 doi: 10.1016/s0735-1097(01)01509-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bergen HR, III, Ajtai K, Burghardt TP, Nepomuceno AI, Muddiman DC. Mass spectral determination of skeletal/cardiac actin isoform ratios in cardiac muscle. Rapid Commun. Mass Spectrom. 2003;17:1467–1471. doi: 10.1002/rcm.1075. [DOI] [PubMed] [Google Scholar]
- 50.Locher MR, Razumova MV, Stelzer JE, Norman HS, Patel JR, Moss RL. Determination of rate constants for turnover of myosin isoforms in rat myocardium: implications for in vivo contractile kinetics. Am J Physiol Heart Circ Physiol. 2009;297:H247–H256. doi: 10.1152/ajpheart.00922.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Swynghedauw B. Developmental and functional adaptation of contractile proteins in cardiac and skeletal muscles. Physiol.Rev. 1986;66:710–771. doi: 10.1152/physrev.1986.66.3.710. [DOI] [PubMed] [Google Scholar]
- 52.Hernandez O, Jones M, Guzman G, Szczesna-Cordary D. Myosin essential light chain in health and disease. Am J Physiol Heart Circ Physiol. 2007;292:H1643–H1654. doi: 10.1152/ajpheart.00931.2006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.