Articulatory Distinctiveness of Vowels and Consonants: A Data-Driven Approach

Abstract

Purpose

The goal of this project was to quantify the articulatory distinctiveness of eight major English vowels and eleven English consonants based on tongue and lip movement time series data using a data-driven approach.

Method

Tongue and lip movements of eight vowels and eleven consonants from ten healthy talkers were collected. First, classification accuracies were obtained using two complementary approaches: Procrustes analysis and support vector machine. Procrustes distance was then used to measure the articulatory distinctiveness among vowels and consonants. Finally, the distance (distinctiveness) matrices of different vowel pairs and consonant pairs were used to derive articulatory vowel and consonant spaces using multi-dimensional scaling.

Results

Vowel classification accuracies of 91.67% and 89.05% and consonant classification accuracies of 91.37% and 88.94% were obtained using Procrustes analysis and support vector machine, respectively. Articulatory vowel and consonant spaces were derived based on the pairwise Procrustes distances.

Conclusion

The articulatory vowel space derived in this study resembled the long-standing descriptive articulatory vowel space defined by tongue height and advancement. The articulatory consonant space was consistent with feature-based classification of English consonants. The derived articulatory vowel and consonant spaces may have clinical implications including serving as an objective measure of the severity of articulatory impairment.

Introduction

Intelligible speech is characterized by the ability to produce discernible distinctions between sounds. The acoustic distinctiveness of vowels and consonants has been studied extensively by investigators from a variety of fields including computer science (i.e., automatic speech recognition), psycholinguistics, neuroscience, and communication sciences and disorders. These studies have been motivated by the need to understand not only the phonetic basis of sounds (Stevens & Klatt, 1974) but also how neuronal processing (e.g., Yoder et al., 2008), auditory perception (e.g., Johnson, 2000), and speaking rate change as a function of speaking task difficulty (e.g., Tsao & Iqbal, 2005), speaking environment (e.g., noise), and talker characteristics (e.g., age, health) (Lindblom, 1990). One commonly used measure of distinctiveness among vowels is the acoustic vowel space area, which is defined by the first and second vowel formants. This measure has been used extensively to investigate declines in speech intelligibility (Neel, 2008; Kim, Mark Hasegawa-Johnson, & Perlman, 2011; Turner, Tjaden, & Weismer, 1995; Weismer, Jeng, Laures, Kent, & Kent, 2001), articulation rate (Zajac et al., 2006), developmental changes in speech (e.g., Lee, Potamianos, & Narayanan, 1999; Rvachew, Mattock, Polka, & Ménard, 2006), and exaggerated speech directed to infants (Green & Nip, 2010; Green, Nip, Mefferd, Wilson, & Yunusova, 2010; Kuhl et al., 1997; Kuhl & Meltzoff, 1997).

In comparison to acoustic-based measures of phoneme distinctiveness, articulatory-based measures have received little attention, due to the logistical difficulty of obtaining articulatory data (e.g., Electromagnetic Articulography, or EMA, is an expensive system and requires careful calibration, compared to, for example, acoustic recordings). Yet articulatory measures have many important clinical and scientific implications including (1) quantifying the degree of articulatory impairment in persons with speech disorders by articulatory information (rather than by acoustic information), (2) advancing knowledge about articulatory-to acoustic relations (Mefferd & Green, 2010), and (3) enhancing phoneme recognition accuracy for speech recognition in noisy environments (King et al., 2007; Livescu et al., 2007) and in disordered speech (Rudzicz, 2011), as well as for silent speech recognition from articulatory movements (Denby et al., 2010; Wang, 2011). Moreover, some research has indicated that articulatory control and coordination may not manifest in speech acoustics. For example, the spatiotemporal variations in tongue movement time-series are not apparent in associated formant time-series (Mefferd & Green, 2010). The development of articulatory-based measures is particularly needed for identifying changes in articulatory control that occur during normal development, treatment, or disease (Wang, Green, Samal, & Marx, 2011).

To date, the articulatory distinctiveness of different phonemes has predominantly been based on the classification of their presumed distinctive articulatory features such as lip rounding, lip opening, lip height, lip contour, and lip area (Potamianos, Neti, Gravier, Garg, & Senior, 2003; Sadeghi & Yaghmaie, 2006; Shinchi, 1998), tongue tip and tongue body height (Richardson, Bilmes, & Diorio, 2000), lip opening and lip rounding (Richardson, Bilmes, & Diorio, 2000; Saenko, Livescu, Glass, & Darrell, 2009), lip width and lip area (Heracleous, Aboutabit, & Beautemps, 2009; Visser, Poel, & Nijholt, 1999), maximum displacement (Yunusova, Weismer, & Lindstrom, 2011), and vocal tract shape geometry (Fuchs, Winkler, & Perrier, 2008; Honda, Maeda, Hashi, Dembowski, & Westbury, 1996). Most of these classification approaches for articulatory data (without using acoustic data) have resulted in only poor to moderate classification accuracy; only a few achieved accuracy of 80% (Yunusova, Weismer, & Lindstrom, 2011). Two significant limitations of the feature-based approaches are that (1) classification is dependent on accurate feature identification and (2) the approaches assume there are isomorphic, simple mappings between chosen features and phonemes. These approaches are also limited because they have typically relied on articulatory features, which do not account for time-varying motion pattern information. More direct approaches such as in this study, where articulatory movement time-series are mapped directly to phonemes, may overcome these limitations.

The goal of this project was to provide a better understanding of the articulatory distinctiveness of phonemes, which has been a long-standing empirical challenge – one that required the development of a novel analytic technique for quantifying the subtle across-phoneme differences in articulatory movements. Specifically, we evaluated the accuracy of a direct-mapping approach for classifying and quantifying the articulatory distinctiveness of vowels and consonants based on articulatory movement time-series data rather than articulatory features. Classification accuracies using statistical shape analysis (Procrustes analysis) and machine learning (support vector machine) on articulatory movements were obtained as a measure of how well the set of vowels and consonants can be distinguished based on articulatory movements. Procrustes distance was then used to quantify the articulatory distinctiveness of vowel and consonant pairs. Finally, the quantified articulatory distinctiveness of vowels and consonants were used to derive both an articulatory vowel space (an articulatory parallel to acoustic vowel space) and an articulatory consonant space.

Methods

Participants

Ten monolingual females, native speakers of English, participated in the study. The average age of the participants was 23.60 years (SD = 9.48, range from 19 to 50). No participant reported hearing and speech problems and prior history of hearing or speech impairments. They were all from the mid-west region of the United States.

Stimuli

Eight major English vowels in symmetrical consonant-vowel-consonant (CVC) syllables, / bab/, / bib/, / beb/, / bæb/, / bɅb/, / bɔb/, / bob/, / bub/, were used as vowel stimuli. The eight vowels are representative of the English vowel inventory and were chosen because they sufficiently circumscribe the boundaries of the descriptive articulatory vowel space (Ladefoged & Johnson, 2011). Therefore, these vowels provide a good representation of the variety of tongue and lip movement patterns. The consonant context was held constant across stimuli to minimize the influence of consonant coarticulation effects on vowel identity. The context / b/, a bilabial, was selected because it had minimum co-articulation effect on the vowels, compared with other consonants such as / k/ and / t/ (Lindblom & Sussman, 2012).

Eleven consonants in symmetrical vowel-consonant-vowel (VCV) syllables (i.e., / aba/, / aga/, / awa/, / ava/, / ada/, / aza/, / ala/, / ara/, / a3a/, / ad3a/, / aja/) were used as consonant stimuli. These consonants were selected because they represent the primary places and manners of articulation of English consonants. Consonants were embedded into the / a/ context because this vowel is known to induce larger tongue movements than other vowels (Yunusova, Weismer, Westbury, & Lindstrom, 2008).

Speech Tasks

All stimuli were presented on a large computer screen in front of the participants and prerecorded sounds were played to help the participants to pronounce the stimuli correctly. Participants were asked to repeat what they heard and put stress on the middle phoneme (rather than the carriers) for each stimulus. Participants were asked to rest (about 0.5 second) between each CVC or VCV production to minimize the co-articulation effect. This rest interval also facilitated segmenting the stimuli prior to analysis. The stimuli were presented in a fixed order (as listed above in Stimuli section) across participants. The stimuli were not presented in a random order because it draws too much attention of the participants. Mispronunciations were rare, but were identified by the investigator and excluded from the data analysis.

Each phoneme sequence was repeated multiple times by each participant. On average, 20.9 valid vowel samples were collected from each participant with the number of samples for each vowel varying from 16 to 24 per participant. In total, 1672 vowel samples with 209 samples for each vowel were obtained and used for analysis. The average number of valid consonant samples collected from each subject was 19.4 varying from 12 to 24 per subject. In total, 2134 consonants samples (with 194 samples for each consonant) were collected and used for analysis in this experiment.

Data Collection

The Electromagnetic Articulograph (EMA, Model: AG500; Carstens Medizintechnik, Inc., Germany) was used to register 3-D movements of the tongue, lip, and jaw during speech. The spatial accuracy of motion tracking using EMA (AG500) was 0.5 mm (Yunusova, Green, & Mefferd, 2009). EMA registers movements by establishing a calibrated electromagnetic field in a volume that can be used to track the movements of small sensors within the volume. The center of the magnetic field is the origin (zero point) of the EMA coordinate system.

Participants were seated with their head within the calibrated magnetic field. The sensors were attached to the surface of each articulator using dental glue (PeriAcryl Oral Tissue Adhesive). The participants were then asked to produce the vowel and consonant sequences at their habitually comfortable speaking rate and loudness.

Figure 1 shows the placement of the 12 sensors attached to a participant's head, face, and tongue. Three of the sensors were attached to a pair of glasses. HC (Head Center) was on the bridge of the glasses; HL (Head Left) and HR (Head Right) were on the left and right outside edge of each lens, respectively. The movements of HC, HL, and HR sensors were used to calculate the movements of other articulators independent of the head (Green, Wilson, Wang, & Moore, 2007). Lip movements were captured by attaching two sensors to the vermilion borders of the upper (UL) and lower (LL) lips at midline. Four sensors - T1 (Tongue Tip), T2 (Tongue Blade), T3 (Tongue Body Front) and T4 (Tongue Body Back) - were attached approximately 10 mm from each other at the midline of the tongue (Wang, Green, Samal, & Marx, 2011). The movements of three jaw sensors, JL (Jaw Left), JR (Jaw Right), and JC (Jaw Center), were recorded but not analyzed in this study.

Figure 1.

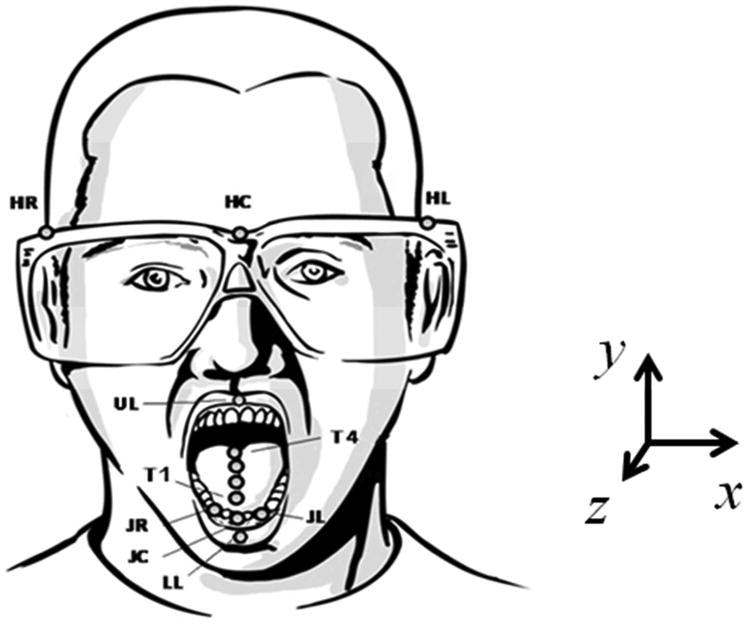
Sensor positions, picture adapted from “Articulatory-to-acoustic relations in response to speaking rate and loudness manipulations,” by A. Mefferd & J. G. Green, Journal of Speech Language and Hearing Research, 2010, 53(5), p. 1209. Sensor labels are described in the text.

Data Preprocessing

Prior to analysis, the translation and rotation components of head movement were subtracted from the tongue and lip movements. The resulting head-independent tongue and lower lip sensor positions included movement from the jaw. The orientation of the derived 3-D Cartesian coordinate system is displayed in Figure 1. Because the movements for the simple vowels and consonants contain only very low frequency components, a low pass filter of 10 Hz was applied to the movement traces prior to analysis (Green & Wang, 2003).

Acoustic signals were recorded simultaneously with kinematic signals directly onto a hard drive of a computer at the sampling rate of 16 kHz with 16 bit resolution. A high quality lapel microphone (Crown Head-worn microphone CM311) was mounted on the forehead approximately 15 cm from the mouth during the recordings. Acoustic recordings were used for segmenting articulatory movement data and for extracting F1 and F2 formant values. First, sequences of movements were aligned with acoustic waveforms. Then the onset and offset of the whole CVC and VCV utterances were identified visually based on acoustic waveform data using a customized Matlab software program (MathWorks Inc. Natick, MA). All manual segmentation results were double checked by the investigator. Occasionally, erroneous samples were collected due to sensor falling off during recording or sounds were not produced correctly. These erroneous samples were excluded in analysis.

Only y (vertical) and z (anterior-posterior) coordinates of the sensors (i.e., UL, LL, T1, T2, T3, and T4) were used for analysis because the movement along the x (lateral) axis is not significant during speech of healthy talkers (Westbury, 1994).

Analysis

Three analyses were conducted: (a) classification using both Procrustes analysis (Dryden & Mardia, 1998) and support vector machine (Boser, Guyon, & Vapnik, 1992; Cortes & Vapnik, 1995), (b) quantifying the articulatory distinctiveness of vowels and consonants using Procrustes distance, and (c) deriving articulatory vowel and consonant space from the distance (distinctiveness) matrices obtained in (b) using multi-dimensional scaling (Cox & Cox, 1994).

Procrustes Analysis

Procrustes analysis is a robust shape analysis technique (Sibson, 1979), which has been successfully applied for object recognition and shape classification (Jin & Mokhtarian, 2005; Meyer, Gustafson, & Arnold, 2002; Sujith & Ramanan, 2005). In Procrustes analysis, a shape is represented by a set of ordered landmarks on the surface of an object. Procrustes distance is calculated as the summed Euclidean distances between the corresponding landmarks of two shapes after the locational, rotational, and scaling effects are removed from the two shapes (or Procrustes matching; see Dryden & Mardia, 1998). A step-by-step calculation of Procrustes distance between two shapes includes (1) aligning the two shapes using their centroids, (2) scaling both shapes to a unit size, and (3) rotating one shape to match the other and obtaining the minimum sum of the Euclidean distances between their corresponding landmarks (Wang, Green, Samal, & Marx, 2011).

An equivalent, but faster method for calculating the Procrustes distance using a complex number representation for the landmark coordinates was used in this experiment. Suppose u and v are two centered shapes represented by two sets of complex numbers. Real and imaginary parts of a complex number represent the two coordinates (y and z of sensor locations) of a landmark. The Procrustes distance d_p between u and v is denoted by Equation (1), where u* denotes the complex conjugate transpose of u. Proof of Equation (1) is given in Dryden & Mardia (1998).

$$d_p(u,v)={\{1-\frac{v\ast uu\ast v}{u\ast uv\ast v}\}}^{1/2}$$ (1)

Procrustes analysis was designed for analysis of static shapes (i.e., shapes do not deform over time). However, a simple strategy was used to extend Procrustes analysis to time-varying shape analysis. In this paper, shapes for phonemes were defined by their sampled motion paths of articulators. First, motion path trajectories (i.e., y and z coordinates) of each articulator were down-sampled to 10 locations spread evenly across time. The predominant frequency of tongue and lip movements is about 2 to 3 Hz for simple CVC utterances (Green & Wang, 2003), thus 10 samples adequately preserve the motion patterns. Then, the sampled motion paths of all articulators were spatially integrated as a composite shape representing each phoneme. The composite shape, integration of 10 locations from each of the six sensors, was used to represent a phoneme shape. Thus, in Equation (1), u is a 1 × 60 matrix of complex numbers; u* is a 60 × 1 matrix of the complex conjugates; the result d_p is a real number within the range between 0 to 1. A similar strategy of spatially integrating shapes at different time points was used for recognition of human motion represented using images (Jin & Mokhtarian, 2005). Figure 2a gives an example of continuous articulatory movements of / bab/; Figure 2b illustrates the corresponding shape in which the 60 circles represent 60 landmarks (10 locations × 6 sensors) of the movements of six sensors sampled to ten time points.

Figure 2.

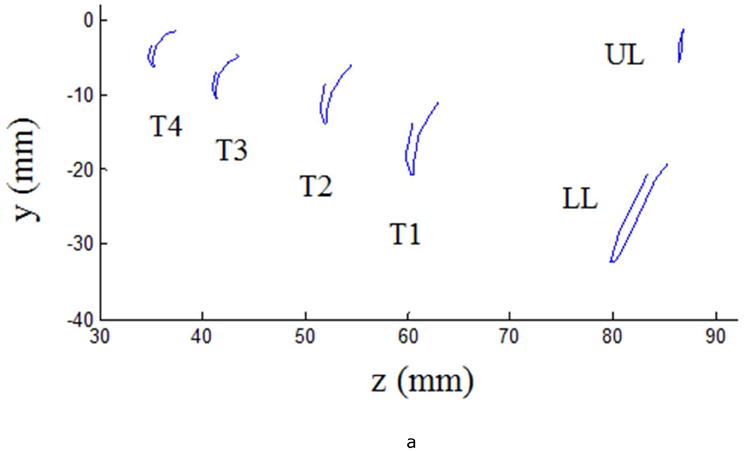
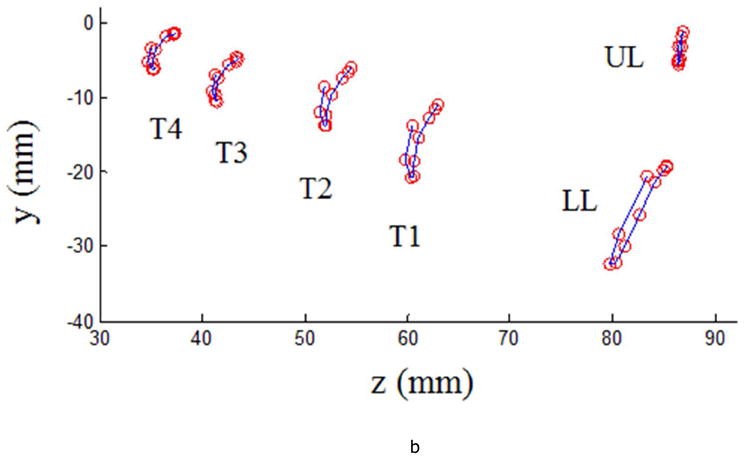
(a) Continuous articulatory movements of / bab/ produced by a single subject; (b) the sampled articulatory movements that form a shape of / bab/ (landmarks are represented by red circles). Articulator labels are described in text.

The following steps, similar to the generalized Procrustes analysis (Gower, 1975), were performed to classify the composite shapes of vowels and consonants for each subject: (1) the average shapes of all samples for each phoneme were calculated and used as references for the phoneme. Average shape of a phoneme is the averaged coordinates of corresponding landmarks of all samples for the phoneme; (2) for each test sample (shape), the Procrustes distances between it and all the average shapes were calculated; and (3) the phoneme that has the shortest distance between its average shape and the testing sample was considered as the recognized phoneme.

Classification accuracy is defined as number of correctly recognized phoneme samples divided by the total number of samples. A classification matrix was used to show how many of the samples from each vowel or consonant were classified into another vowel or consonant. In a classification matrix, a number at row i and column j in the matrix is the percentage of samples of i'th phoneme was classified as j'th phoneme. The classification matrix for a perfect classifier would have 100% along the diagonal and 0% for all the non-diagonal entries.

Then, Procrustes distances between the average shapes of phoneme pairs were calculated and used as a measure of distinctiveness between the pair. Two distance (distinctiveness) matrices (for vowels and consonants, respectively) were obtained from a dataset from each subject. The average distance matrices of all subjects defined the quantified articulatory distinctiveness of vowels and consonants (Wang, Green, Samal, & Marx, 2011).

Support Vector Machine (SVM)

A machine learning classifier (i.e., SVM) was used to provide additional information on classification accuracy to that of Procrustes analysis. SVM, rather than other classifiers, was selected because our prior work showed that SVM outperformed other approaches such as neural networks and decision trees for this application (Wang, Samal, Green, & Carrell, 2009).

In machine learning, a classifier (computational model) predicts classes (or groups, categories) of new data samples on the basis of a training data set, in which the classes are known. In this classification method, a data sample is defined by an array of values (attributes). A classifier makes predictions regarding data classes by analyzing these attributes. The accuracy of the prediction is quantified based on pattern consistency in the data and the classifier's success. SVM is a classifier that tries to maximize the distances between the boundaries of different classes in order to obtain the best generalization of patterns from training data to testing data. SVM classifiers project training data into a higher dimensional space and then separate classes using a linear separator (Boser, Guyon, & Vapnik, 1992; Cortes & Vapnik, 1995). The linear separator maximizes the margin between groups of training data through an optimization procedure (Chang & Lin, 2011). A kernel function is used to describe the distance between two samples (i.e., r and s in Equation 2). The following radial basis function was used as the kernel function K_RBF in this study, where λ is an empirical parameter (Wang, Samal, Green, & Rudzicz, 2012a, 2012b):

$$K_{\mathit{\text{RBF}}}(r,s)=exp(1-\lambda \parallel r-s\parallel )$$ (2)

For more details, please refer to Chang & Lin (2011), which describes the implementation of SVM used in this study.

In this study, a sample (e.g., r or s in Equation 2) is a concatenation of time-sampled motion paths of articulators as data attributes. Initially, the movement data of each stimulus (a vowel or consonant) were time-normalized and sampled to a fixed length (i.e., 10 frames). The length was fixed, because SVM requires the input samples to be fixed-width array. Subsequently, the arrays of y or z coordinates for each articulator were demeaned and concatenated into one sample for each vowel or consonant. Table 1 illustrates how a sample was organized, where UL_y1, one of the attributes, specifies the y coordinate of UL at (normalized) time point one. Overall, each sample contained 120 (6 articulators × 2 dimensions × 10 frames) numbers of attributes. An additional integer (e.g., 1 for / a/, and 2 for / i/) was used for labeling the training data (Table 1).

Table 1. Sample Data Format in Machine Learning Approach (n =10).

Attribute						Label
ULy1, ULy2, … ULyn	ULz1, ULz2, … ULzn	…	T1y1, … T1yn	…	T4z1, … T4zn	Phoneme

Cross validation, a standard procedure to test classification algorithms in machine learning, was used to evaluate the accuracy of articulatory movement classification using SVM. Training data and testing data are unique in cross validation. In this study, Leave-N-out cross validation was conducted, where N (= 8 or 11) is the number of vowels or consonants, respectively. In each execution, one sample for each stimulus (totally N samples) in the dataset was selected for testing and the rest were used for training. There were a total of m executions; where m is the number of samples per phoneme. The average classification accuracy of all m executions was considered the overall classification accuracy (Wang, 2011).

Multi-Dimensional Scaling (MDS)

Multi-dimensional scaling (Cox & Cox, 1994) was used to derive articulatory vowel and consonant spaces based on the distinctiveness matrices of vowels and consonants. MDS is widely used to visualize high dimensional data in a lower dimensional space. Given a set of items and their pair-wise distances (in a symmetric distance matrix), MDS can generate the locations of the points in a coordinate system in which the distance relationships between the items are preserved. The orientation of the space is random and hence does not hold any physical significance. Green & Wang (2003) also used MDS to generate a consonant space based on pair-wise covariance of movements of pellets attached on the midsaggital line of tongue (also named T1, T2, T3, and T4) tracked using x-ray microbeam.

In our use of MDS, the number of dimensions was specified with the input data (i.e., dissimilarity matrix), and then MDS output optimized results in the given number of dimensions. Given an input dissimilarity matrix of phonemes (diagonal numbers are zeros), MDS assigns a location to each phoneme in a N-dimensional space, where N is pre-specified by the user. That is, if N=2, MDS will visualize the data in a 2D space; if N=3, MDS will visualize the data in a 3D space. In this study, the distance matrices between the phonemes were used as dissimilarity matrices. The implementation of MDS in Matlab (MathWorks, Inc. Natick, MA) was used in this analysis. The effectiveness of an MDS outcome can be evaluated by a R² value resulting from a linear regression between the distance matrix obtained from the MDS outcome and the original distance matrix. R² (between 0 to 1) indicates the similarity between the two distance matrices. A larger R² value indicates a better fit between the MDS outcome and the original distance matrix.

Results

Classification Accuracy of Vowels

The average classification accuracy of vowels computed across individual speakers was 91.67% (SD = 5.34) and 89.05% (SD = 11.11) using Procrustes analysis and SVM, respectively. A two-sided t-test was applied on the classification accuracies using the two approaches for each participant. The t-test result showed that there was no significant difference (p < .26) between the accuracies obtained using Procrustes analysis and SVM, which means Procrustes analysis has the similar power as a widely used classifier (i.e., SVM) in vowel classification.

Tables 2 and 3 show the average classification matrices (in percentage) of all subjects using Procrustes analysis and SVM.

Table 2.

Average vowel classification matrix (in percentage) of all subjects using Procrustes analysis. Zeros are not displayed in the tables.

		Classified
		/ a/	/ i/	/ e/	/ æ/	/ Ʌ/	/ ɔ/	/ o/	/ u/
Actual	/ a/	90.53			0.43	3.52	5.08	0.43
	/ i/		98.24	0.91	0.43				0.42
	/ e/		4.19	94.29		0.63			0.89
	/ æ/	3.01		1.25	92.48	2.20	1.06
	/ Ʌ/	1.97			1.48	89.47	5.57	1.51
	/ ɔ/	4.76			0.43	7.89	81.09	5.39	0.43
	/ o/	1.06				5.07	2.93	88.34	2.59
	/ u/					0.63		0.43	98.94

Table 3.

Average vowel classification matrix (in percentage) of all subjects using Support Vector Machine. Zeros are not displayed in the tables.

		Classified
		/ a/	/ i/	/ e/	/ æ/	/ Ʌ/	/ ɔ/	/ o/	/ u/
Actual	/ a/	89.03			1.74	1.25	6.73	0.63	0.63
	/ i/		95.57	4.01					0.42
	/ e/		2.35	97.03				0.63
	/ æ/	2.80		0.63	92.75	1.08	2.75	0.00
	/ Ʌ/	4.32		0.43	0.43	80.36	12.31	1.51	0.63
	/ ɔ/	6.79			1.04	9.29	75.42	6.83	0.63
	/ o/	0.63		0.43		4.18	5.93	85.71	3.13
	/ u/	0.63		1.29			0.45	1.06	96.57

Articulatory Distinctiveness of Vowels

Table 4 shows the average distance matrix (articulatory distinctiveness) computed across all subjects. A larger distance between a vowel pair indicated they are more articulatory distinct. For example, the distances between / a/ and / i/ and that between / a/ and / u/ (0.2506 and 0.2024, respectively) are the largest, suggesting that these vowels are the most articulatory distinct; the distances among / Ʌ/, / ɔ/, and / u/ are the shortest, suggesting that these vowels are least articulatory distinct.

Table 4.

Articulatory distinctiveness between vowel pairs across individuals.

	/ a/	/ i/	/ e/	/ æ/	/ Ʌ/	/ ɔ/	/ o/	/ u/
/ a/	0	0.2506	0.1960	0.1265	0.1087	0.0891	0.1358	0.2024
/ i/	0.2506	0	0.1042	0.1940	0.1911	0.2339	0.2089	0.1461
/ e/	0.1960	0.1042	0	0.1411	0.1504	0.1858	0.1681	0.1406
/ æ/	0.1265	0.1940	0.1411	0	0.1227	0.1248	0.1521	0.1817
/ Ʌ/	0.1087	0.1911	0.1504	0.1227	0	0.0739	0.0814	0.1255
/ ɔ/	0.0891	0.2339	0.1858	0.1248	0.0739	0	0.0999	0.1636
/ o/	0.1358	0.2089	0.1681	0.1521	0.0814	0.0999	0	0.1028
/ u/	0.2024	0.1461	0.1406	0.1817	0.1255	0.1636	0.1028	0

Quantitative Articulatory Vowel Space

The symmetric distance matrix shown in Table 4 was used as a dissimilarity matrix for generating a vowel space using MDS. Figure 3a shows the derived 2-dimensional quantitative articulatory vowel space. As explained previously, in this derived space, the two coordinates are the two optimized dimensions of an MDS solution. Pair-wise distances obtained from the derived space accounts for a large amount of the variance in the original distances as indicated by a regression that yielded a very high R² value of 0.98. MDS can also generate a 3D space (not shown in this paper). However, the third dimension did not contribute significantly to the vowel distinctiveness (R² is also 0.98).

Figure 3.

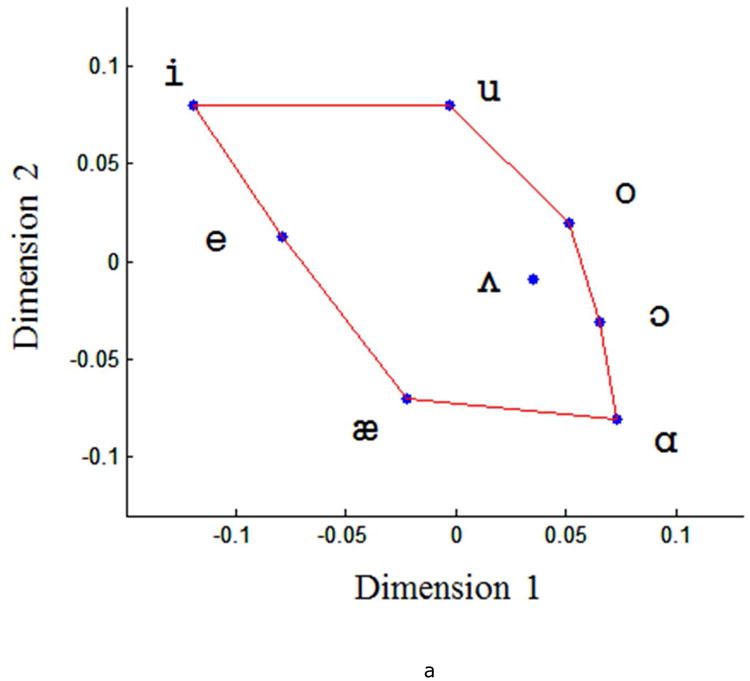
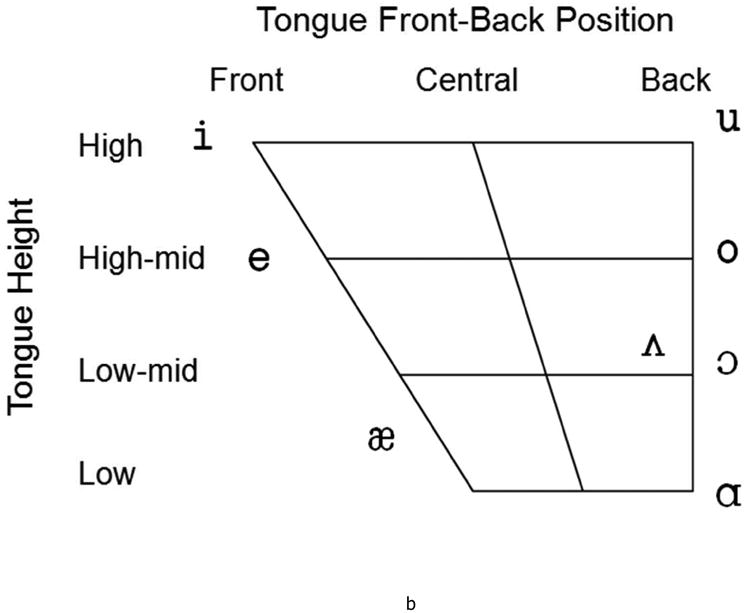
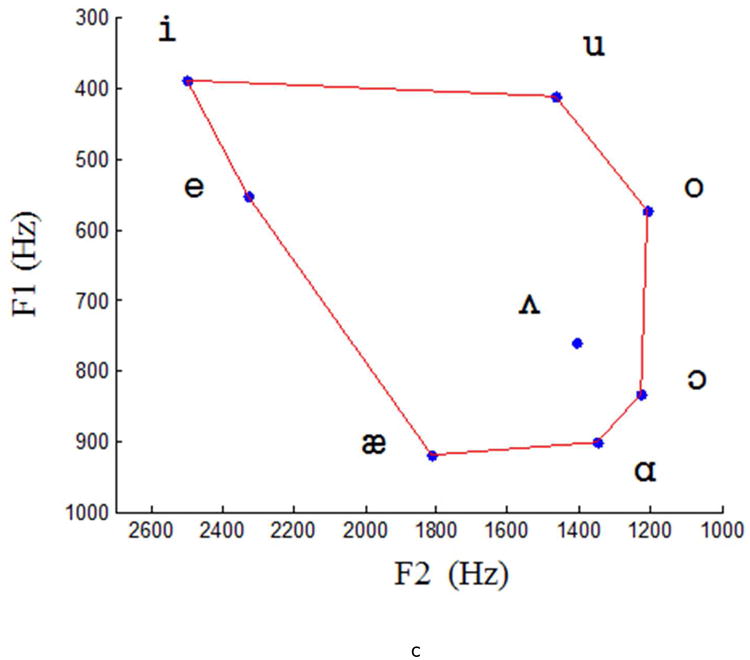
Quantified (a) and descriptive (b) articulatory vowel spaces, and (c) acoustic vowel space including eight major English vowels, picture in panel (b) adapted from A course in phonetics (p. 34), by P. Ladefoged & Johnson, 2011. (6^th ed.) Independence, KY: Cengage Learning. Dimensions in panel (a) are the results of the MDS solution. See Appendix for the formant values in panel (c).

Acoustic Vowel Space

The first and second formants (F1 and F2) of the same eight major English vowels obtained from the synchronously collected acoustic data were used to derive an acoustic vowel space (Figure 3c). The vowel formant values obtained in this study were consistent with those in literature (e.g., Bunton & Story, 2010; Neel, 2008; Rosner & Pickering, 1994; Tsao & Iqbal, 2005; Turner, Tjaden, & Weismer, 1995). Possible slight variation between the formants in this study and those in literature may be due to the dialect or accent effects. As mentioned previously, all our participants are from the mid-west region of the United States. The formant values in Figure 3c are provided in Appendix.

Classification Accuracy of Consonants

The across-talker average accuracies of consonant classification were 91.37% (SD = 4.04) and 88.94% (SD = 6.07) using Procrustes analysis and SVM, respectively. A one-sided t-test showed that the accuracy obtained using Procrustes analysis was significantly higher than that obtained using SVM (p < .01). Tables 5 and 6 show the average classification matrices using Procrustes analysis and SVM, respectively.

Table 5.

Average consonant classification matrix (in percentage) of all subjects using Procrustes analysis.

		Classified
		/ b/	/ g/	/ w/	/ v/	/ d/	/ z/	/ 1/	/ r/	/ 3/	/ d3/	/ j/
Actual	/ b/	94.96		2.88	2.17
	/ g/		94.70	0.50		1.36	0.50		0.53		0.50	1.92
	/ w/	4.03	0.50	93.75	1.31				0.42
	/ v/	1.81		1.03	96.14	0.48			0.56
	/ d/		1.05		0.50	91.17	2.48	1.06	0.53	2.19	1.03
	/ z/				0.56		96.92	1.05	1.06	0.42
	/ 1/		0.50		0.50	1.43	2.55	94.61		0.42
	/ r/		0.48	0.89	1.47		2.11		88.41	3.40	2.17	1.08
	/ 3/		2.98	0.56		0.83	0.50		1.03	83.25	10.32	0.53
	/ d3/					1.58	2.79	0.53	1.06	12.49	81.56
	/ j/	1.08	3.41	1.05		0.53	1.92			2.36	1.56	88.09

Table 6.

Average consonant classification matrix (in percentage) of all subjects using SVM.

		Classified
		/ b/	/ g/	/ w/	/ v/	/ d/	/ z/	/ 1/	/ r/	/ 3/	/ d3/	/ j/
Actual	/ b/	92.32	0.43	3.33	1.89				0.53			1.50
	/ g/	0.42	89.69	0.00	0.00	2.19	0.50	0.50	2.69	0.95	0.50	2.55
	/ w/	2.52	0.43	90.89	1.74	0.50			2.41	0.50		1.00
	/ v/	1.64	0.43	1.48	90.21	0.98	0.56		3.83		0.45	0.42
	/ d/		0.53		0.50	86.67	1.43	2.48	4.05	1.89	1.54	0.92
	/ z/	0.83	0.87		0.56	1.93	91.58	2.81	0.56	0.87
	/ 1/	0.42	0.50		0.45	2.45	3.00	90.90	0.83	0.45		1.00
	/ r/	0.42	1.01	0.56		1.33	1.94	0.50	91.29	2.42		0.53
	/ 3/		1.90			0.53	1.03	0.45	4.24	81.45	9.87	0.53
	/ d3/	0.42				1.48			4.01	9.79	82.78	1.53
	/ j/	0.42	1.82			0.00	0.42		4.33	0.45	2.06	90.51

Articulatory Distinctiveness of Consonants

Table 7 shows the average distance (articulatory distinctiveness) matrix for consonant pairs computed across all subjects. A larger distance between a consonant pair indicates they are more articulatory distinct. The distance between / b/ and / j/ (0.2586) was the largest, representing the greatest articulatory contrast between any two consonants. The distance between / 3/ and / d3/ was the shortest distance (0.0641), representing the least amount of articulatory distinctiveness among any two consonants.

Table 7. Distance Matrix of Consonants.

	/ b/	/ g/	/ w/	/ v/	/ d./	/ z/	/ 1/	/ r/	/ 3/	/ d3/	/ j/
/ b/	0	0.1761	0.1013	0.1035	0.1967	0.1972	0.1957	0.2098	0.2295	0.2546	0.2586
/ g/	0.1761	0	0.1604	0.1608	0.1554	0.1637	0.1682	0.1785	0.1914	0.2121	0.1593
/ w/	0.1013	0.1604	0	0.1068	0.2035	0.2110	0.2157	0.1819	0.2215	0.2485	0.2434
/ v/	0.1035	0.1608	0.1068	0	0.1666	0.1607	0.1740	0.1643	0.1910	0.2156	0.2233
/ d/	0.1967	0.1554	0.2035	0.1666	0	0.1207	0.1416	0.1386	0.1112	0.1257	0.1787
/ z/	0.1972	0.1637	0.2110	0.1607	0.1207	0	0.1029	0.1712	0.1483	0.1639	0.1647
/ 1/	0.1957	0.1682	0.2157	0.1740	0.1416	0.1029	0	0.1978	0.1870	0.2003	0.1846
/ r/	0.2098	0.1785	0.1819	0.1643	0.1386	0.1712	0.1978	0	0.1166	0.1371	0.1791
/ 3/	0.2295	0.1914	0.2215	0.1910	0.1112	0.1483	0.1870	0.1166	0	0.0641	0.1730
/ d3/	0.2546	0.2121	0.2485	0.2156	0.1257	0.1639	0.2003	0.1371	0.0641	0	0.1828
/ j/	0.2586	0.1593	0.2434	0.2233	0.1787	0.1647	0.1846	0.1791	0.1730	0.1828	0

Articulatory Consonant Space

The distance matrix shown in Table 7 was used as a dissimilarity matrix for generating a articulatory consonant space using MDS. Figure 4a gives the derived 2D articulatory consonant space. Similarly to the derived vowels space, the two coordinates in the consonant space are the two optimized dimensions in an MDS solution, which contributed most to the distinctiveness of consonants. An R² value 0.94 was obtained in a regression between the pair-wise distances obtained from the derived space (Figure 4a) and the original distance matrix (Table 7). A 3D articulatory consonant space was also generated using MDS (Figure 4b). Pair-wise distances between consonants obtained from the 3D space yielded an R² value of 0.98.

Figure 4.

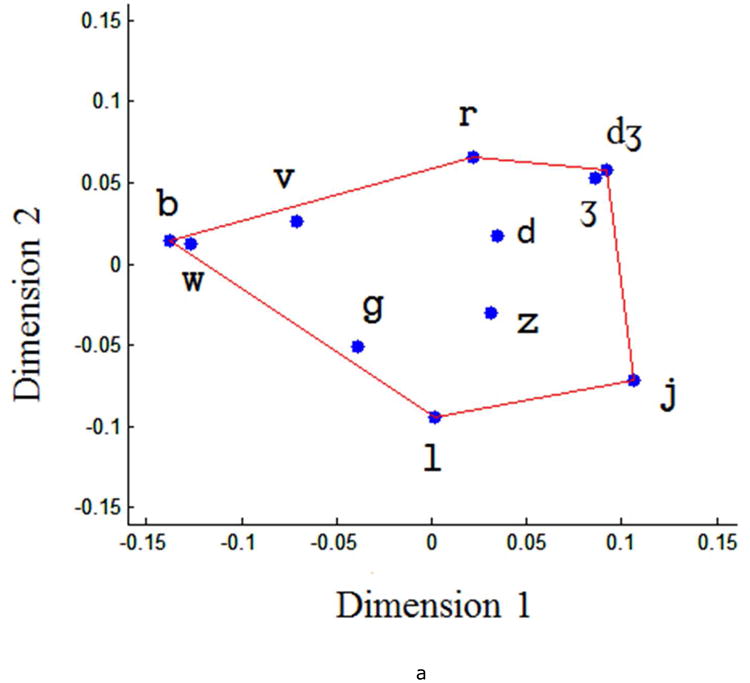
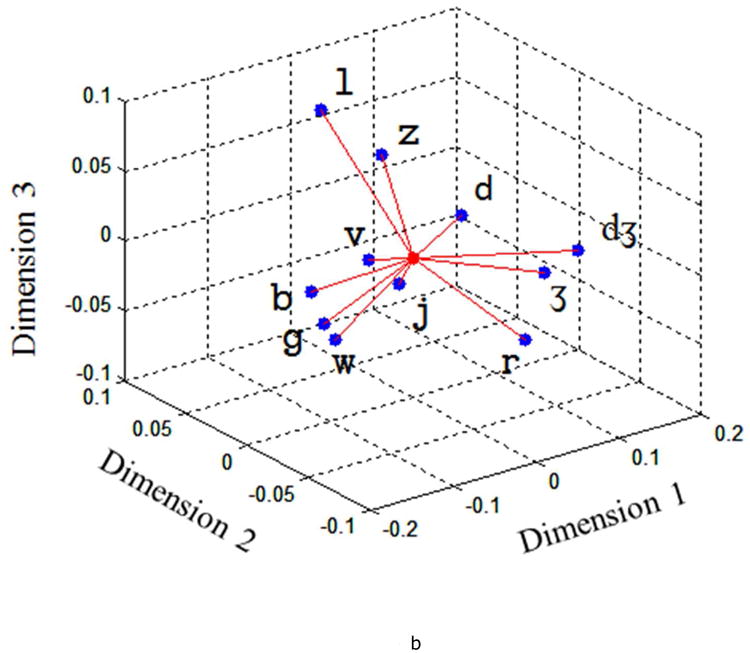
Quantitative articulatory consonant space. Dimensions are results of the MDS solution, which maintain the distance relationships between the data points.

Discussion

High classification accuracies obtained using Procrustes analysis for both vowels and consonants (as similarly high as those obtained using SVM, a widely used classifier) indicate Procrustes analysis is well suited for this articulation analysis. The articulatory distinctiveness of eight English vowels and eleven consonants were then quantified using Procrustes analysis on sparsely sampled lip and tongue movement represented as time series. The dissimilarity matrices for vowels and consonants, when visualized using MDS, were consistent with descriptive schemes that are commonly used to distinguish phonemes based on their unique features (Ladefoged & Johnson, 2011). The scientific and clinical implication of the derived articulatory vowel and consonant spaces are also discussed below, as well as limitations of our approaches.

Classification of Vowels and Consonants

Articulatory position time-series data from multiple articulators were directly mapped to vowels and consonants. This approach differs from prior efforts to classify phonemes from articulatory information, which have primarily been based on extracted articulatory features. The use of statistical shape analysis (i.e., Procrustes analysis) to quantify the differences among phonemes in their articulatory movements is also novel.

The results of this study indicated that both methods (i.e., Procrustes analysis and SVM) were able to classify vowels and consonants accurately and consistently across talkers. The data presented in the classification matrices (Tables 2 and 3) and the distance matrix (Table 4) for vowels indicated that / i/, / e/, / æ/, and / u/ were easier to distinguish than were / Ʌ/, / ɔ/, / o/, and / a/. This result supports the previous findings that low tongue vowels (e.g., / a/) have more articulatory variation than high tongue vowels (e.g., / i/ and / u/, see Perkell & Cohen, 1989; Wang, Green, Samal, & Carrell, 2010). More specifically, our results suggest high and front vowels (i.e., / i/, / e/, / æ/, and / u/) are more articulatory distinct than low and back vowels (i.e., / Ʌ/, / ɔ/, / o/, and / a/). Neel (2008) found that high vowels tend to be more acoustically distinct than low vowels based on the first and second formants of ten representative vowels. Our findings then suggest that more acoustically distinct vowels are also articulated more distinctly, which also agreed with a previous finding in a study on formants and tongue tip locations of two vowels / a/ and / i/ (Mefferd & Green, 2010).

The classification matrices (Tables 5 and 6) and distance matrix (Table 7) for consonants using both approaches indicated that errors occurred most frequently between / r/, / 3/, / d3/, and / j/; this result might be because these sounds are produced with a similar, but not identical, place of lingual articulation.

The high classification accuracies obtained in this study motivates further inquiry into the usefulness of classification for a variety of applications. For example, additional research is required to determine if classification accuracy is a sensitive metric for quantifying the severity of speech impairment or the articulatory changes that occur under different speaking conditions (Mefferd & Green, 2010). In addition, further work is planned to determine if the classification approaches are suitable as the recognition engine for silent speech interfaces (Denby et al. 2010; Fagan et al., 2008; Hueber et al., 2010; Wang, Green, Samal, & Carrell, 2010; Wang, Samal, Green, & Rudzicz, 2012a, 2012b) to facilitate oral communication in patients with moderate to severe speech or voice impairments. Finally, although only female talkers were investigated, we anticipate that the classification of male talkers' vowels and consonants would produce similar results.

Quantified Articulatory Vowel and Consonant Spaces

Although the quantitative articulatory vowel space (Figure 3a) was remarkably consistent with existing qualitative depictions of articulatory vowel space (Figure 3b), the / u/ appeared to be closer to the /i/ in the quantitatively-derived articulatory vowel space than in the descriptive articulatory vowel space (Figure 3b). This finding might be interpreted to suggest that, compared to the /u/, the other back vowels are produced with a more posterior tongue posture. Another explanation, however, may be the backing feature of /u/ was not adequately captured because our most posterior sensor was only on the back of the tongue body and not on the root. More explicitly, both / i/ and / u/ are high tongue vowels, thus tongue backing may be the major information to distinguish them. Because our most posterior sensor was actually on tongue body back rather than tongue root, our approach may not adequately capture the difference between them.

The articulatory vowel space (Figure 3a) was also strikingly similar to the acoustic vowel space obtained from the same participants (Figure 3c). These similarities suggest that, despite the extensive processing of the articulatory movement data, the distinguishing aspects of vowel articulation were preserved in vowel acoustic output.

The 2D articulatory consonant space (Figure 4a) clustered consonants based on place of articulation along Dimension 1. For example, bilabial sounds (i.e., / b/, and / w/), alveolar sounds (i.e., / l/, / z/, and / d/), and post-alveolar sounds (i.e., / 3/ and / j/) were grouped from left to right along Dimension 1. The 3D articulatory consonant space (Figure 4b) clustered the consonants based on the place of articulation as well. For example, alveolar sounds (i.e., / l/, / z/, and / d/), post-alveolar sounds (i.e., / 3/), and bilabial sounds (i.e., / b/, and / w/), were grouped by place of articulation. Based on the data clusters, the manner of articulation did not appear to be represented in the either the 2D or 3D space. Future efforts that encode differences among consonants in their duration may provide a basis for improving the detection of manner differences; duration information was not preserved in our kinematic signals because the articulatory movements were time normalized to the same length prior to classification. In addition, we could not determine if the approaches could distinguish among voiced and voiceless consonants, because our speech samples did not include voice cognates.

The observation that consonants tend to cluster based on place of articulation is not surprising and is consistent with findings reported by Green & Wang (2003), who compared differences among consonants based on tongue and lip movement coupling patterns. Green & Wang (2003) also derived a 3D articulatory consonant space using MDS, but only obtained an R² value of 0.70, which was much lower than the R² (0.98) obtained for the 3D fit in our study. One possible reason that our approach has achieved a better fit than theirs is our approach relied on two dimensions of articulatory movements, rather than only the vertical dimension that was used by Green & Wang (2003).

Another interesting finding was that two principal components were sufficient to capture the variance in articulatory vowel space (R²=0.98), but three components were required to capture the variance in articulatory consonants space (R²=0.98 for 3D space as compared to 0.94 for 2D space). This finding is also consistent with feature-level descriptions of phonemes, which emphasize that two major factors (i.e., tongue height and tongue front-back position) determine the distinctiveness of vowel production but more factors (e.g., manner of articulation, place of articulation, voiced and voiceless, nasality) contribute to the distinctiveness of consonants.

Limitations

The analysis used in the current study provided only a coarse level analysis of the patterns of classification. Additional work is needed to investigate the patterns of misclassification, which may provide more details about the articulatory distinctiveness between those phonemes.

Duration and temporal information play an important role in distinguishing a number of vowels and consonants. However, Procrustes analysis, a spatial analysis, may not encode important temporal features based on, for example, manner-of-articulation. In Procrustes analysis, shapes are required to have the same numbers of data points. Thus, we sampled the articulatory movements for all phonemes to a fixed length (i.e., 10 data points), and consequently lost the duration and temporal information when the phonemes were compared in this study. Future efforts are considered on extending standard Procrustes analysis to compare time-varying shapes with different lengths.

Consonant classification may be enhanced by including distinguishing features such as voicing and nasality. These additions, however, would require the integration of data from sensors that record information about voice and resonance.

In addition, because all of our speech stimuli were embedded in either / b/ context (e.g., / bab/) or an / a/ (e.g., / aba/), the extent to which the current findings generalize to other consonant and vowel contexts is unknown. Additional research is required to determine potential context effects.

Clinical and Scientific Implications of the Derived Articulatory Vowel and Consonant Spaces

The current investigation was not only conducted to improve knowledge about the articulatory distinctiveness of vowels and consonants, but also to develop articulation-based methods that could be used in future studies to quantify the severity of speech motor impairment (Ball, Willis, Beukelman, & Pattee, 2001; Wang, Green, Samal, & Marx, 2011). Just as acoustic vowel space has been extensively used to explain the variance in intelligibility scores for speakers with dysarthria (e.g., Higgins & Hodge, 2002; McRae, Tjaden, & Schoonings, 2002; Tjaden & Wilding, 2004; Weismer, Jeng, Laures, Kent, & Kent, 2001), the derived articulatory spaces may also contribute to understanding intelligibility deficits in clinical populations. In contrast to acoustic analyses, the articulatory level of analysis can be used to directly determine the contribution of specific, compromised articulators to the speech impairment (Yunusova, Green, Wang, Pattee, & Zinman, 2011).

The derived articulatory spaces could also be useful for approaches that seek to intervene in disorders such as apraxia of speech or dysarthria by means of providing EMA visual augmented feedback (e.g., Katz & McNeil, 2010; Katz, Syrika, Garst, & Mehta, 2011). Another potential application is quantifying L2 (the second language) instruction using EMA visual feedback (Levitt & Katz, 2010) or via augmented reality (AR) tutors ‘talking heads’ (e.g. Badin, Elisei, Bailly, & Tarabalka, 2008; Engwall, 201; Kröger, Graf-Borttscheller, & Lowit, 2008; Massaroe, Bigler, Chen, Perlman, & Ouni, 2008; Massaro & Light, 2003).

Summary

Classification of eight vowels and eleven consonants based on articulatory movement time-series data were tested using two novel approaches, Procrustes analysis and SVM. Experimental results using a data set obtained from ten healthy native English speakers demonstrated the effectiveness of the proposed approaches. The articulatory distinctiveness of the vowels and consonants were then quantified using Procrustes analysis. The quantified articulatory distinctiveness of vowels and consonants were used to derive articulatory vowel and consonant spaces, which provided a visual representation of the distinctiveness of vowels and consonants. The clustering of those vowels and consonants in the derived spaces was consistent with feature-level descriptions of differences among the vowels and consonants. For example, the quantified articulatory vowel space resembles the long-standing descriptive articulatory vowel space in classical phonetics. The quantified articulatory distinctiveness of vowels and consonants, and the derived articulatory vowel and consonant spaces have several significant scientific and clinical implications.

Appendix

Mean and standard deviation of F1 and F2 values (Hz) across participants in Figure 3c.

	/ a/	/ i/	/ e/	/ æ/	/ Ʌ/	/ ɔ/	/ o/	/ u/
F1 Mean	901	391	553	919	759	834	575	412
F2 Mean	1349	2450	2329	1812	1408	1227	1210	1469
F1 Std. Dev.	67	101	71	87	60	96	63	43
F2 Std. Dev.	107	362	220	139	146	80	101	179