The Mineral–Collagen Interface in Bone

Abstract

The interface between collagen and the mineral reinforcement phase, carbonated hydroxyapatite (cAp), is essential for bone’s remarkable functionality as a biological composite material. The very small dimensions of the cAp phase and the disparate natures of the reinforcement and matrix are essential to the material’s performance but also complicate study of this interface. This article summarizes what is known about the cAp-collagen interface in bone and begins with descriptions of the matrix and reinforcement roles in composites, of the phases bounding the interface, of growth of cAp growing within the collagen matrix, and of the effect of intra- and extrafibrilar mineral on determinations of interfacial properties. Different observed interfacial interactions with cAp (collagen, water, non-collagenous proteins) are reviewed; experimental results on interface interactions during loading are reported as are their influence on macroscopic mechanical properties; conclusions of numerical modeling of interfacial interactions are also presented. The data suggest interfacial interlocking (bending of collagen molecules around cAp nanoplatelets) and water-mediated bonding between collagen and cAp are essential to load transfer. The review concludes with descriptions of areas where new research is needed to improve understanding of how the interface functions.

Introduction

Interfaces play an important role in all aspects of human activity and in life itself. Everyone who drives an automobile in cold climates, for example, experiences minor (and sometimes major) skids caused by changes in the interface between tire and pavement—a sudden encounter with a patch of ice. This article reviews what is known about the most fundamental interface in bone, the interface between reinforcing mineral particles and the organic matrix in which they are embedded. As will be seen, this interface is crucial to bone’s functionality and remains poorly understood.

Bone is hierarchically structured ([1], see also the paper by Fratzl in this issue), and all of these scales play an important role in bone’s remarkable mechanical properties. In engineering terms, the material bone and the closely related tooth materials dentin and cementum are discontinuously reinforced composites. The reinforcing phase is nanoparticles of a calcium phosphate mineral (carbonated hydroxyapatite, cAp). The matrix in which the cAp nano-platelets are embedded consists primarily of type 1 collagen fibrils but also a significant amount of water, ubiquitous ions of various sorts and a number of different non-collagenous proteins and other macromolecules. The focus here is on the cAp-collagen interface in bone although reference will be made to tooth tissues with similarities to bone, dentin and cementum and to mineralized tendon.

In addition to its mechanical role, bone also serves as a reservoir for calcium homeostasis. Calcium is critical for multiple cell functions, for skeletal development of embryos and for lactation, and dietary calcium input can be irregular. The cAp interface must allow calcium extraction under the right conditions (the action of osteoclasts and possibly osteocytes) and must allow rapid remineralization but must be stable against spontaneous dissolution and must allow some level of load transfer with the surrounding organic matrix if it is to reinforce the matrix.

Bone is a biological composite material dominated by interfaces. At the scale of the osteocyte lacunae and canaliculi, these features possess on the order of 10¹ and 2 × 10² mm² of total surface area per mm³ of bone, respectively.¹ At the hierarchical scale of cAp nanoplatelets and collagen microfibrils, the cAp surface area of ~3 × 10⁵ mm² per mm³ of bone dwarfs even that of the canaliculi.² From nitrogen adsorption measurements, cAp surface area in bone is 1–2 × 10² m²/g (2–4 × 10⁶ mm² per mm³), somewhat higher than the above value [4]. For comparison, crystalline zeolites used in catalysis have surface areas of ~7 × 10⁵ mm² per mm^3.3

Thus, the cAp-collagen interface in bone is a “good news, bad news” story. The good news is that there are so many nanoplatelets that volumetric sampling methods such as X-ray scattering and solid-state nuclear magnetic resonance (ssNMR) can provide precise if indirect measures of average interactions. The bad news is that the interface between an individual cAp nanoplatelet and its surroundings is so small that it is hard to imagine directly measuring quantities like load transfer. One can image such small structures with techniques like transmission electron microscopy (TEM) or perhaps atomic force microscopy (AFM), but the extensive sample preparation and alteration of the boundary conditions of the nanoplatelet’s surroundings are so radical that it is debatable whether the results obtained reflect actual in vivo behavior.

This article’s discussion of the cAp-collagen interface starts with a brief summary of how the properties of the reinforcement, the matrix and their interface(s) interact to produce the composite’s macroscopic behavior. The obvious continuation is the description of the characteristics of the two main phases of the interface: cAp structure is discussed in the second section below followed in the third by a brief review of matrix, mainly collagen but also the associated water, ions and macromolecules such as non-collagenous proteins (NCPs). The fourth section of the review discusses how the mineral comes to be formed within the matrix, something that defines what mineral–collagen-water-ion-NCP interactions are possible. The emphasis is not on the detailed mechanisms of growth and notions such as crystallization from water-mediated ion clusters [6] or from amorphous solid precursors [7, 8]; rather the focus is on growth and limits of growth of the cAp nanophase and its implications for understanding the resulting interface with the matrix. The subject of the fifth section, the 3D spatial dispersion of the mineral phase within the hierarchy of collagen structures, is inextricably linked to the growth processes described in the previous section but deserves separate emphasis because this defines the boundary conditions for interpreting results of experiments related to interface properties or the validity of models of bone properties. This hierarchical scale of interface interactions remains poorly defined and is too often ignored in modeling studies instead of serving as the basis for proper boundary conditions. The sixth section focuses on the nature of the nanoscale interface interactions that might exist and on their strength. The final section focuses on gaps in current understanding, on areas where future research might improve understanding of the cAp-collagen interface, and on emerging techniques and how they might improve understanding of interfaces in bone.

Composites

Composites are materials where two or more dissimilar phases combine to produce properties superior to those of either component. Load, for example, is shared between matrix and reinforcement (collagen and cAp nanoplatelets, respectively, in bone), and this necessitates load transfer from the matrix to the reinforcement embedded in it. Thus, the material properties of a composite material (bone) mostly depend on the (geometric, mechanical, chemical) properties of the isolated phases (cAp, collagen), on the relative amounts of the phases (volume fractions v_i) and on the properties of the interface between the phases. Exactly how the properties of the constituent phases combine has been the subject of much work, reviewed for example in [9].

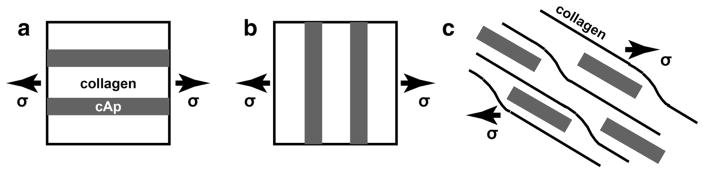
If the phases making up the composite are elastic and there is ideal bonding between the reinforcement and matrix, a simple representation of composite material properties is through their volume fractions, the “rule-of-mixtures” approach assuming both experience either uniform strain (the isostrain or Voigt model) or uniform stress (the isostress or Reuss model). Figure 1a,b pictures these models and indicates the interface; note also that the interfaces essentially extend to infinity. The equations relating the composite Young’s modulus to those of the constituents are E_Voigt = Σ_i (v_i * E_i) and E_Reuss = 1/(Σ_i(v_i/E_i)), where i equals cAp and collagen. Other more complex numerical models exist relating constituent properties and hierarchical organization to E_bone [9], but covering these is beyond the scope of this review.

Fig. 1.

a Voigt model of uniform stress where the loading is parallel to the cAp nanoplatelets. b Reuss model of uniform strain where the loading is perpendicular to the nanoplatelets. c Schematic of finite cAp nanoplatelets in a matrix of collagen molecules

The situation in bone differs from the rule of mixtures models in many ways, and Fig. 1c illustrates some of them. The matrix is neither elastic nor isotropic but consists of long aligned macromolecules (collagen triple helices). Even if the mineral consists only of uniform-sized and -shaped cAp nanoplatelets with a single orientation with respect to the collagen microfibril matrix, the hierarchy of structures in bone (see the review by Fratzl) means that a range of orientations exists with respect to the loading axis, and physiological loading is rarely simple uniaxial but often involves bending or multiaxial stresses. The interface between cAp and collagen is not ideal, and the finite dimensions of the cAp reinforcement offers considerable additional complexity.

Carbonated Apatite

The mineral phase in bone is calcium phosphate and has a structure related to hydroxyapatite (hAp). The nominal formula is Ca₁₀(PO₄)₆(OH)₂, the crystal system is hexagonal, and lattice parameters vary with composition. Forthe inorganically derived material Ca_8.8(PO₄)₆(OH)_1.92, the lattice parameters are a = 9.435 Å and c = 6.865 Å [10]. In bone, the unit cell⁴ of the mineral contains sub-stantial carbonate CO₃, nominally about 5 wt.% in human cAp [11]; because of this, the author prefers to follow Weiner and coworkers [1] and refer to the mineral as cAp instead of hAp. There also is significant citrate content (~2 wt.% [12] ) as well as cation (H, Na, Mg, K, deficiency in Ca) and anion substitutions (F, Cl) into the lattice [11] and perhaps adsorbed to the crystal surfaces.

The mineral phase in bone is frequently termed poorly crystalline, something the data certainly support, but this description is often offered without qualification or definition. Knowing what this means (or does not mean) is essential to understanding the reinforcement-matrix interface. Poorly crystalline cAp can refer to a large amount of substitution within the cAp unit cell, the small dimensions of the cAp nanocrystals and/or possible amorphous calcium phosphate (ACP) associated with the crystalline material.

X-ray diffraction, also termed wide-angle X-ray scattering (WAXS), has been used to study the mineral in bone for many years [13]. Much wider cAp X-ray diffraction peaks are seen from bone (and dentin) compared to synthetic cAp or hAp or tooth enamel. Substitutions in bone’s cAp nanocrystal lattice produce microstrain (also termed rms or root mean square strain); the resulting range in d-spacings (i.e., crystalline interplanar spacings, on the order of 1 Å, something distinct from the D-period in type I collagen, which is the length of the gap plus overlap zone, about 67 nm) within the sampled nanoplatelets is one source of this broadening. Observed microstrains range from 10⁻³ to 10⁻² in dry, powdered human bone (and vary with age) [11] and in hydrated bovine bone [14]. In inorganically synthesized cAp, increasing carbonate content from 1.5–2 to 10 wt.% increases microstrain (X-ray diffraction average via Rietveld refinement for all reflections except 00.l) in a roughly linear fashion from 10–15 × 10⁻⁴ to 40 × 10⁻⁴ [15]; a human enamel specimen is near the bottom of the strain range. Human bone contains ~5 wt.% carbonate [11], and the data suggest that substitutions and not high dislocation densities⁵ are the dominant contribution to microstrain.

In adult human bone (powdered, dehydrated), cAp crystal dimensions range between 30 and 40 nm along the c-axis, between 10 and 20 nm for the 30.0 reflection and 20–25 nm for 21.0 and 31.0 reflections [11]. In hydrated and intact bovine and canine cortical bone, high energy X-ray diffraction reveals c-axis length (corrected for microstrain) of 40 nm and larger, e.g., [14]. Earlier WAXS studies, e.g., [16], which ignore microstrain, report crystallite sizes significantly smaller than those from TEM. Inorganic crystallite domain sizes [15] are comparable to those in bone [11].

In bone, TEM shows cAp in the form of nanoplatelets with dimensions similar to those listed above [16, 17]. Using AFM, a fairly wide range of crystal dimensions is observed. The size depends on whether the crystals are from the interior of collagen fibrils (smaller) or between collagen fibrils (larger) [18]. The average c-axis dimensions from X-ray diffraction are larger than the gap zone in the collagen matrix, and it certainly is possible that the cAp within the fibrils does not exceed the gap length, but the average is made up by cAp platelets on the fibril surfaces. The nanoplatelets have remarkably uniform thicknesses of 3–4 nm and remarkably flat surfaces [19, 20]. One study reports cAp on the exterior of collagen fibrils (as opposed to within fibrils) comprises ~70 % of the total mineral and consists of polycrystalline structures approximately 5 nm thick, 70 nm wide and several hundred nm long [21].

Discussion continues about the presence of ACP in the mineral of mature bone. Setting aside the question of whether ACP exists as a transient phase during platelet growth, radial distribution function studies of bone suggest ACP is not present, at least up to detection limits ~12 % [22], and other diffraction studies come to the same conclusion [23]. Spectroscopists, however, have advanced a model of mineral structure where a solid apatite core is surrounded by an ACP shell [24, 25].

Charge domains observed on the surface of developing enamel suggest this is an important contribution to matrix-cAp interaction in bone [26]. Experiments on bone show the surfaces of cAp have polarizing surfaces that form strong bonds with polar and polarizable molecules [4]. The primary association between amino acids and the hydroxyapatite surface is between carboxylic acid groups and surface calcium ions, and amine groups could interact with oxygens of the phosphate groups [27].

Inorganic apatites with macroscopic dimensions have Young’s moduli on the order of 110–120 GPa [28–30]. For nanoplatelet thickness of 2–4 nm, nowhere within the cAp is farther than two unit cells from a surface, and it would be surprising if the elastic properties were the same as in millimeter- or even micrometer-sized crystals. Such in situ cAp elastic properties can, in fact, be measured in solid samples of bone (and dentin) via high-energy X-ray diffraction by quantifying changes in cAp crystal d-spacing as a function of applied load [14, 31–35], even in the post-yield deformation regime [36–38].

Matrix: Collagen Plus Water Plus Ions Plus Other Macromolecules

The matrix of bone consists of type I collagen stabilized by water and with a significant content of NCPs and other macromolecules. In brief, each type I collagen molecule self-assembles into a triple helix consisting of two α₁ and one α₂ chains; the helix diameter is on the order of 1.25 nm wide and 300 nm long [39] with mass ~285 kDa [40].⁶ Groups of five triple helices appear to be organized into microfibrils with one of the helices running into an adjacent microfibril [43]. The microfibrils are organized into fibrils whose diameters vary in bone (nominally 100–200 nm) and whose lengths are great enough that they are difficult to determine.

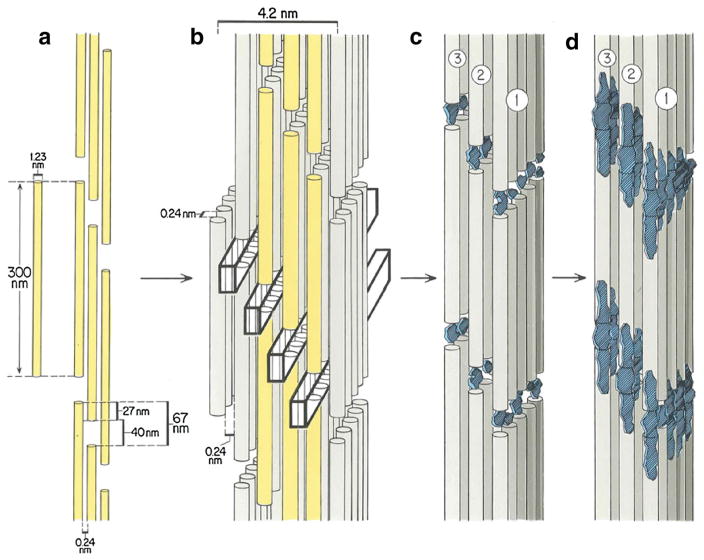
The tertiary collagen structure has a 67-nm periodicity along the molecule axis, a 40-nm gap or hole between the ends of the molecules and a 27-nm overlap region [44, 45]. Figure 2 shows a schematic of the quarter-stagger arrangement; these 2D cross-linked aggregates are packed into strictly registered hole and overlap zones producing open channels running laterally through the structure. The 67-nm periodicity (D-period) is pronounced enough to produce small-angle X-ray scattering (SAXS) peaks whose changes in position (D) can be used for internal strain measurements [31]. Use of synchrotron X-ray microbeams for position-resolved SAXS is now routine with beam diameters ~200 nm or smaller and has added understanding of structures such as the lamellae of osteons [46–49].

Fig. 2.

Schematic of the array of collagen molecules within a mineralized collagen fibril showing the 2D and 3D organization and the intrafibrillar mineral, following the Hodge and Petruska [44] and Landis et al. [45] models. a A single collagen molecule, 1.23 nm in diameter, 300 nm in length and spaced 0.24 nm apart [165], is shown as well as a 2D aggregate of collagen molecules, cross-linked into a quarter-staggered array with characteristic gap (40 nm) and overlap (27 nm) zones [44]. The three columns of collagen molecules are shown in yellow (a, b). (b) Packing of consecutive 2D arrays into 3D assemblages occurs with strict registration of all gap and overlap zones so that channels are created throughout the model [45]. The rectangular prisms (heavy black lines) running away from the viewer indicate these channels. c The cAp crystals, shown in blue, nucleate principally in the collagen gaps and grow preferentially in their c-crystal axis direction. The (100) planes describing the largest developing face of the crystals generally lie parallel to each other and to the collagen molecules associated with the crystals. d Growth of the cAp phase to occupy the entire 40-nm length of the gap. The channels are thought to allow lateral growth of the cAp nuclei into nanoplatelets. As pictured, the cAp has extended beyond the gap zone, but the narrow pore spaces (0.24 nm) [165] between adjacent collagen molecules have unknown capacity to accommodate mineral. Reproduced with kind permission from Springer Science+Business Media: Fig. 1 of [45] (Color figure online)

Water stabilizes the collagen structure, bridging adjacent molecules through hydrogen bonds [40], and bone must be heated in excess of water’s boiling point to remove this bound water. Collagen cross-linking between adjacent molecules occurs when the bone matrix is laid down (enzymatic cross-links), can be as high as one per collagen molecule in young bone and is intrinsic to functionality, hindering the helices from sliding past each other when bone is loaded [50]. Non-enzymatic cross-links form increasingly in older bone and degrade properties (i.e., advanced glycation endproducts, AGEs); these can occur via interaction of the collagen models with sugars [51]. Toughness and strength of bone (but not elastic modulus) decrease significantly with increasing heating-induced collagen denaturation [52].

Collagen possesses functional groups that can interact with cAp or with calcium and phosphate ions [53]. There are frequent clusters of charged amino acids in type I collagen [54] and high charge densities at discrete intrafibrillar sites within the macromolecules [55]. When collagen is stained with heavy metal salts, 12 bands are visible in TEM micrographs [44, 55], and these correspond to the different positive and negative charged domains. In vitro, both positively and negatively charged nanoparticles exhibit binding affinity with collagen fibers [56].

A wide variety of NCPs is present in bone at significant concentrations [57] and appears to be essential in controlling mineral nucleation and growth and facilitating attachment between collagen and cAp [58–60]. Many NCPs are phosphoproteins. The NCPs include small integrin-binding ligand with N-glycosylation (SIBLING) proteins, which provide site-specific binding to collagen [61] and a capacity to interact with or accumulate Ca²⁺ ions in their vicinity [62]. The SIBLINGs include osteopontin (OPN, ~66 kD), bone sialoprotein (BSP, 75 kD) and dentin matrix protein-1 (DMP-1, 37- and 57-kD fragments) [62]. Non-SIBLING proteins in bone include osteonectin (ON, 40 kD), which can bind Ca, and osteocalcin (OC, 6 kD), bone-Gla protein, and these two appear to be the most abundant NCPs in bone.

Mineral Growth and Characteristics

Calcium and phosphate ion products in vertebrate extra-cellular fluid are greater than the solubility product of crystalline forms of calcium phosphate including cAp, and mineral would precipitate spontaneously throughout the organic matrix unless crystallization were inhibited [62]. Such indiscriminate precipitation is not normally observed, although pathological calcification can occur, and the interplay between inhibition and controlled mineralization suggests that many macromolecules modulate the activity of the ions, the details of which are a subject far beyond the scope of this article. It is worth noting that Omelon and Grynpas suggested that inorganic polyphosphates may be important in cAp-collagen mineral nucleation [63]. Data show bone mineral density distribution is essentially constant at the micrometer level in healthy human cancellous bone but changes in diseased tissue [64]; the shape of the histograms of mineral content suggests a two-stage mineralization process with a fast primary phase and a slow secondary phase where the time constants differ by three orders of magnitude [65].

The cAp mineral forms after the collagen matrix has been laid down by the osteoblasts. It nucleates in collagen gap regions within the fibrils (Fig. 2) but also on the fibril surface (see the following section). The cAp crystals within the fibrils grow with their c-axes parallel to the collagen molecule axes. In crystallographic terms, this alignment in a polycrystalline sample is “fiber texture,” and it exists in both cortical bone and in trabeculae of cancellous bone (i.e., the nanoplatelet c-axes and trabecula axes are parallel [66–68]). In dentin where the collagen fibrils are tangential to the tubule axes, the cAp texture, relative to the tubule axis, is axisymmetric [69].

Evidence is accumulating for the role of ACP precursors for cAp mineral in bone, but the distinction (and transition) between very small crystals and amorphous material is nebulous at best. Any fruitful discussion of ACP phases needs careful definition of terms. He and coworkers [70] report that the acidic domains of dentin matrix protein-1 bind calcium in vitro and initiate ACP particles, which crystallize and elongate along the cAp c-axis. Crystalline cAp forms in zebrafish fin rays via transformation of ACP [71]. Nudelman et al. show direct observations of collagen function in synergy with inhibitors of hAp nucleation to actively control mineralization: positive net charge close to the C-terminal end of the collagen molecules promotes infiltration of ACP, and clusters of charged amino acids in gap and overlap regions form nucleation sites controlling conversion of ACP into a parallel array of oriented hAp crystals [72]. Interestingly, spatially confined hAp crystallization in vitro can produce nanocrystal orientation comparable to that in bone through an intermediate ACP phase [73].

In the quarter-stagger collagen molecule arrangement (Fig. 2), there are lateral channels in collagen array, which allow the cAp crystals to broaden into tabular nanoplatelets. This geometry leads naturally to a stack of co-oriented cAp platelets [74–76] within a single fibril and with rotation of orientation between adjacent fibrils. Others have suggested radially symmetric arrangement of collagen molecules within each fibril with corresponding rotations of nearby cAp nanoplatelets [77].

A range of cAp dimensions and properties is found in bone, and these change with age. Human c-axis dimensions increase from 20 to 30 nm at birth to 30 to 40 nm at 20 years and after, but the a-axis dimensions change in the opposite way [11].⁷ A wider distribution of crystallite sizes are seen in juvenile vs. adult dinosaur bone [78]. Age-related alterations in physiochemical properties of mineral crystals correlate with impaired mechanical function of rat cortical bone [79].

The cAp within bone grows within the collagen fibrils (intrafibrillar) and on the surfaces of the fibrils (extrafibrillar). The literature on the size of cAp nanoplatelets frequently does not consider this potentially important factor. For example, it is sometimes difficult to determine which population of mineral is sampled in direct imaging studies with TEM and AFM. Dimensions of cAp nanoparticles derived from WAXS or SAXS inevitably average mineral from both locations, and interpretation of such data must be cautious, at least until sampling volumes drop below (100 nm)³. Strains within cAp are quite large in hydrated bone (via WAXS they are ~1–2 × 10⁻³ [14, 31, 80, 81]); given the small crystallite dimensions and their discontinuous distribution, this suggests the mineralization process produces significant physical constraint on the crystalline phase. Constraint and the accompanying increase in strain energy with growing crystallite thickness may be the reason cAp thickness reaches a fairly well-defined limit. Further, these residual strains demonstrate that load transfer exists between the discontinuously distributed cAp and the organic matrix separating the cAp nanoplatelets.

Dispersion of cAp in Collagen’s Hierarchy of Structures

Beyond the level of the mineral nanoplatelets and collagen triple helices and microfibrils, the organization within and between fibrils is important in defining which interfacial interactions likely affect larger scale properties. The significant range of mineral densities found in bone [82] means that the bone mineral system is highly adaptable. The unfortunate corollary (for researchers) is that it is difficult to generalize from limited data sets obtainable with limited resources. Setting aside the extremely dense whale bulla and rostrum, which contain little collagen (see Fig. 4.1 of [82]), volume fractions of mineral range from 0.25 to 0.45, and bone mechanical properties (elastic modulus, tensile strength, ultimate tensile strain, work of fracture) scale with the amount of mineral present (e.g., Figs. 4.2–4.5 of [82]). On the basis of mechanical testing, some contend that mineral forms a continuous network in normal bone [83, 84], but the author doubts this is possible within the context of mineralization of a pre-existing matrix, of highly aligned nanoplatelets, of partition of intra-and extrafibrillar mineral and of mineral content <45 vol. %. Still, such a “percolating” network of cAp might exist at the fibril level.

It remains unclear whether more cAp is intra- or extrafibrillar, but cAp exists at both positions [85]. One study concludes that 70–80 % of the mineral is within fibrils in bone [86]. On the other hand, neutron diffraction of bone suggests that the majority of mineral is located outside fibrils [87]. Decreased extrafibrillar mineralization in a rickets model leads to deterioration of nanomechanical bone quality [88], so it is clear that the question of the proportion of extra- vs. intrafibrillar cAp is an important one.

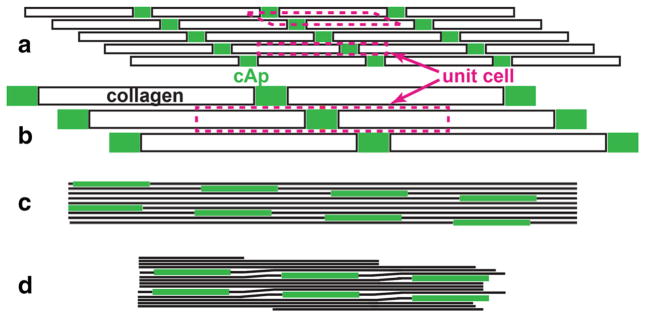
Consider as a lower bound that one-quarter of the volume of all cAp is within the fibril (and the balance is extrafibrillar). Following the quarter-stagger arrangement, Fig. 3 shows where the cAp must fit; for purposes of this rough estimate, treat all structures as extending a unit length (1 nm) into the plane (which leads to an overestimate of the amount of cAp within the fibril). Figure 3a shows two unit cells within the structure. The collagen molecule widths and lengths (1.23 nm and 300 nm, respectively), space between molecules (0.24 nm) and gap and overlap lengths (40 and 27 nm, respectively) are those given by Landis and Jacquet [53]. In Fig. 3b, the volume of the mineralized fibril unit cell is 500 nm³, the volume of the collagen triple helix is 369 nm³, the volume of the space between collagen molecules is (300 − 40)*0.24*1 nm³ = 62 nm³, and the balance of 69 nm³ is the volume of the gap region (nano-platelet thickness of 1.7 nm). On the other hand, one-quarter of the unit cell volume is 125 nm³ (the assumed intrafibrillar volume fraction of cAp), and if the gap distance of 40 nm is invariant, then the corresponding thickness is 3.1 nm, a value substantially larger than the available space. Figure 3c shows 3.1-nm-thick cAp nano-platelets in a quarter-stagger aligned array of rigid collagen molecules; a great deal of free space results between molecules, obviously unrealistic given the fibrils are constrained from large mineralization-induced expansions by their (presumably) closely spaced neighbors. A more reasonable situation is pictured in Fig. 3d where the collagen molecules are distorted in the overlap zones and have only the minimal inter- molecule spacing elsewhere. The free volume in the collagen flexure (overlap) zone could allow growth of additional cAp.

Fig. 3.

Schematics of cAp nanoplatelets in gaps of the quarter-stagger array of type I collagen molecules. In a, b the collagen molecules are indicated by the black bordered rectangles, whereas in c, d they are indicated by the long, thick black line segments. Throughout, the cAp nanoplatelets are indicated by the solid green rectangles. In a, b, the transverse (vertical) scale is greatly exaggerated (for clarity in showing the different unit cells), whereas in c, d, transverse and axial scales are the same; the dimensions of components are those given in Fig. 2. a The dashed magenta lines indicate two possible structural unit cells, each with a different shape. By definition, simple translation of a unit cell can be used to build up the entire structure. These unit cells are different from those within the cAp crystal lattice. b A third unit cell, the one used for the cAp thickness calculation in the text. c Diagram of 3.1-nm-thick cAp nanoplatelets (corresponding to the calculation in the text) within the gaps and surrounded by collagen molecules unrealistically shown as rigid rods. The volume fraction of empty space is greatly increased over that in a, b. d Schematic of 3.1-nm-thick cAp nanoplatelets in a matrix of collagen molecules that have their native packing except in the overlap region where molecules are distorted to maintain the quarter-stagger arrangement. The result is decreased free volume compared to c, but here the open volume is concentrated in the overlap zones (where additional small amounts of cAp may form). Note that there is greater transverse overlap of cAp in this structure than pictured in a, b and that structures at the boundaries of schematic are left incomplete (Color figure online)

The nanoplatelet thickness reported by various methods is 3–4 nm [19, 20], closer to the volume fraction-derived thickness than the allowed width in the idealized quarter-stagger structure. The experimental averages presumably reflect both extra- and intrafibrillar cAp, i.e., of volumetrically unconstrained and constrained material, respectively. One expects that the intrafibrillar cAp does not reach the 3.1 nm thickness calculated above, nor is the free volume as extensive as pictured in Fig. 3d. Nonetheless, cAp extensions to the 40-nm cAp c-axis length might occur, i.e., an analog of what is pictured in Fig. 2d. These extensions would probably be disregarded in direct imaging studies, and, because X-ray scattering measures are weight-fraction-weighted, small volume extensions to the larger main volume of cAp would produce negligible changes. It appears, however, that the cAp must distort the neighboring collagen molecules. This notion is considered further in the following section.

Electrospun type I collagen and collagen-hAp nanofibers [89] provide an interesting window into the effect of nanoparticles within the composite. Tensile tests (in an AFM) of single spun collagen fibers (250–350 nm diameter) reveal properties similar to those of native collagen. For spun fibrils loaded with 6.4–18.5 wt % hAp nanoplatelets, tensile testing yields only slightly increased Young’s modulus (compared to pure collagen fibers) but significantly improved strength, failure strain and toughness. Micrographs of these composites show the hAp nanoparticles tend to cluster, and the hAp probably does not occupy the same intrafibrillar positions as cAp in bone. This result also suggests that the periodicity of cAp nanoplatelets arrays may be extremely important in mineralized fibril elastic behavior.

Interfacial Interactions

Composites’ Interfaces

Optimized performance of a composite requires that bonding at the interface be neither too weak (little or no load transfer to the reinforcing phase) nor too strong (the stiffer reinforcement will fracture at a relatively low strain and will no longer be able to support the applied stress). Given the range of bone densities and of structural hierarchies and the varied mechanical and biological requirements placed on bone, no one interface design can be optimum. Presumably evolution has selected an interface for the cAp-collagen composite that can be formed through efficient biological processes and that provides adequate to superior performance for the varied requirements.

Three broad categories of interfacial “bonding” are summarized in Fig. 4 and include molecular entanglement, intermolecular interactions and mechanical interlocking. Combinations of these types are probably the rule rather than the exception in nature. Molecular entanglement applies to macromolecular interactions, and it is difficult to see how this might apply to the collagen-cAp system in bone unless a highly flexible intermediary molecule were partly entangled with the ordered collagen array and partly in contact with cAp. Intermolecular interactions include covalent bonding, electrostatic attraction (including ionic bonds), van der Waals forces and hydrogen bonds; these might involve direct cAp-collagen interactions or indirect interactions through bridging macromolecules such as NCPs or water. Mechanical interlocking (Fig. 4c) in the collagen-cAp nanosystem might occur as pictured in Fig. 1c.

Fig. 4.

Schematics of interfacial bonding types between reinforcing phase (dark gray) and matrix phase (light gray). a Molecular entanglement: macromolecule A (attached to the reinforcing phase) entangled with macromolecule B (attached to the matrix phase). b Intermolecular interactions. Groups C (of reinforcing phase) forming bonds (black ellipsoids) with groups D (of the matrix). c Mechanical interlocking of the reinforcement and matrix phases. After [166]

The simple model in Fig. 3 suggests that the cAp nanoplatelets grow thicker than the available space in the gap region. The result is that the collagen array is distorted, and this would be a type of mechanical interlocking (Fig. 3d). If the situation is similar to the microfibril model [43], the mineral formed likewise would be subject to mechanical interlocking. The cAp nanoplatelet would also be strained, and this may be the origin of the residual strains seen in WAXS [31, 34, 80, 81]. As the cAp nano-platelet grows thicker, it becomes more highly strained, and the stored elastic strain energy increases; one presumes that eventually it will be too energetically unfavorable to thicken further, and this may be the underlying reason for the remarkably uniform cAp nanoplatelet thicknesses reported. As the WAXS data average over all mineral within the sampled volume, the extrafibrillar and intrafibrillar cAp may contain very different residual strains.

Interactions in Bone

Mineralization-related proteins of various sorts adsorb preferentially on the (100) face of hAp crystals [90]. Binding of BSP to collagen appears to be important for the initiation of bone mineralization [58], and the interaction is probably only partly electrostatic and occurs at a well-defined collagen domain [59]. Loss of BSP appears to lead to impaired endochondral bone development and mineralization [91]. In vitro, OPN inhibits hAp growth on collagen, whereas OC delays nucleation [92]. Expression of phosphophoryn (highly phosphorylated dentin phosphoprotein) can suffice to induce matrix mineralization by mammalian cells [93]. In the presence of bioinspired peptides containing highly phosphorylated Ser-Ser-Asp repeat motifs, collagen fibrils mineralize with cAp in structures similar to those in bone and dentin [94]. Similarly, polyanionic peptides have been used to mimic NCP function and produce cAp mineral in turkey tendon in vitro [95]. In vitro mineralization of collagen in solution with fetuin, a 48-kDa inhibitor of mineralization whose size is thought to exclude it from the fibril interior, demonstrates that intrafibrillar cAp formation is favored by inhibition of extrafibrillar mineralization [96]. On the other hand, type I collagen has been shown to initiate and orient the growth of cAp in the absence of other macromolecules [97]. Size-controlled hAp nanoparticles nucleate in vitro in a chitosan matrix, and this suggests the substrate alone is sufficient to produce mineral observed in bone [98].

Two major NCPs in bone, BSP and OPN, appear to be co-distributed and accumulate in spaces between collagen fibrils [99]. Mineralized tendon with its collagen type I matrix is an important model for bone. Immunocytochemistry of turkey leg tendon reveals OC is present at the surface of, outside of and within type I collagen while that of BSP shows it is localized at the surface of or outside of type I collagen [100]. One expects these observations pertain to bone as well as tendon, but work is needed to confirm this.

Binding sites to calcium (and cAp) are indicated schematically in Fig. 5 for OC, BSP and OPN [60]. In some cases this binding is thought to be involved with crystal nucleation and in others with inhibition of crystal growth. Sites for binding to collagen and for attachment to cells are also shown; Fig. 7 of [41] gives an example of how decorin, a proteoglycan, can link adjacent collagen fibrils.

Fig. 5.

Schematic of protein interactions with cAp. The proteins’ carbon backbones are the wavy structures adjacent to the cAp, helical structures are indicated by the labeled cylinders, and phosphorous is indicated by P. a Osteocalcin (OC, i.e., bone Gla protein BGP) binds to the cAp (100) face through three neighboring γ-carboxy glutamic acid (Gla) residues on the same face of the alpha helix. b The acidic glycoprotein bone sialoprotein (BSP) possesses several sialic acid-containing oligosaccharide chains (s a o). The poly glutamic acid sequences (Glu)_n are thought to constitute sites for cAp nucleation and binding sites with cAp. Binding sites for collagen and for cell attachment are also indicated. c Osteopontin (OPN) instead of (Glu)_n, it contains a poly aspartic acid sequence (Asp)_n that can interact with cAp and is thought to inhibit cAp crystal growth. After [60]

Dorvee and Veis [61] emphasize the importance of hydration layers in mineral formation in cAp, and water is also very important in the mechanical function of bone as demonstrated by changes in behavior upon dehydration (elastic modulus and strength increase, toughness decreases [101]) or treatment with macromolecules or ions. In powdered cortical bone (bovine femora), ssNMR reveals a very ordered (structural) layer of water with protons 2.3–2.55 Å from the cAp surface phosphorous atoms and little evidence of ordered hydroxide, whereas hydrated synthetic cAp (2–4 wt.% carbonate) possesses strong hydroxide bonding with adjacent phosphate and carbonate groups in the mineral (hydrogen bond distance of ~1.96 Å ) [102, 103]. The same approach also demonstrates that water is present within defect sites within the cAp lattice [103, 104].

In vitro immersion of bone in sodium fluoride or sodium phosphate solutions for several days appears to reduce post-yield mechanical properties, whereas sodium chloride has no effect; the phosphate effects are reversible but the fluoride ones are not [105, 106]. Similar effects occur in intact bones soaked in fluoride solution [107]. In vitro exposure of bone to strontium is reported to improve material properties [108]. In vivo and in vitro treatment of bone with raloxifene increased toughness concomitant with increased matrix-bound water through the hydroxyl groups on the raloxifene [36].

Data from ssNMR is interpreted as showing cAp contacts its organic matrix in bone predominantly through polysaccharides, most likely glycosaminoglycans (GAGs) in proteoglycans (PGs) [109]. In bone, ssNMR shows that a significant fraction of protonated phosphates (HPO₄⁻²) are located on the surface of cAp, the concentration of surface HPO₄⁻² is higher in younger, less mature cAp, and the concentration of unprotonated phosphates (PO₄⁻³) is elevated within the cAp lattice compared to the surface [110]. Phosphophoryn binding to cAp is associated with charge arrays on the cAp surface and with the molecule’s phosphorylation [111]. Water-mediated structuring of cAp is suggested through an ACP-like layer [112]. In osteopenic mice (OVX, lactation), bound water is decreased compared to controls as is total water and the space between collagen and inorganic phosphorous [113].

In addition to its use in mapping nanostructure, AFM can also be used to study binding and extensibility of organic molecules attached to well-defined surfaces, typically freshly cleaved mica [57, 114–116]. Mica, a silicate mineral, has surfaces characterized by a sheet-like, hexagonal atomic arrangement whose pattern of charge distribution is thought to be similar to that on the cAp surface. Measured force as a function of retraction distance of the cantilever tip reveals a complex pattern of dissipated energy, in part because it is difficult to isolate a single molecule. Exposure to Ca²⁺ solution increases mica surface coverage by human OPN and bonding between OPN molecules; this bonding can be altered by exposure to solutions such as EDTA [114]. Binding strengths of NCPs and other macromolecules to cAp surfaces do not appear to have been measured.

Older tissues appear to accumulate AGEs (non-enzymatic crosslinks) and through them suffer degraded bone fracture properties [117]. Modeling of mineralized collagen fibrils suggests that enzymatic collagen cross-links minimally affect stress-strain curves and produce a ductile material that fails through debonding of the cAp-collagen interface, while non-enzymatic cross-links inhibit collagen sliding, increase load transfer to cAp and decrease post-yield strain and toughness [118].

Osteogenesis imperfect (OI) is a genetic disorder resulting in brittle bones and caused by mutation of the collagen structure. A mouse OI model has collagen consisting of homotrimers of α₁ helices instead of heterotrimers (two α₁ and one α₂ chains), and this alters collagen structure and cross-linking (decreasing space for mineral nucleation and growth), cAp crystallinity (changed crystal dimensions and orientation) and mechanical properties [119, 120].

Various treatments for osteoporosis appear to affect the interface of cAp with its surroundings in bone. Bisphosphonates act through both physiochemical and biological activities and present a high affinity for adsorption onto hAp and cAp crystals due to the strong attraction of the phosphonate groups for calcium, thereby hindering bone resorption. Data from ssNMR demonstrate a strong interaction between risedronate ions and calcium ions at the cAp surface [121]. In vivo alendronate and in vivo (and in vitro) raloxifene treatments for osteoporosis differ in that the latter (and not the former) produces significant toughening of cortical bone [36].

Interactions During Loading

The increase in bone’s Young’s modulus with increasing cAp content [82] demonstrates cAp’s role in strengthening the collagen matrix. Some speculate that cAp reinforces the composite by hindering sliding of collagen within the fibrils and that cAp actually does not carry load [9]. Recent data with in situ loading and WAXS/SAXS show quite clearly, however, that cAp carries load in bone and in the related material dentin [31, 34, 35, 80, 81, 122]. As discussed above, collagen distortion may, in fact, be an important component of load transfer.

The use of WAXS/SAXS to measure mineral and collagen fibril response to applied stress is based on very simple physical principles. The periodic mineral structures in bone (Bragg plane spacings d with the crystallites and period D defined by the collagen gap plus overlap length in the collagen fibrils) and the multiplicity of nanoplatelet orientations produce cones of scattered X-ray intensity centered around the transmitted beam. X-ray area detectors placed perpendicular to the transmitted beam record rings of intensity whose radii depend on the values of d and D. Application of stress to a bone sample changes d and D along both the direction of the force and, through Poisson contraction, the orthogonal directions. Measurement of the varying radius around the circumference of a ring can be related to the elastic strain present [14, 31].

Measurements of elastic strains (changes in d in WAXS and in D in SAXS) vs. applied load provide a measure of the elastic modulus averaged over all of the cAp in the tissue and over the cAp within the mineralized fibrils, respectively. From the X-ray measurements, apparent moduli $E_{\text{app}}^i={\sigma }_{\text{appl}}/{\epsilon }^i$ can be calculated from the applied stress and the strains in the respective materials (i = cAp or mineralized fibril fib). In canine fibula under compression, $E_{\text{app}}^{\text{cAp}}~40\text{GPa},E_{\text{app}}^{\text{fib}}~18\text{GPa}$ and the modulus from an attached strain gauge ~25 GPa [31]. In compressed bovine incisors, $E_{\text{app}}^{\text{cAp}}$ averages about 27 GPa, $E_{\text{app}}^{\text{fib}}$ about 15 GPa and the ultrasonic modulus about 17 GPa, with positional and inter-individual variation of about 20 % [34]. In bovine femur under compression, $E_{\text{app}}^{\text{cAp}}$ varies from 25 to 29 GPa with transverse anatomical position, and the ultrasonic modulus varies similarly from 17 to 22 GPa ( $E_{\text{app}}^{\text{fib}}$ is not reported) [81]. In tension of the same material, $E_{\text{app}}^{\text{cAp}}$ averages about 20 GPa, $E_{\text{app}}^{\text{fib}}$ about 5 GPa (a surprisingly low value), and the strain gauge modulus is about 20 GPa, with significant differences between anatomical positions [35]. Other X-ray scattering experiments using a small diameter beam and much smaller sample thickness found the ratio of whole tissue strain to collagen strain to mineral strain were 12:5:2 in wet bone [123]; this result is not that different from the above results, especially considering the latter averaged over multiple levels of the structural hierarchy. For comparison, Young’s moduli in macroscopic samples range from ~5 GPa for narwhal tusk to 26 GPa for bovine femur to 32 GPa for axis deer femur [82]; inorganic crystals of various apatites have moduli of 110–115 GPa [28], and type I collagen has E ~1 GPa [124].

Residual stresses (strains) are those present in the material in the absence of externally applied force; these stresses represent something very different from those induced by loading. In metallurgical engineering, one classic example is hammering (shot peening) a plate: compressive residual stresses result in the surface layer and hinder the formation of surface cracks. In bone, residual stresses in cAp represent constraint from the surrounding organic matrix, which may be the mechanism that limits nanoplatelet thickening or a contribution to bone toughness. Dissection of osteonic lamellae reveals residual stresses as large as 110 MPa [125]. From WAXS, compressive residual stresses ~60 MPa exist in millimeter-sized specimens of fixed wet bone, strains that drop to zero after extensive x-radiation [31].⁸ X-ray doses from 3 to 4,000 kGy do not affect cAp or fibril apparent moduli during compression of 1.5-year-old bovine femur samples but cause residual cAp strains to drop considerably and also affect fibrillar residual strains [80].

Time- and cycle-dependent deformation has been monitored by WAXS and SAXS [35, 81, 122], and systematic testing with changing strain rates might provide very valuable information about interfaces. Results of WAXS/SAXS during compression testing of human bone [37] suggested shear deformation involving crystals and fibrils oriented obliquely to the applied stress axis was the dominant deformation mechanism; the shear stress reached a maximum for crystals/fibrils aligned ±30° to the applied load [38]. Under constant applied compressive stress, both cAp and fibrillar strains increased linearly in the steady-state creep regime [122]. In antler, a very rapidly growing bone type with relatively low mineral content, cycling to strains substantially above the yielding point produces increasing amounts of macroscopic hysteresis, but the SAXS-derived fibrillar strain increases linearly with tissue strain (but with a slope less than one), and fibril residual strain also increases linearly [126]; these results and modeling, described below, led this group to conclude that intrafibrillar plasticity through mineral–collagen sliding is the dominant mechanism for the extreme toughness.

An unusual approach to understanding plasticity in bone has been imported from metallurgy: measurement of the activation volume and activation enthalpy for plastic deformation [127]. These quantities carry information on the energy barrier needed to go from the undeformed to deformed state, and this provides important functional information about the interfaces because the collagen backbones and cAp lattices are not being broken. The cited study measured, for fibrolamellar bovine femoral bone, an activation enthalpy of ~1.1 eV and an activation volume of ~1 nm³. The enthalpy is smaller than a typical covalent bond (C–C ~3.6 eV), but much larger than hydrogen bonds (~40 meV), and the result suggests large numbers of hydrogen bonds are being broken. The small activation volume suggests deformation is tightly constrained.

A particularly efficient approach is four-point bending of cortical bone bars where a microbeam is translated across the specimen along the loading direction for each increment of applied deflection; WAXS/SAXS patterns can be recorded at >20 points in <2 min [36]. The beam (diameter <25 μm for photons with energy >60 keV) can be translated laterally to minimize X-ray dose. From the sequence of loads, one can build up a stress-strain curve for each layer of the specimen. Post-test correlation with microstructure (microCT, quantitative backscattered electron mapping, etc.) might be able to isolate the effect of bone structure. Both could be imported into numerical models. This testing could also be done with various perturbations mentioned elsewhere.

Microcracking and failure in bone depend on the loading mode to which it is adapted [128]. For example, mechanical properties (modulus and strength) of narwhal tusk depend strongly on the orientation of the applied load relative to the collagen fibril axis in this highly textured material [129]. Similar orientation effects are reported for plasticity in human bone [37, 38].

Contributions of PGs to the mechanical behavior of mineralized tissue have recently been reviewed [130]. The focus in this summary was on microscale interactions (hydrostatic and osmotic pressure; poroelastic behavior) and on nanoscale mechanisms (sliding filament theory; intramolecular stretching). Via AFM indentation and recovery, the molecular level, calcium-mediated sacrificial bonds are reported to increase stiffness and enhance energy dissipation in bone [131]. Adjacent fibrils may be glued together with a nonfibrillar organic matrix that resists fibril separation [132]. These sacrificial bonds increase energy absorption during fracture, but the bonds can also heal upon release of the load [133], and a network of OPN molecules has been implicated as the source of the bonds [134]. In antler, NCPs glue mineralized collagen fibrils together with fairly weak bonds, producing a very tough material, and AFM measurements of individual fibril pullout energy as a function of pullout rate suggest adhesion is rate dependent [135]. Nanofracture features (dilational bands) have colocalized OC and OPN present, and this correlates with bone toughness and indicates these molecules play a role in interfacial interactions between collagen and cAp [136]. Bone fracture surfaces are covered by NCPs in the form of localized patches of OPN and BSP [115]. In mice lacking OC and OPN, the overall exposure of collagen to cAp is hardly affected, and the contribution of OC-OPN to fracture toughness is attributed to their presence at the extrafibrillar organic-mineral interfaces [137].

Modeling and Numerical Considerations

Numerical modeling of biomineralization was recently reviewed [138], and finite element modeling of bone at the micro and organ scales based on 3D microComputed Tomography (microCT) data sets has been quite successful, e.g., the review of [139]. At the tissue level, focus has concentrated on hierarchical simulation of bone mechanical properties, e.g., [140] and the accompanying papers. Most consider higher levels of the hierarchical structures than the nanoscale cAp-collagen level and rarely more than two scales simultaneously ([141] is an exception). These models can provide reasonable agreement with experiments, but a significant number of assumptions are required.

Modeling of the collagen-cAp building block of bone has not been ignored [122, 124, 142], but these simplified models (and those described below) assumed strongly bonded cAp-collagen interfaces. Numerical analysis of staggered arrays of cAp nanoplatelets embedded in an isotropic matrix with the elastic properties of collagen reveal that mineralized fibril elastic properties change dramatically when the platelets overlap along the fibril axis but still maintain lateral separation [143–145]; a recent review highlights that this micro/nanostructural motif is present in other, quite different mineralized tissues [146]. Quantitative values of interface strength are lacking, to the best of the author’s knowledge, so it is not surprising weak interfaces are not incorporated in the models. The existing models can provide reasonable agreement with experiments, but improved predictive performance awaits incorporation of realistic interfaces. It is worth mentioning one recent study [126], which supposes there is a critical shear above which the cAp and collagen slide past each other within fibrils and uses this parameter within a multiscale model to fit experimental macroscopic and X-ray scattering data. This model plus experiment gives a strong indication that cAp-collagen sliding within the fibril produces the high toughness in antler. Similar observations made in bone suggest extrafibrillar sliding transmitting shear stress to adjacent mineralized fibrils, which maintain a constant tensile stress (from D-period measurements) despite macroscopic plastic deformation [147].

Numerical modeling of the fracture mechanism of hAp nanocrystals shows edge cracks parallel to (001)⁹ produce stress concentration under tensile loading when the crystal thickness is greater than 4.15 nm but not in thinner crystals [148]. This numerical result suggests that thicker crystals would be more prone to crack than thinner ones and that this effect may have been a factor in the evolutionary selection of the thin cAp nanoplatelets observed in bone. Such a consideration probably applies to extrafibrillar mineral but not to that within the fibrils: there is less spatial constraint in the former than the latter (where other considerations dominate).

One group reports mineral forms a continuum in bone [83, 84]. This led another group to conclude citrate ions bridge adjacent cAp nanoplatelets [149]. The author doubts either of these is important in normal bone, but these mechanisms may warrant attention in the extremely highly mineralized whale bulla and rostrum.

Molecular dynamics simulation of the OPN-cAp system suggests that the mechanical properties are governed by electrostatic attraction between the acidic amino acids of OPN and Ca in cAp. The OPN-cAp interaction increases with a higher number of amino acid residues. During deformation, breaking and reforming the OPN-Ca bonds produces a slip-stick type of motion and can dissipate a large amount of energy [150]. In the absence of good numbers for the amount of OPN (and other similar-functioning NCPs), it is difficult to know whether these molecules can provide enough cumulative interaction to explain bone’s properties or whether the experimental associations of NCPs with fracture surfaces are incidental.

As the final topic of this section, consider the number of possible bonding sites on a cAp nanoplatelet and what might be required to produce the observed levels of load transfer to the reinforcement. The lattice parameters of the primitive cAp unit cell are a = 0.94 nm and c = 0.69 nm. The two (100) faces of the nanoplatelet offer by far the most area for bonding, and for purposes of this estimate take the nanoplatelet edge dimensions as 40 nm × 20 nm. Thus, there are (40 × 20)/(0.94 × 0.94) ~10³ unit cells on each (100) face. Consider only Ca²⁺ as bond sites (phosphate groups should also be considered); there is one Ca²⁺ available per unit cell for a total of ~2 × 10³ possible binding sites on both faces. The number of possible Ca bonding sites greatly outnumbers the complementary bonding sites on the collagen molecules adjacent to the nanoplatelet. If binding at the cAp surfaces is what controls cAp-collagen load transfer, the biological questions are what fraction of the Ca sites actually contribute and is their cumulative effect enough to provide the observed effects. Calculations using the maximum number of available sites and characteristic bond strengths could provide an upper bound for load transfer.

Load transfer between cAp and collagen can be through direct interaction or through intermediary water molecules or NCPs. Although no concentration figures appear to exist for NCPs in bone, it appears that there are simply too few of these macromolecules present to provide enough bonding for load transfer, notwithstanding observation of NCPs on bone fracture surfaces and roles in cAp nucleation and growth inhibition. Water certainly could provide large numbers of bonds, and ssNMR data show water ordering at the cAp interface. Molecular dynamics or finite element simulation of an accurate collagen-water-cAp nanoplatelet system under load would be required to judge whether bonding is sufficient for the required load transfer.

Future and Conclusions

Many important results have been obtained on cAp-collagen interface properties, but quantitative understanding of this interface remains elusive, not only its structure but also its function in response to in vivo loads and to accumulated damage. Higher resolution/higher sensitivity studies are needed of the very small volumes comprising the materials bounding the interface and under conditions closer to those in vivo, including realistic boundary conditions. While there have been a wide range of excellent studies, the depth of coverage is rather shallow, leaving the reader unsure how robust the studies’ conclusions are. That is not to say that replicates of ten or more samples are required for each variable (like in studies examining the efficacy of treatment vs. control), but existing approaches need to be repeated by multiple researchers, on different species (with different mineral densities, patterns of locomotion) and on bone perturbed by different treatments but studied by a different modality. Human, bovine and rodent bones have received the most attention by far. Examples of areas of bone research where such depth of coverage has been obtained include bone’s mechanical properties (modulus, strength) as a function of mineral density [82], microCT quantification of trabecular bone architecture [151] and patterns of collagen and cAp orientation in the different lamellae within osteons [49, 152].

Various imaging modes are coming closer to being able to visualize the volume surrounding the cAp-collagen interface in enough detail to detect differences, for example, between bone with normal and impaired toughness. A gap remains between demonstration experiments obtaining a small amount of “baseline” data and between robust interrogation of structural differences, and this is particularly important for studies of the mineral interface. High resolution TEM, for example, has long been capable of studying the nanostructure of bone, but more detailed studies are needed of the many perturbations noted above and with bone from a greater number of individuals in each group. Careful comparison of extra- vs. intrafibrillar cAp and its interfaces is needed in each study and for samples with different mineral densities (see [153] for a recent review). That said, interesting new studies appear constantly [68, 154, 155]. CryoTEM and focused ion-beam (FIB) sample preparation can provide sample conditions closer to those in vivo and so offer great promise if they are systematically applied to the problem of the cAp-collagen interface.

Compared to TEM studies, AFM data on bone are sparse. Additional AFM can certainly improve understanding of the cAp-collagen interface, particularly if more replicates of impaired vs. normal bone are compared. Because AFM can be done in water, studies following hydration/de-hydration/re-hydration of each specimen might be very informative. Observation of changes in wet bone could be quantified following the introduction of different ions or agents (see [36] for such an in situ study of raloxifene’s effect on bone) or during in situ loading and/or nanoindentation. Although the force-response behavior of NCPs attached to mica surfaces has been measured, it does not appear that NCPs attached to cAp have been studied, and such data would be important in determining forces required to debond NCPs from cAp as well as validating (or contradicting!) existing data on NCP stretching in response to loading.

Atom probe studies of mineralized tissues appear to be challenging, but hold considerable promise for clarifying at least the chemical composition of interfaces in bone and related mineralized tissues, as suggested by recent work on dentin [156]. Serial sectioning is possible without demineralization [157], and serial surface viewing with FIB and electron microscopy likewise provides an informative 3D view of bone [154]. Laser scanning confocal microscopy can produce in-plane volume elements (voxels) of 100 nm and can be used to follow damage localization [158], an important advantage when higher resolution, lower field of view techniques are applied to study local differences in interface character. Raman spectroscopy and Fourier transform infrared (FTIR) spectroscopy offer considerable insight into the bonds present within specimens and are widely applied to mineralized tissues [159, 160]. In the context of the cAp-collagen interface, these spectroscopy results are difficult to interpret because current beams have diameters >1 μm and average over many collagen fibrils: contributions from the bulk material dominate over those from interfaces.

X-ray microCT resolution can be obtained below 100 nm, and this scale of tomography is termed nanoCT. A recent X-ray phase contrast tomography imaging study detected the orientations of individual collagen fibrils [161], and one expects that intra- and extrafibrillar domains in bone will soon be visualized using nanoCT. The advantage of this volumetric image technique is that imaging with 25-nm voxels allows one to see the interior of samples with diameters approaching 50 μm. Sample preparation artifacts are, therefore, minimized because regions of interest can be >10 μm from a prepared surface. Radiation damage is a real concern for experiments such as in situ loading studied by synchrotron tomography.

There are quite a number of areas where WAXS/SAXS characterization will contribute to improved understanding of the cAp-collagen interface in bone. One example is observation of changes in residual stress upon dehydration/rehydration/dehydration, with in vitro treatment of bone with agents such as raloxifene (which toughen bone and which appear to affect water at the cAp-collagen interface) or with in situ exposure to different ions (e.g., fluoride vs. phosphate) affecting bone properties. It would be interesting to know the extent to which residual stresses change with age and whether the magnitude of these stresses correlates with changes in fracture toughness. Particularly important will be studies comparing macro (specimen average), fibril and total mineral strains as a function of applied load (simultaneously using strain gage, SAXS, WAXS and load cell data, respectively). Four-point bending of bone monitored with position-resolved WAXS/SAXS measurements and post-test correlations with microstructure (via microCT or SEM) offer a very efficient means of studying the response of different structural levels.

As mentioned above, WAXS mapping is currently routine with ~200-nm-wide beams [69], and beams substantially smaller than 100 nm are available. This suggests WAXS/SAXS mapping in suitably thin specimens (fibril thickness) should be able to detect differences between extra- and intrafibrillar volumes. Alternatively, diffraction tomography [162, 163] with a 50-nm-diameter focused X-ray beam could be used to reconstruct the distribution of mineral with sub-fibril resolution. Collecting these data sets is time consuming, but only a small number of slices would be needed to address questions such as the distribution of mineral between intra- and extrafibrillar locations.

Preparation of samples smaller than a few tens of micrometers across can be done slowly by FIB, by mechanical dissection (e.g., single osteon specimens [46, 47, 152] ) or by using a laser dissection microscope (Fig. 6). The optical micrograph, scanning X-ray diffraction mapping with a beam <250 nm in diameter and nanoCT imaging reveal damage on or near the cuts that does not extend more than a few hundred nm into the specimen. The laser dissection system (Zeiss Palm) can cut bone and dentin samples >25 μm thick with widths considerably narrower than the 35-μm bars shown in Fig. 6.

Fig. 6.

Optical micrograph of bars of dentin machined with a laser dissection microscope (Zeiss Palm system). The thin section was mechanically polished to ~25 μm thickness using 500-grit SiC paper. The very thin, vertically running and somewhat wavy black lines are dentin tubules within the section. The bars are 35 μm across, and the cut surfaces have roughness varying with cutting parameters. Stock SR, Gerkowicz L, Telser A, unpublished data, May 2012

Aged bone often has decreased toughness, and this is linked to increased AGE content. It would be very interesting to see how residual stresses (measured with noninvasive WAXS/SAXS) in cAp and in the mineralized fibril subset of the tissue change with age and with damage such as that produced by high cycle fatigue. Such synchrotron WAXS/SAXS quantification can be done repeatedly on the same specimen with a minimal X-ray dose if the beam is translated to a new area between measurements. Use of X-ray energies >60 keV deposits much less energy in bone specimens compared to energies <50 keV. On the other hand, X-ray-induced damage of bone (collagen cross-linking or perhaps other effects) might be used systematically as a controlled probe of matrix or interface changes’ effect on mechanical behavior; this would require determination of the nature of the damage to the bone matrix or interface of cAp with the surrounding matrix.

The lateral width of ~20 nm for cAp nanoplatelets can be accommodated by aligned gaps, i.e., channels, in the quarter-stagger-related model of Fig. 2 without introducing strain. If the channels extend across the entire fibril diameter (nominally >250 nm), this implies one of several situations exists. The platelets may nucleate every 20 nm or so along the channel and grow until they impinge but remain separate entities. Alternatively, the growing surfaces may be “poisoned” by the macromolecules mentioned above, i.e., a process controlled by the interface. It is also possible that the alignment of the channels extends only 20 nm and adjacent subdomains of the fibril have different orientation. Whatever the actual situation, one must be cautious of interpreting the existing data too rigidly as it is a sampling of what undoubtedly is a range of dimensions within the same tissue.

In order to properly assess the role of NCPs and other macromolecules on cAp-collagen interface properties, one must know the concentrations present and where the molecules are distributed. The author is unaware of such quantification. Although the author is no expert on this type of determination, all reports indicate this is a daunting challenge, and the lack of data is not surprising.

Opportunities for numerical modeling are indicated in the previous section. A detailed model of a 20-nm-wide cAp nanoplatelet with the array of specific binding sites of neighboring collagen molecules (with and without mediating water and/or non-collagenous proteins and/or ACP halo¹⁰; under load applied to collagen) would be an outstanding contribution to understanding the cAp-collagen interface. It would be very interesting to perform an Eshelby inclusion calculation¹¹ [164] for multiple cAp nanoplatelets within a fibril comprised of collagen matrix and constrained by neighboring fibrils; this would establish whether strain energy could indeed limit nanoplatelet thickness. The two-stage mineralization kinetics [65] could also be examined via numerical simulation.

On balance, the author expects water-mediated bonding will eventually be confirmed to play a significant role in the mechanical function of the cAp-collagen interfacial system. He expects that the main contribution will prove to be mechanical interlocking through distortions of the collagen matrix produced by cAp nanoplatelet growth or by the microfibril structure [43]. Considerable experimental and numerical work is required before this latter notion can be accepted or refuted. Until the interface itself can be studied directly, under realistic conditions and with well-controlled modulations (and without confounding signal from the bulk tissue, from extra- vs. intrafibrillar material, etc.), progress depends on new experimental data at other levels of bone’s structural hierarchy and on indirect inferences drawn from these experiments.