Fast Gap-Free Enumeration of Conformations and Sequences for Protein Design

Abstract

Despite significant successes in structure-based computational protein design in recent years, protein design algorithms must be improved to increase the biological accuracy of new designs. Protein design algorithms search through an exponential number of protein conformations, protein ensembles, and amino acid sequences in an attempt to find globally optimal structures with a desired biological function. To improve the biological accuracy of protein designs, it is necessary to increase both the amount of protein flexibility allowed during the search and the overall size of the design, while guaranteeing that the lowest-energy structures and sequences are found. DEE/A*-based algorithms are the most prevalent provable algorithms in the field of protein design and can provably enumerate a gap-free list of low-energy protein conformations, which is necessary for ensemble-based algorithms that predict protein binding. We present two classes of algorithmic improvements to the A* algorithm that greatly increase the efficiency of A*. First, we analyze the effect of ordering the expansion of mutable residue positions within the A* tree and present a dynamic residue ordering that reduces the number of A* nodes that must be visited during the search. Second, we propose new methods to improve the conformational bounds used to estimate the energies of partial conformations during the A* search. The residue ordering techniques and improved bounds can be combined for additional increases in A* efficiency. Our enhancements enable all A*-based methods to more fully search protein conformation space, which will ultimately improve the accuracy of complex biomedically-relevant designs.

1 Introduction

Redesigning a protein’s structure or function has vast potential in biomedical research. One promising technique for protein redesign is computational structure-based protein design (CSPD). Starting from a template protein structure, CSPD algorithms search over amino acid sequences and conformations to predict mutations to the native protein sequence that will have a desired effect on the protein’s biochemical properties. Despite enormous advances in computational power, a major limitation in CSPD is the fact that the conformational space grows exponentially as we increase the number of mutable residue positions or increase the amount of protein flexibility allowed during the design search [1]. Searching these conformational spaces to find protein sequences that will perform biologically important functions requires advanced algorithms.

Proteins are dynamic and can exist in many low-energy, near-native conformations at physiological conditions. If flexibility is ignored or significantly limited during the design search, the search can become brittle and miss biologically favorable conformations and sequences [2]. Therefore, we have developed and implemented algorithms in the CSPD software package OSPREY to model both continuous side-chain and backbone flexibility during the design search [2-5], and to approximate protein binding constants using partition functions over molecular ensembles [6]. We showed that incorporating continuous flexibility in CSPD improves the recovery of native amino acids and finds novel low-energy sequences that are missed by rigid-rotamer techniques [2]. Similarly, ranking sequences based on low-energy protein ensembles with OSPREY improves the results of prospective designs [7, 8]. Applying these methods has led to many successful experimentally validated, biomedically relevant applications, including enzyme design [9, 10], design of protein:protein interaction inhibitors [7, 11], drug resistance prediction [12, 13], and the redesign of anti-HIV-1 antibodies [14-16].

The CSPD problem that OSPREY and other CSPD algorithms solve can be formulated as follows: given the protein design input model (i.e., input protein structure(s), rotamer library, energy function, and allowed protein flexibility), find the amino acid sequence that stabilizes the fold of the given input structure(s). This optimization problem can be solved by computationally searching over amino acid types, side-chain conformations (i.e., rotamers [17, 2, 18]), and backbone movements [3-5] that best accommodate the desired protein fold. The CSPD problem is an optimization over protein conformation and sequence space to find: (i) the global minimum energy conformation (GMEC), (ii) ensembles of low-energy conformations to score conformational entropy (the K* algorithm [6]) and/or (iii) a ranking of protein sequences for experimental testing. While the CSPD problem is NP-hard [19, 20], practical biological designs can be solved with mathematical guarantees by several optimization techniques [21-24]. These provable algorithms guarantee that the optimal solution is found with respect to the input model.

One of the more prevalent provable CSPD techniques is the branch-and-bound algorithm A* [21, 25]. The A* algorithm transforms the CSPD problem into a tree search, where every level of the tree represents a mutable residue position, each leaf represents a conformation in the search space, and every internal node of the tree represents a protein partial conformation (Fig. 1). The total size of the tree is exponential in the number of mutable residue positions. However, the A* algorithm can efficiently search the tree by bounding the energy of every partial conformation and using a best-first search to enumerate a gap-free, in-order list of low-energy protein conformations. In CSPD, a pre-processing dead-end elimination (DEE) pruning step is commonly used before A* to prune rotamers that are guaranteed to not be part of any low-energy protein conformations [26, 27, 8]. After pruning, A* is used to enumerate the remaining conformations or sequences in order of increasing energy.

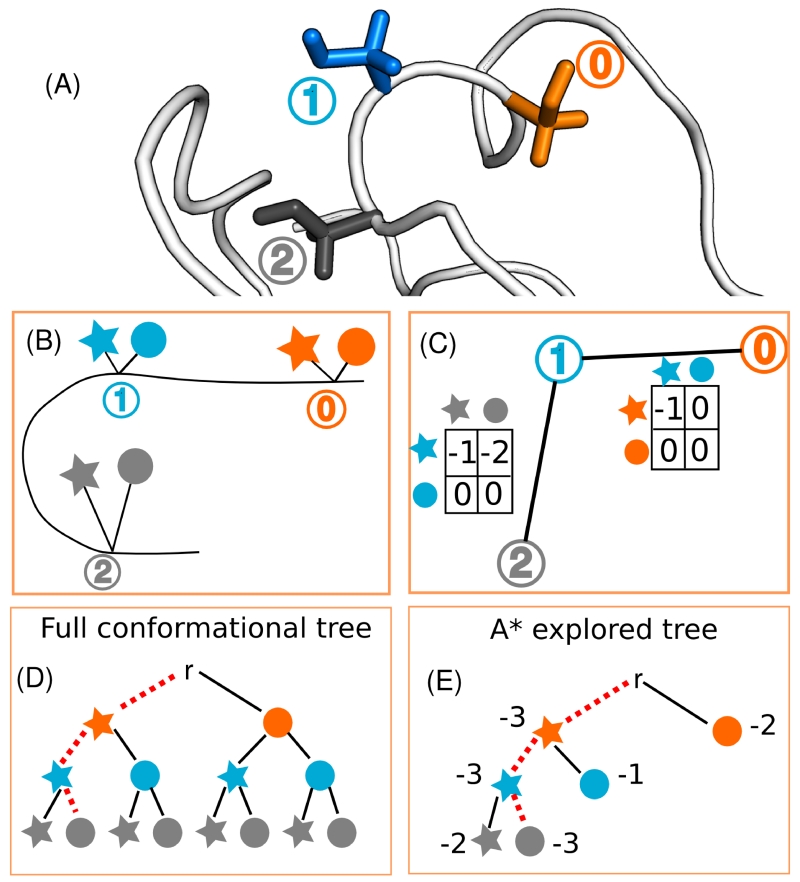
Figure 1. Tree representation of protein conformation space.

(A) A toy example of three serine residues (shown in orange, blue and grey) belonging to the antibody VRC07 (PDB id: 4OLZ [14]), partially shown in white cartoon. (B) A 2D representation of (A), and for the purposes of this toy example, we allow each residue to mutate to only two rotamers (shown here as a star and a circle). (C) Protein design algorithms compute pairwise interactions between rotamers based on an input energy function, and these are shown here in matrices between residue pairs. For simplicity, all internal rotamer energies are zero, and the pairwise energies not shown have a zero value. (D) The protein conformation and sequence space can be represented as a tree. In a tree representation, each level represents a residue, each inner node (each of the nodes between the root of the tree, r, and the leaves of the tree) represents a partially assigned conformation, and each child assigns a rotamer choice for the next residue. Each leaf represents a fully assigned conformation. A näive approach to solve the protein design problem would explore this tree completely. The optimal path is shown in red. (E) Branch-and-bound algorithms such as A* explore a small part of the tree by computing energy lower bounds (called f-scores and shown next to each node) on the possible conformations allowed at each inner node. A* expands nodes in order of their f-score and guarantees that the optimal solution is found (shown in red).

A* enumeration is essential for all CSPD algorithms implemented in OSPREY, including the methods that allow continuous side-chain and backbone flexibility during the design search [2-5], and the ensemble-based methods that approximate protein binding constants by computing partition functions [6]. Specifically, the ensemble-based algorithm, K*, relies on the gap-free, in-order list of conformations generated by A* to provably approximate partition functions used to rank protein sequences. The incorporation of ensemble-based scoring into protein design better reflects protein dynamics and is crucial for accurate designs [7, 13, 28, 29]. A*’s ability to generate a gap-free low-energy ensemble makes it uniquely suited for ensemble-based design in contrast to other provable methods that only find the GMEC, such as integer linear programming (ILP) [22, 30]. The gap-free list generated by A* also allows a set of low-energy sequences to be suggested for experimental testing. Due to inaccuracies in the protein design model, it is rarely expected that every design prediction will work perfectly. Therefore, generating an ordered list of suboptimal sequences is superior to only finding the GMEC [8].

In addition to its use in OSPREY, A* has been used by several other CSPD methods to successfully design novel and improved proteins. A* has been used to design stabilized variants of Cyanovirin-N [31], optimize the binding affinity of an antibody fragment to the integrin VLA1 [32], create calmodulin/M13 variant complexes with novel specificity [33], design HIV-1 protease inhibitors [34], improve the endosomal sorting of granulocyte colony-stimulating factor [35], select candidate residue positions for diversification that improved horseradish peroxidase enantioselectivity [36], design BH3 peptides that can bind Bcl-x_L [37], and design a novel zinc transporter [29]. As designs become more complex, the A* search can become an algorithmic bottleneck in protein design. Improvements to the A* algorithm will not only enable more complex designs, but allow CSPD algorithms to more comprehensively explore protein conformational space. By improving critical CSPD algorithms like A*, protein designers can use more biologically accurate input models, which will greatly improve the accuracy of CSPD and unlock the ability to design biological functions that were previously unattainable by CSPD methods.

In this work we show how the performance of the traditional A* algorithm [21, 8] can be radically improved in two ways: first, by intelligently ordering the search tree (Sec. 2.2), and second, by using improved methods to bound the best outcome of each path in the tree (Sec. 2.3). In Section 2.2 we analyze the ordering of protein residues within the A* tree and the effect the ordering has on performance. We propose several alternatives to the traditional sequential residue ordering, including predefined orders and a new dynamic ordering algorithm (Dynamic A*), that improve the efficiency of A*. In Section 2.3 we focus on improving the lower bounds on the energies of partially defined protein conformations, which are used to guide the tree search in A*. We refer to these lower bounds as f-scores. We analyze and compare the traditional A* f-score vs. improved f-scores computed using established techniques from the field of computational optimization, including linear programming (LP) [22], max-product linear programming (MPLP) [38] and local consistency (LoC) [23]. In Section 3 we present a large-scale study of 29 difficult protein designs that shows the large performance improvements that result from the new residue ordering and f-score methods.

Protein design is an important tool in biotechnology. Due to improvements in computational structural biology (e.g., more protein structures in the PDB database and improved energy functions and rotamer libraries), the protein design problem has been transformed into a computational search problem. Some of the most important remaining challenges are directly related to our ability to search this space efficiently: searching the continuous flexible space of proteins, modeling proteins as dynamic ensembles and enumerating multiple sequence candidates for experimental testing. Our improvements to the A* search enable CSPD protocols that can specifically address these challenges. We detail two such examples in our work. First, we describe a novel A* branching technique, Sequence-A*, that allows A* to directly enumerate sequences rather than conformations. Our improvement of A* f-scores and residue ordering allows Sequence-A* to accurately bound the energies of partial sequences and directly find the best suboptimal sequences. We show that Sequence-A* can generate a gap-free in-order list of low-energy sequences much faster than traditional A* methods. Second, we demonstrate that our improved A* methods can be combined with minimization-aware protein design methods [2, 3] to solve problems that had too many viable rotamers for traditional A* to solve. By improving the capacity of search algorithms, our new methods will allow more accurate and consistent designs, which will translate into novel biological designs.

2 Methods

2.1 Background: The A* Algorithm for the Protein Design Problem

In CSPD, a protein conformation can be represented as a vector of n rotamers a = (a₁, a₂, …, a_n), where n is the number of residue positions allowed to mutate during the design search. The total energy for the conformation a is defined as

$$E\left(\mathbf{a}\right)=E_{\mathrm{templ}}+\sum _{i=0}^{n}E\left(a_i\right)+\sum _{i=0}^n\sum _{j=i+1}^{n}E\left(a_i,a_j\right),$$ (1)

where E_templ is the template energy (i.e., the energy of the backbone atoms and side chain residues that are not allowed to move or mutate), E(a_i) is the internal energy of rotamer a_i plus the energy of a_i with the template, and E(a_i, a_j) is the pairwise energy between rotamers a_i and a_j. In its simplest form, the goal of CSPD is to find the rotamer vector with the lowest energy, known as the GMEC: $\mathbf{g}=\underset{\mathbf{a}}{argmin}E\left(\mathbf{a}\right)$. To reduce the size of the protein conformational search space, DEE can be used to prune rotamers that are guaranteed to not be part of the GMEC [26, 27, 6, 8, 1]. After DEE pruning, many low-energy protein conformations remain unpruned and must be searched to find the lowest-energy structures.

To enumerate protein conformations that remain after DEE pruning, a branch-and-bound algorithm based on the A* algorithm can be used [21, 6]. A* searches protein conformations by representing the design problem as a tree search and traverses only the branches of the tree that might lead to the lowest energy structure. Each level of the tree represents a residue position in the protein that is being designed (Fig. 1). Each internal node in the tree represents a partial rotamer assignment, where the number of assigned rotamers is equal to the node’s depth in the tree. Therefore, every leaf node of the tree is a complete rotamer assignment. Formally, each node x at depth m in the tree contains a partial rotamer assignment p = (p₁, p₂, ⋯, p_m) where p_m is the assigned rotamer at the m^th residue position. The remaining residue positions U = {m + 1, ⋯, n} have not been assigned a rotamer yet. Every node x is scored with an f-score, which is the sum of the partially assigned conformation’s energy g(x) and a bound on the remaining possible rotamer assignments for that node h(x):

$$f\left(x\right)=g\left(x\right)+h\left(x\right).$$ (2)

Since g(x) scores the unique partially assigned conformation at node x, the energy of this partial conformation can be computed exactly:

$$g\left(x\right)=\sum _{i=1}^m\left(E\left(p_i\right)+\sum _{j=i+1}^{m}E\left(p_i,p_j\right)\right)$$ (3)

In contrast, h(x) must estimate the minimum energy of all remaining rotamer assignments for node x. Any function that provides a lower-energy bound for the protein conformations can be used by A* to enumerate low-energy conformations. In [21] the following canonical bound is presented:

$$h\left(x\right)=\sum _{j=m+1}^n\underset{q_j\in Q_j}{min}\left(E\left(q_j\right)+\sum _{i=1}^{m}E\left(p_i,q_j\right)+\sum _{k=j+1}^n\underset{q_k\in Q_k}{min}E\left(q_j,q_k\right)\right).$$ (4)

We refer to the f-score (Eq. 2) that incorporates the above canonical bound (Eq. 4) as the traditional f-score. In Eq. (4), Q_j refers to the set of unpruned rotamers that are allowed at residue position j.

The A* algorithm proceeds by iteratively finding the A* node with the lowest f-score and expanding the node by creating child nodes that assign specific rotamers to the next unassigned residue position. To expand a node at depth m in the A* tree, a child node is created for each rotamer r at residue position m + 1 with the partial rotamer assignment (p₁, ⋯, p_m, r). The A* algorithm progressively expands nodes until the lowest f-score node is a leaf node. This leaf node is guaranteed to be the GMEC because the lower bounds for all remaining conformations are higher than the leaf node’s energy. If desired, A* can continue to enumerate conformations in order of lowest energy, which provides a gap-free, in-order list of low-energy conformations. We refer to the A* algorithm described in this section and presented in [21] as Trad-A*. In Table 1 we summarize the A* method terminology introduced in this section and the remainder of the Methods Section.

Table 1.

Summary of A* method terminology

Term	Definition
Residue (Variable) Orderings
Trad-A* (or Sequential)	Residue positions in the A* search are ordered by their location in the protein’s amino acid sequence.
StaticMinDom	Residue positions are expanded in order of increasing variable domain size (i.e., the number of available rotamers per residue position).
StaticMaxDom	Opposite of StaticMinDom. Residue positions are expanded in order of decreasing variable domain size.
StaticDomCmed	Residue positions are expanded based on the ratio of the variable’s domain size divided by the sum of the median pairwise energies to every other residue posi- tion [23].
StaticHMean	Residue positions are ordered based on the harmonic mean of all the position’s energetic interactions (Eq. 5).
DynMin	The residue position to be expanded is chosen dynamically such that it has the largest minimum f-score.
DynHMean	The residue position to be expanded is chosen dynamically such that it maximizes the harmonic mean of its f-scores.
f -score Methods
Trad-A*	A* nodes are bounded by a sum of the partially assigned conformation’s energy and a bound on the remaining possible rotamer assignments for that node (Eqs. 2-4).
A*-LoC	A* nodes are bounded by the local consistency zero-arity cost function, c∅, com- puted using EDAC [42].
A*-LP	A* nodes are bounded by the solution to the LP relaxation of the CSPD ILP (Eq. 11).
A*-MPLP	A* nodes are bounded using the MPLP algorithm, which approximates the solution to the CSPD LP relaxation.
A* Branching Methods
Conformation-A*	A* enumerates an in-order, gap-free list of low-energy conformations. Each A* node represents a partially assigned conformation.
Sequence-A*	In contrast to Conformation-A*, Sequence-A* directly enumerates protein se- quences rather than conformations. Each A* node represents a partially assigned sequence.

2.2 Ordered A* Trees

The A* algorithm was originally developed for motion planning in robotics as a faster alternative to Dijkstra’s algorithm [25]. While protein design shares some similarities with this motion planning technique, there is a distinct difference between the two problems. In motion planning, each edge in the tree corresponds to a planned motion, and the output of the algorithm is the complete path from tree root to leaf node, which corresponds to the planned robot motion. However, in protein design, only the final leaf node (i.e., the full rotamer assignment) is required as output, so the path that was taken to get to the leaf is discarded. In other words, the order in which the rotamers are assigned to residue positions in the A* tree does not matter for correctness and the path in the protein design A* tree does not have any inherent meaning, in stark contrast to motion planning.

While the residue ordering within the A* tree does not affect correctness (final output conformation and sequence), the complexity (A* runtime) can be drastically affected by the order. Intuitively, if a subtree in the A* tree does not contain the GMEC, it is beneficial to prune it and prevent exploration of this subtree. If the algorithm encountered paths with high energy bounds early in the search, then A* could avoid expanding an exponential number of paths. Encountering paths with high low-energy bounds early can be achieved by ordering the tree such that nodes with high bounds are expanded closest to the root of the A* tree and all its subtrees. Consider the example in Figure 2. Residues 3, 4, and 5 form a clique, such that the choice of a rotamer at one residue significantly affects the choice at the other two residues. If the traditional sequential residue ordering is used for the A* search, all of the nodes at a depth of 1, 2, 3, 4, and 5 must be created (Fig. 2C) in order to guarantee that all other paths do not lead to the GMEC. However, when the ordering is switched (Fig. 2D-E), only one or two levels must be explored in the subtrees that do not lead to the GMEC (Fig. 2D-E). This is well-known in the field of constraint satisfaction problems (CSPs), where depth-first search combined with backtracking is used to find a variable assignment that satisfies all of the problem constraints. Much work has been done developing variable ordering heuristics and evaluating their performance on various CSPs (e.g. [39-41]).

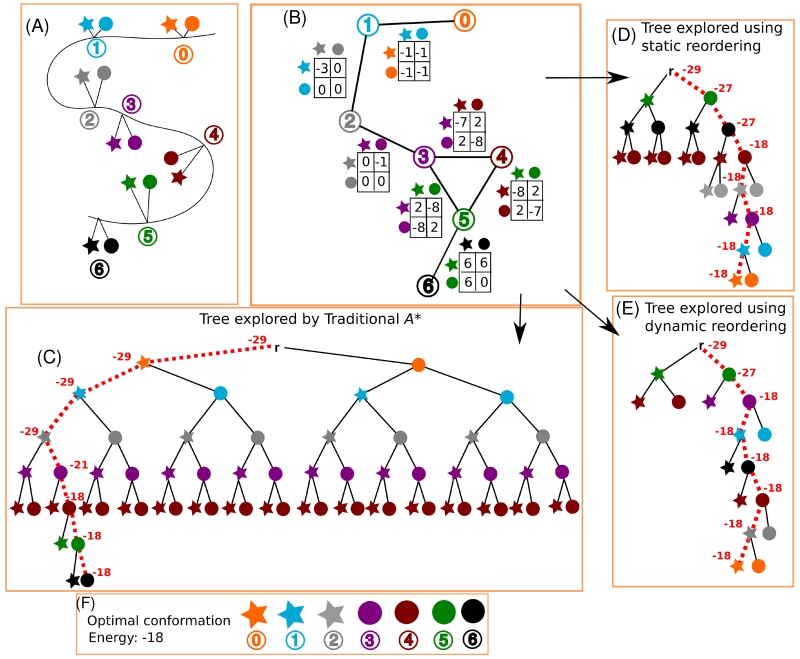
Figure 2. Toy example that demonstrates the effect of residue position reordering on an A* search.

(A) Toy design problem where seven residue positions are each allowed to mutate to two rotamers (represented by a star and a circle). Each residue position is colored by a unique color: orange (position 0), cyan (position 1), grey (position 2), purple (position 3), maroon (position 4), green (position 5), and black (position 6). (B) Diagram showing the pairwise energies between all rotamers in this toy example. For simplicity, assume that all intra-rotamer energies are zero and can be ignored, and that the interactions between pairs that are not joined by an edge are zero. (C-E) The A* algorithm explores only part of the full conformation tree to compute the optimal conformation. A* iteratively expands the node with the lowest f-score (shown by the dotted red path for the nodes in the optimal conformation path) until a leaf is reached. Each expansion results in the creation of new nodes representing the children of the expanded node. To compute the optimal conformation efficiently, it is desirable to expand the fewest number of nodes. The number of nodes expanded can be dramatically reduced by changing the ordering of the tree. (C) The traditional A* algorithm for protein design (Trad-A*) sorts residues in the arbitrary sequential order given by the protein sequence. The bounds on the energies for each inner node in the optimal conformation are shown in red, and the path that leads to the optimal conformation is marked in a thick, red, dashed line. In this toy example, Trad-A* expands 33 nodes, and creates 67 nodes (the 33 expanded nodes plus their children). (D-E) Large speedups in A* can be achieved by a rational ordering of nodes. The energies of each node in the optimal conformation are shown. (D) In a static reordering, residue levels are reordered once before A* runs. In this toy example, A* with static reordering must only expand 13 nodes and create 25 nodes to compute the optimal conformation. (E) In a dynamic reordering, the next level is chosen independently for each path “on the fly” (i.e., as the A* algorithm expands nodes). In this dynamic reordering example, at depth m = 2 the solution path expands position 3 (purple) while the alternative path expands position 4 (maroon). A* with dynamic ordering must expand only 9 nodes, and create a total of 17 nodes, to compute the optimal conformation. (F) The optimal conformation for this example is shown.

The guiding principle behind a good residue ordering is to order the residues such that the number of expanded nodes in the A* tree is small. This can be done by ordering paths so that they fail (i.e., have large bounds) as fast as possible. In the protein design A* search, this can be done by choosing to expand residue positions that will increase the lower bound on the conformations within the tree as much as possible. Based on this idea, we introduce four static (predetermined) residue orderings to replace the traditional sequential ordering. We also present two new dynamic ordering methods that choose which residue position to expand next at each node based on the possible increase in energy bound (i.e., Eq. 2).

2.2.1 Static A* Ordering

The traditional A* enumeration in protein design uses a sequential static ordering of residues in the A* tree. Specifically, depth m in the tree corresponds to the m^th mutable residue in the protein design problem. However, there is no reason why this would be the optimal ordering of residue positions within the tree. We have implemented four alternative variable orderings, StaticMinDom, StaticMaxDom, StaticDomCmed, and StaticHMean to determine how these ordering methods affect the speed and efficiency of the protein design A* search. The StaticMinDom ordering expands residue positions in order of increasing variable domain size (i.e., number of available rotamers per residue position). By expanding variables with a small domain first this greedily minimizes the total size of the A* tree. The StaticMaxDom ordering is the opposite of StaticMinDom and expands residue positions in order of decreasing variable domain size. By expanding residue positions with many rotamers early in the search, the total number of conformations that the h-score must bound for a specific node is reduced, which could lead to a more direct convergence to the GMEC. The StaticDomCmed ordering method is defined in [23] and chooses the residue position to expand based on the ratio of the variable’s domain size divided by the sum of the median pairwise energies to every other residue position. By using the median variable costs, this ordering tries to take into account the lower bound increase that will occur when a specific variable is chosen and find the variable that will increase the lower bound the most. Similar to StaticDomCmed, the StaticHMean ordering scores every position based on the harmonic mean of all the position’s energetic interactions:

$$\mathrm{SHM}\left(i\right)=\sum _{j\ne i}\left(\frac{\mid Q_i\times Q_j\mid -1}{\sum _{\left(q_i,q_j\right)\in \left(Q_i\times Q_j-\left\{\underset{r_i,r_j}{argmin}E\left(r_i,r_j\right)\right\}\right)}{\left(E\left(q_i,q_j\right)-\underset{r_i,r_j}{min}E\left(r_i,r_j\right)\right)}^{-1}}\right).$$ (5)

StaticHMean first normalizes every pairwise interaction between residues i and j by subtracting the minimum pair energy for any pair of rotamers at the two positions ($\underset{r_i,r_j}{min}E\left(r_i,r_j\right)$). Then, StaticHMean computes the harmonic average for each residue pair using the normalized pairwise energies. All the harmonic terms involving a specific residue are summed and used as the residue’s score. Residues are then ordered in the A* tree by decreasing order of this score.

2.2.2 Dynamic A* Ordering

Dynamic A* reordering allows the A* algorithm to choose which residue position to expand next at an A* node based on which residue position will move the search closest to the GMEC energy. This removes the correspondence between the depth in the A* tree and the residue position that exists in traditional A* algorithms. A dynamic A* node contains a set of rotamers P that have been assigned and a set of unassigned residue positions U. There is no requirement that the rotamers in P have sequential residue positions, in contrast to the definition of the partial rotamer assignment p in Section 2.1. Hence, the residue positions in U need not be sequential either. Therefore, dynamic A* adds a step to the traditional A* search where the next residue position to be expanded is chosen from U. Different strategies can be used to choose the next residue position for a given A* node. We tested two ways to choose which residue to expand, DynMin and DynHMean. DynMin chooses the next variable based on the maximum of the variable’s minimum f-score. DynHMean chooses the residue with the maximum harmonic mean f-score (with respect to the parent’s f-score).

In mathematical terms, the next chosen residue position by DynMin is the position i such that:

$$i=\underset{i\in U}{arg\max }\left(\underset{q_i\in Q_i}{min}f\left(P\cup \left\{q_i\right\}\right)\right).$$ (6)

The next residue i for the DynHMean dynamic ordering is chosen as:

$$i=\underset{i\in U}{arg\max }\left(\frac{\mid Q_i\mid }{\sum _{q_i\in Q_i}{\left(f\left(P\cup \left\{q_i\right\}\right)-f\left(P\right)\right)}^{-1}}\right).$$ (7)

A* enumeration with dynamic ordering proceeds by directly choosing the next residue position to expand at each node instead of expanding residue positions in a predetermined order. The traditional A* algorithm in Section 2.1 can be updated to reflect this change:

$$f\left(x\right)=g\left(x\right)+h\left(x\right)$$ (8)

$$g\left(x\right)=\sum _{p_i\in P}\left(E\left(p_i\right)+\sum _{\begin{array}{c}\hfill p_j\in P,\hfill \\ \hfill j>i\hfill \end{array}}E\left(p_i,p_j\right)\right)$$ (9)

$$h\left(x\right)=\sum _{j\in U}\underset{q_j\in Q_j}{min}\left(E\left(q_j\right)+\sum _{p_i\in P}E\left(p_i,q_j\right)+\sum _{\begin{array}{c}\hfill k\in U,\hfill \\ \hfill k>j\hfill \end{array}}\underset{q_k\in Q_k}{min}E\left(q_j,q_k\right)\right).$$ (10)

2.3 Tighter A* f-score Bounds

The residue orderings for A* described in Section 2.2 are founded on the idea that encountering large f-scores early in the search quickly guides the search to low-energy conformations. Another way to increase A* f-scores is to tighten the bounds on the energies of unassigned conformations (Eq. 4). Recall that the f-score of an inner node in the A* tree (e.g., Figs. 1, 2) is a lower bound on the lowest-energy conformation in the node’s subtree. Thus, the tightest value of a node’s f-score is the energy of the lowest energy conformation in the subtree. Although a polynomial-time algorithm that can compute such a tight bound is improbable (because it is as hard as solving the entire problem), it is still possible to tighten the A* algorithm’s f-score in polynomial or average polynomial time.

As defined in the traditional A* search, h(x) is a very overoptimistic bound on the energy of the unassigned conformations. Consider the last term of h(x) in Eq. (4): ${\sum }_{k=j+1}^n\underset{q_k\in Q_k}{min}E\left(q_j,q_k\right)$. This term finds the rotamer q_k with the minimum pairwise energy with q_j over each of the remaining unassigned residue positions. However, there is no consistency constraint: there is no requirement that q_k be the same rotamer for all j = m + 1, ⋯, n. This means different rotamers at position k can contribute to h(x), resulting in a physically infeasible conformation. Ultimately, h(x) finds the lowest local pairwise energy for every unassigned residue pair and does not consider that two different rotamers can not be present at the same residue position in an actual physical conformation. Here we present new A* algorithms for protein design that use established techniques from computational optimization in a novel way to bound unassigned protein conformations. A*-LP uses linear programming (LP) [22] to compute A* f-scores, A*-MPLP computes f-scores with max-product linear programming [38], and A*-LoC uses local consistency methods to improve the f-score [42].

2.3.1 Linear Programming-Based f-score Bounds

The CSPD problem can be formulated as an integer linear program (ILP) [43, 44, 22]. If an ILP is relaxed (i.e., the variables are not restricted to integers) to a linear program (LP) then the solution to this relaxation can be found in polynomial-time [45] or average-case polynomial time (e.g. by the simplex method) [46]. The LP relaxation can find non-physical answers to the protein design problem because fractional rotamers are allowed at residue positions, but the energetic value of the LP solution is always a lower bound on the energy of the protein design solution. Thus, the LP solution can be used as a replacement to the traditional A* f-score.

Here we present the LP formulation of the protein design problem based on [22]:

$$\underset{\mathbf{x}}{min}\sum _{r_i\in Q_i}x\left(r_i\right)E\left(r_i\right)+\sum _{r_i\in Q_i}\sum _{r_j\in Q_j}x\left(r_i,r_j\right)E\left(r_i,r_j\right)$$ (11)

subject to

$$\begin{array}{c}\hfill \sum _{r_i\in Q_i}x\left(r_i\right)=1\text{For all}i\hfill \\ \hfill \sum _{r_j\in Q_j}x\left(r_i,r_j\right)=x\left(r_i\right)\text{For all}\left(r_i,j\right)\text{pairs}\hfill \end{array}$$

where x(r_i), x(r_i, r_j) ∈ [0, 1] and x is the vector of all x(r_i), x(r_i, r_j) indicator variables. When the decision variable x(r_i) or x(r_i, r_j) is set to 1, this corresponds to choosing rotamer r_i or rotamer pair (r_i, r_j) respectively. Note that the LP constraints enforce that the sum of partial rotamers in a specific residue must add up to one, an improvement over the traditional A* algorithm where this sum is unconstrained. The A*-LP algorithm replaces the Trad-A* f-score with the LP solution.

2.3.2 Message Passing-Based f-score Bounds

In practice, the LP solution represents an f-score that tightly bounds the energies of solutions for the protein design problem. However, even though the exact LP bound can be computed in average-case polynomial time using the simplex algorithm [46] and in guaranteed polynomial time using interior point algorithms [45], in practice the time required to solve the LP can become a resource bottleneck. Thus it is desirable to compute f-scores using fast approximation algorithms.

One way to approximate the LP bound is to exploit the weak duality property of linear programs (for a description of duality and dual linear programs, see for example [47-49], and the Appendix of this work). In a linear program any solution that satisfies the constraints is called a feasible solution, while the solution that maximizes the objective function is called the optimal solution. Every linear program (referred to as the “primal program”) has a dual linear program such that any feasible solution to the dual is a lower bound on the optimal solution to the primal. Moreover, the protein design LP also satisfies the strong duality property, which states that the optimal solution to the dual program has the same value as the optimal solution to the primal problem. Thus, any feasible solution of the dual program is a lower bound on the LP solution, and a dual feasible solution that approximates the optimal of the dual program is a tight lower bound on the LP solution.

Several message-passing algorithms [24, 38, 50-53] use the LP strong duality property to compute tight bounds on the LP solution. The Max Product Linear Programming (MPLP) algorithm [38], for example, optimizes the dual of the linear programming formulation in Eq. (11) (the dual is presented in Eq. (13) in the Appendix). MPLP performs a block-coordinate descent in the dual by exchanging messages between residues. Each message, from residue i to residue j “communicates” the likelihood of each rotamer r_j based on the current likelihood of the rotamers at residue i. At each step of the algorithm, a set of dual variables (residue positions) is optimized, while keeping the remaining variables fixed. MPLP is guaranteed to converge, although the convergence value can be lower than the LP solution. We have implemented an MPLP solver in OSPREY and incorporated MPLP into A* to create the new A* algorithm A*-MPLP.

2.3.3 Local Consistency-Based f-score Bounds

An alternative method to calculate A* f-scores can be understood by formulating the CSPD problem as a weighted constraint satisfaction problem (WCSP) [23]. A WCSP is defined by a set of variables that can each take on a discrete set of assignments. Local cost functions are used to weight all possible variable assignments. For the CSPD problem, the WCSP variables are the mutable residue positions that are each allowed to mutate to a discrete set of rotamers. The WCSP local cost functions correspond to the CSPD intra- and pairwise-energy terms. In WCSPs, the cost function can only take on positive integer values, so the CSPD energy function must be scaled between 0 and ∞.

WCSPs are often solved by a branch-and-bound tree search similar to A* [54]. At each node in the tree, local consistency is enforced on the current subproblem defined by the tree node. Local consistency criteria were first developed to solve constraint satisfaction problems (CSPs; [55]), which are a special case of WCSPs where each cost function is a constraint that can either be satisfied or unsatisfied [56, 57]. In CSPs a complete variable assignment is consistent if it satisfies all cost functions. Enforcing local consistency on a CSP progressively eliminates variable assignments that are inconsistent with the constraints, making it possible to find a solution to the problem.

Similar to CSPs, local consistency can be applied to WCSPs. However, since WCSP cost functions are not binary, the goal of WCSP local consistency is to ensure that at least one assignment of each cost function is zero. Two types of local consistency are of particular importance to WCSPs: node consistency, which enforces unary constraints (intra-rotamer energies), and arc consistency, which enforces pairwise constraints (rotamer pair energies) [54]. In practice, node and arc consistency are enforced by transferring energetic costs from pairwise energy terms to lower arity (intra-rotamer or template) energy terms. Ultimately, enforcement of local consistency increases the zero-arity cost function c_∅, which represents the minimum energy of all protein conformations regardless of rotamer assignment (equivalent to the template energy). By construction, c_∅ is a lower bound on the energy of the CSPD solution. Therefore, we can use this bound to compute A* f-scores.

Local consistency is enforced by applying equivalence-preserving transformations to a WCSP, meaning that the CSPD solution is preserved while the underlying structure of the problem is changed. It has been shown that it is NP-hard to find a locally consistent WCSP with a maximum lower-bound [58]. Therefore, several techniques have been developed to find a tight lower bound, such as DAC, FDAC, EDAC [42], and OSAC [59]. Here, we use EDAC to compute A* f-scores in our new algorithm A*-LoC.

2.4 Enumerating Sequences with A*

The A* algorithm used in protein design efficiently generates an in-order, gap-free list of low-energy protein conformations. However, the goal of most protein designs is to find low-energy sequences (rather than conformations) that can be experimentally tested and validated for a desired function. To generate a list of low-energy sequences, A* must often enumerate many conformations that have the same sequences before a new conformation with a unique low-energy sequence is found. To improve the efficiency of searching for low-energy sequences, we have developed a new A* algorithm, Sequence-A*, that uses a modified node expansion technique to directly enumerate sequences.

In Sequence-A*, when a node is expanded, all child rotamers of the same amino acid type are assigned to the same A* node. For example, consider a hypothetical example where three valine and three leucine rotamers are allowed at residue position i. When an A* node is expanded at position i, Sequence-A* will only create two new A* nodes (one for all the valine rotamers and one for all the leucine rotamers), instead of creating six new A* nodes and assigning an individual rotamer to each new node. Therefore, internal nodes in the new A* search tree represent partially assigned sequences instead of partially assigned conformations (as they did in Trad-A*) and leaf nodes now represent fully assigned sequences. Because leaf nodes now represent fully assigned sequences, when the lowest-energy node is returned from the A* tree, this node only represents the lowest-energy sequence. To find the lowest-energy conformation for the returned sequence, the side-chain placement problem must be solved for the sequence. Since the side-chain placement problem is a subproblem of the entire design, it can be solved relatively quickly compared to the entire design problem. To distinguish between Sequence-A* and all previous A* methods that directly enumerate conformations, we refer to the conformation-based methods as Conformation-A*.

Since Sequence-A* nodes now represent partially assigned sequences, the f-score for each node must bound the energy of all sequences that contain the partially assigned sequence. The f-score of each node can be found by calculating a lower energy bound for all possible conformations with the node’s partially assigned sequence. The A*-LP f-score for Sequence-A* is:

$$\underset{\mathrm{x}}{min}\sum _{r_i\in Q_i^{\prime }}x\left(r_i\right)E\left(r_i\right)+\sum _{r_i\in Q_i^{\prime }}\sum _{r_j\in Q_j^{\prime }}x\left(r_i,r_j\right)E\left(r_i,r_j\right)$$ (12)

subject to

$$\begin{array}{c}\hfill \sum _{r_i\in Q_i^{\prime }}x\left(r_i\right)=1\text{For all}i\hfill \\ \hfill \sum _{r_j\in Q_j^{\prime }}x\left(r_i,r_j\right)=x\left(r_i\right)\text{For all}\left(r_i,j\right)\text{pairs}\hfill \end{array}$$

where $Q_i^{\prime }$ is the set of allowed rotamers at residue position i, x(r_i), x(r_i, r_j) ∈ [0, 1], and x is the vector of indicator variables. If position i has been assigned a specific amino acid type, $Q_i^{\prime }$ will be the set of rotamers in Q_i that have that type. If position i has not been assigned yet, $Q_i^{\prime }=Q_i$. Similarly to the A*-LP f-score, it is straightforward to modify the f-score methods in A*-MPLP, A*-LoC, and Trad-A* for Sequence-A*. All four Sequence-A* f-score methods have been implemented and tested in OSPREY.

2.5 Benchmarking Methods

Benchmarking test set

The protein systems from [2] were used as a test set to evaluate the proposed algorithmic improvements. Briefly, crystal structures of protein chains with a maximum resolution of 1.3 Å and less than 100 residues in length were chosen using the PISCES server [60]. Proteins in the test set were chosen such that they had less than 10% sequence identity with all other proteins in the test set. The test set consists of the proteins with the following PDB ids: 1AHO, 1CC8, 1F94, 1FK5, 1G6X, 1I27, 1IQZ, 1JHG, 1JNI, 1L9L, 1LNI, 1M1Q, 1MJ4, 1MWQ, 1OAI, 1OK0, 1PSR, 1R6J, 1T8K, 1TUK, 1U07, 1U2H, 1UCR, 1UCS, 1USM, 1V6P, 1VBW, 1VFY, 1WXC, 1X6I, 1XMK, 1Y6X, 1ZZK, 2AIB, 2B97, 2BT9, 2BWF, 2CC6, 2CG7, 2COV, 2CS7, 2D8D, 2DSX, 2FCW, 2FHZ, 2FMA, 2GOM, 2HBA, 2HIN, 2HLR, 2HS1, 2IC6, 2J8B, 2O9S, 2P5K, 2QCP, 2QSK, 2R2Z, 2RH2, 2RIL, 2WJ5, 2ZXY, 3A38, 3D3B, 3DNJ, 3FGV, 3FIL, 3G21, 3G36, 3HFO, 3I2Z, 3JTZ, 3LAG.

Side-chain placements

Side-chain placement runs selected all residues with < 100% relative side-chain solvent accessible surface area (SASA) and searched over all wild-type amino acid rotamers at each chosen residue position. SASA values were determined with the program NACCESS [61]. The number of flexible residues for each system ranges from 45 to 97 with an average of 71 flexible residues.

Protein core designs

Protein core design runs selected core residues with < 30% relative SASA to mutate during the design search. Each mutable residue was allowed to take on its wild-type identity and mutate to the 5-7 most likely amino acid type substitutions based on the BLOSUM62 matrix [62]. SASA values were determined with the program NACCESS [61]. The number of mutable residues for each system ranges from 11 to 42 with an average of 28 mutable positions per design system.

Protein surface designs

The protein surface designs were similar to the protein core designs, except that all residues with > 50% relative SASA were chosen to mutate during the design search. The number of mutable residues for each design system ranged from 17 to 48 residues, with an average of 28 mutable positions per design system.

Continuous rotamer side-chain placement

The improved A* methods can also be used to improve protein design and side-chain placement with continuous rotamers [2-5]. The A*-LoC-DynMin method was combined with the iMinDEE algorithm [2] to repack the interface residues of the HIV-1 broadly neutralizing antibody, VRC07, bound to gp120 (PDB id: 4OLZ). Interface residues were chosen by computing the contact dots between VRC07 and gp120 using Probe [63] and choosing all residues with at least one contact dot at the interface. In total, 27 gp120 residues and 24 VRC07 residues were flexible during the side-chain placement. An 8 Å shell containing all residues within 8 Å of any interface residue was input to OSPREY as the starting structure.

OSPREY Parameters

The protein design runs used the Richardsons’ Penultimate Rotamer Library [17], while the side-chain placement runs used the Penultimate Rotamer Library doped with the crystal structure side-chain conformations. The objective energy function consisted of the following terms: the AMBER [64] van der Waals and Coulombic potential, EEF1 solvation [65], a hydrogen bond potential [66], an entropic factor [1, 67] and reference energies [68]. The following energy function weights were used: distDepDiel=true, dielectConst=4.0, solvation=0.40, vdwMult=0.95, hbond=3.0, and entropy=5.0. To ensure that a sufficient number of rotamers were present for the enumeration step, only Goldstein DEE pruning [27] was used during the pruning stage. Each design was run on a single Intel(R) Xeon(R) CPU E5-2695 v2 2.40GHz processor with 4 GB of RAM (except the continuous designs were allowed 10 GB of RAM). A design was considered to have failed if it ran out of memory or did not complete within one day of computation. For example, all the difficult side-chain placement and protein core design runs conducted with Trad-A* failed because they ran out of memory. For a given protein system, the same energy matrix and DEE pruning results are used for each enumeration technique. Therefore, to understand the gains from our new enumeration methods, the runtimes reported in this manuscript reflect only the enumeration time, i.e., the time A* took to solve the problem.

A* Enumeration

All combinations of the seven A* variable ordering methods and the four A* f-scores were conducted on each of the design test systems (Table 1). The A*-LP f-score uses the linear program defined as in Equation (11), except that the decision variables for rotamers already assigned at the given node were set to 1. An LP solver was implemented in OSPREY using the Gurobi optimization suite application programming interface (Version 5.6) [69]. A*-MPLP uses MPLP [38] to compute its f-scores. We implemented MPLP within OSPREY and set the number of message-passing iterations to 100, which we found to be a good trade-off between running time and f-score bound tightness based on previous experiments. The A*-LoC f-score uses the local consistency zero-arity cost computed by enforcing local consistency with EDAC on the A* node subproblem to bound the conformations allowed at the A* node. For a residue position that is assigned rotamer r_i within an A* node partial conformation, the costs for all other rotamers at that position, {q_i | q_i ≠ r_i}, were set to infinite energy in the WCSP for that node. Costs for the remaining rotamers were defined by the computed energy matrix. A version of the WCSP solver Toulbar2 [70] (Version 0.9.5) modified to output the results of the initial EDAC bound was integrated with OSPREY to find the zero-arity local consistency bound for each A* node.

3 Results

We tested all the A* enhancements described in the Methods Section (Table 1) on a test set of 73 protein design systems. To assess the benefits of these methods compared to Trad-A*, we focus our analysis on difficult problems: those problems that take over two minutes to run using Trad-A*. Hence, all problems that were solved by Trad-A* in under two minutes were removed from further consideration. We performed two types of designs to test these algorithms. To test exclusively the performance of the ordering methods, we performed side-chain placement designs and further analyzed the 39 difficult design systems. Side-chain placement is a variation of CSPD where no mutations are allowed, so the search is performed on rotamers of the same amino acid type. Then, all combinations of the new methods were tested on protein designs of the cores of the protein test set, 29 difficult designs in total.

3.1 Variable Ordering

We evaluated the static and dynamic variable orderings using side-chain placements of the test protein systems. All residue orderings were tested using the Trad-A* f-score. Four static variable orderings were tested in addition to the standard sequential residue ordering used in Trad-A* [21]. Because the sequential Trad-A* ordering does not use any information about the variable to choose the ordering, this ordering can be considered a random or arbitrary ordering. On the other hand, each new residue ordering is based upon a fail-first principle that tries to order the residue positions in a favorable manner.

Out of the 73 systems tested, 39 were classified as difficult. The sequential Trad-A* algorithm solved 10 of these problems; StaticMinDom solved 9 problems; StaticDomCmed solved 10 problems while StaticMaxDom and StaticHMean solved 13 and 26 systems, respectively. In addition, of the 10 problems solved by sequential ordering, the StaticMinDom, StaticMaxDom, StaticDomCmed, and StaticHMean orderings were each faster than sequential ordering for 8, 6, 9, and all 10 systems, respectively. For the 10 systems that completed with sequential ordering, StaticHMean and StaticMaxDom required the least number of A* nodes (median number of expanded nodes: 3900 and 81000, respectively), while Trad-A*, StaticMinDom, and StaticDomCmed required many more node expansions (362000, 109000, and 129000 nodes, respectively). Overall, these results show that the StaticMaxDom and StaticHMean methods that specifically focus on quickly improving the A* f-score lower bound outperform the other orderings. Our newly proposed dynamic orderings improve upon the StaticMaxDom and StaticHMean orders by specifically analyzing the f-scores of future nodes to find more favorable residue orderings than can be found through static methods.

The dynamic variable orderings, DynMin and DynHMean were able to solve 30 and 31 of the difficult side-chain placement problems, improving upon the static variable orderings. DynMin and DynHMean performed faster than the sequential ordering for all test systems. DynMin and DynHMean expand fewer nodes than the static variable methods in 25 and 29 cases respectively, achieving up to a 2700-fold reduction in the number of expanded nodes (Fig. 3) within the 10 problems that were solved by all methods. The dynamic ordering methods require more computation per node to find the efficient paths through the A* tree; there is an average 43-fold increase in time needed to expand an A* node (51 expanded nodes/second versus 2200 nodes/second). However, the reduction in the number of nodes that must be expanded far outweighs the additional time needed to determine which variable to expand next.

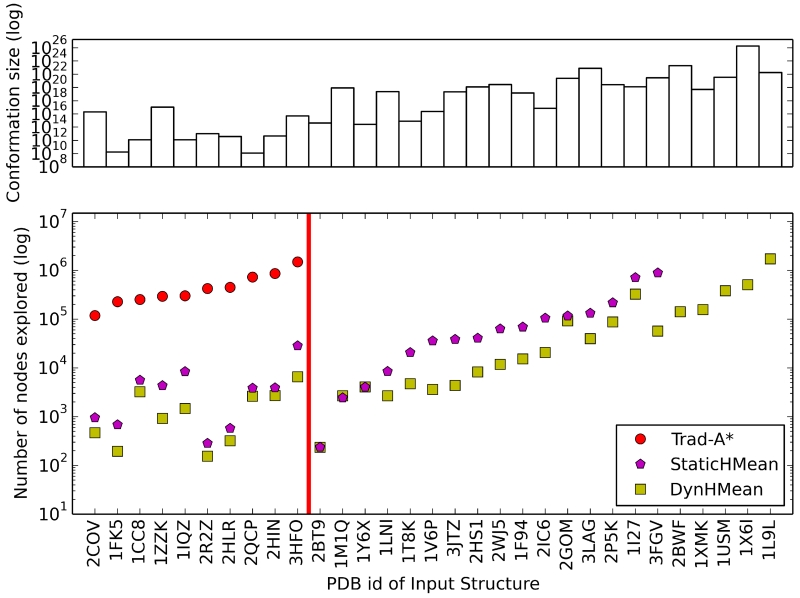
Figure 3. The number of expanded A* tree nodes is greatly reduced by improved variable ordering methods.

Top: The total number of conformations A* had to search through for 31 difficult side-chain placement problems. The size of the conformation space shown is the number of conformations remaining after dead-end elimination pruning. Bottom: The number of A* nodes expanded by three different A* orderings for the 31 side-chain placement problems. Data is shown for the sequential residue ordering used in Trad-A* (red circles), the StaticHMean static variable ordering (purple pentagons), and DynHMean dynamic variable ordering (green squares). The x-axis is labeled by the PDB id used for each side-chain placement problem. All of the runs used the Trad-A* f-score. Trad-A* failed to solve 21 problems (right of the red vertical line) and StaticHMean failed to solve 5 of the problems. For visual clarity the x-axis is ordered first by the number of nodes expanded by Trad-A*, second by StaticHMean, and finally by DynHMean.

3.2 Improved f-scores Methods

We tested the new f-score algorithms A*-LoC, A*-MPLP, and A*-LP by performing 73 protein core designs and selected the 29 difficult designs (i.e., designs that took Trad-A* greater than two minutes to complete) for further analysis. For these designs, each mutable residue was allowed to take on its wild-type identity and several other amino acid types. In this experiment all f-score methods were tested with the sequential variable ordering method. The new f-score methods greatly outperform the standard Trad-A* algorithm (Fig. 4). Trad-A* was only able to solve 5 of the difficult test designs, but A*-LoC, A*-MPLP, and A*-LP were all able to solve 28 of the 29 problems. For the systems that the new f-score algorithms were able to solve, A*-LoC was the fastest algorithm with a median runtime of 26 seconds, while the median times for A*-MPLP and A*-LP were 66 and 52 seconds, respectively. Overall, A*-LP required the least number of expanded nodes (median of 48 nodes), while the median number of expanded nodes for A*-LoC and A*-MPLP were 58 and 57, respectively. A*-LoC was the fastest algorithm, but required the largest number of expanded nodes, implying that there is a tradeoff between speed and f-score accuracy. On average, A*-LoC expanded 2.2 nodes/s, A*-MPLP expanded 1.0 nodes/s, and A*-LP was the slowest at 0.9 nodes/s.

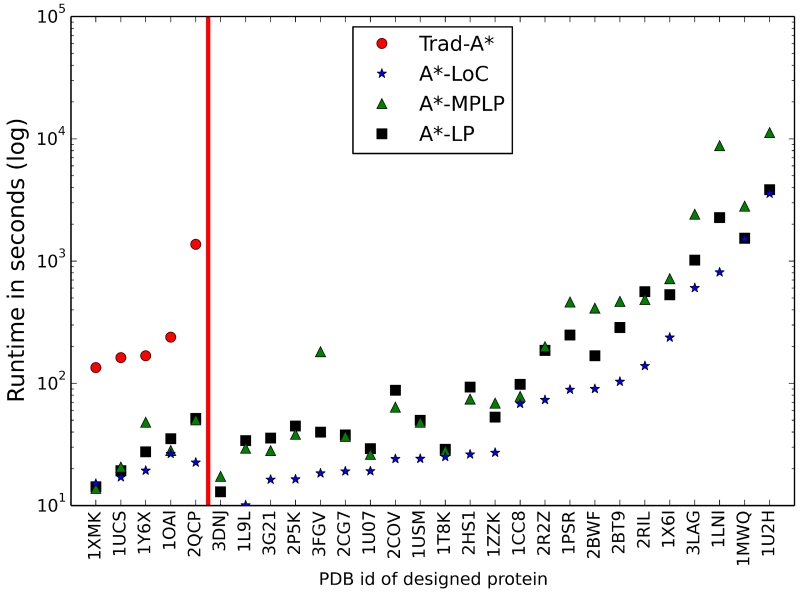
Figure 4. The A* search runtime is greatly reduced by the improved f-score algorithms.

The A* runtimes are shown for the 28 difficult protein core design problems that the new f-score methods could solve. Each run used the Trad-A* sequential variable ordering method. The PDB id for each protein core design is labeled on the x-axis. The three new f-score methods, A*-LoC (blue stars), A*-MPLP (green triangles), and A*-LP (black squares), were able to solve all 28 problems while Trad-A* (red circles) could only solve five problems (left of the red vertical line). For visual clarity the order of designs along the x-axis is sorted first by Trad-A* runtime and then by A*-LoC runtime.

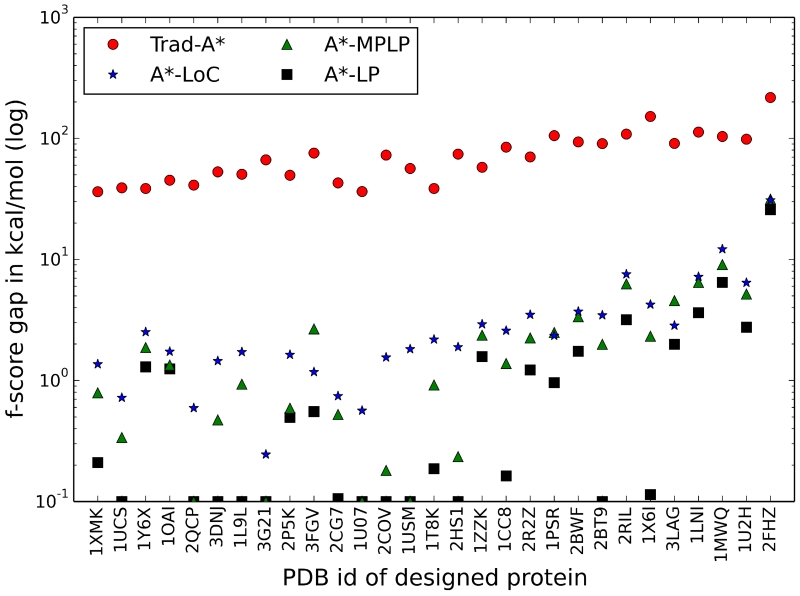
The ability of the new A* f-scores to solve more complex design systems and expand fewer A* nodes is directly related to their ability to produce tight energetic bounds during the A* search. To investigate the accuracy of the improved f-score algorithms we calculated the f-score gap, i.e., the difference between the GMEC energy and the A* root node f-score lower bound, for every design system (Fig. 5). Ideally, if the f-score bound is very accurate, the algorithm can identify the GMEC energy at the root node. This happened 10 times for A*-LP and 4 times for A*-MPLP, but never occurred when using Trad-A* or A*-LoC. However, as shown in Figure 5 the A*-LoC f-scores were always much closer to the actual GMEC energy than the Trad-A* f-scores. The overall accuracy of these f-scores follows a similar trend. The average f-score gap for the 29 difficult design systems was 76 kcal/mol for Trad-A*, while the f-score gaps dropped to 3.9 kcal/mol, 3.1 kcal/mol, and 1.9 kcal/mol for A*-LoC, A*-MPLP, and A*-LP, respectively.

Figure 5. Evaluation of A* f-score accuracy.

The quantity E(g) – f(x₀), referred to as the f-score gap, is shown for all 29 difficult protein core designs, where E(g) is the energy of the GMEC and f(x₀) is the f-score of the A* root node (i.e., the node with no assigned rotamers). The f-score gap represents how accurately an f-score bound approximates the actual GMEC energy. An f-score gap of 0.1 kcal/mol indicates that the f-score was able to exactly bound the GMEC energy. Overall, A*-LP (black squares) produces the tightest bounds, followed by A*-MPLP (green triangles), and A*-LoC (blue stars). The Trad-A* f-score (red circles) always produces the worst bounds and is clearly separated from the other three methods.

To better understand the benefits of the improved f-score algorithms compared to Trad-A*, we now specifically consider the five difficult designs that Trad-A* was able to solve. For these five systems, A*-LoC, A*-MPLP, and A*-LP were all able to solve the designs faster than Trad-A*, with an average reduction in runtime of 19-, 11-, and 11-fold, respectively (Fig. 4). In addition, the new f-score algorithms drastically reduce the number of nodes that A* had to expand compared to Trad-A*. A*-LoC, A*-MPLP, and A*-LP were able to reduce the number of expanded nodes by an average of 6000-, 6300-, and 6500-fold, respectively. Trad-A* was able to expand nodes faster than the other methods (Trad-A*: 1146 nodes/s; A*-LoC: 2.2 nodes/s; A*-MPLP: 1.8 nodes/s; A*-LP: 1.7 nodes/s), but the accuracy of the improved f-score methods drastically outweighs Trad-A*’s ability to quickly process A* nodes.

3.3 Combining Variable Ordering with Improved f-scores

Combining the dynamic variable orderings with the improved A* f-scores yields additional gains over either approach by itself (Fig. 6). All combinations of DynMin with A*-LoC, A*-MPLP, and A*-LP were able to solve all 29 difficult test design problems. The gains are most apparent when analyzing the most complex design systems. Specifically, we consider the five systems that finished with the largest number of expanded nodes for A*-LoC using sequential ordering. When adding DynMin ordering to A*-LoC, the new A* algorithm A*-LoC-DynMin has an average 19-fold reduction in runtime compared to A*-LoC. Similarly, when adding DynMin to A*-MPLP and A*-LP there is an average fold reduction in runtime of 22 and 7, respectively. The number of expanded nodes is also reduced by 15, 12 and 3-fold when adding DynMin to A*-LoC, A*-MPLP, and A*-LP, respectively. Interestingly, adding dynamic variable ordering has a more dramatic effect on A*-LoC and A*-MPLP than on A*-LP. This is likely because the f-score gaps for A*-LP are much smaller than those for A*-LoC or A*-MPLP. Therefore, if the f-score bounds are already very accurate, a beneficial reordering of the A* nodes has a reduced effect compared to looser bounds. This trend is supported by the fact that when we analyzed the five hardest problems that the original A* algorithm was able to solve, we found that adding dynamic reordering improved the number of nodes by an average of 54 fold.

Figure 6. Number of “difficult” protein designs solved by improved A* methods.

Each cell shows the number of difficult protein core designs (N=29) that were solved using the given variable (residue) ordering method combined with the given f-score method. Column headings denote the residue (variable) ordering used for the designs. Row headings denote the f-score method used for the designs. Cells are colored from red (least number of designs solved) to yellow to green (most number of designs solved).

Above, we used protein core packing and protein core design problems as benchmarks to measure the benefits of our new A* methods compared to each other and to traditional A* techniques. However, our new algorithms are not limited to these types of designs, but rather can be used to improve any design that utilizes an A* search. To test the applicability of our algorithms, we have applied the A*-LoC-DynMin algorithm to redesign the surface for each of the 73 proteins in our test set. Surface residues are expected to be much less spatially constrained than protein cores, increasing the total number of biophysically plausible rotamers at surface residues, and making surface designs comparably more difficult than core designs. The A*-LoC-DynMin algorithm was able to provably find the global minimum energy conformation for each surface design tested. The number of residues designed per system ranged from 17 to 48 with an average of 28 mutable residues per system. The median number of conformations that remained after DEE pruning and were input to A*-LoC-DynMin was 10¹³. The median time to solve each design was 17 seconds. The 10 most difficult designs (ranked by the number of A* nodes that had to be expanded), took a median time of 2.5 hours to complete. For these difficult designs, a median of 10³¹ conformations per system remained unpruned after DEE pruning. The largest surface design had 10⁴³ unpruned conformations after DEE pruning, expanded 4875 A* nodes, and took 22.5 hours to complete.

3.4 Protein Design Applications Enabled by the New A* Methods

Direct Enumeration of Sequences for Protein Design

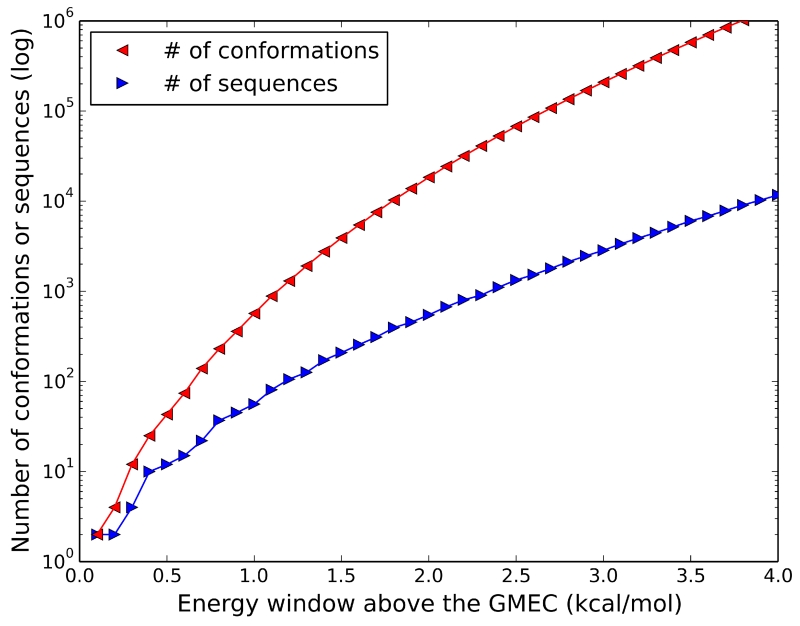
One of the key advantages of A* is its ability to enumerate conformations and sequences in gap-free order of increasing energy. In Conformation-A*, conformations are enumerated in order, but typically many of the lowest-energy conformations have the same sequence or belong to a small number of sequences. An algorithm that tries to find unique sequences by enumerating low-energy conformations will be limited in the number of sequences that it can enumerate because most of the conformations will belong to a small number of sequences. Figure 7 shows an example of how the number of unique sequences grows compared to low-energy conformations for a design of toxin II from Androctonus australis hector (PDB id: 1AHO) using an expanded rotamer library (i.e., rotLib1 from [2]). The number of low-energy conformations grows much faster than the number of unique sequences. When using Sequence-A* (Section 2.4) to directly enumerate sequences, Sequence-A* was able to find all 11717 unique sequences within 4 kcal/mol of the GMEC in 62 minutes. However, when using the Conformation-A* method A*-LoC-DynMin, the design failed to find all the unique sequences within seven days.

Figure 7. The new Sequence-A* algorithm enumerates sequences much faster than Conformation-A*.

To experimentally test protein design predictions, it is often beneficial to predict many low-energy sequences rather than the single GMEC. Conformation-A* methods enumerate conformations in a gap-free, in-order ranking of low-energy conformations. However, most of the low-energy conformations often belong to a small set of protein sequences. Consequently, Conformation-A* enumerates many more conformations than sequences. The number of unique conformations (red) and sequences (blue) are shown for the protein core design of toxin II (PDB id: 1AHO). Each plotted data point shows the number of unique sequences (or conformations) within the given energy cutoff of the GMEC’s energy. Due to the explosion of conformations within 4.0 kcal/mol of the GMEC’s energy, Conformation-A* was unable to find all unique sequences within 4.0 kcal/mol of the GMEC’s energy within seven days. In contrast, by directly enumerating sequences, Sequence-A* was able to find all unique sequences in 62 minutes.

Protein Design with Minimization

When minimization is allowed during a protein design search [2, 3], many rotamer combinations that were easily pruned during a rigid search are now viable and must be considered by A*. The new ordering and f-score A* techniques we presented are needed to efficiently search these difficult minimization-aware design problems that include many rotamer choices with similar energetics. To measure the impact of our new A* algorithms, we conducted a side-chain placement of an antibody-antigen protein-protein interface (PDB id: 4OLZ). The rotamers were allowed to continuously minimize during the search using the iMinDEE algorithm [2]. When using iMinDEE, the A* search no longer enumerates conformations in order of increasing energy, but rather in order of increasing lower-energy bounds. The A*-LoC-DynMin algorithm was able to find the conformation with the lowest-energy bound after expanding a total of 41 nodes. In contrast, Trad-A* fails to find the conformation after expanding 3.5 million nodes. When Trad-A* failed, the best f-score bound was still 21 kcal/mol from the lowest-energy bound. To obtain biologically relevant designs it is important to search accurate energy landscapes of proteins [2, 3, 71-73, 29], which includes allowing protein minimization during the search. Our new enumeration techniques enable the design of complex systems that were previously impractical with the current technology.

4 Discussion

The Trad-A* algorithm is widely used in the field of protein design, but can become a bottleneck for complex protein designs. Improvements in both the A* residue ordering and accuracy of the f-score energetic bounds lead to large speedups in A* runtime and large reductions in the number of nodes explored by A*. The residue orderings designed to increase the current bound in the A* tree as quickly as possible outperformed the traditional sequential ordering. Moreover, A* f-scores using bounds based on solutions to LP, MPLP, or LoC greatly improved upon the traditional A* f-score. All of our new A* enhancements focus on efficiently reducing the number of viable paths in the A* search tree. This allows A* to explore an extremely small fraction of the exponential search space to enumerate all low-energy protein conformations.

The residue ordering and f-score improvements were both designed to increase (i.e., improve) the A* bounds as close to the root of the tree as possible, and can be combined for synergistic improvements in A* enumeration. For example, the most difficult design in our test set (PDB id: 2FHZ; min f-score gap of 26 kcal/mol) could only be solved when novel ordering methods were combined with improved f-score techniques. The potential gains achieved by combining residue ordering with an f-score method are most evident for f-scores that provide large f-score gaps. For f-scores with small f-score gaps, such as A*-LP, the f-score is often close enough to the actual GMEC that few nodes need to be expanded. When only a small number of nodes are required, residue ordering can have minimal effect. Indeed, we see the largest benefits of dynamic ordering with Trad-A* and the least clear effect with A*-LP. However, designs that allow continuous side-chain and/or backbone flexibility during the search [2, 3] result in problems with many low-energy rotamers in the search. For these complex problems it is unlikely that f-score methods can obtain a small f-score gap. In these difficult cases, it will be crucial to have both improved f-scores and residue ordering to efficiently solve the problem.

We have demonstrated that our new algorithms can be directly used to improve the efficiency of both protein core and protein surface designs. Because the algorithms are general, they will likely be useful for many types of real-world design problems, including enzyme design [9, 10], protein-protein interaction design [7, 14], and multistate design [12, 13]. Empirically we have found that tractable problems usually have ≤ 10⁶⁷ conformations remaining after DEE pruning. It is important to note that the number of conformations before DEE pruning does not necessarily correlate with the number after pruning, which is determined by several factors including the energy landscape of the specific protein system (cf. [74]). Here we have focused on using simple and quick pruning methods (i.e., singles Goldstein pruning [27]) to demonstrate the gains in conformation enumeration, but it is expected that combining sophisticated pruning techniques (such as pairs pruning, conformational splitting, and DACS pruning [75-77]) with our new advanced enumeration methods will achieve greater gains.

Both the advanced residue orderings and improved f-scores require additional computation for every expanded A* node compared to Trad-A*. In general, the more advanced/accurate the method, the more computation time is needed for each node. Therefore, there is a clear tradeoff between the amount of time spent per node and the accuracy of the method. For example, in an extreme case, an f-score method that guarantees an f-score gap of zero could be used, but this is as difficult as solving the original CSPD problem. In addition, the optimal variable ordering could be computed, but since there are O(n!qⁿ) ways to order the variables with dynamic ordering, finding the optimal ordering is likely harder than the original CSPD problem (we conjecture this problem may be NP-hard). On the other hand, if very little work is done at each node (e.g., by computing a fast but loose bound or by using the traditional sequential order), the computed bound will be poor, resulting in an unnecessarily large number of nodes that must be expanded. This tradeoff must always be considered when developing new methods to further improve A*. Overall, out of our new A* f-score algorithms, A*-LoC was faster than the other techniques despite producing larger f-score gaps and expanding more nodes than A*-MPLP and A*-LP. By finding the right balance between computation time per node and strength of the f-score bound, A*-LoC was able to outperform all other techniques.

Our new A* algorithms greatly reduce the bottleneck that can arise when using Trad-A* to solve complex biological designs. By reducing the A* bottleneck, new accurate and efficient CSPD methods can be developed. For example, Sequence-A* utilized our new A* improvements and was shown to generate the lowest-energy sequences at least 162 times faster than Conformation-A*. These low-energy sequences can be used to generate a diverse set of designs for experimental testing, which increases the chance that a functional design is found. We also demonstrated the use of our improved A* algorithms for designs that include continuous side-chain and/or backbone flexibility [2, 3]. Allowing continuous flexibility during the design search yields many viable rotamers and conformations that would have been pruned by rigid rotamer methods [2]. Therefore, when including minimization, A* must be able to search through many more conformations compared to less accurate CSPD methods. In the section above entitled “Protein Design with Minimization,” we showed that our new algorithms were able to reduce the number of nodes A* expanded by at least five orders of magnitude.

Computational structure-based protein design has the ability to search large portions of protein conformational and sequence space faster than either experimental or competing computational methods. There have been many successful protein designs, but as the field progresses the demand for larger designs with increased complexity, as well as protein backbone and side-chain flexibility, will continue to grow. The A* algorithm combined with DEE pruning is an effective methodology that can incorporate both continuous flexibility and low-energy ensembles into CSPD. The A* search techniques presented here optimally solve a large class of biomedically-relevant CSPD problems that were previously intractable for A*. This facilitates the development of increasingly accurate CSPD methods that can solve challenging design problems.

A Relationship between f-score methods and proof that the LP-based f-score always improves upon the traditional A* f-score

As we showed in Section 3, the performance of provable branch-and-bound algorithms improves radically if they can compute tight f-score lower bounds on the energy of partial conformations. Tight f-score lower bounds can often be computed by polynomial-time algorithms. In this work we have presented four methods to calculate f-score lower bounds (Trad-A*, A*-LP, A*-MPLP, and A*-LoC). Readers interested in optimization techniques will appreciate that all four f-score lower bounds are related and explore the same optimization space. By understanding this relationship, we can understand why some methods perform better than others. In this Appendix we describe the relationship between the different f-score methods, and prove that the A*-LP f-score always improves upon the traditional Trad-A* f-score.

Before understanding the relationship between f-score methods, however, it is essential to understand the duality property of linear programs (for a more complete explanation, see [47-49]). Every linear program (called the primal LP) is associated with a dual LP. If the primal LP is a minimization, then the dual LP is a maximization and vice-versa. For example, the LP relaxation for protein design presented in Eq. (11) minimizes the protein design objective function. The dual to the protein design LP is a related linear program that maximizes its objective function. There are two important properties associated with duality. The weak duality property of linear programs states that any feasible solution to the dual (i.e., any solution that satisfies the constraints) is a bound on the solution of the primal. In the case of the protein design primal and dual programs, any feasible solution to the dual program is a lower bound on the primal problem. The strong duality property of linear programs [49], which is satisfied for the protein design problem, states that the optimal solution to the primal is equivalent to the optimal solution to the dual. Thus, any feasible solution of the dual program that approximates the optimal of the dual program is a tight lower bound on the LP solution.

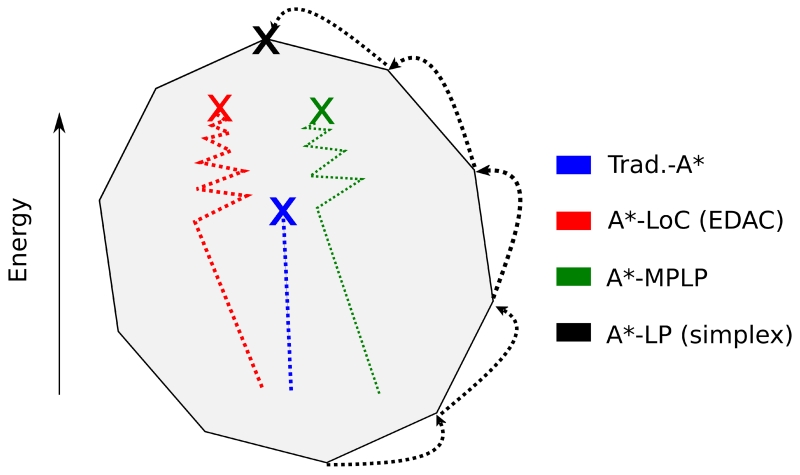
The f-scores used by A*-MPLP, A*-LoC, and Trad-A* are computed by optimization algorithms that approximate the dual LP of the protein design LP (Eq. 11). First, as we described in Section 2.3.2, MPLP directly approximates the optimal solution to the dual of the LP program, and therefore provides an f-score lower bound. In addition, it has also been shown that enforcement of local consistency (used by A*-LoC) searches through the LP dual and approximates the optimal LP relaxation [59]. MPLP and local consistency algorithms are often more efficient than algorithms that find the exact LP relaxation solution. Therefore, there is a clear tradeoff between speed of the f-score computation and tightness of the f-score bound. In addition to these established optimization techniques, in this Appendix we prove that the traditional A* f-score also lies within the dual of the LP formulation of the CSPD problem. This guarantees that the LP solution better estimates protein conformation energies than the traditional A* f-score, and in practice the LP solution is usually a much better bound (Section 3). Figure A1 presents an illustrative toy example showing how all four f-score methods explore the dual of the protein design LP.

To prove that the LP f-score is guaranteed to improve upon the Trad-A* f-score we show that the Trad-A* f-score (as presented in Eq. 2) is always a feasible point in the dual. Since the LP f-score is the optimal value in this dual space, the LP f-score is therefore always higher (and tighter) or equal to the Trad-A* f-score (Figure A1).

We first present the dual of the LP program in Eq. (11). The dual derivation of Eq. (11) is as straightforward as any dual derivation for a linear program, but for convenience we use the dual derived in [38]. Using this derivation, the dual linear program of Eq. (11) can be written as a maximization of minimizations:

$$\underset{\beta }{\max }\sum _i\underset{r_i}{min}\sum _j\underset{r_j}{min}\left({\beta }_{ji}\left(r_j,r_i\right)\right)$$ (13)

subject to the constraints

$$\forall i,r_i,j,r_j:\left({\beta }_{ij}\left(r_i,r_j\right)\right)+\left({\beta }_{ji}\left(r_j,r_i\right)\right)={\theta }_{ij}\left(r_i,r_j\right),$$

where β is the vector of all β_ij variables that are optimized by the dual program. A distinct β_ij(r_i, r_j) variable is defined for each (r_i, r_j) pair, i ≠ j. Therefore, the feasible space of solutions to the dual program are all possible values of the dual objective function such that all β_ij values still satisfy the dual program constraints:

$$f\left(\beta \right)=\sum _i\underset{r_i}{min}\sum _j\underset{r_j}{min}\left({\beta }_{ji}\left(r_j,r_i\right)\right)$$ (14)

subject to the constraints

$$\forall i,r_i,j,r_j:\left({\beta }_{ij}\left(r_i,r_j\right)\right)+\left({\beta }_{ji}\left(r_j,r_i\right)\right)={\theta }_{ij}\left(r_i,r_j\right).$$

We now show that the minimization performed by the f-score of Trad-A* (Eq. 2) always returns a point in the feasible space of the protein design dual linear program (Eq. 14). We first slightly change the f-score of Eq. (2). At the root x₀ of the tree, g = 0 and thus f = h:

$$f\left(x_0\right)=\sum _{i=1}^n\underset{r_i}{min}\left(E\left(r_i\right)+\sum _{j=i+1}^n\underset{r_j}{min}E\left(r_i,r_j\right)\right).$$ (15)

Before we show the relationship to the dual of Eq. (13), note the second sum in Eq. (15) goes from i+1 to n. However, our dual formulation goes from 1 to n so we will reconcile this by introducing a new term,

$${\lambda }_{ij}\left(r_i,r_j\right)=\{\begin{array}{cc}E\left(r_i,r_j\right)\hfill & \text{if}i<j,\hfill \\ 0\hfill & \text{if}i\ge j.\hfill \end{array}\phantom{\}}$$

Because λ_ij is zero for all i ≥ j, we can replace E(r_i, r_j) with λ_ij in the inner sum of Eq. (15) and change the inner sum to add all terms from 1 to n:

$$f\left(x_0\right)=\sum _{i=1}^n\underset{r_i}{min}\left(E\left(r_i\right)+\sum _{j=1}^n\underset{r_j}{min}{\lambda }_{ij}\left(r_i,r_j\right)\right).$$ (16)

In addition, we can move the intra-energy term E(r_i) into the inner sum. Since the inner minimization is independent of the variable r_i, we can move E(r_i) inside the inner minimization as well:

$$f\left(x_0\right)=\sum _{i=1}^n\underset{r_i}{min}\left(\sum _{j=1}^n\underset{r_j}{min}\frac{E\left(r_i\right)}{n}+{\lambda }_{ij}\left(r_i,r_j\right)\right).$$ (17)

It is now straightforward to see that $\frac{E\left(r_i\right)}{n}+{\lambda }_{ij}\left(r_i,r_j\right)+\frac{E\left(r_j\right)}{n}+{\lambda }_{ji}\left(r_j,r_i\right)={\theta }_{ij}\left(r_i,r_j\right)$. Thus, if we set ${\beta }_{ij}=\frac{E\left(r_i\right)}{n}+{\lambda }_{ij}\left(r_i,r_j\right)$ and ${\beta }_{ji}=\frac{E\left(r_j\right)}{n}+{\lambda }_{ji}\left(r_j,r_i\right)$, then the minimization of Eq. (17) always meets the constraint of the dual in Eq. (13) and is therefore a point in the feasible space of the dual. Since the linear program in Eq. (13) maximizes the minimization of Eq. (15), this proves that the LP solution is always greater than or equal to the Trad-A* f-score. Empirically we show in Sec. 3 and Fig. 5 that the LP f-score always results in much tighter bounds. For the difficult designs tested, on average the bounds computed by A*-LP were over 40-fold better (tighter) than Trad-A*, and tighter bounds greatly increase the efficiency of A* (Fig. 4 and Fig. 6).

Figure A1. Several algorithms compute f-score bounds based on the dual of the protein design program.

In the relaxation of the LP formulation of the CSPD problem (the primal problem), the feasible space of solutions is a high-dimensional convex polyhedron. The dual of this formulation is also a convex polyhedron (cartooned here in 2 dimensions in grey) and any solution to the dual is a lower bound on the primal (an f-score lower bound). These f-scores can be used by algorithms, such as A* to find the optimal integer solution to the CSPD problem. The traditional A* algorithm (shown in blue) uses a simple pairwise summation (Eq. 4) to bound the protein design score. We show that the traditional A* f-score is a point in the dual of the LP and it is therefore a worse bound than the LP solution (Appendix). The EDAC algorithm [42] (red) based on local consistency and used in WCSP solvers [70], and the MPLP algorithm [38] (green) approximate the optimal LP relaxation solution. These algorithms are often more efficient than algorithms that find the exact LP solution, such as simplex (in black). Note that in this example simplex finds the optimal solution to the LP dual, which is equivalent to the optimal solution of the LP primal.