The Intravascular Ultrasound Elasticity-Palpography Technique Revisited: A Reliable Tool for the in vivo Detection of Vulnerable Coronary Atherosclerotic Plaques

Abstract

A critical key in detection of vulnerable plaques (VPs) is the quantification of its mechanical properties. From the intravascular ultrasound (IVUS) echogram and strain images, Céspedes et al. (2000) proposed an elasticity-palpography technique (E-PT) to estimate the apparent stress-strain modulus (S-SM) palpogram of the thick endoluminal layer of the arterial wall. However, this approach suffers from major limitations because it was developed for homogeneous, circular and concentric VPs. The present study was therefore designed to improve the E-PT by considering the anatomical shape of the VP. This improved E-PT (IE-PT) was successfully applied to six coronary lesions of patients imaged in vivo with IVUS. Our results demonstrated that the mean relative error of the S-SM decreased from 61.02±9.01% to 15.12±12.57% when considering the IE-PT instead of the E-PT. The accuracy of the S-SM palpograms computed by using the improved theoretical framework was also investigated with regard to noise which may affect prediction of plaque vulnerability.

INTRODUCTION

Vulnerable atherosclerotic plaque (VP) rupture is the leading cause of acute coronary syndrome, myocardial infarction and stroke in the western world (Lloyds-Jones et al. 2010). The morphology of unstable vulnerable coronary lesion consists of a relatively large extracellular necrotic core with a thin fibrous cap (< 65 μm) infiltrated by macrophages (Virmani et al. 2000). The thin-cap fibroatheroma is the precursor lesion that once ruptured, may lead to the formation of a thrombus causing an acute syndrome and possibly death (Virmani et al. 2006). Several intravascular techniques are used to detect coronary VPs in clinics (Vancraeynest et al. 2011), including ultrasound (IVUS) (Rioufol et al. 2002; Carlier and Tanaka 2006), optical coherence tomography (OCT) (Jang et al. 2002; Tearney et al. 2008) and magnetic resonance imaging (IV-MRI) (Larose et al. 2005; Briley-Saebo et al. 2007). Diagnosing unstable VPs, on the other hand, is still imprecise, as the thickness of the fibrous cap alone is not a sufficient predictor of plaque stability (Virmani et al. 2000; Ohayon et al. 2008; Fleg et al. 2012; Maldonado et al. 2012). Biomechanical studies have identified peak cap stress amplitude as an additional key predictor of vulnerability to rupture (Loree et al. 1992; Ohayon et al. 2001; Finet et al. 2004).

Quantifying intraplaque stress distribution, to predict plaque rupture, has been a challenge. To overcome this hurdle, the rate of deformation (strain) of a tissue can be calculated which can then be directly related to the intrapalque stress and its mechanical properties. Ophir and colleagues (Ophir et al. 1991; Céspedes et al. 1993) were the pioneers on developing imaging techniques based on the strain field. Based on their work, several elegant IVUS methods were developed to highlight the spatial strain distribution (i.e. strain-elastogram) over the entire vessel wall (Maurice et al. 2007) or over a restricted thick endoluminal region (Doyley et al. 2001; de Korte et al. 2002). Such IVUS techniques based on the optical flow (Maurice et al. 2004) or time-delay correlation estimation (de Korte et al. 2002) allowed the calculations of intraplaque strain images during the cardiac cycle.

However, these methods did not overcome a main limitation related to the complex geometries of atherosclerotic plaques, which alter the intraplaque strain fields and inhibit direct translation into plaque mechanical properties. Therefore, to complement the characterization of an atherosclerotic lesion from the IVUS echogram and strain images, Céspedes et al. (2000) developed an elegant one-dimensional elasticity-palpography technique (E-PT) to estimate and display an apparent local stiffness (called stress-strain modulus (S-SM) palpogram) of the thick endoluminal layer of the arterial wall (called palpography domain). Although such work presents promising concepts for the identification of atherosclerotic lesions, the current E-PT suffers from major limitations. First, the mechanical solution used to extract the S-SM palpogram was obtained assuming a cylindrical concentric arterial wall made of an homogeneous isotropic incompressible medium and submitted to a uniform outer radial stress distribution (Timoshenko and Goodier 1987). Second, with such a simplified model, it is difficult to correlate the resulting S-SM to the real Young’s modulus distribution in the palpography domain. Such solution is too restrictive and must be used with precaution for atherosclerotic lesions with high eccentricity and non uniform wall thickness.

The present biomechanical study was designed to improve the theoretical framework of the E-PT by considering the anatomical shape of the atherosclerotic coronary artery. This improved elasticity-palpography technique (IE-PT), based on the continuum mechanics theory prescribing the strain field in the palpography region, was successfully applied to six coronary lesions of patients imaged in vivo with IVUS. The robustness and performance of the new IE-PT was investigated with regard to noise which may affect prediction of plaque vulnerability.

MATERIAL AND METHODS

Six patients underwent coronary IVUS, and the extracted plaque geometries were used to simulate strain fields from which the performance of the improved elasticity-palpography technique was tested. Moreover, one idealized concentric and circular non vulnerable plaque geometry with an homogeneous lesion was designed to highlight the main limitations of the native E-PT.

IVUS Study and Plaque Geometries

Patient population

Arteries were explored in patients referred for percutaneous coronary intervention at the Lyon Cardiology Hospital (Hôpital Cardiologique et Pneumologique de Lyon, France) after a first acute coronary syndrome with troponin I elevation. Investigations were approved by the institutional board of the Hospital Cardiology Department and patients consent.

Intravascular ultrasound imaging

Non-ruptured VP geometries were obtained from IVUS scans of the coronary arteries following the protocol described by Rioufol et al. (2002). To avoid vasospasms, IVUS exploration was performed after intracoronary administration of 200 μg of nitroglycerine. The acquired cross-sectional IVUS image of the VP corresponded to the site exhibiting the thinner fibroatheroma cap. IVUS scans were performed with the iLab platform (Boston Scientific, Watertown, MA) equipped with 40 MHz catheters (Atlantis SR Pro 3.6F, Boston Scientific). The spatial resolution of the ultrasound images acquired with the IVUS system was approximately 90 μm in the radial direction (Chopard et al. 2010).

IVUS image analysis

IVUS echogenecity aspects were used to characterize VP components: (i) highly hypoechogenic components (or anechogenic zones), suggestive of quasi-cellular tissues (lipid or cellular deposition); (ii) homogeneous reflective components, suggestive of organized or disorganized fibrosis; or (iii) hyperechogenic components (or bright zones), suggestive of calcified regions (Di Mario et al. 1998). A manual segmentation procedure using ImageJ software (ImageJ, NIH, Bethesda, MD, USA) was performed by a cardiologist to extract the contours of each plaque component.

IVUS measurements and definitions

Each cross-sectional IVUS image of a lesion was quantitatively analyzed. Measurement were made for plaque area (Pla_area, mm²), lumen area (Lu_area, mm²), necrotic core area (Core_area, mm²), calcified area (Cal_area, mm²), degree of stenosis (Stenos_deg, %) as 100 x Pla_area/(Pla_area + Lu_area) and cap thickness (Cap_thick, mm), which was defined as the shortest distance between the lumen and the necrotic core.

Forward Problem: Strain Field Distributions

The files of the digitized contours obtained with ImageJ were imported into MATLAB and then transferred in Comsol (Structural Mechanics Module, version 3.3, Comsol, France) via the LiveLink MATLAB/Comsol toolbox. Radial strain elastograms were obtained by performing static finite element (FE) computations on all VP geometries using Comsol software. The entire plaque geometries were meshed with approximately 15,000 6-Node triangular elements. The center of gravity of the lumen, which was numerically determined as the barycenter (i.e the center of mass) of the lumen area, was used as the origin of the cylindrical coordinate system (r,θ). The strain fields were interpolated on a regular polar mesh with a given radial step resolution of 36 μm and an angular step resolution corresponding to 256 radial directions, which is the resolution one can expect from endovascular elastography (Maurice et al. 2007).

Boundary conditions and material properties

The FE simulations were conducted under the assumption of plane strain. Because instantaneous pressure was not recorded during the IVUS scans of the coronary arteries, we assumed a blood pressure differential ΔP of 1 kPa (or 7.5 mmHg) which corresponds to a realistic pressure gradient occurring between two successive IVUS images recorded during the cardiac cycle. Free boundary condition was assumed at the external diameter of the artery. The mechanical properties of the fibrosis, calcified and soft necrotic core were modeled as isotropic and quasi-incompressible media (Poisson ratio ν = 0.49) with Young’s moduli E_fibrosis = 800 kPa, E_calcified = 5000 kPa and E_core = 5 kPa, respectively (Finet et al. 2004).

Sensitivity study with regard to noise on input radial strain data

To investigate the influence of the noise on the performance of the improved elasticity-palpography technique, a white-noise was added to each FE simulated radial strain field used as input. For the noise model, we used a normal distribution of noise with zero mean and a standard deviation of (a ε_rr + b) β, with a = 0.2%, b = 0.04% and where ε_rr is the local value of the radial strain (Baldewsing et al. 2005; Le Floc’h et al. 2009). The noise field was significantly amplified by increasing β from 1 to 6. For each level of noise β, ten computations in which the noise was spatially randomly distributed were performed and the averaged Young’s modulus of each plaque constituent (± standard deviations) was presented.

Inverse Problem: The Stress-Strain Modulus Palpogram

The stress-strain modulus palpogram of Céspedes et al. (2000)

The S-SM (called E_palpo) was defined by Céspedes et al. (2000) as the local radial stiffness of the thick endoluminal layer of the arterial wall (i.e of the palpography domain). Inspired by the expression of the S-SM obtained for a thick-walled isotropic cylindrical vessel with a specific concentric cylindrical palpography domain, Céspedes et al. (2000) proposed the following S-SM approximation (all details are presented in Appendix I):

$$E_{\mathit{palpo}}^{\mathit{Céspedes}}(\theta )=\frac{\mathrm{\Delta }P/2}{\epsilon (\theta )}\text{with}\epsilon (\theta )=\left|{\int }_{R_i(\theta )}^{R_p(\theta )}{\epsilon }_{rr}(r,\theta )dr\right|$$ (1a, b)

were R_i(θ) and R_p(θ) are the inner and outer radii of the palpography domain, respectively.

The stress-strain modulus palpogram revisited

We revisited the S-SM formulation of Céspedes et al. (2000) to account for both the anatomical shapes of the atherosclerosis plaque and the palpography domain. Based on the relationship between the deviatoric radial stress ${\sigma }_{rr}^{\mathit{dev}}(r,\theta )$, the Young’s modulus E(r,θ) and the radial strain component ε_rr(r,θ) for heterogeneous, isotropic, incompressible and linear elastic continuum medium (Timoshenko and Goodier 1987):

$${\sigma }_{rr}^{\mathit{dev}}(r,\theta )=\frac{2}{3}E(r,\theta ){\epsilon }_{rr}(r,\theta )$$ (2)

we redefined the S-SM as the ratio of the average deviatoric radial stress over the average radial strain along the radial axis:

$$E_{\mathit{palpo}}^{\mathit{new}}(\theta )=\frac{3}{2}\frac{\left|{\int }_{R_i(\theta )}^{R_p(\theta )}{\sigma }_{rr}^{\mathit{dev}}(r,\theta )dr\right|}{\epsilon (\theta )}$$ (3)

where ε(θ) is given by Eq. (1b).

Moreover, knowing that the radial strain ε_rr(r,θ) is proportional to the imposed change of pressure ΔP and inversely proportional to the amplitude of the Young’s modulus E(r,θ):

$${\epsilon }_{rr}(r,\theta )=\frac{3}{2}\frac{\mathrm{\Delta }P}{E(r,\theta )}h(r,\theta )$$ (4)

(where the constant 3/2 was introduced for mathematical convenience only), the expression of the deviatoric radial stress given by Eq. (2) can be rewritten as follow:

$${\sigma }_{rr}^{\mathit{dev}}(r,\theta )=\mathrm{\Delta }Ph(r,\theta )$$ (5)

where h(r,θ) is a new correcting shape function which account for the entire plaque morphology including the geometries of all plaque heterogeneities. Taking advantage of such expression for the deviatoric radial stress, the new S-SM (Eq. 3) becomes:

$$E_{\mathit{palpo}}^{\mathit{new}}(\theta )=\frac{\mathrm{\Delta }P\left|{\int }_{R_i(\theta )}^{R_p(\theta )}h(r,\theta )dr\right|}{\epsilon (\theta )}$$ (6)

Since h(r,θ) is an unknown function that escapes to direct measurements, we computed an approximated correcting shape function h*(r,θ) which accounts for anatomical cross-sectional plaque geometry. Such approximated correcting function was obtained by using a finite element (FE) analysis and by assuming the plaque homogeneous, isotropic and quasi incompressible with Young’s modulus E. This FE simulation was performed in linear elasticity with a loading blood pressure amplitude ΔP. From Eq. (4) and knowing the spatial radial strain distribution we extracted the approximated shape function h*(r,θ) which was used to revisit the S-SM formulation for complex plaque geometries:

$$E_{\mathit{palpo}}^{\text{revisited}}(\theta )=\frac{\mathrm{\Delta }P\left|{\int }_{R_i(\theta )}^{R_p(\theta )}h\ast (r,\theta )dr\right|}{\epsilon (\theta )}$$ (7)

Interestingly, this original revisited S-SM formulation (Eq. 7) allows us to find the real Young’s modulus amplitude E when considering homogeneous isotropic plaque (i.e. $E_{\mathit{palpo}}^{\text{revisited}}(\theta )=E$), whatever their geometries and the palpography domains considered Ω_palpo (with R_i(θ)≤r≤R_p(θ) ).

The Young’s modulus palpogram

To discuss the physical meaning of the native and revisited S-SM formulations given by Eqs. (1) and (7), respectively, we compared them to the circumferential distribution of the averaged Young’s modulus along the radial axis (AYM):

$$\mathit{AYM}(\theta )=\frac{1}{R_p(\theta )-R_i(\theta )}{\int }_{R_i(\theta )}^{R_p(\theta )}E(r,\theta )dr$$ (8)

where E(r,θ) is the spatial distribution of the Young’s modulus.

Moreover, to quantify the accuracy of the reconstructed S-SM palpograms we computed the following mean relative stress-strain modulus error (MR_error):

$${MR}_{\mathit{error}}=\frac{100\left(\underset{0}{\overset{2\pi }{\int }}{E}_{\mathit{palpo}}(\theta )d\theta -\underset{0}{\overset{2\pi }{\int }}\mathit{AYM}(\theta )d\theta \right)}{\underset{0}{\overset{2\pi }{\int }}\mathit{AYM}(\theta )d\theta }$$ (9)

RESULTS

IVUS Study

Six non-ruptured VPs with necrotic cores and calcified areas were identified after extensive IVUS scanning. The geometrical characteristics of the six non-ruptured VPs scanned in vivo (plaques # 2 to 7) and the eccentric circular idealized homogeneous plaque (plaque # 1) were summarized in Table 1. All results presented in our figures were obtained from simulations performed without white noise (i.e β = 0) and with a blood pressure differential ΔP of 1 kPa unless otherwise stated.

Table 1.

Description of atherosclerotic plaque characteristics detected by intravascular ultrasound (IVUS) and modeled.

Plaque #	Origin of the Geometry	Cap Thickness (μm)	Necrotic Core Areas (mm2)	Calcium Area (mm2)	Plaque Area (mm2)	Lumen Area (mm2)	Degree of Stenosis (%)
1	Model	-	-	-	25.13	3.14	89
2	IVUS	93	1.36	-	8.74	2.789	76
3	IVUS	100	5.39	-	16.70	3.24	84
4	IVUS	162	1.20/0.51	-	17.85	6.75	73
5	IVUS	193	2.11	0.40	17.53	3.60	83
6	IVUS	62	3.54	1.60	15.64	4.52	78
7	IVUS	220	2.15/0.70	0.89	16.88	3.62	82

Performance of the Improved Elasticity-Palpography Technique

Importance of considering the correcting stress function

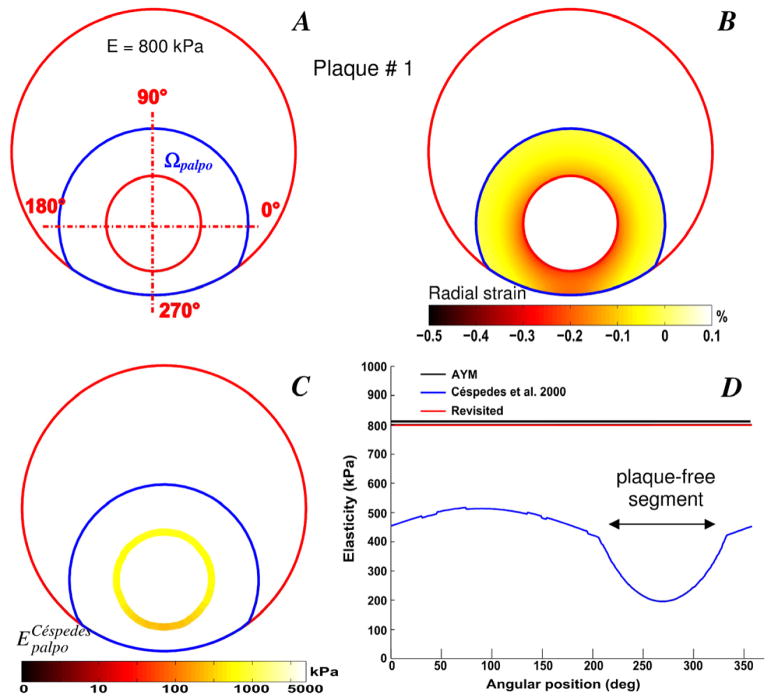
Simulations performed on the idealized eccentric plaque geometry with homogeneous isotropic (E= 800 kPa) and quasi incompressible (Poisson ratio ν = 0.49) atherosclerotic lesion was first presented to highlight the importance of using the revisited S-SM formulation when considering non concentric arterial cross-section with arbitrary palpography domain (see plaque # 1, Fig. 1). The improved S-SM palpogram appears to be less sensitive to the geometries of the arterial plaque and palpography domain than the one derived with the E-PT. The S-SM palpogram computed with the IE-PT remains almost constant and close to 800 kPa - which is also the value of the real averaged Young’s modulus - even in the free-plaque arc length which is the thinnest region of the palpography domain (Fig. 1D).

Figure 1.

Performance of the improved elasticity-palpography technique. A) Contours (in red) of an idealized eccentric and circular plaque model (called plaque # 1) in which the lesion is homogeneous. The palpography domain Ω_palpo is also given (blue contours). B) Radial strain-elastogram computed in the palpography domain. C) Computed native Céspedes et al. (2000) stress-strain modulus (S-SM) palpogram. D) Comparisons between native S-SM of Céspedes et al. (2000), improved S-SM and averaged Young’s modulus (AYM) palpograms.

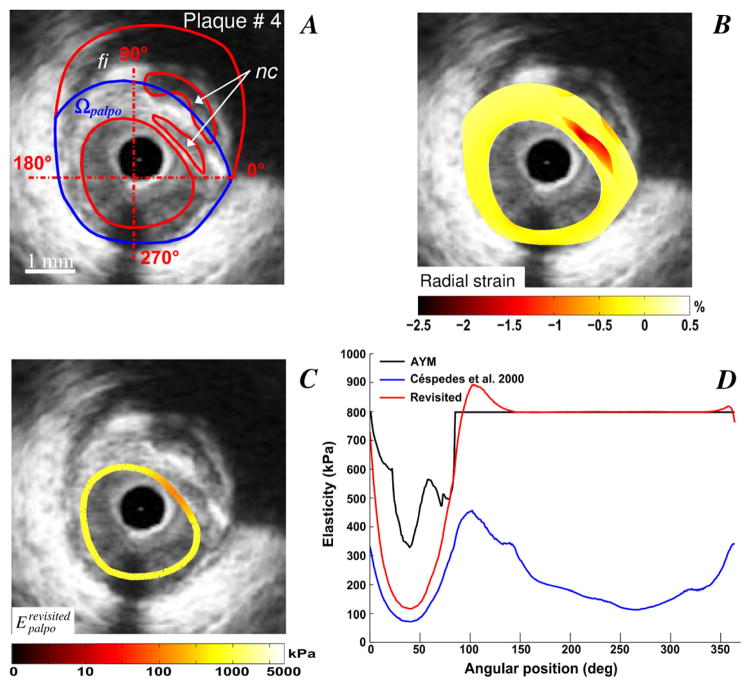
Detection of soft inclusions

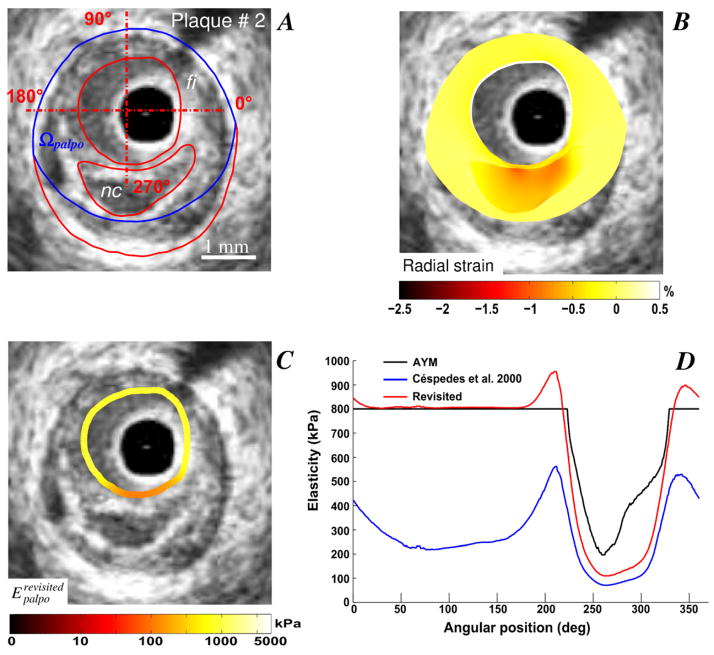
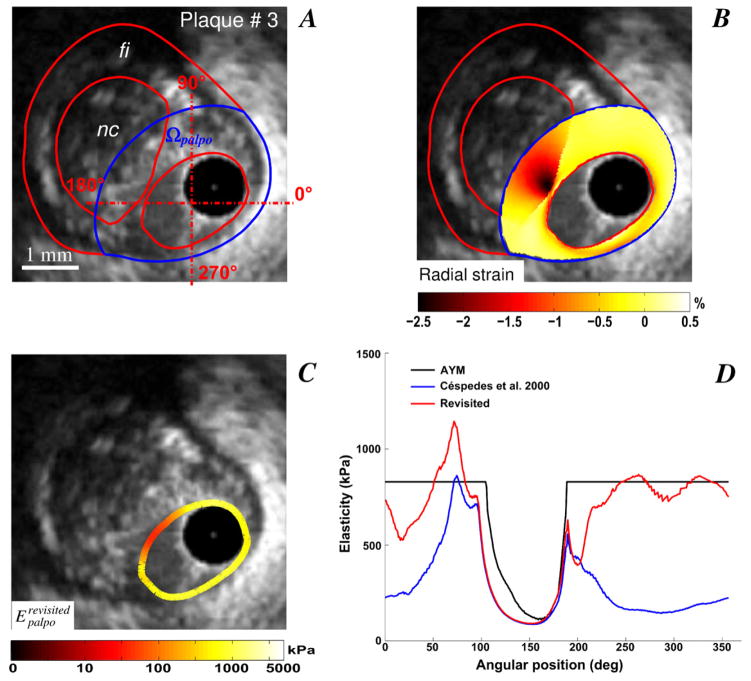
Improved S-SM palpograms obtained for VPs with one (plaques # 2 and 3, Figs. 2 and 3) and two (plaque # 4, Fig. 4) necrotic cores are presented. Necrotic core sites were accurately detected using the IE-PT. The amplitude of the revisited S-SM was found close to the Young’s modulus of the fibrosis (i.e close to 800 kPa) excepted at a soft inclusion locations, for which the S-SM amplitudes were found lower. Compared to the AYM amplitude, the S-SM values at the necrotic core locations were underestimated.

Figure 2.

Performance of the improved elasticity-palpography technique to detect a vulnerable plaque when the whole necrotic core is included in the palpography domain. A) IVUS image of plaque # 2 with plaque constituents (red contours, “nc”: necrotic core; “fi”: fibrous region). The boundaries of the palpography domain Ω_palpo are also given (blue contours). B) Radial strain-elastogram in the palpography domain. C) Computed improved stress-strain modulus (S-SM) palpogram. D) Comparisons between native S-SM of Céspedes et al. (2000), improved S-SM and averaged Young’s modulus (AYM) palpograms.

Figure 3.

Performance of the improved elasticity-palpography technique to detect a vulnerable plaque when only a part of the large necrotic core is included in the palpography domain. A) IVUS image. B) Radial strain. C) Improved S-SM palpogram. D) Comparisons between S-SM palpograms.

Figure 4.

Performance of the improved elasticity-palpography technique to detect a vulnerable plaque with two necrotic cores. A) IVUS image. B) Radial strain. C) Improved S-SM palpogram. D) Comparisons between S-SM palpograms.

Detection of vulnerable plaques with calcified inclusions

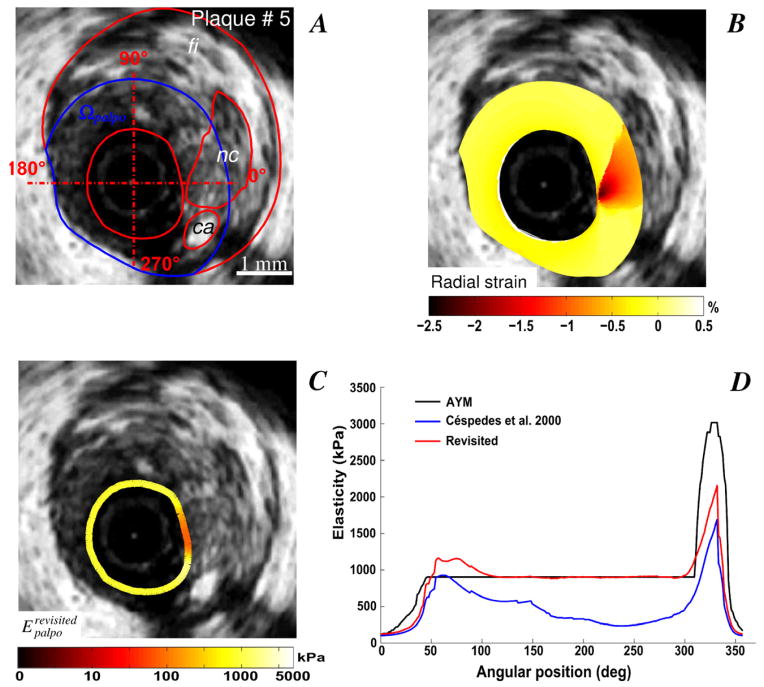
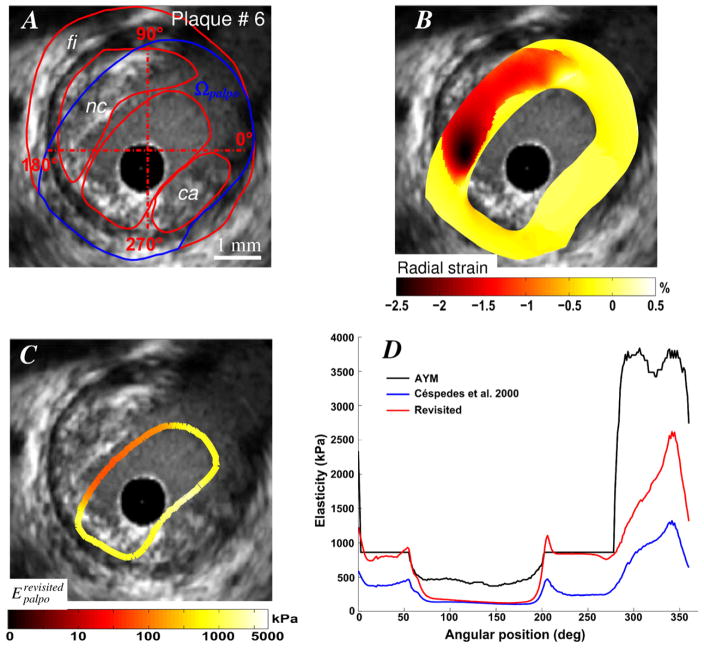
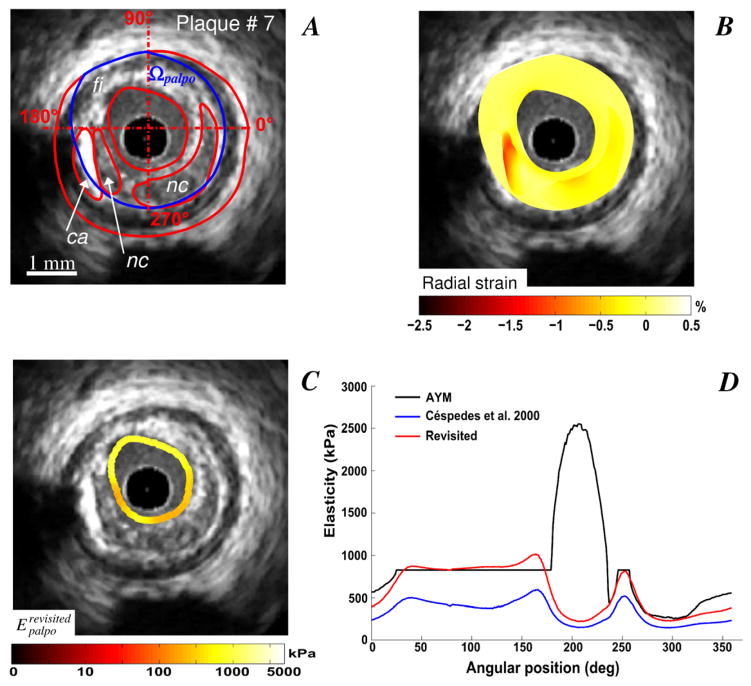
For two VP morphologies (plaques # 5 and 6) with isolated necrotic cores and calcified inclusions (Figs. 5 and 6), the IE-PT detected and differentiated the soft and hard inclusions. Compared to the AYM, the S-SM amplitudes at the calcified inclusion locations were underestimated by almost a factor two. Figure 7 illustrates the abilities of the proposed IE-PT to detect a complex VP (plaque # 7) with adjacent soft and hard inclusions located between 7 and 9 o’clock and one isolated large necrotic core located between 2 and 6 o’clock. The IE-PT successfully detected the isolated soft inclusion adjacent to the calcified area.

Figure 5.

Performance of the improved elasticity-palpography technique to detect a vulnerable plaque with a small calcified inclusion. A) IVUS image. B) Radial strain. C) Improved S-SM palpogram. D) Comparisons between S-SM palpograms.

Figure 6.

Performance of the improved elasticity-palpography technique to detect a vulnerable plaque with a large calcified area. A) IVUS image. B) Radial strain. C) Improved S-SM palpogram. D) Comparisons between S-SM palpograms.

Figure 7.

Performance of the improved elasticity-palpography technique to detect a vulnerable plaque with a small calcified inclusion adjacent to a necrotic core. A) IVUS image. B) Radial strain. C) Improved S-SM palpogram. D) Comparisons between S-SM palpograms.

Comparison between native and improved elasticity-palpography techniques

Our quantitative results demonstrated that the mean relative error of the stress-strain modulus decreased from 61.02±9.01% to 15.12±12.57% when considering the improved elasticity-palpography technique instead of the native (see Table 2). Simulations performed on plaque # 4 (Fig. 4) using the native palpography approach did not differentiate the geometrical effects induced by the shape of the VP to those generated by the mechanical properties of heterogeneous plaque (Fig. 4D). When using the E-PT of Céspedes et al. (2000), the S-SM amplitudes found along the plaque-free segment (i.e. between the angular positions 180 and 300 degrees, Figs. 4A and 4D) were found similar to those computed at plaque segment with necrotic cores (i.e. between 0 and 90 degrees, Figs. 4A and 4D). The IE-PT corrected for such geometric effects since the improved S-SM palpogram highlighted the soft inclusion site only. Similar results were found with all VPs considered in this study (see Figs. 2, 3 and 5).

Table 2.

Results of the mean relative errors (MR_error) made on the palpograms when considering either the native or the revisited elasticity-palpography techniques. The influence of white noise was studied using the vulnerable plaque # 2.

Plaque #	${MR}_{\mathit{error}}^{\mathit{palpo}\mathit{Cespedes}}$ (%)	${MR}_{\mathit{error}}^{\mathit{palpo}\mathit{revisited}}$ (%)
	w/o noise (β = 0)	w/o noise (β = 0)	with noise (β = 2)	with noise (β = 4)	with noise (β = 6)
1	48.97	0.00	-	-	-
2	60.82	11.43	4.70 ± 4.90	14.52 ± 12.46	26.18 ± 16.24
3	61.70	17.30	-	-	-
4	71.26	10.89	-	-	-
5	55.49	8.21	-	-	-
6	73.97	40.18	-	-	-
7	54.89	17.85	-	-	-
	61.02 ± 9.01	15.12 ± 12.57

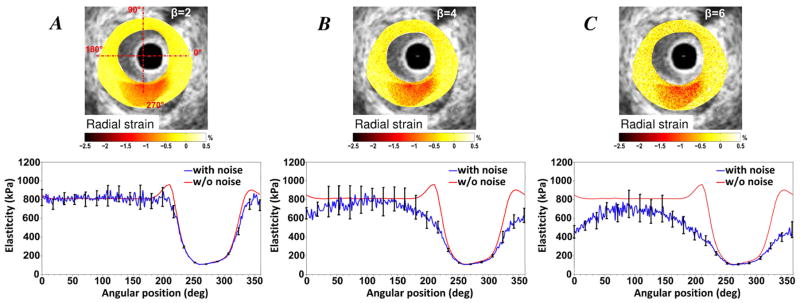
Influence of white noise on stress-strain modulus palpogram

The influence of noise was studied on the vulnerable plaque # 2 (Fig. 8 and Table 2). Based on the definition of the signal-to-noise ratio, we converted our white noise amplitude in dB-scale (see Appendix II). By applying such an approach on plaque # 2, we found that β = 2, 4 and 6 corresponds to noise levels of 13 dB, 7 dB and 3.4 dB, respectively. The robustness of the IE-PT when increasing the white noise level is shown in Fig. 8. According to the performed simulations, the IE-PT was still able to detect the soft inclusion site when introducing significant white noise (β = 6, Fig. 8C). We found that the mean relative error of the stress-strain modulus MR_error increased from 4.70±4.90% with a white noise of β = 2 to 26.18±16.24% with triple the white noise (β = 6) (Table 2).

Figure 8.

Results of the sensitivity analysis performed to investigate the influence of the white noise added to the strain field on the reconstructed improved stress-strain modulus (S-SM) palpogram. Plaque # 2 was used for this study. Row (1): Input radial strain fields obtained with different level of white noise (β=2, 4 and 6). Row (2): Resulting S-SM palpograms obtained with the improved elasticity-palpography technique.

DISCUSSION

A critical key in detection of VPs is the accurate quantification of both the morphology and the mechanical properties of the diseased arteries (Cheng et al. 1993; Finet et al. 2004). Such knowledge could lead to the development of specific therapy for prevention of acute thrombotic events (Libby 2001). Although several endovascular approaches have been implemented to approximate mechanical strain in vivo (de Korte et al. 2002; Kim et al. 2004; Maurice et al. 2007; Wan et al. 2001; Doyley 2012), the spatial plaque Young’s modulus has not yet been determined for ‘real time’ clinical use. Such elasticity map remains difficult to assess since the full inverse problem needs to be solved in continuum mechanics using sophisticated nonlinear mathematical optimization tools and complex procedures (Le Floc’h et al. 2009; Le Floc’h et al. 2010; Richards and Doyley 2011; Le Floc’h et al. 2012; Doyley 2012).

Céspedes et al. (2000) first proposed the E-PT which allows a fast wall stiffness quantification based on the arterial strain and blood pressure measurements. However, this technique suffers from major limitations because it has been developed for homogeneous, isotropic, quasi incompressible, circular and concentric atherosclerotic plaques, only. Therefore in the current study, the native palpography technique was successfully revisited and improved to account for complex plaque and arbitrary palpography domain geometries.

Our results showed clearly the performance of the revisited S-SM formulation which not only improved significantly the accuracy of the native S-SM palpogram, but more importantly, gave a physical meaning to the amplitude of the improved S-SM palpogram.

Has the revisited stress-strain modulus formulation significantly improved the palpography technique?

The native S-SM palpogram neglected the geometric effects induced by the anatomical shape of the atherosclerotic plaque and was derived assuming a circular palpography domain. When using the E-PT, the resulting S-SM values along the plaque-free segment of the atherosclerotic coronary artery were found to be lower than the averaged Young’s modulus amplitudes of the arterial wall. The native S-SM palpogram of plaque # 2 (Fig. 2D), shows such sites with low S-SM amplitudes located between the angular positions 50 and 150 degrees, Figs. 2A and 2C). The IE-PT corrects for such limitation as it account for real plaque and palpography domain geometries. Moreover, simulations performed on the idealized homogeneous lesion (plaque # 1, Fig. 1) clearly illustrate the advantage of considering the new approach. Indeed the exact solution was reached when using the revisited technique while the mean relative error was close to 49% when using the native technique (Table 2). The R-EP technique is less sensitive to geometric effects and can differentiate between plaque elasticity from apparent stiffness, which is dependent on the arterial wall thickness (Fig. 1).

Is the stress-strain modulus palpogram sufficient to detect vulnerable plaques?

The IE-PT is sufficient to detect and identify all VPs without calcified inclusions (see Figs. 2, 3 and 4). More interestingly, the IE-PT appears to be reliable enough to detect complex VPs with calcified inclusions (Figs. 5, 6 and 7). Let us point out that although both resulting S-SM palpograms of plaque # 7 (Fig. 7C), correctly identified the presence of the necrotic core even though a soft inclusion was adjacent to the calcified inclusion and increase the amplitude of the AYM at such site (i.e between the angular positions 180 and 240 degrees, Figs. 7A and 7D), only the R-EP technique was able to correct for the elasticity amplitudes at the plaque-free segment (i.e between the angular positions 30 and 180 degrees, Figs. 7A and 7D).

Is the revisited stress-strain modulus palpogram sufficient to diagnose the degree of stability of vulnerable plaques?

Fibrous cap thickness is often used by interventional cardiologists to diagnose the degree of VP instability. Recent studies (Ohayon et al. 2008; Cilla et al. 2012) have shown that other emergent biomechanical factors such as necrotic core thickness (rather than necrotic core area) and arterial remodeling index are also critical in determining plaque instability. The palpography technique does not permit direct measurements of such key morphologic determinants. Therefore, although the reliability of the IE-PT to detect VPs, this approach is not sufficient to diagnose the degree of stability of VPs.

Is there an optimal size for the palpography domain?

As mentioned previously, the main limitation of the native palpography technique is that we need to consider an optimal circular palpography domain to obtain accurate and reliable S-SM palpograms. Thus the native S-SM appears to be more adaptable for the detection of vulnerable concentric atherosclerotic lesions because its formulation was obtained assuming a cylindrical concentric plaque. The IE-PT may be viewed as an extension of the native formulation allowing the detection of eccentric VPs, which are very common (Glagov et al. 1987). Furthermore, the cardiologist has the flexiblity to choose any arbitrary endoluminal thick layer size and shape as the palpography domain.

Study limitations

A major limitation of this study was that our analysis was performed in the absence of residual strain. The effects of such residual strain have been investigated in an ex vivo study performed by Ohayon et al. (2007) with several human vulnerable coronary plaque samples. We found that residual strain was not negligible and affects mainly the peak cap stress amplitude in the thin fibrous cap. Therefore based on our previous findings, the absence of residual strain should not alter the characterization of the mechanical properties presented in this study, which was the ultimate goal.

A second study limitation was that our study was performed on a relatively small number of cases (n =7). Such atherosclerotic lesions were chosen to be representative of a larger population. Indeed, different necrotic core and calcified inclusion shapes were used to take into account a large variety of clinical cases. Nevertheless, further studies are needed to extend and strengthen the present findings.

Potential clinical implication

Stabilization of vulnerable plaque remains a significant clinical problem (Ylä-Yla-Herttuala et al. 2011; Abela et al. 2011). Studies conducted to analyze the structural variation in the fibrous cap and necrotic core with specific drug treatments (e.g., all statins, angiotensin converting enzyme inhibitors, etc…) revealed an enhancement in plaque stability (Libby et al. 2002; Nozue et al. 2012). As shown in one of our previous study (Finet et al. 2004), a very slight increase in the mechanical properties of plaque constituents, namely the hardening of the lipidic necrotic core, can tilt a VP from instability to stability. The proposed improved elasticity-palpography imaging technique is promising since it provides a non-invasive approach to analyze the evolution of the mechanical properties of atherosclerotic plaques during drug therapies.

APPENDIX I. Formulation of the native stress-strain modulus palpogram

Céspedes et al. (2000) defined the S-SM modulus as the ratio of the average radial stress over the average radial strain along the radial axis:

$$E_{\mathit{palpo}}(\theta )=\frac{\left|{\int }_{R_i(\theta )}^{R_p(\theta )}{\sigma }_{rr}(r,\theta )dr\right|}{\epsilon (\theta )}$$ (A1)

where ε(θ) is the average radial strain (given by Eq. 1b), σ_rr(r,θ) is the radial stress component, and R_i(θ) and R_p(θ) are the non constant inner and outer radii of the palpography domain (Ω_palpo), respectively.

Let us assume that the artery is a thick-walled cylinder (with inner and outer radii R_i and R_o, respectively), isotropic, homogeneous, incompressible, linearly elastic (with Young’s modulus E), submitted to uniform pressure (ΔP) on the inner boundary r = R_i and zero pressure on the outer boundary r = R_o. By assuming plane strain condition and by considering a concentric circular palpography domain Ω_palpo (with R_i ≤ r ≤ R_p), the spatial distribution of the local S-SM (given by Eq. A1) becomes constant through Ω_palpo and equal to:

$$E_{\mathit{palpo}}^{\text{cylinder}}=\frac{\mathrm{\Delta }P\left|{\int }_{R_i}^{R_p}g(r)dr\right|}{\epsilon }$$ (A2)

$$\text{with}\epsilon =\frac{3}{2E}\frac{{\alpha }_o^2}{{\alpha }_{\mathrm{p}}({\alpha }_o^2-1)}\mathrm{\Delta }\mathrm{P}\text{and}{\int }_{R_i}^{R_p}g(r)dr=\frac{({\alpha }_o^2-{\alpha }_p)}{{\alpha }_p({\alpha }_o^2-1)}$$ (A3a,b)

where the constant ε is the absolute value of the compressive average radial strain (with amplitude given by Eq. A3a), α_o and α_p are the relative thicknesses of the arterial wall and of the palpography domain Ω_palpo, respectively (α_o = R_o/R_i and α_p = R_p/R_i). The spatial function g(r) is a correcting shape function which account for the geometry of the thick-walled cylindrical artery. For a specific circular palpography domain only (i.e. when $R_p=[2{\alpha }_o^2/({\alpha }_o^2+1)]R_i$), the amplitude of the uniform local S-SM becomes:

$$E_{\mathit{palpo}}^{\text{cylinder}\ast }=\frac{\mathrm{\Delta }P/2}{\epsilon }$$ (A4)

It is interesting to note that this S-SM (i.e. $E_{\mathit{palpo}}^{\text{cylinder}\ast }$) is not the Young’s modulus E of the isotropic concentric plaque since by substituting Eq. (A3a) into Eq. (A4) we obtain the following relationship:

$$E_{\mathit{palpo}}^{\text{cylinder}\ast }=\frac{1}{3}\frac{{\alpha }_{\mathrm{p}}({\alpha }_o^2-1)}{{\alpha }_o^2}E$$ (A5)

An exact analytical S-SM formula is difficult to derive for heterogeneous, eccentric and complex plaque geometries. Céspedes et al. (2000) were inspired by the simplified S-SM solution obtained for a thick-walled cylindrical vessel (Eq. A4) to propose their S-SM approximation given by Eq. (1a).

APPENDIX II. Converting our white noise in decibel (dB)

To find a correspondence between the imposed white noise and the signal-to-noise ratio SNR (unit: dB) we used the following relationship:

$$\text{SNR}=10{log}_{10}\left(\frac{{\mathrm{A}}_{\text{signal}}^2}{{\mathrm{A}}_{\text{noise}}^2}\right)$$ (B1)

where A_signal and A_noise are the signal and noise amplitudes, respectively. We identified the signal amplitude A_signal to the mean spatial strain amplitude free of noise. Moreover, in our study, we used the following normal distribution of noise A_noise with zero mean and standard deviation σ(r,θ) = (aε_rr(r,θ) + b)β where a = 0.2%, b= 0.04% and β varies from 2 to 6 (Baldewsing et al. 2005; Le Floc’h et al. 2009):

$${\mathrm{A}}_{\text{noise}}(\mathrm{r},\theta )=\text{Normal}\left(0,\sigma {(\mathrm{r},\theta )}^2\right)$$ (B2)

By considering these two expressions of A_signal and A_noise we found:

$$\text{SNR}=10{log}_{10}\left(\frac{{\displaystyle \sum _{\mathrm{r},\theta }}{[{\epsilon }_{\text{rr}}(\mathrm{r},\theta )]}^2}{{\displaystyle \sum _{\mathrm{r},\theta }}{[{\mathrm{A}}_{\text{noise}}(\mathrm{r},\theta )]}^2}\right)$$ (B3)