The Society of Thoracic Surgeons Congenital Heart Surgery Database Mortality Risk Model: Part 1—Statistical Methodology

Abstract

Background

This study’s objective was to develop a risk model incorporating procedure type and patient factors to be used for case-mix adjustment in the analysis of hospital-specific operative mortality rates after congenital cardiac operations.

Methods

Included were patients of all ages undergoing cardiac operations, with or without cardiopulmonary bypass, at centers participating in The Society of Thoracic Surgeons Congenital Heart Surgery Database during January 1, 2010, to December 31, 2013. Excluded were isolated patent ductus arteriosus closures in patients weighing less than or equal to 2.5 kg, centers with more than 10% missing data, and patients with missing data for key variables. Data from the first 3.5 years were used for model development, and data from the last 0.5 year were used for assessing model discrimination and calibration. Potential risk factors were proposed based on expert consensus and selected after empirically comparing a variety of modeling options.

Results

The study cohort included 52,224 patients from 86 centers with 1,931 deaths (3.7%). Covariates included in the model were primary procedure, age, weight, and 11 additional patient factors reflecting acuity status and comorbidities. The C statistic in the validation sample was 0.858. Plots of observed-vs-expected mortality rates revealed good calibration overall and within subgroups, except for a slight overestimation of risk in the highest decile of predicted risk. Removing patient preoperative factors from the model reduced the C statistic to 0.831 and affected the performance classification for 12 of 86 hospitals.

Conclusions

The risk model is well suited to adjust for case mix in the analysis and reporting of hospital-specific mortality for congenital heart operations. Inclusion of patient factors added useful discriminatory power and reduced bias in the calculation of hospital-specific mortality metrics.

The Society of Thoracic Surgeons Congenital Heart Surgery Database (STS-CHSD) began collecting data in 1994 as a quality improvement initiative for congenital cardiac surgeons and hospitals. Participants in the STS-CHSD receive confidential feedback reports comparing each center’s outcomes to the national experience. A key requirement for such feedback reporting is to account for differences in the mix of patients treated at each center by implementing an appropriate case-mix adjustment procedure [1].

For the last several years, mortality reporting in the STS-CHSD has adjusted for a relatively small number of case-mix factors, namely age, weight, and categories of procedural risk, as defined by STS—European Association for Cardio-Thoracic Surgery (EACTS) Congenital Heart Surgery (STAT) Mortality Categories [2, 3]. Because of the increased availability of robust clinical data, it is now possible to develop a more detailed risk model, with adjustment for individual procedure types and for a variety of specific patient characteristics [4].

This report describes the development of the 2014 STS-CHSD Mortality Risk Model for Congenital Cardiac Surgery, which was derived from empirical data and includes adjustment for procedure type and patient factors. The model applies to patients of all ages undergoing operations for congenital heart disease and is intended to facilitate the assessment of mortality outcomes across the entire range of a center’s case mix.

Material and Methods

General Approach

The objective of the study was to develop an operative mortality risk model incorporating procedure type and patient factors to adjust for case mix in the analysis of congenital cardiac surgical outcomes. A working group consisting of statisticians, cardiologists, and cardiac surgeons provided input for the choice of risk factors and the specification of an appropriate statistical model. Coefficients of the final model will be reestimated on a rolling basis to ensure it remains well calibrated for its intended use in the STS-CHSD participant feedback report.

Data Source

The STS-CHSD contains detailed clinical data on more than 300,000 pediatric and congenital cardiac operations since 1998 and currently includes information from 114 participating centers. Data from all pediatric and congenital heart operations at participating centers are transferred to the STS data warehouse hosted by the Duke Clinical Research Institute. Data quality and reliability are ensured through a series of edit checks performed by the Duke Clinical Research Institute during data harvest and through a formal process of site visits and data audits [5]. The Duke University Health System Institutional Review Board approved the study and provided a waiver of informed consent. Although the STS data used in the analysis contain patient identifiers, the data were originally collected for nonresearch purposes, and the risk to patients was deemed to be minimal [6].

End Point

The outcome for this study was operative mortality, defined as death during the hospitalization in which the operation was performed or after discharge but within 30 days of the operation. The rationale for this definition and detailed rules for its application have been published by the STS and the Joint EACTS–STS Congenital Database Committee [7–9].

Cohort Selection

The model’s target population includes patients of all ages undergoing a congenital cardiac operation with or without cardiopulmonary bypass. The 188 types of cardiac procedures that have been designated for mortality reporting in the STS-CHSD feedback report were eligible for the present study [10]. All cardiac operations performed between January 1, 2010, and December 31, 2013, with data collected using the STS version 3.0 data collection form, were initially selected, comprising 98,885 records from 113 centers. The timeframe was chosen to coincide with version 3.0 of the STS data collection form, which added several key patient factors to the STS-CHSD beginning in 2010.

Data from 27 centers with more than 10% missing data on key STS variables were excluded, resulting in the loss of 29,238 records. From the remaining 86 centers, we excluded 11,480 operations occurring after the index operation of each hospitalization, 3,400 operations for patent ductus arteriosus closure in patients weighing 2.5 kg or less, 1,302 operations that could not be assigned to one of the 188 procedure types analyzed in the mortality section of the STS-CHSD feedback report, 937 operations with missing operative mortality status, and 304 operations with missing or invalid data in other key fields, including age, sex, and weight. The final study population included 52,224 records from 86 centers. The first 42 months were used to determine the form of the model and estimate regression coefficients (development sample: n = 44,956 records) and the last 6 months were used for assessing the model’s discrimination and calibration (validation sample: n = 7,268 records).

Assignment of Primary Procedure

The procedures performed during each operation are described in the STS database by using a list of procedure identification codes adapted from the International Pediatric and Congenital Cardiac Code [11, 12]. Among 52,224 operations in the study database, 20,549 operations (39%) involved 1 procedural code and 31,675 (61%) involved 10,862 different combinations of 2 or more procedural codes.

Because estimating the risk for this many unique procedure combinations is not possible, we used an existing algorithm to map combinations of individual procedural codes to the list of 188 distinct primary procedures [13]. According to the algorithm, the primary procedure of an operation is the procedure code associated with the highest STAT Score. Exceptions to this rule are incorporated to allow the analysis of procedures without a STAT Score and to account for procedure combinations for which the component procedure with the highest STAT Score is regarded as a poor reflection of the operation’s actual risk.

Candidate Covariates

Candidate covariates for case-mix adjustment were selected by a group of cardiologists and surgeons after reviewing the STS data collection form, prior STS exploratory analyses, and relevant literature. All candidate variables available in version 3.0 of the STS data collection form were individually assessed from the standpoint of data quality, risk factor prevalence, and precise data definitions.

Potentially relevant preprocedural variables in the STS version 3.0 database are collected under the category headings of demographics, noncardiac congenital anatomic abnormalities, chromosomal abnormalities, syndromes, hospitalization, preoperative factors, diagnosis, and procedure. For screening variables in the preoperative factors category, risk factors were considered for inclusion if their prevalence was at least 2% of the study sample or if the number of deaths among affected patients was at least 20 in any one or more of four age groups in a prior analysis using STS data from 2010 to 2012 [4]. From a list of 12 risk factors meeting this criterion, the factors chosen because of their strong association with outcomes were preoperative/preprocedural mechanical circulatory support, shock persistent at the time of the operation, renal dysfunction or renal failure requiring dialysis (or both), mechanical ventilation to treat cardiorespiratory failure, preoperative neurological deficit, and the presence of any other STS-defined preoperative factor not listed above.

In addition to these variables from the preoperative factors category, the other variables considered on the basis of potential prognostic importance were primary procedure, STAT Category, age, sex, weight, prematurity (birth at <37 weeks’ gestation), prior cardiothoracic operation, presence of any STS-defined noncardiac anatomic abnormality, and presence of any STS-defined chromosomal abnormality or syndrome.

All variables screened for inclusion were retained in the final model. Continuous covariates (age and weight) were modeled as piecewise linear functions with different slope parameters within 4 age groups: neonates (0 to 30 days), infants (31 days to 1 year), children (>1 year but <18 years), and adults (≥18 years). Terms representing the effect of weight on mortality in children and adults were nonsignificant (p > 0.40) and were removed from the model (see the online Supplement for details).

Accounting for Type of Operation

Since 2012, procedural stratification in the STS-CHSD has been based on the STAT Mortality Categories [2, 3]. Briefly, the STAT system assigns operations to 1 of 5 categories on the basis of a similar risk of in-hospital mortality, where category 1 has the lowest risk of death and category 5 has the highest. Details of the STAT Mortality Category assignment are described in the online Supplement and the STS Web site.

The STAT Categories outperform a number of similar procedural stratification methods [2] but have at least two limitations. First, although the STAT Categories were designed to be maximally homogeneous with respect to estimated mortality risk, there is still residual variation in risk across procedures within the same category. Theoretically, if risk differs across procedures in a category, and the mix of procedures differs across hospitals, then it is possible for mortality comparisons across hospitals to be biased. This same limitation would also apply to Risk Adjustment for Congenital Heart Surgery (RACHS-1) [14] categories and, indeed, to any other scheme that involves categorizing operations into a small number of groups.

The second issue is more subtle and statistical. Although STAT Categories were optimal according to an objective statistical criterion, the analysis was not adjusted for covariates, and so the categories may not be optimal for the specific purpose of multivariable modeling. In other words, there may be an opportunity to improve the existing STAT methodology by modeling individual procedure-specific relative risks simultaneously while adjusting for covariates.

Accordingly, two approaches were considered for modeling variation in covariate-adjusted risk across individual primary procedures. Approach 1 involved estimating a separate intercept parameter for each individual primary procedure. Approach 2 involved estimating a separate intercept parameter for each stratum defined by the combination of age group × primary procedure. Approach 2 was motivated by an exploratory analysis that revealed a statistically and clinically important interaction of age × STAT Category and by the belief that a similar age × procedure interaction could exist when analyzing individual primary procedures. Ultimately, approach #2 was selected after developing models using each approach and comparing their performance in the development sample.

Owing to the large number of primary procedures with small sample sizes, estimating procedure-specific intercept parameters using conventional methods was not feasible. Instead, estimation was accomplished using a statistical technique known as empirical Bayes [15]. Briefly, empirical Bayes estimators (also known as shrinkage estimators) use data from the entire ensemble of procedures when estimating the risk for any single procedure. Heuristically, the empirical Bayes estimate for a given procedure is a weighted average of the procedure’s actual observed risk and a model-based estimate of the procedure’s risk derived by borrowing data from other procedures. The model weights an individual procedure’s own data more heavily when the procedure-specific sample size is large enough to be reliable and weights the model-based prediction more heavily when the procedure-specific sample size is too small to be reliable.

To further enhance precision, main effects for STAT Categories were included in the regression model. As a result of including STAT Categories, each procedure’s estimated risk was heuristically a weighted average of its actual observed risk and an empirically derived prediction based on other procedures from the same STAT Category. Estimation was performed using the GLIMMIX procedure in SAS software (SAS Institute Inc, Cary, NC) [16] (see the online Supplement for details).

Missing Data

Variables used for analysis were highly complete as a result of excluding hospitals with frequent missing data and excluding records with missing operative death, age, sex, or weight. Variables with the most missing data were prematurity among infants and neonates (missing 1.2%), prior cardiothoracic operation (missing 0.6%), and any noncardiac congenital anatomic abnormality (missing 0.5%). All other variables were missing in less than 0.5% of records. To retain records with missing data in the analysis, missing binary risk factors were imputed to their most common value. More sophisticated missing data methods, such as multiple imputation, were not used because of the low rate of missing data and because these computationally intensive methods had minimal effect when applied to other STS risk models.

Assessment of Model Discrimination and Calibration

Before the model was used to calculate hospital-specific mortality metrics, its calibration was assessed by comparing observed versus expected mortality rates within subgroups of patients based on deciles of predicted risk. We also assessed discrimination by calculating the C statistic (also known as the area under the receiver operating characteristics curve). The C statistic quantifies the ability of a classification algorithm to separate the target population into groups of patients that will and will not have the end point of interest. A low C statistic does not imply that the model is misspecified or that hospital comparisons will be biased [17]. Nonetheless, the C statistic is widely reported and may serve as a benchmark for comparing alternative models for the same end point in the same target population.

Calculation of Hospital-Specific Mortality Metrics

After finalizing the model, the method of indirect standardization was used to calculate each hospital’s O/E mortality ratio using all 4 years of data. To perform this calculation, each hospital’s expected number of deaths was obtained by summing the predicted probability of death according to the model across all patients at the hospital who met the study’s inclusion and exclusion criteria. The O/E ratio was then calculated as O/E = (observed number of deaths)/(expected number of deaths). A 95% confidence interval (CI) for the O/E ratio was calculated by treating the observed number of deaths as a binomial random variable and treating the expected number of deaths as constant.

An O/E ratio exceeding 1.0 implies that the hospital had more deaths than was expected in light of the hospital’s case mix, whereas an O/E ratio of less than 1.0 implies that the number of deaths was fewer than expected in light of the hospital’s case mix. Hospitals were classified as having lower-than-expected mortality if their 95% CI for the O/E fell entirely below 1, as having higher-than-expected mortality if their 95% CI for the O/E fell entirely above 1, and as having same-as-expected mortality if their 95% CI for the O/E overlapped 1.

Comparison With Simpler Models

To provide context for interpreting the model’s performance and to illustrate the effect of including new risk factors, the discrimination of the final proposed model was compared with 4 simpler models:

• Model 1 included only STAT Categories.

• Model 2 included STAT Categories plus age and weight.

• Model 3 included all variables in the final proposed model, except that the adjustment for procedure type was based on STAT Categories rather than individual primary procedures.

• Model 4 included individual primary procedures but excluded patient factors other than age and weight.

Assessment of model discrimination was based on the validation sample after estimating coefficients in the development sample. Finally, to assess whether the choice of model had a substantial effect on hospital performance results, we computed hospital-specific O/E ratios and 95% CIs using each model in the overall 4-year sample and compared the results.

Sensitivity Analyses

Sensitivity analyses were performed to assess whether inferences about hospital performance were affected by our choice of statistical methodology. First, we assessed how much hospital O/E ratios would change if records with missing mortality status had been imputed rather than excluded. Second, for calculating hospital-specific O/E ratios in the subgroup of pediatric patients, we assessed how much these O/E ratios would change if the risk model had been estimated with adult patients excluded (see the online Supplement for details).

Results

The final study population included 52,224 index operations from 86 centers with 1,931 deaths (3.7%). Records from 27 centers excluded due to more than 10% missing data were generally similar to the study cohort, having similar proportions of neonates (20.9% vs 21.3%), STAT Category 5 operations (4.7% vs 5.0%), and operative deaths (3.4% vs 3.7%). Table 1 reports the characteristics of the study population and summarizes univariable associations between each candidate risk factor and mortality. As expected, operative mortality increased with decreasing age, lower weight, higher STAT Category, prior operations, prematurity, and comorbidities. Neonates comprised 21% of the population but accounted for 58% of deaths.

Table 1.

Distribution of Patient Covariates and Univariable Associations With Mortality^a

Risk Factor	Records No.	Deaths No. (%)	OR (95% CI)	p Value
Age group
Neonates	11,144	1,129 (10.1)	(Reference)
Infants	18,554	564 (3.0)	0.28 (0.25–0.31)	<0.0001
Children	18,407	167 (0.9)	0.08 (0.07–0.10)	<0.0001
Adults	4,119	71 (1.7)	0.16 (0.12–0.20)	<0.0001
Sex
Male	28,326	1,041 (3.7)	(Reference)
Female	23,898	890 (3.7)	1.01 (0.93–1.11)	0.77
Weight
>10th percentile for age group	47,154	1,545 (3.3)	(Reference)
<10th percentile for age group	5,070	386 (7.6)	2.43 (2.17–2.73)	<0.0001
Prematurity among neonates and infants
No	23,908	1,208 (5.1)	(Reference)
Yes	5,447	473 (8.7)	1.79 (1.60–2.00)	<0.0001
STAT Level
1	15,439	103 (0.7)	(Reference)
2	15,275	234 (1.5)	2.32 (1.84–2.92)	<0.0001
3	6,482	190 (2.9)	4.50 (3.53–5.72)	<0.0001
4	12,408	944 (7.6)	12.26 (9.99–15.05)	<0.0001
5	2,620	460 (17.6)	31.71 (25.49–39.45)	<0.0001
Prior cardiothoracic operation
No	37,614	1,536 (4.1)	(Reference)
Yes	14,314	386 (2.7)	0.65 (0.58–0.73)	<0.0001
Any noncardiac congenital anatomic abnormality
No	50,397	1,777 (3.5)	(Reference)
Yes	1,552	139 (9.0)	2.69 (2.25–3.22)	<0.0001
Chromosomal abnormality or syndrome
No	39,975	1,254 (3.1)	(Reference)
Yes	12,099	672 (5.6)	1.82 (1.65–2.00)	<0.0001
Preoperative variables
Mechanical circulatory support
No	51,798	1,851 (3.6)	(Reference)
Yes	283	72 (25.4)	9.21 (7.02–12.08)	<0.0001
Shock at the time of operation
No	51,608	1,785 (3.5)	(Reference)
Yes	473	138 (29.2)	11.50 (9.38–14.10)	<0.0001
Renal dysfunction or Renal failure requiring dialysis (or both)
No	51,504	1,806 (3.5)	(Reference)
Yes	577	117 (20.3)	7.00 (5.68–8.62)	<0.0001
Mechanical ventilator support
No	47,213	1,158 (2.5)	(Reference)
Yes	4,868	765 (15.7)	7.42 (6.73–8.17)	<0.0001
Neurological deficit
No	51,342	1,870 (3.6)	(Reference)
Yes	739	53 (7.2)	2.04 (1.54–2.71)	<0.0001
Any other preoperative factor
No	39,216	1,084 (2.8)	(Reference)
Yes	12,865	839 (6.5)	2.45 (2.24–2.69)	<0.0001

^aFrequency of missing data: prematurity among infants and neonates, 343 of 29,698 (1.2%); prior cardiothoracic operation, 296 of 52,224 (0.6%); noncardiac congenital anatomic abnormality, 275 of 52,224 (0.5%); chromosomal abnormality or syndrome, 150 of 52,224 (0.3%); preoperative factors, including mechanical circulatory support, renal dysfunction or renal failure requiring dialysis (or both), mechanical ventilator support, neurological deficit, and other preoperative factors, 143 of 52,224 (0.3%). All other covariates were 100% complete because patients with missing data were excluded.

CI = confidence interval;

OR = odds ratio.

Covariates in the final model included primary procedure, age, weight among infants and neonates, prior cardiothoracic operation, any noncardiac congenital anatomic abnormality, any chromosomal abnormality or syndrome, prematurity (in neonates and infants), preoperative/preprocedural mechanical circulatory support, shock persistent at the time of the operation, renal dysfunction or renal failure requiring dialysis (or both), mechanical ventilation to treat cardiorespiratory failure, preoperative neurological deficit, and any other preoperative factor. As discussed above, the model used an empirical Bayes estimation technique to adjust for strata defined by the combination of age group × primary procedure and also included STAT Categories to enhance estimation of procedure-specific intercept parameters.

The multivariable association between each model covariate and operative mortality based on the final model is summarized in Table 2. Odds ratios for binary risk factors ranged from 1.35 for the presence of a noncardiac abnormality to 4.27 for preoperative mechanical circulatory support. As expected, mortality risk decreased with increasing age and weight and increased across increasing STAT Categories.

Table 2.

Estimated Odds Ratios and 95% Confidence Intervals From the Final Risk Adjustment Model

Variable	OR (95% CI)	p Value
Age in neonates, per week	0.88 (0.81–0.95)	0.0010
Age in infants, per month	1.05 (0.99–1.11)	0.0796
Age in children, per year	1.00 (0.97–1.03)	0.7886
Age in adults, per year	1.04 (1.02–1.05)	<0.0001
STAT Category 2 vs 1	1.75 (1.24–2.46)	0.0013
STAT Category 3 vs 1	2.49 (1.69–3.68)	<0.0001
STAT Category 4 vs 1	5.14 (3.72–7.11)	<0.0001
STAT Category 5 vs 1	11.40 (7.17–18.14)	<0.0001
Weight in neonates, per 1-kg increase	0.58 (0.51–0.65)	<0.0001
Weight in infants, per 1-kg increase	0.71 (0.65–0.78)	<0.0001
Prior cardiothoracic operation	1.50 (1.27–1.78)	<0.0001
Any noncardiac congenital anatomic abnormality	1.35 (1.09–1.66)	0.0056
Any chromosomal abnormality or syndrome	1.57 (1.40–1.77)	<0.0001
Prematurity (in neonates and infants)	1.39 (1.20–1.60)	<0.0001
Preoperative/preprocedural mechanical circulatory support	4.27 (3.03–6.03)	<0.0001
Shock, persistent at time of operation	3.15 (2.46–4.03)	<0.0001
Renal dysfunction or Renal failure requiring dialysis (or both)	2.12 (1.64–2.73)	<0.0001
Mechanical ventilation to treat cardiorespiratory failure	2.11 (1.88–2.37)	<0.0001
Preoperative neurological deficit	1.91 (1.38–2.65)	<0.0001
Any other preoperative factor	1.61 (1.44–1.80)	<0.0001

CI = confidence interval;

OR = odds ratio.

Figure 1 displays observed versus expected mortality rates across deciles of predicted risk in the validation sample. Supplementary Figures S1 and S2 display observed versus expected mortality rates across deciles of predicted risk within subgroups defined by age group and STAT Mortality Category. Agreement between observed and expected rates was generally excellent, with a slight tendency to overpredict mortality risk in the highest decile.

Fig 1.

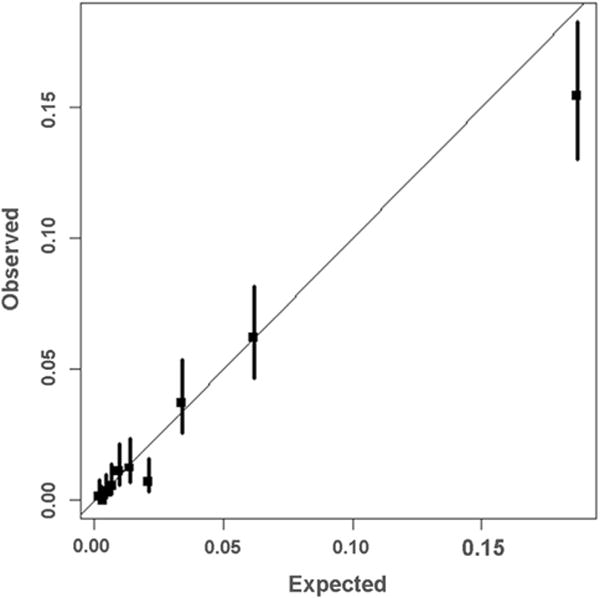
Model calibration in the validation sample. This figure displays observed vs predicted mortality estimates (and the 95% confidence interval) for 10 equally sized groups of patients ordered from lowest to highest risk in the validation sample. Perfect calibration is represented by the 45-degree line.

The C statistic for discrimination in the validation sample was 0.858. For comparison, Table 3 presents C statistics for the final model and 4 other models that were considered as possible candidate models or were calculated for evaluating the final model. As presented in Table 3, the C statistic in the validation sample for a model only adjusting for STAT Categories was 0.787. This C statistic increased to 0.817 when age and weight were added to the model and increased to 0.852 when all risk factors in the final model except primary procedure were added. For comparison, a model with STAT + age + weight + primary procedure (but no other patient-related factors) had a C statistic of 0.831. Of all the models considered, the final selected model had the highest C statistic of 0.858.

Table 3.

Comparison of Model Discrimination (C Statistics) for Alternative Risk Adjustment Models

Model	Covariates	C Statistic
		Development Sample	Validation Sample
1	STAT Levels	0.772	0.787
2	STAT Levels + age and weight	0.818	0.817
3	STAT Levels + age and weight + patient factors	0.862	0.852
4	Primary procedure + age and weight	0.846	0.831
Final	Primary procedure + age and weight + patient factors	0.875	0.858

To further illustrate the effect of adjusting for new patient factors on hospital performance results, we computed hospital-specific O/E ratios and 95% CIs in the overall study sample using the new risk model (which includes new patient factors) and computed these metrics again using model 4 (which excluded these new patient factors). As shown in Figure 2, the exclusion of additional patient factors had a noticeable effect on point estimates of O/E ratios. When each hospital’s O/E ratio based on model 4 was compared with its O/E ratio based on the final model, the O/E ratios differed by a factor ranging from 0.58 to 1.79 (ie, 42% less to 79% more).

Fig 2.

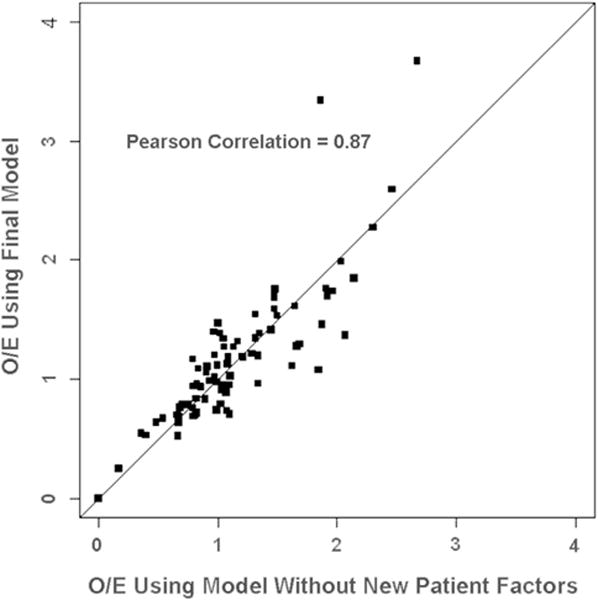
Comparison of hospital observed-to-expected (O/E) ratios calculated using models with and without adjustment for new patient factors. The O/E mortality ratio was calculated as O/E = (observed number of deaths)/(expected number of deaths) for each hospital using a model without patient factors and using a model that included patient factors (final model). Perfect agreement is represented by the 45-degree line.

Furthermore, when hospitals were classified as having lower-than-expected, higher-than-expected, or same-as-expected mortality based on their 95% CI for the O/E ratio, the choice of model mattered. As reported in Table 4, 12 of 86 hospitals (14%) changed categories when model 4 was used in place of the final model.

Table 4.

Cross Tabulation of the Number of Hospitals in Each Mortality Performance Category When Using Models With and Without Adjustment for New Patient Preoperative Factors^a

		Final Model—Includes New Patient Factors
		Higher-Than-Expected Mortality	Same-as-Expected Mortality	Lower-Than-Expected Mortality
Model 4—–Excludes New Patient Factors	Higher-Than-Expected Mortality	8 hospitals	4 hospitals	0 hospitals
	Same-as-Expected Mortality	4 hospitals	61 hospitals	2 hospitals
	Lower-Than-Expected Mortality	0 hospitals	2 hospitals	5 hospitals

^aSee Methods for details.

Sensitivity Analyses

Although records with missing mortality status were excluded from the analysis, a sensitivity analysis was conducted to assess the effect of including these records and imputing mortality status to “alive.” As shown in Supplementary Figure S3, the O/Es calculated with missing mortality excluded vs imputed were nearly identical (Pearson correlation = 0.999).

To assess whether the inclusion of adult patients affected the model’s ability to accurately adjust outcomes of pediatric patients, we performed a sensitivity analysis by reestimating the final model with adult patients excluded. As shown in Supplementary Figure S4, O/E ratios calculated in the subgroup of pediatric patients were nearly identical, regardless of whether adult patients were included or excluded from the estimation of the model (Pearson correlation ≈ 1.0).

Comment

We have described the development, validation, and preliminary results of a new operative mortality risk model for congenital cardiac operations that was created to facilitate outcomes analysis for participants in the STS-CHSD. The model estimates risk for each combination of primary procedure and age group and also adjusts for 12 patient-related variables, including prior operations, comorbidities, and markers of acuity. The model shows good calibration and discrimination, with a C statistic of 0.86, when evaluated in a separate validation sample. Candidate risk models with fewer risk factors exhibited lower discrimination and were also less suited to remove bias from case mix.

One of the strengths of the proposed STS risk model is the method of adjusting for procedural case mix. By adjusting for individual primary procedures, the proposed STS-CHSD model accomplishes a procedural adjustment that is even more granular than STAT Categories. A novel application of empirical Bayes shrinkage estimation was incorporated to account for procedures with small denominators. The estimation procedure also incorporated information from the previously published STAT Categories to facilitate borrowing of information across procedures in the same STAT Category. By including the STAT Category as a main effect and treating the primary procedure × age group combination as random effects, this strategy allowed the model to derive discriminatory power from the STAT Categories without assuming that all procedures within the same STAT Category have identical risk.

In conventional model-based indirect standardization, estimation of provider performance is a two-step procedure that involves first developing a model to predict risk as a function of patient baseline factors and then comparing each provider’s outcomes to the expected rate predicted by the model (ie, by calculating an O/E ratio). An alternative approach, known as hierarchical modeling, involves estimating each provider’s performance simultaneously in a single regression model. The magnitude of between-provider variation in outcomes is estimated while also simultaneously estimating and adjusting for the effect of patient case-mix factors. A fully Bayesian hierarchical model was developed and reviewed by the modeling committee in the course of developing the final STS-CHSD model. The two-stage approach was chosen on the grounds that conventional O/E ratios were more likely to be understood and accepted by the users and consumers of the STS-CHSD feedback report.

The major intended application of the STS risk model is to provide case-mix adjusted mortality metrics for STS-CHSD participants. The model appears to be well suited for this purpose, but there are a number of important limitations and caveats. First, due to the wide heterogeneity of diagnoses and procedures, there is a potential for information loss when only a single summary measure, such as an O/E ratio, is reported. For example, a hospital performing congenital cardiac operations might have lower-than-expected mortality for relatively low-risk simple operations but higher-than-expected mortality for relatively high-risk or complex operations. From the patient’s perspective, a patient would likely prefer the hospital with the best outcomes for that patient’s particular condition. This information is lost when only a single summary is reported. To partially address this limitation, the STS-CHSD feedback report provides separate O/E ratios for subgroups defined by age and STAT Category. An alternative potential strategy would involve reporting outcomes separately for selected individual high-volume procedures. Unfortunately, previous sample size calculations based on STS-CHSD data suggest that few individual procedures would be feasible to analyze [18].

Second, although the model adjusts for several specific patient factors, a large number of potentially important factors were not considered for inclusion. As the number of records in the database grows, the model will be able to be expanded to adjust for an increasing number of such preoperative factors.

Third, regression models make a variety of assumptions that may not be satisfied. For example, the model implicitly assumes that the odds ratio for each binary risk factor is same for all patients and does not interact with other factors such as age or procedure. Large violations of modeling assumptions may introduce bias in the estimation of hospital mortality metrics.

Fourth, even if the fit to the data is adequate, models need to be routinely recalibrated to account for improvements and other changes in outcomes over time. The current plan of the STS-CHSD is to reestimate the model twice yearly to coincide with the production of each STS-CHSD participant feedback report.

Finally, the interpretation of hospital O/E ratios is affected by the exclusion of 27 STS centers with more than 10% missing data. For example, if all United States centers performing congenital heart operations participated in the STS registry and were included, then a hospital’s O/E ratio could be interpreted as a comparison with the national average. Because not all United States centers participate in the STS registry and because only a subset of STS centers were included in this particular analysis, the O/E ratio must be interpreted as a comparison with the subset of centers that were included. Although such a comparison is arguably less relevant than a comparison with the United States national average, it is still internally valid as a comparison among the centers included. Importantly, as noted above, the model will be reestimated for the CHSD participant feedback report twice yearly. Future analyses for the CHSD feedback report will include a higher proportion of STS centers as the proportion of sites with complete data increases.

In conclusion, the risk model appears well suited to adjust for case mix in the analysis and reporting of hospital-specific mortality for congenital heart operations. Inclusion of patient factors added useful discriminatory power and reduced bias in the calculation of hospital-specific mortality metrics.