Neural Mechanisms of Credit Assignment in a Multicue Environment

Abstract

In complex environments, many potential cues can guide a decision or be assigned responsibility for the outcome of the decision. We know little, however, about how humans and animals select relevant information sources that should guide behavior. We show that subjects solve this relevance selection and credit assignment problem by selecting one cue and its association with a particular outcome as the main focus of a hypothesis. To do this, we examined learning while using a task design that allowed us to estimate the focus of each subject's hypotheses on a trial-by-trial basis. When a prediction is confirmed by the outcome, then credit for the outcome is assigned to that cue rather than an alternative. Activity in medial frontal cortex is associated with the assignment of credit to the cue that is the main focus of the hypothesis. However, when the outcome disconfirms a prediction, the focus shifts between cues, and the credit for the outcome is assigned to an alternative cue. This process of reselection for credit assignment to an alternative cue is associated with lateral orbitofrontal cortex.

SIGNIFICANCE STATEMENT Learners should infer which features of environments are predictive of significant events, such as rewards. This “credit assignment” problem is particularly challenging when any of several cues might be predictive. We show that human subjects solve the credit assignment problem by implicitly “hypothesizing” which cue is relevant for predicting subsequent outcomes, and then credit is assigned according to this hypothesis. This process is associated with a distinctive pattern of activity in a part of medial frontal cortex. By contrast, when unexpected outcomes occur, hypotheses are redirected toward alternative cues, and this process is associated with activity in lateral orbitofrontal cortex.

Introduction

In a natural environment, an animal faces numerous objects, which have associations with actions and their outcomes (Gibson, 1979; Cisek and Kalaska, 2010; Hikosaka et al., 2014). To act adaptively, it is important to have accurate predictions of the consequences of choices. However, which prediction an animal makes depends on which object with specific association to an outcome has been used to make the prediction. Unfortunately, single objects in complex environments do not all concur as predictors of future events. In many situations, the animal infers which object is a better predictor of subsequent events. Such inferences about which stimuli in the environment are important might be described as the internal focus of the animal. Thus, once the decision is made, it is according to this hypothesized relationship involving a specific preceding event that responsibility, or credit, for the outcome of the decision is likely to be assigned (Sutherland and Mackintosh, 1971; Mackintosh, 1975). In other words, once the outcome of the decision is apparent, the outcome will be associated with the object that has been focused on.

Orbitofrontal cortex (OFC) and medial frontal cortex (MFC) encode specific sensory events and their relationships with significant events, such as rewards (McDannald et al., 2011, 2014; Noonan et al., 2011; Monosov and Hikosaka, 2012; Klein-Flügge et al., 2013; Howard et al., 2015). However, it has been unclear how representations of specific sensory events in these brain areas and mechanisms of credit assignment are related. We propose that MFC and OFC representations encode focused and alternative associations between sensory events and outcomes, and competitively guide credit assignment by confirming or disconfirming the initial predictions. The problem of assigning credit for current outcomes to earlier choices has been examined in monkeys with lesions and fMRI (Noonan et al., 2010, 2012; Walton et al., 2010; Chau et al., 2015). However, while these previous experiments focused on a particular credit assignment problem involving temporally distributed events, here we consider the more general case where multiple simultaneous cues/objects are present before action and outcome delivery. Furthermore, to rigorously examine the credit assignment problem, it is better that the candidate predictive sensory events are not the choice object themselves as in the previous studies (Noonan et al., 2010; Walton et al., 2010; Chau et al., 2015). Otherwise, the participant's action may suffice to disambiguate the relevant sensory events from irrelevant ones.

To examine the credit assignment problem in the context of multiple cues, we designed a variant of the well known weather prediction task (Knowlton et al., 1996). On each trial, subjects could select one of two cues to guide their decision. Crucially, the choice options were presented separately from the cues to mimic the natural environment with multiple cues (Fig. 1A), and the subjects chose one of them to express their prediction about the weather outcome. It therefore became possible, unlike in previous experiments where only choice stimuli were presented and no separate cue is involved (Boorman et al., 2009; Abe and Lee, 2011; Rushworth et al., 2011; Lee et al., 2012; Donoso et al., 2014; Hunt et al., 2014), to examine how outcome credit is assigned to a preceding cue among multiple simultaneous cues independent of the choice process itself. Furthermore, in this task design, the attended associational knowledge predicting the outcome events can be estimated on a trial-by-trial basis. In the final stage of the trial, subjects saw the actual weather outcome. At this point, subjects could re-evaluate not just the choice they had selected but also their initial internal focus on the association between a specific cue and the outcome.

Figure 1.

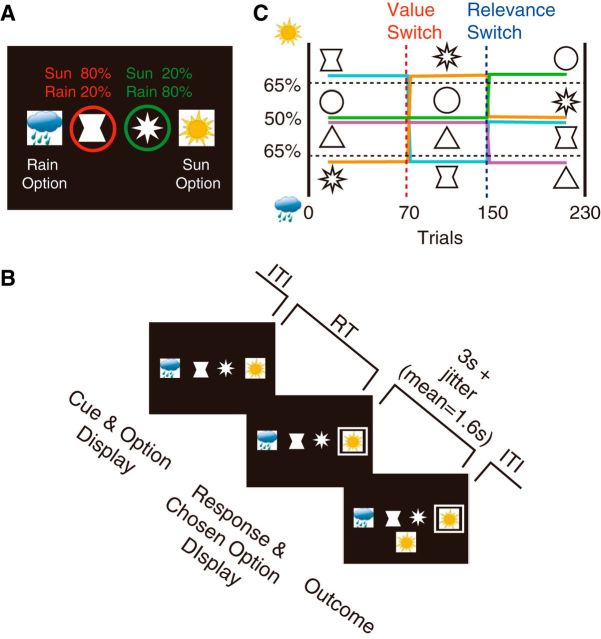
Experimental task design and behavioral results. A, Experimental task. Subjects were presented with two geometrical shapes (from a set of four) in the screen center and, separately, two possible weather prediction options at the left and right of the screen. The two cues predict different outcomes as being more likely (percentages indicated above the cues). B, After the presentation of the information cues and the choice options (Cue & Option Display), they chose one weather prediction by pressing a button (Response & Chosen Option Display), and received feedback about the actual weather outcome (Outcome). C, At each phase of the task schedule, two of four cues were predictive of a weather outcome (relevant cues), while the other two cues were not (irrelevant cues). Two types of changes in association between cues and weather outcomes occurred during the task. During reversal switches, the association of the cue with a specific weather outcome was reversed. During Relevance Switches, the predictive cues became nonpredictive and nonpredictive cues became predictive.

We show that subjects focus more on one cue than another for guiding their decisions and credit assignment is made according to this internal focus. We found that neural mechanisms in MFC and OFC were associated with credit assignment based on the initial focus and on an alternative focus of cue outcome association, respectively.

Materials and Methods

Subjects.

Twenty-six healthy volunteers participated in the functional magnetic resonance imaging (fMRI) experiment. The data of two volunteers were removed because they could not complete the scanning session due to a technical problem. The remaining 24 subjects (17 women; mean age, 23.7 years; SD, 2.8 years) were included in all further analyses. All participants gave informed consent in accordance with the National Health Service Oxfordshire Central Office for Research Ethics Committees (07/Q1603/11) and Medical Sciences Interdivisional Research Ethics Committee (MSD-IDREC-C1-2013-066). Subjects were paid £25 for their participation in the experiment.

Task design.

To mimic the situation where multiple simultaneous antecedent events can cause a subsequent outcome event, we designed a task in which subjects were shown two geometrical cues at the center of a screen and a single weather outcome followed them. This is in contrast to previous experiments where only choice stimuli were presented and no separate cue is involved (Boorman et al., 2009; Abe and Lee, 2011; Rushworth et al., 2011; Lee et al., 2012; Donoso et al., 2014; Hunt et al., 2014). The task is designed to examine how outcome credit is assigned to one preceding cue among many that are simultaneously presented independent of the choice process itself. There were a total of four possible geometrical shapes, each of which was uniquely associated with the outcome. For example, a triangle cue might be more likely to be followed by a sun outcome compared with a rain outcome in one phase of the task. The weather prediction options were displayed on the left and right of the geometrical cues, and their positions were randomized from trial to trial so that the button press used to indicate a given prediction varied from trial to trial. Subjects responded within 4 s (Fig. 1B). Once the response was made, the option chosen was marked by the presentation of a white frame. After the response, there was an interval of 3 s and jitter (drawn from a Poisson distribution). The outcome was then displayed just below the two geometrical shapes to make the association between the cues and the outcomes easier. An intertrial interval of 3 s and jitter (drawn from a Poisson distribution) then followed.

Two geometrical shapes were randomly chosen from the set of four cues (using random values generated by MATLAB). Then, left or right cue positions were randomly assigned to the two cues (again using random values generated in MATLAB). Crucially, the selection of the two cues and the assignment of the cue positions were based on separate sets of random values so that there were no correlations between the two processes (subjects could not predict the identities of the cues from their positions).

The cues had unique predetermined strengths of association to outcomes at each phase of the task, and these were used to calculate the log likelihood ratio of the occurrence of the outcomes given the pair of cues that were presented on each trial. The log likelihood ratios were then transformed to probabilities, which were in turn used to generate the specific outcome at each trial.

Task schedule.

To highlight a particular aspect of the learning process, which assigns credit, or pays more attention, to specific cues than other cues, we designed two types of change in the associative relationship between the geometrical shapes and the weather outcomes. One type of the change in association was reversal of the association value (Value Switch; Fig. 1C). For example, during a reversal switch, the cue that previously predicted the sun became the cue that predicted the rain and vice versa. In this type of switch, the relevance of the cues did not change (relevant cues remained relevant, and irrelevant cues remained irrelevant), but their associative relationship with each specific outcome was reversed. In another type of change, the relevance of the cues changed (Relevance Switch), as follows: the cues that had been strongly predictive of one outcome or the other became predictive of neither outcome (e.g., the strength of association between a cue and an outcome might change from 80% to 50%) and vice versa (e.g., the strength of association between a cue and an outcome might change from 50% to 80%). This novel type of switch in task design was introduced to demonstrate that the learning of cue–outcome association involves not only an isolated cue–outcome association process independent of other cues but also depends on determining the relative importance of cues or, in other words, determining how credit is assigned to specific cues in predicting outcomes. We expected differential credit assignment to the cues to modulate the efficiency of the learning process associating the cues to outcomes. Each of the switch types occurred once in the task, and the order of the switch types was counterbalanced across subjects. The subjects were simply instructed to learn the meaning of each cue and were told that some cues were informative while others were not. The changes in the associations of cues with outcomes were not explicitly instructed before the scanning session.

Model descriptions.

We propose that credit assignment in a multicue environment depends on which cue subjects attend to or select when generating the initial prediction that guides decision making. At the time of outcome, this distinction between cues also modulates the credit assignment process. Therefore, in the formulation of the models, whether and how the cues are distinguished is of great importance. Model 1 does not distinguish the cues. Models 2–4 distinguish cues on the basis of a subjective selection process (or internal hypothesis), which is estimated from the congruency between the choice and the association of the cue to outcomes. Models 5–9 distinguish between cues on the basis of aspects of their objective association with particular outcomes without positing any subjective internal selection process. Models 5 and 6 focus on the predetermined objective strength of association between cues and outcomes, and Models 7–9 focus on the reliability of the objective history of associations. For details of the models, see the descriptions below.

The first model, the Rescorla-Wagner Model (Model 1: Basic RL (reinforcement learning) Model), was the most basic association learning model examined, as follows:

where PV is the prediction variable, which is the sum of the equally weighted cue–outcome association strengths of individual cues (V_c1 and V_c2). PV is transformed to the estimated choice probability with the function p = 1/(1 + e^{(β * (PV − 0.5) + γ * C_n−1)}), where β is the inverse temperature and γ is the factor of choice correlation across trials, also known as “choice stickiness” (C_n−1 is the choice in the previous trial, with sun choice coded as +1 and rain choice coded as −1). V is the cue–outcome association strength of each cue, O is the outcome in the current trial (sun outcome coded as +1 and rain outcome coded as 0), and α is the learning rate shared by both cues. The subscript n corresponds to the current value, and the subscript n + 1 corresponds to the updated value. Note that this model assigned equal weight to each cue in generating the prediction of the outcome in the decision phase and in assigning the credit for the outcome in the outcome phase. The model is based on the empirical finding that the prediction used in the decision appears in the calculation of the prediction error in the outcome phase (Takahashi et al., 2011). The free parameters in this basic association model are inverse temperature (β), choice correlation factor (γ), and learning rate (α; Table 1).

Table 1.

Model comparison of subjectively relevant cue models

Model type	β	γ	α	pw	lw	lw_cor	lw_inc	-LL	BIC
Basic RL (Model 1)	3.45 (1.35, 3.91)	−0.04 (−0.16, 0.07)	0.31 (0.23, 0.36)					2984	3177
Prediction weight (Model 2)	4.29 (1.63, 5.51)	−0.04 (−0.12, 0.13)	0.17 (0.12, 0.25)	0.82 (0.78, 0.93)				2614	2872
Learning weight (Model 3)	4.26 (1.60, 6.02)	−0.04 (−0.10, 0.12)	0.33 (0.26, 0.44)	0.88 (0.76, 0.95)	0.53 (0.38, 0.62)			2541	2863
Learning weight and feedback (Model 4)	4.32 (2.60, 5.27)	−0.03 (−0.10, 0.15)	0.41 (0.26, 0.50)	0.93 (0.82, 1.00)		0.95 (0.62, 1.00)	0.41 (0.26, 0.49)	2364	2751
Prediction weight (cue distinction)	4.31 (1.90, 5.32)	−0.02 (−0.11, 0.14)	0.18 (0.14, 0.24)	0.99 (0.91, 1.00)				2626	2884
Learning weight (cue distinction)	4.42 (2.53, 5.54)	0.00 (−0.10, 0.16)	0.39 (0.32, 0.54)	1.00 (0.94, 1.00)		0.45 (0.28, 0.63)		2552	2875
Learning weight and feedback (cue distinction)	4.21 (1.92, 5.30)	0.01 (−0.09, 0.14)	0.42 (0.31, 0.53)	1.00 (1.00, 1.00)		1.00 (1.00, 1.00)	0.31 (0.10, 0.43)	2457	2844

Estimated values of free parameters are represented as median (25th, 75th percentiles) in each entry. pw, prediction weight; lw, learning weight; lw_corr, learning weight in correct trial; lw_inc, learning weight in incorrect trial; -LL, negative log likelihood; BIC, Bayesian information criterion.

The second model (Model 2) incorporates differential weighting of cues in the prediction generation process at the time of decision making as an additional free parameter [prediction weight (pw)]. At this point, the weight assigned to each cue is either the weight for the cue subjectively selected as the relevant cue (SRC; pw_selected) or the weight for the non-SRC (1 − pw_selected). It is important to realize that we can infer which cue is the SRC, the focus of the subject's hypothesis, and which cue is the non-SRC, on the basis of the history of association between the cues that were presented and the choices that subjects made (the cue–choice congruency; Fig. 2A,B), which reflects how readily the cue and associated outcome come to mind and influence the decision process. The SRC can thus be thought of as the cue that most easily and readily come to mind when two cues are presented together on a given trial. We refer to this model as the Prediction Weight Model (Model 2), as follows:

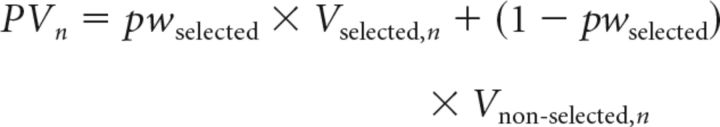In this case, PV is the prediction variable calculated from the sum of the unequally weighted cue–outcome association strengths of individual cues.

Figure 2.

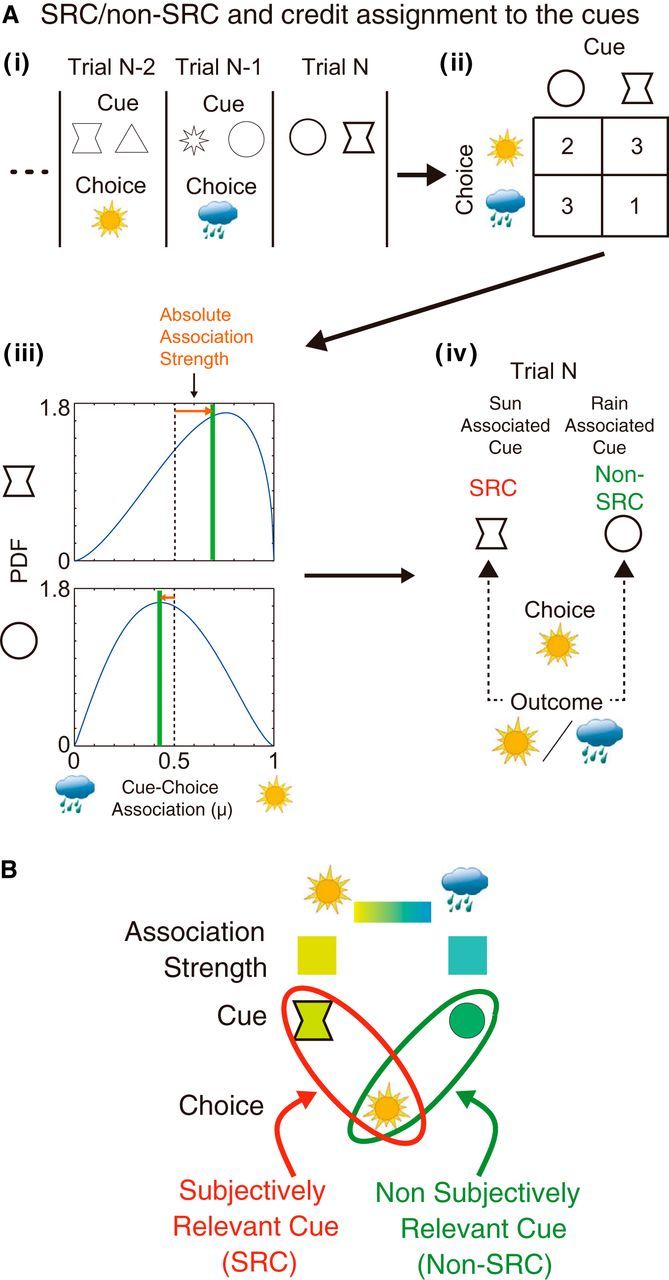
Procedure for estimating subjective cue selection. A, Subjective cue selection (identifying the SRC vs the non-SRC). i, The cue–choice association history reflects each participant's subjective estimate of cue–outcome association. ii, iii, The number of associations between each cue and each choice were, therefore, tallied and discounted with recency-weighted factor of a half-life of six trials (ii) and used to create (iii) β functions (mean value indicated by green lines) summarizing estimates of the subjective strengths of association between each cue and each outcome. iv, These estimates were then compared with the actual choice in the current trial (Trial N). The SRC (shown in red), as opposed to the non-SRC (shown in green), can then be inferred as the cue that was more likely to have guided the participant's choice on the current trial. B, In summary, on each trial, we were able to define the cue that better predicted the subject's current choice as the SRC and the other cue as the non-SRC.

The third model (Model 3) is constructed by further addition of a mechanism of differential credit assignment to each cue (SRC vs non-SRC). This is achieved by the inclusion of an additional free parameter specifying a differential learning weight (lw) for the cues. This means that, at the end of each trial when cue–outcome association strengths of the cues (V_selected and V_nonselected) are adjusted on the basis of the outcome that has just been witnessed, the adjustment is greater (learning is faster) for the cue with the higher learning weight. The learning weight assigned to the SRC in this model (Model 3: Learning Weight Model) was lw_selected, and the learning weight assigned to the non-SRC was (1 − lw_selected), as follows:

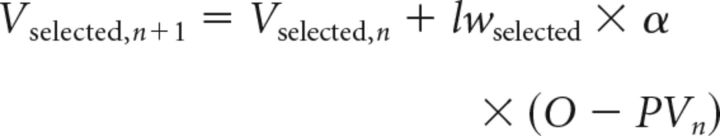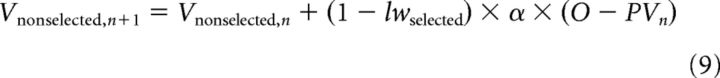The determination of the SRC and non-SRC in the second and the third model (Models 2 and 3) and the next model (Model 4) was, in each case, based on an identical analysis of choice patterns in past trials (Fig. 2A, Table 1). In any such analysis, it is necessary to choose the number of previous trials that will be considered when the choice pattern is investigated to determine the SRC and non-SRC of the current trial. The recency-weighted factor was fixed to a half-life of six trials for all the results presented here; however, the results were consistent across different lengths of half-life. For both pw and lw, the differential weighting factor for the SRC was defined as a free parameter ranging from 0 to 1 [SRC weight = a, non-SRC weight = (1 − a)]. At the time of the decision and prediction generation, the weights simply multiplied the association strength of each cue. At the time of the outcome and credit assignment, the weights multiplied the basic learning rate, which was shared by both cues.

The final model (Model 4: Learning Weight and Feedback Model; Table 1) was similar to the previous models, but, in addition, it distinguished cases of correct and incorrect feedback. Because of this distinction between confirmation and disconfirmation of the initial prediction, there were also two free parameters for learning weights: lw_{selected, correct} and lw_{selected, incorrect} in correct trials (confirmation case), as follows:

and in incorrect trials (disconfirmation case), as follows:

Prediction variables were calculated as in previous models as follows:

We also conducted additional control analyses using models that were fundamentally different in spirit because they used different ways of distinguishing between cues. Instead of inferring individual participants' subjective distinctions between SRCs and non-SRCs, these alternative models adopted optimal strategies of using information by distinguishing between the two cues presented on any trial simply in terms of the objective cue–outcome association in a given task phase (predetermined cue relevance models, Models 5 and 6; Fig. 3A, Table 2) or in terms of the recency-weighted cue–outcome association history (cue–outcome reliability models, Models 7–9; Fig. 3B, Table 2). Thus, while all these models, Models 5–9, were fundamentally different from Models 2–4 (that assumed participants had subjective hypotheses about cue–outcome associations), Models 5–9 shared similarities with one another because they all attempted to determine an “objectively relevant cue” versus an “objectively irrelevant cue” (as opposed to the SRC and non-SRC). They all assumed that cue determination simply reflected the objective history of cue–outcome association in the absence of any subjective hypothesis construction. Although these strategies are more rational ways of performing the current task, actual data in the Results section show that the behavior of human subjects deviated from these rational strategies.

Figure 3.

Procedures of models estimating objective cue selection. A, Predetermined or objective cue relevance (identifying the objectively relevant vs the irrelevant cue). The cue that was objectively of greater relevance for decision making could be determined by the true cue–outcome association history in a given task phase. This corresponds to the cue–outcome association history preprogrammed by the experimenter. In each task phase, two cues were predetermined to be relevant for decision making because of their reliable associations with outcomes (e.g., here, the circle and triangle in the final task phase), while the other two cues were irrelevant for decision making because of their lack of reliable association with outcomes (e.g., here, the hourglass and star cues in the final task phase). B, Cue–outcome reliability in recent history (identifying the recently more reliable vs less reliable cue). i, The designations of the reliable and less reliable cues were based on the cue–outcome associations actually experienced in the recent trial history. ii, iii, The numbers of associations between each cue and each outcome were tallied and discounted with recency-weighted factor of a half-life of six trials (ii) and used to create (iii) a β function, from which the recent predictive reliability of the cues was estimated (inverse of the width of the distribution). iv, The reliability of each of the two cues presented on a given trial was compared to determine which was designated the reliable cue and which was designated the less reliable cue.

Table 2.

Model comparison of predetermined cue relevance and cue–outcome reliability models

Model type	β	γ	α	pw	lw	lw_reli_cor	lw_reli_inc	-LL	BIC
Predetermined cue relevance models
Prediction weight (Model 5)	3.47 (1.34, 3.96)	−0.05 (−0.16, 0.06)	0.16 (0.11, 0.21)	0.81 (0.62, 1.29)*				3004.96	3263.20
Learning weight (Model 6)	3.45 (1.85, 3.94)	−0.06 (−0.18, 0.08)	0.13 (0.09, 0.20)	0.83 (0.42, 1.12)*	1.35 (0.53, 3.95)*			2914.53	3237.32
Cue–outcome reliability models
Prediction weight (Model 7)	3.42 (1.38, 3.90)	−0.05 (−0.15, 0.08)	0.32 (0.23, 0.41)	0.48 (0.44, 0.53)				2975.94	3234.17
Learning weight (Model 8)	3.20 (1.55, 3.94)	−0.06 (−0.12, 0.08)	0.59 (0.43, 0.72)	0.50 (0.46, 0.53)	0.52 (0.20, 0.64)			2951.20	3274.00
Learning weight and feedback (Model 9)	2.88 (1.04, 3.67)	−0.06 (−0.12, 0.07)	0.55 (0.48, 0.83)	0.51 (0.45, 0.53)		0.56 (0.07, 0.81)	0.42 (0.12, 0.69)	2921.86	3309.21

Estimated values of free parameters are represented as the median (25th, 75th percentiles) in each entry. pw, prediction weight; lw, learning weight; lw_reli_cor, learning weight of reliable cues in correct trials; lw_reli_inc, learning weight of reliable cues in incorrect trials; -LL, negative log likelihood; BIC, Bayesian information criterion.

*Note that prediction and learning weights of irrelevant cues were set to 1, and the weights of relevant cues are estimated in reference to the unit weight values of irrelevant cues in predetermined relevance models.

The prediction and learning weights of relevant cues in the predetermined relevance models (predetermined cue relevance-based prediction weight model, Model 5; and predetermined cue relevance-based learning weight model, Model 6; Table 2) were estimated as free parameters, while those of irrelevant cues were set to 1. Thus, the values of the free parameters for the relevant cues were estimated in reference to the irrelevant cues. Because of this approach, it was not necessary to limit the values of the free parameters for the relevant cues to the range between 0 and 1. Note that, unlike the other models, the relevant versus irrelevant cue designation in this model was not determined at a single-trial level but at each task phase. In these models (Models 5 and 6), the following different combinations of cue types might occur: relevant–relevant pair, irrelevant–irrelevant pair, and relevant–irrelevant pair.

Thus, in summary, a model can be devised that was based only on the objective, predetermined cue relevance, without any reference to any subjective hypothesis process, but which was analogous in other respects to the models using a subjective hypothesis process (Model 2–4). Although cue distinction was based on objective predetermined cue relevance in Models 5 and 6, the manner of assigning the prediction weights and learning weights was similar to the models involving subjective cue selection (Model 2–4; Eqs. 4–14). Designations of “selected cue” and “nonselected cue” were replaced by “relevant cue” and “nonrelevant cue,” respectively.

As already mentioned, other variants of objective (optimal) models can be devised in which the cues were again distinguished on the basis of the objective cue–outcome history, but the cue–outcome history that was considered was recency weighted and the cue determinations were made on a single-trial level (Fig. 3B; cue–outcome reliability models: cue–outcome reliability-based prediction weight model, Model 7; cue–outcome reliability-based learning weight model, Model 8; and cue–outcome reliability-based learning weight and feedback model, Model 9; Table 2). Although cue distinction was based on objective cue–outcome reliability in Models 7–9, again the manner of assigning the prediction weights and learning weights was exactly the same as in the three models involving subjective cue selection (Model 2–4; Eqs. 4–14). Designations of selected cue and nonselected cue were replaced by “reliable cue” and “unreliable cue,” respectively.

Model comparisons.

We formally compared the models by examining how well they fit the behavioral data obtained from human subjects. The values of free parameters were fitted for the behavioral data of individual subjects by minimizing the negative log likelihood for individual subjects' data using the fminsearch function of MATLAB. Note that there was no constraint on the fitted parameters from the other subjects or the group of other subjects so that the fitting procedures for each individual subject's data were independent of each other. The median (and 25th, 75th percentiles) values of the fitted parameters were documented in Tables 1 and 2. Note that the estimated values of fitted parameters and negative log likelihoods were stable across the fitting processes with different initial values of the parameters. The negative log likelihoods estimated for individual subjects were transformed to calculate values of the Bayesian Information Criterion (BIC) by considering the number of free parameters. The subsequent comparisons were based on the sum of these individually estimated BIC measures, which penalize the inclusion of additional free parameters severely. Furthermore, we noted that the cue-weighting parameters that had been fitted mostly favored the SRC, during both prediction generation and credit assignment (Table 1). All results of the model fitting are documented in Tables 1 and 2.

fMRI data acquisition.

fMRI data and high-resolution structural MRI data were acquired with a 3 T scanner (Magnetom, Siemens). fMRI data were acquired on a 64 × 64 × 41 grid, with a voxel resolution of 3 mm isotropic, an echo time (TE) of 30 ms, and a flip angle of 90°. We used a Deichmann sequence (Deichmann et al., 2003), in which the slice angle was set to 25° with local z-shimming. This sequence reduces distortions in the orbitofrontal cortex. T1-weighted structural images were acquired for subject alignment using an MPRAGE sequence with the following parameters: voxel resolution, 1 × 1 × 1 mm³ on a 176 × 192 × 192 grid; TE = 4.53 ms; inversion time, 900 ms; and repetition time, 2200 ms. The functional scans were acquired in a single continuous session (run) of ∼50 min (230 trials).

Preprocessing.

fMRI analysis was conducted using the Centre for Functional Magnetic Resonance Imaging of the Brain (FMRIB) Software Library (FSL; Smith et al., 2004). Independent component analyses of the fMRI data were performed using MELODIC to identify and remove obvious motion artifacts and scanner noise (Damoiseaux et al., 2006). Data were then processed using the following default options in FSL: motion correction was applied using rigid-body registration to the central volume (Jenkinson et al., 2002); Gaussian spatial smoothing was applied with a full-width half-maximum of 7 mm; brain matter was segmented from non-brain matter using a mesh deformation approach (Smith, 2002); and high-pass temporal filtering was applied with a Gaussian-weighted running lines filter, with a 3 dB cutoff of 100 s.

GLM analysis.

The analysis of the fMRI data focused on two key aspects of the task. First, for the analysis of decision-related activity, we focused on the time in each trial when decisions were made and used regressors derived from the absolute values of the cue–choice association strengths of the cues. Note that these association strengths correspond to the estimates of the strengths of cue–outcome associations in the models that included a subjective cue selection process (Models 2–4); in the Results section, we explain that models that included a subjective cue selection process provided much better accounts of behavior than the alternative objective models, and so the fMRI analysis was linked to these behavioral models (Models 2–4). In these best-fitting models, the crucial aspect was the distinction between the SRC and non-SRC, which can be conceived as attended or unattended cues. The credits at the time of the outcome were assigned based on this designation of the cues (see the Results section). For this reason, we included separate regressors for the SRC and non-SRC. The absolute values of cue–outcome association for each type of the cues reflect how consistently the cue has been associated with a choice of weather prediction (Fig. 2A) and, therefore, how readily the cue and associated outcome come to mind and influence the decision process.

It may be worth noting that this formulation of the regressors might also be akin to those that might be appropriate for identifying recently proposed “confidence” signals (Lebreton et al., 2015) with high magnitude at the two extremes of sun/rain prediction and lower magnitude at the intermediate range between the extremes.

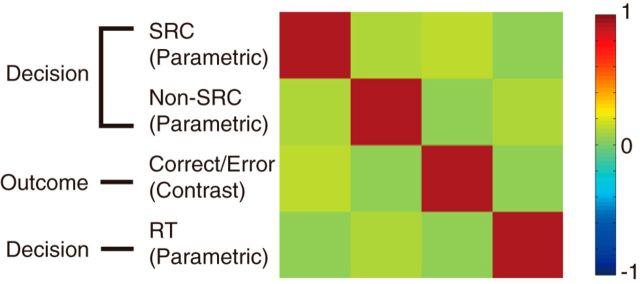
In the whole-brain analysis, the parametric regressors of these values of absolute association strengths, which had onset times aligned to cue and option display, were prepared for the SRC and non-SRC. For the regressors of no interest, we included the contrast (categorical) regressors of correct and error feedbacks with onsets aligned to outcome display, which were coded as 1 and −1, respectively, and the parametric regressors of the reaction time (RT) with onsets aligned to cue and option display (Fig. 4).

Figure 4.

GLM for decision phase analysis. Correlation matrix of regressors in the first fMRI GLM that focused on decision making. The regressors include subjective association strength of the SRC (parametric regressor aligned to decision), the subjective association strength of the non-SRC (parametric regressor aligned to decision), correct/incorrect feedback (1 and −1; contrast regressor aligned to outcome), and RTs (parametric regressor aligned to decision). Magnitudes of correlations are indicated in colors as shown in the color bar (right).

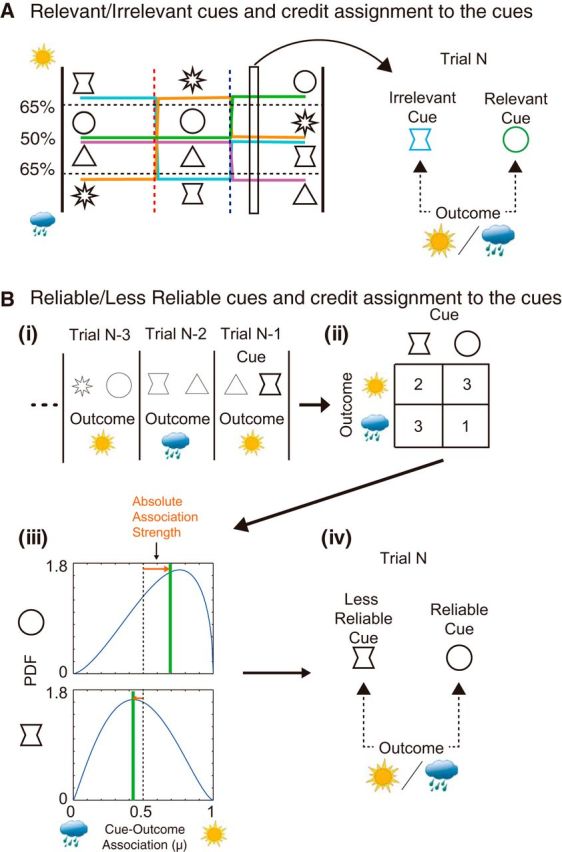
The second fMRI analysis focused on neural activity that was related to learning. More specifically, it focused on the outcome stage of each trial and on activity related to how the encoding of outcome on each trial was related to the choices that subjects made on the next trial on which one of the same stimuli in the current trial was presented (possibly several actual trials in the future because only two of the four possible cues were presented on each trial). Analysis was based on individual cues so that the presence of the same whole pair of the stimuli in the current trial was not necessary and the presence of just one cue in the next trial was sufficient. Therefore, we looked at learning in terms of the effect of the encoding of the outcome delivered in the current trial (T1) on the choice taken in the next trial (T2) when the same cue was presented (Fig. 5A). If the choice in the next trial was the same as the outcome in the current trial (e.g., sun outcome at T1–sun choice at T2), then a more effective learning process had occurred compared with when choice in the next trial was not the same as the outcome in the current trial (e.g., sun outcome at T1–rain choice at T2). Presentations of any one cue were unrelated to presentations of others, so the learning of individual cues can be dissociated and the regressors coding the learning efficiencies for each cue were orthogonal (Fig. 5B).

Figure 5.

Procedure of fMRI analysis at outcome. A, For the fMRI analysis, we are interested in the contrast of the brain states that reflect effective encoding of the current outcome and the brain states that do not reflect effective encoding. We assumed that effective encoding of outcome on a given trial T1 (T1 Outcome) in relation to a specific cue led to the subsequent choice of weather predictions (T2 Choice), which was consistent with the previously experienced outcome (left case, effective encoding at T1). The T2 trials were defined as the subsequent trials when the same cue appeared again. If the encoding of the outcome was not effective at T1, the T1 outcome and T2 choice were less likely to be the same (right, not effective encoding at T1). T1 outcome and T2 choice could be either sun or rain. If they were the same (sun–sun or rain–rain), they were treated as match cases. Otherwise, they were treated as nonmatch cases. The contrasts of the two cases were used for the construction of regressors in the fMRI analyses (inset at top right) for each cue. B, T1 outcome and T0 choice regressors were used as control regressors to account for the part of variance that corresponded to the perseverative tendency of choice in response to a specific cue. Here, T0 means a last trial when the same cue appeared. C, Correlation matrix of regressors in the first GLM. The regressors aligned to outcome included the T1–T2 match/nonmatch contrast of the SRC, the T1–T2 match/nonmatch contrast of the non-SRC, the T1–T0 match/nonmatch contrast of the SRC, and the T1–T0 match/nonmatch contrast of the non-SRC. Magnitudes of correlations are indicated in colors as shown in the color bar (right).

For control analyses, to establish the causal direction of any learning effect, we compared the outcome in T1 with choice in the previous trial (T0) when the same cue had previously appeared. While T1 outcome–T2 choice matches could reflect outcome credit assignment, T1 outcome–T0 choice matches could not; they must reflect the baseline cue–outcome association strength before the learning took place in the current trial. By comparing T1 outcome–T2 choice matches and T1 outcome–T0 choice matches, we could ask how much the subject's cue–outcome association strength in relation to each cue had changed as a consequence of experiencing the outcome.

To perform the analysis of learning-related neural activity, we created categorical regressors in a general linear model (GLM) that distinguished the T1 outcome–T2 choice matches (regressor value = 1) from situations in which choices in the next trial did not follow the outcome in the current trial (regressor value = −1). Thus, in summary, the analysis captured the difference between the brain activity associated with outcome processing that led to an identical choice being made again (e.g., a sun choice after a sun outcome) on a subsequent trial when the same cue was presented and the brain activity associated with outcome processing that did not lead to choice repetition when the same cue appeared. The GLM also included regressors of T1 outcome–T0 choice matches to control for effects of baseline cue–outcome association strength on the neural activity before the credit assignment effect on the current trial. Note, as already mentioned, that the appearance of one cue was not correlated with the appearance of other cues in a given trial so that the regressors of individual cues were not correlated with each other (Fig. 5B). The analysis was focused on neural activity at the time of the outcome onset in each trial.

It is important to note that the GLM included separate regressors for the SRC for T1 outcome–T2 choice matches and for the non-SRC for T1 outcome–T2 choice matches. Moreover, for each of the two regressors above, we included a control regressor (regressor of no interest) that denoted the corresponding T1 outcome–T0 choice match situations: a regressor for the SRC for T1 outcome–T0 choice matches, a regressor for the non-SRC for T1 outcome–T0 choice matches. All the onsets of the regressors were time locked to the onsets of outcome presentation on the T1 trial.

For both the decision-aligned analysis and the outcome-aligned analysis, all regressors were convolved with the FSL default hemodynamic response function (gamma function; mean delay = 6 s, SD = 3 s), and filtered by the same high-pass filter as the data. For group analyses, fMRI data were first registered to the high-resolution structural image using 7 df and then to the standard [Montreal Neurological Institute (MNI)] space MNI152 template using affine registration with 12 df (Jenkinson and Smith, 2001). We then fit a GLM to estimate the group mean effects for the regressors described above. The FMRIB Local Analysis of Mixed Effects (FLAME) was used to perform a mixed-effects group analysis that modeled both “fixed-effects” variance and “random-effects” variance to properly adjust the weight assigned to individual subject's contrast of parameter estimates (COPE) values based on the reliability of the mean values (Beckmann et al., 2003; Woolrich et al., 2004). All reported fMRI z-statistics and p values were from these mixed-effects analyses on 24 subjects. Inference was made with Gaussian random-field theory and cluster-based thresholding, with a cluster-based threshold of z > 2.3 and a whole-brain corrected cluster significance threshold of p < 0.05 (Worsley et al., 1992; Smith et al., 2004). For the analysis of the negative effects of the cue–outcome association strength of the SRC on BOLD activity at the time of decision (this part of the analysis is summarized in Fig. 4), we used a regional mask that restricted the analysis to the entire OFC and MFC, which was based on our a priori hypothesis that the suppression of irrelevant representations occurs in the orbitofrontal cortex (Clarke et al., 2007; Chau et al., 2014). The same large mask was used in our previous analysis of OFC and MFC connectivity (Neubert et al., 2015).

Analysis of region of interest time series.

To examine the learning-related neural activity in the areas highlighted by the whole-brain analyses at the decision time, we conducted additional analyses with separate regressors corresponding to the attended cues (SRC) and unattended cues (non-SRC) at the decision time. The set of regressors used for analysis of decision-related activity was described in the GLM analysis section and is depicted in a correlation matrix in Figure 4. A second part of the analysis focused on the outcome phase of each trial, and, again, it used separate regressors corresponding to the SRC and non-SRC. The rationale for using separate regressors for the analysis of neural activity at both the time of decision making and the time of outcome delivery is that the behavioral analysis showed that not only was decision making particularly influenced by one cue, the SRC, rather than another, but also that the outcome credit assignment process was modulated by the initial internal focus on SRC and its associated outcome (see the Results section). The regressors used at the time of outcome included SRC regressor (T1 outcome–T2 choice match vs nonmatch), non-SRC regressor (T1 outcome-T2 choice match vs nonmatch), SRC regressor (T1 outcome-T0 choice match vs nonmatch), and non-SRC regressor (T1 outcome-T0 choice match vs nonmatch; Fig. 5B). We calculated group means and SEs of effect sizes at each time point for each regressor in the GLM. GLMs were fit across trials at every time point separately for each subject. Effect sizes of the parameter estimates of the regressors were obtained for every time point and for each subject.

With this GLM, we analyzed activity in the posterior MFC (pMFC; area 25) and lateral OFC (lOFC) regions of interest (ROIs). The ROIs were 3-mm-radius spheres centered on activation peaks identified in the first stages of analysis results (described further in the Results section). We avoided “double dipping” by using ROIs identified by decision-related activity (described above as the first stage of the fMRI analysis) for the analysis of learning-related activity (described above as the second stage of fMRI analysis). The extracted BOLD time series from each ROI was then divided into trials with a duration set to the 10 s average duration starting at the delivery of the outcome feedback, and resampled at a 250 ms resolution.

Results

Task and basic behavior

Subjects performed a version of the well known weather prediction task (Knowlton et al., 1996); on each trial, they were shown two geometrical cues, which were drawn from a set of four possible shapes, and asked to predict which single weather outcome was most likely to follow (Fig. 1A,B). Subjects made choices by pressing corresponding left or right buttons to indicate their prediction of sun or rain. The actual outcome, sun or rain, was then displayed below the two shapes.

The task comprised several phases, each consisting of a number of trials (Fig. 1C). Each shape was associated with the outcomes in a different way in the different phases. For example, in one task phase a triangle was more likely to be followed by a sun outcome rather than a rain outcome. At each task phase, two cues were associated with a specific outcome, one with sun and one with rain outcomes. We refer to these as the objectively relevant cues. At the same time, the two other cues did not predict either outcome above chance, and so we refer to these cues as the objectively irrelevant cues. The identities of the cues that were relevant and irrelevant and the links between cues and outcomes were changed during various task phases (Fig. 1C).

Two types of changes occurred. In one type (Value Switch), the objective relevance of the cues remained constant, but the outcomes they predicted were switched. For example, a cue that had predicted a sun outcome now predicted a rain outcome. Irrelevant cues, which were not predictive of either outcome, remained irrelevant cues. In the other type of switch (Relevance Switch), objectively relevant cues, regardless of whether they were relevant for sun or rain predictions, were now irrelevant, and one of the previously objectively irrelevant cues now became relevant to rain predictions while the other became relevant to sun predictions.

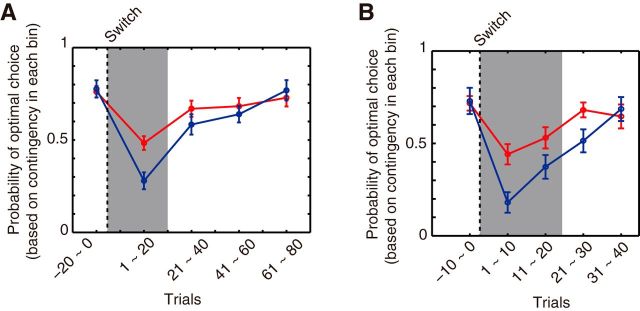
An initial analysis confirmed that identifying which cues were relevant for behavior was an important challenge for the participants in the experiment. This was suggested by the observation that adapting to the changes after a Relevance Switch was more difficult than after a Value Switch (Fig. 6). Both types of switches required subjects to change the way in which they assigned credit for outcomes to cues, but it was only in Relevance Switches that subjects had to move their credit assignment focus away from some cues (the previously relevant cues) and allocate it to other cues (the newly relevant cues). The learning speed for the relevant cue pair after a Relevance Switch was slower, especially in the first 20 trials, than after a Value Switch (Interaction of Switch Type and Time Bin: F_(3.41,78.36) = 2.98, p = 0.031). There were significant performance differences after the two types of switches (paired t test, Trials_1–20: t₍₂₃₎ = 3.36, p = 0.0027; Trials_21–40: t₍₂₃₎ = 1.31, p = 0.20; Trials_41–60: t₍₂₃₎ = 0.66, p = 0.51; Trials_61–80: t₍₂₃₎ = −0.60, p = 0.55; Fig. 1D). The difference in learning efficiency between the two types of switches is due to the difficulty of learning about specific cues when the importance of the cues changes across the Relevance Switch. We therefore focus the subsequent analysis on the learning process in the Relevance Switch.

Figure 6.

Learning curves after switches. A, Performances are displayed as the percentage of responses to the two-cue compound that were of the optimal type according to the postswitch contingency. Compared with Value Switch (shown in red), the learning speed after Relevance Switch (shown in blue) was much slower. Each bin contains data from 20 trials. B, The same data as in A are replotted with the bin size of 10 trials. The range of the trials is now from 10 trials before switch to 40 trials after switch. Data are presented as mean ± SE across 24 subjects.

Subjective selection of the relevant cue to guide behavior

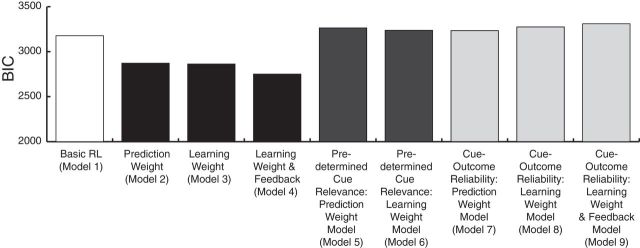
If subjects try to determine cue relevance, then the subjects should be attempting to treat different cues as relevant at different points in the task, possibly at each trial. Ideally, the cue subjects selected as relevant (the SRC) would be an objectively relevant cue, but subjects need to experience cue–outcome contingencies over a number of trials to infer which cues are relevant, and this might contribute to the slower adaptation after Relevance Switches (Fig. 6). There are also likely to be trials in which neither cue is an objectively relevant one, or both cues are objectively relevant but subjects still need to select an SRC to guide the decision. We should, therefore, expect that the SRC on each trial would not necessarily be a cue that was objectively predetermined to be a relevant cue by the program running the task. We tested this idea through formal model comparison contrasting models that differentiated cues as a function of whether or not they were objectively relevant for behavior as determined by the program running the task [Fig. 3A; these models are described as control models in the Materials and Methods section (Predetermined Relevance Models, Model 5 and 6); Table 2] against the basic model that attempted to explain behavior as a result of subjects assigning equal weights to both cues [this model is described as Model 1 in the Materials and Methods section (Basic RL Model)]. However, the former models did not perform better than the latter basic model in explaining the choice patterns of the subjects (Fig. 7, Table 2). We also tried a model in which cue selection was based on the objective reliability of the cue–outcome association actually experienced in the past few trials [Fig. 3B; these models are described as further control models in the Materials and Methods section (Cue–outcome Reliability Models, Model 7–9); Table 2]; we designated the more reliable cue as the one used to guide decisions. Again, these models did not perform better than the basic Model 1 (Fig. 7, Table 2).

Figure 7.

Model comparison. The models of subjective cue selection are shown in black bars. Compared with the basic association model without differential treatment of cues (Basic RL model; Model 1), the model that differentiated SRC and non-SRC at decision stage (Fig. 2; Model 2) explained the subjects' behavior better. The model with differential weighting of the cues at the learning stage (Model 3) explained the subjects' behavior better than the basic model (Model 1). However, this model did not distinguish situations in which the subjects' predictions either matched the weather outcome (correct feedback) or not (incorrect feedback). The model distinguishing the two situations (Model 4) performed still better than the model that did not (Model 3). In fact, Model 4 performed better than any other model (also see Table 1). The models with differential cue weighting based on predetermined cue relevance (Fig. 3A; Predetermined Relevance Weight Model; Models 5–6) are shown in two dark gray bars. The models of recent cue–outcome association history (Fig. 3B; Cue–Outcome Reliability Weight Model; Models 7–9) are shown in three light gray bars. These objective models were not better than Model 1 (also see Table 2).

Because objective (optimal) models (Models 5–9) failed in their attempts to explain subjects' behavior as a result of assigning greater weight to one cue rather than the other as a function of various metrics of their objective relevance for guiding decisions, we next investigated the possibility that subjects attempted to identify relevant cues in subjective and possibly explorative ways (Fig. 2A,B; these models correspond to Models 2, 3, and 4, which are described in the Materials and Methods section). We reasoned that choices made on each trial might reflect each participant's commitment to specific hypotheses about which cue is the SRC and a good predictor of outcome. If in each trial, a participant's choice is guided by an SRC, then we, as experimenters, should be able to tell which cue was the SRC and the focus of the subject's hypothesis on a given trial by looking at the congruency between the choices made on the current trial and the estimates of the associations of cues with outcomes, which were inferred from cue–choice patterns in past trials (Fig. 2).

To do this, first, we estimated subjective associations between cues and outcomes from the proportion of sun/rain choices in past trials in the presence of each cue (Fig. 2A). This measure reflected how readily the cue and associated outcome come to mind and influence the decision process. We could then infer the SRC as the cue most likely to have been the subject's focus in generating the choice made on a given trial; the SRC on a given trial was the cue that predicted the subject's choice on that trial with higher probability through its subjective association with outcomes that had been established by examining behavior on past trials. In other words, the SRC is the cue that most easily and saliently comes to mind when two cues are presented together on a given trial. Such cue–choice congruency (Fig. 2A,B) provides a window revealing the subject's hypothesis—their subjective selection of a relevant cue for predicting outcome. As explained in the Materials and Methods section, we refer to the cue that was congruent with the choice on a given trial as the SRC, and we refer to the other cue as the non-SRC.

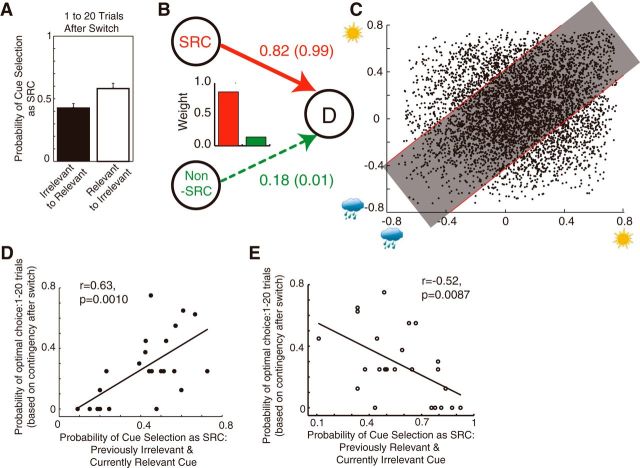
Crucially, the SRC was not always the objectively relevant cue (Fig. 8A). For example, the fraction of objectively relevant cues that were also SRCs was ∼0.4 after a switch, and it rose to ∼0.7 at a maximum later in the task phase. Furthermore, after Relevance Switches, subjects initially continued to rely on the cue that had been relevant in the previous phase (Fig. 8A). In the first 20 trials after a Relevance Switch, the probability of selecting the previously objectively relevant cue as SRC was higher than the probability of selecting the previously objectively irrelevant cue even though this was now the objectively relevant cue (Fig. 8A; unpaired t test, t₍₄₆₎ = 2.77, p = 0.0082). Such analyses provide preliminary evidence that the cue selection process was indeed subjective and did not follow predetermined relevance at a single-trial level of analysis.

Figure 8.

Subjective cue selection and learning after switch. A, In the period between 1 and 20 trials immediately after Relevance Switch, the probability of cue selection was higher for the cue that had previously been relevant but was currently irrelevant compared with the cue that was previously irrelevant but became relevant after the Relevance Switch. Data are presented as mean ± SE across 24 subjects. B, The values of the estimated parameters in Model 2 (Table 1) showed that the weight of the SRC was higher (0.82) than that of the non-SRC (0.18). However, if we apply the free parameter only to unambiguous cases when the difference of the association strengths was >0.3 (the dots outside shaded area in C), the weights were 0.99 for SRC and 0.01 for non-SRC. C, Trials were distinguished according to the difference of the association strengths of cues to outcomes. The ambiguous trials were in the shaded area (<0.3), and unambiguous trials were outside the shaded area (>0.3). Axes correspond to association strengths of two cues present in a given trial. D, The probability of selecting the newly relevant (previously irrelevant) cue as SRC was correlated with the probability of optimal choice in the first 1–20 trials after Relevance Switch (r = 0.63, p = 0.0010). E, Probability of selecting the previously relevant (currently irrelevant) cue as SRC was negatively correlated with probability of optimal choice in the first 1–20 trials after Relevance Switch (r = −0.52, p = 0.0087). Each point represents a value from a single subject.

Furthermore, a formal model comparison shows that the model of subjectively relevant cue selection (Model 2: Subjective Cue Selection-Based Prediction Weight Model) outperformed the objectively relevant cue selection models (Models 5–9) and simpler models lacking any differentiation between cues (Model 1) described above (Fig. 7).

We found that the weight that subjects assigned to the SRC (0.82) was higher than the weight assigned to the non-SRC (0.18; Fig. 8B). It might be argued that if the weights are not 1 for SRC and 0 for non-SRC, then the distinction between the SRC and non-SRC is not completely categorical. One can also argue that the differences in the association strengths of the cues are not large enough to be distinguishable for subjects, especially when the cue–outcome contingencies are changing. To address these issues, we tested additional models in which the weights of the cues were set as equal (0.5) if the difference in the association strengths of cues was small (<0.3; 0.3 is approximately the median difference of association strengths of two cues; Fig. 8C, dots in the gray area). The weights assigned to the cues in trials with larger differences in association strengths could then be estimated as a free parameter. The fitting performance of these models were comparable to the original models of subjective cue selection and still outperformed simpler models (Model 1) lacking any differentiation between cues (Fig. 7, Table 1). Crucially, the weights now assigned to the cues suggested almost perfect differentiation of the cues, as follows: 0.99 for SRC and 0.01 for non-SRC (models noted with “cue distinction” in Table 1 and values in parentheses in Fig. 8B).

We can better understand the link between the new approach we advocate here and a more traditional analysis if we consider the relationship between the probability of selecting objectively relevant cues as the SRC and the learning speeds that participants exhibited after switches. The probability of selecting the objectively relevant cue as the SRC was correlated with performance after Relevance Switches. Participants who were quicker to shift their subjective focus to newly objectively relevant cues adapted faster to the new contingency and vice versa (correlation between probability of selecting the newly relevant cue and probability of optimal choice: r = 0.63, p = 0.0010; Fig. 8D). On the other hand, subjects who continued to rely more on the previously relevant cue performed worse in this transition period (correlation between probability of selecting the previously relevant cue and probability of optimal choice: r = −0.52, p = 0.0087; Fig. 8E). The most plausible interpretation of these relationships is that the cue selection process modulates the learning process, and the subsequent section tests more directly whether the direction of influence (from cue selection to learning) is indeed in this direction.

Mechanisms of confirmation and switch of relevant cues

The subject's internally generated hypothesis about which cue is a relevant predictor of outcome may be used at the time of outcome processing. To examine this possibility, a new model of subject behavior was constructed by including a mechanism for differential credit assignment to each cue. We refer to this model as Model 3 to distinguish it from the basic Rescorla-Wagner model (Model 1) and the Prediction Weight Model (Model 2), which we have already discussed. It included an additional free parameter for differential weights when assigning credit to each of the two cues during learning (lw). The process was not modulated by whether or not feedback was correct or incorrect (Model 3). With this model, more credit for an outcome might be assigned to the SRC than the non-SRC. The weight assigned to each cue was based on whether the cue was the SRC or the non-SRC and was either lw_selected for the SRC or (1 − lw_selected) for the non-SRC (Eqs. 7–9 in Materials and Methods).

The final model (Model 4) was similar to Model 3, but now we also reasoned that when the outcome confirms the initial prediction (correct feedback), the credit for the outcome is assigned to the cue used to generate the initial prediction—the SRC. In contrast, we hypothesized that when the outcome disconfirms the initial prediction (incorrect feedback), the cue not used in the generation of the initial prediction gets more credit for the outcome—the non-SRC. Thus, while model 3 distinguished only the SRC and the non-SRC regardless of the feedback types, Model 4 additionally distinguished cases of correct and incorrect feedback and assigned credit for correct and incorrect feedback preferentially to the SRC and non-SRC, respectively. Because of this distinction between confirmation and disconfirmation of the initial prediction, there were also two free parameters for learning weights, lw_{selected, correct} and lw_{selected, incorrect} (Eqs. 10–13 in Materials and Methods).

To specifically examine these questions, we compared the performances of the models in explaining the subjects' behavior. In addition, we also examined the parameter estimates of the learning weight for each cue (Model 3), and these weights separately for instances of correct and incorrect feedback (Model 4). In summary, these models test not just whether the cues are weighted differently at the time of learning (Model 3), but also whether they are weighted differentially at the time of outcome presentation depending on whether the outcome confirms the subjects' internal beliefs (Model 4).

First, we compared Model 3 with the previous models. The fitting performance of Model 3 (separate learning weights for cues without differentiation of correct and incorrect feedback) was better than the simple association model (Model 1) and comparable to the Prediction Weight model (Model 2; Fig. 7; for the fitting results, see also Table 1). The next model, Model 4, which further distinguished between correct and incorrect feedback cases (confirmation/disconfirmation), was better than Model 3 (Fig. 7). In fact, of all the models, Model 4 provided by far the best account of the data. Crucially, the effects were only found when cues were separated as a function of whether they were the SRC or non-SRC. Analogous effects of learning bias were not found when cues were separated as a function of their objective relevance as predetermined by the task phase (Model 6; Predetermined Cue Relevance-Based Learning Weight Model) or simply as a function of the objective reliability of the cue–outcome contingency actually experienced in recent trials (Models 8 and 9; Cue–Outcome Reliability-Based Learning Weight Model and Learning Weight and Feedback Model; Fig. 7, Table 2). Thus, understanding how the subjects learned from outcomes requires knowing the subjective hypotheses they held about which cues should guide their behavior in each trial.

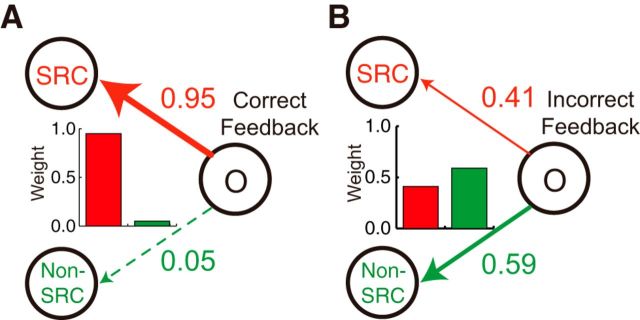
To further test our hypothesis that outcome feedback interacts with the cue that had been the focus of the subject's hypothesis, we examined the estimates of the free parameters corresponding to the learning weights in Model 4 (lw_{selected, correct} and lw_{selected, incorrect}). In the confirmation case, in which the weather outcome was as predicted, the learning weight suggested that the outcome was allocated exclusively to the cue used in the initial generation of the prediction—the SRC [Fig. 9A; in 24 subjects, the values of the median (25th, 75th percentiles) values were 0.95 (0.62, 1.00); Table 1]. Thus, it is as if the subjects were assuming that the initial reliance they had placed on one cue when making their decision had been correct because the outcome conformed to their initial prediction. In contrast, when the outcome disconfirms the initial prediction (disconfirmation case), the learning weights are allocated more to the cue not used in the initial generation of the prediction—the non-SRC [Fig. 9B; the values of the median (and 25th, 75th percentiles) of the SRC were reduced to 0.41 (0.26, 0.49); Table 1]. The differential pattern of the weights in the two cases also explains why Model 4 outperformed even the most similar alternative model, Model 3, which assumed the same weights across the feedback cases. There was still some weight allocated to the SRC even in the disconfirmation case.

Figure 9.

Learning weights after correct and incorrect feedback. A, In the situation when the subjects' predictions matched the weather outcome (correct feedback), the subjects attributed the outcome almost solely to the cue they used to generate the prediction (SRC in the panel). Almost no learning occurred for the other cue (non-SRC in the panel). The learning weights of cues are displayed in bar graphs: a red bar for the SRC; and a green bar for the non-SRC. B, When the subjects' predictions did not match the weather outcome (incorrect feedback), the subjects attributed the outcome more to the cue they did not use in prediction (non-SRC in the panel). Nevertheless, subjects also attributed part of the cause for the outcome to the cue they did use in prediction (SRC in the panel). Conventions are the same as in A.

To briefly summarize, the hallmark of models 2–4 is the distinction between the cues as SRC and non-SRC. We have tried to show that these models are good models by assessing the weights assigned to the cues at the time of decision (Fig. 8B,C, Table 1) and at the time of outcome (Fig. 9, Table 1). To validate the assumptions of these models further, we next show that the probabilities of selecting the cues as SRC after the change of cue relevance were correlated with the learning efficacy after this type of switch.

Specifically, the overall bias to attribute outcomes to the SRC might explain the correlation pattern between the learning efficiency after the switches and the probability of selecting objectively relevant cues as SRCs (Fig. 8D,E). This also suggests that it is important to overcome biases to assign credit for outcomes to the SRC if a participant is to learn well. The importance of overcoming the SRC credit assignment bias is especially true when the cue–outcome contingency changes. In the cases of Relevance Switches, in which the previously relevant cue changed to an irrelevant cue and vice versa, it is easier for subjects to learn the contingency changes if they can attribute the outcome to the non-SRC. In fact, learning efficiency after Relevance Switches was correlated with the estimated weights for the non-SRC (from Model 3, which has overall estimation of the non-SRC weight regardless of outcome; r = 0.54, p = 0.0059).

Neural activity at the time of decision and outcome

The behavioral analyses suggest a link between the process of selecting an SRC at the time of decision making and the process of learning at the time of decision outcome. To make a commitment to a particular hypothesis (a specific cue outcome expectancy), the relevant association must be selectively represented (Fig. 10A). To achieve this selective process, the relevant representation must be relatively enhanced. We already know that there are multiple possible cue outcome associations represented in the lOFC (McDannald et al., 2011, 2011; Klein-Flügge et al., 2013; Howard et al., 2015). However, to commit to a single hypothesis, the irrelevant representations might need to be relatively less active or even suppressed. This is suggested by the parameters of the decision weights estimated in the models of subjective cue selection (Fig. 8B, Table 1). Similarly, it has been reported that irrelevant representations in lOFC become relatively less active, or possibly even suppressed, during reversal learning and decision making with multiple stimulus options (Clarke et al., 2007; Chau et al., 2014). Here we consider evidence that the learning process at the time of outcome presentation also takes place in the same or adjacent brain areas. We show that the process of assigning credit to the SRC is linked to brain areas in which activity enhancements occur at the time of decision making and, in contrast, credit assignment to the non-SRC is linked to areas in which activity is attenuated at the time of decision making (Fig. 10A, compare right and left sides). In both cases, these brain regions should be reactivated at the time of outcome and credit assignment to the SRC and the non-SRC, respectively. Although the exact physiological mechanism underlying such relative attenuation at the time of decision is debatable, our claim here is that this attenuation at the time of decision is specifically related to the representation the SRC and is not associated with other regressors set at the time of decision (non-SRC and RT). This is the brain region where multiple alternative cue–outcome expectancies are held, suggesting that the representations of alternative cue–outcome associations are reactivated at the time of outcome when existing hypotheses are disconfirmed and alternative hypotheses must be considered.

Figure 10.

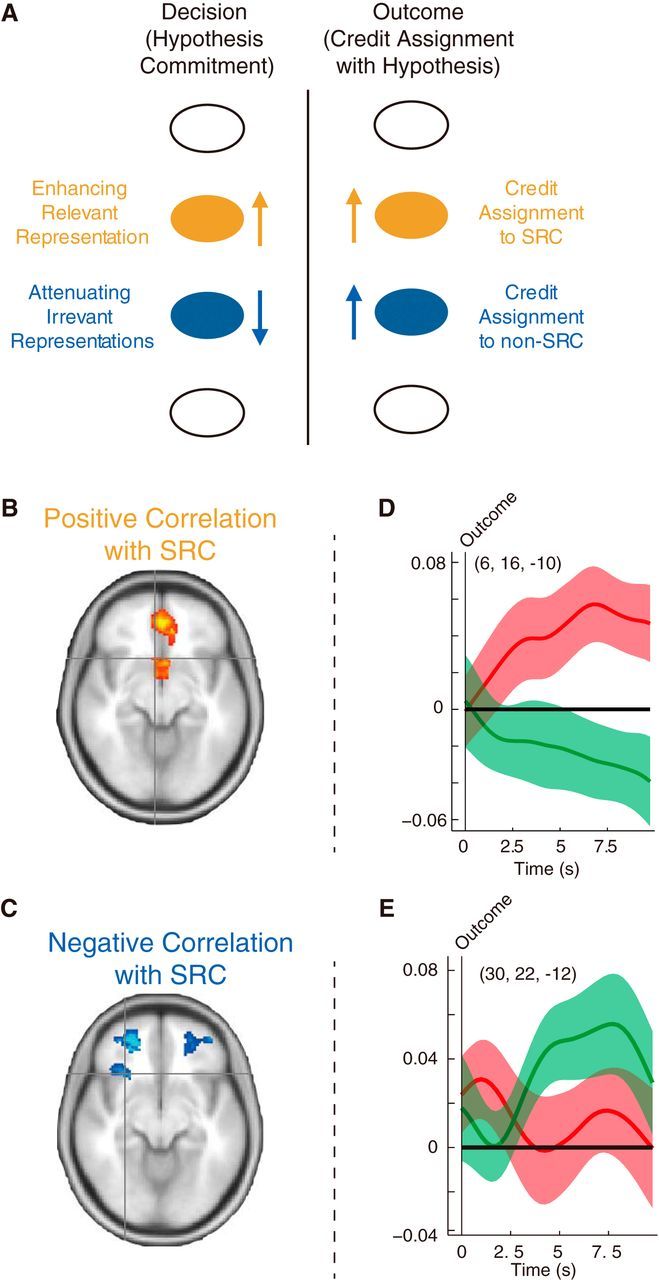
The relationship between decision-related activity and outcome-related activity. A, Neural activity at decision and outcome. The behavioral evidence summarized in Figure 2, A and B, demonstrate that one of the cues present on each trial is selected as the SRC. In this selection process, we reasoned, representation of the SRC is enhanced and the representation of the non-SRC is attenuated. These enhancements and attenuations might take place in different brain regions. In the outcome phase of the task, the brain region with activity correlated with SRC is involved in credit assignment to the SRC. By contrast, the brain region with activity negatively correlated with SRC at the time of decision making should become active in the outcome phase of the trial when a prior hypothesis is disconfirmed, and an alternative hypothesis is considered and credit is assigned to the non-SRC. B, C, Positive and negative correlation with association strength of SRC. The brain regions that, at the time of decision making, showed a positive correlation between activity and the association strength of the SRC were in the MFC. On the other hand, the brain regions with a negative correlation between activity and the association strength of the SRC, at the time of decision making, were in lOFC. This suggests that the MFC and lOFC correspond to the orange and blue mechanisms highlighted on the left-hand side of A above. D, ROI analysis was used to examine the neural activity related to credit assignment to the SRC in MFC. The MFC region that initially showed activity enhancement for the SRC exhibited learning related activity (match/nonmatch contrast), specifically for the SRC (red curve) but not for the non-SRC (green curve). E, ROI analysis of neural activity related to credit assignment to the non-SRC in lOFC. The lOFC area that initially showed activity negatively correlated with the SRC exhibited learning related activity (match/nonmatch contrast) specifically for the non-SRC (green curve) but not for the SRC (red curve).

We found that the neural activity recorded at the time of decision was correlated positively with the cue–outcome association strength of the SRC in MFC (Fig. 10B). In contrast, negative correlations between neural activity and the association strength of the SRC were found in lOFC (Fig. 10C), which included more anterior lOFC (areas 11 and 13) and more posterior lOFC (area 12). These results can be interpreted as suggesting that activity representing the SRC is augmented in MFC. At the same time, the irrelevant representation of the non-SRC is attenuated in lOFC as a function of the association strength of the SRC (in other words, as a function of the saliency of the SRC). As a result of these changes in neural activity, the main hypothesis is more exclusively focused on a particular representation, and fewer resources are allocated to the alternative representations. Alternatively, the current results could mean a reduction of the inputs correlated with the absolute association strength of the SRC because the BOLD signal in general also reflects the input to the lOFC regions. However, we would like to emphasize that any change of the signal to the lOFC region would be due to interaction with the representation of the SRC in MFC. The counterpart of the interaction is likely to be the representation of the non-SRC. The results are consistent with previous evidence that value-related activity in MFC is affected by the direction of attention (Lim et al., 2011), that MFC lesions diminish the normal attentional advantage of reward-associated stimuli and change information sampling strategy (Fellows, 2006; Vaidya and Fellows, 2015), and that irrelevant representations are suppressed in lOFC (Clarke et al., 2007; Chau et al., 2014).

An influential series of fMRI studies emphasized medial OFC (mOFC) and adjacent MFC activity in response to rewards, and lOFC activity in response to negative outcomes (O'Doherty et al., 2001, 2003). But it has been difficult to identify regional variation in neuronal responsiveness to rewards and negative outcomes in macaques (Morrison and Salzman, 2009; Rich and Wallis, 2014) or simple failures to respond to positive and negative outcomes after mOFC versus lOFC lesions (Noonan et al., 2010). We tested for regional differences in correct feedback (positive outcome)-related activity and incorrect feedback (negative outcome)-related activity in the present dataset by including the categorical regressor of correctly/incorrectly predicted outcomes in the first GLM (Fig. 4). Using a conventional cluster-based statistical threshold (z > 2.3, p < 0.01), we could not find evidence for correct or error-related activity in either MFC or OFC. We also tested other regressors (non-SRC and RT) as well with the same procedure but could not find significant activity in MFC or OFC.

Next, we examined how credit for an outcome is assigned more to one cue than to another. It is this process of differential credit assignment to one cue rather than another that was incorporated into both Model 3 and Model 4 to explain behavior. However, the neural basis of differential credit assignment to individual cues is unknown.

To examine neural activity related to the mechanism of learning, we exploited an approach similar to one often used in memory research: we looked at neural activity recorded at one point in time and determined whether it was predictive of behavior at a second time point (Otten et al., 2001). In our experiment, learning should occur at the point in each trial when the actual weather outcome is revealed, and so we focused on activity locked to this time point. We focused on outcome-related activity on a given trial (trial T1), as a function of what subjects did on the next trial (trial T2) when the same cue appeared. We assumed that effective encoding of a particular outcome on T1, in relation to a specific cue, should lead subjects to make a consistent outcome prediction when the same cue was presented on the subsequent trial T2 (Fig. 5A). If the encoding of the outcome is not effective at T1, the T1 outcome and T2 choice are less likely to be the same. If they were the same (sun–sun or rain–rain), they were treated as “match” cases. Otherwise, they were treated as “nonmatch” cases. In other words, we can tell whether subjects assigned the credit for an outcome to a particular cue because they will predict the same outcome on the next trial when the cue is presented.

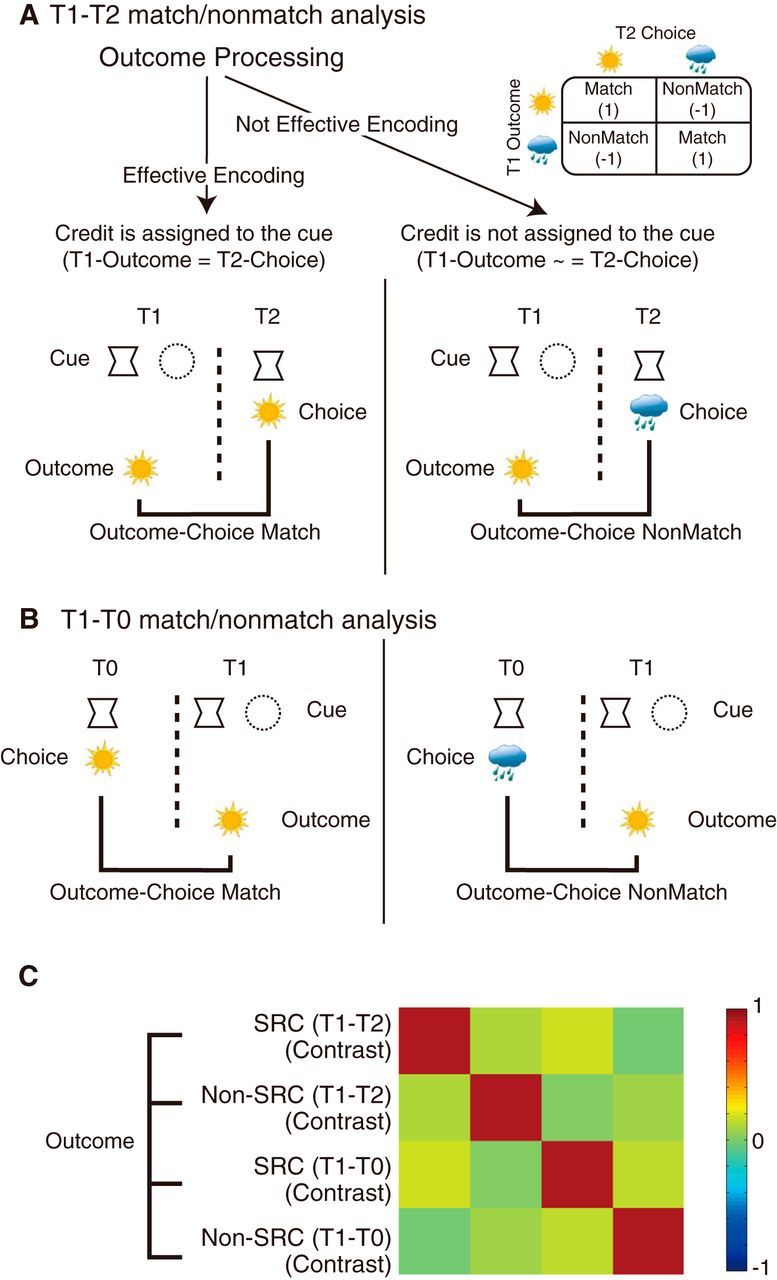
Therefore, to identify neural activity related to assigning credit for an outcome to a cue, we distinguished the two cases (match vs nonmatch) to construct categorical regressors for the fMRI analyses (Fig. 5A, inset at top right). The categorical regressors were time locked to outcome presentation so that the analysis identified learning-related brain activity that led to a match choice (coded as 1), as opposed to a nonmatch choice (−1), being made on a subsequent trial when the same cue reappeared (e.g., a sun choice at T2 after a sun outcome at T1 vs a rain choice at T2 after a sun outcome at T1). Note that we can use independent regressors for each cue to capture learning-related activity corresponding to the SRC and the non-SRC because the appearance of any one cue were uncorrelated with the appearance of others. Thus, we can compare activity in those trials that were followed by a match versus a nonmatch choice on T2 (Fig. 5A). Thus, our fMRI analysis, which was conducted with a standard GLM approach, incorporated the outcome time-locked regressor for the SRC and non-SRC (Fig. 5B): SRC regressor (T1 outcome–T2 choice match vs nonmatch); and non-SRC regressor (T1 outcome–T2 choice match vs nonmatch).

Still, such an approach, in isolation, runs the risk of simply capturing brain activity related to periods of good task performance as opposed to bad task performance. It is, however, possible to identify activity that has a causal role in driving future changes in behavior and controlling for difference in baseline task performance by including additional regressors that code for matches between T1 outcome and the choice that subjects had made on the previous trial (T0): SRC regressor (T1 outcome–T0 choice match vs nonmatch); and non-SRC regressor (T1 outcome–T0 choice match vs nonmatch).

Because the T1 outcome can have no causal consequences for the choice that preceded it, regressors coding for T1 outcome–T0 choice matches and nonmatches provide a strong control for baseline cue–outcome association strengths and differences in performance levels. In summary, the GLM contained four regressors—the two listed above that examined T1 outcome–T2 choice matches and two control regressors that were identical but that compared T1 outcome–T0 choice matches versus nonmatches.

We hypothesized that the brain regions showing positive activity correlations for the SRC, which might reflect enhancement of the representation of the main hypothesis, would be involved in credit assignment to the SRC and that the brain regions showing negative activity correlations with the SRC, which might be related to the attenuation of the irrelevant representations, would be involved in credit assignment to the non-SRC (Fig. 10A). We found a pMFC (x = 6, y = 16, z = −10) region in which match versus nonmatch effects were selective for the SRC (Fig. 10D, red line). The pMFC peak was posterior and ventral to the genu of the corpus callosum in or close to the subgenual cingulate area 25 (Johansen-Berg et al., 2008; Beckmann et al., 2009; Neubert et al., 2015).

In contrast to the situation in which credit for the outcome is assigned according to the favored hypothesis, subjects occasionally switch to the alternative hypothesis that the other cue is more predictive of the outcome when contingencies between cues and outcomes change. We are especially interested in brain regions showing a decrement in activity at the time of the decision, which might be related to the suppression of the irrelevant representations (Fig. 10C). We examined activity in these regions of lOFC at the time of the outcome. We found that activity in posterior lOFC (x = 30, y = 22, z = −12; Fig. 10E) was related to credit assignment to the non-SRC at the time of outcome delivery. The region approximately corresponds to area 12 and is consistent with the results of a previous lesion study with monkeys, which suggested that the more anterior area of lOFC (areas 11 and 13), might not be critical for stimulus–reward learning (Rudebeck et al., 2013). Indeed, we did not find any learning-related activity in areas 11 and 13. Analysis of lOFC activity time courses revealed a high selectivity for the learning effect associated with the non-SRC for the T1 outcome–T2 choice match versus nonmatch contrast (Fig. 10E, green line).

Discussion

By examining how the credit for an outcome is assigned when multiple and simultaneous objects may have predicted it, we have shown that human subjects acted as if they attended more to one cue when predicting the outcome. Moreover, they were also biased to assign credit for an outcome to the cue selected as the relevant predictor of the outcome—the SRC. Importantly, models that lacked the SRC/non-SRC distinction but relied only on the objective cue–outcome associations failed to describe behavior well (Models 5–9; Fig. 7). We identified distinct processes, one related to the confirmation of an initial focus on the SRC, and another related to switching attention to focus on an alternative predictor (Fig. 9). Neural mechanisms in MFC and lOFC were separately mapped to credit assignment processes related to the SRC and non-SRC, respectively.

This approach might appear to contradict well known claims that monkeys combine decision-related evidence from multiple cues (Yang and Shadlen, 2007; Kira et al., 2015). We too have also reported a similar integration process when a similar task was performed by humans (Gould et al., 2012). However, it is important to realize that in all these previous cases data were obtained after an extensive learning and training phase with stable association patterns. From our own and others' experience, we know that subjects cannot integrate all the cue information at the beginning of training and therefore that training started with strong single cues. Thus, it is plausible that the current data might correspond to a stage when subjects are learning the predictive significance of multiple cues.

Previous studies have considered how learning efficiency is related to the rate at which subjects' environments are changing (Behrens et al., 2007). Abrupt state changes in the environment are also modeled in a Bayesian change–point detection framework (Nassar et al., 2010; Wilson et al., 2010). Such processes lead to broad changes in the way in which animals should learn about all cues in their environments. By contrast, the cue selection process in this report enables an animal to learn more about one specific cue rather than another in a multi-cue environment. The important difference from the previous frameworks is that the cue selection process can predict slow learning in cases such as Relevance Switch as opposed to Value Switch (Fig. 6). We therefore have focused our analyses more on the Relevance Switch. The phenomenon may share features with overshadowing in the context of classical conditioning (Mackintosh, 1975, 1976).

Selecting one specific cue among alternatives in the present experiment is not the same as selecting a feature in a dimension (e.g., the color blue or a square shape) from among multiple dimensions (e.g., color, shape, and number) in compound stimuli in the Wisconsin Card Sorting Test (WCST). Nevertheless, it was recently reported that WCST also involves an attention-based action selection and learning process (Wilson and Niv, 2012; Niv et al., 2015). The WCST experiments suggested that participants learned about features when they were explicitly instructed to pay attention to single dimensions, rather than to particular instances of compound cues. In our study, by contrast, participants actively learned about a particular cue, the same one they based their initial hypothesis on, even when they could pay attention to all the potential cues. Whereas optimal learners should focus on specific features in a dimension in WCST, in our test an optimal learner could have learned about both cues regardless of the hypothesis. Furthermore, while feature/dimension-based selection depends on lateral prefrontal areas in humans and other primates (Dias et al., 1996, 1997; Konishi et al., 1998; Niv et al., 2015), the current results and previous reports (Dias et al., 1996, 1997; Noonan et al., 2011) suggest associations between particular instances of information sources, and their associated outcomes involve lOFC and ventral MFC.

Although our task design does not involve an explicit reward, one could still argue for the interpretation of credit assignment based on reward values: reliability of the cue–outcome association might constitute the “value” of the cue in our task because it leads to correct predictions. However, the cue with the more reliable association in a pair in a given trial is used for prediction with only a moderate probability (Fig. 8A). Furthermore, the models assuming more credit assigned to the more reliable cue did not perform better than the basic model (Fig. 7, compare Models 7–9, Model 1).

The mechanism we propose ensures cues already within the subject's focus for guiding behavior are the cues more likely to receive credit for an outcome: 0.95 weight to SRC in the correct feedback case and 0.41 weight to SRC in the incorrect feedback case (Fig. 9). This is a deviation from the prediction of a simple win-stay-lose-shift mechanism, which predicts symmetrical learning weights: near-unity learning weight to SRC in the correct feedback case and almost 0 weight to SRC (near unity learning weight to non-SRC) in the incorrect feedback case. Such a self-confirming process is consistent with the previously reported “confirmation bias” (Nickerson, 1998) and with learning biases seen in animal studies (Mackintosh, 1975, 1976).

While this mechanism might be “circular,” it is important that our analysis methods are not: the key analyses examined how neural activity recorded at the time of outcome predicted a change from the baseline cue–outcome association, which was inferred by comparing past and future choice patterns. Our neural analysis, therefore, included T1–T0 match analyses that controlled for baseline cue–outcome association levels (Fig. 5B). In this way, the SRC-related neural activity of MFC, especially in area 25, could be shown to reflect an aspect of attention-based credit assignment to specific individual cues that was causally important for guiding subsequent decisions. This is consistent with the known role of the area 25 in attention-related decision process (Lim et al., 2011). Thus, MFC represents internal focus, expressed in the choice (Lim et al., 2011; Vaidya and Fellows, 2015) as to which cue should be assigned credit for an outcome.

To counteract the bias to assign credit to the SRC, it is important to be able to switch internal focus to an alternative cue–outcome association especially when cue–outcome relationship changes occur. In such situations, the evidence conveyed by the non-SRC becomes important and encourages switching to an alternative cue on a future trial (Fig. 9). Our data suggest that lOFC, rather than MFC, was important in these situations because its activity selectively predicted such changes (Fig. 10E). This is consistent with the importance of lOFC in other stimulus–reward association learning situations (Kringelbach and Rolls, 2004; Noonan et al., 2010, 2011; Walton et al., 2010), the representations of specific cue–outcome associations in the lOFC (McDannald et al., 2011, 2014; Klein-Flügge et al., 2013), and the function of lOFC in inhibiting irrelevant representation of these specific associations (Clarke et al., 2007; Chau et al., 2014).

An influential series of fMRI studies emphasized mOFC and adjacent MFC activity in response to rewards, and lOFC activity in response to negative outcomes (O'Doherty et al., 2001, 2003). Although we could not find such activity with the correct/incorrect regressor in the whole-brain analysis (Fig. 4) and could not interpret the results as supporting a simple value-based account, the present results did suggest a way in which these potentially disparate results can be reconciled if a key issue is not just whether a positive or negative outcome was received but whether the prediction is confirmed (a case in which we observed MFC activity) or whether the prediction is disconfirmed (a situation in which we observed lOFC activity). Maintenance of the internal focus on the current stimulus and its association with a predicted outcome should tend to occur after a positive outcome because the positive outcome confirms the generally positive expectation (Sharot et al., 2007), and switching of the focus to alternative stimuli and their association with another outcome after a negative outcome occurs because it disconfirms it.

This proposal for reconciling the results of previous studies is also consistent with the finding that mOFC lesions, which did not include area 25 but their proximity in adjacent ventromedial PFC (vmPFC) structures may have deafferented area 25, impair the ability of macaques to focus on the best and second best options, and repeat the best choices in situations in which control animals appear to develop strong attentional bias toward the best choice (Noonan et al., 2010, 2012). We could not find similar learning effects in more anterior vmPFC areas. This might reflect the heterogeneity of brain areas in vmPFC (McNamee et al., 2013; Neubert et al., 2015). It might be the case that selective attentional processes needed for credit assignment in decision making are associated with area 25, whereas the actual decision-making process additionally involves more anterior parts of vmPFC (Monosov and Hikosaka, 2012; Strait et al., 2014).

Our data suggest that MFC and lOFC have unique roles when behavior is guided by a mechanism akin to hypothesis testing: they competitively select the specific association between cues and outcomes that is initially focused on or disengage from it and switch to alternative associations to guide behavior.