Investigating the Stability of Fine-Grain Digit Somatotopy in Individual Human Participants

Abstract

Studies of human primary somatosensory cortex (S1) have placed a strong emphasis on the cortical representation of the hand and the propensity for plasticity therein. Despite many reports of group differences and experience-dependent changes in cortical digit somatotopy, relatively little work has considered the variability of these maps across individuals and to what extent this detailed functional architecture is dynamic over time. With the advent of 7 T fMRI, it is increasingly feasible to map such detailed organization noninvasively in individual human participants. Here, we extend the ability of ultra-high-field imaging beyond a technological proof of principle to investigate the intersubject variability of digit somatotopy across participants and the stability of this organization across a range of intervals. Using a well validated phase-encoding paradigm and an active task, we demonstrate the presence of highly reproducible maps of individual digits in S1, sharply contrasted by a striking degree of intersubject variability in the shape, extent, and relative position of individual digit representations. Our results demonstrate the presence of very stable fine-grain somatotopy of the digits in human S1 and raise the issue of population variability in such detailed functional architecture of the human brain. These findings have implications for the study of detailed sensorimotor plasticity in the context of both learning and pathological dysfunction. The simple task and 10 min scan required to derive these maps also raises the potential for this paradigm as a tool in the clinical setting.

SIGNIFICANCE STATEMENT We applied ultra-high-resolution fMRI at 7 T to map sensory digit representations in the human primary somatosensory cortex (S1) at the level of individual participants across multiple time points. The resulting fine-grain maps of individual digits in S1 reveal the stability in this fine-grain functional organization over time, contrasted with the variability in these maps across individuals.

Introduction

The somatotopic organization of primary somatosensory cortex (S1) is well established in the human brain, both at the level of whole-body topography (Penfield and Boldrey, 1937; Walter et al., 1992; Zeharia et al., 2015) and the more fine-grain organization in the representations of the face and the hand (Moulton et al., 2009; Sánchez-Panchuelo et al., 2010). The somatotopic digit map is the subject of continuing interest, with its relative cortical overrepresentation (Mountcastle, 2005). More generally, it is increasingly clear that the S1 plays a critical role in motor function (Vidoni et al., 2010; Platz et al., 2012; Jacobs et al., 2014).

Studies of human somatotopy have focused considerable effort on attempting to map the representations of digits in the cortex (Baumgartner et al., 1991; Gelnar et al., 1998; Kurth et al., 1998; Francis et al., 2000; Overduin and Servos, 2004; Nelson and Chen, 2008; Schweizer et al., 2008) and the cerebellum (van der Zwaag et al., 2013). Further work has provided evidence for marked topographical differences in the cortical spacing and organization of S1 somatotopy in specific subpopulations, for example, in musicians and individuals with focal dystonia (Bara-Jimenez et al., 1998; Elbert et al., 1998; Meunier et al., 2001; Butterworth et al., 2003; Nelson et al., 2009). Other studies, chiefly using MEG, report a propensity for experience-dependent plasticity in S1 somatotopy (Braun et al., 2000; Schwenkreis et al., 2001; Candia et al., 2003; Stavrinou et al., 2007; Vidyasagar et al., 2014), building upon seminal studies undertaken in nonhuman primates (Allard et al., 1991; Zarzecki et al., 1993). However, the spatial resolution of both MRI and MEG is typically insufficient to make a strong argument about fine-grain digit somatotopy in the somatosensory hand area.

With the increasing prevalence of 7 T MRI scanners, it is now possible to resolve S1 representations of all of the digits in the hand at the level of individual participants. A number of elegant studies at ultra-high field have used tactile stimulation to demonstrate, not only the ability to map digit somatotopy in S1 with a number of paradigms, but also the existence of within-digit somatotopy and cortical overlap between adjacent digit pairs (Sánchez-Panchuelo et al., 2010, 2012; Besle et al., 2013a,b).

Reports of S1 digit maps to date have showcased the novel capabilities of ultra-high-field fMRI (Sánchez-Panchuelo et al., 2012; Besle et al., 2013a,b; Martuzzi et al., 2014; Stringer et al., 2014). In light of the considerable interest in cortical digit maps, and specifically their capacity for plasticity, more thorough cross-sectional and longitudinal analyses are necessary.

Although nonhuman primate data demonstrate considerable intersubject variability in S1 digit somatotopy (Merzenich et al., 1987), little evidence exists to demonstrate stability of the shape and position of S1 digit maps over time. Human studies to date have only considered the reproducibility of isolated individual digit representations or used relatively crude measurements (e.g., center of mass; Vidyasagar and Parkes, 2011; Martuzzi et al., 2014). It therefore remains unclear to what extent reports of intersubject variance in primates could actually reflect intra-individual instability in digit representations in S1. To interpret previous reports of use-dependent plasticity and group variability in human cortical digit representations meaningfully, it is vital to develop a more thorough understanding of S1 digit somatotopy in the healthy population.

Here, we address this fundamental gap in the literature using 7 T fMRI mapping to explore the fine-grain functional organization of S1 at the level of individual human participants. More specifically, we apply a phase-encoding paradigm well validated for sensory body mapping (Sereno and Huang, 2006; Orlov et al., 2010; Sánchez-Panchuelo et al., 2010; Mancini et al., 2012; Zeharia et al., 2015) to investigate whether stable and reproducible maps of individual digits exist in human S1.

Materials and Methods

Participants.

Thirteen healthy control participants (Table 1; mean age: 28.6 ± 5.66; six female) were recruited in accordance with local central university research ethics committee approval (University of Oxford; MSD-IDREC-C2-2013-05). All participants were right handed according to the Edinburgh Handedness Inventory (Oldfield, 1971).

Table 1.

Participant demographic information

	Age	Sex	Handedness	Handedness laterality index	Peak relative head motion (mm)
1	35	F	R	+78	0.20
2	33	M	R	+84	0.13
3	28	M	R	+82	0.32
4	25	M	R	+63	0.26
5	20	F	R	+86	0.35
6	30	F	R	+100	0.81
7	23	F	R	+92	0.20
8	40	M	R	+87	0.41
9	23	M	R	+80	0.53
10	29	F	R	+79	1.25
11	30	F	R	+100	2.65
12	24	M	R	+100	0.54
13	33	M	R	+96	4.11

Handedness laterality index was calculated using the Edinburgh Handedness Score (Oldfield, 1971).

Experimental design.

Participants attended three scan sessions. Two of the sessions were separated by a period of 24 h (0 h and +24 h). The third session took place 4 weeks before or after the other two sessions. During each session, participants underwent a 1 h fMRI scan. One of the sessions also involved an additional scan to acquire a structural image.

MRI acquisition.

fMRI data were acquired using a Siemens 7 T Magnetom system with a 32-channel head coil. An initial functional localizer scan was used to identify hand-movement-related activity to aid slice placement for subsequent task fMRI scans (multislice gradient echo EPI, TR: 3000 ms, TE: 25 ms, flip angle: 90, bandwidth: 1568 Hz, 43 axial slices, 2 × 2 × 2 mm resolution, GRAPPA factor = 2). Task fMRI data were then acquired using a field of view based on the results of the functional localizer; true axial slices were centered on the hand knob activation in the z-axis of the left hemisphere (multislice gradient echo EPI, TR: 1500 ms, TE: 25 ms, flip angle: 90°, bandwidth: 1562 Hz, 22 axial slices, 1.2 × 1.2 × 1.2 mm resolution, GRAPPA factor = 2).

For image registration purposes, single-volume high-saturation EPI images were acquired: one whole brain image and one partial field of view (FOV) image with the same slice placement as the task fMRI. T1-weighted multi-echo magnetization prepared rapid acquisition gradient echo (MEMPRAGE) structural scans were acquired during one of the three sessions (van der Kouwe et al., 2008) using a 3 T Siemens Trio system (TR: 2530 ms, TE: 1.69, 3.55, 5.41 and 7.27 ms, 1 × 1 × 1 mm, GRAPPA factor = 2).

fMRI tasks.

Participants performed a series of tasks involving visually cued movements of individual digits in the scanner: digit 2 (D2: index finger), digit 3 (D3: middle finger), digit 4 (D4: ring finger), and digit 5 (D5: little finger). An active motor task was selected to activate optimally a range of inputs to the cortical somatosensory system, analogous to daily use of the hand. Movement recruits a combination of peripheral receptors encoding a range of somaesthetic modalities, from surface mechanoreceptors to deeper cutaneous receptors and proprioceptors, as well as efference information from the motor system.

During the 3 min functional localizer scan, participants were instructed to appose their right thumb with each of the digits of their right hand sequentially during 15 s movement blocks, contrasted with equivalent periods of rest. All subsequent task fMRI involved individual movements of D2, D3, D4, and D5 in the form of button presses using an MRI-compatible four-finger button-box (manufactured in-house) resting on the participant's right thigh during the scan. Participants were presented with four white circles, corresponding to the four digits of the right hand, shown on a visual display projected into the scanner bore. The displayed circles flashed individually at a constant frequency to cue participants to make button presses at the specified rate. A further discussion of the caveats associated with using an active motor task in the study of S1 is provided in the “Limitations” section below.

A phase-encoding task was used, which involved continuous button presses with no rest periods (Fig. 1A). The task consisted of movement blocks of 8 s in duration, during which participants moved one digit (D2–D5) at a rate of 1 Hz. The phase-encoding forward task cycled through blocks of D2, D3, D4, and D5 in a repeating sequence (8 repetitions of the cycle; Fig. 1A). The phase-encoding backwards task cycled through blocks of D5, D4, D3, and D2 in a repeating sequence (8 repetitions of the cycle). The total duration of the phase-encoding task was 8 min 50 s. The activation maps derived from the phase-encoding forward and backward tasks were averaged voxelwise; further details are provided below.

Figure 1.

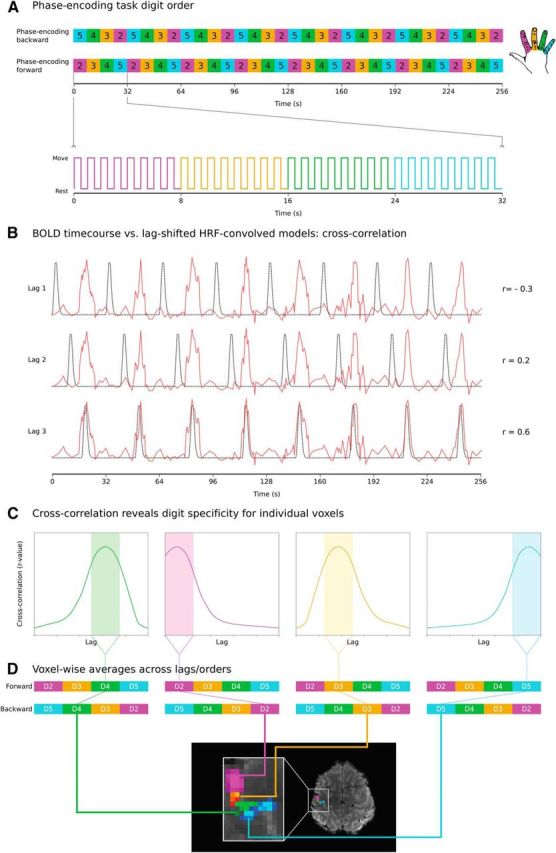
Overview of phase-encoding digit mapping task and analysis. A, Phase-encoding paradigm: 8 × 32 s cycles of continuous button presses at 1 Hz. Each 32 s cycle consists of 4 8 s blocks, with each block cycling through either D2–D5 (forward) or D5–D2 (backward). B, BOLD time courses from individual voxels (1 time course shown) cross-correlated against reference models (8 s “on,” 24 s “off”) shifted iteratively by a number of lags to capture activation throughout the movement cycles. C, Plotting cross-correlation of each voxel's time course as a function of lag reveals peak cross-correlation at a given lag. Four different voxels are shown, each with a cross-correlation peaking in lags corresponding to different digits. D, r-values for each voxel averaged across lags assigned to specific digits. Resulting digit r-value maps for forward and backwards cycled are also averaged to yield voxelwise r-value maps for each digit for one subject/time point (thresholded maps displayed).

A standard block task was also undertaken, which involved movement blocks and rest blocks, both 12 s in duration. A total of four movement blocks were acquired per digit (16 movement blocks total) in a counterbalanced order randomized across visits. During movement blocks, participants were instructed to perform movements of a specific digit at 1 Hz (e.g., D2, D2, D2, D2… ). Each movement block was separated by a rest block. The total duration of the block task was 6 min 24 s.

MRI analysis.

MRI analysis was undertaken using tools from FSL and the Connectome Workbench (Smith et al., 2004; Woolrich et al., 2009; Marcus et al., 2011; Jenkinson et al., 2012). MRI data were projected to cortical surface reconstructions produced with FreeSurfer T1-weighted MEMPRAGE images (Dale et al., 1999; Fischl et al., 2001).

MRI preprocessing.

All fMRI data were subject to the following preprocessing steps: motion correction using MCFLIRT (Jenkinson et al., 2002), removal of nonbrain tissue using the Brain Extraction Tool (Smith, 2002), high-pass temporal filtering (Gaussian-weighted least-squares straight line fitting with σ = 100 s), and spatial smoothing using a Gaussian kernel of FWHM 1.5 mm.

Image registration.

Image registration was undertaken within participants using FLIRT (Jenkinson and Smith, 2001; Jenkinson et al., 2002) and Freesurfer's Freeview. Task fMRI data from the three scan sessions were first registered to a partial-FOV high-saturation EPI image acquired during an additional scan session to avoid biasing any single time point (six degrees of freedom, normalized correlation cost function). The partial-FOV high-saturation EPI image was then registered to the T1-weighted MEMPRAGE image using boundary-based registration (BBR; degrees of freedom: 6, FMRIB's Automated Segmentation Tool white matter segmentation, no search; Greve and Fischl, 2009), initialized with an affine registration matrix. The results of the BBR were used as a starting point for manual alignment of the single-volume partial-FOV high-saturation EPI image to the structural MEMPRAGE white matter and pial surfaces using blink comparison as implemented in Freeview, an approach applied previously in studies of fine-grain topography (Mancini et al., 2012).

Phase-encoding analysis.

The phase-encoding task fMRI data were analyzed using a cross-correlation approach previously applied in retinotopy and more recently for body mapping (Engel et al., 1997; Wandell et al., 2007; Orlov et al., 2010; see “Limitations” section for further discussion. This analysis used cross-correlation to find the time point in the phase-encoding forward (D2–D5) and phase-encoding backwards (D5–D2) tasks at which each cortical voxel responded maximally.

To achieve this, the preprocessed BOLD EPI data were correlated against a series of reference models. The model was composed of a gamma-convolved boxcar: 8 s “on” and 24 s “off” repeated eight times, mirroring the eight 32 s cycles of the phase forward and phase backward tasks (Fig. 1B, black). The model was shifted in time iteratively by a number of lags so that activity throughout the cycle could be modeled (Fig. 1B). This approach increases sensitivity to track a wave of activation (Engel, 2012), in this case associated with the cycles of movement that progress either from D2 to D5 or D5 to D2. A correlation was calculated between the raw BOLD signal of each voxel (Fig. 1B, red) and the reference model at each lag (Fig. 1B, black). Each iteration shifted the model by a given lag (1.5 s). With each lag, the 8 s “on” of each 32 s cycle was time shifted (e.g., model 1: 8 s on/24 s off; model 2: 1.5 s off/8 s on/22.5 s off; model 3: 3 s off/8 s on/21 s off… ), with sufficient shifts to cover 1 32 s cycle. By plotting for each voxel the cross-correlation at each voxel as a function of the lag, a tuning curve was created for each voxel, demonstrating the optimal model fit for that voxel (Fig. 1C). Each lag was assigned to a given digit in the cycle. Voxels responsive to a particular digit demonstrate a peak cross-correlation within the lags corresponding to movement that digit in the cycle.

For each participant and session, the r-values resulting from the cross-correlation analysis specified above (Fig. 1C) were averaged across the lags assigned to the same digit to yield digit maps (D2, D3, D4, D5) for each of the phase-encoding forward and phase-encoding backwards tasks. For each participant and each session, the maps for each digit from the phase-encoding forward and phase-encoding backward tasks were resampled to the single-volume partial-FOV high-saturation EPI space and averaged to give a single voxelwise r-value map for each session and for each digit (Fig. 1D). For each participant, session, and digit, a corresponding voxelwise z-statistic map was calculated on the basis of the distribution of values within the brain tissue of the FOV for which BOLD EPI data were acquired. These soft-edged maps were further masked using a winner-take-all approach to produce digit maps in which each voxel was assigned exclusively to one digit.

Block task analysis.

The block task fMRI data were analyzed using a GLM in the FMRIB Expert Analysis Tool (FEAT). All analysis was undertaken on the single-participant level, using FMRIB's Improved Linear Model (FILM) to estimate time series autocorrelation and to prewhiten each voxel. Each digit was modeled with a separate boxcar regressor with gamma-HRF convolution and its temporal derivative, giving a total of eight regressors. FEAT was used to produce activation maps corresponding to each of the four digits by contrasting a given digit regressor to the rest blocks (e.g., D2 > rest).

Surface projection.

Phase-encoding z-statistic digit maps were projected to 2D surface space using a cortical ribbon mapping method implemented in the Connectome Workbench. This approach estimates the contribution of multiple voxels to one point on the cortical surface and weights the values therein accordingly.

For visualization on the cortical surface of individual participants, winner-take-all z-statistic maps for each digit and time point were thresholded using false discovery rate (FDR) to determine a corrected p-value threshold on the basis of the observed p-value distribution within the data (α = 0.001; Genovese et al., 2002). This resulted in individually defined FDR thresholds for each map under consideration (Table 2).

Table 2.

FDR thresholds for single-participant digit maps

	0 h				+24 h				±4 weeks
	D2	D3	D4	D5	D2	D3	D4	D5	D2	D3	D4	D5
1	5.17 (7.97)	4.17 (10.6)	3.93 (5.87)	4.25 (7.62)	6.16 (9.38)	4.82 (8.13)	4.80 (10.1)	6.28 (11.4)	5.71 (10.1)	4.73 (9.26)	5.78 (11.7)	6.25 (11.2)
2	3.91 (6.53)	2.87 (6.83)	3.96 (5.46)	4.53 (9.32)	5.22 (6.91)	3.07 (5.42)	4.68 (6.63)	4.53 (7.76)	5.19 (8.98)	3.11 (5.93)	5.26 (7.44)	5.48 (8.18)
3	6.21 (9.38)	3.02 (10.7)	4.09 (12.9)	6.85 (9.11)	5.75 (10.6)	4.80 (8.94)	5.02 (12.7)	5.81 (7.53)	6.40 (11.9)	5.45 (8.84)	7.27 (12.3)	6.32 (8.39)
4	5.79 (9.79)	4.90 (8.01)	5.79 (8.91)	3.22 (7.27)	4.83 (7.88)	3.49 (6.75)	5.05 (7.98)	4.16 (6.43)	5.93 (9.47)	3.38 (6.21)	5.52 (9.14)	3.78 (6.73)
5	5.16 (7.90)	4.89 (10.1)	5.71 (8.19)	4.98 (8.02)	5.76 (8.16)	5.53 (8.66)	6.53 (8.22)	3.46 (6.72)	5.69 (8.04)	3.80 (7.02)	3.28 (6.47)	3.43 (5.70)
6	3.02 (5.30)	3.49 (5.86)	3.04 (6.24)	3.52 (6.50)	3.30 (4.60)	3.46 (5.64)	4.97 (6.52)	2.92 (4.20)	2.90 (4.80)	3.21 (9.90)	3.43 (6.41)	3.14 (5.72)
7	4.57 (6.71)	4.46 (6.13)	4.79 (7.78)	3.70 (4.90)	4.04 (5.73)	3.63 (5.63)	3.68 (5.48)	4.99 (7.06)	4.60 (6.31)	3.15 (7.08)	4.50 (7.48)	3.73 (5.11)
8	4.10 (7.99)	4.12 (13.4)	5.57 (7.96)	5.14 (8.28)	4.91 (11.2)	5.97 (14.0)	4.82 (8.58)	6.51 (9.46)	4.86 (9.89)	3.14 (8.10)	5.78 (8.87)	5.85 (10.9)
9	5.48 (8.64)	4.28 (10.5)	7.20 (9.50)	4.77 (6.03)	4.27 (9.61)	2.97 (6.01)	3.14 (9.65)	5.39 (7.20)	5.11 (8.29)	4.13 (5.26)	6.63 (10.0)	5.05 (7.46)

FDR thresholds (maxima in parentheses) for z-statistic phase-encoding derived digit maps for individual participants shown in Figures 3 and 4 across the three time points under study. FDR, False discovery rate (α = 0.001). A two-way repeated measures ANOVA was performed to assess for systematic differences in FDR-defined thresholds, with one factor of digit (D2–D5) and one factor of session (0 h, +24 h, ±4 weeks). There was no significant main effect of session on FDR threshold: F_(2,16) = 0.218, p=0.806, sphericity assumed.

For intersubject comparison, volumetric winner-take-all z-statistic maps were resampled into atlas space using combined volumetric and surface (CVS) registration to achieve accurate and robust alignment with the CVS atlas (Postelnicu et al., 2009) and projected to the atlas 2D surface using the cortical-ribbon mapping method.

Intrasubject reproducibility.

The Dice coefficient (Dice, 1945) was used to assess the reproducibility of phase-encoding digit maps over time, quantifying the spatial similarity of digit map areas. The Dice coefficient varies from 0 (no overlap between digit maps) to 1 (perfect overlap between digit representations). For each digit, the winner-takes-all digit maps for that digit were thresholded (FDR α = 0.001) and overlap was calculated between each possible pairing across each of the three time intervals. Where A and B are the area of the two digit representations, the dice coefficient is expressed as follows:

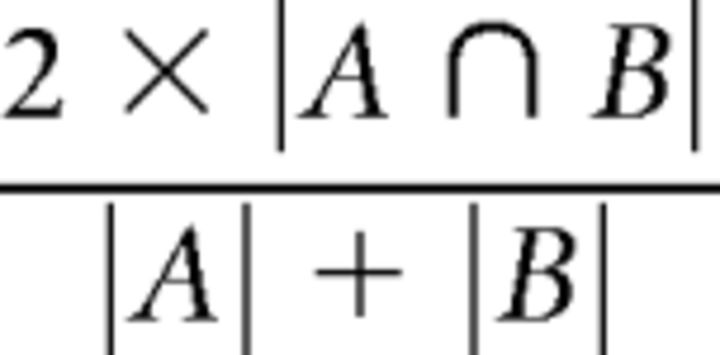Intersubject variability.

The variability in the spatial location of individual digit representations across participants was assessed using the Dice coefficient. Surface-area-based thresholding was applied to the winner takes digit maps such that the maximal 80 mm² of activation within S1 for a specific digit was considered. Digit representations with this surface area were present within S1 for every participant and time point. The interpretability of a Dice coefficient (Eq. 1) calculated across different subjects could be affected by intersubject differences in the size of digit representations. The use of a fixed surface area for each digit representation excluded any effect of intersubject variability in the spatial size of digit maps on intersubject comparisons. Each winner-takes-all digit representation at time point 0 h was compared with each other winner-takes-all digit representation at time point ± 4 weeks across all participants.

Dice coefficients were used to construct a large intersubject Dice comparison matrix (36 × 36 cells) composed of submatrices (9 × 9 cells) for all possible digit pairings. To compare digit representation overlap intrasubject (submatrix diagonal) with digit representation overlap intersubject (submatrix off-diagonals), measures of the matrix dominance ratio (Mdr) were calculated for each submatrix (Greene and Cunningham, 2006). The Mdr of a square matrix K of width and height n can be expressed as follows:

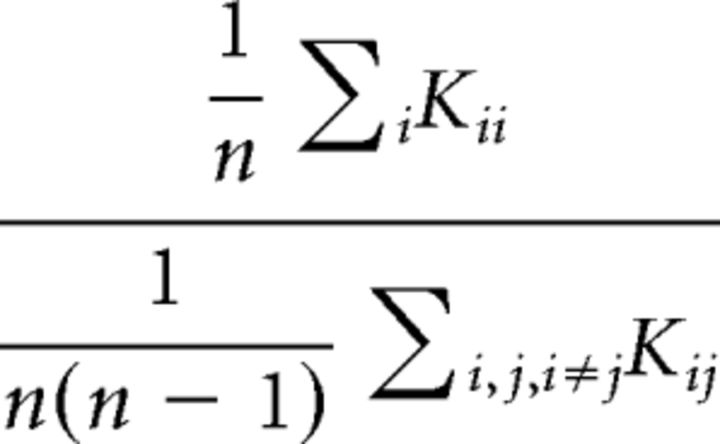Values of Mdr >1 would therefore be observed in cases in which the average Dice overlap of two digit representations within the same subjects (the matrix diagonal) is of greater magnitude than the average Dice overlap made across different subjects (the matrix off-diagonals).

A higher-level matrix of the Mdr values for each digit pairing was constructed, from which an overall Mdr value was calculated. A high value of overall Mdr in this matrix would suggest high matrix dominance in comparisons of “same” digits (e.g., D2–D2, D3–D3… ) and low levels of matrix dominance in comparisons on “different” digits (e.g., D2–D3, D3–D5… ). This in turn would support the hypothesis that intrasubject overlap in “same” digits is greater than intersubject overlap in “same” digits.

Bootstrap resampling was applied to the large intersubject Dice comparison matrix (36 × 36 cells) to quantify the likelihood of observing the reported pattern by chance and therefore the statistical significance of the overall Mdr value.

Additional measures of reproducibility and variability.

In addition to the primary Dice measures of intrasubject reproducibility and intrasubject variability, additional features of the phase-encoding digit maps were assessed. At each time point, soft-edged phase-encoding maps (FDR α = 0.01) were used to assess the amount of overlap between different digit representations within S1. These measures sought to characterize the extent of shared cortical territory between different digit representations, which the winner-takes-all maps do not capture, and to assess the consistency in the extent of this overlap at each time point. The extent of this overlapping shared territory was expressed as a Dice coefficient. The pattern of overlap in these soft-edged digit representations was represented in 4 × 4 matrices for each participant and each time point. The pattern in these matrices were compared using a ranked Mantel test (Mantel, 1967) to quantify both the intrasubject consistency in the overlap pattern and the intersubject variability therein.

In a complementary analysis, peak z-stat coordinates for each digit were calculated with S1 on the inflated cortical surface, allowing for the calculation of geodesic distances between adjacent digits for each time point (D2–D3, D3–D4, D4–D5), which were again assessed for consistency.

Identifying additional digit maps.

To increase statistical power to identify further somatotopic digit maps previously reported in S1 (Iwamura et al., 1980; Pons et al., 1985; Huffman and Krubitzer, 2001), an additional all-session phase-encoding map was produced by coregistering and averaging the forward and backward lags from all three sessions before processing the resulting maps as outlined above using a more liberal FDR threshold (α = 0.01).

Statistics.

All statistical analysis and graphing were undertaken using JMP version 11.0 (SAS Institute) and Statistics Package for the Social Sciences version 19.0 (IBM).

Results

All BOLD EPI data were assessed for excessive motion both visually and using motion estimate outputs from MCFLIRT: data from three participants exhibited visible spin history motion artifact as a result of sharp motion during one or more scan sessions (>1 mm of absolute mean displacement in fewer than five volumes; Table 1); these participants were excluded. Further analysis found no significant or systematic correlation between the task design and motion parameters in the remaining participants. One further participant was excluded on the grounds of an incidental finding. Nine participants were considered in further analysis (Table 1: participants 1–9; mean age: 28.5 ± 6.54; 4 female; −4 weeks: 4 participants; +4 weeks: 5 participants).

Phase-encoding digit maps in S1

The thresholded activation maps from the phase-encoding analysis displayed a clear and specific pattern in the left postcentral gyrus around the anatomically characteristic hand knob (Fig. 2A,D; Yousry et al., 1997). Maps showed a pattern of progression from the lateral-most representation of digit two to the medial-most representation of digit five (Fig. 2C,D), a pattern that was consistent across all participants and time points (Figs. 3, 4). However, the maps showed striking qualitative differences in shape and orientation across participants, consistent with reports of intersubject variability from the nonhuman primate literature (Merzenich et al., 1987).

Figure 2.

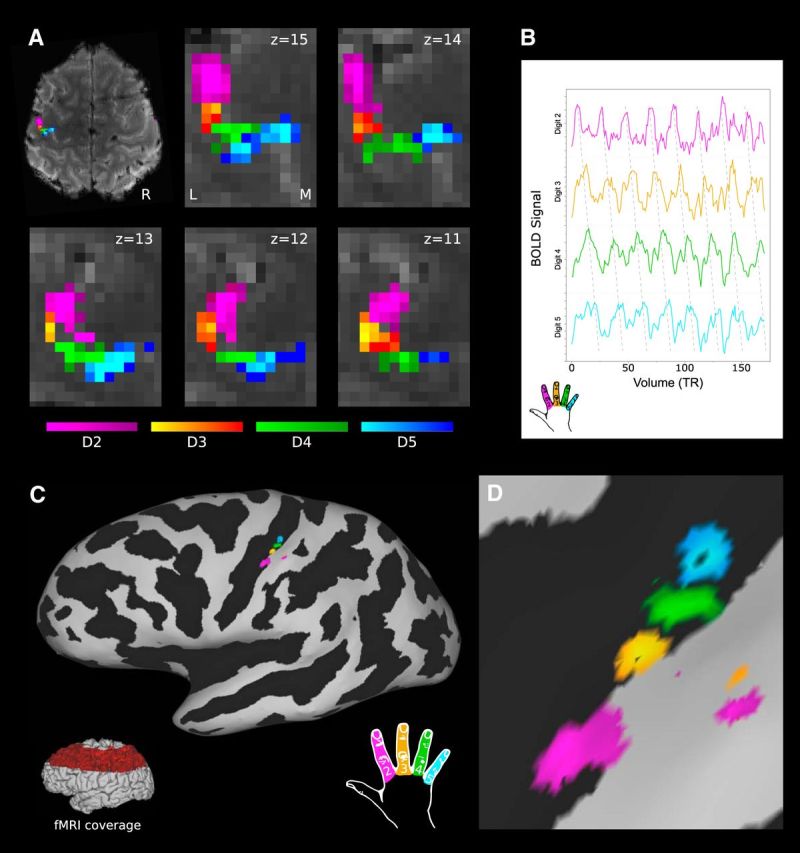
Phase-encoding digit maps from a single participant and time point. A, Digit maps in BOLD EPI volumetric space across five adjacent transverse slices (z: 11–15); FDR threshold (α = 0.001). Pink, D2; orange, D3; green, D4; blue, D5. R, Right; L, lateral; M, medial. B, Post hoc analysis of BOLD signal from individual digit representations in this participant. C, D, Surface projection of digit maps shown on the inflated pial surface (black: sulcal pattern). Red highlighted region (C, inset) indicates coverage of BOLD EPI task fMRI data partial field of view. No masking has been applied within the acquisition field of view.

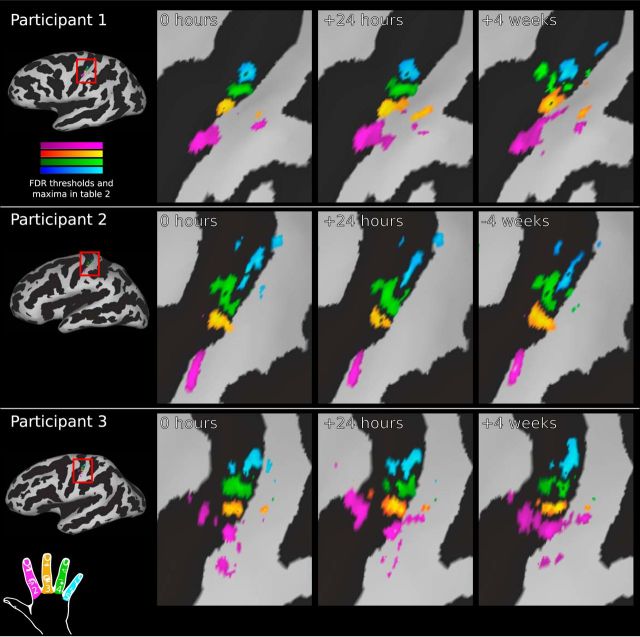
Figure 3.

Temporal reproducibility of phase-encoding digit maps within participants. Shown is a comparison of phase-encoding digit representations at three scan time points for three participants. Although there is a high degree of between-subject variability (as shown by the large differences between rows), there is very little within-subject variability over time (demonstrated by the small differences across each row). Cortical are maps shown on the inflated pial surface with the sulcal pattern in black (positive curvature). Magnification panels are centered on the hand knob of the central sulcus. All digit maps are subject to FDR thresholding (α = 0.001); full details of thresholds and maxima for each time point provided in Table 2; color bars represent a range from zero to maximum.

Figure 4.

Temporal reproducibility of phase-encoding digit maps within participants (continued). Shown is a comparison of phase-encoding digit representations at three scan time points continued from Figure 3 for the remaining participants. All digit maps are subject to FDR thresholding (α = 0.001); full details of thresholds and maxima for each time point provided in Table 2.

Activation was isolated to the S1 on the postcentral gyrus, with minimal extraneous activation within the FOV in which BOLD EPI data were acquired (Fig. 2C); no mask or region of interest (ROI) has been applied to any digit maps presented herein. The Brodmann areas that constitute the S1 cannot be defined accurately on the basis of gross anatomy alone. However, the location of the observed digit representations is broadly anatomically consistent with the location of Brodmann area 3b: on the posterior bank of the central sulcus, posterior to area 3a in the nadir, and anterior to area 1 at the apex of the postcentral gyrus. Some subjects displayed partial additional maps more posteriorly in regions consistent with Brodmann area 2 or 1 (Figs. 3, 4, participants 3 and 9).

A post hoc ROI analysis was used to explore the BOLD signal underlying the phase-encoding digit maps. The average BOLD signal time course was extracted within each digit representation (z > 3.5; Fig. 2B). These showed clear and specific activation patterns in a sequence consistent with the phase-encoding task digit order.

Intrasubject digit map reproducibility over 24 h and 4 weeks

Surface projections of digit maps derived from phase-encoding analysis qualitatively display a striking degree of reproducibility of these fine-grain maps at the single-participant level across both the 24 h and 4 week map–remap intervals (Figs. 3, 4). To assess quantitatively the intra-invidual reproducibility of the phase-encoding derived digit maps, Dice similarity coefficients were used to compare the spatial extent of digit representations across sessions.

A Dice coefficient was calculated between every possible digit pairing and every possible time point pairing (Fig. 5A) within a FreeSurfer anatomically defined ROI of S1 overlapping the fMRI acquisition volume. This analysis demonstrated a very high degree of spatial concordance between “same” digit representations across all time intervals.

Figure 5.

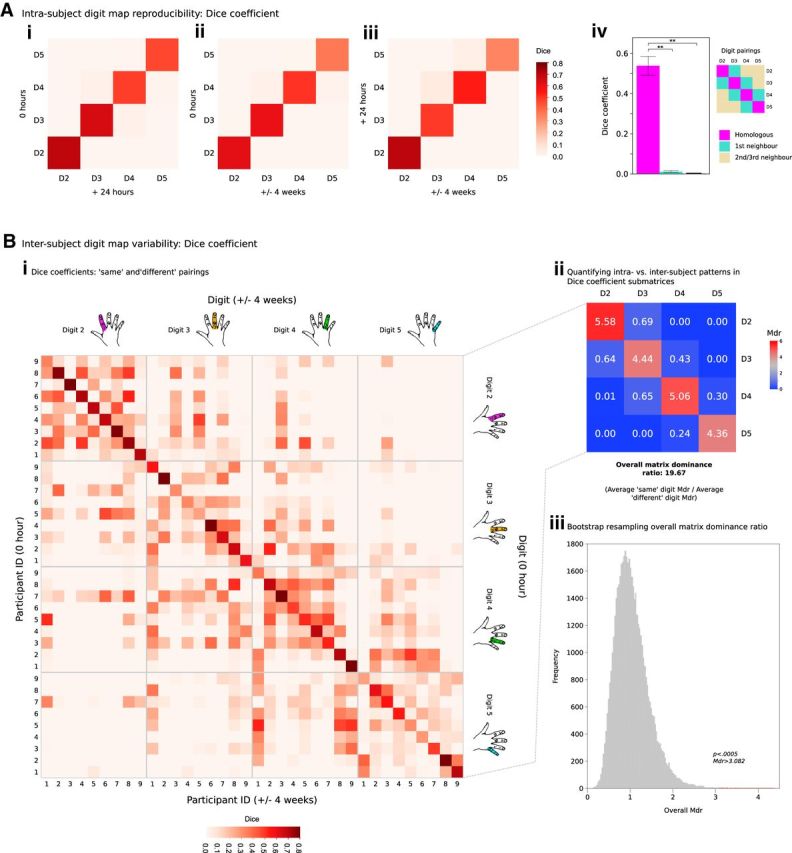
Quantifying intrasubject reproducibility and intersubject variability in phase-encoding digit maps. Ai–Aiii, Dice coefficients demonstrate a clear pattern of reproducibility for maps of homologous digits across the three time points under study compared with first-order and second-/third-order neighbors. Aiv, Dice coefficients for homologous digits were greater than the equivalent value between nonhomologous digit pairings: one-way repeated-measures ANOVA: significant main effect of digit pairing category (homologous, first-order neighbor, second-/third-order neighbor). **Post hoc analysis (Bonferroni adjusted): p < 0.0005. Bi, Dice coefficients comparing all combinations of individual digit representations across different participants (after accounting for differences in digit map size) across 0 h and ± 4 week time points. Bii, Patterns in each digit pair submatrix were summarized by the Mdr (Eq. 2). Mdr >1 suggests greater intrasubject overlap in digit representations; Mdr <1 implies greater intersubject overlap in digit representations. For “same” pairings (e.g., D2–D2), a pattern of high overlap was seen intrasubject (Bi; submatrix diagonals), contrasted with lower overlap values for comparisons intersubject (Bi; submatrix off-diagonals). For “different” pairings (e.g., D2–D4), no such pattern was observed, suggesting that intrasubject consistency is driven by reproducibility of the spatial patterns for the same digits over time. Biii, Calculation of the overall Mdr (from Bii) was subjected to bootstrap resampling (50,000 iterations) to account for the likelihood of observing these dominance ratios by chance. Bootstrapping returned p < 0.0005 for the observed value of overall Mdr, consistent with the notion of intersubject variability in fine-grain digit representations.

The reproducibility matrices were averaged across the two different time intervals and further averaged into three digit pairing categories: homologous digits, first-order neighbors, and second-/third-order neighbors (Fig. 5Aiv) to assess whether the Dice coefficient for homologous digits was significantly greater than the equivalent value between nonhomologous digit pairings. A one-way repeated-measures ANOVA was performed with one factor of digit pairing category. There was a significant main effect of digit pairing category on the Dice coefficient (F_(2,19) = 119.429, p < 0.0005). Post hoc analysis with a Bonferroni adjustment revealed that the Dice coefficient was significantly greater for homologous digit pairings [average Dice coefficient: 0.542, 95% confidence interval (CI): 0.380–0.584] compared with pairings of first-order neighbors (average Dice coefficient: 0.010, 95% CI: 0.000–0.020), and pairings of second- and third-order neighbors (average Dice coefficient: 0.001, 95% CI: 0.000–0.002; all p < 0.0005, Bonferonni adjusted). The same pattern of results was also seen using an equivalent analysis approach on volumetric data rather than surface-projected data.

Intersubject digit map variability

Consistent with qualitative observations (Figs. 3, 4), Dice analysis comparing the spatial location of individual digit representations (Fig. 5Bi) demonstrates a considerable degree of intersubject variability compared with the consistency seen intrasubject. In comparison of “same” digits over time (e.g., D2–D2, D3–D3), the degree of overlap observed intrasubject exceeds that observed intersubject, resulting in values of Mdr >1. This is consistent with the notion of variability in the spatial position of individual digit representations. In contrast, for “different” comparisons (e.g., D2–D4), the degree of overlap observed intersubject exceeds the degree of overlap observed intrasubject, yielding values of Mdr <1. This further strengthens our claim that intrasubject consistency is driven by reproducibility of the spatial patterns for the same digits over time, rather than other irrelevant aspects of the map (e.g., geometrical cluster characteristics).

Values of Mdr for each digit comparison are summarized in Figure 5Bii. From this matrix, a value of overall Mdr was calculated at 19.67 (Eq. 2: average Mdr for “same” digit pairings/average Mdr for “different” digit pairings). To substantiate the observed pattern and value of overall Mdr yielded, we applied bootstrap resampling to the intersubject Dice comparison matrix (50,000 iterations) to account for the likelihood of observing this value by chance (Fig. 5Biii), yielding p < 0.0005.

Overall, the observed pattern of intersubject versus intrasubject Dice overlap provided strong evidence supporting the presence of considerable variability in the spatial distribution of individual digit representations across participants, contrasted with consistency within participants over time.

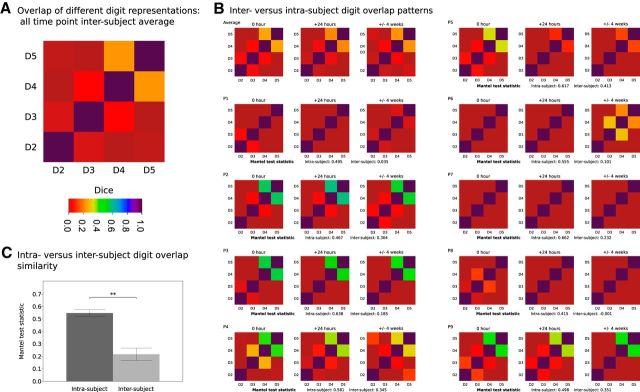
Additional features of cortical digit maps

Measures of shared cortical territory between different digit representations were calculated at each time point (Fig. 6). The intersubject average matrix reveals previously established features of S1 digit representations, with higher overlap in digit pairs such as D4 and D5 and low overlap between D2 and D3 (Fig. 6A), consistent with patterns of daily usage (Ejaz et al., 2015). The similarity of cortical overlap patterns for each participant and time point (Fig. 6B) was assessed using a ranked Mantel test. An intrasubject value was derived for each participant from the average of matrix comparisons within subject but over time. An intersubject value was derived for each participant from the average of matrix comparisons between that subject and all other subjects for a given time point; this was repeated for each time point and the results were averaged. Comparison of the intrasubject versus intersubject Mantel test values revealed greater similarity of values within a given subject compared with across different subjects (paired-sample t test, t₍₈₎= −7.17, p < 0.0005).

Figure 6.

Patterns of overlap between different digit representations. Soft-edged phase-encoding digit maps provide information regarding shared cortical territory of different digit representations. A, Average measures of cortical overlap between different digit representations across all subjects and time points reveal pattern of greater shared territory across functionally coupled digits: the relative independence of D2, with increasing levels of cortical overlap between more synergistic D3/D4 and D4/D5. B, Cortical overlap matrices for individual participants and time points; ranked Mantel test statistics were used to compare matrices. Intrasubject comparisons: average Mantel test statistic for intrasubject comparisons across the three time points. Intersubject comparisons: average of the Mantel test statistic calculated between each participant at a given time point and all other participants at that time point calculated for each time point and averaged. C, Comparison of the intrasubject versus intersubject Mantel test statistics revealed greater similarity of values within a given subject compared with across different subjects (paired-sample t test, **p < 0.0005).

Measures of peak-to-peak distance for adjacent digit representations were calculated at each time point. These measurements are provided in full in Table 3. The intrasubject consistency in these measured was quantified using Cronbach's α, which returned the following values: D2–D3: 0.9714, D3–D4: 0.8526, and D4–D5: 0.8422. These measures support a high degree of consistency across the observed digit maps over time.

Table 3.

Peak-to-peak distances (mm) for single-participant digit maps across sessions

	Digits 2–3			Digits 3–4			Digits 4–5
	0 h	+24 h	±4 weeks	0 h	+24 h	±4 weeks	0 h	+24 h	±4 weeks
1	13.56	12.53	10.53	3.38	3.99	3.61	5.82	2.75	3.55
2	15.48	14.83	15.88	8.00	4.04	3.89	8.67	11.33	10.43
3	5.45	5.14	5.16	7.35	5.19	5.56	5.51	4.67	8.13
4	14.41	16.65	16.49	4.13	3.20	3.24	4.20	11.93	11.82
5	3.48	2.26	6.11	9.11	10.56	8.65	5.06	4.66	5.66
6	13.64	9.72	13.50	5.65	6.40	12.14	6.54	5.81	5.79
7	4.62	3.19	4.62	10.64	16.21	10.64	12.37	11.09	16.87
8	10.99	11.68	9.07	6.66	5.18	5.90	4.25	7.40	4.25
9	10.51	10.32	11.03	10.55	12.10	8.63	4.32	4.85	8.00

Multiple digit maps across S1

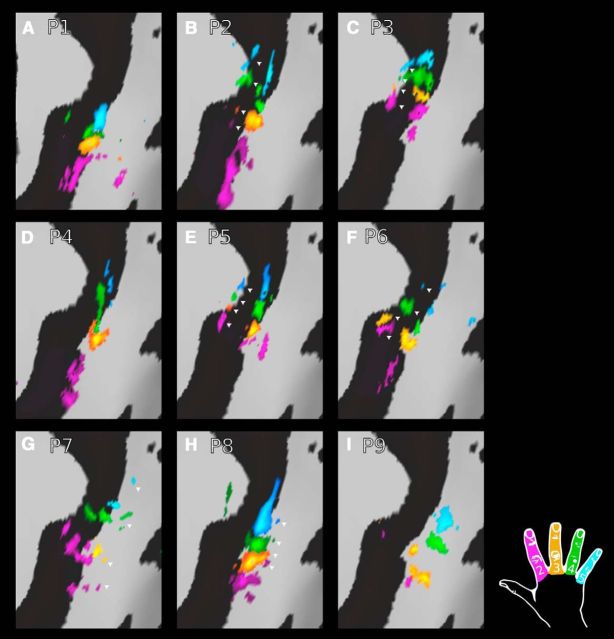
To reveal additional maps previously reported in S1 with weaker digit selectivity (Kaas et al., 1979; Pons et al., 1985; Huffman and Krubitzer, 2001), an all-session average phase-encoding map was produced for each participant and resampled into a common space (FDR thresholding, α = 0.01). Additional maps were seen in a subset of participants. A more anterior map was observed in some individuals (Fig. 7B,C,E,F) and a more posterior map (Fig. 7G,H) in others, both within S1 (see Discussion for further information regarding S1 subdivisions).

Figure 7.

Resolving additional digit maps within S1. An all-session average phase-encoding map was produced for each participant and resampled into a common space (FDR thresholding, α = 0.01). Additional maps were seen in a subset of participants. A more anterior map was observed (arrowheads: B, C, E, F) in some individuals and a more posterior map (arrowheads: G, H) in others, both within S1. In the remaining participants (A, D, I), no clear evidence for additional maps was found.

Strong concordance between phase-encoding and block design activation

To validate finger selectivity identified using the phase-encoding task, concordance with independently derived sets of digit map data from a GLM analysis of the block task was assessed. The normalized β values from the block task GLM contrasts comparing each digit with rest (e.g., D2 > rest) were extracted at the peak voxel of each phase-encoding derived digit representation (Fig. 8). These values were averaged for each digit across the three scan sessions for each participant.

Figure 8.

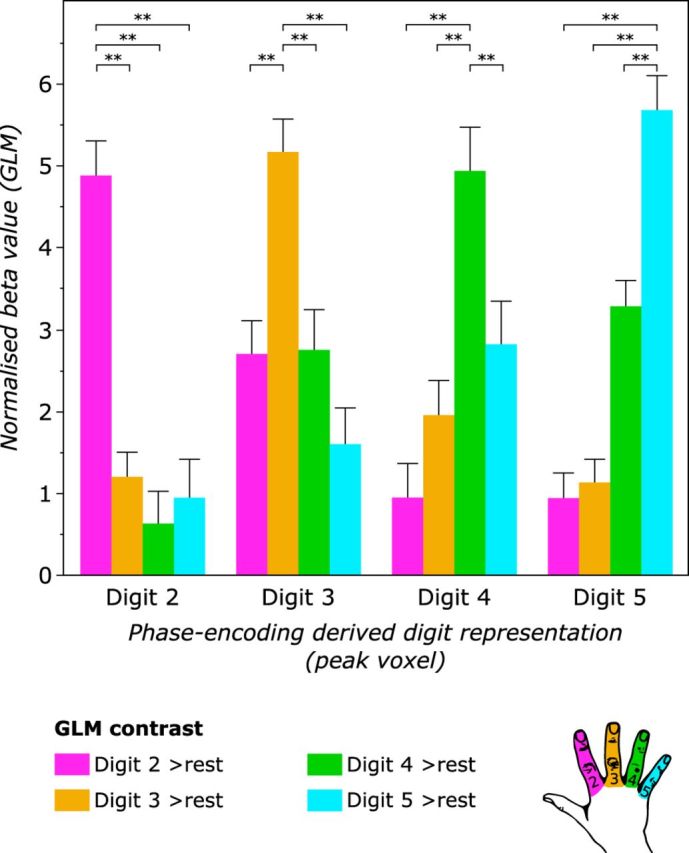
Validation of phase-encoding digit maps using block design data. Beta values from the block design task fMRI data were extracted for each GLM contrast (digit > rest) at the peak voxels of the phase-encoding digit representations (D2–D5). This process was repeated for each of the three scans to derive average values for each participant. For each phase-encoding digit representation, the β value of the homologous GLM contrast (e.g., D2 phase-encoding vs D2 > rest GLM contrast) was significantly greater than for nonhomologous GLM contrasts (e.g., D2 phase-encoding vs D4 > rest GLM contrast). RM-ANOVA: significant interaction between phase-encoding digit representation and the digit contrast of the block design GLM on the normalized β value. **Post hoc t test, p < 0.0005 (uncorrected).

A two-way repeated-measures ANOVA was performed to assess the agreement of the two mapping methods, with one factor of phase-encoding digit representation (D2–D5) and one factor of block design digit representation (D2–D5). There was a significant interaction between phase-encoding digit representation and block design digit representation on the normalized β value (F_(9,72) = 69.15, p < 0.001, sphericity assumed). Post hoc paired-samples t tests demonstrated a significantly stronger relationship between the phase-encoding and block design digit representations for “same” digits compared with “different” digits (all p < 0.0005, uncorrected). For example, the peak voxel for phase-encoding D2 has larger β value for the D2 > rest block task contrast compared with other digit contrasts from the block design (e.g., the D4 > rest GLM contrast). These results indicate an agreement between the two mapping methods: the peak voxel from the phase-encoding-derived map of a given digit shows a maximal normalized β value for the GLM contrast specific to the same digit.

Discussion

In the present study, we report highly reproducible maps of fine-grain digit somatotopy in S1 at the level of individual participants, as demonstrated in all nine participants under study (Figs. 3, 4). These maps were reproducible across up to a 4 week interval (Fig. 5A). The consistency across this interval is particularly striking given the minimally supervised and easily implemented motor task used in this study. Unlike previously reported passive sensory stimulation paradigms used in digit mapping (Huang and Sereno, 2007; Sánchez-Panchuelo et al., 2010; Martuzzi et al., 2014; Stringer et al., 2014), the motor task applied here is more akin to everyday use of the hand.

The map reproducibility observed within individuals was sharply contrasted by a high degree of spatial variability in these maps across different participants. Despite a common ordering and progression of digits along the central sulcus (Figs. 3, 4), the shape and relative position of these representations differed, as has been shown previously in primates (Merzenich et al., 1987). We demonstrate the existence of considerable intersubject variability in the spatial distribution of individual digit representations (Fig. 5B, Table 3). Together, these results robustly demonstrate the presence of very stable fine-grain somatotopy of the four digits under study in human S1, but also highlight the population variability in such detailed functional architecture in the human brain.

Digit maps in Brodmann area 3b and beyond

Using the FDR threshold applied here (α = 0.001), the maps observed at each time point across all participants under study were located in a region anatomically consistent with Brodmann area 3b (Figs. 3, 4). The presence of well delineated maps in Brodmann area 3b is well described in microelectrode mapping studies of individual digits in nonhuman primates (Kaas et al., 1979; Merzenich et al., 1987). The winner-takes-all phase-encoding approach applied herein is well suited to revealing such regions of high digit selectivity. This strong digit selectivity was an important feature in being able to address the question of consistency in such fine-grain cortical organization.

Digit maps in Brodmann areas 3a, 1, and 2 show more limited digit selectivity (Kaas et al., 1979; Pons and Kaas, 1986; Huffman and Krubitzer, 2001). Although it was not possible to resolve evidence for these maps at each time point (Figs. 3, 4), pooling phase-encoding data across the three time points under study to produce an all-session average and using a more liberal FDR threshold provided further insight (Fig. 7). Some individual participants displayed very clear smaller maps anterior and posterior to that presumed to be area 3b. These maps are potentially consistent with Brodmann areas 3a and 1/2, respectively.

Because our data do not allow us to define reliably the constituent Brodmann areas in S1 at the level of individual participants, we are unable to discuss the position of these additional maps. Although atlases do provide Brodmann area boundaries, these vary considerably across individuals and accurate definition would rely on cytoarchitectural information rather than gross anatomy (Zilles and Amunts, 2010). Indeed, certain subdivisions (Brodmann areas 3a/4) are challenging to delineate definitely even on the basis of cytoarchitecture (Mountcastle, 2005).

Digit map reproducibility and variability

In this study, we demonstrate, both qualitatively (Figs. 3, 4) and quantitatively (Fig. 5A), a strikingly high degree of reproducibility in digit somatotopy. Previous work at 7 T has reported measures of digit map reproducibility either only across different runs within a single scanning session (Stringer et al., 2011) or consistency in the relatively crude measure of center of mass location of digit representations in subjects scanned on two occasions with variable intervals between them (Martuzzi et al., 2014). Here, we were able to provide evidence for very clear reproducibility in digit maps based on the 2D area of digit representations on the cortical surface. This was also supported by additional measures of reproducibility: measures of shared cortical territory of different digit representations and peak-to-peak distance between adjacent representations (Fig. 6, Table 3). These same measures also highlight the variability seen across participants.

S1 and motor function

S1 acts broadly as both a processing region for afferent sensory inputs and a more central node in the redirection of incoming sensory information across the sensorimotor network (Mountcastle, 2005). The region shows highly organized reciprocal connections with primary motor cortex (M1) (Darian-Smith et al., 1993; Moore et al., 2000) and is coactivated with M1 during both active and illusory movement of the hand (Porro et al., 1996; Naito et al., 2005). Furthermore, it is increasingly clear that S1 exerts a strong influence on the function of M1 (Sakamoto et al., 1987; Widener and Cheney, 1997; Vidoni et al., 2010; Platz et al., 2012; Jacobs et al., 2014).

In light of the structural and functional interplay between S1 and M1, a natural sensorimotor task such as hand movement will elicit robust activation of S1. The phase-encoding paradigm applied in this study is targeted as resolving the kind of ordered smooth somatotopy reported previously in S1 rather than M1 (Sánchez-Panchuelo et al., 2010; Martuzzi et al., 2014; Stringer et al., 2014). However, other approaches have provided evidence for representation of specific movements or digits in different neuronal populations or cortical regions of M1, although not strictly digit somatotopy (Schieber and Hibbard, 1993; Nudo et al., 1996). Indeed, work in humans suggests that motor representations may be encoded in a higher dimensionality space rather than as individual body parts (Overduin et al., 2012; Diedrichsen et al., 2013; Wiestler et al., 2013). However, recent work combining fMRI and electrocorticography does provide evidence for some ordered digit topography in M1 (Siero et al., 2014).

Digit mapping: plasticity and disease

The presence of stable but variable somatotopic maps raises the possibility of investigating the factors underlying individual differences in cortical functional architecture. In addition, the observation of stability in even the most fine-grain S1 somatotopy provides a firm foundation for studies of plasticity, for example, using within-subject longitudinal study designs. Such work might consider the potential for remapping in health and disease, building upon previous studies using MEG (Braun et al., 2000; Schwenkreis et al., 2001; Candia et al., 2003; Stavrinou et al., 2007). Furthermore, the reproducibility of these maps combined with the short 10 min acquisition time and simple motor paradigm, provides encouraging evidence for the clinical utility of single-participant fMRI. Mapping techniques could be of particular interest in presurgical planning or monitoring longitudinal changes in patient populations (Hirsch et al., 2000; Yoo et al., 2005; Bosnell et al., 2008; Gountouna et al., 2010).

Phase-encoding and digit mapping

We provide evidence of concordance between digit maps derived from phase-encoding and more traditional block designs (Fig. 8). Previous work in body mapping has also demonstrated agreement between phase-encoding maps and mapping results from other fMRI paradigms, including block designs (Orlov et al., 2010; Besle et al., 2013a), event-related designs (Besle et al., 2013a), and resting-state functional connectivity data (Zeharia et al., 2015). The results presented here provide further compelling evidence that the phase-encoding analysis provides a meaningful method of mapping patterns of topography.

Limitations

The use of a motor task in assessing S1 topography has a number of limitations. First, it is not possible to isolate the exact somaesthetic submodality responsible for these maps, which could be induced by stimulation of cutaneous or subcutaneous receptors or deeper proprioceptors. However, typical use of the hand recruits a combination of such receptors, so this task represents a more naturalistic assessment of S1 function than somatosensory stimulation in the absence of movement. In light of the active task applied in this study, it would also be challenging to make inferences about Brodmann area somaesthetic submodality specificity. However, the relevance of submodality segregation in S1 is increasingly called into question (Saal and Bensmaia, 2014).

Given the anatomical enslavement of certain adjacent digit pairs, it is possible that, in moving certain fingers, adjacent fingers will also be moved to a lesser extent. Variability in this enslavement could contribute to the intersubject differences reported in this study. However, given the relatively universal anatomical basis of enslavement (Yu et al., 2010), it seems unlikely that this could account for the considerable variance observed in the functional architecture of the cortex observed here. Moreover, the phenomenon of enslavement is more marked in extension rather than the flexion involved in button press tasks (Yu et al., 2010).

The coverage limitations of ultra-high-resolution fMRI at 7 T constrained the region of interest to S1, preventing any assessment of secondary somatosensory cortex or subcortical gray matter structures, where somatotopy has been reported previously (Lenz and Byl, 1999; Ruben et al., 2001; Huang and Sereno, 2007).

Conclusions

This study robustly demonstrates the presence of stable digit somatotopy of four digits in human S1, as well as the considerable intersubject variability in these representations. The use of fMRI to demonstrate this reproducibility at the level of single participants provides a firm foundation for this noninvasive imaging technique to investigate highly detailed functional organization of the human brain. The mapping paradigm validated in this study has potential applications in the study of sensorimotor plasticity in the context of both learning and pathological dysfunction, as well as in the clinical setting.