Functional Topography of Human Auditory Cortex

Abstract

Functional and anatomical studies have clearly demonstrated that auditory cortex is populated by multiple subfields. However, functional characterization of those fields has been largely the domain of animal electrophysiology, limiting the extent to which human and animal research can inform each other. In this study, we used high-resolution functional magnetic resonance imaging to characterize human auditory cortical subfields using a variety of low-level acoustic features in the spectral and temporal domains. Specifically, we show that topographic gradients of frequency preference, or tonotopy, extend along two axes in human auditory cortex, thus reconciling historical accounts of a tonotopic axis oriented medial to lateral along Heschl's gyrus and more recent findings emphasizing tonotopic organization along the anterior–posterior axis. Contradictory findings regarding topographic organization according to temporal modulation rate in acoustic stimuli, or “periodotopy,” are also addressed. Although isolated subregions show a preference for high rates of amplitude-modulated white noise (AMWN) in our data, large-scale “periodotopic” organization was not found. Organization by AM rate was correlated with dominant pitch percepts in AMWN in many regions. In short, our data expose early auditory cortex chiefly as a frequency analyzer, and spectral frequency, as imposed by the sensory receptor surface in the cochlea, seems to be the dominant feature governing large-scale topographic organization across human auditory cortex.

SIGNIFICANCE STATEMENT In this study, we examine the nature of topographic organization in human auditory cortex with fMRI. Topographic organization by spectral frequency (tonotopy) extended in two directions: medial to lateral, consistent with early neuroimaging studies, and anterior to posterior, consistent with more recent reports. Large-scale organization by rates of temporal modulation (periodotopy) was correlated with confounding spectral content of amplitude-modulated white-noise stimuli. Together, our results suggest that the organization of human auditory cortex is driven primarily by its response to spectral acoustic features, and large-scale periodotopy spanning across multiple regions is not supported. This fundamental information regarding the functional organization of early auditory cortex will inform our growing understanding of speech perception and the processing of other complex sounds.

Introduction

Neural representations of a sound's constituent frequencies are preserved in topographically organized neurons from cochlea to cortex, perhaps providing a foundation for the specialized processing architectures built upon it. Historically, this “tonotopic organization” was thought to run parallel to Heschl's gyrus (HG) in humans, with high frequencies represented medially and low frequencies represented laterally (Pantev et al., 1995; Howard et al., 1996; Wessinger et al., 1997; Lockwood et al., 1999). In contrast, most recent research has shown tonotopy oriented orthogonally or obliquely to HG, with a high-low-high gradient following posterior–anterior (as in nonhuman primates; Hackett, 2011) or posteromedial–anterolateral axes (Formisano et al., 2003; Humphries et al., 2010; Woods et al., 2010; Da Costa et al., 2011; Striem-Amit et al., 2011; Langers and van Dijk, 2012; Moerel et al., 2012; Herdener et al., 2013). Although this latter configuration is currently more widely accepted (Baumann et al., 2013; Saenz and Langers, 2014), conflicting reports exist (Talavage et al., 2000, 2004; Schönwiesner et al., 2002; Barton et al., 2012). Because functional topography is used to delineate subregions of sensory cortex, this lack of consensus has stunted characterization of low-level acoustic processing in human auditory cortex, including even primary auditory cortex.

A related challenge to studies of early auditory sensory cortex is identifying the acoustic features critical for analyzing complex sounds. Several groups have proposed a trade-off between spectral and temporal processing (Zatorre and Belin, 2001; Bendor and Wang, 2008; Scott et al., 2011; Kusmierek and Rauschecker, 2014); however, the exact nature of the spectral and temporal features being processed by different subregions of auditory cortex is unclear. Neuroimaging studies assessing temporal processing typically manipulate how quickly stimuli change in time; yet, these manipulations can also induce pitch perception. For example, when white noise (WN) is temporally modulated at rates high enough to be resolved within the hearing range of humans (>20 Hz), it is perceived to have pitch matching the modulation frequency (i.e., “periodicity pitch”; Miller and Taylor, 1948; Pollack, 1969; Burns and Viemeister, 1981). By contrast, WN modulated at frequencies below the human hearing range (<20 Hz) may be more likely to be perceived as having no pitch, or a pitch matching its (approximate) center frequency. Thus, a critical challenge is separating responses to temporal frequency from spectral frequency and/or periodicity pitch.

In this study, we used high-resolution fMRI to measure responses to two basic spectral and temporal acoustic features: center spectral frequency and rates of temporal modulation. First, we measured tonotopic organization using pure tones (PTs), narrow bandpassed noise (N-BPN), and broad bandpassed noise (B-BPN). Then, sensitivity to the temporal features of sound was assessed using amplitude-modulated (AM) white noise at several periodic rates, including AM rates high enough to convey pitch. Across the same regions of auditory cortex, we measured strength(s) and relative direction(s) of (1) tonotopy and (2) topographic organization by AM rate (possible “periodotopy”). We also determined the extent to which AM-rate topography, if found, could be explained by responses to spectral information present in AMWN. With this approach, we hoped to resolve long-standing controversies regarding functional organization and topographic mapping of human auditory cortex, which should contribute to faster convergence with the nonhuman primate literature.

Materials and Methods

Participants

Thirteen individuals (eight female; mean age, 26.5; SD, 3.7 years) gave informed consent to participate in this experiment. All volunteers reported having normal neurological histories and normal hearing.

Stimulus presentation

Stimuli were created in Matlab (MathWorks) and were all ∼2.5–3.0 s in duration, with a 44.1 kHz sampling rate and 32 kbit/s bit rate, and presented during the delay between acquisition of echoplanar images (EPIs) in a sparse-sampling paradigm. All stimuli were matched for root mean squared power; this method is a common way to “normalize” auditory stimuli in perceived amplitude intensity or level. During each fMRI run, stimuli from a single stimulus category (i.e., narrow bandpassed noise, spectral bandwidth, or temporal modulation stimuli, as described in following sections) were presented in pseudorandom order, minimizing the number of immediately adjacent trial repetitions. In each run, stimulus-absent “silent” trials were interspersed among auditory stimuli within this pseudorandom order.

Narrow bandpassed noise stimuli

Center frequency responses were assessed using trains of narrow (1/6 octave) bandpassed noise bursts centered on each of five frequencies (225, 602, 1611, 4311, 11535 Hz) and the temporal envelope evenly modulated at 4 Hz. Twenty trials were presented at each frequency over two fMRI runs.

Spectral bandwidth stimuli

Sensitivity to spectral center frequency was also assessed using stimuli with a variety of spectral envelopes. PTs and broad (1 octave) BPN were centered on three center frequencies: 250, 1495, and 8938 Hz. WN, which theoretically consists of a signal with infinite bandwidth and constant power spectral density, was bandpassed at 200 Hz and 12.8 kHz so that it covered a range of the frequency spectrum equivalent to the range covered by N-BPN and B-BPN combined (i.e., from 1 octave flanking 250 Hz B-BPN to 1 octave flanking 8938 Hz B-BPN). The spectrum was flat over this range, so we retain the name “WN” for convenience. Harmonic complex tone stimuli had a fundamental frequency of 250 Hz and were combined with a series of octave-spaced harmonics (i.e., 500, 1000, 2000, 4000, and 8000 Hz). Amplitude envelopes of all stimuli were modulated at 4 Hz. Center frequencies for PT and B-BPN stimuli were presented 20 times each over two runs; 26 trials were presented for WN and harmonic-tone stimuli over two runs. Data associated with WN and harmonic-tone stimuli are not discussed further in this manuscript. Due to time constraints, these scans were not run in one volunteer.

Temporal modulation stimuli

Sensitivity to temporal envelope was assessed using AMWN at six different rates: 0 (i.e., no modulation), 1.3, 3.3, 8.3, 20.8, and 52.1 Hz. AM rate randomly varied by a factor of 20% throughout each 2.6-s-long stimulus [“variable duty cycle” as in the studies by Zatorre and Belin (2001), Seifritz et al. (2003), and Boemio et al. (2005)]. Each AM rate was presented 24 times over two runs; unmodulated WN (0 Hz) was presented 20 times over two runs. AMWN stimuli were bandpassed at 20 and 16 kHz (center frequency, 565.7 Hz). Due to time constraints, these data were not collected for one participant (different than the participant referenced in the paragraph above).

Amplitude oddball task

Participants performed an amplitude “oddball” task during the fMRI experiment. On a small percentage of trials (∼4–7%), stimuli were presented with unequal amplitude in the right and left ear (e.g., softer volume in right ear than the left). Participants were asked to respond to these oddball trials with a button in their right hand. On nonoddball trials (i.e., trials with equal volume in left and right ears), participants were to respond with a left-hand button press. When stimulation was absent, participants were asked to randomly choose the left or right button with roughly equal frequency. This task was chosen to minimize task-related differences across conditions and to monitor participants' alertness during the scan.

Image acquisition

Images were acquired using a 3.0-Tesla Siemens TIM Trio scanner. Functional EPIs were acquired using a sparse-sampling event-related fMRI paradigm: repetition time (TR), 7 s; TR delay, 5 s; echo time (TE), 33 ms; flip angle, 90°; 28 axial slices; 1.5 × 1.5 × 1.9 mm³ resolution. The field of view of functional images included auditory cortex, subcortical structures superior to the midbrain, and ventral prefrontal cortex. A high-resolution anatomical scan (MPRAGE) was also performed for each subject with the following parameters: TR, 2530 ms; TE, 3.5 ms; inversion time, 1100 ms; flip angle, 7°; 176 sagittal slices; matrix size, 256 × 256 mm²; 1 × 1 × 1 mm³ resolution.

Image processing and analysis

Functional imaging analyses were completed using BrainVoyager QX (Brain Innovation). Functional images from each run were corrected for motion in six directions using a sinc function, corrected for linear trend, high-pass filtered at 3 Hz, and spatially smoothed using a 3 mm³ full width at half maximum (FWHM) Gaussian filter. Data were then coregistered with anatomical images and interpolated into Talairach space (Talairach and Tournoux, 1988) at 2 × 2 × 2 mm³ using a sinc function.

Group and single-subject analyses using the general linear model (GLM) were executed in single voxels to assess the relationship between fMRI signal and our experimental conditions (i.e., regressors; Friston et al., 1995). In this sparse-sampling fMRI design (Hall et al., 1999), a single EPI was acquired at the estimated peak of the blood-oxygenation-level-dependent (BOLD) response to each trial (∼4 s), and the EPI TR was long (7 s) to minimize contamination of BOLD responses across trials (Hall et al., 2000). Thus, an event-related boxcar design was used, and GLM regressors were not convolved with a hemodynamic response function. Random-effects models were used for group analyses to reduce the influence of interindividual variability (Petersson et al., 1999).

For N-BPN and AM stimuli, one-way ANOVAs determined whether the fMRI signal in each voxel was statistically different across trials in these conditions (i.e., for frequency and AM rate, respectively). ANOVA results could be considered a proxy for “frequency selectivity” (N-BPN) or “AM-rate selectivity” (AM stimuli); however we assume, as have others (Formisano et al., 2003; Talavage et al., 2004; Schönwiesner and Zatorre, 2009; Langers and van Dijk, 2012; Schönwiesner et al., 2014), that voxels not demonstrating statistically different responses to frequency and AM rates may nevertheless contain meaningful information regarding frequency and AM rates. Therefore, we did not restrict topographic analyses to voxels significant in these one-way ANOVAs (see also Humphries et al., 2010). Instead, all analyses were restricted to temporal cortex and included only those voxels that had a significant fMRI response to any stimulus condition (single-voxel threshold, t₍₁₂₎ = 2.179, p < 0.05), and smoothed with a modest (3 mm³ FWHM) Gaussian kernel before post hoc tests (e.g., ANOVAs and preference maps, as described in the sections Statistics and Topographic gradient estimation below).

Statistics

N-BPN scans.

The GLM analyses for these runs included all five N-BPN stimuli (225, 402, 1611, 4311, 11535 Hz) as regressors, with oddball trials included in a separate regressor. Silent baseline trials (24 total across two runs) were not included in the GLM per convention (Friston et al., 1998). Maps of “frequency preference” were calculated (Figs. 1C,D) by determining, for each voxel, the stimulus frequency for which the fMRI signal (t value) was maximal. For comparison with frequency preference maps of PT and B-BPN stimuli (below) that use only three frequencies, we also created “N-BPN3” frequency preference maps using three of five available frequencies (225, 1611, and 11535 Hz). Each of these preference maps was smoothed with a modest (3 mm³ FWHM) Gaussian kernel.

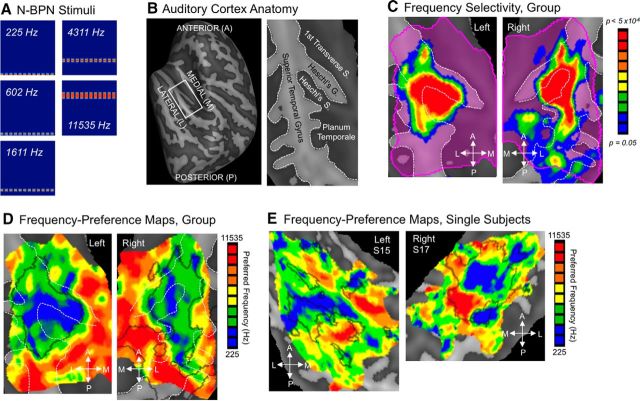
Figure 1.

Frequency selectivity in human auditory cortex. A, N-BPN stimuli are displayed in spectrograms; x-axes span 0 to 3 s, and y-axes span 0 to 16 kHz (linear scale). B, The anatomy of the superior temporal cortex is shown using a reconstruction of a group-averaged cortical surface (left), flattened to display all structures in the same plane (right). The borders of major sulci and gyri are marked with white dashed lines. In all subsequent figures, data are presented in this manner, on flattened cortical surfaces with sulci/gyri outlined in white dashed lines. C, Voxels with statistically different BOLD responses to five frequencies of N-BPN are shown, indicating clear frequency selectivity. Such voxels were present throughout the left and right superior temporal plane (key at right; right hemisphere flipped around the AP axis to match the left). D, Group frequency-preference maps or tonotopic maps are shown, whereby color represents the preferred stimulus frequency (i.e., the frequency with the highest BOLD response), as shown in the key at right. Black outlines mark the outline of the clusters from B. E, Single-subject maps of preferred frequency are displayed for two representative subjects (S15, S17). Black outlines mark regions of significant frequency selectivity for each subject as for group maps in D (p < 0.01).

PT and B-BPN scans.

For these runs, all six PT and B-BPN stimuli (three frequencies each) were included as regressors in the GLM: 225, 1495, and 8393 Hz for PT; 225, 1495, and 8393 Hz for B-BPN. WN, HS and oddball trials were also included as regressors. Silent baseline trials (24 total across two runs) were not modeled. As described above, frequency preference maps were calculated separately for PT and B-BPN. Each of these maps was smoothed (3 mm³ FWHM Gaussian kernel).

In a complementary assessment of tonotopy, all single-frequency maps for PT, N-BPN3, and B-BPN were used to construct maps of frequency preference independent of spectral bandwidth. For each voxel, we first calculated the best response (i.e., highest t value) for low frequencies (250 Hz). We performed the same calculation for middle center frequencies (1495, 1611, and 1495 Hz for PT, N-BPN, and B-BPN, respectively) and high frequencies (8393, 11535, 8393 Hz, respectively). The resulting maps were smoothed (3 mm³), and maps of frequency preference were created.

Temporal modulation scans.

Statistical analyses for these runs used a GLM including one regressor for each AM rate (0, 1.3, 3.3, 8.3, 20.8, 52.1 Hz) and a separate regressor for oddball trials; again, silent trials (32 across two runs) were not modeled. Maps of “AM-rate preference” were created by calculating the AM rate to which each voxel responded maximally (i.e., largest t value) and smoothed (3 mm³ FWHM).

Parametric sensitivity to AM rate was assessed in an additional GLM with a parametric regressor for AM stimuli (regressor weights, −1, −0.6, −0.2, 0.2, 0.6, 1) and “boxcar” regressors for oddball stimuli (regressor weight, 1). Parametric relationships between voxel time courses and AM rate were considered significant at a threshold of t₍₁₁₎ > 3.50, p < 0.005, with a cluster correction of k > 120 mm³ (p_corr < 0.05 using Monte Carlo simulations; Forman et al., 1995).

Topographic gradient estimation

To characterize any organization present in preference maps for spectral frequency and AM rate, we measured the strength and direction of gradient organization in each preference map using Matlab 2013a (MathWorks). Flattened cortical surface maps were smoothed in BrainVoyager (15 iterations), imported into Matlab using NeuroElf version 0.9c, interpolated into an isotropic array, and analyzed using Matlab. Gradient magnitude and direction were calculated at each vertex using the Sobel Gradient Operator (imgradient function, Image Processing Toolbox version 8.2), transformed back into native surface maps, and exported to BrainVoyager for visualization.

Topographic gradients were quantified for statistical analysis in Matlab. Histograms of gradient direction were computed for each map; these histograms were weighted by the strength of the local gradient at each vertex. The shape of these weighted distributions were then smoothed (25 neighbors) and fitted with functions containing mixtures of either two or four Gaussians. The fit of these curves to the weighted histograms was measured using maximum likelihood estimates to assess the degree to which one and two axes of frequency organization (i.e., two and four gradient directions) were present in these maps (Matlab's Curve Fitting Toolbox). Three goodness-of-fit metrics were calculated for two- and four-Gaussian models, including r², Akaike and Bayesian information criteria (AIC and BIC, respectively). The latter were calculated as AIC = log(MSE) + 2 * k/n and BIC = log(MSE) + k * log(n)/n, where MSE is the mean squared error of the model, k is the number of model terms, and n is the number of observations (Qi and Zhang, 2001). Gradient strength was also recorded for every vertex (i.e., point) in a given map regardless of local direction, and a two-way ANOVA (spectral frequency stimuli) and a t test (AM-rate stimuli) were used to measure differences in gradient strength across hemispheres and stimulus type for spectral frequency stimuli (PT, N-BPN, B-BPN), with post hoc t tests corrected for multiple comparisons using the Bonferroni method. Because fMRI signal in each 3D voxel is reflected in many 2D vertices on the cortical surface (and, correspondingly, there are many more vertices than voxels contributing to these maps), the degrees of freedom for the ANOVA error terms were adjusted to reflect the number of 3D voxels (683 in right and 628 in left auditory cortex) rather than the number of vertices to avoid inflating significance of the voxelwise statistical tests on these group maps. In addition, spatial similarity between group tonotopic and AM-rate topography was calculated using Pearson's r for each hemisphere, and for auditory subregions defined using reversals in tonotopic maps, with a Bonferroni correction for the total number of regions analyzed.

Cross-validation of group topographic maps

Previous studies have demonstrated that topographic maps in individual subjects can be interrupted by vascular artifacts (Winawer et al., 2010) and significantly influenced by gyrification (Da Costa et al., 2011), the latter of which can be quite variable in superior temporal cortex (Rademacher et al., 2002; Schneider et al., 2005). Thus, we rely on group topographic maps in the current analyses. To measure the reliability of group topographic maps, we executed cross-validation analyses for each map (N-BPN, PT, B-BPN, AMWN) using a leave-one-out approach. In these analyses, multiple group maps of preferred frequency (N-BPN, PT, B-BPN) and AM rate were created as described above, with data from one subject omitted in each iteration, yielding 12 N-BPN, 11 PT, 11 B-BPN, and 11 AMWN maps (data not acquired for one subject for PT, B-BPN, and AMWN conditions). Spatial similarity was assessed among each group of maps by calculating mean pairwise Pearson's r (Haxby et al., 2001). Spatial correspondence was high and consistent across map iterations [N-BPN mean (SD), r = 0.78 (0.03); PT mean (SD), r = 0.74 (0.05); B-BPN mean (SD), r = 0.70 (0.04); AMWN mean (SD), r = 0.71 (0.06)].

Displaying functional maps on the cortical surface

Given the size and convoluted nature of superior temporal cortex, it is sometimes difficult to appreciate its functional organization in 3D images, which can require multiple 2D slices to create a discontinuous display of auditory cortex in its entirety. Therefore, we used Freesurfer software (http://surfer.nmr.mgh.harvard.edu/) to reconstruct the cortical surfaces of our subjects, so that all of auditory cortex could be viewed in a single, continuous image. In an automated procedure, anatomical MR images were corrected for intensity bias and segmented into cortical gray and white matter to reconstruct gray- and white-matter surfaces (Dale et al., 1999). Reconstructed surfaces were inflated, spherized, and aligned with Freesurfer's template average (Dale et al., 1999). To display group statistics, a study-specific average of these surfaces was then computed, imported into BrainVoyager, and aligned with functional maps at 2 × 2 × 2 mm³ resolution for visualization. For displaying single-subject statistics, individual surfaces were imported from Freesurfer for each subject. For both averaged and individual reconstructions, each cortical surface was inflated, cut to isolate the superior temporal cortex, and flattened in BrainVoyager. Importantly, using BrainVoyager QX, distances between the nodes on the surface (which correspond to corners of 3D voxels bordering the gray and white matter surfaces) were corrected for distortions caused by the process of inflation and flattening; thus, the distances between the nodes more accurately reflected their actual “native” distance in the original 3D volume. Statistical maps were displayed on these flattened cortical surfaces using linear interpolation of data 1 mm interior and 3 mm exterior to the boundary between white and gray matter.

Results

Spectral frequency topography

FMRI responses to PT and BPN bursts with different bandwidths were measured across the superior temporal plane (STP) in both hemispheres. A large region of STP was responsive to sound, as indicated by significantly greater fMRI activity to any acoustic stimulus compared to stimulus-absent trials (Fig. 1). Many of these voxels also exhibited differences in responses to the various center frequencies of N-BPN (one-way ANOVA, F_(4,48) > 2.57, p < 0.05), indicating significant frequency selectivity. These voxels were concentrated in central STP along the middle and lateral sections of Heschl's gyrus and sulcus, and along lateral STP. Topographically organized preferences for stimulus frequency, or tonotopic maps, were demonstrated by displaying the N-BPN center frequency to which each voxel responded maximally (akin to a “best voxel frequency”). These maps were verified in random-effects group analyses (Fig. 1D) and in single-subject analyses (Fig. 1E). Highly frequency-selective regions mostly preferred low stimulus frequencies and formed a fan-like shape, as originally suggested in early studies of tonotopic organization of core auditory subfields in nonhuman primates (Morel and Kaas, 1992; Morel et al., 1993). Frequency-selective areas preferring higher frequencies were relatively smaller, yet readily apparent.

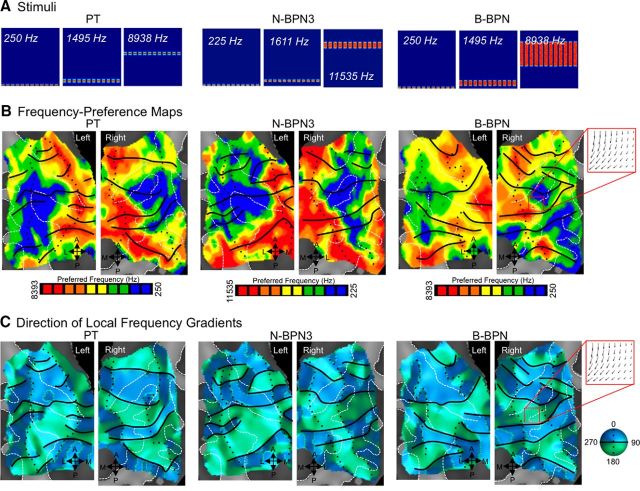
Tonotopic organization was apparent for all three stimulus types (Fig. 2), and frequency-gradient flow was quantified in group maps to compensate for idiosyncrasies in anatomy and vasculature (Rademacher et al., 2002; Winawer et al., 2010). Frequency gradients progressed mainly along two, roughly orthogonal axes in tonotopic maps for all three stimulus bandwidths tested: PT, N-BPN3 (three frequencies), and B-BPN. In weighted distributions of tonotopic gradient direction, two axes (four directions) were apparent, particularly in the right hemisphere and for B-BPN (Fig. 3). One of these gradient axes progressed roughly in the anterior–posterior direction and contained several reversals (i.e., 180° changes in gradient direction). These anterior–posterior gradients are consistent with those thought to delineate core regions in the majority of previously published literature (Baumann et al., 2013), and were oriented roughly perpendicular to Heschl's gyrus and parallel to the STG. The other tonotopic axis extended medial to lateral and contained few reversals. Instead, this medial–lateral gradient reflected preferences for high frequencies medially, and low frequencies laterally. This arrangement of orthogonal tonotopic gradients was apparent for all stimulus bandwidths (PT, N-BPN3, and B-BPN).

Figure 2.

Measuring tonotopic gradients. A, Stimuli are displayed in spectrograms for PTs, N-BPN (3 frequencies; N-BPN3), and B-BPN; x-axes span 0 to 2.6 s, and y-axes span 0 to 16 Hz (linear scale). B, Group frequency-preference (tonotopic) maps are shown on cortical surfaces; color indicates the center frequency eliciting the greatest BOLD activity. Data for three stimulus types are shown, including PT, N-BPN3, and B-BPN. Note the similarity between N-BPN3 and N-BPN maps in Figure 1D. Isofrequency contours are marked as black (solid and dotted) lines based on frequency reversals determined from gradient maps in C. C, Local frequency gradients are displayed, where color indicates the gradient direction at each point on the tonotopic maps from B, moving from low to high frequencies. Black lines mark gradient reversals between 0/360 and 180° (green to blue, respectively), and black dotted lines mark reversals between 90 and 270° (dark to light colors, respectively). An example of gradient flow is illustrated in a red inset at the right in B and C, and the corresponding points on the rightmost maps are marked. Arrows indicate the direction of tonotopic gradient flow, from low to high frequencies.

Figure 3.

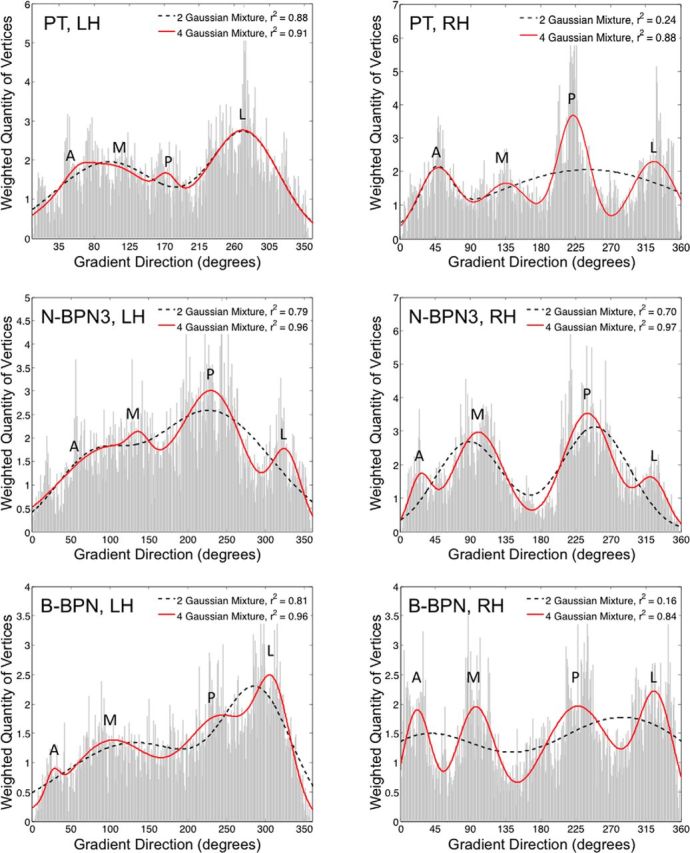
Quantifying tonotopic frequency gradients. For each tonotopic map, the quantity of vertices (i.e., points on the map) exhibiting a given tonotopic gradient direction are displayed. Distributions are given for left- and right-hemisphere maps in left and right columns, respectively, and for PT, N-BPN3, and B-BPN maps in the top, middle, and bottom rows, respectively. Functions containing mixtures of two (black dashed lines) or four (red lines) Gaussians/peaks were fitted to each distribution to assess overall patterns in gradient direction in each tonotopic map. The amount of variance accounted for by these two- and four-Gaussian mixtures is displayed in insets (r² value). Additional goodness-of-fit measures were compatible with r² values; both the AIC and BIC were less for four- than two-Gaussian models, indicating a better fit (two-Gaussian model AIC, −2.84, −3.12, −2.36; four-Gaussian model AIC, −4.44, −3.41, −4.02; two-Gaussian model BIC, −2.78, −3.06, −2.29, four-Gaussian model BIC, −4.31, −3.28, −3.89 for PT, N-BPN3, B-BPN, respectively). The approximate gradient direction is indicated for each peak: A, anterior; M, medial; P, posterior; L, lateral.

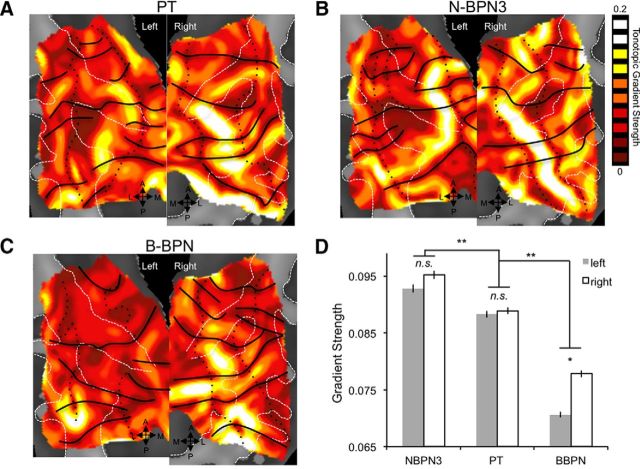
The strength of frequency gradients in these group maps differed both across stimulus bandwidth and between hemispheres (two-way ANOVA; Fig. 4). Frequency gradients were strongest for narrow-band stimuli (significant main effect of stimulus bandwidth). In particular, gradient strength was strongest for N-BPN3 stimuli, followed by PT and then B-BPN (post hoc t tests, p_bonf < 0.05). Overall, gradients were also stronger in right auditory cortex (significant main effect of hemisphere). However, this latter main effect may be driven by stronger gradients in B-BPN maps in the right hemisphere compared to left B-BPN maps (significant stimulus-by-hemisphere interaction; p < 0.05 × 10⁻⁵ for all significant main effects and interactions). Indeed, although mean gradients in N-BPN3 and PT maps did not differ significantly between hemispheres (p_bonf > 0.05), gradients were stronger in right B-BPN maps compared to left B-BPN maps (p_bonf < 0.05).

Figure 4.

Strength of tonotopic gradients in human auditory cortex. A–C, Strength of frequency organization is displayed for tonotopic gradients in maps for PT (A), N-BPN (B), and B-BPN stimuli (C). Reversals in frequency organization are marked as in Figure 2B. A region of high gradient strength is located near central Heschl's gyrus and sulcus, and may correspond to A1. D, Average gradient strength is plotted for each of the maps in A–C; error bars reflect the SEM across map voxels. Significant differences between stimulus bandwidths are shown by double asterisks. A significant hemisphere by stimulus bandwidth interaction is marked with a single asterisk.

Temporal frequency topography: responses to AM rate

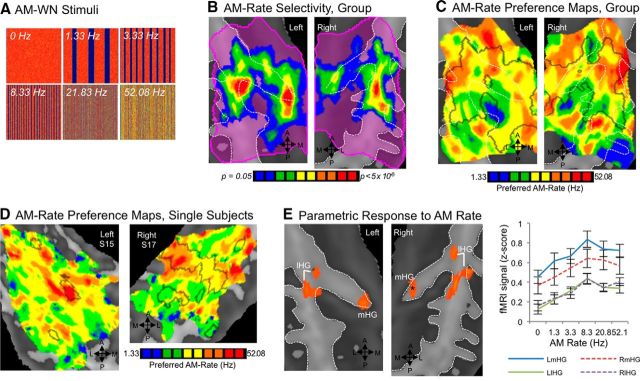
Compared to spectral frequency, relatively smaller regions of the STP exhibited differences in fMRI signal to different rates of AMWN stimuli (one-way ANOVA, F_(5,55) > 2.38, p < 0.05; Fig. 5). Central, posteriormost, and anteriormost regions responded with roughly equal magnitude to all stimulus conditions. In contrast, a midmedial region located on the medialmost segment of HG and a midlateral subregion adjacent to the lateralmost part of HG both exhibited highly significant differences across AMWN rates. Predominantly, they responded more to stimuli with higher/faster rates of change in amplitude envelope than to stimuli modulated at slower rates (Fig. 5C–E).

Figure 5.

Selectivity for rates of temporal modulation in white noise. A, AMWN stimuli are displayed in spectrograms; x-axes span 0–2.6 s, and y-axes span 0–16 kHz (linear scale). B, Voxels with statistically different BOLD responses to six temporal rates of AMWN are located on medial (mHG) and lateral HG (lHG), and adjacent superior temporal gyrus. Color marks significant voxels (p < 0.05); a key is given at the right. C, Group maps for preferred modulation rate are shown, where the color of each voxel represents the preferred AM rate (i.e., the rate with the highest BOLD response), as shown in the key on the side. D, Single-subject maps of preferred modulation rate are displayed, with black outlines indicating regions with statistically different BOLD responses to the six AMWN stimuli for each subject. E, Significant parametric relationships between BOLD activity and AM rate are displayed in orange (p_corr < 0.05), with mean activity per AM-rate condition plotted for each of these clusters at right. The asterisk marks a subthreshold cluster on the right mHG (p < 0.005, k = 112 mm³).

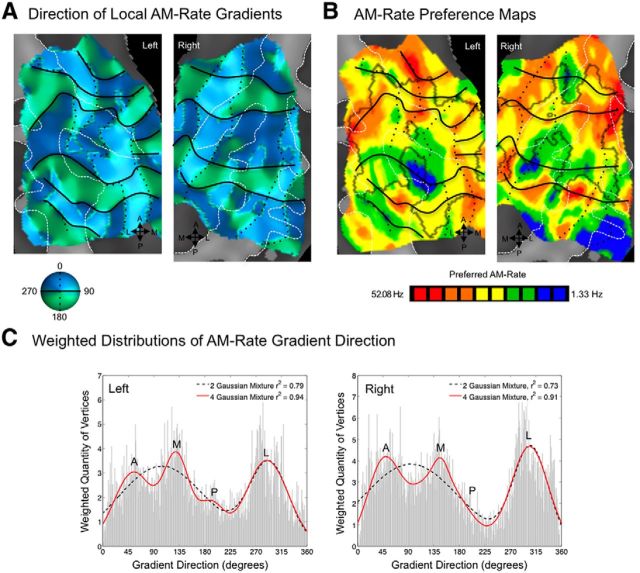
Functional organization by preferred rate of temporal modulation (periodotopy) was much less clear by comparison to spectral-frequency organization (tonotopy). In group maps, modulation rate preferences were relatively more punctate (Figs. 5C, 6); however, a pattern somewhat like that seen for frequency organization was apparent. In a weighted histogram of local gradient directions, three or four peaks were present, with a four-Gaussian mixture function explaining 94% of variance in the shape of the distribution (Fig. 6C). In other words, two axes (four gradient directions) were also present in these temporal-frequency maps. Gradients were also stronger in the right-hemisphere group map (mean strength, 0.15) compared to left (mean strength, 0.13; t test, p_bonf < 0.05).

Figure 6.

Topographic organization by preferences for temporal modulation rate in auditory cortex. A, Gradient maps for preferred AM rate are shown, where color indicates the gradient direction moving from low to high AM rates. Black lines mark gradient reversals between 0/360 and 180° (green to blue, respectively), and black dotted lines mark reversals between 90 and 270° (dark to light colors, respectively). B, Group maps of AM rate preferences are displayed on cortical surfaces; color indicates the rate eliciting the greatest BOLD activity. Reversals from A are displayed, marking contours sharing similar responses to AM rate in B. C, Distributions are plotted for vertices exhibiting local gradient directions 0–360°, weighted by the strength of the gradient at each vertex. Functions containing mixtures of two (black dashed lines) or four (red lines) Gaussians were fitted to the shape of these distributions to assess overall patterns in gradient direction. A goodness of fit (r² value) for two- and four-Gaussian mixtures is displayed in the upper right corner of each box. Additional goodness-of-fit measures were compatible with r² values; the AIC and BIC were less for four- than two-Gaussian models, indicating a better fit (AIC, −1.92 and −3.08 for two- and four-Gaussian models; BIC, −1.86 and −2.95 for two and four-Gaussian models, respectively). A, Anterior; M, medial; P, posterior; L, lateral.

The medialmost and lateralmost aspects of HG also demonstrated parametric sensitivity to temporal rate. These fields responded most robustly to WN with high AM rates (i.e., ≥8 Hz), while responding less robustly to stimuli with slower rates and unmodulated WN (Fig. 5E).

Relationships between neural responses to spectral and temporal frequency

AMWN stimuli used in the current experiment also convey pitch; specifically, periodicity at faster AM rates (>20 Hz) can convey pitches matching the AM rate (Miller and Taylor, 1948; Pollack, 1969; Burns and Viemeister, 1981). In comparison, stimuli with slower AM rates (<20 Hz) may be perceived to have no pitch or a pitch matching the center spectral frequency of these stimuli (565.7 Hz). To measure the extent to which preferences for AM rates could be explained by the pitch conveyed, we performed correlation analyses (Fig. 7) between spectral-frequency preference maps using all stimulus bandwidths (Fig. 8C,D) and temporal-frequency maps (Fig. 6). A small amount of overall variance in AM-rate maps could be explained by spectral frequency responses in the right-hemisphere group maps (Pearson's r = −0.08, p = 0.03). This negative relationship indicates that, at least to some extent, voxels that prefer high AM rates also tend to prefer low spectral center frequencies in PT, N-BPN, and B-BPN stimuli. Conversely, voxels that prefer low temporal frequencies tend to prefer high center frequencies in PT, N-BPN and B-BPN. This negative relationship was particularly pronounced in the right putative A1/medial belt (ML) and in parabelt, as defined using reversals in tonotopic gradients (r = −0.41, p_bonf < 0.0001 and r = −0.28, p_bonf < 0.0001, respectively). Negative correlations between spectral-frequency and temporal-frequency maps were also present in left putative A1/ML and parabelt, mimicking the right hemisphere (A1/ML, r = −0.123, p_bonf = 0.02; parabelt, r = −0.117, p_bonf = 0.03). However, when considering left-hemisphere maps as a whole, there was no significant correlation between the maps (r = 0.02, p = 0.52). Negative spatial cross-correlations in the putative medial belt (right, r = −0.12, p_bonf = 0.02; left, r = −0.14, p_bonf = 0.007) were also affected by an overall preference for higher spectral frequencies regardless of temporal-frequency preference.

Figure 7.

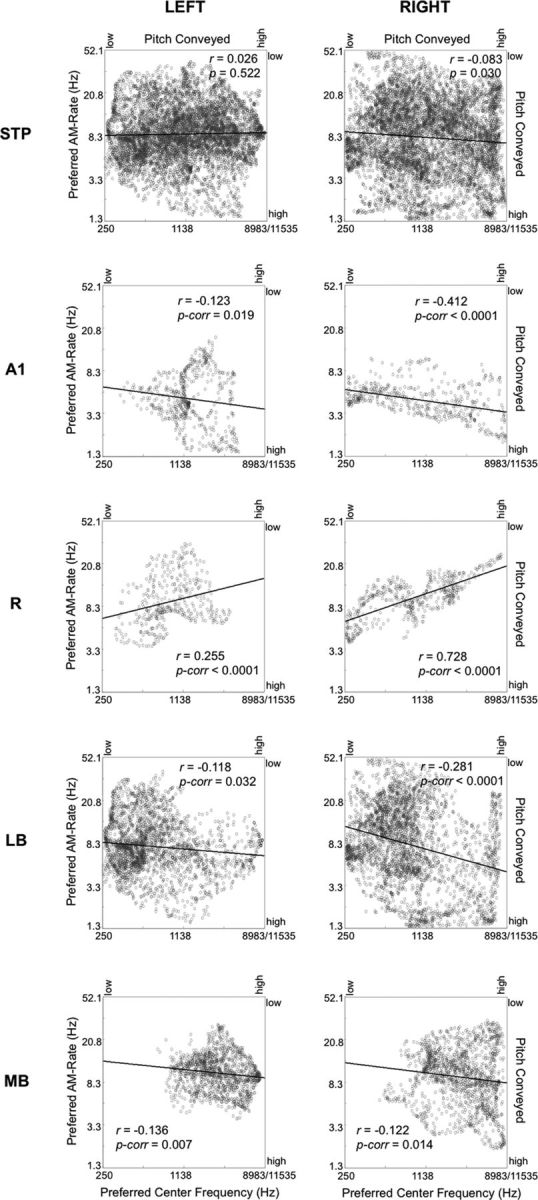
Spatial correspondence between AM-rate maps and tonotopic maps for all of auditory cortex (top row) and selected regions/areas of auditory cortex (bottom rows). Scatter plots are shown, where each data point represents each voxel's preferred rate of AMWN (left y-axis) and preferred spectral center frequency (bottom x-axis). Dominant pitch conveyed is also displayed for AMWN (right y-axis) and center frequency (top x-axis). Negative correlations suggest that AM-rate preference might be explained by spectral/pitch information conveyed by AMWN stimuli. Data for preferred center frequency were taken from group tonotopic maps including all stimulus bandwidths (i.e., PT, N-BPN, and B-BPN). Black lines mark the best linear fit to each scatter plot (Pearson's r). Auditory cortical fields analyzed include the entire STP, putative core subfields A1 and R, the lateral belt (LB), and the medial belt (MB).

Figure 8.

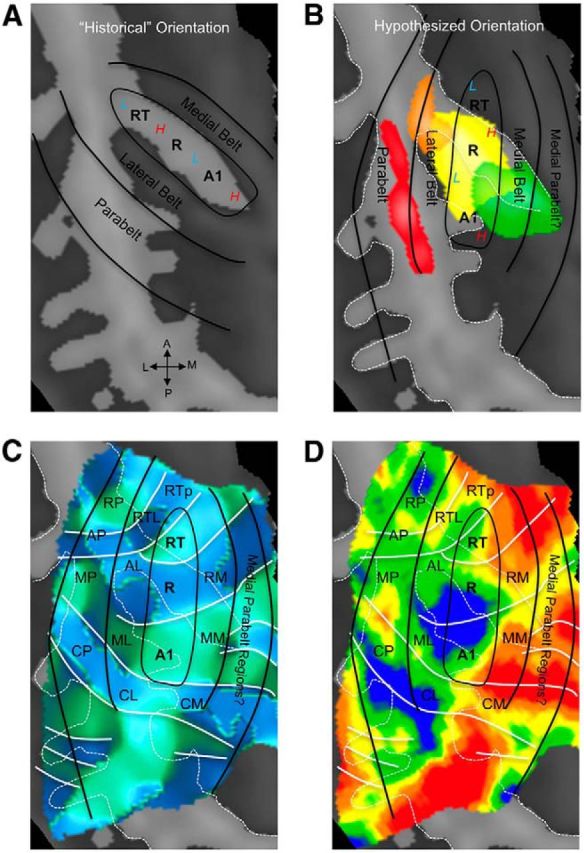
Hypothesized positions of auditory cortical regions coincide with probabilistic maps of koniocortical areas in humans. A, Previous neuroimaging research placed the orientation of core auditory fields along HG, with high frequencies represented medially (red “H”) and low frequencies represented laterally (blue “L”). B, Our current data confirm an orientation of core regions oblique to HG, with high and low frequencies alternating from posterior to anterior. In this scheme, our functional definition of core regions overlaps with the koniocortical/primary region Te1.0, as defined from underlying cytoarchitecture (Morosan et al. 2001; Rademacher et al., 2002), which is shown in yellow according to the Wake Forest University PickAtlas (Maldjian et al., 2003). Medial, nonprimary region Te1.1 is shown in green, the lateral region Te1.2 in orange, and Te3.0 in red. C, A map of frequency-gradient direction is shown, derived from a map of frequency preference independent of stimulus bandwidth (i.e., including responses to PT, N-BPN, and B-BPN together). White lines indicate the position of gradient reversals as in Figures 2 and 6. The hypothesized locations of the putative core, belt, and parabelt regions are marked by solid black lines, along with hypothesized subregions homologous to those identified in nonhuman primates. D, A group tonotopic map is displayed, which matches gradient map displayed in C. Data from all stimulus frequencies and bandwidths were used to create this map. Reversals that appear to delineate subregions in C remain in D. All panels display a group-average cortical surface (right hemisphere), and white dashed lines mark major sulci and gyri. Auditory subfield names are taken from the nonhuman primate literature for convenience and follow these abbreviations: R, rostral; C, caudal; M, medial; A, anterior; L, lateral belt; P, parabelt; T, temporal; p, pole. Note that “M” refers to “medial belt” when occurring as the second letter of a two-letter abbreviation (e.g., CM, caudomedial belt).

Discussion

In this study, we characterized the functional topography of human auditory cortex by measuring fMRI responses to center frequency of tones and bandpassed noise, and to temporally modulated noise. Tonotopic gradients along the anterior–posterior axis are compatible with previous reports (Baumann et al., 2013; Moerel et al., 2014; Saenz and Langers, 2014); however, we also demonstrate a second medial–lateral gradient, compatible with early studies of tonotopy in humans (Romani et al., 1982; Pantev et al., 1995; Howard et al., 1996; Wessinger et al., 1997). Large-scale organization in AM-rate preferences, or “periodotopy,” when present, was often related to the pitch conveyed: low pitch at high AM rates or high pitch conveyed by the center frequency of WN more evident at low AM rates. Previous studies assessing topography using temporally modulated stimuli (Barton et al., 2012; Herdener et al., 2013) may also share this confound. Thus, our findings question the utility of using such stimuli to assess periodotopic organization and/or the temporal fidelity of auditory cortex responses.

Functional topography in auditory cortex

Two axes of tonotopic organization were suggested by our data: one oriented anterior–posterior and another medial–lateral. Reversals in the former are likely to mark borders between subregions within core and surrounding belt (Galaburda and Sanides, 1980; Rauschecker et al., 1995; Fullerton and Pandya, 2007), whereas reversals in the latter did not seem to delineate cortical subregions. Instead, the medial–lateral axis may reflect preference for low frequencies in lateral STP and either (1) a preference for high frequencies in medial belt (Fig. 1C) and/or (2) a relatively higher number of smaller subregions in medial belt (Fig. 1D). Spectral frequency appeared to be the main driver of functional organization in early auditory areas, reflecting the unidimensional nature of auditory sensory epithelia.

The presence of two tonotopic axes in our data does not mean that other types of functional topography are not present (Schreiner and Winer, 2007), nor does it necessarily preclude the possibility that the medial–lateral tonotopic axis is an epiphenomenon of “periodotopy” (i.e., organization by preferred pitch). Indeed, periodotopy has been demonstrated in the auditory brainstem and cortex of nonhuman primates and other animals (Schreiner and Langner, 1988; Langner et al., 2009; Baumann et al., 2011, 2015). However, current evidence supporting large-scale periodotopic organization across the whole of human auditory cortex is mixed. Previous empirical support consists of MEG studies where spatially resolving periodotopy is difficult (Langner et al., 1997; Alho et al., 2012), and two previous fMRI studies reporting conflicting orientations of periodotopy [“clover leaf” (Barton et al., 2012) and high-to-low rates organized along the medial-to-lateral axis (Herdener et al., 2013)]. Other fMRI studies that have measured responses to temporally modulated sound (i.e., not to demonstrate periodotopy per se) also do not clearly indicate periodotopy in our view (Giraud et al., 2000; Langers et al., 2003; Schönwiesner and Zatorre, 2009).

Studies of periodicity pitch and temporal sensitivity face a similar challenge: temporally modulated stimuli (like AMWN) can convey pitch both by their center frequency and their fundamental/temporal frequency. In our data, large-scale organization by AM rate was not evident in group maps, and, when quantified, similarities to tonotopic maps were apparent. Gradients in AMWN maps extended along two, roughly orthogonal axes: one anterior to posterior and another medial to lateral. AMWN maps and tonotopic maps were negatively correlated spatially in some regions, suggesting that (1) preference for high AM rates may reflect preference for low-frequency periodicity pitch in these stimuli and (2) preference for low AM rates may reflect preference for the higher center/spectral frequency of AMWN. This was particularly apparent in right auditory cortex, which may be biased toward spectral processing (Zatorre and Belin, 2001; Schönwiesner et al., 2005), and in lateral auditory cortex bilaterally, which is sensitive to pitch and harmonicity (Griffiths et al., 1998; Schneider et al., 2005; Lewis et al., 2009; Leaver and Rauschecker, 2010).

Unlike responses to center/spectral frequencies, only small nonoverlapping foci in medial HG and lateral HG/STP exhibited significantly different responses to AM rates in our data. Activity in these same regions showed a significant positive correlation with AM rate, such that the highest AM rates elicited the highest response. Together, these data suggest regional, not global, sensitivity to AM rate in auditory cortex, and the presence of large-scale organization by preferred AMWN (periodotopy) in human auditory cortex is not supported by our data. Instead, different subregions might be sensitive to periodicity pitch (lateral region; Griffiths and Hall, 2012) and may exhibit local periodotopy (Barton et al., 2012), whereas others may respond with greater temporal fidelity to the rapid changes in high rates of AMWN (medial region; Kusmierek and Rauschecker, 2009; Schönwiesner and Zatorre, 2009; Herdener et al., 2013).

Functional topography delineates subregions of human auditory cortex

In histological studies, core, or “koniocortical,” auditory cortex has been consistently shown to occupy the central part of Heschl's sulcus (HS), HG, and the first transverse sulcus in humans and can be differentiated into two or three subfields approximately oriented along the anterior–posterior axis (Brodmann, 1909; Galaburda and Sanides, 1980; Rivier and Clarke, 1997; Clarke and Rivier, 1998; Hackett et al., 2001; Morosan et al., 2001; Fullerton and Pandya, 2007), though its exact location varies relative to individual macroanatomy (Rademacher et al., 1993, 2002; Morosan et al., 2001). Our data also support the idea that core auditory cortex occupies central HG/HS. Voxels in central HG/HS were highly selective for center/spectral frequency and exhibited the strongest tonotopic gradients across all stimulus bandwidths. This is consistent with previous work in nonhuman primates (Recanzone et al., 1993, 2000; Kosaki et al., 1997) and recent neuroimaging research in humans (Schönwiesner et al., 2014) showing a high degree of frequency selectivity in central HG/HS. Core subfield A1 also responds with greater temporal fidelity than more anterior rostral (R) and rostrotemporal (RT) core subfields (Bendor and Wang, 2008; Kusmierek and Rauschecker, 2009); however, responses to AM rates were not significantly different in central HG/HS in our data. Perhaps future research better able to address temporal fidelity of responses in these and other regions will be more informative.

In our data, lateral auditory regions were also frequency selective, indicative of the role these areas play in spectral and/or pitch processing (Overath et al., 2008; Schönwiesner and Zatorre, 2009; Giordano et al., 2013). Previous human neuroimaging studies in humans implicated several parts of lateral auditory cortex in pitch processing, including lateral HG (Griffiths et al., 1998; Patterson et al., 2002; Penagos et al., 2004; Schneider et al., 2005; cf. Hall and Plack, 2009), the location of which is compatible with a homologous region identified in nonhuman primates at the border of A1 and the anterolateral belt (AL; Bendor and Wang, 2005, 2006). In our data, lateral subregions, perhaps homologues of monkey AL (Rauschecker et al., 1995), showed greater responses to low center frequencies and to high AM rates conveying low pitch, supporting the relevance of pitch processing for lateral auditory regions.

Medial auditory cortex was less selective for center frequency; however, part of medial HG was selective for high AM rates. Given medial HG also preferred high center frequencies in tonotopic maps, responses to AMWN in this region are unlikely to have been affected by the spectral content of AMWN. Instead, this preference for high AM rates could indicate greater temporal fidelity in responses and/or a preference for processing sounds at shorter time windows. Indeed, neuroimaging studies have shown a preference for high temporal rates in medial HG (Schönwiesner and Zatorre, 2009; Herdener et al., 2013), and in nonhuman primates, some regions of medial belt respond at shorter latencies, in particular the caudomedial belt area (Kusmierek and Rauschecker, 2009, 2014; Camalier et al., 2012). Neurons that respond well to high center frequencies also respond at shorter latencies than neurons preferring low frequencies (Bendor and Wang, 2008; Kusmierek and Rauschecker, 2009); this may explain the behavior of this medial HG in our study. Addressing these issues with methods better able to resolve the temporal dynamics of neural responses in auditory cortex like combined MEG/EEG and fMRI (Dale et al., 2000) or multiband fMRI (Uðurbil et al., 2013; cf. Harms et al., 2005) will be better able to test these hypotheses.

Conclusions

In this study, we characterized the functional topography of human auditory cortex, and explored how its subregions process low-level acoustic features important for processing complex natural sounds, an approach hitherto pursued mostly in nonhuman primates and other species (Rauschecker, 1998; Schreiner and Winer, 2007). Although basic, this information is fundamental to our understanding of auditory and sensory processing as a whole. Using functional topography in this way will allow us to independently identify regions and pathways as homologous to other species, thus providing a more complete and generalized knowledge of auditory processing. Given the keen interest in determining the relative contribution of processing streams originating from anterior/ventral versus posterior/dorsal auditory regions (Romanski et al., 1999; Rauschecker and Tian, 2000) to higher cognitive functions, including speech and language (Hickok and Poeppel, 2007; Rauschecker and Scott, 2009; Bizley and Cohen, 2013; Bornkessel-Schlesewsky et al., 2015), it is critical to understand the role these early auditory–sensory subregions play (Hackett, 2011). Together, studies like these will ultimately form a complete picture of complex acoustic analysis in the human brain.

Notes

Supplemental material for this article is available at http://users.bmap.ucla.edu/∼aleaver/functional_topography/. Sound files for example stimuli used in this study are available for review and download. This material has not been peer reviewed.