Abstract
Obtaining accurate displacement estimates along both axial (parallel to the acoustic beam) and lateral (perpendicular to the beam) directions is an important task for several clinical applications such as shear strain imaging, modulus reconstruction and temperature imaging, where a full description of the two or three dimensional (2D/3D) deformation field is required. In this study we propose an improved speckle tracking algorithm where axial and lateral motion estimations are simultaneously performed to enhance motion tracking accuracy. More specifically, using conventional ultrasound echo data, this algorithm first finds an iso-contour in the vicinity of the peak correlation between two segments of the pre- and post-deformation ultrasound radiofrequency echo data. The algorithm then attempts to find the center of the iso-contour of the correlation function that corresponds to the unknown (sub-sample) motion vector between these two segments of echo data.
This algorithm has been tested using computer-simulated data, studies with a tissue-mimicking phantom, and in vivo breast lesion data. Computer simulation results show that the method improves the accuracy of both lateral and axial tracking. Such improvements are more significant when the deformation is small or along the lateral direction. Results from the tissue-mimicking phantom study are consistent with findings observed in computer simulations. Using in vivo breast lesion data we found that, compared to the 2D quadratic subsample displacement estimation methods, higher quality axial strain and shear strain images (e.g. 18.6% improvement in contrast-to-noise ratio for shear strain images) can be obtained for large deformations (up to 5% frame-to-frame and 15% local strains) in a multi-compression technique. Our initial results demonstrated that this conceptually and computationally simple method could improve the image quality of ultrasound-based strain elastography (SE) with current clinical equipment.
Keywords: ultrasound, elasticity imaging, elastography, speckle tracking, strain elastography, shear strain
Introduction
Ultrasound-based strain elastography (SE; (Shiina et al., 2015)) (Ophir et al., 1991; O'Donnell et al., 1994; Hall et al., 2003), an imaging modality complementary to conventional ultrasound, is a surrogate for manual palpation to assess variations in tissue elasticity. In SE, tissue elasticity information can be readily estimated from ultrasound radiofrequency (RF) echo data acquired by obtaining an RF echo frame, deforming the tissue, obtaining another RF frame, and then tracking displacements that occurred between those two frames of RF data. Since several orders of magnitude difference between the elastic modulus of normal and abnormal tissues exists in many organ systems, SE has been successfully applied to clinical management of neoplasms and cardiovascular diseases, including non-invasive differentiation of breast tumors (Itoh et al., 2006; Regner et al., 2006; Burnside et al., 2007), monitoring thermal ablation for liver tumors (Kolokythas et al., 2008; Rubert et al., 2010), characterizing thyroid lesions (Rago et al., 2007; Bae et al., 2007), imaging vascular plaques (Cespedes et al., 1997) and assessing the age of deep vein thrombosis (Xie et al., 2004).
To further develop SE techniques, all components of the displacement vector field and/or their spatial derivatives will be required. Both axial and lateral displacements are needed to estimate shear strains (Konofagou and Ophir, 1998a; Rao et al., 2008), to measure thermal expansions for estimating temperature distributions (Simon et al., 1998; Miller et al., 2004), and to reconstruct modulus distributions through mathematical inversions (Kallel and Bertrand, 1996; Zhu et al., 2003; Oberai et al., 2004). However, in typical SE systems, lateral (and elevational) displacement estimates (perpendicular to the ultrasound beam) are lower in quality as compared to that of axial displacement estimates.
Previous efforts to improve estimation of non-axial motion have been well documented and can be divided into two categories. Methods in the first category require significant modifications of the ultrasound imaging system (e.g. special beamforming or rapid beam steering). A method independently proposed by Jensen (Jensen and Munk, 1998) and Anderson (Anderson, 1998) attempted to introduce non-axial oscillations/modulations in their respective imaging point spread functions. Techavipoo et al. used “angular compounding” to improve lateral displacements (Techavipoo et al., 2004). Methods in the second category (Lubinski et al., 1996; Konofagou and Ophir, 1998a; Chen et al., 2004; Ebbini, 2006; Brusseau et al., 2008; Zheng et al., 2007) fall into the area of (software) image processing. Particularly, in order to improve displacement estimation, tissue incompressibility has been frequently used to explicitly tie relevant axial and lateral displacements together. For instance, Konofagou and Ophir (Konofagou and Ophir, 1998b) proposed a subsample estimation approach where axial and lateral displacements can be iteratively improved by re-correlating ultrasound echo signals through instantaneous motion compensations. In more recent work by Brusseau et al. (Brusseau et al., 2008), they formulated motion tracking between two echo frames as an optimization process to find local 2D affine transformations. Therefore, both axial and lateral translations can be jointly solved using constrained nonlinear programming. Viola and Walker (Viola et al., 2008) proposed multi-dimensional tracking using spline functions. Since this extension enables them to simultaneously solve the axial and lateral displacements, their work nicely fits into the category of coupled subsample displacement estimation. Rivaz et al. have also applied physical constraints to simultaneously regularize axial and lateral speckle tracking using multiple (time) frames of RF echo data to improve displacement estimations (Rivaz et al., 2014). Their method also yielded good results. To improve lateral displacements, an assumption of tissue incompressibility can also be applied directly to an estimated displacement vector field as an off-line “de-noising” method. Our group (Zheng et al., 2007) has implemented a partial differential equation (PDE)-based method. Our formulations were derived based on the calculus of variation and solved using finite difference scheme.
Our objective in this study was to develop an alternative method to improve both axial and lateral speckle tracking using conventional ultrasound echo data acquired by clinical imaging systems. The remainder of the paper is structured as follows. In the Methods and Materials Section, the correlation function between the pre- and post-deformation echo signals was derived. We then demonstrated that isocontours of the “log-compressed” correlation function were a series of ellipses sharing an isocenter. The center of any of these ellipses corresponds to the peak of the correlation function. This approach simultaneously estimates both axial and lateral displacements by locating the center of one of these ellipses in a least square sense. In the Results Section, the coupled tracking algorithm was tested using Field II-simulated RF echo signals (Jensen, 1991), data acquired from a tissue-mimicking phantom (Pavan et al., 2012), and in vivo breast tissue data (Hall et al., 2003). Closing remarks are provided in the Discussion and Conclusion Sections.
Materials and Methods
A. Theoretical Background
In linear systems theory the radiofrequency (RF) echo signals of a medical ultrasound system are modeled based on the shift-invariant point spread function (PSF) (Meunier and Bertrand, 1995; Jensen, 1991; Li and Zagzebski, 1999) as follows:
| (1a) |
| (1b) |
where s is the RF echo signal consisting of a set of A-lines, h is the system PSF, z is the acoustic impedance difference of tissue modeled by a 2D Gaussian random field and, x and y are lateral and axial coordinates, respectively. In Eqns. (1a) and (1b), s1 and s2 are two grossly aligned segments of RF signals and are only separated by a subsample displacement vector (dx, dy). The log-compressed cross-correlation function (between s1 and s1) can be written as follows,
| (2a) |
| (2b) |
where C1 and C2 are related to the ultrasound system parameters but are two constants for two given signals s1 and s2. In Eqns. (2a) and (2b), Δx and Δy represent a uniform grid from which a correlation map can be obtained. Eqn. (2a) indicates that, in the vicinity the correlation peak, the (log-compressed) correlation function can be approximated as a second-order polynomial surface. The role of subsample speckle tracking is to find locations corresponding to the true maximum of the correlation function ρ (Eqn. (2a)). Therefore, one approach to estimate the subsample displacements is to fit correlation values in the proximity of the correlation peak (at the integer level) to 1D (Cespedes et al., 1995) or 2D (Zahiri Azar et al., 2010) quadratic functions. Our method takes a different approach. We set the right hand side of Eqn. (2a) equal to a constant K. Consequently, as seen from Eqn. (2b), an iso-contour of the log-compressed correlation function ρ is an ellipse. To this end, locating the center of this ellipse (dx, dy) is equivalent to finding the theoretical peak of the correlation function ρ, i.e., the correlation function ρ reaches its maximum when and only when Δx = dx and Δy = dy
In short, this method of estimating the unknown (subsample) displacement vector (dx, dy) is to first select one correlation value K around the (integer level) correlation peak, then to fit the chosen iso-contour to an ellipse, in a least-squares sense, to determine the center of the fitted ellipse. The center of the fitted ellipse is mathematically equivalent to the unknown (subsample) displacement vector (dx, dy). A brief derivation of Eqn. (2a) is provided in Appendix for the sake of completeness.
B. Implementation of the coupled subsample displacement estimation
The coupled subsample displacement estimation technique involves three steps for a given subsample displacement estimate: (1) estimate the initial displacement and strain using a modified block matching (MBM) algorithm (Jiang and Hall, 2011), (2) shift and stretch the post-deformation kernel locally using integer displacement and axial strain estimates (assuming that tissue is locally incompressible) to maximize cross correlation, and (3) calculate the correlation function in the neighborhood of its peak to determine the center of one iso-contour of the correlation function. Essential implementation details are provided below.
In the first step, the MBM algorithm (Jiang and Hall, 2011) was used to obtain initial displacement vectors at the integer level (dxi, dyi). This MBM algorithm starts motion tracking from a set of “high quality seeds” to avoid large tracking errors due to “false correlation peaks” (Walker and Trahey, 1995). More details can be found in a previous publication (Jiang and Hall, 2011).
In the second step, initial displacements obtained from Step 1 were used to shift the search kernel on the post-deformation RF frame by the amount of the integer displacements estimated. This process is known as (partial) “motion-compensation” (Alam and Ophir, 1997). In the third step, to simultaneously calculate subsample displacement estimates (dx, dy), we first calculated a discretely-sampled correlation function with improved resolution (e.g. 0.05-mm [lateral] × 0.005-mm [axial]) around the vicinity of the correlation peak known from the integer displacement estimation in Step 1. A fast B-spline interpolation developed by Unser et al. (Unser, 1991) was used to locally up-sample the RF data so that the search kernel can ‘translate’ beyond the integer level. Therefore, the resolution of the correlation map can be improved without up-sampling the entire RF data sets. To choose an iso-contour near the correlation peak, the following empirical equation was used to determine the value of K (Eqn. 2b):
| (3) |
where ρi,j is the peak correlation value located at the ith row and the jth column of the correlation map. Consequently, the selected K value is the averaged correlation values among one-ring and two-ring neighbors of the correlation peak ρi,j at the integer level. To obtain the subsample displacement vector (dx, dy), we fit coordinates of the selected iso-contour (at the correlation value K defined by Eqn. (3)) to an ellipse (Fitzgibbon et al., 1996). It is worth noting that the selected iso-contour should be close to the correlation peak ρi,j because Eqn. (2a) is only valid in the vicinity of the correlation peak. However, selecting a value that is too close to the peak of the (discretely sample) correlation function will result in fewer points to define the iso-contour, causing problems for the subsequent fitting of the ellipse. Therefore, Eqn. (3) represents a practical balance. The final high quality displacement vector (tdx, tdy) was the sum of the integer displacement vector (dxi,dyi) from Step 1 and the subsample displacement vector (dx, dy) from the current step (i.e. Step 3).
C. Strain Estimation
The axial and shear strains can be estimated as follows,
| (4) |
| (5) |
In this study, we estimated local axial strain and shear strain using a least-square method (Kallel and Ophir, 1997).
D. Recovery of Large Deformations Using Multiple-Step Accumulation
Many correlation-based tracking algorithms provide low quality displacement estimates for in vivo tissue when single-step deformation is large (e.g. frame-average strain is greater than 2%). However, large tissue deformation may be recovered through accumulations of smaller deformation in a multi-step process (Jiang et al., 2006; Du et al., 2006) as follows. Given a sequence of N ultrasound echo fields under a monotonic compression, sequential motion tracking was first performed between two adjacent frames using any above-described motion tracking algorithm (including the coupled tracking) to obtain (N-1) frames of displacement fields. More formally, the ith displacement field represents the 2D displacement vector field obtained between the ith and (i+1)th RF echo frames. Next, those displacement and strain frames in this sequence were mapped to the coordinate system of the first ultrasound echo frame using B-spline interpolations to provide spatially-registered data for the analysis described below (subsection F).
E. Experimental Validation
The coupled subsample displacement estimation algorithm was tested using computer-simulated data, tissue-mimicking phantom data, and in vivo breast tissue data. The first test was to compute bias errors and variances using FIELD II-simulated RF signals (Jensen, 1991). A virtual phantom (40mm × 40mm × 10 mm) was uni-axially compressed under the plane strain condition from 0.1% to 5% to generate pre- and post-deformation RF echo data. Density of randomly positioned point scatterers was set to be approximately 35 scatterers per mm3, satisfying the Rayleigh scattering condition (Rao et al., 1990). The virtual phantom was imaged with a 192-element linear array probe using 64 active elements. The simulation used a 6 MHz center frequency with a 50% of fractional bandwidth and sampling frequency was 50 MHz (i.e. 15.4 μm spacing between adjacent samples along an A-line). A single transmit focus was set at 20 mm depth, and dynamic receiving focusing was modeled to generate the RF lines. In total, 150 RF lines were simulated along a width of 30 mm for each frame, resulting in a line spacing of 198 μm.
The bias errors of axial and lateral displacements were calculated by comparing the estimated axial and lateral displacement fields to the known axial and lateral displacement fields. Error variances obtained by this 2D coupled tracking algorithm were compared to the 1D and 2D quadratic subsample estimation methods (Zahiri Azar et al., 2010). All three methods have been incorporated into the MBM algorithm (Jiang and Hall, 2011).
In the second test, a tissue mimicking (TM) phantom (10 cm × 10 cm × 10 cm) (Pavan et al., 2012) was used to demonstrate the coupled tracking algorithm in a controlled setting. The spherical target (10mm diameter) was approximately four times stiffer than the background. RF echo data were acquired using a Siemens SONOLINE(tm) Antares (Siemens Medical Solutions Inc., Mountain View, CA) equipped with a multi-row linear array transducer (VFX9-4) sampling at 40 MHz and the AXIUS Direct Ultrasound Research Interface (URI) software package (Nock et al., 2002). The ultrasound transducer was pulsed at 8.89 MHz. The phantom was compressed using an acyclic plate (a 17 cm square) by 1%.
The third test compared the performance of the coupled tracking algorithm to the 2D quadratic interpolation algorithm using in vivo breast tissue data. Tests 1 and 2, and data available in the literature, provide a basis to argue that the 2D quadratic algorithm out-performs the 1D quadratic subsample displacement estimation algorithm (Zahiri Azar et al., 2010). From an archived database of ultrasound scans of human breast lesions, 2 RF echo data sets (one fibroadenoma [FA] and one invasive ductal carcinoma [IDC]) were arbitrarily chosen. The detailed protocol for acquisition of that data was previously reported (Hall et al., 2003).
Two metrics were chosen to compare the performance among three above-mentioned methods. The first metric, the “displacement quality metric” (DQM) (Jiang et al., 2006), is the product of the normalized cross correlation (NCC) among the pre-deformation and motion-compensated post-deformation RF echo fields (a measure of motion tracking accuracy applied to the entire region of interest) and the cross correlation between two consecutive motion-compensated strain images (a measure of strain image consistency) (Jiang et al., 2006). NCCs were used to assess above-mentioned correlations. Therefore, all DQM values lied between 0 and 1, with 1 indicating the best result. More details of this metric can be found in an early publication (Jiang et al., 2006).
The second metric is the weighted contrast-to-noise ratio (CNR) (Song et al., 2004):
| (6) |
where I and σ2 denote means and variances of signals, and subscripts b and t represent the background and target, respectively. To calculate the CNR using Eqn. (6) for each strain image, the lesion was manually segmented (representing the ‘target’) and the rest of strain image represented the ‘background’. w is a weighting of the area of the target and the background to the total area given by wx= areax / areatotal. Consideration of the weighted area is necessary because the target and the background contribute differently to the noise estimates (Song et al., 2004).
Performance comparison among these three algorithms were done off-line on a Windows 7 computer (1.8-GHz, i5-CPU, 8GB, VAIO, Sony Inc., Tokyo, Japan) using ANSI C and the MEX interface to Matlab (Mathworks Inc., MA, USA). Of note, in the first test, large deformations among numerical phantoms were tracked both in a single step and in a multiple step fashion (every 0.5%), whereas large deformations in two in vivo breast lesion data (test 3) were tracked in a multi-step fashion (see Section II-D). In the second test, single step (1%) tracking was done for the tissue-mimicking phantom. For all three subsample displacement estimation algorithms, displacement estimation spacing was approximately 0.5 mm × 0.5 mm.
Results
A. Numerical Phantom Results
Results are shown in Table 1 where approximately 2000 statistically independent realizations were used to estimate error variances and absolute values of the mean errors (i.e. estimation bias) for a 1% compression. For all three methods, results in Table 1 indicated that the displacement estimate biases were reasonably low, and the coupled tracking method had the lowest bias for all kernel sizes investigated. Through an analysis of tracking error variances, we found that the coupled tracking algorithm also consistently out-performed both the 1D and 2D quadratic subsample displacement estimation methods. For instance, when the search kernel was 0.63 [axial] × 1.0 [lateral] mm both axial and lateral error variances were among the lowest, and the coupled tracking algorithm outperformed the 1D and 2D quadratic subsample methods by factors of 4.8 and 2.2, respectively, for lateral displacements. Axial speckle tracking improved, relative to the 1D and 2D interpolation results, by factors of 2.9 and 1.2, respectively, for the same search kernel. However, the performance improvement decreased as the kernel size increased beyond that size (Table 1).
Table 1.
Tabulated results of tracking errors using three different subsample algorithms: the coupled tracking algorithm, the 1D-quadratic interpolation method and the 2D-quadratic interpolation method. The kernel sizes are also provided in terms of samples and beamlines (values in parentheses).
| Kernel Size (axial height × lateral width) | Subsample Methods | Axial Displacement Error | Lateral Displacement Error | ||
|---|---|---|---|---|---|
|
|
|
||||
| Absolute Mean (mm) | Variance (mm2) | Absolute Mean (mm) | Variance (mm2) | ||
| 0.23 × 0.6 mm (15 × 3) | 1D-Quad | 9.1×10-5 | 4.8×10-6 | 6.8×10-4 | 3.6×10-3 |
| 2D-Quad | 10.8×10-5 | 2.9×10-6 | 10.0×10-4 | 2.8×10-3 | |
| Coupled | 2.1×10-5 | 3.0×10-6 | 0.8×10-4 | 1.3×10-3 | |
|
| |||||
| 0.32 × 0.6 mm (21 × 3) | 1D-Quad | 8.5×10-5 | 5.6×10-6 | 6.8×10-4 | 4.0×10-3 |
| 2D-Quad | 10.9×10-5 | 4.1×10-6 | 10.0×10-4 | 3.5×10-3 | |
| Coupled | 3.5×10-5 | 2.3×10-6 | 1.1×10-4 | 1.1×10-3 | |
|
| |||||
| 0.63 × 0.2 mm (41 × 1) | 1D-Quad | 10.0×10-5 | 3.8×10-6 | 6.0×10-4 | 3.1×10-3 |
| 2D-Quad | 13.2×10-5 | 2.0×10-6 | 9.8×10-4 | 2.0×10-3 | |
| Coupled | 4.4×10-5 | 1.5×10-6 | 0.8.×10-4 | 1.0×10-3 | |
|
| |||||
| 0.63 × 1.0 mm (41 × 5) | 1D-Quad | 9.8×10-5 | 2.9×10-6 | 7.2×10-4 | 2.4×10-3 |
| 2D-Quad | 10.1×10-5 | 1.2×10-6 | 9.9×10-4 | 1.1×10-3 | |
| Coupled | 3.3×10-5 | 1.0×10-6 | 0.5×10-4 | 0.5×10-3 | |
|
| |||||
| 0.94 × 1.4 mm (61 × 7) | 1D-Quad | 8.9×10-5 | 2.1×10-6 | 10.0×10-4 | 1.7×10-3 |
| 2D-Quad | 9.8×10-5 | 1.2×10-6 | 11.0×10-4 | 0.71×10-3 | |
| Coupled | 3.4×10-5 | 1.1×10-6 | 1.1×10-4 | 0.5×10-3 | |
|
| |||||
| 1.86 × 1.0 mm (121 × 5) | 1D-Quad | 5.8×10-5 | 3.5×10-6 | 15.0×10-4 | 2.0×10-3 |
| 2D-Quad | 7.8×10-5 | 3.0×10-6 | 14.0×10-4 | 1.3×10-3 | |
| Coupled | 1.0×10-5 | 2.8×10-6 | 3.1×10-4 | 1.2×10-3 | |
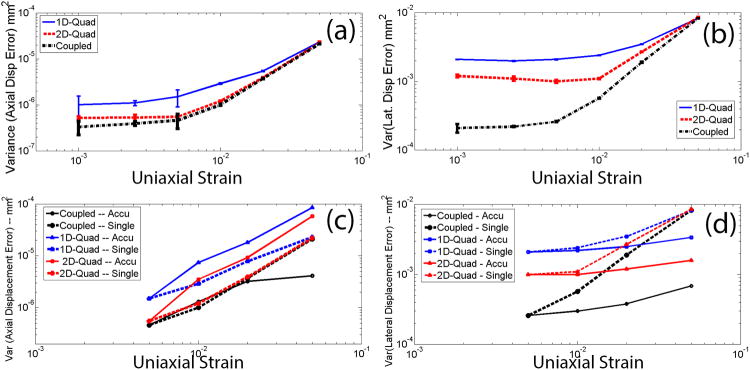
The simulations were repeated for different applied deformation (0.1–5% uniaxial strain) using a kernel size of 0.6-mm (axial length) by 1.0-mm (lateral width). Results using a single-step tracking strategy are plotted in Figs. 1(a) and 1(b) where error bars denote one standard deviation from 5 realizations. Of note, the search kernel (0.6 × 1.0 mm) is close to an ‘optimal’ tracking kernel that results in ‘lowest’ axial and lateral error variances for all three methods (see Table 1). Figs. 1(a) and 1(b) show that the error variances of both axial and lateral displacement estimates were lower when the coupled tracking method was used. Particularly, the coupled tracking method improved the lateral tracking more significantly, as compared to its improvements to the axial tracking. We also found that the greatest improvement with the coupled algorithm occurred at the low deformations, for instance, by approximately factors of 1.7 and 5 at the 0.1% strain for axial and lateral tracking, respectively, as compared to the 2D quadratic subsample method.
Figure 1.
Plots of the estimated (a and c) axial and (b and d) lateral error variances among displacement estimates with simulated RF data using a search kernel size of 0.6 × 1.0 mm. The deformation levels varied from 0.1% to 5% strain. In (a) and (b), all error variances were obtained using a single step tracking strategy. In (c) and (d), error variances obtained from multiple steps (0.5% per step) were compared to those obtained from the single-step tracking strategy.
When a multi-step tracking strategy was employed (i.e. accumulating displacements tracked from every 0.5% deformation), the coupled tracking algorithm maintained substantially lower error variances both for axial and lateral tracking (see Figs. 1(c) and 1(d)). The improvement rate by the coupled tracking algorithm was significant at 5% accumulated strain (i.e. improvement factors of approximately 20 and 3 for axial and lateral tracking, respectively, as compared to using the 2D quadratic subsample method).
B. Axial Strain and Shear Strain Results from the TM phantom
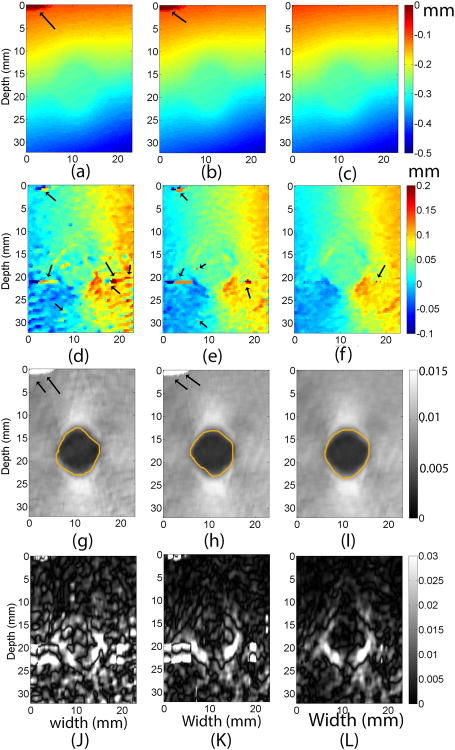
Results from the tissue-mimicking phantom under a 1.0% compression are shown in Fig. 2. Similar to the simulation results in Fig. 1, comparable axial displacements (Figs. 2a-c) were obtained from the phantom experiment. The estimated CNR values from axial strain images obtained from three methods were 4.2 (1D-Quad), 4.3 (2D-Quad) and 5.2 (Coupled), respectively. The lateral displacement images (Figs. 2d-f) contained significant noise compared to their axial counterparts. Consequently, the full shear strain images (Figs. 2J-L) had lower target detectability. Nevertheless, the coupled method improved the lateral tracking (Fig. 2f) and the subsequent shear strain image (Fig. 2L). Consistent with visible perception, the estimated CNR values from shear strain images obtained from three methods were 0.22 (1D-Quad), 0.32 (2D-Quad) and 0.49 (Coupled), respectively.
Fig. 2.
Images of the tissue mimicking phantom containing a spherical target using three different subsample displacement estimation methods. Images in the first, second and third columns were obtained using the 1D quadratic interpolation method, the 2D quadratic interpolation method, and the coupled tracking method, respectively. The top row, (a) - (c), is axial displacement images, while (d) - (f) are lateral displacement images, (g)-(I) are axial strain images and (J)-(L) are (full) shear strain images. The arrows on all images point to potential tracking errors. The contours in axial strain images segment target boundaries and were used for calculations of CNRs. A 3 × 3 median filter was applied to lateral displacement estimates for display.
C. Axial Strain Results from In vivo Breast Tissue Data
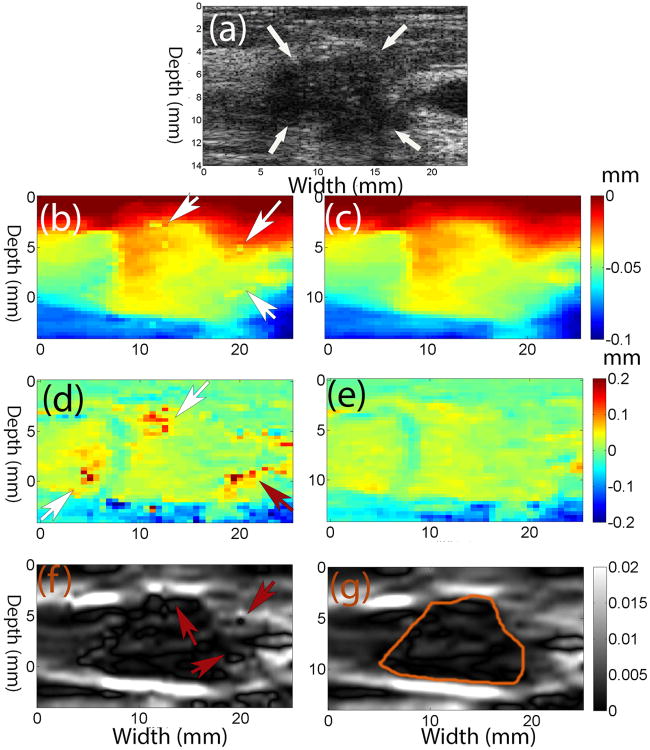
Representative results from in vivo invasive ductal carcinoma (IDC) data were used to demonstrate the performance of the coupled tracking method. The frame-average strain was approximately 1%. Figs. 3b, 3d and 3f show that the 2D quadratic subsample method makes some suspected errors (see arrows), while the coupled tracking method is able to avoid them. The general appearance of the axial and lateral displacement images (Figs. 3c and 3e) obtained using the coupled tracking method is smoother as compared to results from the 2D quadratic method (Figs. 3b and 3d).
Fig. 3.
a) B-mode image of an in vivo invasive ductal carcinoma (IDC), (b), (d) and (f) axial and lateral displacement (in mm) and axial strain images obtained using the 2D quadratic interpolation method, respectively, compared to (c), (e) and (g) those obtained using the coupled tracking method. The arrows in (a) point to the IDC, while arrows in (b), (d) and (f) point to the possible tracking errors. The contours in axial strain images were the segmented target boundaries and were used for calculations of CNRs.
d. Shear Strain Results from In vivo Breast Tissue Data
Figures 4b and 4d show images of axial shear (Thitaikumar et al., 2008) (i.e. the second term on the right hand side of Eqn. (5)) and full shear strain (i.e. Eqn. (5)), respectively, occurring in the IDC (shown in Fig. 3) obtained using the coupled tracking algorithm. The full shear strain image of the same IDC using the 2D quadratic subsample method is displayed in Fig. 4c. The lesion is clearly visible in the full shear strain image obtained with the coupled tracking method. However, the detectability of the lesion in Fig. 4c is low since the lateral displacement estimates obtained with the 2D quadratic subsample method are lower quality (see Fig. 3e vs. Fig. 3d).
Figure 4.
(a) B-mode, (b) axial shear and (d) full shear strain images estimated from the in vivo IDC breast lesion using the coupled tracking method. For comparison, a full shear strain image estimated using the 2D quadratic interpolation method is shown in (c). Arrows in the B-mode image point to the breast lesion. Arrows in (d) point to a tissue interface that cannot be seen in the axial shear image (b). The frame-average axial strain is approximately 1%.
Similarly, Figs. 5c and 5d show (full) shear strain images for the in vivo fibroadenoma (FA). In both breast lesions, tissue interfaces identified by high shear regions in the full shear strain image (see arrows in Figs. 4d and 5d) are more consistent with the layered tissue structures shown on the corresponding B-mode images (see Figs. 4a and 5a).
Figure 5.
(a) B-mode, (b) axial shear and (d) full shear strain images estimated from the in vivo FA using the coupled tracking method. For comparison, a full shear strain image estimated using the 2D quadratic interpolation method is shown in (c). Arrows in the B-mode image point to the breast lesion. Arrows in (d) point to visible interfaces that cannot be seen in the axial shear image (b). The frame-average axial strain estimated by the coupled subsample displacement estimation method is approximately 1%.
e. Performance Assessment
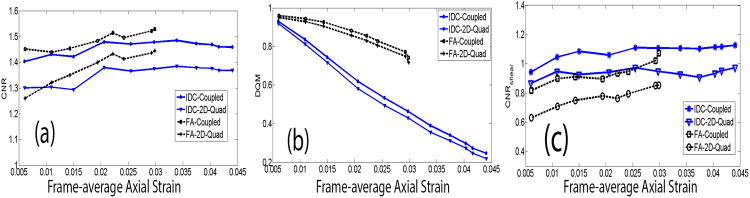
Estimated DQM and CNR values of (accumulated) axial strain images using the coupled tracking and the 2D quadratic subsample methods were plotted in Figs. 6(a) and 6(b), with respect to different axial deformations for the in vivo IDC (Figs. 3 and 4) and the FA (Fig. 5). Figure 6c shows a plot of estimated CNR values of (accumulated) full shear strain images obtained from the in vivo IDC and FA breast lesions with respect to their axial deformations.
Figure 6.
Plots comparing (a) CNR of axial strain images, (b) DQM values, and (c) CNR of (full) shear strain images obtained from an in vivo IDC and an in vivo FA using two subsample methods: the coupled tracking method and the 2D quadratic subsample method. All metrics in all three figures were plotted with respect to accumulated frame-averaged axial strains.
In all three plots, large deformations were accumulated from displacement estimates obtained from two adjacent RF echo frames (Methods Section D). Higher DQM and, CNR values of the axial strain and shear strain images were obtained using the coupled subsample displacement estimation method, as compared to the 2D quadratic sub-sample method. This observation is consistent with a subjective analysis of Figs. 3, 4 and 5. The improvement ratio in DQM values for the coupled subsample displacement estimation algorithm is only 5.4%±3.7% (mean ± standard deviation), while the improvement ratio in CNR values of axial strain images is higher (8.0% ± 2.2%). The improvement ratio in CNR values of (full) shear strain images is 18.6% ± 5.3%. The image sequences corresponding to data in Fig. 6 can be found in Movies 1 (IDC) and 2 (FA) in the supplement materials. In both movies, accumulated axial strain and (full) shear strain images obtained from the coupled tracking and the 2D quadratic method are compared side by side as the tissue being deformed.
Discussion
In this study, we have quantitatively demonstrated that the coupled tracking method can improve both the accuracy of motion tracking (DQM and displacement estimate error variances) and the quality of axial strain and full shear strain images (CNR). It is worth noting that the displacement estimate bias of the coupled tracking method was also the lowest (Table 1), as compared to both the 1D and 2D quadratic interpolation methods. Here, we stipulate one possible explanation. Equation (2a) showed that the underlying correlation function can be represented by a second-order polynomial, so the advantage of the coupled algorithm could be viewed, to some extent, as an averaging process – estimating the center of an ellipse from multiple angular locations. Cespedes et al. have demonstrated that 1D sub-sample displacement estimation can be iteratively reconstructed by first finding two locations with equal correlation values around the correlation peak (integer level) and, then using the middle point between those two locations as the peak (sub-sample level) of the correlation function (Cespedes et al., 1995). They showed that their method has a lower displacement estimate bias, as compared to the 1D quadratic interpolation method.
Our preliminary results (Figs. 1c and 1d) showed that the coupled tracking algorithm has lower noise sensitivity for displacement estimate accumulation (using a 0.5% axial strain increment), largely due to lower lateral tracking errors. Recall that, in the framework of multi-compression tracking (Jiang et al., 2006; Du et al., 2006), we first track tissue deformations through a long sequence of echo data and then map all deformations back to the initial reference state through interpolations before accumulation. That is why both axial and lateral displacements play roles in the displacement accumulation. Hence, we anticipate that the availability of the coupled tracking algorithm may help for nonlinear modulus inversion (Hall et al., 2009; Oberai et al., 2009; Goenezen et al., 2012). The initial result is encouraging and therefore warrants further investigations.
Recently, the use of the axial shear strain alone has shown value in characterization of breast lesions (Thitaikumar et al., 2008). However, to fully quantify “shearing” as a surrogate for tissue connectivity around a breast lesion, contributions from the lateral shear strain cannot be ignored. Figs. 4 and 5 demonstrated that horizontal interfaces around those two breast lesions could not be identified in the axial shear strain images. Although there has not been a demonstration of the clinical use of the full shear strain imaging, the feasibility of obtaining full shear strain data using conventional ultrasound echo data is the first step toward exploring its clinical utility.
The coupled tracking method is straightforward and enhances image quality using conventional ultrasound signals. However, it is worthwhile to note that this method is restricted to signals from “linear” medical ultrasound systems (Meunier and Bertrand, 1995). While coded excitation methods (Chiao and Hao, 2005) may provide improved signal-to-noise ratio and resolution, they could complicate speckle tracking by confounding nonlinear contributions to received echo signals.
Currently, we have implemented the coupled subsample displacement estimation algorithm in Matlab (Mathworks Inc., MA) for the convenience in algorithm testing. The method runs offline and requires approximately 20 minutes (on an i5 CPU with 8GB memory) to obtain a 50 × 50 grid of displacement estimates. Since coupled tracking in the ROI are completely independent, translating the current implementation to a multi-core GPU (NIVIDIA Inc., Santa Clara, CA), together with algorithm optimization, will likely lead to high quality displacement and strain images in real-time (> 20 frames/second).
Conclusions
The theoretical basis for a novel coupled sub-sample estimation algorithm is presented. Computer simulation results show that the method improves the accuracy of both lateral and axial tracking, as compared to the 1D and 2D quadratic sub-sample displacement estimation methods. The improvement is more significant at small deformations (e.g. 0.1%-0.5%) and along the lateral direction (e.g. factors of 10 and 6, respectively, as compared to the 1D and 2D quadratic subsample estimation methods, respectively at the 0.1% deformation). From the in vivo breast lesion data investigated, we found high quality displacements and shear strains can be estimated for large accumulated deformations (up to 5% frame-to-frame and 15% local strains). Particularly, the coupled tracking method can improve the contrast-to-noise ratios (18.6±5.3%) among full shear strain images. Our initial results demonstrated that the proposed method could be used to improve displacements for strain elastography (SE) with current clinical equipment.
Supplementary Material
Acknowledgments
This study was partially supported by NIH grants R01CA140271 and R15CA179409. The computing time for FIELD II simulations was provided by a grant from Michigan Tech's Superior HPC cluster (Dr. Gowtham and Dr. Pengfei Xue). We want to thank Dr. Bo Peng and Mr. Yu Wang at the Michigan Tech for their assistance for Field II simulations and data processing. We also thank our colleagues at the Charing Cross (London, UK) for providing breast data.
Appendix: Derivation of 2D Correlation Function
Based on the linear systems description of ultrasound imaging systems (Meunier and Bertrand, 1995), two 2D segments of RF signals, before and after a small deformation, can be expressed as follows:
| (A1) |
| (A2) |
where s is the RF echo signal consisting of a set of A-lines, h is the system point spread function (PSF) and z is the scatterer distribution function. The subscripts 1 and 2 in Eqn. (A2) denote the pre- and post-deformation data, respectively. In Eqns. (A1) and A(2), since the displacement vector (dx, dy) is at the subsample level, the same coordinate system (x, y) has been used, implying that two segments of signals are from the same sample volume.
The cross correlation between those two signals s1and s2 can be written as follows (Wagner et al., 1988),
| (A3) |
where 〈…〉 represents the ensemble average, Δx and Δy are a pair of dummy variables representing a uniform grid from which the cross-correlation between the pre- and post-translation RF signals s1 and s2 is calculated, and * denotes the conjugate.
We assume that the tissue of interest contains a homogenous distribution of scatterers with uniform scatterering strength and uncorrelated microstructures, resulting in fully developed speckle envelope signal. Therefore, the following equation holds (Li et al., 2001)
| (A4) |
where a0 is the scattering strength and δ(*) is a 2D Dirac-delta function. Hence, Eqn. (A3) can be rewritten as follows,
| (A5) |
Eqn. A(5) demonstrates that correlation function between s1and s2 from the same sample volume can be represented by the “auto-correlation” function of the system's PSF (Li et al., 2001). Strictly, Eqn. (5) is not the auto-correlation function of the PSF because of the presence of a subsample deformation (dx, dy).
We also assume that the 2D PSF h(x, y) is separable in the axial and lateral dimensions. This assumption is valid near the focal depth (Wagner et al., 1983). Furthermore, the PSFs in Eqns. (A1) and (A2) can be modeled using axial and lateral components of Gaussian envelopes as follows,
| (A6) |
where σx and σy are characteristic widths in the lateral and axial directions, respectively, and are related to the lateral and axial bandwidths of the ultrasound system.
As described by Wagner et al. (Wagner et al., 1988), we evaluate the integral in Eqn. (A5) along the lateral and axial directions separately,
| (A7) |
Ix and Iy can be obtained through regular integrations,
| (A8) |
| (A9) |
After a simple reorganization of Eqns. (A7-9), the “log-compressed” correlation function [log(ρ)] can be expressed as follows,
| (A10) |
where C1, C2 and C3 are three constants.
It is worth noting that, in Eqn. (A6), only the Gaussian envelope of the PSF is included. This simplification appears to be adequate to model the correlation function in the proximity of correlation peak (Rao and Varghese, 2006). If we assume that the PSF is a Gaussian modulated cosine function, in the vicinity of the correlation peak, the form of the log-compressed cross-correlation function will be more complex but approximately remain Gaussian.
References
- Alam SK, Ophir J. Reduction of signal decorrelation from mechanical compression of tissues by temporal stretching: applications to elastography. Ultrasound in Medicine & Biology. 1997;23:95–105. doi: 10.1016/s0301-5629(96)00164-0. [DOI] [PubMed] [Google Scholar]
- Anderson ME. Multi-dimensional velocity estimation with ultrasound using spatial quadrature. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1998;45:852–61. doi: 10.1109/58.677757. [DOI] [PubMed] [Google Scholar]
- Bae U, Dighe M, Dubinsky T, Minoshima S, Shamdasani V, Kim Y. Ultrasound thyroid elastography using carotid artery pulsation: preliminary study. J Ultrasound Med. 2007;26:797–805. doi: 10.7863/jum.2007.26.6.797. [DOI] [PubMed] [Google Scholar]
- Brusseau E, Kybic J, Deprez JF, Basset O. 2-D locally regularized tissue strain estimation from radio-frequency ultrasound images: theoretical developments and results on experimental data. IEEE Trans Med Imaging. 2008;27:145–60. doi: 10.1109/TMI.2007.897408. [DOI] [PubMed] [Google Scholar]
- Burnside ES, Hall TJ, Sommer AM, Hesley GK, Sisney GA, Svensson WE, Fine JP, Jiang J, Hangiandreou NJ. Differentiating benign from malignant solid breast masses with US strain imaging. Radiology. 2007;245:401–10. doi: 10.1148/radiol.2452061805. [DOI] [PubMed] [Google Scholar]
- Cespedes EI, de Korte CL, van der Steen AF, von Birgelen C, Lancee CT. Intravascular elastography: principles and potentials. Seminars in Interventional Cardiology. 1997;2:55–62. [PubMed] [Google Scholar]
- Cespedes I, Huang Y, Ophir J, Spratt S. Methods for estimation of subsample time delays of digitized echo signals. Ultrasonic Imaging. 1995;17:142–71. doi: 10.1177/016173469501700204. [DOI] [PubMed] [Google Scholar]
- Chen X, Zohdy MJ, Emelianov SY, O'Donell M. Lateral speckle tracking using synthetic lateral phase. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control. 2004;51:540–50. [PubMed] [Google Scholar]
- Chiao RY, Hao X. Coded excitation for diagnostic ultrasound: a system developer's perspective. IEEE Trans Ultrason Ferroelectr Freq Control. 2005;52:160–70. doi: 10.1109/tuffc.2005.1406543. [DOI] [PubMed] [Google Scholar]
- Du H, Liu J, Pellot-Barakat C, Insana MF. Optimizing multicompression approaches to elasticity imaging. IEEE Trans Ultrason Ferroelectr Freq Control. 2006;53:90–9. doi: 10.1109/tuffc.2006.1588394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebbini ES. Phase-coupled two-dimensional speckle tracking algorithm. IEEE Trans Ultrason Ferroelectr Freq Control. 2006;53:972–90. doi: 10.1109/tuffc.2006.1632687. [DOI] [PubMed] [Google Scholar]
- Fitzgibbon AW, Pilu M, Fisher RB. Proceedings of the 1996 International Conference on Pattern Recognition (ICPR '96) Volume I - Volume 7270. IEEE Computer Society; 1996. Direct Least Squares Fitting of Ellipses. [Google Scholar]
- Goenezen S, Dord JF, Sink Z, Barbone PE, Jiang J, Hall TJ, Oberai AA. Linear and nonlinear elastic modulus imaging: an application to breast cancer diagnosis. IEEE Trans Med Imaging. 2012;31:1628–37. doi: 10.1109/TMI.2012.2201497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall TJ, Oberai AA, Barbone PE, Sommer AM, Gokhale NH, Goenezen S, Jingfeng J. Engineering in Medicine and Biology Society, 2009 EMBC 2009; Annual International Conference of the IEEE; 3-6 Sept. 2009; 2009. pp. 1967–70. vol. Series. [DOI] [PubMed] [Google Scholar]
- Hall TJ, Zhu Y, Spalding CS. In vivo real-time freehand palpation imaging. Ultrasound in Medicine & Biology. 2003;29:427–35. doi: 10.1016/s0301-5629(02)00733-0. [DOI] [PubMed] [Google Scholar]
- Itoh A, Ueno E, Tohno E, Kamma H, Takahashi H, Shiina T, Yamakawa M, Matsumura T. Breast disease: clinical application of US elastography for diagnosis. Radiology. 2006;239:341–50. doi: 10.1148/radiol.2391041676. [DOI] [PubMed] [Google Scholar]
- Jensen JA. A model for the propagation and scattering of ultrasound in tissue. The Journal of the Acoustical Society of America. 1991;89:182–90. doi: 10.1121/1.400497. [DOI] [PubMed] [Google Scholar]
- Jensen JA, Munk P. A new method for estimation of velocity vectors. IEEE Trans Ultrason Ferroelectr Freq Control. 1998;45:837–51. doi: 10.1109/58.677749. [DOI] [PubMed] [Google Scholar]
- Jiang J, Hall TJ. A fast hybrid algorithm combining regularized motion tracking and predictive search for reducing the occurrence of large displacement errors. IEEE Trans Ultrason Ferroelectr Freq Control. 2011;58:730–6. doi: 10.1109/TUFFC.2011.1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang J, Hall TJ, Sommer AM. A novel performance descriptor for ultrasonic strain imaging: a preliminary study. IEEE Trans Ultrason Ferroelectr Freq Control. 2006;53:1088–102. doi: 10.1109/tuffc.2006.1642508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kallel F, Bertrand M. Tissue elasticity reconstruction using linear perturbation method. IEEE Transactions on Medical Imaging. 1996;15:299–313. doi: 10.1109/42.500139. [DOI] [PubMed] [Google Scholar]
- Kallel F, Ophir J. A least-squares strain estimator for elastography. Ultrasonic Imaging. 1997;19:195–208. doi: 10.1177/016173469701900303. [DOI] [PubMed] [Google Scholar]
- Kolokythas O, Gauthier T, Fernandez AT, Xie H, Timm BA, Cuevas C, Dighe MK, Mitsumori LM, Bruce MF, Herzka DA, Goswami GK, Andrews RT, Oas KM, Dubinsky TJ, Warren BH. Ultrasound-based elastography: a novel approach to assess radio frequency ablation of liver masses performed with expandable ablation probes: a feasibility study. J Ultrasound Med. 2008;27:935–46. doi: 10.7863/jum.2008.27.6.935. [DOI] [PubMed] [Google Scholar]
- Konofagou E, Ophir J. A new elastographic method for estimation and imaging of lateral displacements, lateral strains, corrected axial strains and Poisson's ratios in tissues. Ultrasound in Medicine & Biology. 1998a;24:1183–99. doi: 10.1016/s0301-5629(98)00109-4. [DOI] [PubMed] [Google Scholar]
- Konofagou E, Ophir J. A new elastographic method for estimation and imaging of lateral displacements, lateral strains, corrected axial strains and Poisson's ratios in tissues. Ultrasound Med Biol. 1998b;24:1183–99. doi: 10.1016/s0301-5629(98)00109-4. [DOI] [PubMed] [Google Scholar]
- Li PC, Cheng CJ, Yeh CK. On velocity estimation using speckle decorrelation. IEEE Trans Ultrason Ferroelectr Freq Control. 2001;48:1084–91. doi: 10.1109/58.935727. [DOI] [PubMed] [Google Scholar]
- Li Y, Zagzebski JA. Frequency domain model for generating B-mode images with array transducers. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1999;46:690–9. doi: 10.1109/58.764855. [DOI] [PubMed] [Google Scholar]
- Lubinski MA, Emelianov SY, Raghavan KR, Yagle AE, Skovoroda AR, O'Donnell M. Lateral displacement estimation using tissue incompressibility. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1996;43:247–56. doi: 10.1109/58.660158. [DOI] [PubMed] [Google Scholar]
- Meunier J, Bertrand M. Ultrasonic texture motion analysis: theory and simulation. IEEE Transactions on Medical Imaging. 1995;14:293–300. doi: 10.1109/42.387711. [DOI] [PubMed] [Google Scholar]
- Miller NR, Bamber JC, ter Haar GR. Imaging of temperature-induced echo strain: preliminary in vitro study to assess feasibility for guiding focused ultrasound surgery. Ultrasound in Medicine & Biology. 2004;30:345–56. doi: 10.1016/j.ultrasmedbio.2003.11.016. [DOI] [PubMed] [Google Scholar]
- Nock LF, Brunke SS, Jiang H, Mai JJ, Trahey GE, Von Behren P. IEEE Ultrasonics Symposium, Oct 8-11 2002, (Munich, Germany, 2002) (Proceedings of the IEEE Ultrasonics Symposium, vol Series 2) Institute of Electrical and Electronics Engineers Inc.; 2002. pp. 1571–3. [Google Scholar]
- O'Donnell M, Skovoroda AR, Shapo BM, Emelianov SY. Internal displacement and strain imaging using ultrasonic speckle tracking. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1994;41:314–25. [Google Scholar]
- Oberai AA, Gokhale NH, Doyley MM, Bamber JC. Evaluation of the adjoint equation based algorithm for elasticity imaging. Physics in Medicine & Biology. 2004;49:2955–74. doi: 10.1088/0031-9155/49/13/013. [DOI] [PubMed] [Google Scholar]
- Oberai AA, Gokhale NH, Goenezen S, Barbone PE, Hall TJ, Sommer AM, Jiang J. Linear and nonlinear elasticity imaging of soft tissue in vivo: demonstration of feasibility. Phys Med Biol. 2009;54:1191–207. doi: 10.1088/0031-9155/54/5/006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ophir J, Cespedes I, Ponnekanti H, Yazdi Y, Li X. Elastography: a quantitative method for imaging the elasticity of biological tissues. Ultrasonic Imaging. 1991;13:111–34. doi: 10.1177/016173469101300201. [DOI] [PubMed] [Google Scholar]
- Pavan TZ, Madsen EL, Frank GR, Jiang J, Carneiro AA, Hall TJ. A nonlinear elasticity phantom containing spherical inclusions. Phys Med Biol. 2012;57:4787–804. doi: 10.1088/0031-9155/57/15/4787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rago T, Santini F, Scutari M, Pinchera A, Vitti P. Elastography: new developments in ultrasound for predicting malignancy in thyroid nodules. J Clin Endocrinol Metab. 2007;92:2917–22. doi: 10.1210/jc.2007-0641. [DOI] [PubMed] [Google Scholar]
- Rao M, Varghese T. Correlation analysis of the beam angle dependence for elastography. J Acoust Soc Am. 2006;119:4093–101. doi: 10.1121/1.2195290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao M, Varghese T, Madsen EL. Shear strain imaging using shear deformations. Med Phys. 2008;35:412–23. doi: 10.1118/1.2825621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao N, Mehra S, Hui Z. Ultrasonics Symposium; Proceedings, IEEE 1990; 4-7 Dec 1990; 1990. pp. 1435–40. 1990, vol Series. [Google Scholar]
- Regner DM, Hesley GK, Hangiandreou NJ, Morton MJ, Nordland MR, Meixner DD, Hall TJ, Farrell MA, Mandrekar JN, Harmsen WS, Charboneau JW. Breast lesions: evaluation with US strain imaging--clinical experience of multiple observers. Radiology. 2006;238:425–37. doi: 10.1148/radiol.2381041336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivaz H, Boctor EM, Choti MA, Hager GD. Ultrasound elastography using multiple images. Medical image analysis. 2014;18:314–29. doi: 10.1016/j.media.2013.11.002. [DOI] [PubMed] [Google Scholar]
- Rubert N, Bharat S, DeWall RJ, Andreano A, Brace C, Jiang J, Sampson L, Varghese T. Electrode displacement strain imaging of thermally-ablated liver tissue in an in vivo animal model. Med Phys. 2010;37:1075–82. doi: 10.1118/1.3301603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiina T, Nightingale KR, Palmeri ML, Hall TJ, Bamber JC, Barr RG, Castera L, Choi BI, Chou YH, Cosgrove D, Dietrich CF, Ding H, Amy D, Farrokh A, Ferraioli G, Filice C, Friedrich-Rust M, Nakashima K, Schafer F, Sporea I, Suzuki S, Wilson S, Kudo M. WFUMB guidelines and recommendations for clinical use of ultrasound elastography: Part 1: basic principles and terminology. Ultrasound Med Biol. 2015;41:1126–47. doi: 10.1016/j.ultrasmedbio.2015.03.009. [DOI] [PubMed] [Google Scholar]
- Simon C, Vanbaren P, Ebbini ES. Two-dimensional temperature estimation using diagnostic ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control. 1998;45:1088–99. doi: 10.1109/58.710592. [DOI] [PubMed] [Google Scholar]
- Song X, Pogue BW, Jiang S, Doyley MM, Dehghani H, Tosteson TD, Paulsen KD. Automated region detection based on the contrast-to-noise ratio in near-infrared tomography. Appl Opt. 2004;43:1053–62. doi: 10.1364/ao.43.001053. [DOI] [PubMed] [Google Scholar]
- Techavipoo U, Chen Q, Varghese T, Zagzebski JA. Estimation of displacement vectors and strain tensors in elastography using angular insonifications. IEEE Transactions on Medical Imaging. 2004;23:1479–89. doi: 10.1109/TMI.2004.835604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thitaikumar A, Mobbs LM, Kraemer-Chant CM, Garra BS, Ophir J. Breast tumor classification using axial shear strain elastography: a feasibility study. Phys Med Biol. 2008;53:4809–23. doi: 10.1088/0031-9155/53/17/022. [DOI] [PubMed] [Google Scholar]
- Unser M. Fast B-spline Transforms for Continuous Image Representation and Interpolation. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1991;13:277–85. [Google Scholar]
- 60.Viola F, Coe RL, Owen K, Guenther DA, Walker WF. MUlti-Dimensional Spline-Based Estimator (MUSE) for motion estimation: algorithm development and initial results. Ann Biomed Eng. 2008;36:1942. doi: 10.1007/s10439-008-9564-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner RF, Insana MF, Smith SW. Fundamental correlation lengths of coherent speckle in medical ultrasonic images. IEEE Trans Ultrason Ferroelectr Freq Control. 1988;35:34–44. doi: 10.1109/58.4145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner RF, Smith SW, Sandrik JM, Lopez H. Statistics of speckle in ultrasound B-scans. 1983;SU-30:156–63. [Google Scholar]
- Walker WF, Trahey GE. Fundamental limit on delay estimation using partially correlated speckle signals. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1995;42:301–8. [Google Scholar]
- Xie H, Kim K, Aglyamov SR, Emelianov SY, Chen X, O'Donnell M, Weitzel WF, Wrobleski SK, Myers DD, Wakefield TW, Rubin JM. Staging deep venous thrombosis using ultrasound elasticity imaging: Animal model. Ultrasound in Medicine and Biology. 2004;30:1385–96. doi: 10.1016/j.ultrasmedbio.2004.08.015. [DOI] [PubMed] [Google Scholar]
- Zahiri Azar R, Goksel O, Salcudean SE. Sub-sample displacement estimation from digitized ultrasound RF signals using multi-dimensional polynomial fitting of the cross-correlation function. IEEE Trans Ultrason Ferroelectr Freq Control. 2010;57:2403–20. doi: 10.1109/TUFFC.2010.1708. [DOI] [PubMed] [Google Scholar]
- Zheng R, Le LH, Sacchi MD, Ta D, Lou E. Spectral ratio method to estimate broadband ultrasound attenuation of cortical bones in vitro using multiple reflections. Phys Med Biol. 2007;52:5855–69. doi: 10.1088/0031-9155/52/19/008. [DOI] [PubMed] [Google Scholar]
- Zhu Y, Hall TJ, Jiang J. A finite-element approach for Young's modulus reconstruction. IEEE Transactions on Medical Imaging. 2003;22:890–901. doi: 10.1109/TMI.2003.815065. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.