Retrospective Revaluation: The Phenomenon and Its Theoretical Implications

Abstract

Retrospective revaluation refers to an increase (or decrease) in responding to conditioned stimulus (CS X) as a result of decreasing (or increasing) the associative strength of another CS (A) with respect to the unconditioned stimulus (i.e., A-US) that was previously trained in compound with the target CS (e.g., AX−US or just AX). We discuss the conditions under which retrospective revaluation phenomena are most apt to be observed and their implications for various models of learning that are able to account for retrospective revaluation (e.g., Dickinson and Burke, 1996; Miller and Matzel, 1988; Van Hamme and Wasserman, 1994). Although retroactive revaluation is relatively parameter specific, it is seen to be a reliable phenomenon observed across many tasks and species. As it is not anticipated by many conventional models of learning (e.g., Rescorla and Wagner, 1972), it serves as a critical benchmark for evaluating traditional and newer models.

1. Introduction

1.1. Retrospective revaluation: Definition

Retrospective revaluation (RR) is commonly defined as a change in the response eliciting potential of a target conditioned stimulus (CS) as a result of associative revaluation of a ‘companion’ cue with which the target has previously been compounded (see Table 1). One instance of RR is unovershadowing, which refers to an increase in responding to a target cue (X) as a result of associative deflation (i.e., extinction) of cue A after X was initially trained in an overshadowing situation with A (i.e., reinforced in compound with companion cue A [i.e., AX−US]). Another instance of RR is backward blocking, which refers to a decrease in responding to target CS X as a result of associative inflation (i.e., reinforcement) of A after X was initially trained in an overshadowing situation with A (i.e., AX−US). A further example of RR is backward conditioned inhibition, which refers to an increase in the Pavlovian conditioned inhibitory response potential of target CS X as a result of associative inflation (i.e., reinforcement) of cue A after X was initially presented in compound with A either after Pavlovian conditioned inhibition treatment (i.e., A-US trials interspers3ed with AX− trials) or simply without reinforcement (i.e., AX−). Note that in this case the change in conditioned inhibitory status of the target cue is directly related to the change in associative strength of the companion cue, which is just the opposite of the RR that is often observed when the excitatory status of the target CS is assessed.

Table 1.

Two generic examples of retrospective revaluation. Posttraining associative deflation (extinction) and inflation (more conditioning) of companion cue (A).

Group	Phase 1	Phase 2	Test X
Control (overshadowing)	AX-US	B−	Cr
Unovershadowing	AX-US	A−	CR*
Backward blocking	AX-US	A-US	cr*

Note.

^*indicates phenomenon of retrospective revaluation relative to the Control group. A is a ‘companion’ cue that is trained in compound with the target cue X. B is another (noncompanion) cue. US is a unconditioned stimulus. - indicates nonreinforcement. Cr indicates a moderate conditioned response. CR indicates a robust conditioned response. cr indicates a weak conditioned response.

1.2. Retrospective revaluation: History

RR was first reported by Kaufman and Bolles (1981). In a single-experiment paper, they reported an increase in conditioned suppression by rats to CS X as a result of nonreinforced CS A trials (A−) following AX−US trials (i.e., unovershadowing, aka recovery from overshadowing). Despite the potential considerable theoretical importance of RR, Kaufman and Bolles’ report drew little attention, perhaps because they did not determine whether the observed increase in behavioral control by X was specific to X (i.e., the cue that was previously paired with A) and they used repeated CS X test trials with RR appearing only on the middle test trials rather than the first (or last) trial. Additionally, their paper appeared in a nonrefereed journal. A few laboratories (including that of the present first author) tried unsuccessfully to conceptually replicate the effect. These investigators considered pooling and publishing their failures to replicate, but decided to first make additional efforts with different parameters, specifically, using longer duration CSs than they had previously used, based on Kaufman and Bolles having employed relatively long (30 s) CSs. These efforts resulted in a replicable RR effect (Matzel, Schachtman, and Miller, 1985). Notably, this success at obtaining RR with relatively long CSs suggests that RR is positively correlated with the strength of the within-compound association between X and A because longer duration CSs increase the effective pairing of the two cues; moreover, longer CSs increase the amount of operational extinction of A during the RR treatment assuming the same number of trials are administered. Importantly, Matzel et al. also demonstrated that their RR effect was stimulus specific to the target CS that had previously been paired with the revalued cue (A).

The same year as the Matzel et al. (1985) report was published, Shanks (1985) reported RR in humans using a contingency judgment task. He found that pairing the companion cue A with the outcome (O) following AX−O pairings decreased ratings of the X−O contingency. This procedure, AX−O trials followed by A−O trials, constitutes backward blocking which is an instance of RR occurring as a result of associative inflation of the companion cue as opposed to the previously discussed deflation of the companion cue. Moreover, Shanks’ research demonstrated RR using humans as opposed to nonhuman subjects and a task quite different from the conditioned suppression preparations previously used with nonhuman subjects by Kaufman and Bolles (1981) and Matzel et al. (1985).

Since 1985, there have been numerous reports of RR with rodents and human subjects across diverse tasks (e.g., Pavlovian conditioning, contingency learning, causal learning, evaluative conditioning) and from different independent laboratories (e.g., Aitken, Larkin, and Dickinson, 2000; Blaisdell, Gunther, and Miller, 1999; Boddez, Baeyens, Hermans, and Beckers, 2011; Chapman, 1991; De Houwer and Beckers, 2002a, 2000b; Denniston, Savastano, Blasidell, and Miller, 2003; Dickinson and Burke, 1996; Hallam, Matzel, Sloat, and Miller, 1990; Larkin, Aitken, and Dickinson, 1998; Liljeholm and Balleine, 2006, 2009; Matzel, Shuster, & Miller, 1987; McConnell, Urushihara, and Miller, 2010; Melchers, Lachnit, and Shanks, 2006; Miller and Matute, 1996; Shevill & Hall, 2004; Tassoni, 1995; Urushihara and Miller, 2010; Van Hamme and Wasserman, 1994; Wasserman and Berglan, 1998; Zanon, De Houwer, Gast, and Smith, 2014). In addition to RR being seen to modulate excitatory cue competition, RR has been reported with conditioned inhibition where, following inhibition training of CS X, inflation or deflation of the excitatory cue that was used during inhibition training has been found to increase (i.e., backward conditioned inhibition) or decrease, respectively, the inhibitory potential of X (Amundson, Wheeler, and Miller, 2005; Chapman, 1991; Larkin, Aitken, and Dickinson, 1998; Miller, Hallam, Hong, and Dufore, 1991; Hallam, Matzel, Sloat, and Miller, 1990; but see Miller, Hallam, and Grahame, 1990).

In contrast to these many demonstrations of RR, there have also been several reports of failures to observe RR (e.g., Dopson, Pearce, and Haselgrove, 2009; Holland, 1999; Williams, 1996). Notably, the reported failures to obtain RR have all been with nonhumans, suggesting that RR is more readily obtained with humans than nonhumans. However, in light of the many successful observations of RR with both nonhumans and humans, RR appears to be a reliable phenomenon and its occurrence is now widely accepted even if its theoretical implications still often receive short shrift. Admittedly, like most learning phenomena, it is parameter dependent; moreover, the parameters that yield RR appear to be more limited than those that yield basic learning phenomena such as simple acquisition and extinction or even cue competition (e.g., overshadowing and blocking). That the parameters necessary to produce RR are relatively limited is not surprising because RR is a higher-order effect relative to these other learning phenomena in that RR requires that at least two of these simpler effects both occur and interact.

1.3. Constraints on the phenomenon of retrospective revaluation

1.3.1. Strength of within-compound association

All studies designed to assess the relationship of the magnitude of RR to the strength of the within-compound association between the target CS and its companion cue have reported a positive correlation. For example, Aitken, Larkin, and Dickinson (2001) and Larkin, Aitkin, and Dickinson (1998) observed this positive correlation with human subjects. We have also repeatedly observed this relationship in our laboratory using rats as subjects, although with nonhuman subjects assessment of the within-compound association is necessarily indirect. For instance, Amundson, Witnauer, Pineno, and Miller (2008, Experiment 3) reported that an inhibitory within-compound association established prior to overshadowing treatment attenuates the overshadowing effect, and that degradation of the inhibitory within-compound association following overshadowing treatment increased the magnitude of the overshadowing effect (i.e., decreased responding to the target cue, a RR effect). Moreover, the previously mentioned finding that RR was more readily observed with longer CS durations (Matzel et al., 1985) is also consistent with the magnitude of RR directly depending on the strength of the within-compound association because longer CSs should produce stronger within-compound associations between the target CS and companion cue.

1.3.2. Number of revaluation trials

Early efforts at producing RR in our laboratory often failed. Not unreasonably, our working assumption was that RR treatment (typically associative deflation of the target CS’s companion cue) should continue until the companion cue stopped eliciting responding. This assumption was predicated on the view that responding was a reliable index of the associative status of the companion cue. However, over decades of research we have become ever more aware that simple responding to a cue is often an inadequate measure of its associative status. A recent example of this is reported by Denniston, Chang, and Miller (2003), who found that sub-zero extinction treatment reduced subsequent recovery from extinction. With respect to RR, although we often found that moderate numbers of extinction trials (e.g., 30) with the companion cue following cue competition treatment was sufficient to eliminate responding to the companion cue, a larger number of associative deflation trials with the companion stimulus was required to produce a robust RR effect. For example, Blasidell, Gunther, and Miller (1999) found that 200 extinction trials of a blocking CS were inadequate to produce RR (recovery from blocking in this instance) with their parameters, but 800 trials yielded RR.

1.3.3. RR from associative deflation stronger than RR from associative inflation

The RR effect observed as a result of associative deflation of the companion cue (e.g., recovery from OV) is ordinarily more robust than that observed as a result of associative inflation (e,g., backward blocking; Larkin, Aitkin, and Dickinson, 1998; Liljeholm and Balleine, 2006; Miller and Matute, 1996; but see Shanks, 1985; Wasserman and Berglen, 1998). Although none of these demonstrations perfectly controlled for potential differences in response scaling between inflation and deflation effects, the consistency of the basic conclusion suggests that it is not purely an artifact of measurement. Although there are numerous accounts of why, following training of a target CS in compound with a companion cue, associative deflation of the companion tends to have greater impact than inflation of the companion (see section 3), this asymmetry appears to be reliable.

1.3.4. Distinctiveness of the target cue and its companion

Liljeholm and Balleine (2009) reported that high physical similarity between the target cue and its companion results in mediated extinction. In contrast, when the compounded cues were distinct from each other, RR emerged. Similarly, Balleine, Espinet, and Gonzalez (2005) found that acquired distinctiveness, in addition to physical distinctiveness, of the compounded cues enhances RR.

1.3.5. Context dependence of RR

Boddez, Baeyens, Hermans, and Beckers (2011) observed that testing the target CS in the context in which the companion cue had been revalued increased RR.

2. Accounts of retrospective revaluation

The behavioral phenomenon of RR is real, but what causes it? Here we describe various accounts of RR. Importantly, the occurrence of RR challenges most traditional accounts of learning such as that of Rescorla and Wagner (1972) which assumes that (a) a CS must be present on a trial for it to change associative status, and (b) that responding to CS is a direct monotonic function of the strength of the association between the CS and outcome. The phenomenon of RR is basically a change in responding to a target CS as a result an inverse change in the strength of the association between the target CS’s companion cue and the outcome. Based on assumption (b), the Rescorla-Wagner model must conclude that RR reflects new learning about the target CS when the associative status of its companion cue is altered. But in light of revaluation of the companion cue occurring in the absence of the target CS, this conclusion violates assumption (a).

2.1. Comparator hypothesis

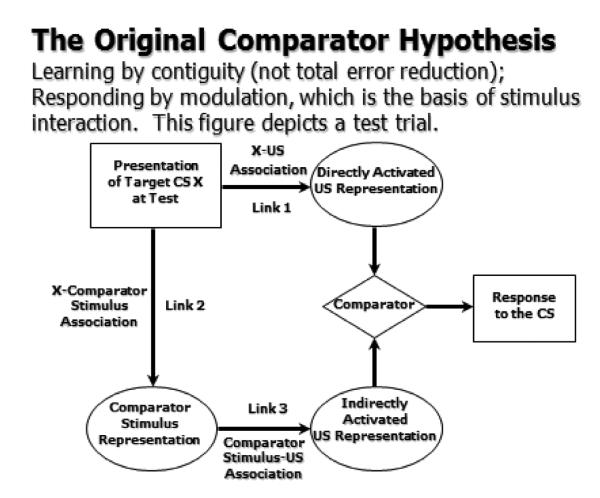
The comparator hypothesis (CH, Miller and Matzel, 1988) was the first model of learning capable of accounting for RR. The CH was elaborated upon by Denniston et al. (2001) and further developed and mathematically formalized by Stout and Miller (2007). Like the Bush and Mosteller (1955) model, the CH assumes that acquisition requires only contiguity and a discrepancy between what is predicted by the target CS in question and the experienced outcome. Unlike most models of learning, the CH emphasizes information processing that occurs at the time of test as opposed to during acquisition. Thus, cue competition such as overshadowing is assumed to arise not from a learning deficit, but a failure to express the target CS-outcome association despite its having been encoded during training. The basis for this response deficit is that at test expression of the traditional target CS-outcome association (Link 1 in Figure 1), based on direct activation of the outcome representation by the CS, is down modulated by indirect activation of the outcome representation which is activated by the CS activating the representation of the companion cue (Link 2) which in turn activates the indirect representation of the outcome (Link 3). Figure 1 depicts a test trial on which the target CS is presented. Alternatively stated, unlike many contemporary models of learning in which responding to a target cue is montonically related to the absolute strength of the target-outcome (X−O) association, the CH assumes responding to X is down modulated at test by the degree to which other cues that are associated with X have their own associations with O. Alternatively stated, responding to X is monotonically related to the strength of the X−O association relative to how well O is predicted by background cues that were present during conditioning of X (or are otherwise associated with X).

Figure 1.

Original comparator hypothesis (after Miller & Matzel, 1988). This figure depicts a test trial.

According to the CH, RR treatment (i.e., extinction of the companion cue or pairings of the companion with the outcome) does not produce a change in associative status of the target CS, but a change in its response potential (i.e., a change in performance rather than new learning about the target). As stated above, conditioned responding is not proportional to strength of target CS-US association, but to the change in the likelihood of the US relative to the associative strength of the target CS’s companion cue. The CH account of RR assumes that in cue competition situations (e.g., overshadowing), the absence of responding to the target cue is not due to an absence of a cue-US association, rather it is present but latent. Critically, behavior is not a veridical window on memory. However, the CH, like the Rescorla-Wagner model, retains the view that a CS must be present on a trial for it to undergo a change in associative status. RR does not reflect a change in the target cue’s associative status, but only its expression.

2.2. Van Hamme and Wasserman (1994)

Van Hamme and Wasserman (VH&W, 1994, also see Wasserman and Berglan, 1998) proposed a model of associative learning explicitly designed to account for RR. Their model is a simple variant of the Rescorla and Wagner (1972) model that rejects the Rescorla and Wagner assumption that a CS must be present for a change in its associative status to occur. Instead, VH&W posit that a subject can learn about an absent CS on a given trial if an associate of the CS is present on that trial. The Rescorla-Wagner equation for a change in the associative strength (V) of CS X as a result of trial N is:

$$\Delta {{\text{V}}_{\text{CS}}}^{\text{N}}={\alpha }_{\text{CS}}{ß}_{\text{US}}({\lambda }_{\text{US}}-\Sigma {{\text{V}}_{\text{Total}}}^{\text{N}})$$ (1)

where λ is the maximum associative strength that the US can support on that trial, and ß is the associability of the US which is a positive number between 0 and 1 when the US is present and a smaller positive number when the US is absent. Critically, in the Rescorla-Wagner model, α is the associability of the CS which is a positive number between 0 and 1 when the CS is present and 0 when the CS is absent. It is this last point that precludes learning about the CS on a trial on which the CS is absent. The VH&W model differs from the Rescorla-Wagner model only in positing that α for any given CS is a nonzero negative number between 0 and −1 on a trial on which the target CS is absent but a cue associated with the target is present. This causes ΔV_CS to be nonzero and of the opposite sign as the change in the associative status of the companion cue on the trial on which the companion cue is revalued and the target CS is absent. By this means, the VH&W model can account for most forms of RR including recovery from overshadowing due to associative deflation of the companion cue and backward blocking due to associative inflation of the companion cue.

Although the VH&W model rejects the Rescorla and Wagner (and CH) position that a cue must be present on a trial for it to change associative status, the model (like that of Rescorla and Wagner) emphasizes information processing at the time of acquisition. This contrasts with the CH which emphasizes information processing at the time of testing. Note that all contemporary accounts of RR depend on there being a within-compound association between the target CS and its companion cue. But they differ with respect to when the within-compound association is in play: during RR treatment (e.g., VH&W), or at test (e.g., CH). Is RR due to new learning about the absent target CS as proposed by VH&W (and subsequently by Dickinson and Burke [see below]), or modified expression of a previously acquired target CS-outcome association as proposed by the CH? It is highly likely that information processing at both the time of training and the time of testing is important, but most investigators favor oversimplification in the interests of tractability.

Van Hamme and Wasserman (1994) implied that for RR to occur, there had to be a with-compound association between the target CS and the outcome, but neither Van Hamme and Wasserman (1994) nor Wasserman and Berglan (1998) mathematically formalized the VH&W model. Witnauer and Miller (2011) did formalize it by assuming that the magnitude of change in the associative strength of the target CS was directly proportional to the strength of the within-compound association. Witnauer and Miller (2011) also fit a number of RR data sets with VH&W model and the CH, and found that both models did well, with the VH&W model fitting some of the data marginally better than the CH and the CH doing marginally better with other data.

2.3. Dickinson and Burke (1996)

Just as Van Hamme and Wasserman (1994) modified a widely cited model of learning that could not account for RR (i.e., the Rescorla-Wagner model) so that it could do so, so too Dickinson and Burke (1996) modified Wagner’s (1981) SOP model which was also unable to account for RR. Although space precludes a detailed description of the original SOP model, their modification of SOP (MSOP) differs from SOP only in positing that new learning occurs to a target CS representation that, although physically absent, is retrieval activated into an A2 memory state on an operational RR trial by the presentation of a [companion] cue that had previously been presented in compound with the target CS. If the outcome is not presented during RR treatment and the representation of the outcome is also retrieval activated into the A2 state (i.e., associative deflation of the companion cue), MSOP posits that the association between absent target CS and the absent outcome will be strengthened (e.g., recovery from overshadowing). In contrast, if the outcome is presented along with the companion cue during the RR treatment (i.e., associative inflation of the companion cue), the representation of the outcome will be activated into an A1 memory state while the representation of the target CS is activated into an A2 memory state, which should result in a strengthening of an inhibitory target CS-outcome association. This in turn should decrease responding to the target CS (i.e., backward blocking and similar phenomena). Thus, MSOP provides a second account of RR that, like VH&W, emphasizes new learning about the target CS that occurs on an RR treatment trial.

2.4. Chapman (1991)

Chapman (1991) proposed that RR was due to the stimuli presented during RR treatment initiating rehearsal of prior compound training. This account works well in the case of posttraining associative deflation of the target CS’s companion cue, but is arguably challenged by the observation that posttraining inflation yields a RR effect in the opposite direction (i.e., reduced responding to the target). If the RR treatment initiates rehearsal of prior compound training including the pairings of the target CS and outcome, one might expect associative inflation of the companion cue to increase rather than decrease responding to the target and in fact do so more robustly than associative deflation of the companion cue because the presence of the US on during the RR treatment should enhance rehearsal of the target-US association. That is, two stimuli (the companion cue and outcome) as in inflation treatment should stimulate more rehearsal of the target-outcome pairings than one stimulus (the companion cue alone) as in deflation treatment.

2.5. Other accounts of retrospective revaluation

All four of the above accounts of RR depend upon the existence of an within-compound association between the target CS and the companion cue. The CH (Miller and Matzel, 1988; Denniston et al., 2001; Stout and Miller, 2007) posits that within-compound associations are critical at the time of test in determining how the X−O association will be expressed, whereas VH&W, MSOP, and Chapman’s (1991) rehearsal account all assume that within-compound associations play a critical role at the time of RR treatment. In contrast, Connor, Lolordo, and Trappenberg (2014) have proposed an elemental, neural network account of RR that they assert is free of within-compound associations. However, in their description of the model, they state “previously paired stimuli … come to activate similar ensembles of neurons.” (p. 22). To us, this appears to be a variant of within-compound associations and leaves their account similar in most respects to that of VH&W. Moreover, Ghirlanda (2005; also see Markman, 1989; Tassoni, 1995) provides accounts of RR that appear to basically be a variant of the principle underlying the VH&W model. Thus, all of these additional accounts of RR in one way or another assume that RR is a dependent on the within-compound association between the target CS and the revalued companion cue.

Mitchell, Killedar, and Lovibond (2005) provide an explanation of RR based on propositional reasoning. However, in our view their model is not well specified and its predictions are largely post hoc. Jamieson, Hannah, and Crump (2010) have proposed an interesting instance-type model account of RR, but its being an instance model makes it so different from the models discussed above that introducing it here would constitute too much of a digression from the focus of this review.

2.6. A semantic issue

A basic assumption of the VH&W and MSOP accounts of RR is that subjects learn about a CS on a trial on which it is absent, and in some instances when the outcome (O) is also absent, specifically post-training [with respect to the target cue] associative deflation of the target’s companion cue. That is, this sort of RR consists of an increase in responding to the target CS based on the CS-outcome association, without a new experience with either the CS or outcome. Clearly this involves some sort of reorganization of previously acquired information, but do we want to call it learning? The present authors’ working definition of learning is the incorporation of information from the external world. By this definition, if neither the CS nor the outcome occur on the treatment trial, no new learning concerning the target CS-outcome association can occur. This suggests that RR arises from changes in the companion cue-outcome (or CS-companion cue) association, with the CH being one such formulation of this approach. However, for those investigators who favor the VH&W (or the like) account, the CS-outcome association itself is revalued as a result of the RR treatment trials on which neither the target nor outcome were present. Here we see that the CH and VH&W models use distinctly different definitions of ‘learning,’ which is worthy of note in order to facilitate discussion. But as this is a semantic issue, it does not shed light on when the critical cognitive process(es) underlying RR takes place, even if we choose not to call it ‘learning’: at the time of deflation or inflation of the companion cue, or at test. We note at least one other prominent example of an increase in recall without further pairings of the two associates, that being the testing effect. The testing effect refers to the oft repeated observation that after initial learning, cued retrieval practice of the association enhances later recall and is seen with both nonhuman (e.g., Miller, 1982) and human subjects (e.g., Karpicke and Roediger, 2008). Here too the observed enhancement of responding could be regarded as new learning that occurs at the time of retrieval practice, or simply improved retrieval of what the subject had previously learned.

3. Implications of posttraining inflation of companion cues being weaker than deflation

Most RR research has focused on the effects of posttraining deflation, both because it is theoretically more interesting (i.e., it bears on the existence of latent associations) and because it is a more robust phenomenon. However, the observation that the RR effects of posttraining associative inflation of a companion cue are weaker than deflation of the companion cue (e.g., Larkin, Aitken, and Dickinson, 1998; Hallam, Matzel, Sloat, and Miller, 1990; but see Shanks, 1985) is itself informative with respect to evaluating accounts of RR.

Denniston, Miller, and Matute (1996) and Miller and Matute (1996) note that the CH anticipates the greater efficacy of posttraining deflation than inflation of the companion cue because deflation of the companion not only weakens Link 3 but potentially also weakens Link 2 (assuming backward extinction occurs, i.e., presentation of cue A alone weakens the effective strength of the X–>A association), whereas inflation strengthens Link 3 (as demoted by ‘inflation’) but also potentially weakens Link 2 (see Figure 1). As the magnitude of the RR effect predicted by the CH depends on the product of Link 2 and Link 3, deflation treatment, that likely attenuates both Links 2 and 3, should yield greater RR than inflation treatment, that strengthens Link 3 but potentially weakens Link 2.

The VH&W model, contrary to most observations, anticipates equal or stronger RR with inflation of a companion cue than deflation. This prediction stems from the associability of the US (or outcome) being equal or greater than the associability of the US when it is absent but an associate of it, such as the companion cue, is present.

MSOP’s predictions concerning the relative magnitude of RR induced by inflation as opposed to deflation are complex (e.g., Aitken, Larkin, and Dickinson, 2001; Larkin, Aitken, and Dickinson, 1998). However, Dickinson and his colleagues clearly interpret MSOP as anticipating weaker inflation effects than deflation effects. One source of this prediction is that, on RR treatment trials on which both the target CS’s companion cue and the outcome are presented, the presence of the companion cue should activate part of the representations of both the target CS and the outcome into the A2 memory state, while the presence of the outcome should activate other parts of the representation of the outcome into the A1 memory state. This partial activation of the outcome representation into the A1 memory state while the target representation is in the A2 state should produce an inhibitory CS-outcome association that partially counteracts the increase in the excitatory CS-outcome association resulting from their conjoint activation in A2.

Chapman’s (1991) rehearsal account of RR anticipates that with more cues to initiate rehearsal, greater RR should be observed. As both the companion cue and the outcome are cues associated with the prior target CS-outcome pairings, the account erroneously predicts that RR induced by inflation of the target cue should be greater than that induced to deflation of the companion cue.

Thus, we see that larger RR effects with deflation than inflation of the companion cue is problematic for the VH&W model and Chapman’s (1991) rehearsal account, but not the CH or MSOP. Denniston, Miller, and Matute (1996) and Miller and Matute (1996) have suggested an additional account of why RR produced by inflation is weaker than RR produced by deflation. Specifically, based on functional considerations, they proposed that although subjects readily increase the functional status of an association about an outcome, they are resistant to reducing the functional status of an association concerning a biological significance outcome such as a US because a nonfunctional response has a lower cost than failing to respond when such a response would be functional. Moreover, Denniston et al. (1998) and Miller and Matute(1998) presented evidence supportive of this assumption in the form of finding the greater efficacy of pasttraining deflation relative to inflation of a companion cue is eliminated when the comparison between inflation and deflation is embedded in a sensory preconditioning paradigm in which both compound training and the RR treatment occur before the outcome is paired with a biologically significant US. Although this account of the greater efficacy of deflation relative to inflation may well at least partial account for the asymmetry, it does not stem from any of the proposed accounts of RR described in Section 2 and consequently does not differentiate between these accounts.

4. Higher-order retrospective revaluation

Just as behavior reflecting a target CS-outcome association can be altered by associative deflation or inflation of the CS’s companion cue, so too might the influence of the companion cue-outcome itself be influenced by the associative status of any companion cue that the CS’s companion cue might have. We refer to such companion cues as higher-order companion cues with respect to the target CS. Consider training subjects on both XA−outcome and AB-outcome trials. If CS X is regarded as the target CS, A is the 1^st-order companion cue of X. Similarly, B is the 1^st-order companion cue of A, making it potentially a 2^nd-order companion cue to X. There are two questions to be asked concerning higher-order RR: Does it actually occur, and if it does, what does it tell us about the nature of RR in general.

There are now multiple reports, from different laboratories, of the occurrence of higher-order RR in both human (e.g., De Houwer and Beckers, 2002a, 2002b; Numata and Shimazaki, 2009) and nonhuman subjects (e.g., Denniston et al., 2003, Experiment 4). Changes in responding to a target CS are in the opposite direction to that of a revalued 1^st-order companion cue, and changes in responding to the target CS are typically in the same direction to that of a revalued 2^nd-order companion cue. Moreover, De Houwer and Beckers (2002a; see Table 2) extended their experiments to 3^rd-order RR. Using the allergy task with human subjects, they administered XA− outcome, AB-outcome, and BC-outcome trials, with X serving as the target CS, and then in different conditions revalued (i.e., operationally extinguished) A, B, or C. Associative deflation of A (X’s 1^st-order companion cue) increased ratings of X, deflation of B (X’s 2^nd-order companion cue) increased ratings of A but increased ratings of X, and deflation of C (X’s 3^rd-order companion cue) increased ratings of both B and X but decreased ratings of A. Additionally, as the order of RR increases, the magnitude of the RR effect decreases. This decrease is not surprisining because each higher-level of RR depends on all levels of RR below it, and RR at each level constitutes a partial reversal of the behavioral control at the level immediately below it.

Table 2.

Design summary [simplified] and data of De Houwer and Beckers (2002a, Experiment 2)

Group	Initial Training Re	valuation Test X
Deflate 1st	XA-O / AB-O / BC-O / D-O / E-	A- / D-O / E-	61
Inflate 1st	XA-O / AB-O / BC-O / D-O / E-	A-O / D-O / E-	14
Deflate 2nd	XA-O / AB-O / BC-O / D-O / E-	B- / D-O / E-	23
Inflate 2nd	XA-O / AB-O / BC-O / D-O / E-	B-O / D-O / E-	50
Deflate 3rd	XA-O / AB-O / BC-O / D-O / E-	C- / D-O / E-	48
Inflate 3rd	XA-O / AB-O / BC-O / D-O / E-	C-O / D-O / E-	21

Note. X, A, B, and C were counterbalanced cues; D and E were filler cues. O represents the outcome (i.e., the occurrence of an allergic reaction) in a fictitious patient. - represents omission of the allergic reaction. Slashes separate interspersed trials. Test X indicates mean ratings of the target cue (X). A = 1^st-order companion cue to X (the extinction of which yielded a change in responding to X that was inverse to that seen to A). B = 1^st-order companion cue to A and therefore 2^nd-order companion to X (the extinction of which yielded a change in responding to A that was inverse to that to B and consequently a change in responding to X that was in the same direction as that to A). C = 3^rd-order companion cue to X (the extinction of which yielded a change in responding to B that were inverse to that to C, and consequently a change in responding to A that was in the same direction as that to C, and consequently a change in responding to X that was inverse to that seen to C). Ratings of A, B, and C were also reported and consistent with this interpretation but not depicted here in the interests of simplification. Thus, the influence of A on responding to X represents 1^st-order RR, the influence of B on responding to X represents 2^nd-order RR, and the influence of C on responding to X represents 3^rd-order RR.

In De Houwer and Beckers’ (2002) experiments, A-outcome trials following AB-outcome | and BC-outcome training resulted in increased ratings to A, decreased ratings to B, and increased ratings to C (relative to an unovershadowing [A−] control). McLaren et al. (2012) conducted two experiments in which a similar higher-order RR design was used. In one experiment, they used a conventional human contingency learning procedure. Subjects in this experiment were tasked with rating the allergenic potential of a cue at test based on memory of cue-outcome (and potentially cue-cue) contingencies from training. Unsurprisingly, McLaren et al. observed increased ratings to A and decreased ratings to B as a result of posttraining A-outcome trials (relative to an unovershadowing control). However,, McLaren et al. observed decreased ratings to C (again, relative to an unovershadowing control) as a result of posttraining A-outcome trials. That is, revaluation of B (1^st-order RR) and C (2^nd-order RR) were in the same direction relative to each other. In another experiment, McLaren et al. used a higher-order RR design in a questionnaire-based procedure (instead of a conventional human contingency learning procedure). Subjects in this experiment received a list of all training trials on the same page. This procedure produced results that agree with De Houwer and Beckers’ (i.e., decreased ratings to B and increased ratings to C). McLaren et al. posited that the human contingency learning procedure involves a larger memory load than the questionnaire procedure. McLaren et al. speculated that participants in the human contingency learning procedure are less likely to use inferential reasoning in judging the value of higher-order companions to the treatment cue. In this framework, the pattern of results observed by De Houwer and Beckers reflects the operation of inferential reasoning, which is potentially outside of the domain of associative models. Notably, this issue is complicated by Denniston et al.’s (2003) successful conceptual replication of De Houwer and Beckers’ results with rats as subjects. The observation that rats show this pattern of data is evidence against McLaren et al.’s interpretation that higher-order RR is based on inferential reasoning, provided one assumes that rats don’t engage in inferential reasoning.

Turning to the theoretical implications of higher-order RR, both De Houwer and Beckers (2002a, 2000b) and Denniston et al. (2003) concluded that the pattern of results observed in higher-order RR (i.e., responding to the target CS changing in the opposite direction as 1^st- and 3^rd-order companion cues, but in the same direction as 2^nd-order companion cues) was anticipated by the extended CH (Denniston et al., 2001), but neither the VH&W nor MSOP models could explain the consequences of 2^nd-order RR. However, this conclusion concerning the VH&W and MSOP models was based on qualitative estimations of what these models predicted. Actual simulations conducted by Witnauer and Miller (2011) found that the VH&W model as well as the CH anticipated the observed alternation in the direction of change in responding to the target CS with increasing order of RR. In contrast, MSOP was not able to account for this pattern of results. The unexpected success of the VH&W model in this situation is a good example of why quantitative simulations of learning models are valuable; even seemingly simple models can challenge our ability without quantitative simulations to estimate what they really predict. In this case, post hoc inspection of the VH&W simulation determined that the success of the VH&W model in accounting for 2^nd-order RR originates in (a) its postulate that neural representations of a cue that is absent but has an associate that is present has negative associabilites, and (b) the product of two negative associabilities being a positive associability. In summary, higher-order RR does occur and the pattern of results that it produces is anticipated by the CH and the VH&W model, but not MSOP.

5. Further assessment of the CH and VH&W models with respect to retrospective revaluation

5.1. Stimulus relative validity

Although the CH and the VH&W model provide convergent predictions with respect to most cases of RR, McConnell, Urushihara, and Miller (2010, Experiment 1) designed an experiment for which the CH predicts results diametrically opposed to those predicted by the VH&W model (as well as other acquisition-focused accounts such as MSOP). This was a RR experiment, but one with an unusual twist (see Table 3). Specifically, a stimulus relative validity paradigm was used. The basic relative validity phenomenon is that subjects exposed to interspersed AX+ and BX− trials (where the letters depict cues, + indicates a US, − indicates nonreinforcement, and +/− indicates 50% reinforcement) respond weaker to CS X than subjects exposed to AX+/− and BX+/−. This result occurs despite X being paired with the US on 50% of the training trials in both conditions. McConnell et al. (2010, Experiment 1) trained an Experimental group and a Control group on two stimulus relative validity problems (AX+ and BX−, and CY+ and DY−) in Phase 1, using the same parameters that Cole, Barnet, and Miller (1995) had previously found to yield the conventional stimulus relative validity deficit in responding to CS X. Then in Phase 2, the Experimental group was given many (240) extinction trials with a compound of B and C (BC). The CH predicts that the BC extinction trials should have increased stimulus control by Y but not X because C was the cue previously reinforced in compound with Y (making it an effective comparator stimulus for Y), whereas B was the cue nonreinforced in compound with X (leaving it an ineffective comparator stimulus for X). In contrast, the VH&W model predicts equal enhancement of stimulus control by X and Y as a result of extinction of the BC compound because B should have activated the representation of X (with a negative associability) and at the same time C should have activated both the representation of Y (with a negative associability) and an unfulfilled expectation of the US (i.e., a negative error term [see Equation 1]). The product of the [equal] negative associabilities of X and Y and the negative valued error term should have been a positive number, causing VH&W to predict equal RR (i.e., increases in stimulus control) by X and Y. For slightly different reasons, MSOP makes the same predictions as the VH&W model. Specifically, during the BC− trials, B should activate X into A2 and C should activate both Y and the US into A2. Thus, there should be excitatory learning about both X and Y because of simultaneous A2 activation of X, Y, and the US. In fact, one interpretation of MSOP predicts stronger retrospective revaluation of X than Y. Specifically, the B-X association should be stronger than the C-Y association after Phase 1 because BX trials were nonreinforced and CY trials were reinforced. Activation of the US in A1 during CY− outcome trials should reduce learning of the C-Y association. During the Phase 2 BC- treatment, more X elements than Y elements should be A2-activated; thus, increments in the B-X association should be greater than increments in the C-Y association. Thus, McConnell et al.’s results failed to produce evidence of A2-A2 learning of a previously null X-US association (see section 5.2 for further discussion concerning this prediction). McConnell et al.’s data clearly indicated that extinction of BC increased behavioral control by CS Y but not CS X, which is consistent with the prediction of the CH.

Table 3.

Design [simplified] of McConnell, Urushihara, and Miller (2010, Exp. 1) which was designed differentiate VH&W (and MSOP) from CH accounts of retrospective revaluation using a relative validity procedure.

Group	Phase 1	Phase 2	CH predict	VH&W predict
Exp	(AX-US / BX-) & (CY-US / DY-)	many BC-	X?->cr*	X?->CR
			Y?->CR*	Y?->CR*
Ctrl	(AX-US / BX-) & (CY-US / DY-)	Context only	X?->cr*	X?->cr*
			Y?->cr*	Y?->cr*

Note. Conditioned stimuli (CSs) A, B, C, and D were click train, tone, white noise, and flashing light, counterbalanced; Target CSs X and Y were buzzer and SonAlert, counterbalanced. The US was a footshock. - indicates nonreinforcement. CR indicates robust conditioned responding; cr indicates weak conditioned responding.

^*indicates reponsing actually observed.

5.2. Learning a new association between associatively activated pairs

Some models of RR assume that learning about an absent cue is driven by associative activation of the absent cue (and the outcome). For example, MSOP assumes that unovershadowing treatment (i.e., extinction of the overshadowing cue alone after target training consisting of overshadowing treatment) results in associative activation of both the target cue and the outcome into the A2 memory state. Simultaneous activation of target cue and outcome elements in A2 produces increments in the strength of the target cue-outcome association. Relatedly, Witnauer and Miller’s (2012) modification of the VH&W model assumes that unovershadowing is driven by activation of the target cue through overshadowing cue-target cue within-compound associations. Of course, unovershadowing per se involves increments in the strength of a pre-existing cue-outcome association. These models also predict that a retrospective revaluation treatment can establish a new cue-outcome association. Experimental tests of this prediction have led to inconsistent results. Dwyer et al. (1998) conducted a conditioned flavor preference procedure in which a relatively low value flavor cue (Cue X; peppermint) was presented in Context 1. During separate sessions, a second low-value flavor (Cue A; almond) was paired with a high value flavor (outcome; sucrose) in a distinctly different context (Context 2). In a subsequent phase of the experiment, Cue A was presented in either Context 1 or 2. MSOP (and Witnauer and Miller’s modified VH&W model) predict that presentation of Cue A in Context 1 should result in simultaneous associative activation of both X (by Context 1) and the outcome (by Cue A), which should establish an excitatory association de novo between X and the outcome, thereby increasing flavor preference for X relative to a control group that received presentation of Cue A only in Context 2. Dwyer et al.’s observations agreed with MSOP’s predictions; however, Le Pelley and McLaren (2001) failed to observe a similar effect in a human contingency learning procedure. Moreover, as previously mentioned, Denniston et al. (2003) also failed to see such as effect in rats. Thus, the existing literature is mixed concerning whether a new association can be formed between associatively activated representations of stimuli.

5.3. Counteraction and recovery from counteraction

The term cue interaction refers to when a target cue is trained in compound with a companion cue and that presence of the companion cue influences subsequent responding to the target. Cue competition (e.g., overshadowing, blocking) and conditioned inhibition are two of the best known instances of cue interaction. Being able to account for cue interaction is regarded as an acid test of any model of learning to be regarded as viable. Most models of learning that can account for RR explain cue interaction in such a way that they anticipate training a target cue in compound with two companion cues of the same associative status will augment cue interaction relative to training in compound with only one companion cue. For example, VH&W and MSOP both predict enhanced blocking (i.e., reduced responding) to a target CS trained in the presence of two previously conditioned blocking cues relative to the presence of a single blocking cue. In contrast to this prediction, Witnauer, Urcelay, and Miller (2008) found that multiple companion cues counteract each other, such that training in compound with two companion cues actually has less impact on responding to the target than does training in compound with a single companion cue. In their critical experiment, Witnauer et al. observed less blocking of X after Phase 1 training of A+ / B+ and Phase 2 training of ABX+, than after Phase 1 training of A+ / B+ and Phase 2 training of AX+ training. Both VH&W and MSOP predict greater blocking by A and B than by A alone. VH&W assumes that λ_US – (V_A + V_B + V_X) will produce weaker excitatory learning about X than λ_US – (V_A + V_X). In contrast, the extended CH assumes that each companion cue (e.g., A and B) serves as both a first-order and second-order comparator cue (Denniston et al., 2001); thus, A and B are capable of competing with each other, thereby reducing their potential to compete with X.

Critically, the extended CH (Denniston et al., 2001) is unique among contemporary models capable of accounting for RR in anticipating both counteraction and RR after counteraction, which takes the form of release from counteraction. Urcelay and Miller (2006) demonstrated that overshadowing and degraded contingency (i.e., extra US presentations interspersed among target CS-US pairings during training) treatments counteract each other’s potential to reduce responding to a target CS. In a conditioned lick suppression experiment, rats received either compound (overshadowing) or elemental reinforced training of the target CS and, orthogonally, they received either unsignaled US presentations during the intertrial intervals (degraded contingency) or no extra-trial presentations of the US (control). Unsurprisingly, both the simple overshadowing group (i.e., omitting the unsignaled US presentations) and the elemental degraded contingency group showed less suppression to the target than the simple elemental conditioning group (i.e., overshadowing and degraded contingency effects were observed when the treatments were administered separately). Interestingly, strong suppression was observed in the group that received both compound conditioning and degraded contingency treatments. The extended CH explains this effect by asserting that the overshadowing stimulus and the training context (the companion cue that drives the degraded contingency effect) each serve as a comparator stimulus for the other, thereby undermining the potential of each of these two stimuli to down-modulate behavioral control by the target CS. A follow-up experiment demonstrated that the counteraction between overshadowing and degraded contingency is sensitive to RR. Specifically, posttraining associative extinction of either the overshadowing cue or the training context reduced responding to the target cue. Notably, the RR experiment was embedded in a sensory preconditioning procedure because, like backward blocking, the RR treatment was expected to reduce responding to a target cue that had previously been established as a strong excitor. For more detailed discussion of counteraction and release from it including numerous additional examples of both phenomena, see Urcelay and Miller (2006), Urushihara and Miller (2006), and Witnauer, Urcelay, and Miller (2008); however, it should be noted that some failures to observe counteraction have been reported (Nagaishi and Nakajima, 2008; Nakajima and Imada, 1999).

5.4. Context dependence of RR treatment

In section 1.3.5, we noted that RR effects appear to the specific to the context in which RR treatment occurred (Boddez, et al., 2011). These observations suggest that the memory of initial training survives RR treatment, with test context determining whether responding reflects initial training alone or RR treatment as well. As only the CH account of RR assumes that a veridical memory of initial training survives RR treatment, one might view this observation of context specificity as supportive of the CH. But the CH fails to provide an account of why RR effects should be context specific. Consequently, the observed context specificity of RR at best only weakly supports the CH account of RR. However, most of the models that explain RR fail to make realistic assumptions about memory retrieval (but see McLaren et al., 2012); thus, the failure of these models to explain the context dependence of RR treatment could reflect simplifying assumptions about memory retrieval rather than errors in their treatment of RR.

5.5. The challenge of differentiating between the CH and VH&W accounts of RR

Rephrasing the basic question concerning the various accounts of RR, the CH asserts that RR is the result of new learning about the companion cue that takes place during RR treatment, whereas the VH&W and MSOP accounts of RR assert that RR is the consequence of new learning about the target CS that takes place during RR treatment despite the target not being present on the RR treatment trials. At first blush, one might think that a simple way to differentiate these two families of accounts would be to alter the associative status of the companion cue after the RR treatment. Along this line of thinking, one might argue that, if the RR treatment altered the target- outcome association as proposed by the VH&W and MSOP models, this alteration would be impervious to further changes in the associative status of the companion cue; in contrast in the CH framework, further modification of the associative status of the companion cue would be expected to impact subsequent expression of the target-outcome association that was established during training of the target CS (usually in compound with the companion cue). However, this expectation based on the VH&W and MSOP models is faulty in that these models actually predict that revaluation of the companion cue following initial RR treatment is simply more RR treatment that will induce yet further learning about the target-outcome association, causing these models to make predictions indistinguishable from those of the CH.

6. Assessing the CH and VH&W models beyond retrospective revaluation

Although both CH and VH&W (1994) were proposed initially to address RR, they are general models of learning. Hence, here we briefly consider how they fare beyond RR, keeping the discussion short as this takes us somewhat away from RR. Not surprisingly, we find that both models have their strengths and weaknesses. Among their strengths are their abilities to account for positively decelerating acquisition curves, negatively decelerating extinction curves, conditioned inhibition, cue competition, and the US-preexposure effect.

The US-preexposure effect refers to observation that pretraining exposure to the US (or outcome) retards development of subsequent behavioral control by the target cue (X). It is ordinarily explained as a consequence of a context-US association formed during US-preexposure blocking subsequent acquisition of behavioral control of X during X-US pairings. Both the CH and the VH&W model explain the US-preexposure effect in this manner although they have quite different accounts of blocking. Evidence for blocking by the context in this situation comes from the observation that a context shift between US-preexposure and the X-US pairings attenuates the observed retardation. An operation analogous to US-preexposure is exposure to the US alone following the CS-US pairings (US-postexposure). The CH anticipates US-postexposure effects should be as large as US-pretraining effects. In contrast, VH&W, like the RW model on which it is based, anticipates no effect of US-posttraining exposures on subsequent responding to the target cue because the US-alone presentations should not activate an expectation of the CS (i.e., the error in expectancy should be zero). The data here are mixed. Ordinarily no effect of US-posttraining exposure on responding to the target CS is observed, but Urushihara, Wheeler, and Miller (2004) found that if the US-postexposure procedure was embedded in a sensory preconditioning paradigm (AX−O, followed by O alone, followed by pairing O with a US), making it an outcome-postexposure procedure, a decrement on responding to the target CS is observed. This has been interpreted in a functional framework as subjects being more resistant to reducing the potential to respond to a signal for a biologically significant outcome (i.e., a US) than for an outcome that is not biologically significant (also see the above comments concerning a similar effect of the biological significance of the outcome on the occurrence of backward blocking). Thus, in some situations an outcome- postexposure effect is observed, but the effect is almost always weaker than the equivalent outcome-preexposure effect. In summary, the CH clearly fails here in that the observed outcome-postexposure effect is weaker than the outcome-preexposure effect whereas the CH anticipates that they will be equal, but the VH&W model also fails in predicting no outcome-postexposure effect at all.

The CH is unique among accounts of RR in predicting that not only will RR be positively correlated with the strength of the within-compound association between the target CS and its companion cue, but that the same correlation will be observed in conventional cue competition such as overshadowing and conventional (i.e., forward) blocking. However, several reports suggest that such a positive correlation does not obtain in simple cue competition (e.g., Aitken, Larkin, and Dickinson, 2001; Matzel, Brown, and Miller, 1987; Melchers, Lachnit, and Shanks, 2004). This lack of a correlation is a distinct failure of the CH. Related to this inaccurate prediction of the CH, the model anticipates that matched parameters forward and backward blocking will be of equal strength. In contrast to this prediction, many studies have found forward blocking to be much stronger than backward blocking (e.g., Chapman, 1991). This constitutes another failure of the CH.

The VH&W model, being essentially the Rescorla and Wagner (1972) model modified only to account for RR, has many of the same weaknesses as the Rescorla-Wagner model. For example, it fails to account for (a) latent inhibition (e.g., Lubow and Moore, 1959), (b) the observation that under select training conditions a given CS can pass tests for both conditioned excitation and conditioned inhibition (e.g., Matzel, Gladstein, and Miller, 1988), and (c) recovery from extinction (e.g., Bouton and Bolles, 1979). Additionally, the VH&W model fails to account for second-order conditioning and the observation that, given interspersed A-US and AX− trials, small numbers of AX− trials make X a second-order excitatory CS, whereas large numbers of AX− trials make X an inhibitory CS (Stout, Escobar, and Miller, 2003), whereas the formalized CH (Stout and Miller, 2007) does account for this. Notably, sensory-preconditioning, like backward conditioned inhibition (see section 1.1), is an example of RR in which the change in behavioral control of the target CS is in the same direction as that of the revalued companion cue. Relatedly, Espinet et al. (1995) observed that interspersed, nonreinforced interspersed exposure to compounds AX and BX followed by reinforcement of A results in inhibitory behavioral control by B. Presumably, AX− / BX− trials establish an inhibitory within-compound association between A and B. Notice that the so- called Espinet effect could be viewed as an example RR in which the change in behavioral control by the target CS (B) is in the opposite direction as that of the revalued companion cue (A).

The CH clearly anticipates each of the above phenomena except recovery from extinction. With recovery from extinction, it succeeds only to the extent that it views extinction as at least in part something other than the erasure of associations that is assumed by VH&W, but the CH fails to explain how extinguished associations come to be later expressed in renewal and spontaneous recovery situations.

All of the models considered above except MSOP are trial-wise models. As such, they fare poorly with timing effects (e.g., when does responding occur during a presentation of a CS), which demand real-time rather than trial-wise models. Moreover, all of the above models without exception assume retention of only summary statistics as opposed to a multitude of separate episodic events (i.e., instance theories). Obviously real-time models and instance models are more plausible, but they are less tractable and often fail to make unambiguous predictions that can be tested in the laboratory.

Perhaps most critically, the VH&W and MSOP models, like the Rescorla and Wagner (1972) model (also see Barto and Sutton, 1988), assume that learning is driven by total error reduction (i.e., minimizing the difference between the outcome expected on that trial based on all cues present on that trial and the outcome that occurs on that trial, λ_US − ΣV). In recent years, there has been wide acceptance of the principle of total error reduction, an acceptance that in our view has been at least partially driven by a bandwagon effect. This has occurred despite considerable data inconsistent with it (see Witnauer, Urcelay, and Miller, 2014, for a review). Perhaps most notable among the behavioral observations challenging the total error reduction principle is Rescorla’s (2000, 2001, 2008) finding that two cues matched in associability (through counterbalancing) that are reinforced together in compound (i.e., same total error) change differentially as a function of their different associative strengths going into that trial. This observation strongly suggests that learning is driven by local error reduction (a.k.a. individual error reduction, i.e., minimizing the difference between the outcome expected on that trial based individually on each specific cue being revalued on that trial and the outcome experienced, λ_US − V_X) as was suggested long ago by Bush and Mosteller (1955) and Mackintosh (1975), and is assumed by the CH. Rescorla recognized the challenge of his data for a total error reduction mechanism, but rather than rejecting total error reduction, he proposed a hybrid model of learning in which learning is driven by the product of total error reduction and local error reduction (i.e., [λ_US − ΣV]*[λ_US − V_X]). Rescorla argued for retaining the total error reduction term in order to be able to account for cue competition as a learning deficit. Notably, some TER inspired models are able to explain Rescorla’s (2000) data; however, these models make additional assumptions about representation, memory retrieval, and attention (among others, e.g., McLaren et a., 2012; Harris, 2006; Schmajuk, 2009). In contrast, the CH views cue competition as a deficit in performance rather than a deficit in learning, and uses comparator processes active at test to account for cue competition. This allows the CH to use the parsimonious Bush and Mosteller (1955) local error term to drive associative acquisition and explain Rescorla’s (2000, 2001, 2008) data, which neither the VH&W or MSOP models can do.

More generally, the VH&W model focuses exclusively on acquisition processes while ignoring processes underlying retrieval and response generation. The CH uses a simpler acquisition rule and focuses largely on processing of information, perhaps oversimplifying acquisition processes. The problems listed above tend focus on failings of the VH&W model because it was designed only to extend the Rescorla-Wagner model to account for RR rather than address other shortcomings of the Rescoral-Wagner model. But surely there are major problems with all contemporary models of learning including the CH. Many of the above problems arise from the oversimplifying assumptions that were used to make the CH and VH&W models tractable. At the same time, development and empirical assessment of these models has advanced our understanding of basic cognitive processes underlying learning. In our view, the three major contributions of the CH are that (a) it challenges the need for the assumption that learning on any given trial is driven by total error reduction rather than local error reduction, (b) it draws attention to information processing that occurs at test, and (c) it acknowledges the existence of latent memories.

7. Conclusions

The phenomenon of RR has proven and continues to prove useful as a benchmark for assessing models of learning. Moreover, it forces acceptance of either the view that response deficits in cue interaction paradigms are largely due to cognitive processes that occur at the time of test (i.e., the CH), and/or that learning about a cue can occur on a training trial on which the target cue is not present (i.e., the VH&W and MSOP models).

Highlights.

• Retrospective revaluation treatment changes the response potential of an absent cue.

• Treatments involve changes in the associative status of companion cues.

• Retrospective revaluation challenges most models of associative learning.

• Several recently proposed models of learning anticipate basic retrospective revaluation.

• All models are challenged by at least some aspects of retrospective revaluation.