Impact of Shoulder Abduction Loading on Brain-Machine-Interface in Predicting Hand-opening and closing in Individuals with Chronic Stroke

Abstract

Background

Many individuals with moderate and severe stroke are unable to use their paretic hand. Presently, the effect of conventional therapy on regaining meaningful hand function in this population is limited. Efforts have been made to use brain-machine interfaces (BMI) to control hand function. To date, almost all of BMI classification algorithms are designed for detecting hand movements with a resting arm. However, many functional movements require simultaneous movements of arm and hand. Arm movement will possibly impact the detection of intended hand movements, specifically for individuals with chronic stroke who have muscle synergies. The most prevalent UE synergy --- flexor synergy --- is expressed as an abnormal coupling between shoulder abductors and elbow/wrist/finger flexors.

Objective

We hypothesized that due to flexor synergy, shoulder-abductor activity would affect the detection of the hand-opening (a movement inhibited by flexion synergy) but not the hand-closing task (a movement facilitated by the flexion synergy).

Methods

We evaluated the accuracy of a BMI classification algorithm in detecting hand-opening versus closing after reaching a target with two different shoulder-abduction loads in six individuals with stroke.

Results

We found a decreased accuracy in detecting hand-opening when a stroke individual intends to open the hand while activating shoulder abductors. However, such decreased accuracy with increased shoulder loading was not shown during detecting a hand-closing task.

Conclusions

This study supports that one should consider the effect of shoulder abduction activity when designing BMI classification algorithms for the purpose of restoring hand function in individuals with moderate to severe stroke.

I. INTRODUCTION

Stroke is the leading cause of disability in the United States. About 40% of all individuals after a stroke are not able to use their paretic hand [1]. Presently, for individuals with severely affected upper extremity (UE) post stroke, the evidence that conventional therapy can restore meaningful hand function is limited [2–6]. Therefore, exploring the usage of a brain-machine interface (BMI) to control a neuroprosthesis that provides an artificial means to regain basic hand function merits further investigation.

Since 2008, the effect of BMI-mediated detection of activities, such as grasping or finger extension, has been tested in individuals with stroke [7–17]. However, these BMI studies have detected the intention of hand movements in isolation without consideration of the effect of arm activity on the hand. In reality, arm activity is often required to implement functional motor tasks, such as reaching and grasping an object. This clear gap between the current BMI classification algorithm design and real-world requirements could significantly impact the effectiveness of the targeted neuroprosthetics and negatively influence a stroke user’s willingness to use it.

The importance of exploring the effect of proximal arm activity on detecting a hand-task in individuals with stroke comes from the loss of independent joint control in the paretic arm due to the abnormal muscle synergies. The most prevalent muscle synergy [18, 19], the so-called flexor synergy, is expressed as an abnormal coupling between shoulder abductors and elbow/wrist/finger flexors in the paretic upper limb. Recent research in our lab provided evidence demonstrating that due to the flexor synergy, lifting the paretic arm resulted in synergy-related finger/wrist EMG activity and thus reducing the ability of a more severely impaired stroke individual to generate volitional wrist/finger extension [20]. Furthermore, we found that synergy-induced abnormal muscle coactivation patterns were associated with changes in cortical activity [21]. Therefore, it is likely that synergic activities also impact the accuracy of a BMI classification algorithm. As previous studies already shown that abduction affected the elbow/wrist/finger extension more than flexion, we hypothesized that shoulder abduction would affect the detection of a hand-opening (i.e., a task inhibited by the synergy) but not a hand-closing task (i.e., a hand movement that is less affected by the synergy as compared to opening).

II. Method

A. Subject

Six subjects with chronic hemiparetic stroke were recruited for this study (see Table 1 for subject information). All the subjects sustained a unilateral lesion at least 1 year before participating in the study. The following inclusion criteria were applied to the participants: 1) without motor impairment in the non-paretic limb; 2) without brainstem and/or cerebellar lesions; 3) without severe concurrent medical problems (e.g. cardiorespiratory impairment); 4) without acute or chronic pain in the upper extremities or spine; 5) able to provide informed consent; 6) able to elevate the paretic limb against gravity up to horizontal and generate some active elbow extension, and 7) able to understand the required tasks. The level of impairment severity were evaluated using the upper extremity portion of the Fugl-Meyer Motor Assessment (FMA) [22]. Participants scoring 10 to 60 out of 66 on the FMA were admitted in the study. All of subjects provided written consent that was approved by the Institutional Review Board of Northwestern University prior to participating in this study.

TABLE I.

Subject Information

Patient	Age	Sex	Affected hand	Dominant hand	Site of Lesion	Time since incident (y)	FMS (/66)	FMS for hand (/14)
S1	63	M	L	R	R. Corona radiata	5.3	43	8
S2	52	M	L	R	R. IC & R. Put & R. Cl	13	10	1
S3	61	M	L	R	R. Thalamus & IC-G	7.6	24	3
S4	55	F	R	R	L. Dorsal Lateral SMA & PM. Subcortical white matter.	9.2	35	3
S5	58	M	L	R	R Posterior frontal cortex with MC involvement	2.5	46	7
S6	60	F	R	R	L Th, IC, BG, Put, GP	4.9	16	1

^*S are subjects after stroke,

M = Male, F = Female, R =Right limb, L = Left limb, N/A = Not available, IC = Internal Capsule, SMA = Supplementary Motor Area, LS = Lateral Sulcus, ICG = Internal Capsule, Genu, Put = Putamen, Cl = Claustrum, FMS = Fugl-Meyer Scores, MC = Motor cortex, BG = Basal ganglia, GP = Globus pallidus, Th = Thalamus.

B. Experimental setup

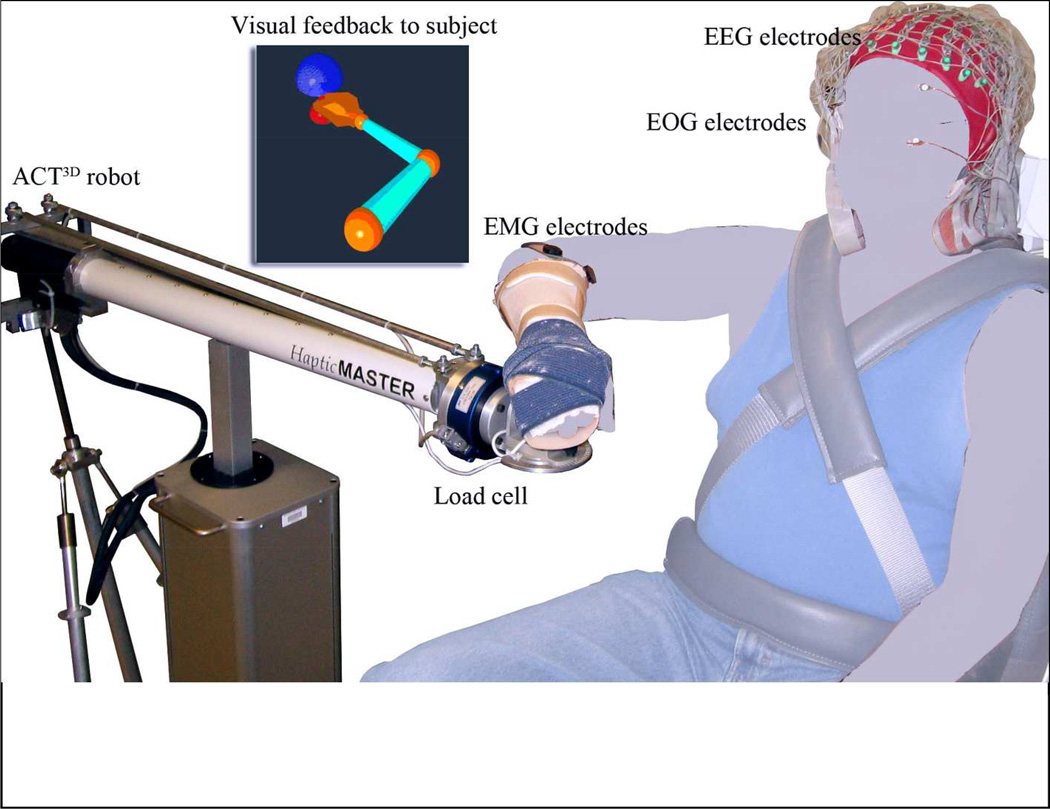
The Arm Coordination Training (ACT^3D) robot was used to modulate the shoulder load during motor tasks. This admittance controlled robot can generate constant shoulder abduction loads during reaching tasks, as shown by both kinetic and kinematic data, and can thus precisely modulate the amount of flexion synergy expressed at more distal joints of the paretic upper limb [23–26].

During the all the experiments, participants sat in a Biodex chair that restrained the trunk and pelvis with straps to prevent motion during the experiment. Each subject’s forearm was strapped into a forearm-hand orthosis attached to the end effector of the ACT^3D robot. At the start of the experiment, the subject’s limb lengths were measured and entered into the computer in order to scale the OpenGL-rendered graphical representation of the limb (avatar). Then the tested arm was positioned at a “home position” of a 45° shoulder flexion angle, 75° shoulder abduction angle, and 90° elbow flexion angle (see figure 1); and the “target position” was set as far as the tip of the hand could reach based on segment lengths with the configuration of a 95° shoulder-flexion angle, 75° shoulder-abduction angle, and 0° elbow-flexion angle.

Figure 1.

Experimental Setup. The tested arm is required to move from the “home position” (red dot) to the “target position” (blue dot) at a comfortable speed at which point the subject either opens or closes the hand.

Before data collection, a short training/preparation session was conducted to help subjects to get familiar with the motor tasks and associated feedback. At the beginning of a trial, the subject was instructed to move the paretic arm to the home position and relax there for 3 seconds. During this phase, the target position appeared as a blue or green sphere, with the color indicating a hand opening (blue) or closing (green) trial. The home target then disappeared indicating to the subject that s/he should reach at a comfortable speed for the target within 2 seconds (i.e., the reaching phase). The average duration of the reaching phase was about 1–1.5 seconds. A monitor continuously displayed an avatar of the true position of the tested arm/hand during the reaching phase. In some instances, subjects were unable to reach the target. In this case, they were instructed to perform the task to the best of their ability. After reaching or attempting to reach the target for more than 2 seconds, the target position changed to yellow and the position of the avatar then went to the target position where it was frozen. Upon seeing the yellow target, the subject was instructed to concentrate on either opening or closing the hand for 1 to 2 seconds while holding his/her arm in the same posture.

The hand opening/closing tasks were performed with 2 different shoulder loads: the “supported” condition, where subjects were supported by a frictionless haptic table generated by the robot; or the “unsupported” condition, during which the virtual table was lowered by 5 cm, requiring the subject to actively elevate and hold the paretic arm against gravity above the haptic table. When performing the hand task during the “unsupported” condition, a beeping sound was given to the subject when the paretic arm touched the table. All subjects were able to elevate the paretic arm once hearing the beeping sound. If during an a block of 20–30 trials, there were 3 consecutive trials with a short beeping signal, the data collection was paused and a longer resting period was incorporated before starting the next block. Overall, 4 different tasks (opening /closing tasks in supported or unsupported conditions) were performed by each subject. Subjects finished the opening and closing tasks under the supported condition on the first day and the unsupported condition 2 or 3 days later. In each condition, opening and closing tasks were performed randomly in several blocks of 20–30 trials for a total of 120–200 trials for each task. The experiment for each session lasted approximately 4 hours, including 2 hours for setup time and 2 hours for data collection. To minimize fatigue, a resting period of 8–20 seconds between trials was implemented as well as a 10–20 minute period between blocks.

We simultaneously collected EMG signals from the wrist/finger extensors (extensor carpi radialis longus & brevis and the extensor digitorum) and flexors (flexor carpi radialis and the flexor digitorum superficialis) of the tested arm, as well as 160-channel EEG from the scalp and 2-chanel electrooculography (EOG) signals from above and beneath the eye (Biosemi, Inc., Active II, Amsterdam, The Netherlands) during each session (see figure 1). All signals were collected with the reference placed at both ears and sampled at 1024 Hz.

C. EEG Data analysis

The 160-channel EEG signals were first visually inspected to identify and remove channels constantly contaminated by noise (i.e., channels with bad contact or movement artifacts). On average, about 8–10 peripheral channels were eliminated. The remaining EEG signals were then aligned to the onset of wrist/finger flexor (for closing task, or for opening task when the activity of wrist/finger extensors was absent) or wrist/finger extensor (for opening task). Subsequently, they were segmented from −1 s to 1 s with 0 representing the onset of EMG activity. The segmented EEG signals were then baseline corrected by removing the average voltage level during the baseline phase (−1 to −0.8 s) from all data points in the segment. Subsequently, a finite-difference Surface Laplacian [27] transformation was applied to each EEG channel as a spatial high-pass filter to reduce the smearing effects caused by the head volume conductor and to increase the signal-to-noise-ratio [28]. This resulted in the elimination of the outermost electrodes (about 29 channels), and thus a spatial pattern of activation was generated by a total of about 120 electrodes throughout all sessions. Additionally, visual inspection of the processed signals was performed to remove trials contaminated by ocular or movement artifacts. Within each shoulder load condition, 80–150 trials remained for the two hand tasks combined. These remaining trials were then down-sampled to 256 Hz and exported to MATLAB for further analysis.

In the MATLAB environment, a classification algorithm utilizing time-frequency synthesized spatial patterns (TFSP) [29–31] with a newly-added rejection scheme was implemented as follows:

First, for a single trial of EEG data, the signal from one channel was decomposed into 13 frequency bands using constant Q value (Q = 4) band-pass filters with their center frequencies ranging from 5–34 Hz. Subsequently, the Hilbert transform was used to extract profiles of the oscillatory activities, which were then divided into 72 equal-length time intervals (55 ms of each interval) with a 50% overlap. Next, the instantaneous power (i.e., integration of the profile) was calculated in each of the time–frequency bins, and thus the EEG signal from a single channel was represented by a 72×13 matrix of coefficients. The above processing was repeated in all channels. As a result of above decomposition process, a single trial EEG signal was characterized by a series of spatial features represented in each of the 72×13 time-frequency bins (t-f bins).

After decomposing spatial feature onto 72×13 t-f bins, the classification of the hand-opening/closing tasks was performed for the supported and unsupported conditions separately. Under a given shoulder load, we first calculated the characteristic spatial patterns for each hand task in each of the specific t-f bins by averaging all the spatial patterns within such specific t-f bin (i.e., for a given shoulder load, the characteristic spatial patterns (P) for hand-opening $P_{op}(t,f)=\frac{1}{N}{\sum }_{n=1}^N{p}_{op}{(t,f)}_n$ and for hand-closing $P_{cl}(t,f)=\frac{1}{M}{\sum }_{m=1}^M{p}_{cl}{(t,f)}_m$, where n and m were the indices of trials; and N and M were the total number of the trials in the training datasets for opening and closing task, respectively). Then, a similarity judgment S_p(t, f) within a specific time–frequency bin (t,f) was made by comparing correlation coefficients between the spatial pattern of a testing trial (p) and the two characteristic spatial patterns (P) as follows:

$$S_p(t,f)=\{\begin{array}{c}\hfill 1,\mathit{\text{corrcoef}}(p(t,f),P_{op}(t,f))-\mathit{\text{corrcoef}}(p(t,f),P_{cl}(t,f))>T{h}_{rej}\hfill \\ \hfill 0,\left|\mathit{\text{corrcoef}}\right(p(t,f),P_{op}(t,f))-\mathit{\text{corrcoef}}(p(t,f),P_{cl}(t,f)\left)\right|\le T{h}_{rej}\hfill \\ \hfill -1,\mathit{\text{corrcoef}}(p(t,f),P_{cl}(t,f))-\mathit{\text{corrcoef}}(p(t,f),P_{op}(t,f))>T{h}_{rej}\hfill \end{array}$$ (1)

A Sp(t, f) equal to 1 or −1 indicated a detection result of hand-opening or a hand-closing trial; and 0 represented an uncertain judgment. As shown in the equation (1), at this first-level, the correlation coefficient between the testing trial and the 2 characteristic patterns was used to quantify the distance between the testing trial and the characteristic pattern. The decision of one t-f bin went to the class whose characteristic pattern was closer to the testing trial. A rejection scheme was added to the original TFSP BMI algorithm at each of the time-frequency bins. When the difference in the similarity judgment was smaller than the rejection threshold (Th_rej), the corresponding grid did not contribute to the final decision-making. The output of the first-level Sp(t, f) by each of the t-f bins was then used at the second level to determine a final decision. The second level synthesis worked akin a voting system, in which each individual (equal to each of the t-f bins) voted, and the final judgment went to the decision that was agreed by most of the individuals. All the accepted grids shared the same voting rights, and the final judging decision R(p) regarding the class of a testing trial was made by summing the results over the entire 72×13 time–frequency grids as follows: R(p)= sign (sum(Sp(t,f))). A positive R(p) indicated that a majority of bins judge that the current trial was a hand-opening event, while a negative one indicated a hand-closing event. No trial would be rejected completely unless R(p)= sign (sum(Sp(t,f))=0, which never happened in any test trials to date.

Finally, we calculated the true positive rate (TPR, defined as the number of hand-opening trials that were correctly recognized, normalized by the number of total hand-opening trials) and true negative rate (TNR, defined as the number of hand-closing trials that were correctly recognized, normalized by the number of total hand-closing trials). The BMI algorithm was repeated with a rejection threshold of 0 to 0.95 with a step increase of 0.05. The leave-four-out cross validation method [32] was used to test the overall performance under either the supported or unsupported conditions with each of the given rejection thresholds.

In order to understand the neural underpinnings of our results, we further identified the t-f bins that performed differently under ‘supported’ and ‘unsupported’ conditions, separately for each of the 2 hand tasks. To implement this, we first gave a score equal to 1, −1 or 0 to each of the t-f bins, if it detected a single trial correctly, falsely, or refused to make a decision, respectively. The final recognition score of a t-f bin was then calculated by summing the scores cross all of the trials with the rejection threshold setting as 0.35 (i.e., the overall optimal rejection threshold). Subsequently, we used a one-way Repeated Measure of Analysis of Variance (RMANOVA) to identify t-f bins with a significant change in the recognition score when a different level of limb support was applied (dependent factor: recognition score, independent factor: ‘supported’ vs. ‘unsupported’ condition, samples are different trials, p<0.05). These t-f bins were defined as shoulder-load sensitive t-f bins (SS t-f bins). Finally, we counted the number of SS t-f bins in Theta (4–7 Hz), Alpha1 (8–10 Hz), Alpha2 (10–13 Hz), Beta1 (13–20 Hz), and Beta2 (20–30 Hz) bands before and after the EMG onset.

To explore the spatial features, we reconstructed the cortical activity of subject S2 from 0 to 50 ms while performing hand-opening and hand-closing tasks using his paretic left arm under the supported and unsupported conditions. Inverse source reconstruction was conducted using the LORETA method (Lp=1) [33, 34] based on ensemble-averaged EEG signals and a subject-specific boundary element head model developed by subject-specific anatomic MRI. Although the inverse procedure was performed over the whole cortex, only the activities in the region of interest (ROI), consisted of the bilateral the premotor (PM), supplementary motor area (SMA, including both preSMA and SMA proper), primary motor (M1) and primary somatosensory (S1) cortices were shown. Due to the absence of MRI data in the remaining 5 subjects, cortical activity reconstruction was not performed in the other 5 subjects.

Statistical analyses were applied to detect the difference at a p<0.05 significance level or a trend of reaching significance at a p between 0.05 and 0.1.

III. Results

Overall, equal numbers of hand opening and closing trials were used: A two-way ANOVA (hand task, support level) analysis result showed no significant difference in the trail numbers between the hand-opening and closing tasks (p=0.78, F=0.07) or between the unsupported versus supported conditions (p=0.40, F=0.75).

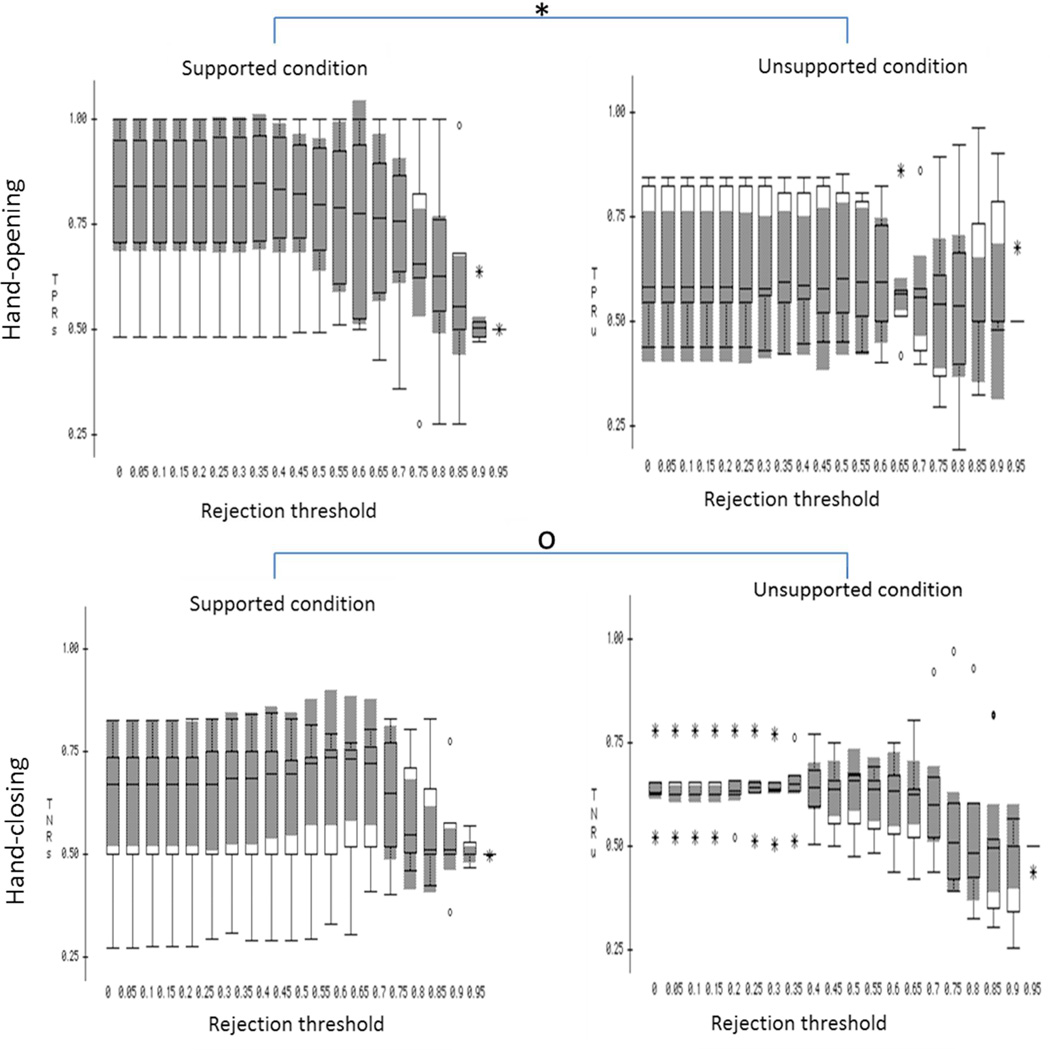
The box plots of true positive rates (TPR) and true negative rates (TNR) under the supported and unsupported conditions with each of the rejection thresholds were plotted in figure 2. Results from a one-way MANOVA (independent factor: shoulder abduction load with the rejection threshold as the nested factor; dependent factors: TPR and TNR) showed that shoulder abduction load significantly influenced the accuracy rate for detecting hand-opening (F=28.737, p<0.0001) but not the accuracy rate for detecting a hand-closing (F=0.0824, p>0.1). Scheffe post-hoc tests showed that the classification algorithm detected the hand opening with significantly higher accuracy during the supported condition as compare to the unsupported condition (mean difference =12.8%, p<0.0001).

Figure 2.

The box plot of the BMI performance over the 6 subjects under supported (left column) and unsupported (right column) conditions with different rejection thresholds applied. *p<0.0001 and °p>0.1. In this figure, the applied rejection threshold was indicated in the x-axis, and the TPR or TNR was indicated in the y-axis.

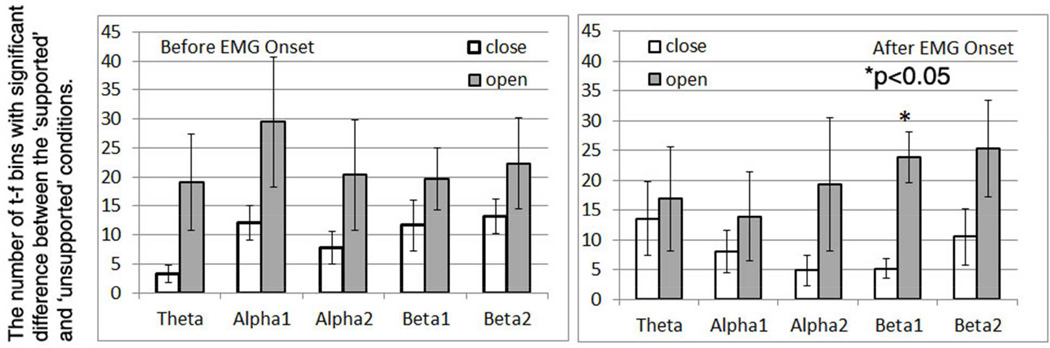
Across-subjects mean and standard errors of the number of shoulder-load sensitive t-f bins (SS t-f bins) were shown in Figure 3. As shown in figure 3, overall more SS t-f bins were found for the hand-opening task (gray bars of figure 3) than for the hand-closing task (white bars). A three-way RMANOVA was used to test the effect of the time window (2 levels--- before and after EMG onset), frequency band (5 levels) and hand task (2 levels --- opening and closing tasks) on the number of SS t-f bins. Results of RMANOVA reported a significant effect of the hand task (F=9.854, p=0.0257) on the number of SS t-f bins but not the other two factors (time window: F=0.091, p=0.7745; and frequency band: F=0.353, p=0.839). There were no significant interactions between these three within-subject factors, either. A non-parametric Friedman post-hot test reported a significantly greater number of SS t-f bins in low beta band (13–20 Hz) after EMG onset for hand opening task as compared to closing task (p<0.05). No other significant results were found by the post-hoc analysis.

Figure 3.

The numbers of t-f bins with significant difference in recognition score between the ‘supported’ and ‘unsupported’ conditions at different frequency bands during the time window of before EMG onset (left) and after EMG onset (right).

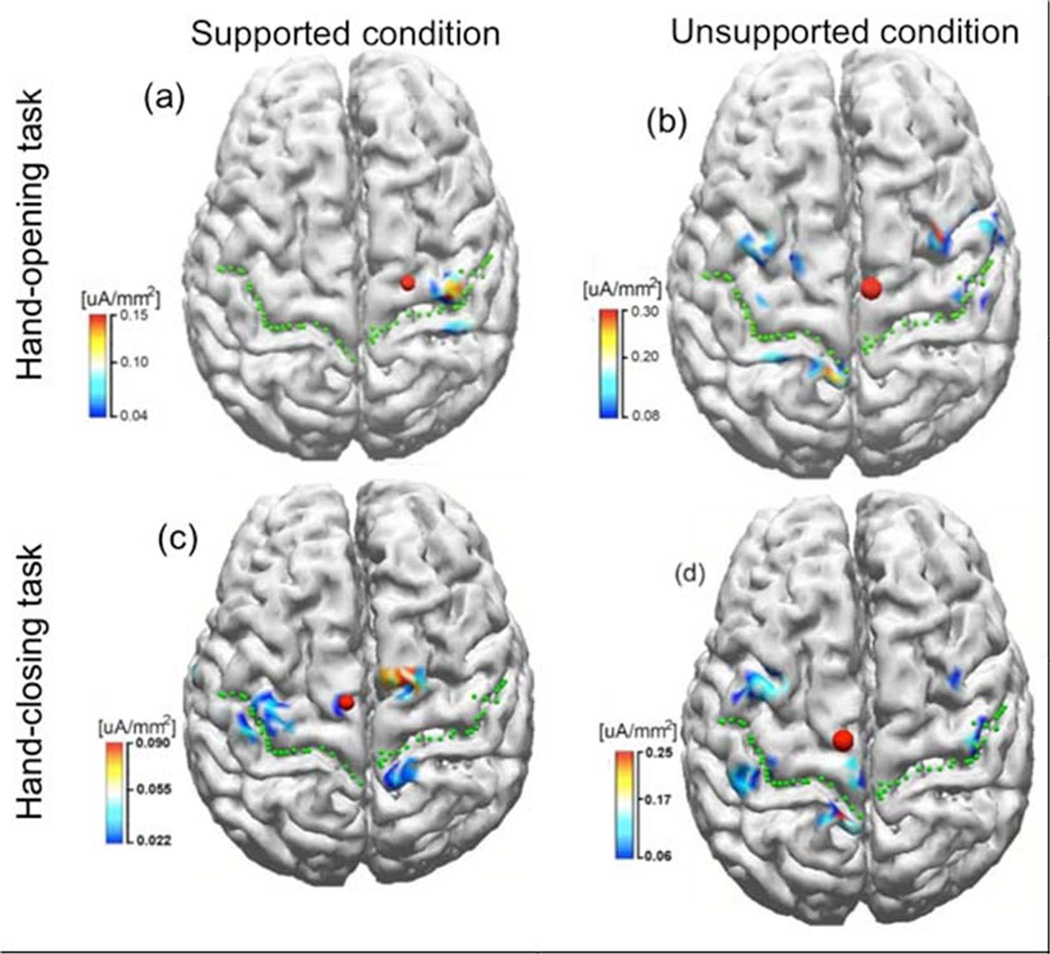
Cortical activities of subject S2 from 0 to 50 ms while performing hand-opening and - closing tasks with the paretic left arm during supported and unsupported conditions were shown in figure 4. As illustrated in Figure 4, during the supported condition, only the contralateral M1/S1 cortical regions were involved in the hand-opening task (figure 4 a); however, bilateral activity was detected during the hand-closing task (figure 4 c). Thus the spatial patterns during the supported condition for the two hand tasks were quite different. However, during the unsupported condition, bilateral cortical activity was observed for both the hand-opening and - closing tasks (see figure 4 b and d). The similarity in cortical spatial patterns for the two hand tasks during the unsupported condition reduced the accuracy of the classification algorithm.

Figure 4.

The inverse results in stroke subject S2 when performing tasks of hand-opening (the upper row) and hand-closing (the lower row) using his paretic arm (left arm) under supported (left column) and unsupported conditions (right column), respectively. The green dot lines indicate the central sulcus and the red dots represent the center of gravity (CoG) of the cortical activity within ROI.

IV. Discussion

Our results obtained from the paretic arm of 6 subjects with chronic hemiparetic stroke showed a significant reduction in the accuracy of detecting the hand opening with an increased shoulder abduction load. However, such shoulder-abduction induced reduction in the accuracy was not demonstrated in hand-closing task.

The loss of independent joint control in individuals of stroke affects the accuracy in detecting the hand-opening task

We believe that the SABD-load induced reduction in the accuracy for detecting hand-opening task is due to changes in brain activity that also results in a flexor synergy. Previous reports from our laboratory have shown that the flexion synergy decreases the ability to reach [25, 26] and open the hand [21], when increased shoulder abduction loading was applied. The main underlying neural mechanism is postulated to be an increased reliance on brainstem descending pathways, like the cortico-reticular spinal tract (CRST), due to the loss of corticospinal tract (CST) fibers from the lesioned hemisphere. It is well known that CST monosynaptically facilitates contralateral extensor and flexor muscles [35], and ipsilateral CST activation of spinal motoneurons is absent or very weak [36]. In contrast, CRST is a bilaterally organized system. Previous studies have shown that CRST projects to both motoneurons and interneurons involved in digital control [37]. CRST tends to facilitate flexors and suppress extensors ipsilaterally, and the reverse contralaterally [38–40]. Thus it is possible that the ipsilateral CRST and remaining CST projections are both effective resources to drive hand-closing regardless of the supporting conditions. The case of hand opening is more complex. As we already know that ipsilateral CRST suppresses extensors. Therefore, residual CRST from the non-lesioned ipsilateral side may not be a good backup for hand opening, and hand opening may be primarily depended on contralateral residual CS. Such dependence on contralateral residual CST is also reflected as the greater paralysis of finger extensors regardless of shoulder abductor activity [41]. During the supported condition, using contralateral residual CST for opening task versus using bilateral CRST and CST for closing task might allow for the detection of the two hand tasks. However, when additional shoulder abductor muscle was required, ipsilateral CRST was used for both hand-tasks and contralateral cortical activity related to hand opening might no longer be detectable. This explanation was supported by the cortical activity results from a single subject, as shown in figure 4. It was also supported by the significant change of the number of SS t-f bins in detecting hand opening at lower beta band (13–20 Hz) after EMG onset when different SABD loading was required. As reported before, cortico-muscular communication conducted via the CRST oscillates in a lower frequency band (10–15 Hz) [42, 43] than that conducted via CST that is in a higher frequency band [15–40 hz see 44]. Our finding of a significant difference in the number of SS t-f bins for hand-opening task in the low beta band probably also reflects that CST and CRST were used to drive hand opening during the ‘supported’ as compared to the ‘unsupported’ condition.

In short, our results show that shoulder loading has a significant impact on the accuracy of detecting a hand-opening task in individuals with stroke, presumably because hand-opening is more exclusively dependent on activity in the contralateral lesioned hemisphere via the lateral CST. Conversely, the impact of shoulder abduction loading on the detecting of hand-closing task is not significant, presumably because hand-closing can be generated by both contralateral cortical activity via the CST and ispilateral cortical activity via the CRST.

Possible limitations in the interpretation of our data

Previous literature has shown that the human brain, even after a stroke, can still adapt to a BMI device to improve performance [12]. Because we always conducted experiments under the supported condition on the first day, and experiments under the unsupported condition about 2 or 3 days later, it is reasonable to expect that the effect of learning could impact our findings. In case a subject learned from the 1^st day’s experiment, any potential learning effects should favor the unsupported condition, and thus, imply an even lower detection rate under an unsupported condition if there is no effect of learning. Therefore, the order of the experiments should not invalidate our results. If anything it should only strengthen them. Furthermore, there is no reason to believe that the effect of learning would affect the hand-opening and -closing tasks differently. Because of the above 2 reasons, we ruled out an effect of learning on our findings.

Results of conducting the experiments in a fixed sequence could also be affected by some random differences: such as the subject’s overall mental state, noise from random sources, day-to-day impedance differences between electrodes and skin, and so on. These differences will be reflected as baseline differences and have been removed from analysis. Furthermore, because of their random nature, there is no reason to believe that noise from random sources should bias one testing condition over another.

Other possible confounding factors that may impact our signals are muscle fatigue and EMG contamination of EEG activity. It is possible that, the subject may be more fatigued on the 2^nd day than that on the 1^st day. To avoid this issue, we have separated the 2 experiments by 2 or 3 days. In order to limit the effects of muscle fatigue within a day, we included longer resting periods between trials and between blocks for experiments in the unsupported condition. No subjects reported fatigue during or after the experiment. We also checked the frequency spectrum of EMG data. We did not find a significant difference in the EMG spectrum between the first 10 and last 10 trials. Therefore, no clear evidence of muscle fatigue was found. Consequently, we argued that muscle fatigue was not a primary contributor to the observed decrease in BMI performance when a greater shoulder abduction load was applied.

Additionally, higher muscle artifacts might be introduced to EEG signals under the unsupported condition as compared to the supported condition. The increased EMG activity mostly affected the outside EEG electrodes, which were removed from further analysis, thereby reducing their influence on EEG signals. Furthermore, we argued that if EMG activity indeed contaminated EEG to a greater extent when the arm was not supported, then it should have affected both the opening and closing tasks similarly. However, our results showed that different shoulder loads only significantly affected the accuracy in detection of the hand-opening task. To further confirm that EMG did not affect time-frequency bins differently for various conditions, a two-way repeated measure of ANOVA (i.e., supporting conditions and the hand tasks) was used to compare the spectrum in two control frequency bands: 30–40 Hz and 40–50 Hz. In these two bands, the spectrum should not be significantly modulated by a brain signal change but could very easily be modulated by an EMG artifact signal. Repeated measures of MANOVA did not report any significant effects (p>0.1).

The difference in sensory input under the supported and unsupported conditions as well as additional motor output for shoulder abduction under unsupported condition could also contribute to the changes in BMI performance. We argued that the sensory input and motor output caused by shoulder abductor activation were the same to both hand-opening and hand-closing task. However, we only observed the changes in the BMI performance for hand-opening task but not for hand-closing task. Therefore, the common sensorimotor information caused by the shoulder activity cannot explain selective changes in the BMI performance for the hand-opening task only but not for the closing task.

Finally, our discussion of possible neural mechanisms for our findings (i.e., shoulder loading affects the BMI performance of hand opening task but not closing task) was partially based on imaging results from a single subject. Imaging results on increased number of subjects are required for a more solid answer to the neural mechanisms. In short, our results provide for the first time evidence that shoulder loadings impact the BMI performance differently for hand opening as opposed to closing task.

Clinical implications and future directions

In this paper, we provided evidence of a decreased accuracy of the classification algorithm in detecting hand opening when an individual after a stroke intended to activate the hand while also activating shoulder abductors. This conclusion is based on the off-line performance of the TFSP algorithm. However, this conclusion is likely generalizable to real-time applications as well. Our conclusion about shoulder activity impacting the accuracy in detecting hand tasks can probably also be generalized to other joints, such as the elbow and the wrist; and to other synergetic patterns, such as the impact of shoulder adduction on the detection of the hand-closing task. In short, our results demonstrate the necessity of considering the impact of multi-joint activity when designing a BMI device such as a neuroprosthetics for potential future clinical usage in individuals with stroke and suggest that regaining more independent shoulder and elbow control may be vital to improve BMI performance for the purpose of recapturing basic hand function.