Abstract
Automated nuclear detection is a critical step for a number of computer assisted pathology related image analysis algorithms such as for automated grading of breast cancer tissue specimens. The Nottingham Histologic Score system is highly correlated with the shape and appearance of breast cancer nuclei in histopathological images. However, automated nucleus detection is complicated by (1) the large number of nuclei and the size of high resolution digitized pathology images, and (2) the variability in size, shape, appearance, and texture of the individual nuclei. Recently there has been interest in the application of “Deep Learning” strategies for classification and analysis of big image data. Histopathology, given its size and complexity, represents an excellent use case for application of deep learning strategies. In this paper, a Stacked Sparse Autoencoder (SSAE), an instance of a deep learning strategy, is presented for efficient nuclei detection on high-resolution histopathological images of breast cancer. The SSAE learns high-level features from just pixel intensities alone in order to identify distinguishing features of nuclei. A sliding window operation is applied to each image in order to represent image patches via high-level features obtained via the auto-encoder, which are then subsequently fed to a classifier which categorizes each image patch as nuclear or non-nuclear. Across a cohort of 500 histopathological images (2200 × 2200) and approximately 3500 manually segmented individual nuclei serving as the groundtruth, SSAE was shown to have an improved F-measure 84.49% and an average area under Precision-Recall curve (AveP) 78.83%. The SSAE approach also out-performed 9 other state of the art nuclear detection strategies.
Index Terms: Feature representation learning, automated nuclei detection, Stacked Sparse Autoencoder, breast cancer histopathology
I. Introduction
With the recent advent of cost-effective whole-slide digital scanners, tissue slides can now be digitized and stored in digital image form [1]. Digital pathology makes computerized quantitative analysis of histopathology imagery possible. The diagnosis from a histopathology image remains the “gold standard” in diagnosing considerable number of diseases including almost all types of cancer. For breast cancer (BC), the Nottingham Histologic Score system enables the identification of the degree of aggressiveness of the disease, largely based off the morphologic attributes of the breast cancer nuclei. The arrangement and topological features of nuclei in tumor regions of breast histopathology thus represent important histologic based biomarkers for predicting patient outcome [2]. Accurate determination of breast cancer grade is important for guiding treatment selection for patients. Since the scoring system is highly correlated to nuclear appearance, accurate nuclei detection is a critical step in developing automated machine based grading schemes and computer assisted decision support systems for digital pathology. Additionally, the quantitative assessment of lymphocytes in breast tissue has been recently recognized as a strong prognostic predictor of favourable outcome [3]. Consequently it has become important to be able to automatically identify the extent of lymphocytes in digitized pathology images. However, qualitative estimation of the extent of lymphocytic infiltration in breast pathology images by pathologists is still largely subjective and manual quantification is laborious, tedious, and hugely time consuming. Hence, there is a need to develop algorithms for automated detection of individual nuclei.
Additionally, the identification of the location of individual nuclei can also allow for automated characterization of spatial nuclear architecture. Features that reflect the spatial arrangement of nuclei (e.g. via graph algorithms such as the Voronoi, Delaunay Triangulation, Minimum Spanning Tree) have been shown to be strongly associated with grade [2] and cancer progression [4]. Thus there are compelling reasons to find improved, automated, efficient ways to identify individual cancer nuclei on breast pathology images.
The rest of the paper is organized as follows: A review of previous related works is presented in Section II. A brief review of basic autoencoder and its architecture is presented in Section VI. A detailed description of Sparse Stacked Autoen-coder (SSAE) is presented in Section III. The experimental setup and comparative strategies are discussed in Section IV. The experiment results and discussions are reported in Section V. Concluding remarks are presented in Section VI.
II. Previous Related Work
Accurate detection of nuclei is a difficult task because of the complicated nature of histopathological images. Hematoxylin and Eosin (H&E) are standard stains that highlight nuclei in blue/purple and cytoplasm in pink in order to visualize the structure of interest in the tissue [5]. The images are complicated by (1) the large number of nuclei and the size of high resolution digitized pathology images, (2) the variability in size, shape, appearance, and texture of the individual nuclei, (3) noise and non-homogenous backgrounds. Most current nuclei detection/segmentation methods on H&E stained images are based on exploiting low-level hand-crafted features [6], such as color [7]-[22], edge [23]-[28], contextual information [29]-[31], and texture [32], [33]; see Table I for a detailed enumeration of some of these approaches.
Table I.
The categorization of different nuclei detection approaches
| Categorize | Nuclei Detection Approaches | |
|---|---|---|
| Hand-crafted feature based | color-based | blue ratio [7], [8] |
| unsupervised color clustering [9] | ||
| local thresholding [10] | ||
| local adaptive thresholding [11] | ||
| color deconvolution [12], | ||
| singular value decomposition (SVD) [13], | ||
| adaptive thresholding & morphological operation [14] | ||
| gaussian mixture model & EM [15] | ||
| LoG filter [16], distance-constrained LoG filter [17] | ||
| iterative voting [18] | ||
| single path voting & mean-shift [19] | ||
| iterative kernel voting [20] | ||
| multi-scale distance map-based voting [21] | ||
| region-based voting [22] | ||
| edge-based | adaptive H-minima transform [23] | |
| watershed [24], [25] | ||
| multi-scale morphological close & adaptive thresholds [26] | ||
| gradient & morphological operation [27] | ||
| circular Hough transform [28] | ||
| contextual information based | Region-growing and markov random field [29] | |
| spectral graph [30] | ||
| graph mining [31] | ||
| texture-based | diffused gradient vector field [32], [33] | |
| Deep Learning based | Convolutional autoencoder neural network [34] | |
As Table I illustrates, most of the detection approaches are based on hand-crafted features. A number of these approaches, including ones previously presented by our group [15] have yielded high degrees of detection accuracy. However, since most of these approaches are dependent on either color or intensity related attributes, it is not clear how these approaches would generalize from one site to another. To the best of our knowledge, none of the approaches in Table I have been extensively tested on multi-site data.
Recently, significant progress has been made in learning image representations from pixel (or low) level image features to capture high level shape and edge interactions between different objects in images [35]. These higher level shape cues tend to be more consistently present and discernible across similar images across sites and scanners compared to lower level color, intensity or texture features. These low level image attributes tend to be more susceptible to signal drift artifacts. Deep learning (DL) is a hierarchical learning approach which learns high-level features from just the pixel intensities alone that are useful for differentiating objects by a classifier. DL has been shown to effectively address some of most challenging problems in vision and learning since the first deep autoencoder network was proposed by Hinton et al. in [36]. An appealing attribute of DL approaches for histopathology image analysis is the ability to leverage and exploit large numbers of unlabeled instances. Consequently, in the last couple of years there has been interest in the use of DL approaches for different types of problems in histopatho-logical image classification. For instance, in [34], the authors employed a convolutional autoencoder neural network architecture (CNN) with autoencoder for histopathological image representation learning. Then a softmax classification is employed for classifying regions of cancer and non-cancer. The work in [34], however, only used one-layer autoencoder for high-level feature representation.
Unlike CNN-based feature representation which involves convolutional and subsampling operations to learn a set of locally connected neurons through local receptive fields for feature extraction, the approach presented in this paper (illustrated in Figure 2) employs a full connection model for high-level feature learning. Autoencoder or Stacked Sparse Autoencoder (SSAE) is an encoder-decoder architecture where the “encoder” network represents pixel intensities modeled via lower dimensional attributes, while the “decoder” network reconstructs the original pixel intensities using the low dimensional features. CNN is a partial connection model which stresses importance of locality while SSAE is a full connection model which learns a single global weight matrix for feature representation. For our application, the size of nuclear and non-nuclear patches was set to 34 × 34 pixels. Additionally each image patch may contain up to a single object (in this case a nucleus) that would be appropriate for construction of a full connection model. Therefore, we choose to use SSAE instead of CNN in this paper. On the other hand, SSAE is trained, bottom up, in an unsupervised fashion, in order to extract hidden features. The efficient representations in turn pave the way for more accurate, supervised classification of the two types of patches. Moreover, this unsupervised feature learning is appropriate for histological images since we have a great deal of unlabeled image data to work with; image labels typically being expensive and laborious to come by. This higher level feature learning allows us to efficiently detect multiple nuclei from a large cohort of histopathological images. In our preliminary work [37], we employed the SSAE framework for learning high-level features corresponding to different regions of interest containing nuclei. These low-dimensional, high-level features were subsequently fed into a Softmax Classifier (SMC) for discriminating nuclei from non-nuclear regions of interest within an independent testing set. In this paper, we extend the framework presented in [37] to automatically detect multiple nuclei from whole slide images. To attain this goal, locally maximal confidence scores are computed by sliding a window across the entire image in order to selectively identify candidate image patches for subsequent nucleus classification. Each automatically selected image patch is then fed into a trained classifier, yielding a binary prediction for absence or presence of a nucleus in each image patch.
Fig. 2.
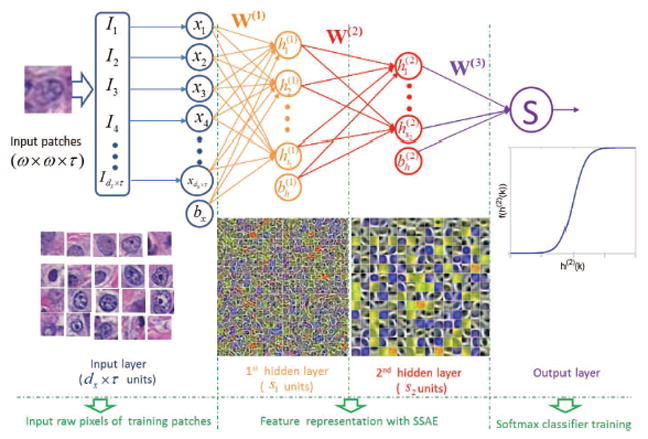
Illustration of Stacked Sparse Autoencoder (SSAE) plus Softmax Classifier (SMC) for identifying presence or absence of nuclei in individual image patches.
Note that our approach is focused on nuclei detection and not on nuclear segmentation, i.e. explicitly extracting the nuclear boundaries [15], [25]. However our approach could be used to provide initial seed points for subsequent application of segmentation models such as watershed [10], [38], active contour [15], and region-growing approaches [29].
The major contributions of this paper are:
Different from hand-crafted feature representation based methods, the SSAE model can transform the input pixel intensities to structured nuclei or non-nuclei representations. Therefore, the SSAE based framework is able to learn high-level structure information from a large number of unlabeled image patches. Our approach is thus fundamentally different from a number of existent handcrafted methods that rely on low-level image information such as color, texture, and edge cues.
By training the SSAE classifier with unlabeled instances, the SSAE model employs a hierarchical architecture for transforming original pixel signal intensities of input image patches into the corresponding high-level structural information. During the classification stage, each image patch to be evaluated is fed into the hierarchical architecture and represented by a high-level structured representation of nuclei or non-nuclei patches.
Using a sliding window approach enables rapid traversal across large images for detection of individual nuclei efficiently. Locally, maximal confidence scores are assigned to individual image patches and used to identify candidate patches which are then fed to a subsequent classifier. This two-tier classification reduces the computational burden on the classifier, sieving out non-candidate nuclear patches and thus making the overall model more efficient.
To sum up, this paper integrates the SSAE based framework for learning of high-level features associated with nuclei. Our approach also employs a sliding window scheme for efficiently detecting nuclear patches.
III. Stacked Sparse Autoencoder (SSAE)
The stacked autoencoder is a neural network consisting of multiple layers of basic SAE (see Figure 1) in which the outputs of each layer are wired to the inputs of each successive layer [39]. The review of the basic SAE is presented in the Appendix. In this paper, we considered the two layer SAE, which consists of two hidden layers, and the Stacked Sparse Autoencoder (SSAE) to represent the two layer SAE. The architecture of SSAE is shown in Figure 2. For simplicity, we did not show the decoder parts of each basic SAE in the Figure 2.
Fig. 1.
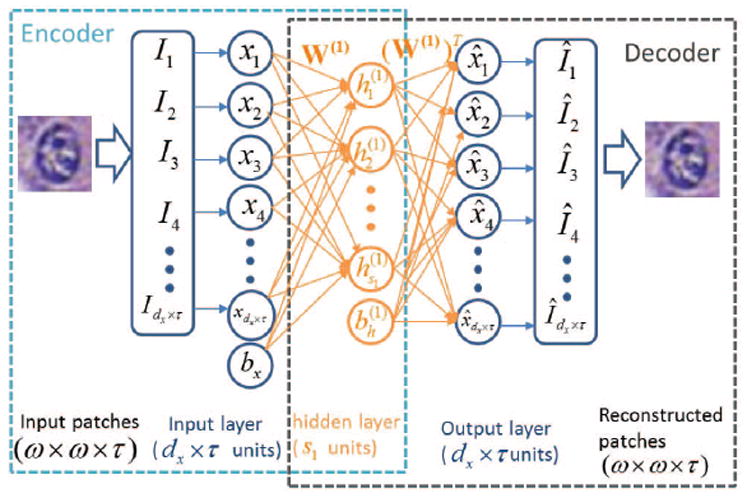
Illustration of the architecture of basic Autoencoder (AE) with “encoder” and “decoder” networks for high-level feature learning of nuclei structures. The “encoder” network represents dx × τ input pixel intensities corresponding to an image patch via a lower s1 dimensional feature. Then the “decoder” network reconstructs the pixel intensities within the image patch via the s1 dimensional feature.
A. SSAE for high-level feature learning
Similar to SAE, training an SSAE involves finding the optimal parameters θ = (W, bh, bx) simultaneously by minimizing the discrepancy between input and its reconstruction. After the optimal parameters θ are obtained, the SSAE yields a function that transforms input pixel intensities of an image patch to a new feature representation of nuclear structures.
As Figure 2 shows, with SSAE, each training patch x(k) of pixel intensities is represented by a high-level structured representation of nuclei or non-nuclei patches h(2)(k) in the second hidden layer of the model. All the training patches can be written as where for each k ∈ {1, 2, … , N}, {h(2) (k), y(k)} is a pair of high-level features and its label. For the two class classification problem considered in this paper, the label of the k–th patch is y(k) ∈ {0, 1}, where 1 and 0 refer to the nuclear and non-nuclear patches, respectively. Note that in the SSAE learning procedure, the label information Y is not used. Therefore, SSAE learning is an unsupervised learning scheme. After the high-level feature learning procedure is complete, the learned high-level representation of nuclear structures, as well as its label , are fed to the output layer.
B. The output layer: Softmax Classifier (SMC)
Softmax classifier (SMC) is a supervised model which generalizes logistic regression as
| (1) |
where is a sigmoid function with parameters W(3). When the input z of SMC is a high-level representation of nuclear structures learned by SSAE, the SMC’s parameter W(3) is trained with training set to minimize the cost function. By minimizing the cost function with respect to W(3) via the gradient descent based approach [39], the parameter W(3) can then be determined.
C. The trained SSAE+SMC for nuclei detection
After training, the parameters θ of SSAE and W(3) of SMC are determined. With these parameters, SSAE+SMC is ready for nuclei detection. The detection procedure is shown in Figure 3. During detection process, each image patch detected by a sliding window is first represented by high-level feature h(2)(k). This is then fed to the SMC (function (1)) and produces a value between 0 and 1 that can be interpreted as the probability of the input image patch corresponding to a nucleus or not.
Fig. 3.
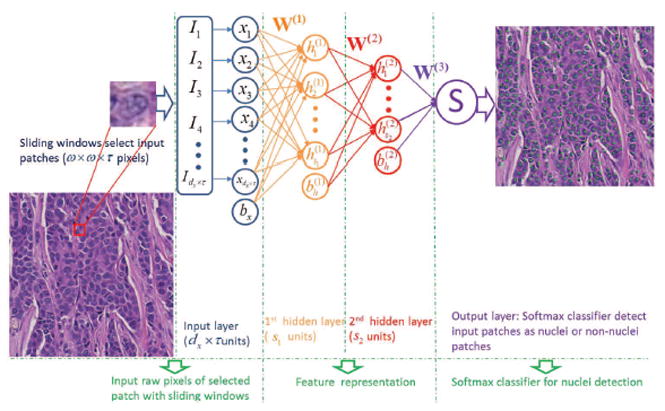
Illustration of SSAE+SMC for nuclei detection on breast histopathology. With a sliding window scheme, the randomly selected image patches from the histopathologic images are fed into a trained SSAE+SMC model for detecting presence or absence of nuclei. If a nucleus is found to be present, a green dot is then placed in the center of that corresponding image patch.
IV. Experimental Setup
A. Dataset
A set of 537 H&E stained histopathological images were obtained from digitized glass slides corresponding to 49 lymph node-negative and estrogen receptor-positive breast cancer (LN-, ER+ BC) patients at Case Western Reserve University. The size of each image is about 2200 × 2200 pixels and there are about 1500 nuclei in each image. The H&E stained breast histopathology glass slides were scanned into a computer using a high resolution whole slide scanner, Aperio ScanScope digitizer, at 40x optical magnification. The images were randomly split into two subgroups for training (37 images) and testing (500 images). We also ensured that images from the same patient were not simultaneously in the training and testing sets. The complete access to the full dataset is provided with this link: http://engineering.case.edu/centers/ccipd/data/TMI2015.
B. Parameter setting
In this paper, the patch size is defined as ω × ω = 34×34 = 1156 pixels which is big enough to contain a nucleus within the patch under 40X optical magnification resolution images. Each patch size has three color channels. Therefore, τ = 3. In the first layer, or input layer, of SAE and SSAE (Figures 1, 2, and 3), the input is the vector of pixel intensities corresponding to a square patch. This vector is represented as a column vector of pixel intensities with size (342 ×3)×1. Therefore, there are dx = s0 = 34×34×3 = 1156×3 input units in the input layer. The first and second hidden layers have = s1 = 400 and = s2 = 225 hidden units, respectively. The nl of SAE and SSAE are 2 and 3, respectively.
C. Generation of training sets
A pathologist manually placed a dot in the center of each nucleus from each of the 37 images that comprised the training set. Each nuclear patch is generated from a 34 × 34 square image window, employing the annotated dot as the center of the window. The size of each patch was chosen to be big enough to contain a nucleus within the patch. Each nuclear patch was chosen in a way that it only contained a single nucleus within it. The non-nuclear patches were randomly generated by identifying those 34 × 34 square image windows whose centers are far away (greater than 34 pixels) from the pathologist identified nuclear centers. The non-nuclear patches do not contain any nuclei or only contain a part of a nucleus. Our training set comprised of 14,421 nuclear and 28,032 non-nuclear patches extracted from 37 training images. These training patches were then employed for training the SSAE and SMC models.
D. Ground truth generation
For all 500 testing images considered in this study, the objective was to automatically detect the location of the nuclear regions. Since it was tedious and time consuming to have an expert pathologist manually detect each and every nucleus in each of the 500 images (to provide ground truth for quantitative evaluation), the expert was asked to randomly pick regions of interest on the digitized images where clusters of nuclei were visible. The expert then proceeded to meticulously place a dot in the center of each nucleus within the randomly chosen ROIs (400 × 400) on each of the 500 digitized images considered in this study. Consequently, quantitative evaluation of the different models was limited to these 500 ROIs across the 500 images.
E. Training the SSAE+SMC
Before training, the SSAE network was initially assigned a set of hyperparameters θ′ = (θ, W(3), s1, s2, α, β) which includes the network parameters θ = (W, bh, bx), the weight of SMC (W(3) in (1), number of units in 1st (s1) and 2nd (s2) hidden layers, the weights of the sparsity term (α in Eq. (7)), and regularization term (β in Eq. (7)). For 37 images in the training set, we used 10-fold cross validation, where each fold consisted of 30 training and 7 validation images. For each fold, the patches from the training images are used for training the SSAE model based on the procedure just described in this section. Then the SSAE model is employed for detecting nuclei in the validation images. The detection performance on the validation images is used for choosing the best set of hyperparameters. We used F-measure and Average Precision (defined in (5) and (6)) to evaluate the performance of the model. Finally, the hyperparameters θ′ with the highest F-measure and Average Precision (AVeP) were chosen as the final set of model parameters.
The architecture of SSAE+SMC is shown in Figure 2. We employ the greedy layer-wise approach for training SSAE by training each layer in a sequential manner. The training procedure includes the three following steps:
First, a Sparse Autoencoder (SAE) is applied to the pixel intensity of image patches in training set X to learn primary representation h(1)(x) on the pixel intensities by adjusting the weight W(1);
Next, the input pixel intensities are fed into this trained sparse autoencoder, obtaining the primary representation activations h(1)(x) for each input image patch x. These primary representations are used as the “input” to the other sparse autoencoder to learn the secondary representation h(2)(x) on these primary representations by adjusting the weight W(2);
Following this, the primary representation is fed into the second SAE to obtain the secondary representation activations h(2)(x) for each of primary representation h(1)(x) (which correspond to the primary representation of the corresponding input image patches x). These secondary representations h(2)(x) are treated as “input” to a SMC, and it is trained to map h(2)(x) to digitally label Y by adjusting the weight W(3).
Finally, all three layers are combined to form a SSAE with 2 hidden layers and a final SMC layer capable of detecting the nuclei.
The model involves the SSAE being trained bottom up in an unsupervised fashion, followed by a Softmax classifier that employs supervised learning to train the top layer and fine-tune the entire architecture. It is easy to see that the label Y is not used during the training procedures 1) and 2), until the Softmax classifier is trained. Therefore we can conclude that SSAE learns feature representations in an unsupervised manner.
F. The trained SSAE+SMC for nuclei detection
The detection procedure for the trained SSAE+SMC is shown in Figure 3. The red square in Figure 3 is an example of a selected image patch for nuclei detection. Each 34 × 34 × 3 image patch is first converted into a 1156 × 3-dimensional vector. Then each input image patch yields an output based on Equation (1). If the output value is ≈ 1, this patch will be identified as a nuclear patch; otherwise not.
G. Sliding window detector
Our strategy involves identifying the presence or absence of a nucleus within every individual image patch in a histopathologic image. A sliding window scheme is used to select candidate patches. Since the sliding window detector will typically evoke multiple responses around target nuclei, non-maxima suppression is applied to only retained those evoked responses above a pre-defined threshold. The threshold and overlapping rate for the non-maxima suppression algorithm are empirically defined as 0.8 and 30%, respectively.
H. Experimental design and comparative strategies
In order to show the effectiveness of the SSAE+SMC model, the model is compared against 8 other state of the art models (see Table III).
Table III.
Models considered in this work for comparison with the SSAE+SMC model
| Acronyms | Description |
|---|---|
| EM | Expectation-Maximum Algorithm |
| BRT | Blue Ratio Thresholding |
| CD | Color Deconvolution |
| SMC | Softmax Classifier |
| AE+SMC | Single layer Autoencoder plus Softmax Classifier |
| SAE+SMC | Single layer Sparse Autoencoder plus Softmax Classifier |
| STAE+SMC | Stacked Autoencoder plus Softmax Classifier |
| TSAE+SMC | Three layer Sparse Autoencoder plus Softmax Classifier |
| CNN+SMC | Convolutional Neural Network plus Softmax Classifier |
-
SSAE+SMC versus hand-crafted feature based nuclei detection methods: We compare SSAE+SMC with extant nuclei detection methods, including Expectation-Maximization (EM) based [15], Blue Ratio (BR) [7], and Color Deconvolution (CD) based [12] algorithms. EM algorithm has been employed to detect nuclei in our previous work in [15]. These methods are described in these papers [7], [12], [15] and we direct interested readers to these papers for a detailed description of the methods.
The implementation of the EM based nuclei detection was based on our previous work in [15]. BR and CD algorithms for nuclei detection were implemented based on the paper [7], [12], respectively.
SSAE+SMC versus other feature representation based classification models: We compare SSAE+SMC with SMC classifier which employs SMC directly on the pixel intensities, where a SMC is learned from pixel intensities of training set to detect nuclei via the methods described in Section III-B. In the SSAE+SMC based framework (Figure 3), the features learned by SSAE are treated as “input” to SMC for detection. In this experiment, we additionally attempt to show the efficiency of sparsity constraint on the hidden layer. We compare SSAE with the Stacked Autoencoder (STAE) without the sparsity constraint, where α = 0 in Eq. (7).
We therefore compare the SSAE+SMC against three other models (see Table III) to evaluate the efficiency in detecting nuclei from histopathological images as follows:
Softmax Classifier (SMC): In this model, the input z of SMC in (1) are pixel intensities of an image patch and the SMC’s parameter W(3) is trained with training set to minimize the cost function. Then SMC (1) with W(3) determined during training is integrated with the sliding window detector (see Section IV-G) to detect presence of a nucleus within each image patch selected by the sliding window.
AE+SMC: The parameter α in (7) controls the sparsity constraint on the hidden layer of AE. If the sparsity constraint is removed by setting α ≡ 0, the SAE is reduced to a one layer AE model. The input z of SMC in (1) is learned via a single layer of AE and the SMC is trained and employed for nuclei detection in a way similar to that described in Section IV-H2 (1). Then SMC (1) is coupled with AE to detect presence or absence of a nucleus within each image patch selected by the sliding window.
STAE+SMC: Stacked AE (STAE) is a neural network consisting of multiple layers of basic AE in which the outputs of each layer are wired to the inputs of the successive, subsequent layer. STAE involves a two layered AE which in turn comprises of two basic AEs. The input z of SMC in (1) is a feature learned via use of a two layer of AE from pixel intensities of a image patch. The SMC is subsequently trained and evaluated using the approach discussed in Section IV-H2 (1).
I. SSAE+SMC vs SAE+SMC
The aim of this experiment was to show the efficiency of using a “deep” versus “shallow” architecture when it comes to representing high level features using pixel level intensities. A comparative evaluation of the following various architectures was performed.
SAE+SMC: In this model, the input z of SMC in (1) is a feature learned via use of a single layer of SAE from pixel intensities of an image patch. The SMC is subsequently trained and evaluated using the approach discussed in Section IV-H2 (1).
TSAE+SMC: Three Layer Sparse Autoencoder (TSAE) is a neural network consisting of three layers of basic Sparse AE in which the outputs of each layer are wired to the inputs of next layer. There are dx = 34 × 34 × 3 = 1156 × 3 input units in the input layer. The first and second hidden layers have = 400, = 225, and = 100 hidden units, respectively. The input z of SMC in (1) is a feature learned via use of a three layer SAE from pixel intensities of an image patch. The SMC is subsequently trained and evaluated using the approach discussed in Section IV-H2 (1).
J. SSAE+SMC versus CNN+SMC
The aim of this experiment was to compare SSAE and CNN for the problem of nuclei detection. The implementation of CNN is based on the CAFFE framework [40]. We used one convolutional layer, one pooling layer, one full connection layer, and an output layer. For the convolutional and pooling layers, 25 feature maps of fixed 11 × 11 convolutional kernel and 8 × 8 pooling kernel were used, the feature map having been obtained as a result of applying a convolutional or max-pooling operation across an image. In the output layer, 225 neurons are fully connected with output/classifier.
For simplicity, the training and detection procedures of SMC, AE+SMC, STAE+SMC, SAE+SMC, and TSAE+SMC in Table III are omitted since they are almost identical to the strategies used for SSAE+SMC, shown in Figure 3. For CNN training,readers can refer to the CAFFE framework [40]. The detection procedure is the same as illustrated in Figure 3. For each of six models, sliding window detectors are first employed to select image patches before feeding to the models. Then high-level features are extracted via the models and these features are then subsequently input to SMC. Finally, the trained SMC (1) classifies each image patch as either having or not having a nucleus present.
K. Evaluating the effect of window size
The aim of this experiment was to analyze the effect of window size on the detection accuracy of SSAE+SMC framework. The classification accuracy of SSAE+SMC is computed by averaging the F-measure value across all 500 images as the size of the sliding window changes.
L. Evaluating the effectiveness of the step size for sliding window operator
The aim of this experiment was to analyze the effect of step size as the window slides across the images on the detection accuracy of SSAE+SMC framework. The classification accuracy of SSAE+SMC is computed by averaging the F-measure across all 500 images as the step size of the sliding window changes.
M. Performance Evaluation
The quantitative performance of SSAE+SMC and different models shown in Table IV are analyzed by using the metrics in Equations (2)–(6), respectively. The performance of automatic nuclei detection is quantified in terms of Precision, Recall or True Positive Rate (TPR), False Positive Rate (FPR), F-measure, and Average Precision (AveP).
Table IV.
The mean associated with Precision, Recall, and F-measure and Average Precision (AveP) with boots trapping method for EM, BRT, CD, SMC, AE+SMC, STAE+SMC, TSAE+SMC, TSAE+SMC, CNN+SMC, and SSAE+SMC for nuclei detection in over 500 breast histopathology images
| Model | Precision (%) | Recall (%) | F-measure (%) | AveP (%) |
|---|---|---|---|---|
| EM | 66.38 | 78.73 | 70.84 | 54.78 |
| BRT | 84.40 | 61.87 | 71.04 | 49.25 |
| CD | 77.75 | 75.80 | 75.61 | 59.48 |
| SMC | 78.05 | 78.39 | 79.56 | 68.29 |
| AE+SMC | 83.51 | 77.40 | 79.85 | 68.09 |
| SAE+SMC | 84.52 | 77.93 | 80.68 | 70.51 |
| STAE+SMC | 83.71 | 82.98 | 83.12 | 78.29 |
| TSAE+SMC | 88.35 | 77.15 | 82.26 | 73.48 |
| CNN+SMC | 88.28 | 77.60 | 82.01 | 73.65 |
| SSAE+SMC | 88.84 | 82.85 | 84.49 | 78.83 |
Here True Positive (TP) is defined as the number of nuclei correctly identified as such by the model. In the paper, the correct detection of nuclear patches (true positives) was identified as those instances in which the distance between the center of the detected nuclear window and the closest annotated pathologist identified nucleus was less than or equal to 17 pixels. FP and FN refer to false positive and false negative errors, respectively. Other measures such as Precision, Recall, F-measure, FPR are defined in Equations (2)-(5). In (6), Average Precision (AveP) involves computing the average value of p(r) over interval between r = 0 and r = 1 and the precision p(r) is a function of recall r. Therefore, AveP shows the average area under Precision-Recall curve (see Figure 7(a)).
Fig. 7.
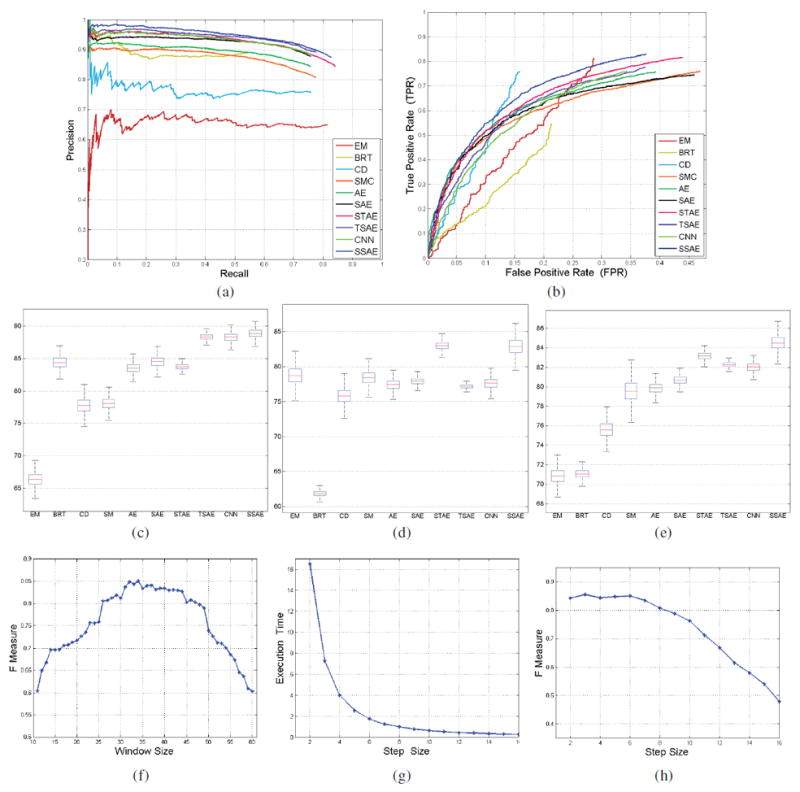
The precision-recall curves (a) and ROC curves (b) on the detection accuracies of SSAE+SMC compared to EM, BRT, CD, SMC, AE+SMC, STAE+SMC, TSAE+SMC, and CNN+SMC; The estimated confidence intervals of Precision (c), Recall (d), and F-measure (e) with bootstrapping method for different methods; (f) The F-measure value on the nuclei detection accuracies of SSAE+SMC with variable window size; The effectiveness of SSAE+SMC model with different step size on the execution time (g) and F-measure value (h).
We also draw the precision-recall curves and Receiver Operating Characteristic (ROC) curves to assess the performance of nuclear detection provided by different models.
V. Experimental Results and Discussion
A. Qualitative results
The visualization of learned high-level features in the first and the second hidden layers from training patches with SSAE are shown in Figures 5(a) and 5(b), respectively. These features show that the SSAE model enables the uncovering of nuclear and non-nuclear structures from training patches.
Fig. 5.
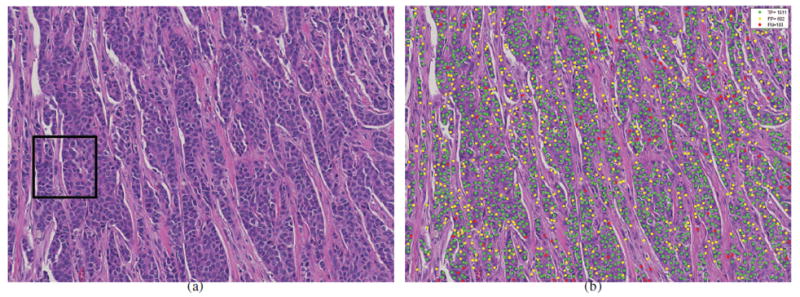
The nuclei detection results (b) of SSAE+SMC for a large breast histopathological image (a) from a whole-slide image of a patient. The green, yellow, and red dots represent the true positive (TP), false positive (FP), and false negative (FN) with respective to groundtruth, respectively.
Qualitative detection results of SSAE+SMC for a whole-slide breast histopathological image (Figure 5(a)) is shown in Figure 5(b). The detection results of EM, BRT, CD, SMC, AE+SMC, STAE+SMC, SAE+SMC, CNN+SMC, and SSAE+SMC models on a magnified region of interest (ROI) are illustrated in Figures 6(b)-(j), respectively. In these images, the green, yellow, and red dots represent the nuclei that had been correctly detected (true positive detection), the non-nuclei that had been wrongly detected as the nuclei (false positive detection), and the nuclei that were missed with respect to the manually ascertained ground truth delineations, respectively. The SSAE+SMC model was found to outperform the other 8 models with respect to the ground truth (see Figure 6(a)). These results appear to suggest that SSAE+SMC works well in learning useful high-level features for better representation of nuclear structures.
Fig. 6.
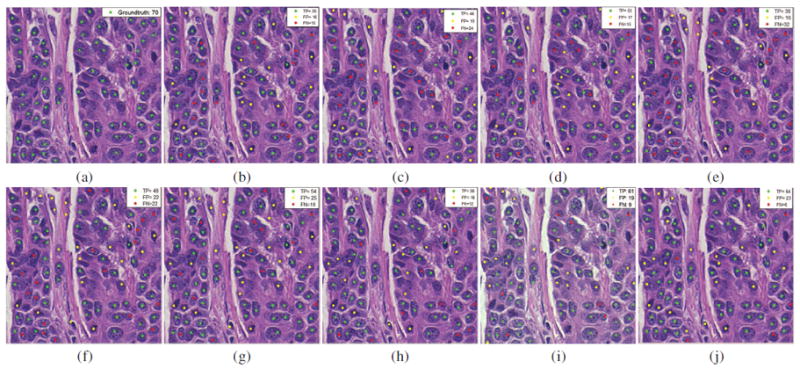
The nuclear detection results of EM (b), BRT(c), CD(d), SMC (e), AE+SMC (f), SAE+SMC (g), STAE+SMC (h), CNN+SMC (i), and SSAE+SMC (j) models for a 400 × 400 patch selected from the black square region in Figure 5 (a). The ground truth of manually detected nuclei are shown as green dots in (a). (b), (c), (d), (e), (f), (g), (h), and (i). The green, yellow, and red dots in these images represent the TP, FP, and FN with respective to ground truth, respectively.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
B. Quantitative results
Figure 7(a) shows the precision-recall curves corresponding to nuclear detection accuracy with respect to the EM, BRT, CD, SMC, AE+SMC, STAE+SMC, SAE+SMC, TSAE+SMC, CNN+SMC, and SSAE+SMC models across 500 images, respectively. Each point on the X-axis and Y-axis represents the precision and recall in Equations (2) and (3), respectively. Each model is quantitatively evaluated using AveP, as shown in Table IV. The results appear to suggest that SSAE+SMC achieves the highest AveP. Each of the ROC and Precision-Recall curves (Figures 7 (a), (b) respectively) were generated by sequentially plotting the confidence scores (in descending order) associated with the various nuclear detection methods considered in this work. Precision-recall and ROC curves were generated for each detection method considered across 500 images. High precision or True Positive Rate corresponds to a method with a more accurate nuclear detection result. For the nuclear detection problem, we only had information pertaining to the total number of manually identified nuclear patches (or positive patches). However information on the total number of patches without nuclei (or negative patches) was not available. Therefore, to compute False PositiveRate (FPR), we estimated the total number of negative patches with sliding window scheme across the randomly chosen ROIs on each of the 500 images. The window slides across each ROI image row by row from upper left corner to the lower right (the step size was fixed at 6 pixels). The number of negative patches is the sum of all the patches across the 500 images excluding well-centered and annotated patches as well as those instances in which the distance between the center of the patch window and the closest annotated pathologist identified nucleus was less than or equal to 17 pixels. Also, for Figure 7 (b), since the total number of False Positive detections is always smaller than the estimate of the total number of negative patches, the FPR can never reach 1. The trajectory of the ROC curves is therefore only plotted for a false positive fraction of 0.4. The ROC curve (see Figure 7 (b)) shows that SSAE+SMC results in superior detection performance compared to other models. Moreover, Figures 7 (a) and Table IV show that SSAE+SMC tend to outperform SAE+SMC and TSAE+SMC in terms of AVeP. While the results appear to suggest the importance of a “deeper” architecture compared to a “shallow” architecture in representing high-level features from pixel intensities, the relatively poor performance of the three layered SAE+SMC model as compared to the SSAE+SMC model suggests that increasing the number of layers may result in overfitting. Dropout is a popular approach employed for avoiding overfitting problems associated with deep networks. The dropout approach was originally proposed in [41], [42]. The Autoencoder model with dropout is also called “Denoising Autoencoder (DAE)”. The name “Denoising” is meant to reflect the idea of DAE. DAE is a simple variant of the basic autoencoder (AE). It is trained to reconstruct clean “repaired” input data from a corrupted version of DAE. The idea is to add some noise, such as additive Gaussian noise, to the input data in the input layer. Recently, the authors in [43] employed “drop-out” to add noise to the hidden layer. We tried to implement “drop-out” in our work. But the “drop-out” implementation did not yield any gains on performance in our experiments. Therefore, we decided to exclude it from the paper. The estimated confidence intervals of Precision, Recall, and F-measure in a confidence level of 95% with the bootstrapping method for different methods are shown in Figures 7 (c), (d), and (e), respectively. The means of Precision, Recall, and F-measure of SSAE+SMC and comparative models are shown in Table IV. As expected, SSAE yields the highest F-measure of 84.49%.
C. Sensitivity Analysis
Figure 7(f) shows the sensitivity of window size (X-axis) on the detection accuracy (Y-axis) of SSAE+SMC model. The curves in Figure 7(f) show that the SSAE+SMC achieves the best F-measure value when the window size is around 34 pixels. As a result, we chose a window size of 34 pixels for all subsequent experiments. Figures 7(g) and 7(h) show the execution time and F-measure of the SSAE+SMC model as a function of step size. They show the effect of step size on the computational efficiency and detection accuracy of the SSAE+SMC model. The figures show that both execution time and F-measure value significantly decrease as the step size increases.
As expected, the SSAE achieves better performance in detecting nuclei as compared to hand-craft feature based methods. This also appears to be related to the ability of the SSAE model to better capture higher level structural information, yielding better discriminability of nuclei versus non-nuclei.
D. Computational Consideration
All the experiments were carried out on a PC (Intel Core(TM) 3.4 GHz processor with 16 GB of RAM) and a Quadro 2000 NVIDIA Graphics Processor Unit. The software implementation was performed using MATLAB 2014a. The training set included 14421 nuclei and 28032 non-nuclei patches. The size of each patch was 34 × 34 pixels. We compared the computational efficiency of SSAE+SMC against 9 other state of the art strategies. The execution time for each of these models is shown in Table V. In terms of training time, the four autoencoder based models, and the CNN model, need longer training times while EM, CD, and BRT did not require a training phase. Also, the deeper the architecture (more layers), the longer the training time required. However, once the autoencoder models were trained, the models were actually more efficient compared to the EM, CD, and BRT models in terms of run time execution.
Table V.
The execution time of EM, BRT, CD, SMC, AE+SMC, STAE+SMC, SAE+SMC, TSAE+SMC, CNN+SMC, and SSAE+SMC models on the training set and the corresponding run time when evaluated on a test image of dimensions 2200 × 2200 pixels
| Model | Training Time | Detection Time (in seconds) |
|---|---|---|
| EM | – | 820 |
| BRT | – | 310 |
| CD | – | 132 |
| SMC | 50 min | 34 |
| AE+SMC | 1.24 hour | 45 |
| SAE+SMC | 1.36 hour | 45 |
| STAE+SMC | 2.11 hour | 45 |
| TSAE+SMC | 3.64 hour | 45 |
| CNN+SMC | 4.53 hour | 122 |
| SSAE+SMC | 2.15 hour | 45 |
VI. Concluding Remarks
In this paper, a Stacked Sparse Autoencoder framework is presented for automated nuclei detection on breast cancer histopathology. The Stacked Sparse Autoencoder model can capture high-level feature representations of pixel intensity in an unsupervised manner. These high-level features enable the classifier to work very efficiently for detecting multiple nuclei from a large cohort of histopathological images. To show the effectiveness of the proposed framework, we compared “deep” structure (Stacked Sparse Autoencoder and Stacked Autoencoder) over “shallow” structure (Sparse Autoencoder and general Autoencoder) in representing high-level features from pixel intensities. The efficiency of sparsity constraint on hidden layers is also shown. We further compared Stacked Sparse Autoencoder plus Softmax Classifier with Expectation-Maximization, Blue Ratio Thresholding, Color Convolution, Convolutional Neural Network based nuclei detection method, which are some of the popular nuclei detection models. Moreover, we qualitatively evaluate the sensitivity of parameters of sliding window for both computational efficiency and detection accuracy. Both qualitative and quantitative evaluation results show that Stacked Sparse Autoencoder plus Softmax Classifier outperforms a number of different state of the art methods in terms of the nuclear detection accuracy. Finally, the presented nuclei detection framework can provide accurate seed points or vertices for developing cell-by-cell graph features that can enable characterization of cellular topology features on tumor histology [2]. In future work, we will integrate the Stacked Sparse Autoencoder framework with cell-graph based feature extraction methods to better characterize breast histopathological images.
Fig. 4.

The visualization of learned high-level features of input pixel intensities with three layers SAE. (a) shows the learned feature representation in the first hidden layer (with 400(20 × 20) units). The learned high-level feature representation in the second hidden layer (with 225 (15 × 15) units) and third hidden layer (with 100 (10 × 10) units) is shown in (b) and (c), respectively. As expected, (a) shows detailed boundary features of nuclei and other tissue while (b) and (c) show high-level features of nuclei. Also, the overfitting problem is presented in (c) when learning high-level features of nuclei in the third layer.
Table II.
Enumeration of the symbols used in the paper
| Symbol | Description | Symbol | Description | ||
|---|---|---|---|---|---|
|
| |||||
| EM | Expectation-Maximum Algorithm | BRT | Blue Ratio Thresholding | ||
| SMC | Softmax Classifier | CD | Color Deconvolution | ||
| SAE+SMC | Single layer Sparse Autoencoder plus Softmax Classifier | AE+SMC | Single layer Autoencoder plus Softmax Classifier | ||
| TSAE+SMC | Three layer Sparse Autoencoder plus Softmax Classifier | STAE+SMC | Stacked Autoencoder plus Softmax Classifier | ||
| CNN | Convolutional Neural Network | BC | Breast Cancer | ||
| ER+ | estrogen receptor-positive | LN- | lymph node-negative | ||
| k,N,dx ,dh,l, nl,sl, ω, τ | positive integers | k | the kth patch | ||
| N | number of entire training patches | l | lth layer (l ∈ {0, 1, 2, … , nl}) | ||
| X = (x(1),x(2), … ,x(N))T | set of entire training patches | Y = (y(1),y(2), … , y(N))T | label set of training patches | ||
| x(k) | vector of intensity for kth patch | y(k) | the label of kth patch | ||
| nl | number of layers | sl | number of neurons in layer l | ||
| ω | number of rows (columns) of input image patches | τ | number of channels of input patches input layer of network | ||
| 0th layer | |||||
| dx | number of pixels (or input units) in training image patch (or input layer) |
|
number of hidden units in lth layer ith element of vector hl(k) at layer l | ||
|
|
feature vector at layer l |
|
or kth patch or the ith unit in the lth softmax classifier function | ||
|
| |||||
| θ | parameter set | hidden layer for kth patch | |||
| x̂ | reconstruction (decoder) of input x | xˇ | the encode of x | ||
| dθ̂(·) | decoder with parameter θ̂ | eθˇ(·) | encoder with parameter θˇ | ||
| W(l) | weight matrix of lth layer | bh (bx) | bias of hidden (input) layer | ||
|
|
connection between ith neuron in layer l – 1 and jth neuron in layer l |
|
image patch k being a dx dimensional vector of real numbers | ||
| LSAE (θ) | cost function of SAE | J(W(3)) | cost function of softmax classifier | ||
| ‖·‖2 | L2 norm | KL(·‖·) | Kullback-Leibler (KL) divergence | ||
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Nos. 61273259,61272223); Six Major Talents Summit of Jiangsu Province (No. 2013-XXRJ-019), and the Natural Science Foundation of Jiangsu Province of China (No. BK20141482); the National Cancer Institute of the National Institutes of Health under award numbers R01CA136535-01, R01CA140772-01, R21CA167811-01, R21CA179327-01; the National Institute of Diabetes and Digestive and Kidney Diseases under award number R01DK098503-02, the DOD Prostate Cancer Synergistic Idea Development Award (PC120857); the DOD Lung Cancer Idea Development New Investigator Award (LC130463), the Ohio Third Frontier Technology development Grant, the CTSC Coulter Annual Pilot Grant, and the Wallace H. Coulter Foundation Program in the Department of Biomedical Engineering at Case Western Reserve University. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
APPENDIX
Brief Review of Sparse Autoencoder
Sparse Autoencoder (SAE) is an unsupervised feature learning algorithm which aims to learn a high-level structured representation of nuclei or non-nuclei patches. The architecture of SAE for high-level feature learning of nuclei structures is shown in Figure 1. In general, the input layer of the SAE consists of an encoder which transforms input image patch x into the corresponding representation h, and the hidden layer h can be seen as a new feature representation of the input image patch. The output layer is effectively a decoder which is trained to reconstruct an approximation x̂ of the input image patch from the hidden representation h. Basically, the purpose of training an autoencoder is to find optimal parameters by minimizing the discrepancy between input x and its reconstruction x̂. By applying the back-propagation algorithm, the autoencoder tries to decrease the discrepancy between input and reconstruction as much as possible by learning an encoder and decoder networks (See Figure 1), which yields a set of weights W and biases b.
The cost function of an Sparse Autoencoder (SAE) comprises three terms as follows [39]:
| (7) |
The first term is an average sum-of-squares error term which describes the discrepancy between input x(k) and reconstruction x̂(k) over the entire data. In the second term, n is the number of units in hidden layer, and the index j is summing over the hidden units in the network. KL(ρ‖ρ̂j) is the Kullback-Leibler (KL) divergence between ρ̂j, the average activation (averaged over the training set) of hidden unit j, and desired activations ρ. The third term is a weight decay term which tends to decrease the magnitude of the weight, and helps prevent overfitting. Here
| (8) |
where nl is the number of layers and sl is the number of neurons in layer l. represents the connection between ith neuron in layer l − 1 and jth neuron in layer l.
Contributor Information
Jun Xu, the Jiangsu Key Laboratory of Big Data Analysis Technique and CICAEET, Nanjing University of Information Science and Technology, Nanjing 210044, China.
Lei Xiang, the Jiangsu Key Laboratory of Big Data Analysis Technique and CICAEET, Nanjing University of Information Science and Technology, Nanjing 210044, China.
Qingshan Liu, the Jiangsu Key Laboratory of Big Data Analysis Technique and CICAEET, Nanjing University of Information Science and Technology, Nanjing 210044, China.
Hannah Gilmore, Department of Pathology-Anatomic, University Hospitals Case Medical Center, Case Western Reserve University, OH 44106-7207, USA.
Jianzhong Wu, the Jiangsu Cancer Hospital, Nanjing 210000, China.
Jinghai Tang, the Jiangsu Cancer Hospital, Nanjing 210000, China.
Anant Madabhushi, the Department of Biomedical Engineering, Case Western Reserve University, OH 44106-7207, USA.
References
- 1.Gurcan MN, Boucheron LE, Can A, Madabhushi A, Rajpoot NM, Yener B. Histopathological image analysis: A review. Biomedical Engineering, IEEE Reviews. 2009;2:147–171. doi: 10.1109/RBME.2009.2034865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Basavanhally A, Feldman MD, Shih N, Mies C, Tomaszewski JE, Ganesan S, Madabhushi A. Multi-field-of-view strategy for image-based outcome prediction of multi-parametric estrogen receptor-positive breast cancer histopathology: Comparison to oncotype dx. J Pathol Inform. 2011;2 doi: 10.4103/2153-3539.92027. 01/2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mahmoud SMA, Paish EC, Powe DG, Macmillan RD, Grainge MJ, Lee AHS, Ellis IO, Green AR. Tumor-infiltrating cd8+ lymphocytes predict clinical outcome in breast cancer. Journal of Clinical Oncology. 2011;29(15):1949–1955. doi: 10.1200/JCO.2010.30.5037. [DOI] [PubMed] [Google Scholar]
- 4.Lewis J, Ali S, Luo J, Thorstad WL, Madabhushi A. A quantitative histomorphometric classifier (quhbic) identifies aggressive versus indolent p16-positive oropharyngeal squamous cell carcinoma. The American Journal of Surgical Pathology. 2014;38(1):128C137. doi: 10.1097/PAS.0000000000000086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Veta M, Pluim JPW, van Diest PJ, Viergever MA. Breast cancer histopathology image analysis: A review. Biomedical Engineering, IEEE Transactions. 2014 May;61(5):1400–1411. doi: 10.1109/TBME.2014.2303852. [DOI] [PubMed] [Google Scholar]
- 6.Irshad H, Veillard A, Roux L, Racoceanu D. Methods for nuclei detection, segmentation and classification in digital histopathology: A review. current status and future potential. Biomedical Engineering, IEEE Reviews. (99):1–1. 2013. doi: 10.1109/RBME.2013.2295804. [DOI] [PubMed] [Google Scholar]
- 7.Chang H, Han J, Borowsky A, Loss L, Gray JW, Spellman PT, Parvin B. Invariant delineation of nuclear architecture in glioblastoma multiforme for clinical and molecular association. Medical Imaging, IEEE Transactions. 2013 Apr;32(4):670–682. doi: 10.1109/TMI.2012.2231420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Irshad H, Jalali S, Roux L, Racoceanu D, Hwee LJ, Le Naour G, Capron F. Automated mitosis detection using texture, sift features and hmax biologically inspired approach. Journal of Pathology informatics. 2013;4(Suppl) doi: 10.4103/2153-3539.109870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cataldo SD, Ficarra E, Acquaviva A, Macii E. Automated segmentation of tissue images for computerized ihc analysis. Computer Methods and Programs in Biomedicine. 2010;100(1):1–15. doi: 10.1016/j.cmpb.2010.02.002. [DOI] [PubMed] [Google Scholar]
- 10.Oberlaender M, Dercksen VJ, Egger R, Gensel R, Sakmann B, Hege H. Automated three-dimensional detection and counting of neuron somata. Journal of Neuroscience Methods. 2009;180(1):147–160. doi: 10.1016/j.jneumeth.2009.03.008. [DOI] [PubMed] [Google Scholar]
- 11.Nielsen B, Albregtsen F, Danielsen HE. Automatic segmentation of cell nuclei in feulgen-stained histological sections of prostate cancer and quantitative evaluation of segmentation results. Cytometry Part A. 2012;81(7):588–601. doi: 10.1002/cyto.a.22068. [DOI] [PubMed] [Google Scholar]
- 12.Ruifrok AC, Johnston DA. Quantification of histochemical staining by color deconvolution. Analytical and quantitative cytology and histology/the International Academy of Cytology [and] American Society of Cytology. 2001;23(4):291–299. [PubMed] [Google Scholar]
- 13.Vink JP, Van Leeuwen MB, Van Deurzen CHM, De Haan G. Efficient nucleus detector in histopathology images. Journal of microscopy. 2013;249(2):124–135. doi: 10.1111/jmi.12001. [DOI] [PubMed] [Google Scholar]
- 14.Petushi S, Garcia FU, Haber MM, Katsinis C, Tozeren A. Large-scale computations on histology images reveal grade-differentiating parameters for breast cancer. BMC Medical Imaging. 2006;614(1) doi: 10.1186/1471-2342-6-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fatakdawala H, Xu J, Basavanhally A, Bhanot G, Ganesan S, Feldman M, Tomaszewski JE, Madabhushi A. Expectation maximization-driven geodesic active contour with overlap resolution (emagacor): Application to lymphocyte segmentation on breast cancer histopathology. Biomedical Engineering, IEEE Transactions. 2010;57(7):1676–1689. doi: 10.1109/TBME.2010.2041232. [DOI] [PubMed] [Google Scholar]
- 16.Byun J, Verardo MR, Sumengen B, Lewis GP, Manjunath BS, Fisher SK. Automated tool for the detection of cell nuclei in digital microscopic images: application to retinal images. Mol Vis. 2006;12:949–960. [PubMed] [Google Scholar]
- 17.Al-Kofahi Y, Lassoued W, Lee W, Roysam B. Improved automatic detection and segmentation of cell nuclei in histopathology images. Biomedical Engineering, IEEE Transactions. 2010 Apr;57(4):841–852. doi: 10.1109/TBME.2009.2035102. [DOI] [PubMed] [Google Scholar]
- 18.Parvin B, Yang Q, Han J, Chang H, Rydberg B, Barcellos-Hoff MH. Iterative voting for inference of structural saliency and characterization of subcellular events. Image Processing, IEEE Transactions. 2007 Mar;16(3):615–623. doi: 10.1109/tip.2007.891154. [DOI] [PubMed] [Google Scholar]
- 19.Qi X, Xing Y, Foran DJ, Yang L. Robust segmentation of overlapping cells in histopathology specimens using parallel seed detection and repulsive level set. Biomedical Engineering, IEEE Transactions. 2012 Mar;59(3):754–765. doi: 10.1109/TBME.2011.2179298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schmitt O, Hasse M. Radial symmetries based decomposition of cell clusters in binary and gray level images. Pattern Recognition. 2008;41(6):1905–1923. [Google Scholar]
- 21.Wang H, Xing F, Su H, Stromberg A, Yang L. Novel image markers for non-small cell lung cancer classification and survival prediction. BMC Bioinformatics. 2014;15(1):310. doi: 10.1186/1471-2105-15-310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Xing F, Su H, Neltner J, Yang L. Automatic ki-67 counting using robust cell detection and online dictionary learning. Biomedical Engineering, IEEE Transactions. 2014 Mar;61(3):859–870. doi: 10.1109/TBME.2013.2291703. [DOI] [PubMed] [Google Scholar]
- 23.Jung C, Kim C. Segmenting clustered nuclei using h-minima transform-based marker extraction and contour parameterization. Biomedical Engineering, IEEE Transactions. 2010 Oct;57(10):2600–2604. doi: 10.1109/TBME.2010.2060336. [DOI] [PubMed] [Google Scholar]
- 24.Yan Y, Zhou X, Shah M, Wong STC. Automatic segmentation of high-throughput rnai fluorescent cellular images. Information Technology in Biomedicine, IEEE Transactions. 2008 Jan;12(1):109–117. doi: 10.1109/TITB.2007.898006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ali S, Madabhushi A. An integrated region-, boundary-, shape-based activecontour for multiple object overlap resolution in histological imagery. IEEE Trans Med Imaging. 2012 Jul;31(7):1448–1460. doi: 10.1109/TMI.2012.2190089. [DOI] [PubMed] [Google Scholar]
- 26.Yan C, Li A, Zhang B, Ding W, Luo Q, Gong H. Automated and accurate detection of soma location and surface morphology in large-scale 3d neuron images. PLoS ONE. 2013;8(4):e62579–04. doi: 10.1371/journal.pone.0062579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Esmaeilsabzali H, Sakaki K, Dechev N, Burke R, Park EJ. Machine vision-based localization of nucleic and cytoplasmic injection sites on low-contrast adherent cells. Medical & Biological Engineering & Computing. 2012;50(1):11–21. doi: 10.1007/s11517-011-0831-2. [DOI] [PubMed] [Google Scholar]
- 28.Filipczuk P, Fevens T, Krzyzak A, Monczak R. Computer-aided breast cancer diagnosis based on the analysis of cytological images of fine needle biopsies. Medical Imaging, IEEE Transactions. 2013 Dec;32(12):2169–2178. doi: 10.1109/TMI.2013.2275151. [DOI] [PubMed] [Google Scholar]
- 29.Basavanhally A, Ganesan S, Agner S, Monaco JP, Feldman MD, Tomaszewski JE, Bhanot G, Madabhushi A. Computerized image-based detection and grading of lymphocytic infiltration in her2+ breast cancer histopathology. Biomedical Engineering, IEEE Transactions. 2010;57(3):642–653. doi: 10.1109/TBME.2009.2035305. [DOI] [PubMed] [Google Scholar]
- 30.Bernardis E, Yu SX. Pop out many small structures from a very large microscopic image. Medical Image Analysis; Special Issue on the 2010 Conference on Medical Image Computing and Computer-Assisted Intervention; 2011. pp. 690–707. [DOI] [PubMed] [Google Scholar]
- 31.Faustino GM, Gattass M, de Lucena CJP, Campos PB, Rehen SK. A graph-mining algorithm for automatic detection and counting of embryonic stem cells in fluorescence microscopy images. Integrated Computer-Aided Engineering. 2011;18(1):91–106. [Google Scholar]
- 32.Li G, Liu T, Nie J, Guo L, Malicki J, Mara A, Holley SA, Xia W, Wong STC. Detection of blob objects in microscopic zebrafish images based on gradient vector diffusion. Cytometry Part A. 2007;71(10):835–845. doi: 10.1002/cyto.a.20436. [DOI] [PubMed] [Google Scholar]
- 33.Liu T, Li G, Nie J, Tarokh A, Zhou X, Guo L, Malicki J, Xia W, Wong STC. An automated method for cell detection in zebrafish. Neuroinformatics. 2008;6(1):5–21. doi: 10.1007/s12021-007-9005-7. [DOI] [PubMed] [Google Scholar]
- 34.Cruz-Roa A, Arevalo Ovalle J, Madabhushi A, Gonzalez Osorio F. A deep learning architecture for image representation, visual interpretability and automated basal-cell carcinoma cancer detection. In: Mori Kensaku, Sakuma Ichiro, Sato Yoshinobu, Barillot Christian, Navab Nassir., editors. Lecture Notes in Computer Science; MICCAI 2013; Springer Berlin Heidelberg; 2013. pp. 403–410. [DOI] [PubMed] [Google Scholar]
- 35.Bengio Y, Courville A, Vincent P. Representation learning: A review and new perspectives. Pattern Analysis and Machine Intelligence, IEEE Transactions. 2013;35(8):1798–1828. doi: 10.1109/TPAMI.2013.50. [DOI] [PubMed] [Google Scholar]
- 36.Hinton GE, Salakhutdinov R. Reducing the dimensionality of data with neural networks. Science. 2006;313(5786):504–507. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- 37.Xu J, Xiang L, Hang R, Wu J. Stacked sparse autoencoder (ssae) based framework for nuclei patch classification on breast cancer histopathology. Biomedical Imaging: From Nano to Macro, 2014. ISBI ’14; IEEE International Symposium; 2014. [Google Scholar]
- 38.Meyer F. Topographic distance and watershed lines. Mathematical Morphology and its Applications to Signal Processing. 1994;38(1):113–125. Signal Processing. [Google Scholar]
- 39.Ng A. Sparse autoencoder. CS294A Lecture notes. 2011:72. [Google Scholar]
- 40.Jia Y, Shelhamer E, Donahue J, Karayev S, Long J, Girshick R, Guadarrama S, Darrell T. Caffe: Convolutional architecture for fast feature embedding. arXiv preprint arXiv:1408.5093. 2014 [Google Scholar]
- 41.Vincent P, Larochelle H, Lajoie I, Bengio Y, Manzagol P. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J Mach Learn Res. 2010 Dec;11:3371–3408. [Google Scholar]
- 42.Vincent P, Larochelle H, Bengio Y, Manzagol P. Extracting and composing robust features with denoising autoencoders. Proceedings of the 25th International Conference on Machine Learning; New York, NY, USA. 2008. pp. 1096–1103. ICML ’08, ACM. [Google Scholar]
- 43.Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. J Mach Learn Res. 2014 Jan;15(1):1929–1958. [Google Scholar]


