Application of back-propagation artificial neural network and curve estimation in pharmacokinetics of losartan in rabbit

Abstract

In order to develop pharmacokinetic model, a well-known multilayer feed-forward algorithm back-propagation artificial neural networks (BP-ANN) was applied to the pharmacokinetics of losartan in rabbit. The plasma concentrations of losartan in twelve rabbits, which were divided into two groups and given losartan 2 mg/kg by intravenous (Iv) and intragastrical (Ig) administration, were determined by LC-MS. The BP-ANN model included one input layer, hidden layers, and one output layer was constructed and compared with curve estimation based on the time-concentration data of losartan. The results showed the BP-ANN model had high goodness of fit index and good coherence (R > 0.99) between forecasted concentration and measured concentration both in Iv and Ig administration. The residuals of each concentrations generated by BP-ANN model were all smaller than Curve estimation. The pharmacokinetic result showed there was no significant difference between measured and simulated pharmacokinetic parameters including AUC_(0-t), AUC_(0-∞), MRT_(0-t), MRT_(0-∞), T_1/2 V and C_max (P > 0.05). In conclusion, the BP-ANN model has remarkably accurate predictions ability, which better than Curve estimation, and can be used as a utility tool in pharmacokinetic experiment.

Introduction

Artificial neural network (ANN), one of widely used statistical learning algorithm in machine learning and cognitive science, is inspired by biological neural networks and basically consists of several non-linear processing units which called neurons or nodes [1]. These units connected by some parameters are in a massive parallel architecture. For example, the first unit has input neurons which send data via synapses (or neurons or nodes) to the second unit of neurons, and then via more synapses to the third unit of output neurons. More complex ANN models have more units of neurons and capture complex and non-linear relationships from large amounts of data and acquire the knowledge through a learning process. It has applied to broad categories include system identification and control [2], quantum chemistry [3], pattern recognition [4]. In medical areas, it has been used to diagnose cancers [5], predict mortality risk of liver failure [6], predict pharmaceutical properties of dosage forms, concentration of antibiotics and risk factors of some diseases [7]. However, it is rare to find its application in drug metabolism, especially in pharmacokinetics study.

Pharmacokinetics, a fundamental scientific discipline, provides a mathematical basis to assess the time course of drugs and their effects in the body [8]. Application of pharmacokinetic values to individualize pharmacotherapy can help doctors adjust dosage accurately and rapidly [9]. Losartan is an angiotensin II receptor antagonist drug mainly used to treat hypertension. It also used as a probe drug to evaluate metabolic ability of CYP2C9 in vivo and vitro [10,11]. In order to obtain its pharmacokinetic character in clinical and laboratory works, the concentration of losartan should be determined frequently. Generally, 10 to 12 specimens should be collected in a pharmacokinetic experiment [12]. The more specimens are collected, the better are the pharmacokinetic results. These series of specimens should be taken at corresponding time, especially the sampling time and sampling frequency must be consistent. Therefore, development of pharmacokinetic model of losartan will be useful in drug metabolism studies, and this pharmacokinetic model can be used for reference by other drugs.

In this study, an ANN model of losartan was developed by back-propagation learning algorithm, and the ability of fitting accuracy of ANN in pharmacokinetics were compared with the simulation results of curve regression.

Materials and methods

Chemicals and animals

Losartan (> 98%) and the internal standard atropine (IS) purchased from Sigma-Aldrich Company (St. Louis, MO, USA). HPLC grade acetonitrile and methanol purchased from Merck Company (Darmstadt, Germany). A total of 12 Japanese male rabbits weighed 2.1 ± 0.15 kg were obtained from Wenzhou Medical College Laboratory Animal Center (Wenzhou, China), and housed under controlled conditions (25 ± 1°C, RH 55 ± 10%) with a natural light-dark cycle. All experimental procedures were conducted according to the Institutional Animal Care guidelines and approved ethically by the Administration Committee of Experimental Animals, Laboratory Animal Center of Wenzhou Medical University, Zhejiang Province, China.

Instrumentations

Agilent 1200 Series liquid chromatograph equipped with a quaternary pump, a degasser, an autosampler, a thermostatted column compartment, and a Bruker Esquire HCT mass spectrometer (Bruker Technologies, Bremen, Germany) equipped with an electrospray ion source. An ASUA laptop computer with an Intel (R) Core (TM) i5-2430M processor 2.40 GHz, Random Access Memory 2 GB and a Windows 7 operating system.

Pharmacokinetic study

Twelve rabbits were divided by randomization in 2 groups (n=6), group Iv and group Ig. Group IV was administered losartan 2 mg/kg intravenously, Group Ig administered losartan 2 mg/kg intragastrically (Ig). Blood samples (0.5 mL) were directly collected into the heparinized tube from the marginal ear veins at 5, 15, 30, 45, 60, 90, 120, 180, 240, 300, 360, 480, 600, 720 after administration. After centrifugation at 3000 × g for 5 min, plasma was separated and determined by the developed LC-MS method.

The determination of target ions were performed in SIM mode, (m/z 423.1 for losartan and m/z 338 for IS) and positive ion electrospray ionization interface. Chromatographic separation was achieved on an Agilent Zorbax SB-C18 column (150 mm × 2.1 mm, 5 μm particle) at 30°C. Mobile phase was a mixture of mobile phase A (0.1% formic acid in water) and mobile phase B (acetonitrile), setting flow rate at 0.4 mL/min. The gradient elution programme was conducted. The validation of determination method was according to previous literature [13].

Bp-ANN modeling

The back-propagation artificial neural network (Bp-ANN), a kind of multilayer feed forward neural network was applied. The main characteristics of BP-ANN are the signals transmit forward and the errors transfer reversely, which can be used to develop a non-linear ANN model of a system. The structure of BP-ANN includes one input layer, hidden layers, and an output layer. The representation of structural drawing is illustrated in Figure 1.

Figure 1.

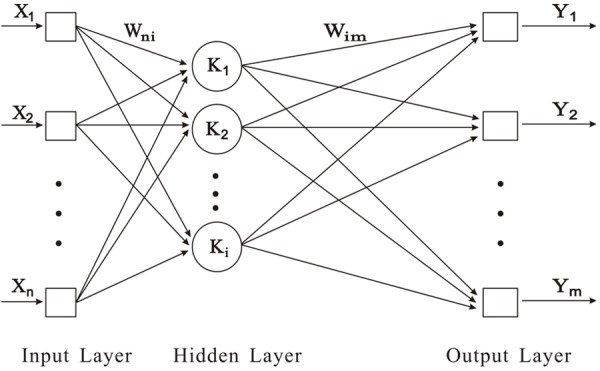
Topology of BP Artificial Neural Network, X₁, X₂,…X_n are the input values, Y₁, Y₂,…Y_m are the predictive values, Wni and Wim are the weights. The input signals transmit from the input layer to the hidden layers and then to the output layer.

The node numbers of hidden layer were based on the formula of m = √(n + l) + a, where m is the number of the nodes in the hidden layer, and n is the number of nodes in the input layer, l is the number of nodes in the output layer, a is a constant from 1 to 10 [12]. The input layer included 13 neurons (sampling times), and the plasma concentrations were selected as the output data. The transfer function of the hidden layers nodes was tansig, and the transfer function of the output layer nodes was purelin. When all of the parameters of BP-ANN were completed, it was performed in Matlab R2011a.

Regression modeling and statistical analysis

In order to assess the accuracy of BP-ANN model, eleven methods of curve estimation, which included logarithmic, inverse, quadratic, cubic, compound, power, S, growth, exponential, logistic, were developed by using SPSS statistical software, version 16.0. The sampling times were selected as independent variable, and the plasma concentrations were selected as dependent variable. The results of regression modeling were assessed according to fitted parameters which analyzed by ANOVA.

The results of predicted concentrations at each time points generated by BP-ANN and curve estimation were compared with the real measured concentration by One-way ANOVA analysis. The residuals of each concentration were calculated and analyzed.

Results

BP artificial neural networks

After the model was trained and well performed in two groups, the good fitness was indicated by following four values: mean square error (MSE), magnitude of the gradient, the number of validation checks, correlation coefficient. The mean squared error is the default performance function for feed forward the average squared error between the network outputs and the target [14]. The correlation coefficient was used to assess the relationship between the outputs of network and the targets [15]. The results showed MSE and gradient was 3.12 × 10^-12, 1.11 × 10^-4 at epoch 118 in Ig-group and 1.05 × 10^-12, 9.79 × 10^-5 at epoch 51 in Iv-group. The correlation coefficients of two groups were both > 0.999. That indicated BP-ANN performed well in pharmacokinetics of Ig and Iv administration, and Iv pharmacokinetics was more high accuracy than Ig pharmacokinetics.

Curve estimation model

The model summaries of curve estimation were showed in Table 1. The results indicated the best optimal model for Iv and Ig administration was Logarithmic and Cubic, which both have statistical significance (P < 0.05). The determinant coefficient of Logarithmic curve estimation for Iv administration was higher than Ig administration, which indicated Iv administration was suitable for fitting.

Table 1.

The model summary of losartan after 1 mg/kg Ig and Iv administration in rabbits

Equation	Ig administration		Iv administration
	R2	P	R2	P
Linear	0.20 ± 0.10	0.17 ± 0.12	0.66 ± 0.09	< 0.01
Logarithmic	0.04 ± 0.04	0.55 ± 0.21	0.96 ± 0.02	< 0.01
Inverse	0.29 ± 0.03	0.06 ± 0.02	0.60 ± 0.12	< 0.01
Quadratic	0.43 ± 0.02	0.06 ± 0.01	0.85 ± 0.08	< 0.01
Cubic	0.77 ± 0.10	< 0.05	0.92 ± 0.05	< 0.01
Compound	0.07 ± 0.05	0.45 ± 0.19	0.89 ± 0.08	< 0.01
Power	0.11 ± 0.06	0.31 ± 0.15	0.82 ± 0.08	< 0.01
S	0.65 ± 0.10	< 0.01	0.35 ± 0.10	< 0.05
Growth	0.07 ± 0.05	0.45 ± 0.19	0.89 ± 0.08	< 0.01
Exponential	0.07 ± 0.05	0.45 ± 0.19	0.89 ± 0.08	< 0.01
Logistic	0.07 ± 0.05	0.45 ± 0.19	0.89 ± 0.08	< 0.01

Comparison of Bp-ANN and curve estimation

The predicted concentrations generated by Logarithmic and Cubic model were compared with Bp-ANN model. Based on the developed BP-ANN, Logarithmic and Cubic model, the predicted concentrations of Ig and Iv administration were generated. Their concentration-time curves were showed in Figure 2. The results indicated that Bp-ANN model was obviously better than Cubic model in Ig administration. In Iv administration, the predicted concentrations of losartan were consistent with the measured concentration both in Bp-ANN and Logarithmic model. It seemed there was no obvious difference between Bp-ANN and Logarithmic model. However, the residuals of predicted concentrations were showed Bp-ANN model was better than Logarithmic model, as BP-ANN had smaller residuals (Figure 3).

Figure 2.

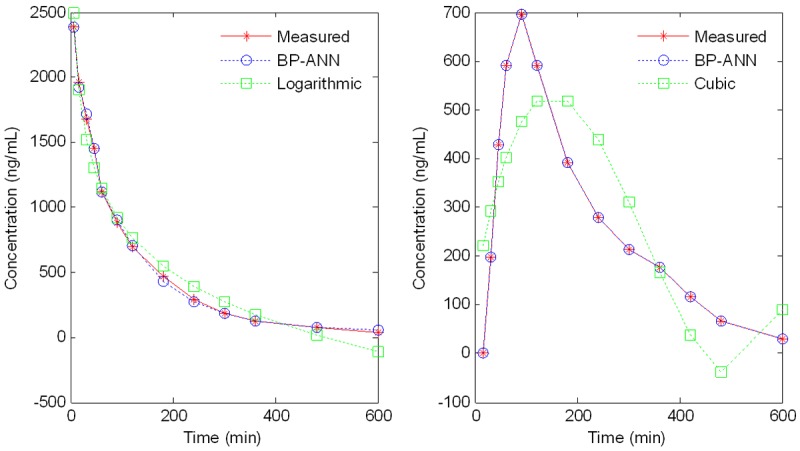
The measured (*) and predicted concentrations-time curve of BP-ANN (o) and Curve estimation (□) after Ig and Iv administration.

Figure 3.

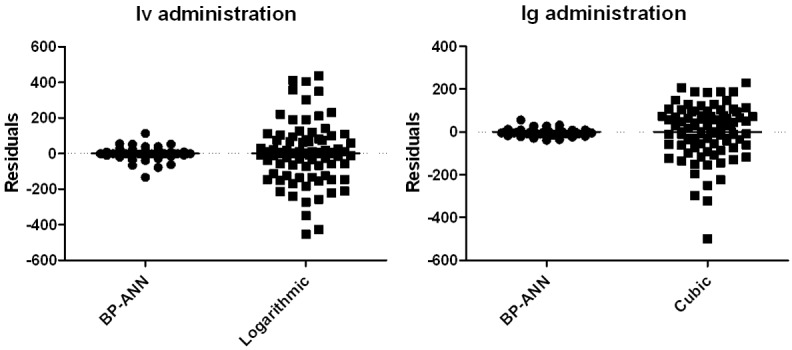
The residuals of each concentrations of BP-ANN and Curve estimation after Ig and Iv administration.

Pharmacokinetic parameters

The measured and simulated pharmacokinetic parameters of losartan by Ig and Iv administration were all calculated in two-compartmental model. The pharmacokinetic results showed the AUC_(0-t), AUC_(0-∞), MRT_(0-t), MRT_(0-∞), T_1/2, V and C_max calculated by the concentrations in measured data were almost equal to simulated data of BP-ANN. whatever it was Ig or Iv administration. There was no significant difference (P > 0.05) between measured and simulated data, the results of pharmacokinetic parameters were listed in Table 2.

Table 2.

The measured and predicted pharmacokinetic parameters of losartan Ig administration 2 mg/kg in rabbits (Mean ± SD)

		Ig administration		Iv administration
Parameters		Measured	Predicted	Predicted	Predicted
AUC(0-t)	μg/mL*min	148.83 ± 13.63	148.88 ± 13.70	257.94 ± 46.84	257.62 ± 47.07
AUC(0-∞)	μg/mL*min	152.48 ± 14.35	152.53 ± 14.42	266.02 ± 54.34	265.44 ± 54.30
MRT(0-t)	min	196.34 ± 14.38	196.36 ± 14.38	125.10 ± 10.32	124.70 ± 10.74
MRT(0-∞)	min	209.16 ± 21.63	209.17 ± 21.62	143.84 ± 23.99	142.90 ± 24.96
t1/2	min	88.66 ± 20.32	88.66 ± 20.32	127.82 ± 35.90	126.27 ± 36.26
Tmax	min	90.00 ± 0.00	95.00 ± 12.25	5.00 ± 0.00	5.00 ± 0.00
CL/F	L/min/kg	0.01	0.01	0.01 ± 0.00	0.01 ± 0.00
V/F	L/kg	1.67 ± 0.31	1.67 ± 0.31	1.38 ± 0.20	1.37 ± 0.23
Cmax	μg/mL	0.69 ± 0.14	0.68 ± 0.14	2.38 ± 0.48	2.38 ± 0.48

Discussion

The BP-ANN method was based on the standard back-propagation algorithm. Its principle as follows: after input signal is presented to the network, the consequent error vector across output units will be calculated and back-propagated to update the weights [16,17]. The next signal is then presented and the process repeated. BP-ANN has integrated system, explicit algorithmic process, data identification and simulation function, and also owns the excellent ability to solve nonlinear problem. Generally, the structure of BP-ANN is determined by the number of hidden layers, neural and activated form of the function of neurons [18]. The learning process continues until the desired output signals is less than a preset value.

In this study, three layers BP network with tansig function as excitation function was developed, the learning rate was 0.05, as a large learning rate may cause the problem of oscillation. The results showed the BP-ANN had high goodness of fit index according to this kind of experiment’s setting. There was good coherence between forecasted concentration with real measured concentration both in Iv and Ig administration, One-way ANOVA showed they were no statistical difference (P > 0.05). Although, the logarithmic algorithm also obtained high goodness of fit index in Iv administration, the BP-ANN was still better than it, because of its smaller residuals. In Ig administration, which has more complicated time-concentration curve than Iv administration, the advantage of BP-ANN was fully embedded. The Figure 2 showed the BP-ANN model reached high accuracy distinctly.

We also calculated the pharmacokinetic parameters according to the predicted concentration generated by BP-ANN model. Equally unsurprisingly, the results showed that AUC_(0-t), T_max, MRT_(0-t), MRT_(0-∞), T_1/2, V and C_max of BP-ANN model were almost equal to the measured, there was no significant difference (P > 0.05). Therefore, it’s obviously the BP-ANN model was better than curve estimation of SPSS. More importantly, we can predict the drug concentration at any time point during the pharmacokinetic study by BP-ANN. If some of time points were lost in experiment, we can predict them by BP-ANN model.

Conclusion

In this paper, a BP-ANN model was used to simulate the concentration of losartan in rabbit after Ig and Iv administration. The results showed that BP-ANN has remarkably accurate predictions ability which better than curve estimation of SPSS. BP-ANN can be used as a utility tool to improve the accuracy and convenience of pharmacokinetic experiment.

Disclosure of conflict of interest

None.