Reanalysis of Earth rotation observations reconciles them with globally averaged sea-level change in the 20th century.
Keywords: Climate change, Earth sciences, Earth rotation, sea level
Abstract
In 2002, Munk defined an important enigma of 20th century global mean sea-level (GMSL) rise that has yet to be resolved. First, he listed three canonical observations related to Earth’s rotation [(i) the slowing of Earth’s rotation rate over the last three millennia inferred from ancient eclipse observations, and changes in the (ii) amplitude and (iii) orientation of Earth’s rotation vector over the last century estimated from geodetic and astronomic measurements] and argued that they could all be fit by a model of ongoing glacial isostatic adjustment (GIA) associated with the last ice age. Second, he demonstrated that prevailing estimates of the 20th century GMSL rise (~1.5 to 2.0 mm/year), after correction for the maximum signal from ocean thermal expansion, implied mass flux from ice sheets and glaciers at a level that would grossly misfit the residual GIA-corrected observations of Earth’s rotation. We demonstrate that the combination of lower estimates of the 20th century GMSL rise (up to 1990) improved modeling of the GIA process and that the correction of the eclipse record for a signal due to angular momentum exchange between the fluid outer core and the mantle reconciles all three Earth rotation observations. This resolution adds confidence to recent estimates of individual contributions to 20th century sea-level change and to projections of GMSL rise to the end of the 21st century based on them.
INTRODUCTION
Earth rotation observations
Munk’s enigma of 20th century sea-level rise (1) is based on three Earth rotation observations that are summarized in Fig. 1. First, analysis of Babylonian, Chinese, Arab, and Greek eclipse observations (2–5) suggests a slowing of Earth’s rotation rate sufficient to produce a clock error [defined as the difference between the time of occurrence of an eclipse, which is measured in terrestrial time (a theoretically invariant time scale), and universal time, which is fixed to Earth’s rotation at 1820 C.E.] of 16,000 s or ~4.5 hours since 500 B.C.E. (vertical bars, Fig. 1A). Correction of this record for tidal dissipation (6) yields a residual nontidal acceleration of Earth’s rotation that integrates into a clock error of ~6000 s (3–5) over the same period (difference between the observations and the green line, Fig. 1A). Although this clock error is characterized by decadal to millennial time scale fluctuations (with the former being evident in astronomic measurements over the past two centuries), the Munk analysis (1) and the present study are concerned only with the very long-term trend in the time series.
Fig. 1. Munk’s enigma of global sea-level rise (1).
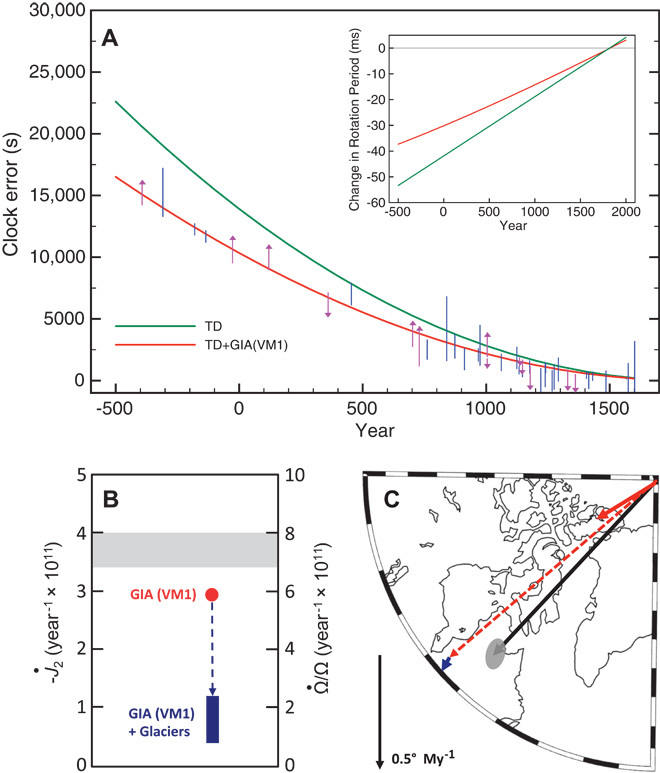
(A) Clock error from 500 B.C.E. to 1600 C.E. inferred from untimed partial solar eclipses (magenta; arrows reflect allowable bounds) and untimed total and annular solar eclipses (blue lines) listed in Appendix B of Stephenson (4) [see also Stephenson and Morrison (3)]. The green line represents the clock error associated with the slowing of Earth’s rotation due to tidal dissipation (TD) (3, 6). The red line represents the clock error computed by adding to the green line the signal due to GIA, as predicted using the VM1 viscosity profile (13, 14) and the ICE-5G ice history (15). (Inset) Change in the rotation period associated with the red and green lines in the main frame, also plotted relative to the value for 1820 C.E. (B) Rate of change of the J2 harmonic from 1976 to 1990. The shaded region represents the satellite-derived (7–9) observational constraint on the secular rate of change in the J2 harmonic from 1976 to 1990. The red dot represents the predicted J2 rate due to ongoing GIA computed using the VM1 viscosity model (13, 14) and the ICE-5G ice history (15). The blue bar represents the correction to the GIA prediction associated with the melting of glaciers (including those at the periphery of the Greenland Ice Sheet) tabulated by Vaughan et al. (18). The vertical range of the blue bar reflects the uncertainty in this melt contribution (0.7 ± 0.1 mm/year). The right ordinate scale maps the J2 rate into an associated acceleration of Earth’s axial rate of rotation (11). (C) TPW rate over the 20th century. The black arrow with error ellipse represents the secular rate of TPW relative to mantle reference frames as inferred from astronomic and geodetic data (12). (The black arrow at the bottom left of the map shows the amplitude scale for the TPW vector.) The dashed red line and the solid red line represent the TPW vector associated with ongoing GIA computed using the viscosity model VM1 and either the standard (11) or the revised ice age rotational stability theory (21), respectively. The blue line represents the TPW signal driven by the melting of glaciers (18). The fact that the GIA predictions based on the VM1 viscosity model (and, in the case of the TPW datum, the old rotation theory) fit all three rotation observables and do not allow for any excess signal associated with modern ice mass flux. Frame (B) defines Munk’s enigma.
The second and third observations considered by Munk (1) involve changes in the magnitude (Fig. 1B) and orientation (Fig. 1C) of Earth’s rotation vector during the 20th century. We limit our discussion to estimates based on observations up to 1990 to avoid signals associated with the onset of major polar ice mass flux and the acceleration of mountain glacier melting beginning in the early 1990s and continuing to the present (7–10). Satellite geodetic estimates of the second-degree zonal harmonic of Earth’s geopotential (the J2 harmonic) from 1976 to 2012 are characterized by nonlinearity, which was modeled in the early 1990s as two linear segments with a slope break (7) or as a quadratic (9). Considering time windows of 10 years’ duration or greater ending in 1990, the time series of the J2 harmonic in Cheng et al. (9) yields best-fitting linear trends in the range of −3.4 × 10−11 to −4.0 × 10−11 year−1 (gray shading, Fig. 1B). This value maps into an associated rate of change in Earth’s rotation rate (11) of 1/Ω × dΩ/dt = 7.4 ± 0.6 × 10−11 year−1, which is equivalent to an increase in Earth’s rotation period (or length of day) of ~6 millionths of a second per year. Finally, astronomic and geodetic observations up to the early 1990s yield estimates of the secular motion of the rotation vector relative to various mantle reference frames (12) [that is, true polar wander (TPW)] of ~1° million year (My)−1 in the direction of the Hudson Bay (black arrow, Fig. 1C).
RESULTS AND DISCUSSION
Munk’s enigma
Superimposed on the frames of Fig. 1 are predictions of the glacial isostatic adjustment (GIA) signal in the three anomalies in Earth’s rotation (see Materials and Methods), calculated by adopting the VM1 mantle viscosity (13, 14) profile (Fig. 2), the ICE-5G (version 1.2) model of the last glacial-interglacial cycle (15), and the rotational stability theory developed by Wu and Peltier (11). [Munk (1) cited GIA results based on model VM1 and the rotation theory of Wu and Peltier (11).] Since the end of the last deglaciation (~5000 years before the present), the continuing postglacial rebound of polar regions has decreased the oblateness of Earth, contributing to an increase in Earth’s rotation rate. The amplitude of the increase predicted using the VM1 ICE-5G GIA model, when added to the tidal dissipation signal, yields an excellent fit to the total clock error estimated from ancient eclipses (red line, Fig. 1A; inset shows changes in the period of rotation associated with the two curves in the main frame). It also provides a reasonable fit to (though an underestimate of) the J2 rate inferred from satellite observations (red dot, Fig. 1B) and the TPW magnitude and direction estimated from astronomic and geodetic observations (dashed red arrow, Fig. 1C). The level of misfit associated with the prediction of TPW is acceptable given that the observed 20th century TPW rate may have a relatively significant contribution from mantle convective flow (16). Indeed, a recent paleomagnetic analysis suggests a mean TPW rate over the last 40 My of ~0.2° My−1 (17), which is similar in magnitude to the level of misfit in Fig. 1C.
Fig. 2. Mantle viscosity profiles adopted in this study.
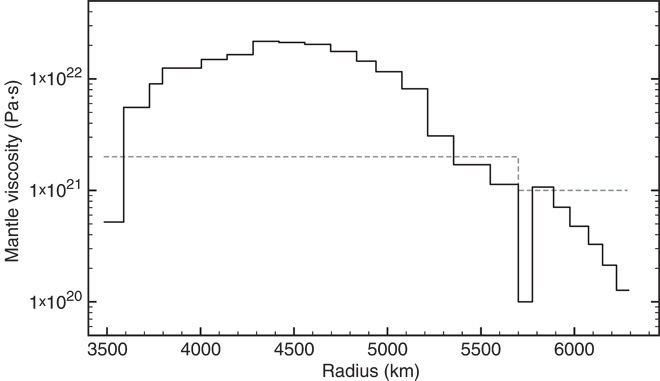
The dashed gray line and the solid black line represent the VM1 (13, 14) and MF (26) radial profiles of viscosity from the base of the lithosphere to the CMB. The former has a viscosity jump of a factor of 2 at the 670-km boundary between the upper mantle and the lower mantle. The latter (a 23-layer model) is characterized by an increase in viscosity of greater than two orders of magnitude from the base of the lithosphere to the deep mantle and is consistent with inferences based on observations related to both GIA (24–26) and mantle convection (27–31).
The fits to the three observables in Fig. 1 are obtained without any additional signal due to modern mass flux from ice sheets and glaciers. This modern signal would not affect the eclipse predictions, but it would contribute to the rate of change in both the J2 harmonic and the position of the rotation axis. As an example, the blue lines in Fig. 1 (B and C) show the signals associated with the melting of glaciers tabulated in the recent Fifth Assessment Report of the Intergovernmental Panel on Climate Change (18). The mass loss from these glaciers over the period 1900–1990, including those in the periphery of the Greenland Ice Sheet, is equivalent to a global mean sea-level (GMSL) rise of 0.7 ± 0.1 mm/year (18). Including this melt signal slows the rotation rate of Earth (because mass moves away from high latitudes) and leads to a significant misfit to the satellite geodetic estimate of the J2 rate. Furthermore, as noted by Munk (1), including any additional polar ice mass flux to increase the total 20th century GMSL rise to ~2 mm/year would add a signal of ~4 × 10−11 year−1 to the J2 rate for each millimeter per year of equivalent GMSL rise (19) and would further increase the misfit to the J2 rate. TPW driven by modern glacier melting is predicted to be relatively small (blue arrow, Fig. 1C), but polar ice sheet melting would likely introduce a significant misfit to the TPW observation because mass flux from either the West Antarctic or the Greenland Ice Sheet equivalent to a GMSL rise of 1 mm/year would drive a polar wander speed in excess of 1° My−1 (20). In any case, it is clear that any significant level of modern mass flux from glaciers or ice sheets would destroy the GIA (VM1)-based fits to the J2 rate and (likely) the TPW rate summarized in Fig. 1; thus, the 20th century enigma in GMSL rise (1) is defined.
A previous study of the enigma (20) suggested that uncertainty in the satellite-derived rate of change in the rotation rate (Fig. 1B) might have been significantly underestimated by not incorporating uncertainty in the signal associated with the 18.6-year body tide, which would introduce room for a modern melt signal. However, more recent analyses of the satellite record (9) have confirmed the robustness of the error bar in Fig. 1B. Mitrovica et al. (20) also noted that the rotational stability theory adopted to compute the GIA signal in Fig. 1C [dashed red arrow (11)] is inaccurate (21); the adoption of a revised theory reduces the magnitude of the TPW prediction (based on the viscosity model VM1) by ~80% relative to the calculation using the earlier, less accurate rotational stability theory (11), and the fit described by Munk (1) disappears (solid red arrow, Fig. 1C). [Adopting the revised rotation theory of Mitrovica et al. (21) in place of the earlier theory (11) has negligible impact on calculations of the rotation period or clock error.]
Resolving the enigma
According to Munk (1), “[among] possible resolutions of the enigma are: a substantial reduction from traditional estimates (including ours) of 1.5–2 mm/yr global sea-level rise; a substantial increase in the estimates of 20th century ocean heat storage; and a substantial change in the interpretation of the astronomic record” (p. 6550). As we demonstrate here, the first and third of these possibilities play a role in resolving the enigma, and an additional contribution comes from an improvement in the GIA model that Munk (1) applied.
A recent probabilistic analysis of a global database of tide gauge records (22) has estimated a GMSL rise of 1.2 ± 0.2 mm/year in 1900–1990. The Fifth Assessment Report of the Intergovernmental Panel on Climate Change estimated three contributions to GMSL rise over this period: melting of glaciers (0.7 ± 0.1 mm/year, as noted previously) (18), thermal expansion (0.4 ± 0.1 mm/year) (10), and net anthropogenic storage of water on land (−0.11 ± 0.05 mm/year) (10). These signals add to a GMSL rise of ~1.0 mm/year, and the consistency of this value with the new probabilistic estimate suggests that the 20th century sea-level budget can be closed without additional contributions from polar ice sheet mass loss (22). That is, if we accept the new GMSL estimate over the period 1900–1990, we need not consider any melt signal in addition to the glacier contribution shown in Fig. 1 (B and C). In contrast, an earlier analysis of the global tide gauge records estimated a GMSL rate of 1.5 ± 0.2 mm/year for 1900–1990 (10, 23), a value that would likely require additional ice melting beyond the glacier contribution cited by Vaughan et al. (18).
Despite the reduced estimates of the 20th century GMSL rise, it is important to recognize that a fundamental aspect of Munk’s enigma remains intact. The J2 rate, or equivalently the nontidal rate of change in the axial rate of rotation (Fig. 1B), is consistent with the nontidal clock error since 500 B.C.E. (that is, integrating the satellite-inferred rate twice yields a clock error consistent with the latter) (1). Therefore, if one were to adopt a different GIA model that introduced a misfit between the GIA prediction of the J2 rate and the satellite geodetic estimate of the rate that was consistent with the signal from glacier melting (equivalent to a GMSL rise of ~0.7 mm/year), then this same GIA model would predict a clock error that was inconsistent with the nontidal signal in Fig. 1A. We can express this inconsistency in another way. In the absence of some other signal contributing to the J2 rate, and assuming that recent estimates of 20th century glacier melting (18) are reasonably accurate, the mantle viscosity model VM1 (used in the GIA prediction in Fig. 1B) cannot be correct. Thus, it follows that there must be an additional non-GIA signal contributing to the clock error in Fig. 1A. This would precisely represent the type of “substantial change in the interpretation of the astronomic record” that Munk (1) hypothesized, and we turn to this issue next.
Our conclusions based on the viscosity model VM1 are unaltered if we adopt, instead, a more recent revision, VM2, which is formally paired with the ICE-5G ice history (15) (fig. S1). These viscosity models are at odds with a suite of GIA-inferred viscosity profiles that increase by several orders of magnitude from the base of the lithosphere to the core-mantle boundary (CMB) (24–26). The latter are consistent with inferences of the radial profile of viscosity based on data sets associated with mantle convection (27–31). Indeed, this consistency has been established explicitly in joint inversions of GIA and convection data (26), and we adopt, as an illustration in the calculations below, an example from this class of viscosity models (Fig. 2; henceforth model MF). Model MF will be paired with the global ice history described by Fleming and Lambeck (32).
The prediction of the J2 rate due to GIA based on the viscosity model MF is shown in Fig. 3B (red dot). The amplitude of the GIA prediction exceeds the observed value by ~2 × 10−11 year−1 (that is, the GIA calculation predicts a decreasing oblateness of Earth at a rate greater than observed); thus, in contrast to the GIA calculation based on model VM1 (Fig. 1B), it provides room for an additional signal from modern ice mass flux. Indeed, adding the signal from glacier melting to the GIA prediction based on the viscosity model MF yields a total J2 rate that is in accord with the geodetic observation (blue bar, Fig. 3B). This is the first plank in our resolution of the sea-level enigma.
Fig. 3. Revised analysis of Munk’s enigma (1).
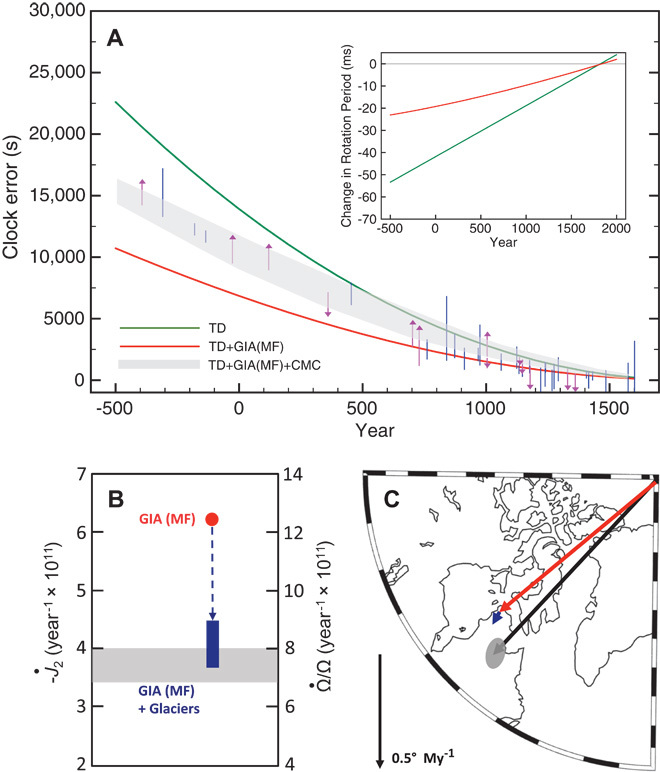
(A) Integrated clock error (as in Fig. 1A) inferred from ancient eclipse observations. The green line represents the clock error associated with the slowing of Earth’s rotation due to tidal dissipation (TD) (3, 6). The solid red line represents the clock error computed by adding to the green line a signal due to ongoing GIA predicted using the MF viscosity profile (26) and the global ice history of Fleming and Lambeck (32). The shaded region bounds three predictions of the total clock error computed by adding to the solid red line the three time series of clock error in Fig. 4 associated with angular momentum exchange between the fluid outer core and the mantle (CMC) (33). (Inset) Change in the rotation period associated with the red and green lines in the main frame relative to the value for 1820 C.E. (B) Rate of change of the J2 harmonic from 1976 to 1990. As in Fig. 1B, the shaded region represents the satellite-derived (7–9) observational constraint on the secular rate of change in the J2 harmonic from 1976 to 1990. The red dot represents the predicted J2 rate due to ongoing GIA computed using the MF model (26). The blue bar represents the correction to the GIA prediction associated with the melting of glaciers (including those at the periphery of the Greenland Ice Sheet) tabulated by Vaughan et al. (18) (0.7 ± 0.1 mm/year). (C) TPW rate over the 20th century. The black arrow with error ellipse represents the secular rate of the TPW relative to mantle reference frames as inferred from astronomic and geodetic data (12). The solid red line represents the TPW signal associated with ongoing GIA computed using the viscosity model MF (26) and the rotational stability theory described by Mitrovica et al. (21). The blue line represents the TPW signal driven by the melting of glaciers (18).
To understand the difference in the J2 rate predicted using the models VM1 and MF, fig. S2 shows a prediction of the GIA signal for a suite of Earth models in which the viscosity of the upper mantle is fixed at 5 × 1020 Pa·s and the viscosity of the lower mantle (that is, below a depth of 670 km) varies by more than two orders of magnitude. The figure provides an important insight into the sensitivity of the predictions to deep mantle viscosity: at low viscosities, the predicted GIA signal is small because these models have relaxed close to equilibrium by the present day, whereas at very high viscosities, the small GIA signal reflects the inherently sluggish adjustments of such models at all times (19). A maximum GIA signal is thus predicted for intermediate values of deep mantle viscosity. The predictions of the J2 rate based on the viscosity models VM1 and MF are superimposed on fig. S2 at an x-axis location given by their maximum lower mantle viscosity. The GIA prediction based on the VM1 model is relatively small because the low viscosity of this model yields a small level of residual isostatic disequilibrium; in contrast, model MF belongs to a class of intermediate viscosity models that yields a relatively large GIA signal.
Next, we consider TPW inferred from astronomic and geodetic observations up to 1997. The GIA prediction of TPW, computed using the rotational stability theory of Mitrovica et al. (21) and based on the MF model, is shown in Fig. 3C (red arrow) together with the signal from glacier melting. As discussed in the context of Fig. 1C, the residual misfit in the amplitude of the TPW (~0.1° My−1) is comparable to estimates of the TPW rate driven by mantle convective flow based on both viscous flow modeling (16) and paleomagnetic analysis (17). This is the second plank in our resolution of the sea-level enigma.
Finally, we turn to the clock error inferred from the ancient eclipse record. Figure 3A shows this record, together with the tidal dissipation signal (both reproduced from Fig. 1A), and a time series computed by adding to the latter signal the GIA prediction of the clock error computed using the viscosity model MF. The significant misfit between the latter (red line) and the observed eclipse record, which increases to ~6000 s by 500 B.C.E., illustrates an important point made earlier in the text; namely, adopting any GIA model that yields a residual between the observed J2 rate and the predicted rate due to GIA that is sufficient to accommodate a signal from ongoing glacier melting (Fig. 3B) will lead to a misfit between the clock error prediction based on the same GIA model and the eclipse observations. As we also noted previously, the latter misfit (as in Fig. 3A) implies that there is an additional unidentified signal in the clock error time series associated with a net slowing of Earth’s rotation over the past three millennia.
The nontidal acceleration of Earth’s rotation since 500 B.C.E., as inferred from the eclipse record, is characterized by millennial-scale fluctuations superimposed on a quadratic background form (3–5). A study of angular momentum exchange between the core and the mantle, derived by inverting observed magnetic field variations from 1000 B.C.E. to 1900 C.E. for flow at the CMB and by using theoretical arguments to reconstruct the flow field throughout the outer core, predicts a millennial-scale variability (33) (Fig. 4, inset). Furthermore, this prediction suggests a mean increase in Earth’s rotation period over the past 2500 years as a result of core-mantle coupling. To consider the impact of this process on our predictions and to recognize the uncertainty associated with the oscillatory signal superimposed on the mean increase, we have performed calculations using three different time series of changes in the rotation period up to 1820 C.E. (Fig. 4, inset): the raw prediction by Dumberry and Bloxham (33), the best linear trend through this prediction, and a constant offset equal to the mean rotation period from 1000 B.C.E. to 1820 C.E. relative to the value for 1820 C.E. The clock error signal associated with each of these time series is shown in the main frame of Fig. 4. Moreover, the shaded region in Fig. 3A represents the computed bound on the total clock error mapped out by adding the signals in Fig. 4 to the combined ice age and tidal dissipation signal in Fig. 3A (red line). This bound is in excellent agreement with the total clock error inferred from the eclipse record, and the consistency supports the argument for a mean slowing in Earth’s rotation rate due to core-mantle coupling over the time span sampled by these ancient observations. Identifying this coupling as an important signal in Earth’s rotation provides the third and final plank in our resolution of the sea-level enigma.
Fig. 4. Impact of core-mantle coupling on Earth’s rotation.
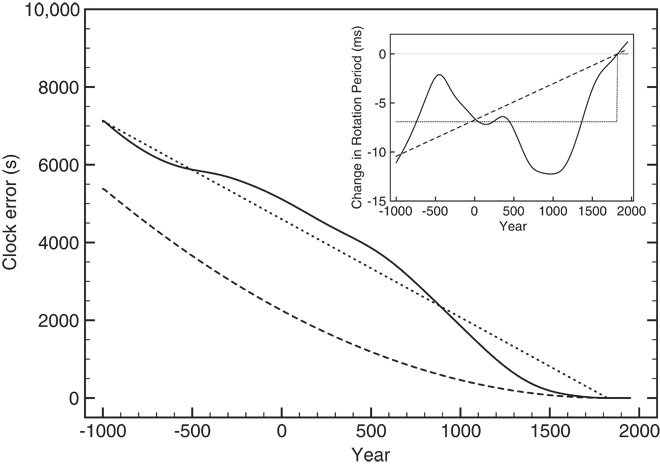
(Inset) Change in rotation period due to angular momentum exchange between the fluid outer core and the mantle, as computed by Dumberry and Bloxham (33) (solid line), relative to the value for 1820 C.E. Dashed and dotted lines represent the best-fitting linear trend through the solid line and the mean pre–1820 C.E. value of the solid line, respectively. (Main frame) Clock error computed by integrating the three time series in the inset.
Further discussion
The simultaneous reconciliation (Fig. 3) of the three rotation observations described by Munk (1) involves, in the case of the J2 rate and the TPW, glacier melting equivalent to a GMSL rise of ~0.7 ± 0.1 mm/year (18). A question arises: How much additional ice melting from 1900 to 1990 is possible before these constraints are violated? In regard to the J2 datum, the glacier melt signal in Fig. 3B could be augmented by polar ice sheet melting with an equivalent GMSL rise of up to ~0.2 mm/year, or by additional melting of glaciers (with the exception of Greenland) at a GMSL rise of up to ~0.3 mm/year, before the predicted (GIA plus melt) signal misfits the observational constraint (19). These values are sufficiently small that it is unlikely that the additional melting would introduce a significant misfit to the TPW datum (Fig. 3C). Note that adding this total melt signal (GMSL rise of ~1.0 mm/year) to estimates of thermal expansion (GMSL rise of 0.4 ± 0.1 mm/year) and net anthropogenic storage of water on land (GMSL rise of −0.11 ± 0.05 mm/year) for the period 1900–1990 (10) indicates that the GMSL rate adopted by Munk (1) (1.5 to 2.0 mm/year) was too high when considering records from the first 90 years of the century.
It is possible that one could find a mantle viscosity profile that yielded a GIA-induced J2 rate that was higher than the value predicted using the MF model (Fig. 3B) and that this would provide room for even higher modern melt rates. However, in this case, we emphasize that the GIA plus core-mantle coupling model would have to remain consistent with the eclipse record of clock error (Fig. 3A), whereas the GIA plus melt signal would have to satisfy the TPW datum.
CONCLUSIONS
Munk’s argument (1) that the GIA-induced perturbations in Earth’s rotation predicted using the viscosity model VM1 fit three different observational constraints and thus leave no room for Earth rotation signals associated with ice mass flux due to 20th century global warming has been an enduring, unanswered enigma in modern climate research. Our reanalysis of the issue demonstrates that the VM1 model is not consistent with any of these observations if one accounts for the signal from the melting of glaciers before 1990 (10, 18), a more accurate theoretical treatment of GIA-induced TPW (21), and the signal due to core-mantle coupling in ancient eclipse observations (33). Addressing each of these issues and adopting a GIA prediction that satisfies numerous independent analyses of mantle viscosity (24–31) reconcile all three observations when a glacier melting rate consistent with recent tabulations for the period (10, 18) (equivalent GMSL rise of ~0.7 mm/year), or up to ~1 mm/year, is included in the analysis. Adding this melt signal to estimates of globally averaged ocean thermal expansion [~0.4 mm/year (10)] yields a total that is consistent with analyses of 20th century GMSL based on tide gauge records (22, 23). Confronting Munk’s elegant statement of the enigma has thus improved our understanding of Earth’s rotation spanning the last three millennia and the individual sources of sea-level rise in the century before the early 1990s. The reconciliation also adds confidence to ongoing efforts to project this rise to the end of the current century and beyond.
MATERIALS AND METHODS
The GIA calculations described in the text adopt the pseudo-spectral formalism of Kendall et al. (34) to compute gravitationally self-consistent sea-level changes in a rotating Earth model using an input ice load history and radial profile of mantle viscosity. The latter inputs are specified in the text. All calculations were performed up to spherical harmonic degree and order 256, and incorporated time-varying shoreline geometry. We assumed a spherically symmetric, self-gravitating, and Maxwell viscoelastic Earth model that is elastically compressible (35). The load-induced Earth rotation changes that form part of the sea-level algorithm are based on the methodology of Mitrovica et al. (21), although the TPW calculations in Fig. 1C and fig. S1C (dashed red lines only) are based on the earlier, less accurate theory of Wu and Peltier (11) for consistency with the GIA results cited by Munk (1).
Supplementary Material
Acknowledgments
This paper is dedicated to the memory of John Wahr, a distinguished scholar, generous colleague, and friend. Funding: Funding was provided by Harvard University, National Science Foundation awards ARC-1203414 and ARC-1203415, National Oceanic and Atmospheric Administration grant NA10OAR4170075, New Jersey Sea Grant project 6410-0012, and a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada. This paper is a contribution to the PALSEA2 (Paleo-Constraints on Sea-Level Rise) project of Past Global Changes/IMAGES (International Marine Past Global Change Study). Author contributions: J.X.M. performed all ice age calculations. All authors contributed to the analysis of Earth rotation observations and to the writing of the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/1/11/e1500679/DC1
Fig. S1. Munk’s enigma of global sea-level rise (1): the VM2 model.
Fig. S2. Sensitivity of GIA predictions of the J2 rate to variations in mantle viscosity.
REFERENCES AND NOTES
- 1.Munk W., Twentieth century sea level: An enigma. Proc. Natl. Acad. Sci. U.S.A. 99, 6550–6555 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Stephenson F. R., Morrison L. V., Whitrow G. J., Long-term changes in the rotation of the Earth: 700 B.C. to A.D. 1980. Philos. Trans. R. Soc. London Ser. A 313, 47–70 (1984). [Google Scholar]
- 3.Stephenson F. R., Morrison L. V., Long-term fluctuations in the Earth’s rotation: 700 BC to AD 1990. Philos. Trans. R. Soc. London Ser. A 351, 165–202 (1995). [Google Scholar]
- 4.F. R. Stephenson, Historical Eclipses and Earth’s Rotation (Cambridge Univ. Press, Cambridge, 1997), 464 pp. [Google Scholar]
- 5.Stephenson F. R., Historical eclipses and Earth’s rotation. Astron. Geophys. 44, 2.22–2.27 (2003). [Google Scholar]
- 6.Christodoulidis D. C., Smith D. E., Williamson R. G., Klosko S. M., Observed tidal braking in the Earth/Moon/Sun system. J. Geophys. Res. 93, 6216–6236 (1988). [Google Scholar]
- 7.Roy K., Peltier W. R., GRACE era secular trends in Earth rotation parameters: A global scale impact of the global warming hypothesis? Geophys. Res. Lett. 38, L10306 (2011). [Google Scholar]
- 8.Nerem R. S., Wahr J., Recent changes in the Earth’s oblateness driven by Greenland and Antarctic ice mass loss. Geophys. Res. Lett. 38, L13501 (2011). [Google Scholar]
- 9.Cheng M., Tapley B. D., Ries J. C., Deceleration in the Earth’s oblateness. J. Geophys. Res. 118, 740–747 (2013). [Google Scholar]
- 10.J. A. Church, P. U. Clark, A. Cazenave, J. M. Gregory, S. Jevrejeva, A. Levermann, M. A. Merrifield, G. A. Milne, R. S. Nerem, P. D. Nunn, A. J. Payne, W. T. Pfeffer, D. Stammer, A. S. Unnikrishnan, Sea level change, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex, P. M. Midgley, Eds. (Cambridge Univ. Press, Cambridge, 2013). [Google Scholar]
- 11.Wu P., Peltier W. R., Pleistocene deglaciation and the Earth’s rotation: A new analysis. Geophys. J. R. Astron. Soc. 76, 753–791 (1984). [Google Scholar]
- 12.Argus D. F., Gross R. S., An estimate of motion between the spin axis and the hotspots over the past century. Geophys. Res. Lett. 31, L06614 (2004). [Google Scholar]
- 13.Peltier W. R., Postglacial variations in the level of the sea: Implications for climate dynamics and solid-Earth geophysics. Rev. Geophys. 36, 603–689 (1998). [Google Scholar]
- 14.Tushingham A. M., Peltier W. R., Validation of the ICE-3G model of Würm-Wisconsin deglaciation using a global data base of relative sea level histories. J. Geophys. Res. 97, 3285–3304 (1992). [Google Scholar]
- 15.Peltier W. R., Global glacial isostasy and the surface of the ice-age Earth: The ICE-5G (VM2) model and GRACE. Annu. Rev. Earth Planet. Sci. 32, 111–149 (2004). [Google Scholar]
- 16.Steinberger B., O’Connell R. J., Changes of the Earth’s rotation axis owing to the advection of mantle density heterogeneities. Nature 387, 169–173 (1997). [Google Scholar]
- 17.Doubrovine P. V., Steinberger B., Torsvik T. H., Absolute plate motions in a reference frame defined by moving hot spots in the Pacific, Atlantic, and Indian oceans. J. Geophys. Res. 117, B09101 (2012). [Google Scholar]
- 18.D. G. Vaughan, J. C. Comiso, I. Allison, J. Carrasco, G. Kaser, R. Kwok, P. Mote, T. Murray, F. Paul, J. Ren, E. Rignot, O. Solomina, K. Steffen, T. Zhang, Observations: Cryosphere, in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex, P. M. Midgley, Eds. (Cambridge Univ. Press, Cambridge, 2013). [Google Scholar]
- 19.Mitrovica J. X., Peltier W. R., Present-day secular variations in the zonal harmonics of the Earth’s geopotential. J. Geophys. Res. 98, 4509–4526 (1993). [Google Scholar]
- 20.Mitrovica J. X., Wahr J., Matsuyama I., Paulson A., Tamisiea M. E., Reanalysis of ancient eclipse, astronomic and geodetic data: A possible route to resolving the enigma of global sea-level rise. Earth Planet. Sci. Lett. 243, 390–399 (2006). [Google Scholar]
- 21.Mitrovica J. X., Wahr J., Matsuyama I., Paulson A., The rotational stability of an ice-age Earth. Geophys. J. Int. 161, 491–506 (2005). [Google Scholar]
- 22.Hay C. C., Morrow E., Kopp R. E., Mitrovica J. X., Probabilistic reanalysis of twentieth-century global sea-level rise. Nature 517, 481–484 (2015). [DOI] [PubMed] [Google Scholar]
- 23.Church J. A., White N. J., Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 32, 585–602 (2011). [Google Scholar]
- 24.Nakada M., Lambeck K., Late Pleistocene and Holocene sea-level change in the Australian region and mantle rheology. Geophys. J. Int. 96, 497–517 (1989). [Google Scholar]
- 25.Mitrovica J. X., Haskell [1935] revisited. J. Geophys. Res. 101, 555–569 (1996). [Google Scholar]
- 26.Mitrovica J. X., Forte A. M., A new inference of mantle viscosity based upon joint inversion of convection and glacial isostatic adjustment data. Earth Planet. Sci. Lett. 225, 177–189 (2004). [Google Scholar]
- 27.Richards M. A., Hager B. H., Geoid anomalies in a dynamic Earth. J. Geophys. Res. 89, 5987–6002 (1984). [Google Scholar]
- 28.Ricard Y., Fleitout L., Froidevaux C., Geoid heights and lithospheric stresses for a dynamic Earth. Ann. Geophys. 2, 267–286 (1984). [Google Scholar]
- 29.Forte A. M., Peltier R., Viscous flow models of global geophysical observables: 1. Forward problems. J. Geophys. Res. 96, 20131–20159 (1991). [Google Scholar]
- 30.King S. D., Masters G., An inversion for the radial viscosity structure using seismic tomography. Geophys. Res. Lett. 19, 1551–1554 (1992). [Google Scholar]
- 31.Panasyuk S. V., Hager B. H., Inversion for mantle viscosity profiles constrained by dynamic topography and the geoid, and their estimated errors. Geophys. J. Int. 143, 821–836 (2000). [Google Scholar]
- 32.Fleming K., Lambeck K., Constraints on the Greenland Ice Sheet since the Last Glacial Maximum from sea-level observations and glacial-rebound models. Quat. Sci. Rev. 23, 1053–1077 (2004). [Google Scholar]
- 33.Dumberry M., Bloxham J., Azimuthal flows in the Earth’s core and changes in length of day at millennial timescales. Geophys. J. Int. 165, 32–46 (2006). [Google Scholar]
- 34.Kendall R., Mitrovica J. X., Milne G. A., On post-glacial sea level. II. Numerical formulation and comparative results on spherically symmetric models. Geophys. J. Int. 161, 679–706 (2005). [Google Scholar]
- 35.Wu P., Peltier W. R., Viscous gravitational relaxation. Geophys. J. R. Astron. Soc. 70, 435–485 (1982). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/1/11/e1500679/DC1
Fig. S1. Munk’s enigma of global sea-level rise (1): the VM2 model.
Fig. S2. Sensitivity of GIA predictions of the J2 rate to variations in mantle viscosity.


