DRUG-TARGET INTERACTION PREDICTION BY INTEGRATING CHEMICAL, GENOMIC, FUNCTIONAL AND PHARMACOLOGICAL DATA

Abstract

In silico prediction of unknown drug-target interactions (DTIs) has become a popular tool for drug repositioning and drug development. A key challenge in DTI prediction lies in integrating multiple types of data for accurate DTI prediction. Although recent studies have demonstrated that genomic, chemical and pharmacological data can provide reliable information for DTI prediction, it remains unclear whether functional information on proteins can also contribute to this task. Little work has been developed to combine such information with other data to identify new interactions between drugs and targets. In this paper, we introduce functional data into DTI prediction and construct biological space for targets using the functional similarity measure. We present a probabilistic graphical model, called conditional random field (CRF), to systematically integrate genomic, chemical, functional and pharmacological data plus the topology of DTI networks into a unified framework to predict missing DTIs. Tests on two benchmark datasets show that our method can achieve excellent prediction performance with the area under the precision-recall curve (AUPR) up to 94.9. These results demonstrate that our CRF model can successfully exploit heterogeneous data to capture the latent correlations of DTIs, and thus will be practically useful for drug repositioning.

1. Introduction

In recent years, drug repositioning or drug repurposing has become an increasingly popular trend in drug discovery.^1–4 The main goal of drug repositioning is to reuse existing or abandoned drugs and identify their new therapeutic functions. Recent literature reveals that drugs often possess the so-called promiscuity property,^5,6 that is, individual drugs can act on other off-target proteins in addition to the original target. This property provides a strong theoretical support for drug repositioning.

In silico prediction of drug-target interactions (DTIs) has been widely applied in drug repositioning, since it can significantly reduce time and cost of drug development. Molecular docking methods have been commonly used in predicting new DTIs if structure coordinates of both proteins and drugs are available.^7–10 When three-dimensional (3D) structures of molecules are absent, we need to depend on other approaches to perform DTI prediction. The structure-free approaches can be roughly divided into two categories: ligand-based and network-based methods. Ligand-based methods exploit ligand similarity to identify new targets that can interact with a query drug.^11,12 Although with some successful stories, ligand-based approaches have di±culty in identifying new interactions associated with novel binding scaffolds.¹³ Network-based methods^14–20 detect the latent correlation features of DTIs to predict new interactions, and recently have become a popular tool for drug repositioning and drug development. A key challenge in network-based prediction approaches lies in integrating heterogeneous data for accurate DTI prediction. Traditional DTI prediction approaches often relate genomic and chemical data with DTI networks to perform new prediction.²¹ Recently, pharmacological data such as drug side-effets have also been taken into consideration,^{18,20,22–24} and the results suggest that incorporating more data into DTI prediction can further improve prediction accuracy. Most existing network-based approaches mainly rely on the sequence similarity to measure the closeness of two targets. The sequence similarity, however, is not necessarily sufficient enough to characterize the shared patterns of DTI profiles between two targets.

Functional similarity enables us to compare two proteins with respect to their molecular and biological functions.²⁵ It is defined mainly based on Gene Ontology (GO) terms, which indicate the biological roles of gene products. This measure can identify functionally-related proteins regardless of homology, and hence provide additional information about the similarity of two targets aside from their genomic data. Based on functional similarity, we can construct biological space for proteins and analyze their DTI patterns from a different angle.

Although numerous approaches^{18,20,23,24,26} have been proposed to integrate genomic (i.e., protein sequences), chemical (i.e., chemical substructures of drugs) and pharmacological (i.e., drug side-effects) data for predicting unknown DTIs, functional information has not been well exploited in DTI prediction. To our knowledge, little work has been developed to systematically integrate functional information on proteins with the aforementioned data to predict missing interactions between drugs and targets. In this paper, we present a new approach to address the DTI prediction problem by systematically integrating large-scale chemical, pharmacological, genomic and functional data and DTI network information into a unified framework. Our method applies a probabilistic graphical model, called conditional random field (CRF), to encode the complicated network associated with drugs and targets, and predict new DTIs. We apply a stochastic gradient ascent approach plus the contrastive divergence (CD) algorithm²⁷ to train our graphical model and capture the hidden correlations between drugs and targets. Tests on two benchmark datasets derived from multiple publicly-available databases show that our CRF model can effectively integrate multiple sources of information and achieve excellent prediction performance, with the area under the precision-recall curve (AUPR) up to 94.9. These results indicate that our approach can have potential applications in drug repositioning.

In summary, the following contributions are made in this paper: (1) Introduction of functional data into DTI prediction and construction of biological space for proteins using the functional similarity measure; (2) Development of a new machine learning approach that can systematically integrate heterogeneous data into a unified framework to predict unknown DTIs; and (3) Promising testing results on two benchmark datasets.

2. Methods

2.1. Conditional Random Field Framework

Conditional random field (CRF) is a probabilistic graphical model or a variant of Markov random field^28–30 that was first proposed for object recognition and image segmentation.³¹ Now it has been widely used in many fields such as shallow parsing,³² named entity recognition,³³ topic distillation,³⁴ social recommendation³⁵ and molecular structural modelling.³⁶ We apply a binary CRF model^34,35 to formulate our DTI prediction problem.

Let {d_i} ≤ i ≤ n_d be the set of known drugs and {t_j} 1 ≤ j ≤ n_t, be the set of targets, where n_d and n_t represent the total numbers of drugs and targets respectively. We use X to denote observed data, including known DTIs and various similarity scores, such as sequence similarity scores for proteins and chemical similarity scores for drugs. In other words, X stands for a set of binary indicators representing known drug-target interactions, and positive variables representing observed similarity scores. For each drug d_i, we construct a CRF on an undirected graph G = (V_t, E_t), where V_t = {t_t} is the set of targets and each edge in E_t represents the similarity between a pair of targets. Let vector Y = (y₁, y₂, ^... y_nt) denote the prediction, where each y_j is a binary random variable representing the prediction of target t_j, that is, y_j = 1 if the predicted interaction between drug d_i and target t_j is true, and y_j = 0 otherwise. We call this model the target-based CRF. Similarly, for each target t_j, we construct a CRF on an undirected graph G = (V_d, E_d), where V_d = {d_d} is the set of drugs and each edge in E_d represents the similarity between a pair of drugs. We call the second model the drug-based CRF. For the convenience of description, next, we will mainly use the target-based model as an example to illustrate the learning and prediction procedures of our CRF model unless otherwise specified.

For each target-based CRF, we define a joint probability distribution conditioning on observation X. In the underlying graph, each node represents a target t_i or its associated binary random variable y_i, and each edge connecting two nodes represents the dependency between these two nodes. Hereinafter, we will slightly abuse the notation and use terms ‘node’ and ‘random variable’ interchangeably. The undirected graphical model possesses the so-called conditional independence property,³⁷ which states that the conditional distribution of node y_i is independent of all other nodes given its ‘neighbors’ (i.e., all other nodes that y_i is connected to). By connecting similar proteins together, we indeed assume that the conditional state of a target depends only on the states of other proteins with high similarity. Details about how to construct edges between targets will be described in Section 3.1.

In a CRF model, the energy of a joint configuration Y given X can be defined as follows:

$$E(Y\mid X)=\sum _i{a}_{i}f(y_i\mid X)+\sum _{i,j}{b}_{ij}g(y_i,y_j\mid X)$$ (1)

where f (y_i|X) is a local node feature function defined based on the state of y_i, g(y_i, y_j|X) is a relational edge feature function defined based on states of both y_i and y_j, and a_i ≥ 0 and b_ij ≥ 0 are weight parameters that need to be learned from training data. In our DTI prediction framework, we let all target-based or drug-based CRFs share the same parameters a_i and b_ij. Then the joint probability density function of Y given X can be defined as

$$p(Y\mid X)=\frac{1}{Z\left(X\right)}\exp (-E(Y\mid X))$$ (2)

where Z (X) = Σ_Y exp (−E(Y | X)) is the normalizing constant, also called partition function. We define functions f (·) and g (·) as followings:

$$f(y_i\mid X)=-{(y_i-H_{x_i}\left(y_i\right))}^2$$ (3)

$$g(y_i,y_j\mid X)=-H_{x_i,x_j}{(y_i-y_j)}^2$$ (4)

where H_xi (y_i) represents the observed feature of target t_i, and H_xi,xj (y_i − y_j) represents the relational feature measure of y_i and y_j given observation X. In our framework, we let H_xi (y_i) be the average number of observed drug interactions for target t_i, and let H_xi,xj (y_i − y_j) be the difference between binary variables y_i and y_j. By defining the above two feature functions, we indeed add a penalization when (1) predictions for two connected nodes are different, and (2) the prediction of a given node deviates from its average state. Unlike in Ref. 35, which assumes that all nodes share the same parameter a and all edges share the same parameter b, here in our model all weight parameters a_i, b_ij are set to be different values for individual nodes and edges. This parameter setting is more flexible to capture information from data and can avoid potential improper assumptions about weight parameters. Our test results (details are not shown in the paper) suggest that this new parameter setting can yield better performance than the original version³⁵ which chooses a relatively rigid parameter setting.

2.2. Parameter Training

In the training process, we aim to learn parameters a_i and b_ij from training data. We use stochastic gradient ascent³⁸ as an optimization method to maximize the conditional log-likelihood of training data. To simplify the notation, we use vector θ to denote parameters (a_i, b_ij), and function vector h to denote (f, g). Then the probability density function in Eq. (2) can be rewritten as

$$p_{\theta }(Y\mid X)=\frac{1}{Z_{\theta }\left(X\right)}\exp (\theta \cdot h)$$ (5)

Thus we can derive the following conditional log-likelihood:

$$L_{\theta }=\sum _{i=1}^{n_t}\log \left(p(y_i\mid X)\right)=\sum _{i=1}^{n_t}[\theta \cdot h(y_i\mid X)-\log \left(Z_{\theta }\left(X\right)\right)]$$ (6)

Since each component of θ is non-negative, we let $\theta =(\exp \left({\theta }_1^{\prime }\right),\cdots ,\exp \left({\theta }_{n_t}^{\prime }\right))$. For simplicity, we use exp (θ′) to represent $\theta =(\exp \left({\theta }_1^{\prime }\right),\cdots ,\exp \left({\theta }_{n_t}^{\prime }\right))$. Then we have

$$L_{\theta }=\sum _{i=1}^{n_t}\left[e^{{\theta }^{\prime }}\cdot h(y_i\mid X)-\log \left(Z_{\theta }\left(X\right)\right)\right]$$ (7)

The gradient in Eq. (7) is

$$\frac{\partial L_{\theta }}{\partial {\theta }^{\prime }}=\theta \cdot \sum _{i=1}^{n_t}[h(y_i\mid X)-E_{\theta }\left(h(Y\mid X)\right)]$$ (8)

where E_θ(h(Y|X)) is the expectation of h (Y |X) and Y|X follows the distribution p_θ defined in Eq. (5).

To apply the gradient ascent method, we need to deal with the expectation term in Eq. (8). It is algebraically intractable to directly calculate this expectation, and one possible solution is to employ some simulation techniques such as Markov Chain Monte Carlo (MCMC) to approximate its value. A Gibbs sampling method was used in Ref. 35 to sample a sequence of Y following the current distribution p_θ and then approximate E_θ(h(Y|X)) by

$$E_{\theta }\left(h(Y\mid X)\right)=\frac{1}{L}\sum _{i=1}^{L}h(\widetilde{y_i}\mid X)$$ (9)

where {ỹi}, 1 ≤ i ≤ L, is the sampled sequence, and L is the total number of sampling iterations. Sampling such sequence often proceeds as follows: We first randomly pick some initial value y₀, and then sample each variable using the current value according to its conditional distribution. Normally, after some burn-in period, the distribution of y_i can approximate distribution p_θ.

Although Gibbs sampling is a popular method to approximate the expectation, it su®ers from heavy computational cost, which is impractical in our case. Here we apply another sampling algorithm, called contrastive divergence (CD), which was first proposed in Ref. 27. The CD algorithm has been successfully used to train restricted Boltzmann machines³⁹ and it can be easily implemented. The basic idea of the CD algorithm is to substitute E_θ(h (Y|X)) in Eq. (8) by E_pT (h(Y|X)), where p_T represents the distribution of data transformed by T cycles of Gibbs sampling.²⁷ In practice, T is often chosen to be one. Although the CD algorithm may lead to biased estimates, the bias is small in general.⁴⁰ In practice, the CD algorithm can provide an effcient method to approximate the log-likelihood function.^27,39,40

2.3. Predicting New Drug-Target Interactions

To predict unknown drug-target interactions for a query drug given observation X, we compute the conditional probability distribution p (y_k|y_−k, X) for each target t_k, where y_−k denote the all other targets except t_k. For i ≠ k, y_i = 1 if target y_i is known to interact with the query drug, and y_i = 0 otherwise. We then calculate the conditional expectation of y_k as the prediction score of the interaction between target y_k and the query drug.

3. Results 3.1. Constructing Conditional Random Field

In our CRF model, an edge connecting two nodes indicates the relational dependency between them, and we assume that two connected nodes should share high similarity. One natural approach for constructing edges in the underlying graph is to connect two nodes if their similarity score is above a threshold. By choosing different threshold values we should be able to tune the number of edges in the graph. This construction method, which we call the threshold-based approach, could yield an unbalanced graph in which some nodes may have much fewer neighbors than others. This situation would make it difficult for inferring the states of those neighbor-free nodes. To avoid this problem, we used another approach to construct the underlying graph. For each node t_i, let N_i be the set of top K nodes that have the highest similarity scores with t_i, and we connect two nodes t_i and t_j if t_i ∈ N_j or t_j ∈ N_i. We refer to this new approach as the degree-based approach, which ensures that the degree of each node in the underlying graph is at least K and roughly balanced, and thus can prevent the existence of ‘isolated’ nodes. In practice, we should not choose a large value of K in order to train our CRF model efficiently on a large-scale dataset. Our sensitivity analysis shows that our results did not vary much for different K values (Supplementary Material S2). We can also combine the above two approaches to get an integration-based approach for constructing edges, that is, we connected two nodes mainly based on a similarity score threshold but also added more connections to a node if its degree is less than K. The comparison results show that different construction approaches did not influence much on prediction performance when choosing K ≥ 2 (Supplementary Material S3). In the following analysis, the underlying graph of our CRF model was constructed mainly based on the degree-based approach, unless otherwise specified. We chose K = 4 when a single similarity measure was used and K = 2 when multiple similarity measures were used. This parameter was fixed throughout all our tests.

We tested the following six different approaches in our conditional random field framework:

• Genomic approach (GEN): The target-based CRF was constructed using the sequence similarity measure.

• Functional approach (FUN): The target-based CRF was constructed using the functional similarity measure.

• Integrated Genomic-Functional approach (IGF): The target-based CRF was constructed using the sequence and functional similarity measures simultaneously. In other words, two nodes were connected if they satisfied the sequence or functional similarity criterion.

• Chemical approach (CHEM): The drug-based CRF was constructed using the chemical similarity measure.

• Pharmacological approach (PHAR): The drug-based CRF was constructed using the sidee®ect similarity measure.

• Integrated Chemical-Pharmacological approach (ICP): The drug-based CRF was constructed using the chemical and side-effect similarity measures simultaneously. In other words, an edge was constructed if it was valid under the chemical or side-effect similarity measure criterion.

In addition, we investigated the combination of two independent predictions from target-based and drug-based CRFs respectively. For any given drug-target pair, let S_d denote the prediction score using the drug-based CRF model and S_t denote the prediction score using the target-based CRF model. Then our final score for this query drug-target pair is

$$S=\alpha S_d+(1-\alpha )S_t$$ (10)

In the current version of our program, we fixed α = 0.5. By fine-tuning the parameter ®, we may achieve better results than our current tests. Our final approach integrated chemical, pharmacological, genomic and functional data simultaneously:

• Full Integration approach (FI): The final prediction was the simple linear combination of both integrated chemical- pharmacological (ICP) and integrated genomic-functional (IGF) approaches using Eq. (10).

Our program was implemented in Matlab (2010 b) based on the UGM package developed by Mark Schmidt (http://www.di.ens.fr/~mschmidt/Software/UGM.html). UGM is a Matlab toolbox that implements various tasks in discrete undirected graphical models with pairwise potentials. We used the default parameters of functions in the UGM package throughout all our tests.

3.2. Datasets

To demonstrate the predictive power of our approach, we first tested it on a dataset derived from the KEGG database^41,42 which contains experimentally-verified drug-target interactions. We call this dataset the first dataset. All drugs in the first dataset have molecular weight more than 100. In order to obtain pharmacological information we only included those drugs that also have side-e®ect records in the SIDER database.⁴³ As a consequence, in total 875 drugs and 249 proteins with 2596 drug-target interactions were obtained in the first dataset.

To compare with other existing approaches, we tested our algorithm on another dataset that has been published in Ref. 24, where all drugs have records in SIDER, JAPIC and AERS. JAPIC and AERS are two public databases about drug side-effects. More details about these two databases can be found in Ref. 24. The data we tested here is slightly different from the original data which contains 359 drugs and 226 proteins with 1188 drug-target interactions. We excluded six proteins that do not have any GO annotation and two drugs that have no interaction with the remaining proteins. Thus the new dataset includes 357 drugs and 220 proteins with 1174 drug-target interactions. We call this new dataset the second dataset. Descriptive statistics about the first and second datasets are provided in Supplementary Material S1.

Chemical similarities between drugs were calculated using the graph kernel approach,⁴⁴ where chemical structure information of drugs was taken from the KEGG database. Side-effect similarities between drugs were calculated using the same method as in Ref. 24, where pharmacological information was obtained from the SIDER database. Sequence similarities between proteins were computed using local alignment kernel approach.⁴⁵ Functional similarities between proteins were calculated using online software FunSimMat,^46,47 in which functional similarity scores were derived from GO terms annotated with biological process and molecular function. In both datasets that we have tested, most pairs of proteins or drugs were dissimilar. In the first dataset, less than 3% of all drug pairs had chemical similarity score greater than 0.85 (all similarity scores were normalized to 1), and less than 1% of all protein pairs had sequence similarity score greater than 0.85. In the second dataset, less than 2% of all drug pairs had chemical similarity score greater than 0.85, and less than 1% of all protein pairs had sequence similarity score greater than 0.85.

3.3. Performance Evaluation

We used the Receiver Operator Characteristic (ROC) curve and the Precision-Recall (PR) curve to evaluate the performance of our algorithm. In addition, we also computed the AUC (area under ROC curve) and AUPR (area under PR curve) scores. In our performance evaluation, true positives were those correctly predicted interactions, while false positives were those predicted interactions that were not present in the tested dataset. For highly-unbalanced data, the PR curve is usually considered to be a better criterion to assess the prediction performance, since it can punish more false positive examples.^16,19,48 Thus our analysis mainly focused on AUPR, although in many cases AUC and AUPR were positively correlated. Our tests were performed mainly using a 10-fold cross-validation procedure. In this procedure, all DTIs were randomly partitioned into 10 equal size subsamples. Each subsample was in turn used as validation data to test our algorithm, and the remaining nine subsamples were used as training data.

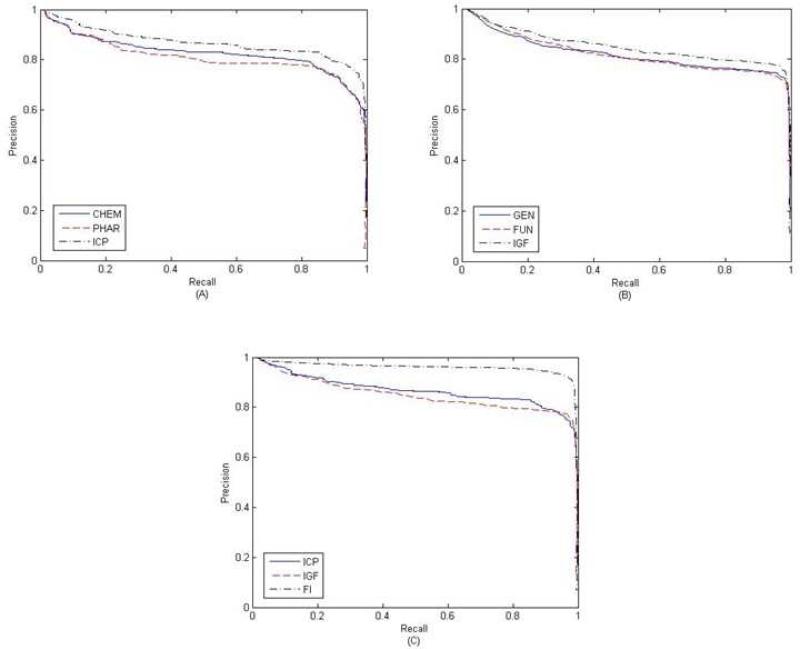
Table 1 summarizes the test results on the first dataset using the 10-fold cross-validation procedure. Under the target-based CRF framework, integrating both genomic and functional data achieved better performance than other two approaches, with the AUPR score improved by > 3%. When both chemical and pharmacological data were integrated into the drug-based CRF framework, the results outperformed each single-similarity based approach with the AUPR score improved by > 4%. When integrating all available information, the FI approach achieved the best performance with AUPR > 94. Figure 1 shows the AUPR curves for different approaches tested on the first dataset. These results demonstrate that incorporating additional information about drugs and proteins can further improve prediction accuracy. To check the robustness of our model, we also performed a 5-fold cross-validation test, and only observed a slight decrease in AUC and AUPR values (Supplementary Material S4).

Table 1.

Prediction results on the first dataset using 10-fold cross-validation. Both AUC and AUPR scores are normalized to 100. The best result is shown in bold.

Approach		Evaluation Criterion
		AUC	AUPR
Target-based CRF	GEN	97.3	80.7
	FUN	97.7	80.9
	IGF	98.0	83.9
Drug-based CRF	CHEM	96.0	81.5
	PHAR	96.6	79.9
	ICP	98.1	85.9
Full Integration Approach (FI)		99.2	94.9

Fig. 1.

PR curves for different approaches on the first dataset. (A) PR curves for drug-based CRFs. (B) PR curves for target-based CRFs. (C) PR curves for the FI approach.

3.4. Comparison Results

To compare with other existing approaches, we tested our algorithm on the second dataset, i.e., the benchmark dataset published in Ref. 24. Here we mainly compared our approach with the pairwise kernel regression (PKR) method proposed in Ref. 24, which claimed that PKR outperformed many other state-of-the-art methods on the same data. As in Ref. 24, we also tested seven different approaches, including AERS-freq-based pharmacogenomic approach (AERS-freq), AERS-bit-based pharmacogenomic approach (AERS-bit), SIDER-based pharmacogenomic approach (SIDER), JAPIC-based pharmacogenomic approach (JAPIC), chemogenomic approach (CHEM), integrated pharmacogenomic approach (INTEG-P) and integrated pharmaco-chemogenomic approach (INTEG-PC). These different methods, as suggested by their names, are defined mainly based on input data, and more details about them can be found in Ref. 24 or Supplementary Material S5 of this paper. In addition, we tested an additional approach that combines chemical, side-effect, sequence and functional data together. This approach was not included in Ref. 24 and we referred to it as ‘INTEG-ALL’. Table 2 shows the comparison results between our conditional random field (CRF) model and the pairwise kernel regression (PKR) model.

Table 2.

The comparison results between our CRF and PKR methods. The second dataset was tested in our CRF model using 3-fold cross-validation. The results for PKR were taken from Ref. 24 in which pair-wise cross-validation corresponds to our 3-fold cross-validation test here. Note that the INTEG-ALL approach was absent in Ref. 24. The best score is shown in bold.

Approach	AUPR
	CRF	PKR
AERS-freq	85.7	80.6
AERS-bit	85.4	81.3
SIDER	87.3	76.8
JAPIC	91.2	87.7
CHEM	87.7	79.7
INTEG-P	90.7	87.4
INTEG-PC	90.4	88.5
INTEG-ALL	91.5	\

As shown in table 2, our method outperformed the PKR model over all different tests. In particular, our approach can improve the AUPR score by up to 10.5 when only SIDER-based information was used. Furthermore, the results produced by CRF were not as sensitive to different input data as those produced by PKR. For example, the AUPR score of PKR based on JAPIC was about 10% larger than that based on SIDER, whereas the test of our algorithm on SIDER-based data can still yield decent performance. These comparison results indicate that our method is more robust to input data than PKR, and may have a better capacity to handle noise in data.^a

4. Conclusion

In this article, we introduced functional data into DTI prediction and developed a probabilistic graphical model to predict new drug-target interactions using known drug-target interactions and various similarity scores for both drugs and targets. Our model can integrate chemical, pharmacological, genomic and functional data systematically, and predict new DTI interactions with high accuracy. We demonstrated that incorporating functional information of targets can further improve prediction performance.

Currently, our algorithm uses a simple linear combination of independent predictions from drug-based and target-based CRFs respectively. In the future, we will extend our model into a more sophisticated framework that can better integrate both drug-based and target-based CRF models. In addition, we will incorporate other data such as drug-drug interaction (DDI) and protein-protein interaction (PPI) information into DTI prediction. We hope that by incorporating these additional information our model can reveal mechanism of drug action to a greater extent. Currently we only evaluated our approach based on benchmark data. We will explore the practical applications of our prediction algorithm, e.g., identifying novel drug-target interactions for drug repositioning.