Large-scale probabilistic 3D organization of human chromosome territories

Abstract

There is growing evidence that chromosome territories (CT) have a probabilistic non-random arrangement within the cell nucleus of mammalian cells including radial positioning and preferred patterns of interchromosomal interactions that are cell-type specific. While it is generally assumed that the three-dimensional (3D) arrangement of genes within the CT is linked to genomic regulation, the degree of non-random organization of individual CT remains unclear. As a first step to elucidating the global 3D organization (topology) of individual CT, we performed multi-color fluorescence in situ hybridization using six probes extending across each chromosome in human WI38 lung fibroblasts. Six CT were selected ranging in size and gene density (1, 4, 12, 17, 18 and X). In-house computational geometric algorithms were applied to measure the 3D distances between every combination of probes and to elucidate data-mined structural patterns. Our findings demonstrate a high degree of non-random arrangement of individual CT that vary from chromosome to chromosome and display distinct changes during the cell cycle. Application of a classic, well-defined data mining and pattern recognition approach termed the ‘k-means’ generated 3D models for the best fit arrangement of each chromosome. These predicted models correlated well with the detailed distance measurements and analysis. We propose that the unique 3D topology of each CT and characteristic changes during the cell cycle provide the structural framework for the global gene expression programs of the individual chromosomes.

Introduction

Spatial positioning has emerged as a fundamental principle governing nuclear processes and, together with the field of genomics, has led to a paradigm shift in the study of gene regulation (1–5). Understanding the regulation and coordination of thousands of genes at any given time will require more precise information on how these genes are spatially arranged and expressed within the three-dimensional (3D) context of the cell nucleus (1,2,4,6–9). It is widely assumed that the 3D arrangement of chromosome territories (CT) and the spatial positioning of genes within the CT are linked to genomic function and regulation (10–14). While elucidating the details of the non-random arrangement of CT has been a challenging endeavor (15–20), recent investigations have identified probabilistic interchromosomal networks of large subsets of CT with cell-type specificity and alterations in the cell cycle (21,22) and in malignant breast cancer cells (23–25).

Similarly, limited progress has been made in understanding the overall shape and 3D organization of chromatin within individual CT (topology) (26–35). CT display a wide range of 3D shapes from regular ellipsoid-like to highly irregular (36,37). Properties that could influence the global organization of individual CT include heterochromatin/euchromatin (38), gene density (37,39), RIDGES/anti-RIDGES (34) and gene activity (40,41). A higher degree of irregularity in CT shape is found with increasing gene density (37). For example, despite being nearly identical in sequence length, the gene-rich CT17 is less compact and much more irregular in shape than the gene-poor CT18 (37). The potential influence of gene activity on shape irregularity is demonstrated in female cells, in which one homolog of the X chromosome is inactivated (Xi) and more regular in comparison to its active counterpart Xa (40,41).

If there are distinct differences among CT in overall shape, how is the chromatin arranged three dimensionally at the global level of the entire CT? Limited studies using multi-in situ hybridization (FISH) and computer analysis have revealed distinct 3D organization and specificity for relatively short regions (<5 Mb) within CT (31,34,42). Organization of larger regions has been limited to investigations of chromatin folding by the method of polymer modeling and mean squared distances (MSDs) (43,44) with only one previous study (43) analyzing entire human chromosomes (CT4, 5 and 19). These studies have led to general models of chromatin loops and higher level folding that are of potentially great significance (43–48), but do not directly address the precise organization of the chromatin within individual CT.

As a step toward understanding the overall 3D architecture of chromatin within individual CT, we have combined the tools of 3D microscopy, multi-FISH, computer imaging and computational geometric analysis to analyze six labeled regions spanning each CT in the G1 and S phase of WI38 normal diploid human fibroblasts. We find that on a global level, each CT has a specific folding pattern with limited alterations across the cell cycle. A classic data-mining computational geometric algorithm termed the k-means (49–52) was applied to determine the best fit probabilistic 3D topology of the labeled probes across each CT. The 3D topological models derived from this geometric approach were specific for each CT and had a high degree of non-randomness compared with models generated from random simulations. Moreover, the overall patterns were generally similar in G1 and S phase. An exception was CT17 where the degree of variation in the individual data points was similar to random simulation. We conclude that CT have a probabilistic non-random 3D organization at the global level that may provide the structural basis for the overall regulation of genomic function specific for each CT.

Results

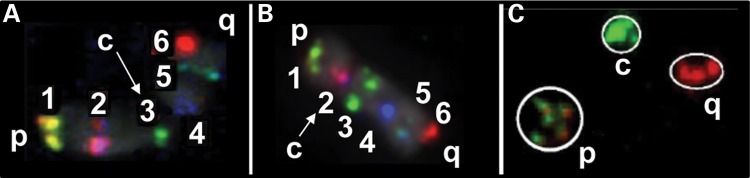
Multifluor 3D FISH, computer imaging and computational geometric approaches (see Materials and Methods) were used to study the global intrachromosomal 3D organization (topology) of a subset of six human chromosomes (1, 4, 12, 17, 18 and X) in WI38 diploid human fibroblasts during the G1 and S phases of the cell cycle. This subset of chromosomes is representative of the entire genome with a broad range in size and a weighted average gene density (6.8 genes/Mb) nearly identical to the entire female genome (6.7 genes/Mb). Within each CT, six regions (sub-telomeric p and q, centromeric, and three others spaced between the centromere and telomeres) were labeled with digoxigenin (dig), biotin (bio) or dinitrophenol (DNP) either alone or in combinations of dig-bio, dig-DNP or bio-DNP. CT were labeled with DEAC/aqua (chrombios). Details of the probes for each chromosome are presented in Table 1. The overall average distance between consecutive (1_2, 2_3 … 5_6) probes was 28.3 Mb. Metaphase FISH was performed to confirm that each bacterial artificial chromosome (BAC) probe labels the selected region on each chromosome (Fig. 1A and B). To ensure that the selected probes are representative of their region in interphase, three different regions within CT4 were labeled with five BACs spanning 10 Mb (15 probes in total). The close proximity of each set of five BAC labels in interphase, demonstrates that the individual probes are representative of the region selected on the chromosome (Fig. 1C).

Table 1.

BAC probes representing regions on six selected chromosomes

chr 1		chr 4		chr X		chr 12		chr 17		chr 18
RP11-	Mb	RP11-	Mb	RP11-	Mb	RP11-	Mb	RP11-	Mb	RP11-	Mb
82D16	2.2	81L5	14.7	91D5	0.4	467M14	0.3	629C16	0.4	324G2	0.2
133B9	47.2	738E22	57.7	509C1	32	113B6	33.8	64J19	21.1	808F20	13.5
799C6	111	698A19	88.5	949B21	62.5	1148K3	51.3	698D9	39.6	138H11	32.2
1008K23	159	571L19	100	349D15	94.8	114G18	80.5	42M14	50.6	10I6	48.1
957E7	200	81F5	137	137A15	129	110L13	108	352P21	67.4	3K7	62.9
81J5	238	196K19	185	402H20	154	394D10	132	258N23	80.7	89N1	77.8

Figure 1.

BAC probes label appropriate regions within CT in both metaphase and interphase. Metaphase FISH was performed in order to ensure that the probes label the appropriate region on the chromosomes. Six probe labeling in metaphase is presented for chromosome 1 (A) and chromosome 12 (B). Five BAC probes were labeled within each of three ∼10 Mb domains (15 probes in total) at the beginning, middle and end of CT4 (C). All five probes for each region were found to be in close proximity on the interphase CT, and hence, representative of their region.

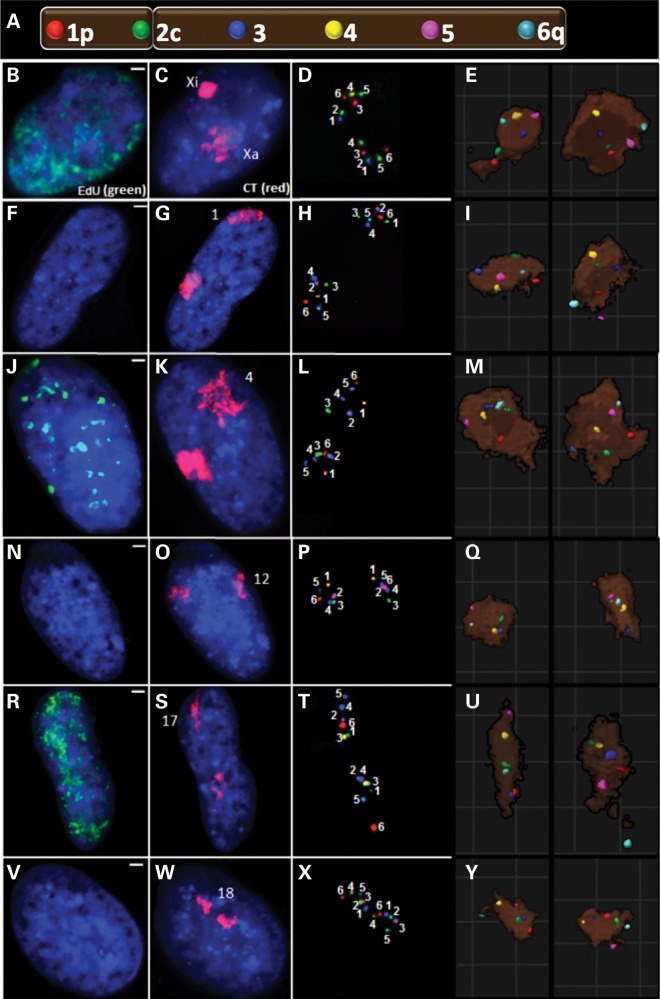
Multi-fluor 3D FISH was then performed on the six CT during interphase. Representative images are shown in Figure 2. EdU was used to distinguish S phase (Fig. 2 B, J and R) from non-S phase cells (Fig. 2F, N and V). G1 cells were identified in the non-S population by excluding G2 cells detected by doublet BAC signals which occur only after replication (e.g., probes 3 and 5 in Fig. 2L). Applying computer analysis and computational geometric algorithms to the images enabled investigation of: (a) the intrachromosomal organization of the six labeled regions relative to the CT center and periphery; (b) intrachromosomal organization relative to the nuclear periphery; (c) spatial orientation of CT homologs; (d) pairwise 3D distance measurements among all combinations of the six labeled regions; (e) chromatin folding properties of the individual CT and (f) the overall global pattern and most probabilistic 3D model for each CT.

Figure 2.

Six-probe FISH for 3D topology. A diagram illustrates BAC probe labeling of six regions across each chromosome (A). Two of these probes were located near the telomeres (1p and 6q); one was located near the centromere (2c on chromosomes 12, 17, 18 and X or 3c on the metacentric chromosomes 1 and 4) with the remaining probes spaced between the centromeric probe and the telomeres. Representative images are displayed for CTX (B–E), CT1 (F–I), CT4 (J–M), CT12 (N–Q), CT17 (R–U) and CT18 (V–Y). S (B, J, and R) versus non S (F, N and V) phase cells were distinguished by the presence of EdU replication labeling. In addition to whole-chromosome painting (C, G, K, O, S, W), the six regions were labeled with biotin (BIO), digoxigenin (DIG) or dinitrophenol (DNP) alone or in combinations of BIO–DIG, BIO–DNP or DIG–DNP (D, H, L, P, T, X). In order to find the maximal labeling efficiency, the labeling scheme was altered depending on each probe's labeling intensity. As a result, the numbers in these images represent the region within the CT as defined by that given color combination. For ease of comparison, these probes were pseudocolored (E, I, M, Q, U, Y) in their corresponding 3D reconstructions to match the labeling scheme of (A).

Positioning of regions within CT relative to the nuclear periphery

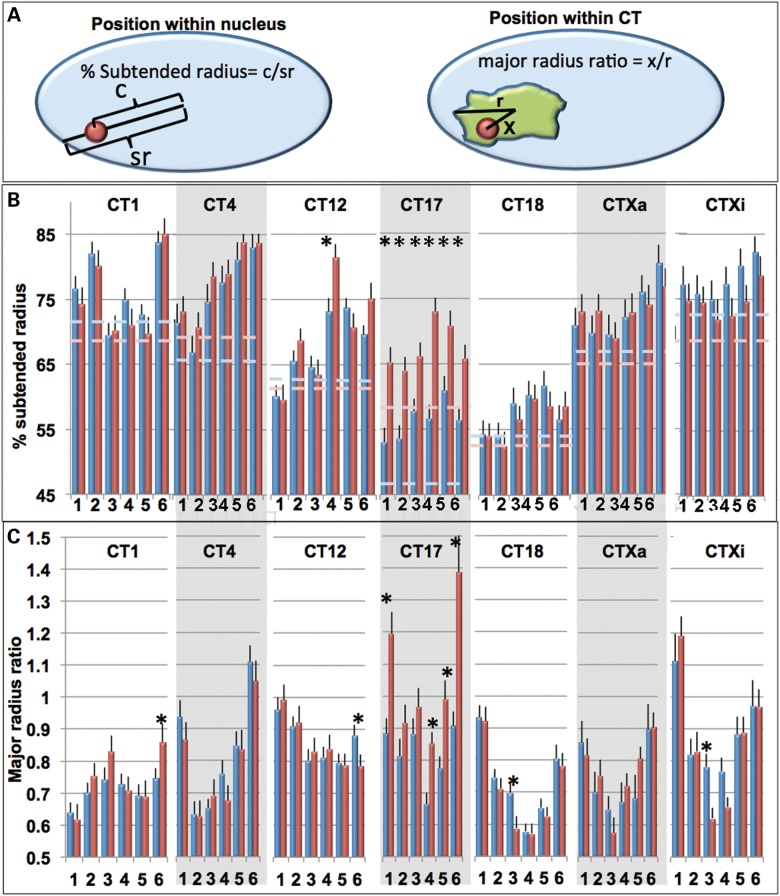
The spatial orientations of the six labeled regions within each CT relative to the nuclear periphery were measured by the percent subtended radius (% SR, see Materials and Methods, Fig. 3A). Specific distance profiles were detected for each CT (Fig. 3B) with some CT (CT1, 4 and 12) having greater variation in radial positioning of the six regions than others (CT17, 18 and X). The great majority of probe regions were closer to the nuclear periphery than the subtended radius of the entire CT (Fig. 3B). Moreover, the overall subtended radius probe profiles did not change significantly (P < 0.05) from G1 to S phase; with the exception of the entire CT17 profile which was strikingly more peripheral in S phase (Fig. 3B).

Figure 3.

Intrachromosomal organization relative to the CT or nuclear periphery. Distances of labeled regions relative to the nuclear periphery were determined as a percent of their subtended radii (SR, the distance from the nuclear center to the nuclear periphery projected through the probe center).The distances from each BAC labeled region relative to the CT center were normalized relative to the major radius of the CT (major radius ratios, MRR). Schematics of these measurements are illustrated in (A). The %SR (B) and MRR values (C) for CT1, 4, 12, 17, 18, Xa and Xi are shown in G1 (blue) and S (red). Dashed lines in (B) represent the % SR of the entire CT in G1 (light blue) and S (pink) phase. Error bars denote SEM. *Indicates statistical significant differences between G1 and S for SR values (t-test, P < 0.05).

Organization of regions within CT

The positioning of regions within the CT was determined by the ratio between the probe distance to the CT center of gravity and the major radius of the CT (major radius ratio, MRR, Fig. 3A). A MRR of 0 indicates that the region is located exactly at the CT center. A value of 1 indicates that it is on the periphery of the CT, and a value >1 indicates that the region is within an extension away from the main CT body. The overall patterns of MRRs were specific for each CT. At least one of the telomeric regions of each CT and both telomeric regions of CT4, 17, 18 and X were located at or near the CT periphery. CT17-p, 17-q and Xi-p were frequently located within a projection outside the CT (Figs. 2D–E, T and U, 3C). The overall MRR profiles in G1 versus S phase were not significantly different except for CT17 where four of the six regions showed large increases in MRR during S phase including the two telomeric regions which extend outside the main CT body in S and positions 4 and 5 (adjacent to the q-arm telomere) which reposition closer to the CT periphery (t-test, P < 0.05). Random simulations were performed using a computer algorithm in which six points were chosen randomly inside the territory of the CT. Since the volume is greatest around the border of a 3D ellipsoid, the MRR for randomly selected points within the CT were between 0.7 and 1.0 and, in contrast to the experimental data, did not show significant variations in their average MRR (Supplementary Material, Fig. S1).

Homologous CT orientations

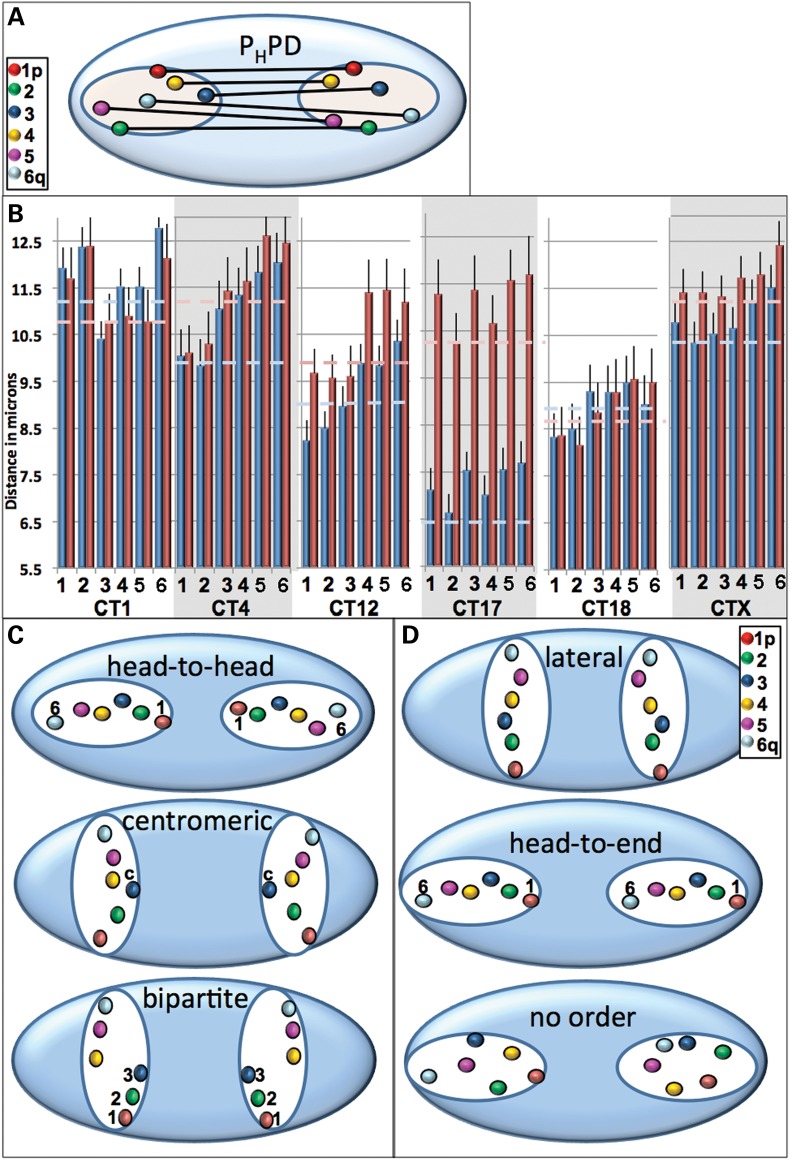
Deciphering the arrangement of the pairwise homologous probe distances (Fig. 4A) revealed that the patterns varied from chromosome to chromosome and showed cell cycle alterations for some CT (Fig. 4B). Three major orientation types between homologous chromosomes observed are illustrated in Figure 4C and include: (a) head-to-head—where p arm telomeres are nearest and the distance between consecutive regions increases such that the q arm telomeres are the furthest; (b) bipartite—where distances between the entire Region 1–3 are closer than the distances in the entire region 4–6; (c) centromeric—where the centromeres are closest. If all homologous probes are equidistant, the CT would be oriented laterally, head-to-end or not ordered (Fig. 4D).

Figure 4.

Internal orientation of homologous CT pairs. The 3D distances between the six labeled regions for each homologous CT pair were measured. A schematic diagram demonstrating these measurements is shown in (A) and experimental values in microns are presented in (B). Based on the pairwise distances between homologous probes, preferred patterns of spatial arrangement could be head-to-head (where the p arm telomeres were nearest and the distance between consecutive regions increased such that the q arm telomeres were the furthest), bipartite (distances between the entire region 1–3 are closer than the distances in the entire region 4–6) or centromeric (the centromeres are closest, C). If all homologous probes are equidistant, the CT would be oriented laterally, head-to-end or not ordered (D). Dashed lines in (B) represent the CT center to center distance for the entire CT in G1 (light blue) and S (pink) phase. Error bars denote SEM. Statistically significant differences in the 3D distances (P < 0.05) were found for the centromeric probe 3 in the G1 phase of CT1 compared with the other probes; between probes 1 or 2 and 5,6 in both G1 and S phase for CT4; between probes 1 and 4,5 6; 2 and 4,5,6 and 3 and 6 in G1 phase for CT12; between 1 and 4,5; 2 and 4,5,6; 3 and 4,5 in the S-phase of CT12 and between all the probes in G1 versus S for CT17.

CT1 in G1 revealed a centromeric orientation with the centromeres (Position 3 probes) closer together than all the other probes (Fig. 4B). This arrangement was altered in S phase where no significant differences were found in the CT1 probes. A head-to-head orientation (Fig. 4C) was determined for CT4 in both G1 and S phase and in the G1 phase of CT12 which switches to a bipartite arrangement during S phase (Fig. 4B). Since no significant differences were found in either G1 or S phase for the probe distances of CTX, 17 and 18, their orientations are potentially head-to-end, lateral or patternless (Fig. 4B and D). Most of the probe distances were either greater than the center-to-center distances between CT homologs or not significantly different (Fig. 4B, dashed lines). There was a modest increase during S phase in the distances between homologs (≤1 µm) with the exception of CT17 which increased by ∼ 4 µm. As a result, the individual probe homologs in CT17 are much further apart in S compared with the G1 phase (Fig. 4B).

MSD profiles

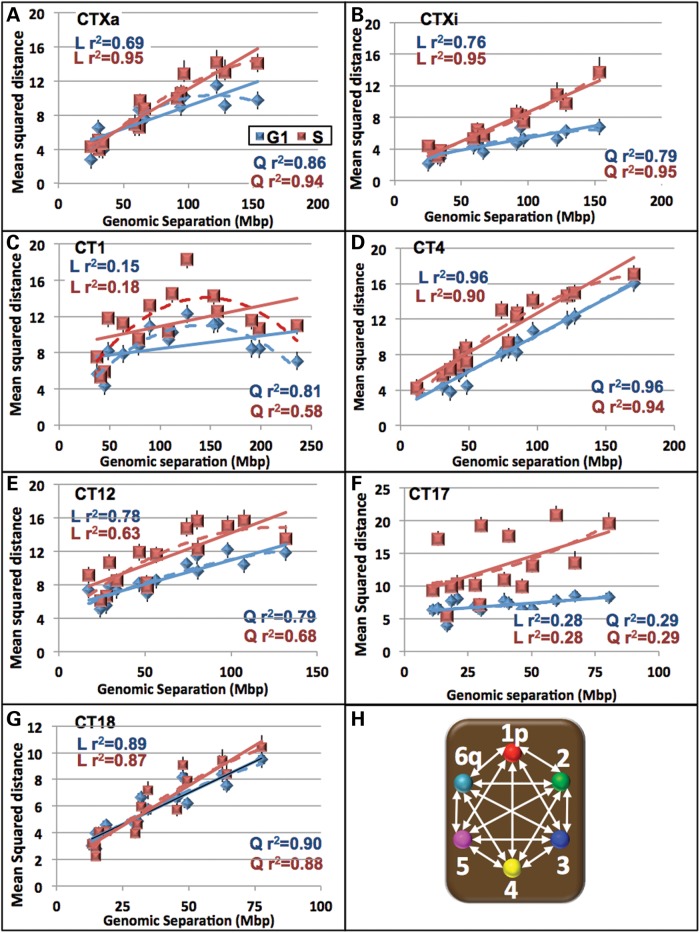
As a first step in examining the chromatin folding among this sub-set of CT, we calculated the 3D pair-wise probe distances between the six probes (15 distances, Fig. 5H) in the G1 and S phases (Supplementary Material, Figs S2 and S3) and plotted the MSDs against their genomic separation (Fig. 5). The MSD profile patterns were specific for each CT with values varying up to 4-fold for each CT (Fig. 5). For the gene poor CT4 and CT18, the MSDs displayed relatively large linear increases with genomic separation that did not plateau (Fig. 5D, G and Supplementary Material, Fig. S4) respectively). CT1, 12 Xa and Xi (S phase) showed much lower increases in MSDs with CTXa and CT12 reaching a plateau at ∼100 Mb in G1 and S phase, respectively (Fig. 5A–C and E). The MSDs for CT17 showed minimal changes with genomic separation and did not conform to either a linear or quadratic relationship (Fig. 5F). A sharp decline in the MSD was found in CT1 for genomic separations ∼160 Mb which is consistent with this CT bending back upon itself (Fig. 5C). Corresponding MSD plots of random simulations for each CT had uniform MSDs across the entire genomic sequence (Supplementary Material, Fig. S5).

Figure 5.

The relationship between mean squared distances and the genomic separation varies among chromosomes. The mean squared interphase distances between the six probes (a total of 15 distances) were plotted against their genomic separation for CTXa (A), Xi (B), 1 (C), 4 (D), 12 (E), 17 (F) and 18 (G). An illustration of these 15 distance measurements is shown in (H). Linear trendlines (solid) and quadratic (dashed) are shown for G1 (blue) and S (red). r² values for the linear (L) and quadratic (Q) trendlines are displayed on the graphs. While CTXa (S phase), Xi (S phase), 4 and 18 displayed a strong linear relationship between the mean squared distances and genomic separation, CT12 and Xi (G1) showed only a moderate linear relationship. CT1 (G1 and S) and CTXa (G1) fit a quadratic trend better and CT17 does not fit either a linear or quadratic trend.

Folding ratio analysis of CT

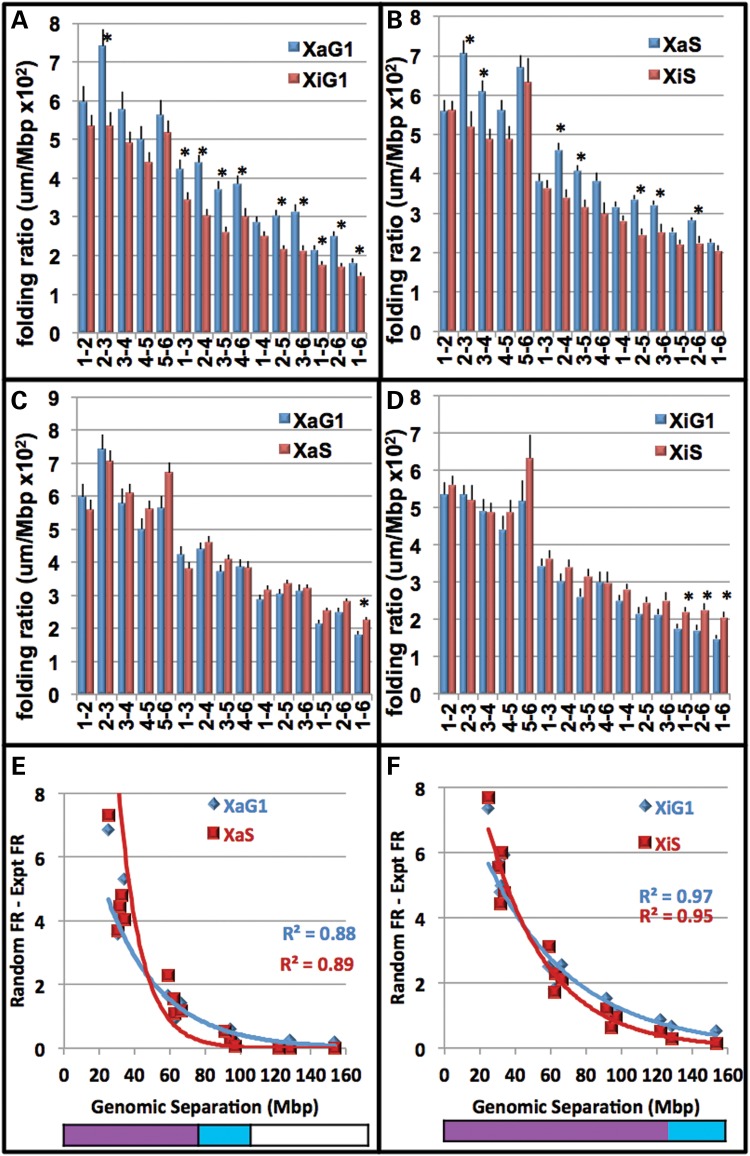
To further decipher the 3D folding of the six labeled regions within the CT, the spatial distances were expressed as a ratio of their respective sequence lengths along the chromosome (folding ratios, FR, microns per Mb, Figs. 6 and 7). Each CT displayed a unique FR profile of these 15 spatial distances (Figs. 6 and 7, Supplementary Material, Fig. S6) with different degrees of alterations in G1 versus S phase from 11 of 15 distances for CT17 to 3 of 15 distances for CT18. While Xi and Xa had only one and three cell cycle changes in FRs (Fig. 6C and D), comparision of Xa versus Xi at G1 and S revealed 10 and 15 differences, respectively, (Fig. 6A and B). Interestingly, a majority of the FR values in CTXa are significantly greater than those in CTXi (Fig. 6, t-test, P < 0.05).

Figure 6.

FRs of regions within the active and inactive CTX are nonrandom across large sequence lengths during the cell cycle. The FR is defined as the spatial distance (microns) between any two given regions divided by their respective Mb sequence length. A higher number indicates a greater distance per Mb. FRs were plotted for the 15 distances from FISH labeling of the six regions within CTXa (blue) and Xi (red) in G1 (A) and S (B). Error bars denote SEM. Ten significant differences (indicated by *) were determined between Xa and Xi in G1 and 7 in S (t test, P < 0.05). Comparisons of these FRs between G1 (blue) and S (red) are also shown for CTXa (C) and CTXi (D). One significant difference (*) was determined between G1 and S for CTXa and 3 for Xi (t test, P < 0.05). Next, six points were randomly generated within the experimental CT space. To determine the level of non-randomness across sequence lengths, the FRs for the distances between the experimental FRs (FRe) were subtracted from the corresponding random FRr. FRr − Fre values for all 15 pairwise distances within the CT are then plotted against their respective genomic separation (Mb) for CTXa (E) and CTXi (F). Positive FRr − FRe values occur when experimental distances are closer together than randomly generated points. A value of zero indicates that experimental and random regions are equidistant. Negative values occur when experimental distances are further apart than predicted by the random simulations. Trendlines within the graphs are exponential. The bottom color-bars indicate statistically significant differences between FRe and FRr (P < 0.05, t-test): blue, significant in G1; red significant in S; purple, significant in G1 and S; white, not significant.

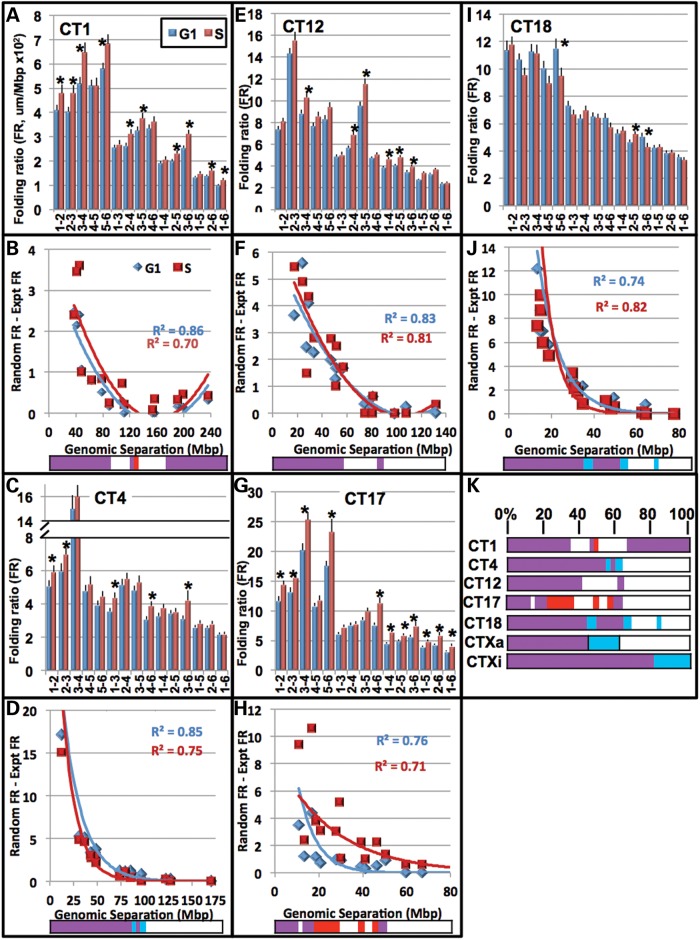
Figure 7.

FRs of regions within the autosomes are nonrandom across large sequence lengths during the cell cycle. The FR is defined as the spatial distance (microns) between any two given regions divided by their respective sequence length. A higher number indicates a greater distance per Mb (see Fig. 6 legend for more details). FRs were plotted for the 15 distances that result from FISH labeling of the six regions in G1 (blue) and S (red) for CT1 (A) CT4 (C), CT12 (E), CT17 (G) and CT18 (I). Error bars denote SEM. Significant differences between G1 and S (P < 0.05, t-test) are indicated with asterisks. FRr − FRe values for all 15 pairwise distances within the CT are then plotted against their respective genomic separations (Mb) (see Fig. 6 legend for more details) for CT1 (B) CT4 (D), CT12 (F), CT17 (H) and CT18 (J) in G1 (blue) and S (red). A positive FRr − FRe value indicates that randomly generated points are further apart compared with experimental. A value of zero indicates that random and experimental regions are equidistant and negative values demonstrate that experimental distances are further apart than predicted by random simulations. Trendlines within the CT1 and 12 graphs are quadratic, while those in CT4, 17 and 18 are exponential. The bottom color bars indicate statistically significant differences between FRe and FRr (P < 0.05, t-test): blue, significant in G1; red significant in S; purple, significant in G1 and S; white, not significant. Alignment of the significance color-bars for the subset of seven CT are displayed as the normalized percent of maximum separation in (K).

To determine the patterns of non-randomness across sequence lengths, the experimental FR (FRe) was subtracted from the random FR (FRr) for each individual pairwise combination of probes. Positive FRr − FRe values indicate that randomly generated points are further apart than the experimental. A value of zero would show that random and experimental regions are equidistant, while a negative value would reveal experimental distances that are further apart than predicted by the random simulations. FRr − Fre values for all 15 pairwise distances within the CT are then plotted against the respective genomic separation. This analysis revealed significantly closer distances than predicted by random simulations for all the CT (Figs. 6 and 7). As the sequence lengths between the regions increased, the experimental pairwise distances approached exponentially the pairwise distances calculated between randomly generated points (Figs. 6 and 7).

The sequence length at which the spatial distances become random-like was CT specific and revealed different patterns of non-random and random-like organization. For example, the distances in CTXi (in G1) were significantly nonrandom across the entire chromosome (∼150 Mb, Fig. 6F), while CT17 was significantly non-random only up to ∼18 Mb (Fig. 7H). In CT1 the distances become similar to a random distribution at ∼80 Mb, but subsequently folds back on itself to a non-random configuration at ∼160 Mb (Fig. 7). Interestingly, 160 Mb is also the length of genomic separation where the MSD regression plot shows a ‘bend’ for CT1 (Fig. 5C).

Furthermore, these FR profiles fit trendlines which are unique for each chromosome (Figs. 6 and 7). While the entire CT1 and 12 did not fit exponential trendlines, they did fit quadratic trendlines indicating that the ends of these CT fold back upon themselves (Fig. 7). This, however, was nonrandom only in the case of CT1 (Fig. 7). In contrast, the other CT fit exponential trendlines (Figs. 6 and 7) with differing coefficients and exponents (Supplementary Material, Fig. S7) indicating that each CT has its own nonrandom nature across sequence lengths. Moreover, if only the first ∼60% of CT1 or 12 is considered, they fit exponential trendlines (Supplementary Material, Fig. S8).

The relative sequence lengths at which distances are non-random (P < 0.05) or random are displayed as color-bar profiles with blue indicating significantly nonrandom in G1, red in S, purple in both G1 and S and white random in both G1 and S (Figs. 6 and 7). All the CT except CT12 displayed at least some differences between G1 and S in their color-bar profiles. While some regions are altered, non-randomness across large sequence distances is significantly maintained across the cell cycle. Moreover, when the distances from each individual position were plotted separately (e.g., 1–2, 1–3, 1–4, 1–5, and 1–6; 2–1, 2–3, 2–4, 2–5, 2–6; etc.), each region within the CT fit trendlines of different exponential values (Supplementary Material, Figs S8–14).The q arm of CT4 for example, conforms closer to an exponential trendline than its p arm counterpart. These finding indicate significant levels of heterogeneity in nonrandomness across the individual CT.

Best fit probabilistic 3D topologies of CT

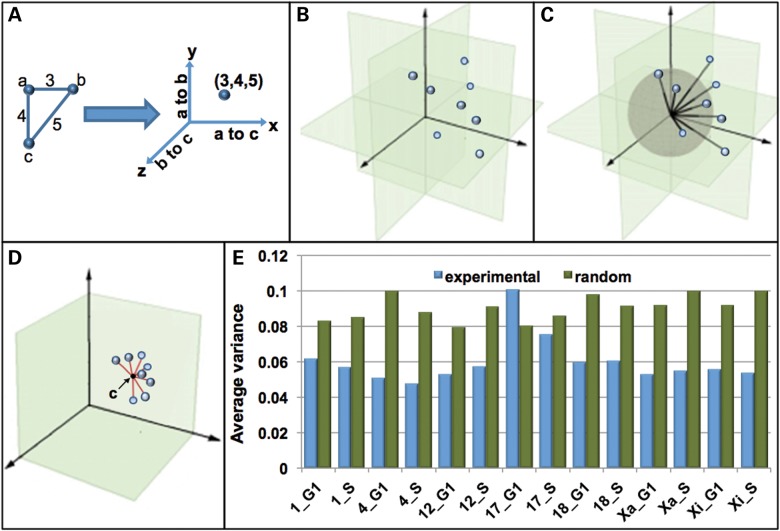
Based on the MSD profiles and FRs, we hypothesized that individual CT might have preferred topologies which potentially change across the cell cycle. We were particularly interested in determining whether CT are organized into 3D topological patterns and the probability with which CT fold into those patterns. To more concretely determine CT topology, a well-recognized clustering and pattern recognition algorithm (k-means (49–52), see Materials and Methods) was used to determine the degree of non-randomness in the 3D positioning of the 6 BAC probe positions within CT. In this approach the 15 point-to-point 3D distances (Fig. 5H) are plotted in a graph with 15 orthogonal planes (x, y, z, x′, y′, z′ etc.). The 15 distances for each CT are, therefore, represented by one point within this graph (Fig. 8B). Each point consequently has a line connecting it to the origin (Fig. 8C). These lines all intersect a sphere of a given size (Fig. 8C). In order to normalize CT of different sizes, each point is projected onto that sphere. The distances relative to the center of these points can be used to determine variability of the CT topologies (red lines in Fig. 8D, variance). The clustering program has the capacity to automatically categorize the points into groups (clusters) demonstrating the same 3D structure. In this study, each CT had points that fell under the same cluster (K-means = 1) and no variation in the topological arrangement was found within CT homologs. Furthermore, with the exception of CT17, random simulations revealed variance that ranged from 34 to 98% greater than that of the experimental data (Fig. 8E).

Figure 8.

CT 3D topology using a k-means based program. A geometric computational algorithm to determine the best fit 3D arrangement of the distance data sets for each CT was developed based on the k-means method. In this program each probe-to-probe distance (PPD) is plotted on an orthogonal plane such that all 15 distances within a CT are represented as a single point on a graph. A schematic diagram of this process (A) is shown for three hypothetical probes (a, b and c) with distances of 3 (a–b), 4 (a–c) and 5 (b–c). This is performed for all CT in the population (B). These points are connected to the origin by a line. All of these lines pass through a unit sphere depicted in gray (C). In order to normalize CT of different sizes, these points are then projected onto this unit sphere (D). The variance within the population is then measured as the distance from the center point within the cluster (black point, c) to each individual point (red lines). Smaller average distances relative to the center point indicate lower variability within the population (D). The average variances for each CT in G1 and S are shown and compared with random simulation (E). The center point within the cluster (c) will have 15 coordinates which correspond to 15 distances in 3D space.

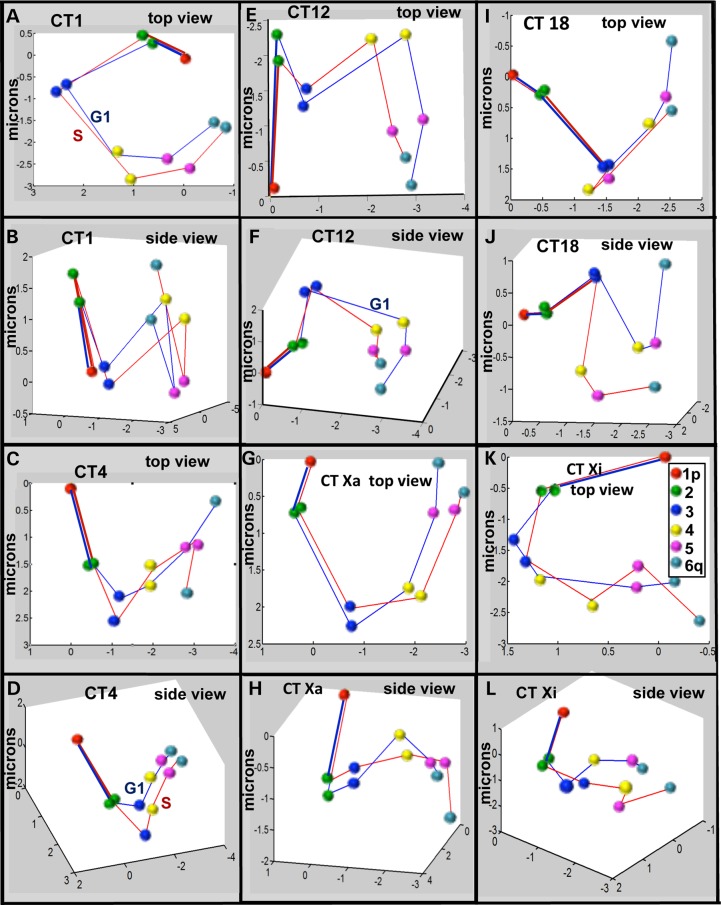
The center point within the cluster will have 15 coordinates which correspond to 15 distances in 3D space. These 15 distances represent the best fit from the overall population of six probe data analyzed by the k-means algorithm. Best fit models of the 3D topology were then determined from these center points by a realization algorithm that converts the 15 distances to the six coordinate points in 3D (see Materials and Methods for details) and are displayed in Figure 9. For ease of comparison between G1 and S, Position 1 and the trajectory to Position 2 within G1 and S were overlaid. We find that each CT has its own preferred topological model (Fig. 9) with CT1, 12 and Xa in G1 showing different degrees of bending back on themselves, while CT4, 18 and Xi are more linear.

Figure 9.

Probabilistic 3D models of CT topology. The 15 distances obtained from the coordinates of the center point of the population in the k-means algorithm are graphed and represent the best fit 3D probabilistic models of CT topology. Position 1 and the trajectory to position 2 are overlaid in order to compare topology between individual CT in G1 and S phase. The points corresponding to the 3D positions of the six probes are identified by the color scheme in (K) and are connected by blue lines for CT in G1 and red lines for CT in S. Top and side views of these 3D models are shown for CT1 (A, B), CT4 (C, D), CT12 (E, F), CTXa (G, H), CT18 (I, J) and CTXi (K, L).

The k-means 3D models of Figure 9 generally agree with the FR analyses and a manual visual categorization of individual image sets of CT (see Supplementary Material, Fig. S18). CT1 (G1 and S), CTXa (G1 and S) and CTXi (G1) appear loop-like from the top view. Upon rotation of the models, bending of the CT onto itself are observed in all cases except Xa in S phase which shows minimal bending. In contrast, CT4, 18 and Xi (S-phase) have a linear appearance from the top 2D view. This linearity (although in a zigzag manner) is maintained even when the CT are rotated 360°. The regions in CT12 are arranged in a ‘W-shaped’ conformation from the top view in both G1 and S phase. In 3D, however, the telomeric region bends back, especially in S phase. Importantly, the spatial distance plots for each CT (Fig. 5 and Supplementary Material, Fig. S16) fit similar trends as seen in this modeling, with CT1 and Xa (in G1 phase) bending back on itself and CT4, 18 Xa (in S phase) and Xi being linear. CT12 in S phase, which visually shows more bending than in G1 phase, was also found to fit better in a quadratic trendline (Supplementary Material, Fig. S16). These relationships were not seen in random simulations (Supplementary Material, Figs S5 and S17). The 3D models of all CT depict only minor alterations across cell cycle with the exception of CTXi. A bent CTXi in G1 becomes more linear in S phase. It is important to note that since the variance for CT17 indicates that there is a high degree of variability from cell to cell which is virtually random-like, no corresponding model is displayed for CT17.

Discussion

It is widely accepted that the 3D arrangement of CT and the spatial positioning of genes within them are linked to genomic function and regulation (1,5–11,14,53). Our understanding, however, of the 3D spatial arrangement of individual CT and their orientation within the cell nucleus is much more limited. With this in mind we have combined the tools of multi-fluor 3D FISH with a suite of computer imaging and geometric computational data mining algorithms to systematically investigate the organization of a subset of six chromosomes within the cell nucleus of WI38 normal diploid fibroblasts in the G1 and S periods of the cell cycle. This six chromosome subset was selected to be representative of the entire genome in chromosome size: (large—CT1, 4; intermediate—CT12, X; and small—CT17, 18); gene density: (high—CT17; intermediate—CT1, 12; low—CT4, X, 18) and gene activity (CTXa versus Xi). Within each of these CT, six regions including the sub-telomeric- p and q, centromeric, and three other approximately equidistant regions were labeled with BAC probes. The 3D distances were then determined among all the probes (15 measurements) as well as their positions within the overall CT and nucleus.

It is important to study nuclear positioning of different chromosomal regions because it is reflective of their gene density and transcriptional activity. It is well-established that heterochromatin is concentrated on the nuclear periphery while euchromatin is enriched in the nuclear interior (54–56). Moreover, at least in certain cell types, gene rich chromosomes are found more toward the inside of the nucleus (39,57). Within CT the gene rich and transcriptionally active regions are usually found at the chromosome border, while the gene poor regions are located more interiorly (58). Since different chromosomes have different arrangements across the sequence length of these gene rich and gene poor regions (34), our findings of differences in the positioning of six probes spanning each CT are likely reflecting the specificity of genomic expression at the global CT level. These results demonstrate common features as well as differences that are specific for the global arrangement of each CT. For example, the intrachromosomal arrangement of the BAC probes with respect to both the nuclear periphery and within the CT were specific for each CT and displayed only minor differences between G1 and S phase (Fig. 3). One exception was CT17 which displayed major differences between G1 and S phase in both these properties.

While it has been established that radial positioning of CT is either dependent on size or gene density (39,59,60), not many studies have focused on how the two CT homologs orient during interphase. A non-random chromosome orientation has been demonstrated such that both homologs of mouse CT11 were positioned either parallel to the periphery or with their telomeric or centromeric ends pointing toward the nuclear periphery or center (61). To gain insight into how CT homologs are oriented with respect to each other in the nucleus, we analyzed the distances between the six homologous probes (1a_1b, 2a_2b, etc) for each CT homolog pair (Fig. 4). Based on the pairwise homologous probe distances, we determined that: homologs CT4 and 12 (in G1) are positioned head to head (p telomere closest, q telomere farthest, Fig. 4); homologs CT1 (in G1) are oriented centromerically (centromeres are the closest); and homologs CT12 (in S phase) are bipartite (distances between first three probes shorter than last 3 probe). Since the differences in homologous probe distances in CT17, 18 and X were not statistically significant, we propose that these CT could be present laterally, head to end or patternless (Fig. 4). A random positioning between the two homologs of CTX was previously suggested, while CT7, 8 and 16 were reported to have a non-random preferential relative location of the two copies (62). Specificity in the spatial orientation of some of the CT homologs demonstrated in our study are consistent with previous studies demonstrating a non-random probabilistic arrangement of CT within the cell nucleus (21,22,24).

It has been demonstrated that the positioning of specific subchromosomal regions within the CT are altered in a physiologically responsive manner. Upon active expression certain genes are positioned on chromatin loops that project out of the CT. This has been demonstrated for the major histocompatibility complex on CT6 (63), HOX genes on CT11 (64), and the epidermal differentiation complex on CT1 (65). In contrast, some studies report that both active and inactive genes are found at the CT boundary (66) and that genes are evenly distributed throughout the CT regardless of their level of expression (67,68). Most recently, single-cell Hi-C studies confirmed earlier studies demonstrating that active domains tend to be at the interface of CT (69). Our analysis further revealed that at least one of the telomeres of each chromosome was located at or near the CT periphery. The most striking examples of this were the telomere regions of 17-q during S phase and Xi-p which were positioned on projections extending from the main CT body (Figs. 2 and 3). Interestingly, the labeled q-telomeric region of CT17 contains the gene for tubulin cofactor D, which is a cell cycle regulated protein and plays a role in cell division (70). Similarly, the pseudoautosomal region on chromosome X, which is homologous to a region on the Y chromosome and escapes X-inactivation (71), was found to be the most peripheral in the inactive X in comparison with all other regions in Xi or its Xa counterpart.

Numerous efforts have been made to explain chromatin folding within the CT in terms of polymer models (43–46). Studies involving both FISH and chromosome capture (3 C and Hi-C) techniques have been performed to fit chromosomes or regions of chromosomes to the proposed polymer models (47,72,73). While the Hi-C approach has been instrumental for understanding higher order chromatin domains of 1–10 Mb across the entire chromosome and defining specific sequences within these domains such as the TADs (74–76), the multi-FISH approach used in this study is necessary for analyzing sequences separated by the much larger genomic distances that range up to the full length of the chromosome (∼80–240 Mb). In the only previous whole chromosome study using microscopy, CT4, 5 and 19 were shown to behave according to a ‘random walk or giant loop’ based on a MSD analysis (43,45). These investigations demonstrated a large increase in MSD within ∼2 Mb followed by a much more gradual increase in MSD extending the length of each chromosome (43). In contrast, other studies over more limited genomic distances have shown that physical distances plateau beyond 5–10 Mb leading to several other models that also take into account functional properties of the genome (44,77). Mateos-Langerak et al. (44), for example, reported that within a 25–75 Mb window there is no increase in the average physical distance beyond 3–10 Mb in the q-arms of chromosomes 1 and 11.

Our studies of MSD demonstrate folding properties among this sub-set of 6 chromosomes that are chromosome specific. The gene poor CT4 and 18 increased linearly without reaching a plateau across the entire genomic sequence while the more gene rich CT1 and 12 increased at lower rates with CT12 approaching a plateau at very high genomic separation (≥100 Mb) and CT1 reaching a plateau at ∼ 100 Mb before bending back upon itself at ∼160 Mb (Fig. 5). In contrast, the very gene rich CT17 revealed wide scatter in MSD versus genomic separation in S phase and no significant differences in G1 phase across the entire chromosome. Random simulations plots of all the chromosomes were very different from the actual CT determinations and uniformly showed little or no changes in MSD across the entire simulated CT (Supplementary Material, Figs S5 and S17). We thus conclude that at large genomic separations each CT displays a different profile of genomic to spatial distances which are non-random with the exception of CT17 which is very similar to its random simulation.

Previously, it was reported that even within a small region of 4.3 Mb, the chromatin follows different folding properties (31). This argues for heterogeneity in the overall arrangements of different CT in the cell nucleus. Analysis of more individual chromosomes with these approaches should be helpful in developing more sophisticated models that fit the variety of CT topologies suggested by our findings and others.

Strikingly, the average MSD in CT17 were almost twice the distances observed in CT4 and CT18 for similar short range genomic separation. Previous studies have found higher spatial distance between two probes in the gene rich RIDGES than the gene poor anti-RIDGES (34,44). CT17 is gene rich and has been reported to have a much more open structural configuration as compared with the gene poor CT18 (37). Notably, CT4 is also the fourth most gene poor human chromosome (78). Similarly, the MSD found in the inactive X (CTXi) were significantly lower than not only its active counterpart (CTXa), but also other CT with comparable genomic separation. It has been previously reported that the inactive CTXi has a higher compaction (compaction factor = 1.9) and significantly shorter distances than Xa for genomic segments of ∼30–50 Mb (41). In active chromosomes, it has been shown that CT are composed of chromatin domain clusters which are surrounded by a channel system termed the interchromatin compartment (10,13). However within the inactive X CT this structure is collapsed and the chromatin domain clusters are much closer together (79). These studies are consistent with our studies comparing the inactive CTXi to other CT. Consequently, we hypothesize that gene density and gene activity significantly affect the overall CT topology.

To directly analyze the patterns of chromatin folding across the CT at the global level, we determined the FRs versus genomic separation. Each CT had a FR profile characteristic for that CT (Figs. 6 and 7). Gene rich CT17 and CT1 had the most differences in profile during the cell cycle, while the gene poor CT4 and 18 had considerably less alterations. CTX displayed minimal cell cycle differences, but striking profiles differences between Xa and Xi. This suggests a close relationship between gene activity and global folding of the X CT.

Comparison of the FR profiles of CT with random simulations revealed a high degree of non-randomness in these profiles. All the CT except CT17 showed large stretches (∼40–125 Mb) of non-random folding (Figs. 6 and 7). Moreover, the patterns of non-random folding were specific for each CT (Fig. 7K). CT1 showed the most unusual pattern with the two ∼80 Mb ends non-random and a central region predominantly randomly folded. This correlated precisely with the bending of this CT as determined by the MSD analysis (Fig. 5). The gene rich CT17 and intermediate gene dense CT12 had the highest levels of random folding (∼60–75%) while gene poor CT4 and 18 had significantly lower levels (>30%). The two X-CT homologs varied in nonrandom folding as well as having striking cell cycle differences with 100% versus ∼60% nonrandom folding in G1 and ∼80% versus ∼40% in S phase for Xi and Xa, respectively. The random-rich CT17 also displayed cell cycle differences in their profiles with significantly less random folding in S phase. Minor cell cycle differences were also detected for CT4 and 18 but the CT1 and 12 profiles were virtually identical in G1 and S phase. We conclude that each CT has a unique pattern of nonrandom folding which undergo minor alterations between G1 and S phase in some of the CT.

A number of investigations of higher order chromatin structure have applied computational geometric methods to 3D multi-FISH data ranging from the Mb level to the entire CT (34,35,41,80). For example, a novel data mining and pattern recognition algorithm termed the chromatic median has enabled elucidation of probabilistic networks of interchromosomal associations in the cell nucleus which were cell-type specific and highly altered in corresponding malignant breast cancer cells ((21–23,81). Other studies have looked at the shape and regularity of a large subset of CT using computational algorithms (37). A geometrical morphometrics approach and statistical shape theory for 3D reconstruction and visualization of the mean positions of five consecutive probes on a 3.7 Mb region of chromosome X provided the evidence for a non-random organization that differed between Xa and Xi (42). Similarly a nonrandom organization in a 4.3 Mb region of CT14 in mice was shown (31) and significant differences in organization in RIDGE and anti-RIDGE regions were demonstrated for chromosomes 1 and 11 in six different cell lines (34). Recently, integrated yeast 3C data were used to model 3D chromatin structures based on a Bayesian inference framework (82). This approach, however, is designed to model chromatin structure at a level ≤1 Mb.

The specificity and non-randomness in folding of the CT demonstrated in this study prompted us to determine if each CT had a preferred 3D arrangement. A classic clustering and pattern recognition algorithm (k means) was applied (49–52) to determine the best fit probabilistic arrangement (topology) in the 3D positioning of the six BAC probe positions within each CT. The analysis revealed that all the images evaluated for each CT cluster into a single most probable 3D arrangement and no significant differences were detected in the probe arrangements between CT homologs.

Comparisons with random simulations revealed that all the CT except CT17 showed significant levels of non-randomness in the preferred 3D models. CT1 (G1 and S), CTXa (G1 and S) and CTXi (G1) appear loop-like from the top view. Upon rotation of the models, a bending is observed in CT1, Xa and Xi (G1) onto itself. In contrast, CT4, 18 and Xi have a linear appearance from the top 2D view. This linearity (although in a zigzag manner) is maintained even when the CT are rotated 360°. The regions in CT12 (G1 and S) are arranged in a ‘W-shaped’ conformation from the top view, such that it appears to be linear and looping at the same time. This is in agreement with the MSD plot in which CT12 only moderately fit both linear and quadratic trendlines (Fig. 5E, Supplementary Material, Fig. S16E). Indeed, all the 3D models correlate well with the spatial positioning analysis. In addition, only minor alterations in 3D arrangement were detected across the cell cycle except for CTXi, which shows striking differences in conformation between G1 and S phases. CTXi appears loop like in G1 and becomes more linear in the S phase, which is also in accordance with the MSD analysis (Fig. 5B). It is important to note that since the variance for CT17 indicates that there is a high degree of variability from cell to cell which is virtually random-like, no corresponding 3D model is displayed for CT17.

In conclusion, while the recent advancements in chromosome capture techniques such as Hi-C enable identification of the intricacies of chromatin looping and folding, their application identifies specific DNA interactions within chromatin domains ≤10 Mb (74,76). Several physical models have been proposed to explain the organization of chromatin at even higher levels of organization but their application to resolving the global 3D topology of individual chromosomes has been limited (44). Our findings, using multi-FISH 3D imaging for six different chromosomes combined with computational and pattern recognition algorithms, establishes both specificity and uniqueness in the overall global folding of each chromosome as well as some cell cycle related alterations. We propose that these differences in structural organization and changes during the cell cycle are related to the global expression programs of the individual chromosomes.

Materials and Methods

Cell culture

WI38 (ATTC) were grown in advanced Dulbecco's Modified Eagle Medium supplemented with 10% serum and penicillin–streptomycin at 37°C, 5% CO₂.

Experimental design

A subset of six chromosomes was chosen ranging in size (large- chr1, 4; intermediate- chr12; small- chr17, 18) and gene density (low- chr4, 18; intermediate- chr1, 12; high- chr17). Chromosome X was chosen to study the differences between the inactive (Xi) versus the active homolog (Xa). Chromosome paints were labeled with DEAC (Chrombios GMBH, Nussdorf, Germany). Within each chromosome, six BAC probes (Health Research Incorporated at Roswell Park Cancer Institute) representing sub-telomeric- p and q, centromeric and three approximately evenly spaced regions (Table 1), were nick translated with digoxigenin (dig, invitrogen), biotin (bio, invitrogen) or DNP (Invitrogen, Carlsbad, CA) either alone or in combinations of dig-bio, dig-DNP or bio-DNP.

DNA FISH and immunofluorescence

Cells were grown on coverslips and pulsed with EdU (20 µM, Invitrogen) for 30 min. Cells were fixed with 4% paraformaldehyde for 10 min followed by 100 mm glycine/PBS washes (3×) for 20 min. Coverslips were stored in 50% formamide/2×SSC at 4°C for up to several days. Denaturation of cells was performed at 75°C for 9 min in 70% formamide/2×SSC. BAC probes representing selected regions (Table 1) were denatured for 10 min at 75°C. The cells were then hybridized with the probes and whole chromosome paints (DEAC fluorophore, Chrombios GMBH, Nussdorf, Germany) for 72 h followed by three post hybridization washes of 30 min each (wash I: 50% formamide in 2×SSC and 0.05% Tween; wash II: 2×SSC with 0.05% Tween; and wash III:1×SSC). Coverslips were then immunolabeled with anti-BIO rabbit, anti-DNP rat and anti-DIG sheep (1:50) antibodies for 1 h followed by incubation with anti-rabbit-alexa 647, anti-rat-alexa 488, anti-sheep-alexa 594 (1:50, Molecular Probes) for 35 min. DAPI was used to visualize the nuclei. Cells were mounted in vectashield/DAPI (1:2000, Vecta Laboratories) and 300–400 images were acquired with fluorescence microscopy. The coverslips were then removed from the slide and treated with the click-it EdU kit Alexa 488 (Life Technologies, Chicago, IL) following the manufacturer's protocol with minor variations. The coverslips were then remounted and the previously imaged cells were identified and re-acquired to identify EdU+ and EdU− cells. G2 cells were excluded manually by the visual presence of doublet signals for probes in EdU− cells.

Microscopy and image analysis

Images were acquired with an Olympus BX51 upright microscope (100×plan-apo, oil, 1.4 NA) equipped with a Sensicam QE (Cooke Corporation, USA) digital charge-coupled device camera, motorized z-axis controller (Prior) and Slidebook 4.0 software (Intelligent Imaging Innovations, Denver, CO). Optical sections were collected at 0.5 µm intervals through the z-axis. Nearest neighbor deconvolution was performed using Slidebook 4.0. The CT were segmented manually into binary images using ImageJ’s threshold feature. The CT borders in each section were visualized using a narrow range of thresholds to ensure proper thresholds were chosen. Furthermore, the selected threshold was decreased until background is excluded and the optimal threshold was reached (24). An in-house program called eFISHent (24), was used to measure in 3D a large number of parameters including: volumes, minimal border-to-border distances between CT (PBDs), distances between centers of gravity (PCDs), distances between peripheries and centers (PBCDs), the distance of the line projecting from the nuclear center through the center of the chromosome/BAC region to the nuclear periphery (subtended radii, SR), minimal peripheral distance to the nuclear periphery, centroid x, y, z coordinates and major and minor axes. The pairwise distances between BAC probes (PPD) are also measured. ∼50 image sets (100 chromosomes) were analyzed for each CT in each phase (G1 or S) of the cell cycle.

Random simulations

While many simulations are done using an artificial nucleus and preset volumes run many times (22), to more accurately mimic the experimental conditions, we have simulated the precise nuclear and CT volume and shape for each image set. The random simulation program reads the experimental data to determine whether probes were within the CT mask across the entire CT populations. The percent of probes which were outside each CT and the average distance from the CT boundary was calculated for those probes found outside the CT mask. Next the simulation program selected an equal number of points within and outside the experimental CT masks. These points were selected outside the CT space at similar distances from the CT boundary as the experimental data. These random simulations were then analyzed to determine the distance measurements precisely as the experimental data.

Identification of Xa and Xi territories

The images obtained after labeling CTX were merged with the DAPI image of the respective nucleus. The co-localization of one of the copies of CTX with the highly intense DAPI region in the nucleus (Barr Body) resulted in the identification of the X inactive (41). The Barr body was easily recognizable in ∼85% of the image sets. Image sets in which this distinction could not be made were not used for analysis.

Statistics

Averages and SEMs (STDEV function and dividing by the square root of n) were calculated using Microsoft excel. P-values were calculated using Microsoft excel's TTEST (two-tailed, heteroscedastic) function.

K-means and 3D modeling

Modeling to determine the most probabilistic arrangement of the six labeled regions for each CT was performed using a classic and well proven data mining and pattern recognition algorithm termed the k-means which has been successfully applied to a number of different problems in computer science (49–52). Briefly, within each CT, 15 point to point 3D distances are measured between the six labeled regions. Each distance is then plotted on an orthogonal plane such that all of the distances within a CT are represented as a single point on a graph (with 15 orthogonal planes). A schematic diagram of this process is shown for three probes a, b and c with distances of 3 (a–b), 4 (a–c) and 5 (b–c, Fig. 6A). This is done for all CT in the population (Fig. 6B). These points within the graph are normalized by projecting them onto a unit sphere (Fig. 6C). The variance within the population is then measured as the distance from the mean or center point within the cluster to each individual point (smaller average distance relative to the center point indicates a lower variability within the population, Fig. 6D).

For 3D modeling the mean point (which is the center of this cluster in 15 dimensions) is mapped back to the corresponding six points (called pattern points) in 3D space by using a 3D realization algorithm (developed by our group). In this realization process, the 15 pairwise distances between the 6 pattern points are optimized to be as close as possible to the 15 coordinates of the mean point. Once the 6 pattern points are generated, they can be viewed as a rigid structure in 3D space. To align this pattern with the six BAC probes of each chromosome, we first use a matching algorithm to determine the best rigid transform for the six BAC probes of each chromosome and then apply the resulting transform on the probes to achieve the best alignment (83).

Supplementary Material

Supplementary Material is available at HMG online.

Conflict of Interest statement. None declared.

Funding

This research was supported by grants from the National Institutes of Health (GM-072131) to R.B., the National Science Foundation (IIS-0713489, IIS-1115220 and IIIS-1422591) to J.X. and R.B. and the University at Buffalo Foundation (9351115726) to R.B.