Spatial sequence coding differs during slow and fast gamma rhythms in the hippocampus

SUMMARY

Spatiotemporal trajectories are coded by “theta sequences”, ordered series of hippocampal place cell spikes that reflect the order of behavioral experiences. Theta sequences are thought to be organized by co-occurring gamma rhythms (~25–100 Hz). Yet, the question of how sequences of locations are represented during distinct slow (~25–55 Hz) and fast (~60–100 Hz) gamma subtypes remains poorly understood. We found that slow gamma-associated theta sequences activated on a compressed time scale and represented relatively long paths extending ahead of the current location. Fast gamma-associated theta sequences more closely followed an animal’s actual location in real time. When slow gamma occurred, sequences of locations were represented across successive slow gamma phases. Conversely, fast gamma phase coding of spatial sequences was not observed. These findings suggest that slow gamma promotes activation of temporally compressed representations of upcoming trajectories, whereas fast gamma supports coding of ongoing trajectories in real time.

INTRODUCTION

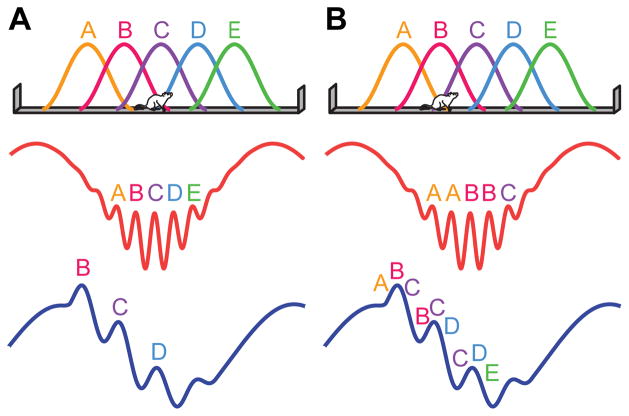
The hippocampus is central to episodic memory and spatial navigation (O'Keefe and Nadel, 1978), both of which rely on sequences of spatiotemporal information. “Theta sequences” (Dragoi and Buzsaki, 2006; Foster and Wilson, 2007; Gupta et al., 2012; Skaggs et al., 1996) are precisely ordered series of spikes from place cells, hippocampal neurons that fire in specific spatial locations (O'Keefe, 1976; O'Keefe and Dostrovsky, 1971). Theta sequences provide temporally compressed representations of spatial paths, which activate within individual cycles of the extracellular theta oscillation (~6–10 Hz) and may be important for encoding or retrieval of spatial memories (Dragoi and Buzsaki, 2006; Foster and Wilson, 2007; Gupta et al., 2012; Wikenheiser and Redish, 2015). A second type of oscillation in the hippocampus, gamma (~25–100 Hz), is thought to interact with theta to temporally organize theta sequences (Dragoi and Buzsaki, 2006; Gupta et al., 2012; Lisman, 2005; Lisman and Jensen, 2013). The prevailing theory of how sequences of spatial locations are represented within theta-nested gamma rhythms posits that discrete spatial locations, not sequences of locations, are coded within individual gamma cycles (Dragoi and Buzsaki, 2006; Jensen and Lisman, 1996; Lisman and Jensen, 2013). A hypothesis that arises from this theory is that spatial paths represented during slow gamma are shorter than paths represented during fast gamma (Figure 1A), because fewer slow gamma cycles than fast gamma cycles occur within a theta cycle (Belluscio et al., 2012).

Figure 1. Schematics illustrating two theories of theta-nested gamma rhythms.

(A) The first schematic illustrates the leading theory of gamma coding during theta sequences. According to this theory, longer paths are coded during fast gamma than during slow gamma. This is because more gamma cycles occur within a theta cycle during fast gamma, and, according to this theory, discrete locations (i.e., A–E) are coded within individual gamma cycles. (B) A novel theory of theta-nested gamma, supported by our present results. In this theory, longer paths are coded during slow gamma than during fast gamma. This is because sequences of locations, rather than single locations, are coded within individual slow gamma, but not fast gamma, cycles.

Accumulating evidence indicates that slow and fast gamma rhythms represent distinct processing states in the hippocampal network. Slow and fast gamma occur on distinct theta phases (Colgin et al., 2009), and different types of hippocampal processing also occur on distinct theta phases (Hasselmo et al., 2002). Additionally, slow and fast gamma exhibit different relationships with behavior (Cabral et al., 2014; Carr et al., 2012; Kemere et al., 2013; Takahashi et al., 2014; Yamamoto et al., 2014; Zheng et al., 2015). Also, place cells represent space differently during slow and fast gamma, coding locations ahead of the animal during slow gamma and behind the animal during fast gamma (Bieri et al., 2014). Yet, the question of whether longer sequences are represented during fast gamma and shorter sequences during slow gamma, as hypothesized above, has not yet been investigated. The current study addresses this gap in knowledge by comparing spatial trajectories coded by place cell ensembles during theta sequences associated with slow or fast gamma. The results support a novel model of spatial sequence coding during theta-nested slow and fast gamma rhythms (Figure 1B).

RESULTS

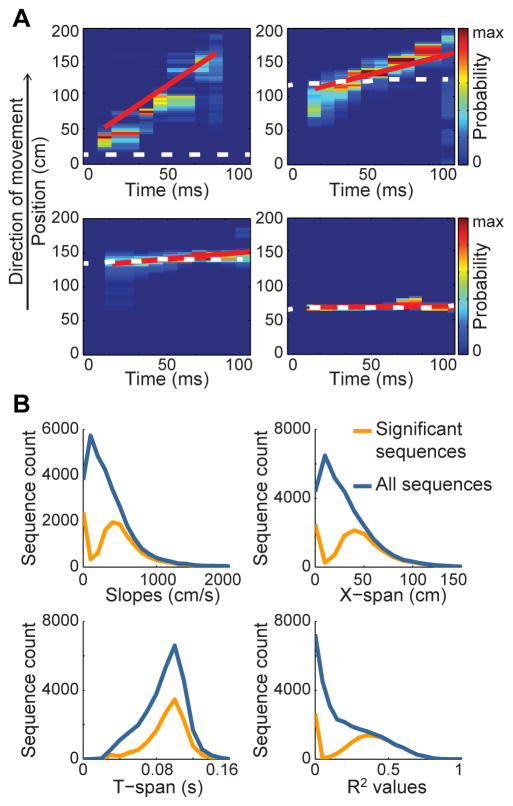
The local field potential (LFP) and spiking activity from 604 place cells were recorded in hippocampal area CA1 (Figure S1) of 7 rats traversing a linear track. The spatial path represented by place cell ensemble activity during individual theta cycles was estimated using a Bayesian decoding approach (Bieri et al., 2014; Brown et al., 1998; Gupta et al., 2012; Jensen and Lisman, 2000; Zhang et al., 1998; see Experimental Procedures). A regression line was fit to the position estimates from each decoded “theta sequence” of place cell spikes (Figure 2A). The regression line was subsequently used to measure the slope (cm/s), distance (‘x-span’, cm), and duration (‘t-span’, ms) of each sequence (Figure 2B). Each of these measures provides information about how spatial trajectories are represented by theta sequences. Slope measures the spatial distance represented by a sequence in a given amount of time and thus can be used to quantify temporal compression of sequences. ‘X-span’ estimates the length of a represented trajectory, and t-span reflects the time period of sequence activation. Sequences of ordered locations that were unlikely to arise by chance were classified as “significant sequences” (see Experimental Procedures). Theta sequences have previously been defined as sequences that occur in forward order (Foster and Wilson, 2007; Gupta et al., 2012), or in other words exhibit a “sweeping forward structure” (Feng et al., 2015). Thus, it is unclear how to interpret theta sequences with negative slopes (i.e., sequences occurring in reversed order). For this reason, theta sequences with negative slopes were excluded from analyses presented in the main text (analyses of sequences with negative slopes are shown in Figure S2). Sequences with negative slopes (n = 17193) constituted a minority of the total sequences (n = 48098), and only a minority (36%) of sequences with negative slopes were defined as significant. In contrast, a majority (64%) of sequences exhibiting positive slopes were defined as significant.

Figure 2. Characterization of theta sequences.

(A) Example theta sequences showing the animal’s actual location (white dotted line), the predicted location based on Bayesian decoding of ensemble place cell activity (color-coded according to probability), and the associated best fit regression line (red line). (B) The distribution of slopes, x-span, t-span, and R² values of the regression lines for significant sequences (orange) and all decoded sequences (blue). See also Figure S1.

Sequences of place cells represent longer and more temporally compressed paths during slow gamma than during fast gamma

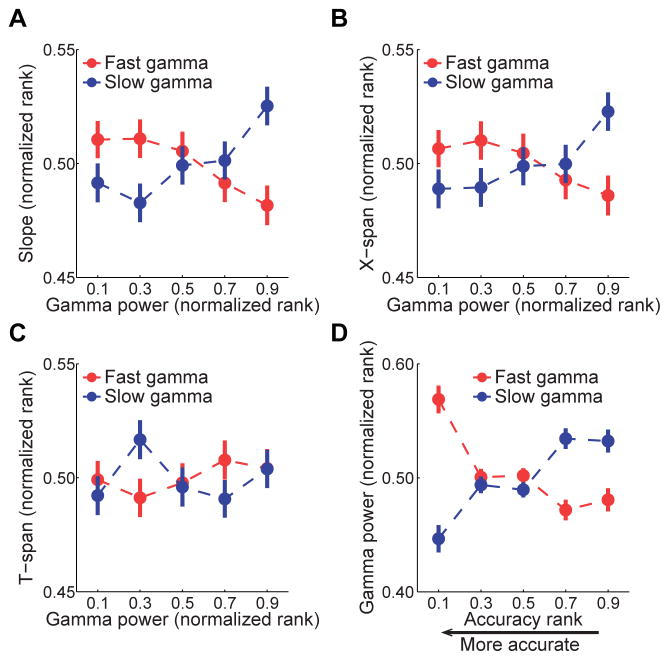
Theta sequences provide compressed representations of sequences of locations (Dragoi and Buzsaki, 2006; Foster and Wilson, 2007; Gupta et al., 2012; Skaggs et al., 1996), and ensembles representing different locations are thought to be activated within separate gamma cycles (Dragoi and Buzsaki, 2006; Gupta et al., 2012; Harris et al., 2003). If individual locations within a path are represented within discrete gamma cycles, then longer paths should be represented on a faster time scale during fast gamma compared to slow gamma (Figure 1A). To test this hypothesis, we first examined the relationship between slow and fast gamma power and the slope of the regression line, which measures the degree of temporal compression of sequences. Specifically, temporally compressed sequences represent longer distances per unit time and are thus associated with steeper slopes, whereas sequences with flatter slopes (i.e., closer to 0) more closely represent current location. We compared slope values during slow gamma-associated theta sequences and fast gamma-associated theta sequences (“slow gamma sequences” (n = 2958) and “fast gamma sequences” (n =2883); see Experimental Procedures; examples shown in Figure 3). We found that slopes were significantly higher during slow gamma sequences than during fast gamma sequences (503.2 ± 7.5 vs. 473.9 ± 7.4 cm/s; Z = 3.4, p = 0.001, Mann Whitney U-test). The difference between slopes increased when we compared slow and fast gamma sequences exhibiting maximal slow and fast gamma power, respectively (i.e., top 20% of slow or fast gamma sequences, ranked according to increasing power; 544.2 ± 18.8 vs. 481.8 ± 18.2 cm/s; Z = 2.8, p = 0.006). Thus, we next tested whether temporal compression of significant sequences increased as a function of slow gamma power and decreased as a function of fast gamma power. Using the combined set of slow and fast gamma sequences, we found a significant interaction effect of gamma power and gamma type (i.e., slow or fast) on slope (Figure 4A; multiple regression model interaction term; b = 0.09, t(11678) = 4.6, p < 0.001), suggesting that temporal compression of sequences was differentially affected by slow and fast gamma. Slow gamma power and slope were positively correlated (Figure 4A; b = 0.04, t(5839) = 3.0, p = 0.001), supporting the hypothesis that temporal compression of sequences increased as slow gamma rhythms increased. In contrast, slopes decreased as fast gamma power increased (Figure 4A; b = −0.04, t(5839) = −3.2, p = 0.001).

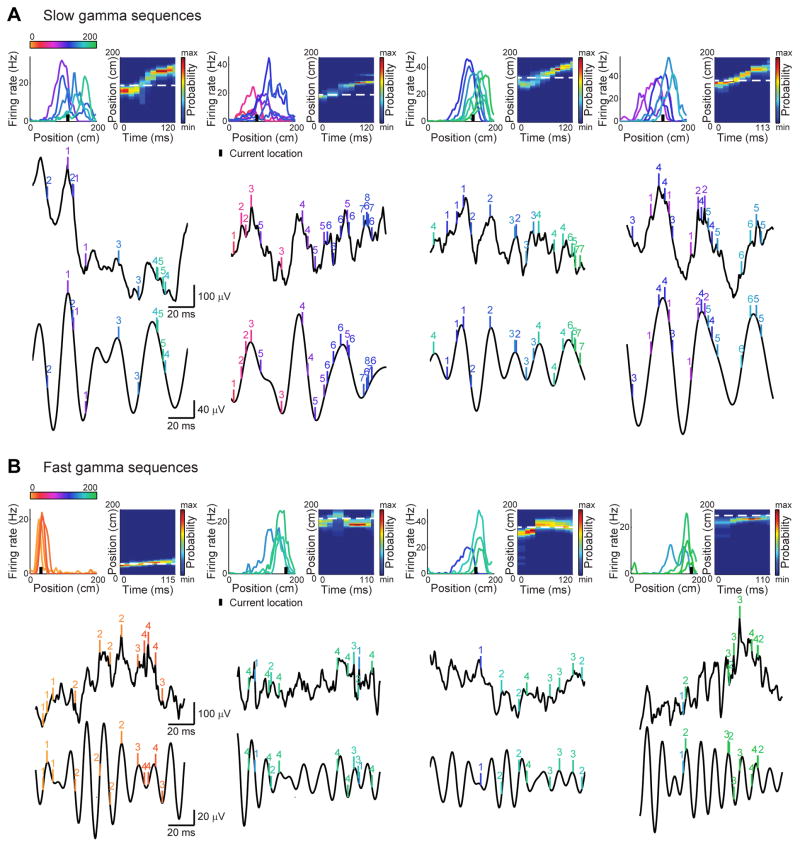
Figure 3. Example slow gamma sequences and fast gamma sequences.

Examples were selected from five different rats. (A) Examples of slow gamma sequences. The top row (left) shows rate maps for ensembles of simultaneously recorded place cells, ordered according to their place fields’ centers of mass (color-coded according to center of mass locations on the track). The black bar indicates the animal’s current location. The top row (right) shows color-coded spatial probability distributions (resulting from Bayesian decoding analyses) for the example theta sequences. White dashed lines indicate animals’ actual locations. The middle row shows raw CA1 recordings, and the bottom row shows corresponding slow gamma bandpass-filtered (25–55 Hz) versions. Vertical tick marks indicate spike times from the corresponding place cell ensembles. Each cell’s number identifier indicates its order within the theta sequence. (B) Same as (A) but for example fast gamma sequences.

Figure 4. Effects of fast and slow gamma power on properties of theta sequences.

Slope, x-span, and t-span measures were ranked across all significant sequences and normalized, such that 0 indicates the lowest value and 1 indicates the maximal value. Gamma power measures were ranked separately for each gamma type. (A) Sequence slope increased with slow gamma power and decreased with fast gamma power. (B) Path length (x-span) increased with slow gamma power and decreased with fast gamma power. (C) Temporal duration (t-span) of sequences did not change depending on gamma. (D) Sequence accuracy relative to the animal’s actual location was estimated based on slope and mean prediction error (see Experimental Procedures). High fast gamma power was associated with high accuracy, and high slow gamma power was associated with low accuracy. Data are shown as mean ± SEM. See also Figures S2–S4.

The finding that sequences represent more space per unit time during slow gamma may reflect an increase in the length of the represented path during slow gamma, or representation of similar path lengths across shorter periods of time. To distinguish these possibilities, we separately analyzed x-span (i.e., length of decoded trajectory) and t-span (i.e., temporal duration of activation) of each sequence. First, we compared x-span values during slow and fast gamma sequences. We found that x-spans were significantly longer during slow gamma sequences than during fast gamma sequences (45.0 ± 0.6 vs. 42.9 ± 0.6 cm; Z = 2.9, p = 0.004). The effect size increased when we compared those slow and fast gamma sequences with particularly strong gamma (i.e., top 20% of slow or fast gamma sequences, ranked by ascending power; 47.7 ± 1.4 vs. 43.6 ± 1.5 cm; Z = 2.4, p = 0.02). We next tested whether x-span measures changed according to slow or fast gamma power. We found that x-spans were differentially related to slow and fast gamma power (Figure 4B; multiple regression model interaction term; b = 0.07, t(11678) = 3.9, p < 0.001). Slow gamma power and x-span were positively correlated (Figure 4B; b = 0.04, t(5839) = 3.0, p = 0.003), indicating that relatively long paths were represented when robust slow gamma rhythms were present. In contrast, x-span decreased significantly with increasing fast gamma power (Figure 4B; b = −0.03, t(5839) = −2.5, p = 0.01). These findings suggest that place cells represent longer paths during slower gamma rhythms, which is unexpected considering how spatial locations are thought to be coded during theta-nested gamma (Figure 1A). This same pattern of results was maintained when sequences with negative slopes were included in analyses and when relatively flat slopes and relatively steep slopes were analyzed separately (Figure S3). Also, the results were not explained by changes in animals’ running speed, acceleration, or jerk (Figure S4 A–C), nor position on track or time within a testing session (Figure S4 D–E).

In contrast to x-span results, t-spans of slow and fast gamma sequences were not different (78.2 ± 0.5 ms for slow gamma sequences and 78.4 ± 0.5 ms for fast gamma sequences; Z = 0.7, p = 0.4). Also, no significant gamma power by gamma type interaction was found for t-span (multiple regression model interaction term; b = −0.01, t(11678) = −0.8, p = 0.4), and t-span did not change as a function of gamma power (b = 0.004, t(11678) = 0.5, p = 0.7; Figure 4C). These findings suggest that sequences of place cells activate across similar time periods regardless of gamma power or gamma type.

Sequences of place cell spikes more accurately represent ongoing trajectories during fast gamma than during slow gamma

The finding that shorter and longer paths are represented during fast and slow gamma, respectively, suggests that spatial representations more closely follow an animal’s current position during fast gamma but extend a greater distance away from the current position during slow gamma. To test this hypothesis, we devised a metric that combined slope and prediction error measures to assess accuracy of decoded sequences. A sequence was considered accurate (i.e., the decoded path closely tracked the animal’s actual position) if it had a flat slope and a low prediction error (see Experimental Procedures). We found that different gamma types showed different relationships to accuracy (Figure 4D; multiple regression model interaction term; b = 0.2, t(11678) = 8.1, p < 0.001). High fast gamma power correlated with high accuracy (b = −0.09, t(5839) = −5.4, p < 0.001), whereas high slow gamma power correlated with low accuracy (b = 0.1, t(5839) = 6.1, p < 0.001). These findings suggest that sequences more accurately follow an animal’s current location during fast gamma than during slow gamma.

Prediction error was calculated by subtracting the actual position from the decoded position; thus, positive prediction errors indicate that decoded positions are ahead of the actual position, whereas negative prediction errors indicate that decoded positions are behind the actual position. Our previous results showed that place cells tend to code positions ahead of the animal during slow gamma and behind the animal during fast gamma (Bieri et al., 2014). We tested whether place cells were again more likely to code positions ahead of the animal during slow gamma and behind the animal during fast gamma in our present data set (which includes 604 CA1 cells, 351 of which were also used in the Bieri et al. study; see Experimental Procedures). Consistent with our previous results, prediction errors were significantly higher during slow gamma than during fast gamma (Z = 5.0, p < 0.001, Mann-Whitney U-test). Also, prediction errors were significantly positive during slow gamma (Z = −3.25, p = 0.001, Wilcoxon Signed Ranks Test) and significantly negative during fast gamma (Z = −5.34, p < 0.001, Wilcoxon Signed Ranks Test). The above collection of results suggests that place cells code relatively long paths extending ahead of the current position on a compressed time scale during slow gamma and code ongoing paths on a slower time scale during fast gamma.

Slow gamma phase coding of spatial information

Place cell spikes occur at progressively earlier theta phases as an animal moves through a cell’s place field, and thus spikes’ theta phases provide spatial information (“theta phase precession”; O'Keefe and Recce, 1993; Skaggs et al., 1996). However, current hippocampal gamma theories assume that gamma phase variations do not code spatial information (Lisman and Jensen, 2013). Yet, the phase of ~30 Hz gamma oscillations in prefrontal cortex was shown to code the order of sequentially presented objects (Siegel et al., 2009), raising the possibility that slow gamma phase coding of sequences also occurs in the hippocampus. If sequences of locations, not individual locations, were represented at different phases within slow gamma cycles, it would help explain why relatively long paths are represented on a relatively compressed time scale during slow gamma (Figure 1B).

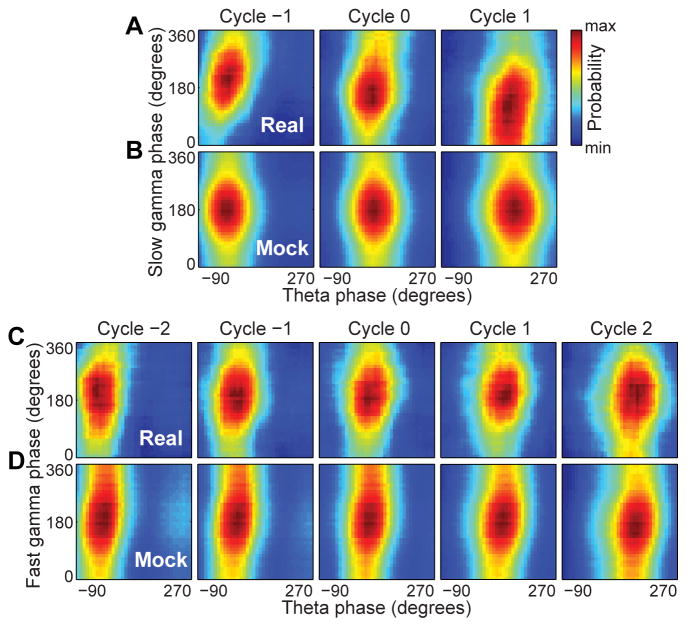
To address the question of whether slow or fast gamma phases code spatial information, we assessed whether slow and fast gamma phases of spikes changed systematically as theta sequences progressed (Figure 5). We ordered individual gamma cycles during fast gamma sequences and slow gamma sequences (3 and 5 gamma cycles per theta cycle for slow and fast gamma, respectively; Figure S5A–E), centered at the gamma cycle with the highest number of spikes (cycle ‘0’; Figure S5F, I). Cycles occurring before cycle 0 were labelled with descending integer values, and cycles occurring after cycle 0 were labelled with increasing integer values. The slow gamma phase of place cell spikes significantly shifted across successive slow gamma cycles (Figure 5A; W(4) = 125.2, p < 0.001; p < 0.001 for all pairwise comparisons; Multi-sample Mardia-Watson-Wheeler test). In contrast, place cells did not shift their fast gamma firing phase preference across successive fast gamma cycles (Figure 5C; W(8) = 8.3, p = 0.4). Slow gamma phase variations across cycles were not due to differences in spike density (Figure S5G–H, J–K).

Figure 5. Slow gamma phase precession.

Gamma cycles within theta cycles were ordered, centered at cycle 0 (i.e., gamma cycle with maximal spiking). (A) Probability distributions of slow gamma phases of spikes across slow gamma cycles within slow gamma sequences. Slow gamma phases of spikes shifted systematically across successive slow gamma cycles. (B) Probability distributions of mock slow gamma phases of spikes across mock slow gamma cycles in slow gamma sequences. Mock slow gamma spike phases did not shift significantly across mock slow gamma cycles within slow gamma sequences. Preferred spike phases shifted significantly less across mock cycles than across real slow gamma cycles. (C) Probability distributions of fast gamma phases of spikes across successive fast gamma cycles within fast gamma sequences. Spikes’ preferred fast gamma phase did not significantly change across successive fast gamma cycles. (D) Probability distributions of mock fast gamma phases of spikes across mock fast gamma cycles generated from fast gamma sequences. Preferred firing phases of spikes within mock fast gamma cycles did not change significantly across the sequence. See also Figure S5.

Theta phase precession has previously been shown to be slightly disrupted during periods of slow gamma, with spikes tending to occur across a more limited range of theta phases during slow gamma than during fast gamma (Bieri et al., 2014). This finding was maintained in the present data set. Theta phase distributions of spike times during slow and fast gamma sequences were significantly different (data randomly downsampled such that each cell had equal numbers of phase estimates in slow and fast gamma sequences, as in Bieri et al. (2014); Watson-Wheeler test, W(2) = 6.6, p = 0.04). For each cell, we also compared theta phase precession for slow and fast gamma sequences using circular-linear regression analysis (Kempter et al., 2012; Schlesiger et al., 2015). For cells exhibiting significant theta phase-position correlations (i.e., significant circular-linear correlations) during both slow and fast gamma sequences, we found significantly different theta phase-position correlations for slow and fast gamma sequences (Chi-square goodness-of-fit test, X²(4) = 21.5, p = 0.0003). Specifically, theta phase precession slopes for fast gamma sequences were significantly more negative than slopes for slow gamma sequences (paired t-test, t(78) = 2.1, p = 0.04).

Still, theta phase precession was largely maintained during slow gamma. Thus, it is possible that the observed slow gamma phase precession was simply an epiphenomenon of theta phase precession. That is, slow gamma phase precession could occur as a result of segmentation of theta sequences. To test this possibility, we cut each slow gamma-associated theta cycle into contiguous segments using a “period” randomly selected from the range of slow gamma periods (i.e., 1/55–1/25 second). The slow gamma phases for each of these mock slow gamma cycles were assigned by designating the first and last time points in the mock gamma cycle as 0 and 360 degrees, respectively, and linearly interpolating phase values for intervening time points. Theta and mock gamma phases of spikes occurring within these mock slow gamma cycles were measured. For each slow gamma sequence, this procedure to produce mock slow gamma cycles and associated slow gamma spike phases was repeated 1000 times and averaged to generate the probability distributions shown in Figure 5B. Although theta phases of spikes advanced in both real and mock data sets, slow gamma phase precession was not apparent across mock slow gamma cycles (Figure 5B). The mean phase shift across successive slow gamma cycles for the real data was −46.0 degrees, which was significantly different than the phase shifts observed across the sets of successive mock slow gamma cycles (−0.01 ± 2.9 degrees, mean ± angular deviation; 95% confidence intervals for mock data: [−5.7, 5.7] degrees, p < 0.0001). This finding supports the conclusion that slow gamma phase precession was not epiphenomenal to theta phase precession and segmentation of theta sequences. Analogous analyses were performed for fast gamma (Figure 5D), using contiguous segments with periods randomly selected from the range of fast gamma periods (i.e., 1/100–1/60 second). Not surprisingly, considering that spikes did not exhibit fast gamma phase precession in the real data, mock fast gamma phases of spikes did not systematically change across successive mock fast gamma cycles (Figure 5D). The mean phase shift across successive real fast gamma cycles was −6.0 degrees, which was not significantly different than the phase shifts across mock fast gamma cycles (−6.2 ± 2.9 degrees, mean ± angular deviation; 95% confidence intervals for mock data: [−11.9, −0.4] degrees, p = 0.95). These results were maintained when an alternative method was used to construct mock gamma cycles (Figure S5L).

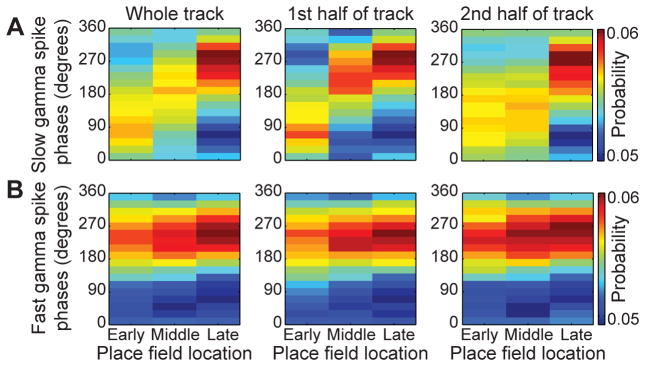
The finding that slow gamma phases of groups of place cell spikes change systematically across theta sequences raises the hypothesis that slow gamma phases of spikes code spatial information. To test this hypothesis, we investigated whether place cells fired on different gamma phases depending on the location of their place fields. We grouped place cells that fired during each theta sequence into three categories based on the location of their peak firing rate along the trajectory of the track. “Early” place cells fired near the beginning of the trajectory, “middle” place cells fired in the middle, and “late” place cells fired near the end. We then estimated the mean phase of slow or fast gamma at which spikes occurred for place cells within each spatial category. Spike phases during slow gamma sequences were significantly different depending on spatial category (Figure 6A; W(4) = 81.0, p < 0.001; Multi-sample Mardia-Watson-Wheeler test), with early and late slow gamma phases coding early and late place field locations, respectively. On the other hand, spike phases during fast gamma sequences did not change significantly across place field locations (Figure 6B; W(4) = 7.0, p = 0.1). The results were not due to a differential distribution of slow and fast gamma across different track locations (Bieri et al., 2014) because the effects persisted when sequences occurring on the first and second halves of the track were analyzed separately (Figure 6A & 6B; first half of the track, W(4) = 41.5, p < 0.001 for slow gamma phases and W(4) = 3.3, p = 0.5 for fast gamma phases; second half of track, W(4) = 55.1, p < 0.001 for slow gamma phases and W(4) = 2.4, p = 0.7 for fast gamma phases). These findings suggest that slow gamma phases provide information about spatial location, whereas fast gamma phases do not code spatial information.

Figure 6. Slow gamma phases coded spatial information, but fast gamma phases did not.

Place cells were categorized by their place field location (‘Early’, ’Middle’, and ‘Late’ correspond to place fields near the beginning, middle, and end of the track, respectively). (A) Cells fired on different phases of slow gamma according to their place field location, for slow gamma sequences that occurred across the whole track (left), on the first half of the track (middle), or on the second half of the track (right). (B) Cells tended to fire on a similar fast gamma phase, regardless of where their place field was located or where their corresponding fast gamma sequence occurred on the track. See also Figure S6.

A previous study described two classes of place cells that fire at different phases of gamma (trough-firing pyramidal cells, termed “TroPyr”, and rising phase-firing pyramidal cells, termed “RisPyr”; Senior et al., 2008). This previous study did not distinguish between slow and fast gamma, leaving open the possibility that each place cell class is selectively driven by a gamma subtype. The gamma phase of TroPyr and RisPyr spikes varied differently across a theta cycle (Senior et al., 2008), which could be related to the different gamma phase variations exhibited by spikes during slow and fast gamma. This proposition was not supported by the present data, however. Although slow and fast gamma power were negatively correlated, as reported previously (Colgin et al., 2009), firing rates of individual cells were positively correlated during slow and fast gamma sequences (Figure S6). This finding suggests that place cells are equally active during either gamma type and not selectively activated during slow or fast gamma.

Number of fast gamma cycles per theta cycle increases with path length

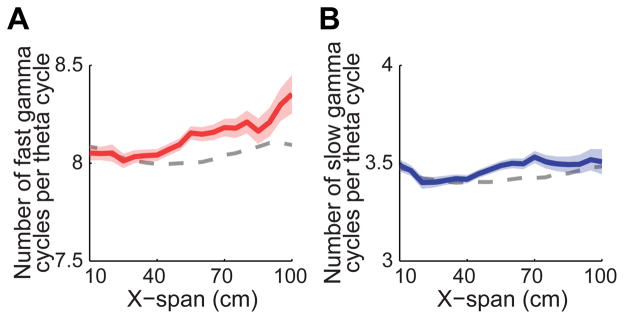
A previous study showed that the number of gamma cycles within a theta sequence increases with increasing path length (Gupta et al., 2012). However, this study measured gamma across a broad range of frequencies (i.e., 40–100 Hz). Here, we investigated whether the number of gamma cycles within a theta sequence changed with path length separately for slow and fast gamma (Figure 7). We found a significant interaction effect between path length and gamma type on number of gamma cycles within a theta cycle (multiple regression model interaction term; b = −0.002, t(5571) = −2.1, p = 0.04). The number of fast gamma cycles within a theta sequence was positively correlated with path length (Figure 7A; b = 0.002, t(2761) = 3.2, p = 0.001), but the number of slow gamma cycles per theta sequence did not significantly change with path length (Figure 7B; b = 4.8×10⁻⁴, t(2810) = 0.8, p = 0.4). These results are consistent with the hypothesis shown in Figure 1B. That is, if sequences of locations are represented within slow gamma cycles, then the number of slow gamma cycles would not be expected to change much with path length. However, if different locations are represented across successive fast gamma cycles, then the number of fast gamma cycles would increase with increasing path length, as was observed. These fast gamma findings are consistent with previously reported results (Gupta et al., 2012). Gupta and colleagues reported ~11–12 gamma cycles within a theta cycle. This relatively high number of gamma cycles per theta cycle is consistent with fast gamma but not slow gamma (Belluscio et al., 2012; Figure S5A–E); that is, ~11 slow gamma cycles would span ~275 ms and thus would not fit within the time span of a theta cycle (i.e., ~125 ms).

Figure 7. Number of gamma cycles per theta cycle increased as a function of decoded path length for fast gamma but not slow gamma.

For fast gamma sequences (A), the number of fast gamma cycles per theta cycle increased as a function of x-span. For slow gamma sequences (B), the number of slow gamma cycles per theta cycle did not significantly change as a function of x-span. The expected gamma cycle count versus path length relationships (gray dashed lines) were estimated based on relationships of path length and gamma cycle count to running speed (see Experimental Procedures), as in an earlier study (Gupta et al., 2012). Data are presented as mean± SEM.

DISCUSSION

These data show that sequences of place cell spikes code relatively long trajectories that extend ahead of the animal on a compressed time scale within slow gamma cycles. Slow gamma phases of place cell spikes were found to progressively decrease as animals advanced through series of locations, with early and late slow gamma phases representing early and late locations, respectively. In contrast, place cell ensembles more accurately represented current locations during fast gamma. Spikes occurred at similar fast gamma phases, regardless of sequence progression or spatial information carried by the spike.

Place cells have previously been shown to predict upcoming locations (Muller and Kubie, 1989). Such predictive firing during active navigation has been observed at decision points and linked to subsequent goal destinations (Johnson and Redish, 2007; Wikenheiser and Redish, 2015). Predictive firing by place cells has also been associated with the occurrence of slow gamma (Bieri et al., 2014). In addition, slow gamma has been shown to be enhanced when previously experienced sequences guide an animal’s path (Cabral et al., 2014). Sequences are believed to be stored in, and retrieved from, CA3 (Jensen and Lisman, 1996; Levy, 1996; Wallenstein et al., 1998; Wallenstein and Hasselmo, 1997), and CA3 transmits activity to CA1 during slow gamma (Colgin et al., 2009; Kemere et al., 2013; Schomburg et al., 2014). This collection of findings supports the hypothesis that slow gamma promotes the retrieval of place cell sequences from CA3 as animals plan and envision future trajectories. However, this kind of predictive function would require temporal compression of spatial sequences to allow a rapid “look ahead”, and the afore-mentioned studies did not investigate how this would occur. The present results suggest a way in which such temporal compression arises during theta-related behaviors. Specifically, sequential locations may activate at the slow gamma time scale during retrieval, thereby providing a more compressed time scale than the theta time scale of encoding.

The present results were limited to theta-related behaviors (i.e., active movement). However, sequences also activate in a temporally compressed manner during sharp wave-ripples (SWRs) (Diba and Buzsaki, 2007; Lee and Wilson, 2002; Nadasdy et al., 1999), and sequences replayed during awake SWRs were recently shown to predict animals’ future trajectories toward goal locations (Pfeiffer and Foster, 2013). Interestingly, slow gamma increases during awake SWRs, with stronger slow gamma coinciding with higher fidelity replay (Carr et al., 2012). Considering these prior findings from SWR-associated behaviors together with the current results during theta states raises the possibility that slow gamma promotes temporally compressed spatial memory representations during both active exploration and rest. However, different mechanisms likely regulate sequence compression during SWRs compared to sequence compression during theta. Hippocampal neurons receive high frequency shunting inhibition during ripples, preventing most cells from firing (English et al., 2014). This shunting inhibition likely prevents spikes from occurring across a wide range of slow gamma phases, as was seen in the present study. In line with this viewpoint, trajectories coded within SWRs jumped from one location to another across slow gamma cycles (Pfeiffer and Foster, 2015), rather than activating within slow gamma cycles.

Regarding the functional significance of fast gamma, previous studies have shown that fast gamma links CA1 to inputs from the medial entorhinal cortex (Colgin et al., 2009; Kemere et al., 2013; Schomburg et al., 2014), which convey information about current location (Brun et al., 2002; Hafting et al., 2005; Zhang et al., 2013). Additionally, place-based navigation is thought to rely on fast gamma (Cabral et al., 2014), and place cells represent recent locations, not upcoming locations, during fast gamma (Bieri et al., 2014). Also, fast gamma frequencies increase with increasing running speeds, which may enable faster transitions across sequentially coded locations as running speeds increase (Ahmed and Mehta, 2012; Zheng et al., 2015). These findings support the hypothesis that fast gamma supports coding of current spatial positions, rather than activating previously stored memories. The present results provide additional support for this hypothesis by showing that fast gamma sequences code relatively short paths that closely follow an animal’s position in real time.

In addition, our findings provide the first evidence of gamma phase coding of spatial sequences and reveal that phase coding occurs selectively during slow gamma. Specifically, sequences of locations were represented within individual slow gamma cycles, with increasing slow gamma phases coding successive positions within a spatial sequence (Figure 6). It is unlikely that this finding relates to theta phase shifts of slow gamma amplitude peaks that have been reported at increased running speeds in mice (Chen et al., 2011), firstly because our mock slow gamma results do not support this conclusion (Figure S5L). Moreover, we did not observe such shifts in rats (Zheng et al., 2015). The observed slow gamma phase precession contrasts with prevailing theories of spatial coding during theta-nested gamma, which assume that discrete locations are coded within individual gamma cycles and that gamma phase variations do not provide spatial information (Dragoi and Buzsaki, 2006; Jensen and Lisman, 1996; Lisman, 2005; Lisman and Jensen, 2013). However, there is a precedent for slow gamma phase coding of sequences. In the prefrontal cortex, different phases of ~30 Hz gamma have been shown to code series of items maintained in short-term memory (Siegel et al., 2009). In contrast to slow gamma, we found no evidence of fast gamma phase coding. Spikes preferentially occurred at the same fast gamma phase across successive fast gamma cycles within a theta sequence, in agreement with theories of theta-nested gamma in the hippocampus (Dragoi and Buzsaki, 2006; Jensen and Lisman, 1996; Lisman, 2005; Lisman and Jensen, 2013).

The ability of the hippocampus to handle sequences of spatiotemporal information is a dynamic process, involving both encoding of ongoing events and retrieval of previously stored memories. Earlier work indicated that encoding and retrieval optimally occur at different theta phases (Hasselmo et al., 2002). At the encoding phase, inputs from entorhinal cortex dominate, and long-term potentiation in hippocampal synapses is enhanced. At the retrieval phase, inputs from CA3 are strong, whereas inputs from entorhinal cortex and long-term potentiation mechanisms are attenuated. The hypothesis that fast and slow gamma play roles in encoding and retrieval, respectively, is consistent with this earlier work in that fast and slow gamma preferentially occur at different theta phases (Colgin et al., 2009). However, in the earlier study (Hasselmo et al., 2002), encoding and retrieval occurred within the same theta cycles, whereas the present results, and previous results (Colgin et al., 2009), have found that slow and fast gamma tend to occur on different theta cycles. This difference may be explained by the behavioral tasks. In the present study, and in Colgin et al. (2009), rats were merely running through familiar environments. In tasks explicitly requiring encoding and retrieval, perhaps slow and fast gamma would be observed more often on the same theta cycles.

The current study suggests a possible mechanism for achieving dual encoding and retrieval functions through different gamma subtypes. During sequence retrieval, an initial cue may trigger the first ensemble in a linked sequence of place cell ensembles. The relatively long slow gamma period may then allow successive items within the stored sequence to be retrieved rapidly, until gamma-modulated inhibition (Buzsaki et al., 1983; Penttonen et al., 1998; Soltesz and Deschenes, 1993) arrives and shuts down place cell firing. In contrast, the short period of fast gamma may ensure that only one cell assembly is activated per fast gamma cycle. This type of scheme may be well-suited for coding sequences of discrete locations in ongoing behavior, preventing preemptive retrieval of locations that previously followed the current location but may or may not become part of the current trajectory. These dual slow and fast gamma mechanisms may also explain how spatial memories can be encoded in real time but later retrieved in a time-compressed manner.

EXPERIMENTAL PROCEDURES

Subjects

Seven male Long-Evans rats weighing ~350–500 g and ~4–10 months of age were used in the study. Data from four of these rats were included in a previous study (Bieri et al., 2014). Rats were maintained on a reverse light/dark cycle (lights off from 8 a.m. to 8 p.m.) and tested during the dark phase. After surgery, animals were singly housed in cages (40 cm x 40 cm x 40 cm) constructed from clear acrylic and containing enrichment materials (e.g., plastic balls, cardboard tubes, and wooden blocks). Rats recovered from surgery for at least 1 week prior to the start of behavioral testing. During the data collection period, rats were placed on a food deprivation regimen that maintained them at ~90% of their free-feeding body weight. All experiments were conducted according to the guidelines of the United States National Institutes of Health Guide for the Care and Use of Laboratory Animals under a protocol approved by the University of Texas at Austin Institutional Animal Care and Use Committee.

Recording drive implantation

Recording drives were surgically implanted above the right hippocampus (in mm: AP 3.8, ML 3.0, DV 1 in six rats; AP 5.0, ML 5.0, DV 1 in one rat). Bone screws were placed in the skull, and the screws and the base of the drive were covered with dental cement to affix the drive to the skull. Two screws in the skull were connected to the recording drive ground.

Testing procedures

Following the post-surgery recovery period, rats were trained to run three 10-minute sessions per day on a linear track. The linear track was 2 m long, 10 cm wide, and placed 64 cm above the floor. Rats were trained to run back and forth on the track, receiving small pieces of sweetened cereal or vanilla cookies at the ends. Every rat was trained on the linear track for at least 3 days prior to the start of recording to ensure familiarity with the environment. Between recording sessions, rats rested for ~10 minutes in a towel-lined, elevated ceramic container.

Results, statistics, and data analyses

Data were analyzed using custom software written in MATLAB (MathWorks, Natick, MA), unless indicated otherwise. Statistics were computed with MATLAB, SPSS 22 (IBM), R 3.1.1 (R Foundation for Statistical Computing, Vienna, Austria), and Oriana 4.02 (Kovach Computing Services, Pentraeth, Wales, UK). Mann-Whitney U-tests were used to compare sequence properties for slow gamma sequences and fast gamma sequences. Wilcoxon signed-rank tests were used to test if mean prediction errors during slow gamma and fast gamma sequences were significantly different from zero. Multiple regression analyses were applied to test for gamma type × gamma power interaction effects on theta sequence properties. Then, linear regression analyses were performed separately for each gamma type to test for correlations between gamma power and theta sequence properties. Comparisons of gamma phase distributions across successive gamma cycles (Figure 5), or across different place field location categories (Figure 6), were performed using multi-sample Mardia-Watson-Wheeler tests. Data are presented as mean ± SEM, unless indicated otherwise. Additional analysis methods are described in detail below and in the Supplemental Experimental Procedures.

Detecting individual theta cycles for Bayesian decoding

LFP signals were band-pass filtered for theta (6–10 Hz) and delta (2–4 Hz), and the time-varying power for each was determined as described in the “Oscillatory power estimation” section of the Supplemental Experimental Procedures. For theta cycle selection, a single LFP signal was chosen for each session by identifying the channel with the highest time-averaged theta power and at least one recorded CA1 cell. Periods of theta activity were defined using the theta-delta power ratio (Csicsvari et al., 1999). Specifically, theta power was required to be at least three times greater than delta power. Data with insufficient theta activity were not included in analyses. Individual theta cycles were cut at the theta phase with the lowest number of spikes (typically at the peak or close to the peak) from all recorded CA1 cells during that session.

Bayesian decoding analyses

The most likely position represented by spiking activity from CA1 place cells was estimated using a Bayesian decoding approach (Bieri et al., 2014; Brown et al., 1998; Gupta et al., 2012; Jensen and Lisman, 2000; Zhang et al., 1998). Recording sessions with fewer than 20 cells were not analyzed, and only theta cycles containing at least three active place cells and a running speed greater than 5 cm/s were decoded. Place fields were constructed for each recording session on the linear track, as described in the ‘‘Place fields’’ section of the Supplemental Experimental Procedures. Decoding was performed for each theta cycle using a 40 ms sliding time bin shifted by 10 ms at each step. The probability of the animal to be at position x, given the number of spikes n from each cell collected in the time bin t was estimated using Bayes rule:

$$P(x\mid n)=\frac{P(n\mid x)\times P(x)}{P(n)}$$

P(n|x) was estimated using the firing rates from the experimentally obtained place fields in the same 10 minute linear track session. It was assumed that the firing rates of different place cells were statistically independent and that the number of spikes from each cell followed a Poisson distribution (Jensen and Lisman, 2000; Zhang et al., 1998). P(n), the normalizing constant, was set so that P(n|x) summed to 1. P(x) was set to 1.

Theta sequence analysis and significance determination

Theta sequences were characterized by first determining the longest contiguous set of time bins (length of each bin = 40 ms, 10 ms sliding window) that contained spikes. If spikes did not persist across an entire theta sequence, then contiguity was considered to be broken when there were 2 or more adjacent time bins (i.e., 50 ms or longer) without spikes. The temporal duration of the longest set of contiguous time bins was defined as the “t-span” of the sequence. For each time bin within the t-span, 1000 spatial positions were randomly selected from a weighted distribution, i.e., the probability distribution P(x|n) of positions obtained from the Bayesian decoding analyses (see above), and fit with a regression line. The slope of the regression line defined the slope of the theta sequence. The path length (“x-span”) of the theta sequence was defined as the difference between positions associated with the start and end of the regression line.

To determine if a theta sequence was significant, we employed the following shuffling approach. For each sequence, we circularly shifted the probability distribution of estimated positions by a random distance at each time bin 1000 times (same as “column-cycle” shuffle described in Davidson et al., 2009 for sharp wave-associated sequences). Two methods were used to detect significant sequences. First, we compared the R² value of the linear regression of each sequence to its corresponding shuffled versions to determine significance. Specifically, sequences with an R² value > 95% of R² values for shuffled data were classified as significant sequences. However, this classification excluded sequences that accurately followed an animal’s actual position and thus exhibited R² values that were close to 0 (see Figure 2). In order to allow such sequences to be defined as significant, we used a second definition of significance for those sequences with R² values close to 0 (i.e., lowest 10% of R² values). For these sequences, the residual sum of squares (RSS) of the linear regression was compared between each sequence and corresponding shuffled versions. These sequences were then defined as significant if they exhibited an RSS value < 95% of RSS values for shuffled data.

Because theta sequences have previously been defined as sequences occurring in a forward order (Foster and Wilson, 2007), sequences with negative slopes were excluded from all analyses, except Figure S2, in which sequences with negative slopes were analyzed separately. Theta sequences with negative slopes may represent a different phenomenon with different underlying mechanisms than theta sequences with positive slopes, considering that reverse replay during awake sharp waves is thought to arise from different mechanisms and serve a different function than forward replay (Colgin and Moser, 2006; Diba and Buzsaki, 2007; Foster and Knierim, 2012; Foster and Wilson, 2006).

Categorization of slow gamma sequences and fast gamma sequences (Figures 3–7 & Figures S3–S6)

To categorize slow and fast gamma sequences, significant sequences were first ranked according to their slow gamma power and fast gamma power (ranked separately for slow and fast gamma). A rank of 0 corresponded to lowest power, and a rank of 1 corresponded to highest power. Slow gamma sequences and fast gamma sequences were then defined as those significant sequences exhibiting power rank values for the gamma type of interest that were above 0.5 and power rank values for the other gamma type (i.e., not the gamma type of interest) that were below 0.5.

The total number of theta sequences detected was 48098. Of the 48098 sequences, 18059 were defined as significant; 13537 of these significant sequences had positive slopes (i.e., activated in forward order). Of the 13537 significant sequences with positive slopes, 2958 were classified as slow gamma sequences, and 2883 were classified as fast gamma sequences.

Sequence accuracy (Figure 4D)

To assess how accurately a theta sequence represented an animal’s current location, we applied the following method to the combined set of slow and fast gamma sequences. First, two measures, slope and mean prediction error (i.e., the average difference between the actual position of the animal and the position of the regression line that was fit to the sequence), were separately ranked. Lower rank values corresponded to lower numerical values. The slope rank and the mean prediction error rank for each sequence were then averaged and normalized between 0 and 1 to create an accuracy measure. Accuracy measures close to 0 corresponded to high accuracy, and accuracy values close to 1 corresponded to low accuracy (i.e., accuracy scores were high when slopes and prediction errors were low, and accuracy scores were low when slopes and prediction errors were high).

Phase analyses

The time varying phases of slow gamma, fast gamma, and theta were determined by Hilbert transformation of respective bandpass filtered signals (25–55 Hz for slow gamma, 60–100 Hz for fast gamma, and 6–10 Hz for theta). Oscillatory peaks were defined as 0° for theta, and oscillatory troughs were defined as 0° for slow and fast gamma. Degrees were defined in this way to allow plotting from 0° to 360° for both theta and gamma, given that cycles were cut according to the phase associated with minimal spiking (peak-to-peak for theta and trough-to-trough for gamma; see “Detecting individual theta cycles for Bayesian decoding” section above and Figure S5).

Estimation of gamma phase shifts across gamma cycles (Figures 5 & S5)

The gamma cycle with maximal spiking across all simultaneously recorded cells was defined as cycle 0 (Figures S5F & S5I). Cycles occurring before cycle 0 were numbered with decreasing integer values, and cycles occurring after cycle 0 were numbered with increasing integer values. Incomplete cycles at the beginning or end of the sequence were excluded from analyses. Gamma phases and theta phases of spike times were estimated for place cells that spiked within at least 2 slow gamma cycles within a theta cycle or at least 3 fast gamma cycles within a theta cycle. The number of cycles analyzed within each theta sequence was limited to 3 (cycles -1 to 1) for slow gamma and 5 (cycles -2 to 2) for fast gamma. These selection criteria correspond to the estimated average number of cycles encompassed within a gamma episode, based on the well-defined theta-gamma coupling bands seen in Figures S5A & C. 2–D histograms of gamma phases and theta phases for spikes from each cycle number were plotted using 30° bins, and were smoothed across 5 bins.

Categorization of place cell locations (Figure 6)

Within each significant slow or fast gamma sequence, active place cells were ordered according to the spatial location of their peak firing rate using all spikes recorded within a given session. The peak firing positions of active cells in each sequence were ranked, and then normalized between 0 and 1, in order to group cells into three categories. The cells representing relatively early locations (i.e. closest to the beginning of the track, 0 (start position) < peak firing position rank ≥ 1/3), middle locations (i.e. 1/3 < peak firing position rank ≥ 2/3), and relatively late locations (i.e. 2/3 < peak firing position rank < 1 (end position)) were placed in “Early”, “Middle” and “Late” categories, respectively. Histograms of spike phases for each spatial category were plotted using 20° bins and smoothed across 7 phase bins.

Number of gamma cycles as a function of path length (Figure 7)

Individual gamma cycles were defined from trough to trough, using the time point closest to when the gamma phase was 0°. For each significant slow or fast gamma sequence, the total number of slow or fast gamma cycles per theta cycle was counted, and the corresponding x-span (i.e., path length of decoded sequence) was found. The expected gamma cycle number vs. x-span relationship, based solely on the relationships of these variables to running speed, was estimated by multiplying the gamma cycle number vs. running speed relationship by the running speed vs. x-span relationship (as in Gupta et al., 2012). The gamma cycle number vs. running speed relationship was estimated by calculating the average number of gamma cycles per theta cycle for each set of sequences falling within a given running speed bin (bin width = 5 cm/s). The running speed vs. x-span relationship was determined by creating an n₁ × n₂ matrix, where n₁ is the running speed bin number and n₂ is the x-span bin number. For each element in the matrix, the number of sequences exhibiting that particular set of running speed and x-span values was then counted. The number of sequences within each x-span column of the matrix was then normalized across running speeds such that summation of the measures within each column = 1.