Ultrafast fiber lasers based on self-similar pulse evolution: a review of current progress

Abstract

Self-similar fiber oscillators are a relatively new class of mode-locked lasers. In these lasers, the self-similar evolution of a chirped parabolic pulse in normally-dispersive passive, active, or dispersion-decreasing fiber (DDF) is critical. In active (gain) fiber and DDF, the novel role of local nonlinear attraction makes the oscillators fundamentally different from any mode-locked lasers considered previously. In order to reconcile the spectral and temporal expansion of a pulse in the self-similar segment with the self-consistency required by a laser cavity's periodic boundary condition, several techniques have been applied. The result is a diverse range of fiber oscillators which demonstrate the exciting new design possibilities based on the self-similar model. Here, we review recent progress on self-similar oscillators both in passive and active fiber, and extensions of self-similar evolution for surpassing the limits of rare-earth gain media. We discuss some key remaining research questions and important future directions. Self-similar oscillators are capable of exceptional performance among ultrashort pulsed fiber lasers, and may be of key interest in the development of future ultrashort pulsed fiber lasers for medical imaging applications, as well as for low-noise fiber-based frequency combs. Their uniqueness among mode-locked lasers motivates study into their properties and behaviors and raises questions about how to understand mode-locked lasers more generally.

1. Introduction: limits to nonlinear pulse propagation in dispersive media

Numerous variations of interferometry, spectroscopy, and microscopy are now ubiquitous techniques in science and technology, and have enabled many important developments in both. Ultrafast optical pulses are increasingly common in modern laboratories, typically on the scale of femtoseconds (10^–15s) but occasionally reaching the attosecond regime (10^–18 s) [1, 2]. These pulses provide the finest temporal resolution currently possible as well as the greatest peak intensities. They are therefore enabling scientific and technological tools, not only for ultrafast time-resolved measurements and frequency metrology, but for high-intensity physics, precise materials-processing, and surgery. Mainstream applications in chemical analysis, medical imaging and manufacturing are emerging. To enable these mainstream applications as well as to lower the cost and expertise required of research users, ultrafast fiber lasers are an important technology. In recent years, ultrafast fiber lasers have just begun to compete in performance with conventional sources. Although they lag behind in many important respects, they provide significant advantages in terms of cost, complexity, and maintenance, and many sources are now commercially available.

In the rest of this section we will give an accessible overview of existing mechanisms of pulse formation in mode-locked lasers based on the concepts of average-cavity solitons and dissipative solitons. A recent review on average-cavity dispersion-managed solitons was written by Turitsyn et al [3]. An introduction to normal-dispersion lasers was provided by Wise et al [4]. A more technical review of lasers based on normal dispersion is by Renninger et al [5], and a broader overview of dissipative solitons was provided by Grelu and Akhmediev [6]. While this article focuses on self-similar fiber oscillators, a more general review of self-similarity in ultrafast optics was written by Dudley et al [7]. In the next section, we will briefly review progress on self-similar oscillators where self-similar evolution occurs in a passive fiber (passive similariton, or passive self-similar, lasers). Then, we will discuss more intensively the recent progress on oscillators incorporating self-similar evolution in a gain fiber (amplifier similariton, or active self-similar, lasers). We will then touch on self-similar lasers in other contexts, and highlight the differences between passive and active similariton lasers. Finally, we will describe some new developments extending the latter beyond the limits of the gain medium, and discuss future possibilities for this work.

In most femtosecond-pulse lasers, pulse formation results from the average balance of up to several different forces that act on the electric field envelope in the laser cavity, leading eventually to a stationary self-consistent pulse. As the pulse modifies the local refractive index via the optical Kerr effect, it imposes a self-phase modulation (SPM) on itself which depends on the shape of the pulse. Pulses called solitons are characterized by an envelope phase balance: their shape causes a self-phase modulation which precisely cancels the phase that arises from linear group-velocity dispersion (GVD). Hence, they maintain a constant temporal phase and pulse shape as they propagate. In addition to these phase modulations, amplitude modulations of the envelope may also contribute to pulse shaping. These modulations are dissipative processes, caused by linear or nonlinear gain and loss, such as by a spectral filter or saturable absorber. Most often, phase modulations are of primary importance and the resulting pulses have a constant temporal phase (i.e. unchirped). Relatively recently, dissipative solitons (DS) have emerged as an important alternative, where the phase and amplitude modulations are of roughly equal importance, and where the pulses may have more complex temporal phases.

The most common femtosecond lasers are based on soliton pulse formation. In general, laser cavities contain a variety of components which have different GVD, leading to a position-dependent GVD referred to as a ‘dispersion map’. When the average GVD of a cavity is anomalous, soliton-like pulses will form as the nonlinear self-phase modulation will balance the GVD in an average sense [8–11]. In 1984, it was demonstrated that a pair of prisms can provide adjustable anomalous GVD with low loss [12]. Although the majority of femtosecond lasers contain almost exclusively materials with normal dispersion at the lasing wavelength, prism pairs or other geometric means allows averaged-cavity soliton pulse formation in a variety of situations and wavelengths. In all cases, saturable absorbers and spectral filters may play secondary roles in stabilizing the pulse and allowing the laser to start from noise.

The average-cavity soliton picture applies to a variety of lasers. Er-doped fiber lases near 1550 nm, in the anomalous-dispersion regime of fused silica. Er:fiber lasers therefore operate in the soliton mode (except when the waveguide dispersion is deliberately stronger than the material dispersion, as in dispersion-shifted fiber). For Yb:fiber and Ti:sapphire, devices like fiber Bragg gratings, dispersion-engineered photonic crystal fiber, or prism pairs and chirped mirrors, can add anomalous dispersion beyond the normal dispersion of the silica fiber or sapphire crystal. This can make the average-cavity dispersion anomalous and therefore allow the cavity to support soliton-like pulse-formation. Although the parameters vary by several orders of magnitude among these systems, they are qualitatively similar. Much of this understanding stems from modelling the nonlinear propagation of the electric field pulse envelope by the cubic Ginzburg–Landau equation (CGLE),

$$\frac{\partial A(z,t)}{\partial z}=(g-l)A(z,t)+\left(\frac{1}{\Omega }-\mathrm{i}\frac{D}{2}\right)\frac{{\partial }^{2}A(z,t)}{\partial t^2}+(\alpha +\mathrm{i}\gamma ){\mid A(z,t)\mid }^{2}A(z,t)$$ (1)

with the terms on the right side corresponding to the gain and loss, gain dispersion/spectral filtering, GVD, saturable absorption, and self-phase modulation respectively. The CGLE is an average-cavity equation: the parameters correspond essentially to the cavity-averaged values. Note that the imaginary terms on the right correspond to phase modulations and the real terms correspond to amplitude modulations. In absence of the latter, the CGLE is simply the common nonlinear Schrödinger equation (NLSE), whose fundamental soliton solutions are the basis for soliton mode-locked lasers. Hence although all stationary solutions of the CGLE are strictly speaking dissipative solitons (their existence is characterized by a balance between loss and gain), we refer to these anomalous-dispersion solutions with the shorthand ‘soliton pulse-formation’ to emphasize the fundamental importance of the phase-modulations. This terminology reflects how the NLSE soliton acts as an average-cavity nonlinear attractor even in the presence of some amplitude modulations.

An important, related class of average-cavity solitons in mode-locked lasers is the normal-dispersion dissipative solitons of the CGLE with an additional quintic nonlinear gain/loss term, δ|A|⁴A, i.e. the cubic-quintic GLE [6, 13]. With normal average cavity dispersion (D positive) and self-focusing media (γ positive, which is the case for most transparent materials), balance of the phase-only terms is impossible. However, self-phase modulation generates new frequencies at the edges of the pulses. A spectral loss element, such as spectral filter or the limited gain bandwidth of the gain medium, may therefore act as a temporal amplitude modulator that can balance the linear spreading of the pulse from GVD. Amplitude modulations are therefore on equal footing with phase modulations. To differentiate from the solitons above, we use the shorthand terminology ‘dissipative soliton pulse-formation’. For DS pulse-formation, the saturable absorber is key in allowing the laser to start from noise and stabilizing it in the steady-state, and (in contrast to the solitons discussed above) its characteristics also influence the exact shape of the stable soliton.

All average-cavity lasers are limited by the maximum nonlinear self-phase modulation that can be balanced by other effects. A pulse with intensity I(t,z) accumulates a temporal nonlinear phase shift

$${\Phi }^{\mathrm{NL}}(t,z)=\frac{\omega }{c}\int n_{2}I(t,z)\mathrm{d}z$$ (2)

At some critical level of nonlinear phase shift (roughly π and 10π for soliton and DS pulse formation respectively [14]), balance becomes impossible; the pulse cannot be stabilized. In the mode-locked laser, the laser either cannot be mode-locked or pulses undergo fission into multiple stable pulses per round trip. In the former case, before reaching steady-state a pulse formed from noise experiences wave-breaking [15] and eventually disintegrates. The enhanced nonlinear interaction length in a waveguide compared to in homogenous media is therefore a primary challenge in generating high-power pulses from fiber lasers. This is because a relatively low energy pulse in fiber can experience a much higher nonlinear phase shift than in an oscillator without a waveguide.

For solitons, an effective way of reducing nonlinearity is to force the pulse to temporally ‘breathe’. This is done by placing alternating segments of large normal and anomalous GVD with nearly identical magnitudes, so that the pulse duration oscillates periodically. This evolution gives rise to the so-called dispersion-managed soliton. For all fiber lasers, a common approach to avoid excessive nonlinear phase is to simply reduce the intensity by increasing the mode diameter of the fiber [16–20]. Although this approach works well to increase the pulse energy, fibers with increasingly large mode area (LMA fibers) tend to sacrifice many practical benefits of fiber, including flexibility, insensitivity to environmental conditions, cost, and ease of manufacturing and integration.

2. Self-similar parabolic pulses in passive and active fiber

Regardless of the fiber used, the ultimate performance limit of average-cavity soliton and DS-based ultrafast fiber lasers is set by the maximum nonlinear phase shift. A question of key interest is therefore if an alternative pulse-formation mechanism is possible, without such a limit on the nonlinear phase. This question is closely related to one considered by Anderson and colleagues: are there pulses which, in passive fiber, can avoid wave-breaking? That is, are there solutions to the NLSE with normal dispersion (β₂ > 0),

$$\frac{\partial A(z,t)}{\partial z}=-\mathrm{i}\frac{{\beta }_2}{2}\frac{{\partial }^{2}A(z,t)}{\partial t^2}+\mathrm{i}\gamma {\mid A(z,t)\mid }^{2}A(z,t),$$ (3)

such that wave-breaking cannot occur? Anderson et al showed that wave-breaking will be avoided provided the pulse acquires a monotonic frequency sweep (or ‘chirp’) as it propagates [21]. Intuitively, GVD causes a quadratic phase shift in the frequency domain. For a chirped pulse, a quadratic temporal phase shift is likewise a quadratic spectral phase shift. Anderson et al showed that pulses whose temporal intensity distribution was quadratic (parabolic pulses) and which had a quadratic temporal phase (i.e. a linear frequency sweep or chirp) would never experience wave-breaking. These solutions to the NLSE take the form

$$A(z,t)=\{\begin{array}{cc}{a}_o\left(z\right)\sqrt{1-{(t∕\tau \left(z\right))}^2}{\mathrm{e}}^{\mathrm{i}b\left(z\right)t^2},\hfill & \text{if}\mid t\mid ⩽\tau \left(z\right)\hfill \\ 0,\hfill & \text{if}\mid t\mid >\tau \left(z\right)\hfill \end{array}\phantom{\}}$$ (4)

Such a pulse evolves self-similarly: it continuously broadens in both time and frequency, but remains a scaled replica of itself in the time domain. Shortly thereafter, Tamura and Nakazawa noticed that the self-similar evolution could reduce wave-breaking in a short-pulse fiber amplifier [22]. Fermann et al showed analytically that a self-similar pulse, now often called an ‘amplifier similariton’, occurs in a fiber with gain, where propagation is described by a modified NLSE:

$$\frac{\partial A(z,t)}{\partial z}=-\mathrm{i}\frac{{\beta }_2}{2}\frac{{\partial }^{2}A(z,t)}{\partial t^2}+\mathrm{i}\gamma {\mid A(z,t)\mid }^{2}A(z,t)+\frac{g}{2}A(z,t)$$ (5)

Notably, and in contrast to the wavebreaking-free self-similar parabolic evolutions in passive fiber, the parameters of the asymptotic self-similar evolution in a gain fiber is determined completely by the fiber parameters. There is a single, quantitatively-unique asymptotic self-similar evolution in the gain fiber. Of course, launching pulses of different energy will produce parabolas with different durations and bandwidths at the end of a finite length gain fiber with a finite gain. However, these pulses are part of the same self-similar evolution, a single trajectory though phase space we refer to as the nonlinear attractor. This evolution is characterized by a constant chirp (equal to g/(6πβ₂)) with the bandwidth and pulse duration growing with the pulse energy as $E_p^{1∕3}$. Fermann et al also experimentally confirmed this in a Yb-doped fiber amplifier [23]. In large part enabled by self-similarity analysis of the modified NLSE (equation (5)) and similar equations, many analytic results are now known for the properties of self-similar pulses in passive fibers and amplifiers [24]. Although some work has been done [25–27], there are still relatively few analytic results for self-similar oscillators. Nonetheless, many insights from the single-pass systems can be applied, with some care, to oscillators.

The amplifier similariton solution provides several promising properties for high-power fiber lasers and amplifiers. These properties come along with two important caveats. The first property is that the similariton has no nonlinear phase limit and therefore permits in principle the highest-power fiber amplifiers or lasers. However, whether in an amplifier or laser, the similariton is strictly a solution to the above NLSE with constant gain, GVD and the Kerr nonlinearity (equation (5)). Of these, the requirement of constant gain can be somewhat relaxed [28]. At high pulse energies, Raman scattering may disrupt the self-similar evolution. Under typical amplifier conditions however, the self-similar evolution will be disrupted by the finite gain bandwidth of the amplifier [29, 30]. As the pulse bandwidth becomes comparable to the gain bandwidth, the frequency sweep may deviate from a monotonically-increasing form, which leads ultimately to wave-breaking. The second caveat applies to lasers. In order for a laser cavity to produce a stable pulse train, the periodic evolution of the pulse through the cavity must be self-consistent. How can such a periodic evolution be possible if the similariton evolves in a constant-scaling fashion? This seems to be a non-trivial challenge. However, by solving it, another important property of the similariton becomes apparent.

This final key property is that the amplifier similariton is a nonlinear attractor of the NLSE with gain [23]. Any launched pulse will asymptotically evolve towards the same ultimate self-similar trajectory, although the propagation distance required will be greater the further a pulse is from the asymptotic solution [23, 28, 31]. In contrast to the average-cavity pulse-formation mechanisms described in the introduction, an amplifier similariton laser has a nonlinear attractor present only in the gain segment of the fiber. This local nonlinear attraction can simplify the cavity design problem and in fact turns out to allow for radical new approaches to cavity design that allow circumvention of the gain-bandwidth limitation.

3. Summary of mode-locking regimes in fiber lasers

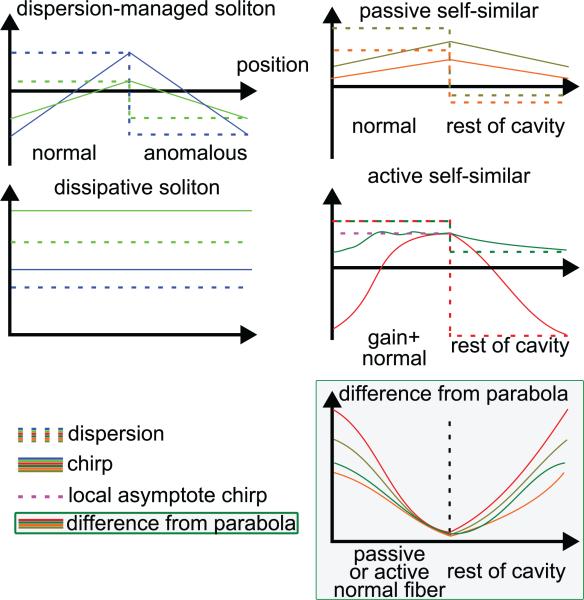
Before describing the state of research on self-similar fiber lasers, we briefly summarize the important properties and distinctions between the known mode-locking regimes to help establish the novel aspects of the self-similar regimes. Figure 1 illustrates, for each regime, two possible chirp evolutions through the laser cavity. For the dispersion-managed soliton, the average cavity dispersion is the most important pulse shaping parameter. Nonlinear and anomalous linear dispersive phase modulations balance in an average sense. Two cavities with different average dispersion values but identical nonlinear phase will in general produce different stable pulses. For the dissipative soliton, a combination of spectral filtering, average normal dispersion, and nonlinear dispersion balance in an average sense. Given the same nonlinear phase and spectral filtering, oscillators with different average dispersion will produce different pulses. From one perspective the passive self-similar laser is based around a local self-similar parabolic evolution in passive normal dispersion fiber. However, the necessity of meeting periodic boundary conditions and the existence of multiple potential parabolic asymptotic evolutions in the passive fiber mean that the stable pulses may in fact be more insightfully understood in terms of the average cavity parameters. Therefore, two cavities that differ only in terms of average dispersion will produce different pulses. For the passive self-similar, the self-similarly evolving parabola converts nonlinear dispersion into linear normal dispersion. In an average sense, nonlinear and normal linear dispersion hence balance anomalous dispersion while self-similar spectral broadening balances with spectral loss. For active self-similar lasers, the most important element is the local nonlinear attraction to the asymptotic self-similarly evolving amplifier similariton in the normal dispersion gain fiber. In the limiting case of an ideal, infinite-length normal dispersion gain fiber, the pulses emerging from the gain fiber are independent of the cavity's average dispersion or even spectral filtering. In practice, the pulses are not completely independent because the gain fiber's length is finite and only pulses starting sufficiently close to the asymptotic self-similar pulse will reach it by the end of the fiber.

Figure 1.

Conceptual depiction of mode-locking regimes. Each of the top four plots show two possible evolutions within a cavity operating in the given regime, but with different average dispersion. Dotted lines indicate the local dispersion of the cavity, while solid lines depict the pulse chirp. In the bottom-right plot, solid lines correspond to the difference of the pulse from a parabolic shape (smaller values correspond to more parabolic pulses), and the dotted line shows the division between the passive or active normal dispersion fiber and the rest of the cavity.

This distinction arguably implies that the passive self-similar oscillator has more commonality with the dispersion-managed and dissipative soliton regimes than with the active similariton. Although this implication is true, the passive self-similar laser exhibits the self-similar evolution of a chirped parabolic pulse. As is depicted in the grey-highlighted plot (bottom right), for active (passive) self-similar lasers, the pulse rapidly becomes parabolic within the normal dispersion gain (passive) fiber segment and evolves self-similarily before being pulled away in the rest of the cavity. Hence, local self-similar evolution is still typically an important element in the passive self-similar laser. However, like dissipative and dispersion-managed solitons, if the cavity's dispersion and spectral filtering were somehow distributed evenly throughout the cavity, the steady-state pulses from passive self-similar laser would be unchanged. This is emphatically not true for the active self-similar laser.

4. Fiber lasers based on self-similar evolution in passive fiber

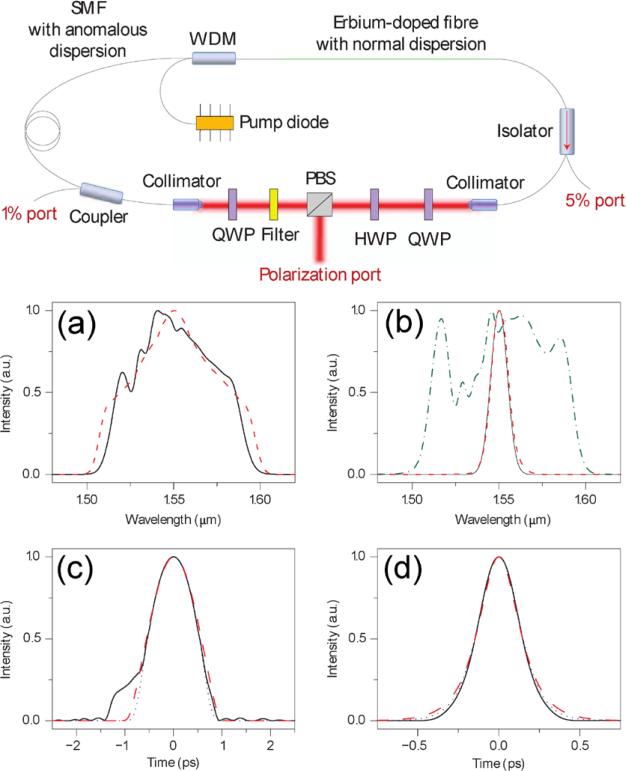
The development of self-similar lasers followed a conceptual trajectory similar to single-pass systems. The first self-similar laser was based on the passive self-similar evolution [32]. Figure 2(a) shows the conceptual schematic of such a laser. The primary evolution occurs in a long passive fiber (single mode fiber, SMF). The short gain fiber provides some gain narrowing but negligible nonlinearity and dispersion, and was chosen so as to avoid the amplifier similariton attractor and minimize disruption of the passive similariton. A saturable absorber starts the pulse and stabilizes it against noise, and the DDL restores the pulse to near its transform limit (i.e. restores the temporal phase to near-constant). Figure 2(a) shows a simulation of the round-trip evolution in such an oscillator. Note how the evolution is self-consistent: at the end of the round-trip the pulse is restored precisely to its state at the beginning of the round-trip. The primary nonlinear pulse evolution occurs in a 6 m passive fiber, and the round-trip pulse evolution is made periodic by the gain filter and anomalous dispersion DDL. The laser produced 10 nJ, 4 ps parabolic pulses which were compressed to 130 fs outside the cavity. Figures 2(c) and (d) show the spectrum and autocorrelations of the chirped and compressed pulse.

Figure 2.

Passive self-similar laser. (a) Conceptual schematic of the passive similariton fiber laser. SMF: single mode passive fiber, DDL: dispersive anomalous delay line. (b) Simulation result showing the steady-state evolution of the pulse spectral bandwidth and time-bandwidth product over one round-trip. (c) Experimental spectrum of the oscillator (inset linear scale). (d) Experimental intensity autocorrelation traces of the output pulse (chirped) and compressed pulse. (b)–(d) from from [32].

Although shorter and higher-energy pulses are now possible from fiber lasers, it is worth emphasizing the advance in performance the passive self-similar oscillator enabled at the time. The 10 nJ pulse energy more than tripled the best result from a comparable dispersion-managed soliton oscillator [33]. Perhaps more importantly, the oscillator had a normal average GVD and represented an approach scalable even further beyond soliton oscillators. Using conventional and dispersion-shifted fiber to create the dispersion map, Ruehl et al demonstated an all-fiber Er:fiber laser which generated 6.2 nJ pulses that could be compressed to 64 fs [34]. They also demonstrated a Yb:fiber version [35] but, without a strong spectral filter or dispersion compensation, the performance was relatively limited. Although these demonstrations are impressive, it seems plausible that the best performance of a passive self-similar laser has not yet been reached. Theoretical work has suggested that perhaps the asymptotic parabola need not be reached: by using intermediate states reached during the evolution towards the asymptotic state [36], stable novel pulses can be obtained. Practically, these intermediate states are chirped triangle-shaped pulses that occur for cavities like figure 2(a), except with relatively higher gain and smaller net dispersion. Scientifically, these triangle states are a reminder of the large volume of unexplored parameter space, which may produce pulses with both new and interesting characteristics as well as exceptional dechirped peak power.

5. Fiber lasers based on self-similar evolution in gain fiber

Although amplifier similaritons in mode-locked fiber lasers were theoretically predicted as early as 2001 [37], it was not until 2010 that lasers with self-similar evolution in the gain segment were demonstrated. Figure 3 shows the conceptual schematic of such a laser.

Figure 3.

Conceptual schematic of a mode-locked amplifier similariton laser.

The mode-locked operation can be understood as follows. A pulse enters a normal-dispersion gain fiber. In principle, this pulse can be arbitrarily far from the asymptotic parabola. In practice however, a pulse somewhat close to the asymptotic solution is required to reach it by the end of the gain fiber. During the process of self-similar amplification, a parabolic pulse with a broadened spectrum and positive linear chirp is formed. After the gain fiber, part of the pulse is coupled out of the oscillator. In order to ensure a self-consistent cavity, before passing the pulse back into the gain fiber, its bandwidth and duration must be reduced. It may be passed through a dispersive delay line (DDL), which brings the pulse closer to its transform-limit, or through a narrow spectral filter which restores the pulse bandwidth. With these measures, and with a saturable absorber to start the pulse from noise and help stabilize it, the pulse may again reach the asymptotic amplifier similariton form and stable mode-locking may occur. Under typical conditions of most experiments so far, the spectral filter is of primary importance. However, the key is that the pulse be restored to a state well within the basin of attraction of the local nonlinear attractor in the gain fiber.

Theoretical work showed that a chirped parabolic pulse which is very close to the amplifier similariton can be formed in a fiber laser cavity. It was pointed out that a strong saturable absorber and large SPM are necessary to have stable amplifier similaritons in a mode-locked cavity [37–39].

Surprisingly, the first experimental demonstration of an amplifier similariton in a mode-locked fiber laser employed a somewhat different technique to ensure self-consistency, namely the soliton attractor in an anomalous-dispersion passive fiber [41]. Thus, the laser was called a soliton-similariton fiber laser. Figure 4 shows the schematic and experimental results of the soliton-similariton fiber laser. Nonlinear polarization evolution (NPE) is used as an effective saturable absorber. After a gain fiber wherein the pulse evolves to the amplifier similariton, the pulse passes through the polarizing beamsplitter (PBS), which implements the loss of the NPE saturable absorber. The NPE rejection port is, as is commonly done, used as a convenient output port. The pulse remaining in the cavity then passes through a spectral filter (12 nm bandwidth (BW)). The filtered pulse evolves into a soliton in a subsequent segment of anomalous-dispersion SMF. Given an arbitrarily long SMF, the spectral filter should not be strictly required, as the soliton is also a nonlinear attractor. In practice the spectral filter likely plays a role in stabilizing the laser, and greatly reduces the length of fiber necessary for the pulse to adjust itself to the soliton solution. As the soliton formed after filtering is relatively near the initial condition required for the self-similar evolution, it evolves into an amplifier similariton in the gain fiber. Therefore, this laser has two distinct nonlinear attractors in each round trip. The spectral bandwidth increases to 85 nm in the normal-dispersion Er-doped fiber. Overall, the spectral breathing ratio (which is defined as the ratio of maximum to minimum bandwidth) of the evolution is 7. Large spectral breathing is a signature of the self-similar evolution, and is indicative of the relatively large nonlinear phase shift the pulse acquires.

Figure 4.

Soliton-similariton laser. Top: schematic of the soliton-similariton fibre laser. QWP: quarter wave plate; HWP: half wave plate; PBS: polarizing beamsplitter; WDM: wavelength-division multiplexer. Bottom: (a) and (b) show the spectra from simulation (red dashed) and experiment(black) from the 5% and 1% output ports. (b) also shows the output spectrum from the NPE port (broader, green dashed line). (c) and (d) show the pulse temporal profiles inferred from the PICASO algorithm [40] for the simulation and experiment at the 5% and 1% output ports. From [41].

A similariton can be established in a mode-locked fiber laser without the help of soliton formation (or an anomalous-dispersion segment). In fact, most work has not used a DDL, but instead only a narrow spectral filter to stabilize the amplifier similariton evolution in an all-normal dispersion cavity. The first such laser was demonstrated by Renninger et al [42]. The schematic of the laser is shown in figure 5. The combination of a grating and fiber-coupled collimating lens comprises a narrow-bandwidth (4 nm) Gaussian filter. The pulse then evolves to a chirped parabolic pulse in the gain fiber. The evolution can be quantified by comparing the pulse shape to a parabola with the same peak power and energy. This showed that the pulse rapidly reshaped until it was virtually parabolic and, furthermore, the exact chirped parabola expected analytically [23, 28].

Figure 5.

All-normal dispersion amplifier similariton laser. Top: schematic of an all-normal dispersion amplifier similariton fiber laser. Bottom: experimental (a) cross-correlation of the pulse from the grating reflection (solid) with a parabolic (dotted) and sech² (dashed) fit; (b) interferometric autocorrelation of the dechirped pulse from the NPE output; and spectra from the (c) grating reflection and (d) NPE output. From [42].

The 5 nJ pulse energy achieved by the all-normal-dispersion similariton laser was lower than has been observed with DS oscillators, but no attempt was made to maximize the pulse energy in the initial work, and 5 nJ is still quite high for a fiber oscillator. In addition, the pulse duration was remarkably short—shorter than that produced by any prior all-normal dispersion laser. As the amplifier similariton evolution produced linearly-chirped pulses with large bandwidth, ~60 fs pulses could be obtained by external compression with a grating pair. By using the same cavity design with Er-doped, dispersion-shifted fiber, pulses with 3.5 nJ pulse energies and ~70 fs pulse duration were achieved [43].

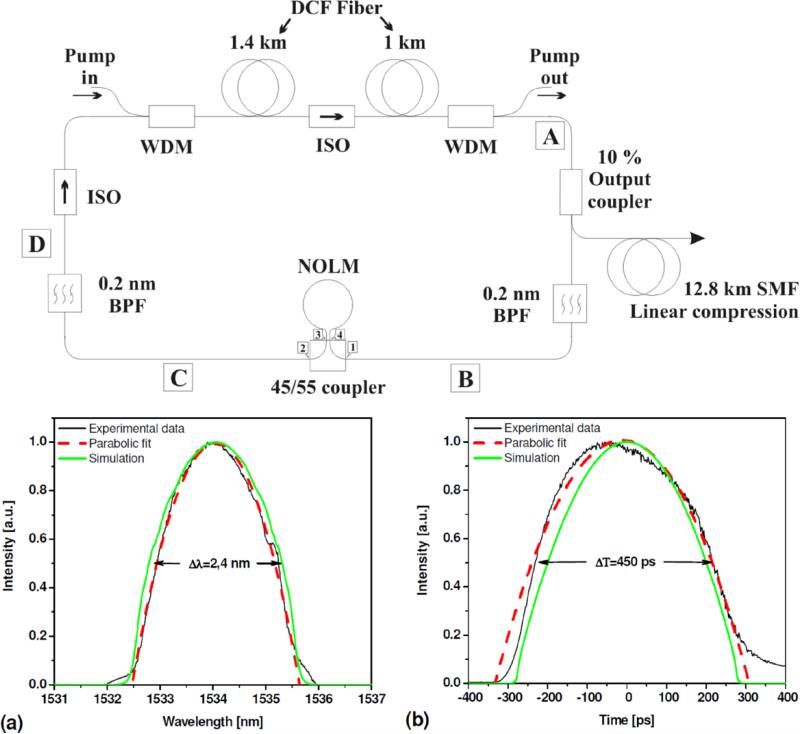
The mode-locked amplifier similariton was realized not only with rare-earth doped gain fibers, but also with Raman gain [44] (figure 6). The Raman amplifier similariton laser was realized using all-fiber components, with a 2.4 km dispersion-compensating fiber (DCF) for the gain fiber and a nonlinear optical loop mirror (NOLM) as the saturable absorber. The laser generated 22 nJ and 450 ps chirped parabolic pulses at 1534 nm, which were compressed in SMF to ~6 ps. While this performance is clearly unique, the novel implementation is also quite valuable. Although much work has been done, understanding of amplifier similariton oscillators is still immature compared to knowledge of average-cavity soliton and DS oscillators. In particular, most work so far has been done within a fairly narrow region of the possible parameter space, which limits the extent to which we can make conclusions about amplifier similariton oscillators in general. The laser demonstrated by Aguergaray et al hence, beyond being attractive for many applications, provides several useful data points: the use of a very long gain fiber, the use of Raman gain, the all-fiber design, the ultra-low 64 kHz repetition rate and use of a NOLM saturable absorber. These features are all unique among amplifier similariton oscillators and, in fact, relatively unique among mode-locked fiber lasers more generally. The demonstration of fiber lasers based on self-similar pulse evolution in such disparate settings is evidence of the robust nature of the process.

Figure 6.

Raman self-similar laser. Top: schematic of a Raman amplifier similariton laser. Bottom: (a) and (b) are the laser output pulse and spectrum with a least-square parabolic fitting respectively. From [44].

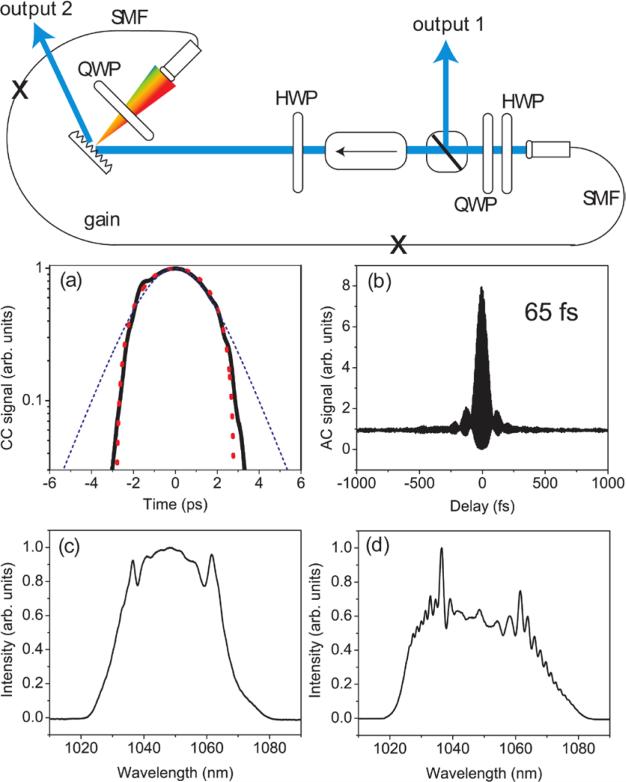
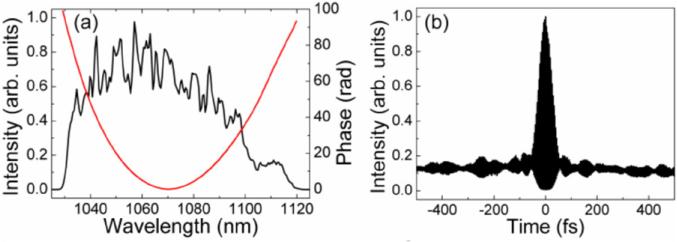
Nie et al firmly established the benefit of the amplifier similariton oscillator for short pulses. Using roughly the same cavity design as Renninger et al these workers obtained >10 nJ pulse energies with remarkably short pulse duration [45] (figure 7). The pulses were dechirped to ~42 fs pulses using multiphoton intrapulse interference phase scan (MIIPS) [46], which is a spatial light modulator (SLM)-based pulse shaping/measurement technique. The resulting 250 kW peak power is among the highest achieved by a femtosecond fiber laser constructed with standard small-core fiber.

Figure 7.

High-performance all-normal dispersion self-similar laser. (a) Output laser spectrum (black) and measured phase of the output pulses (red). (b) Experimental interferometric autocorrelation, AC FWHM 57 fs. From [45].

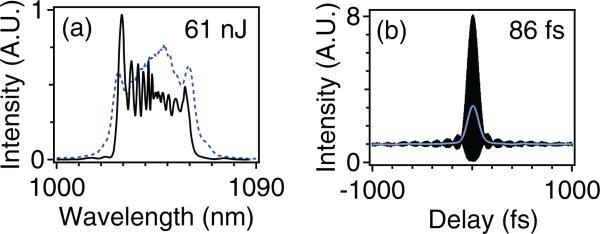
The pulse energy of an amplifier similariton laser can be scaled up by using large mode area fibers such as a chirally coupled core (CCC) fiber [47, 48]. CCC fiber has a secondary core helically wrapping around a large central core to selectively couple out higher order modes. For fibers of typical lengths (~a few meters), CCC fiber is effectively single-mode. With a Yb-doped CCC fiber, the pulse energy was successfully scaled up to ~60 nJ with a compressed pulse duration of <90 fs (figure 8). Again, NPE was used as a saturable absorber while a grating / collimator combination served as a spectral filter.

Figure 8.

Large mode area fiber all-normal dispersion self-similar laser. Experimental output of the CCC similariton laser (a) NPE output (solid) and intracavity (dashed) spectra; (b) dechirped AC. From [47].

6. Other self-similar lasers

Both passive and active self-similar pulses have been considered in the context of solid-state systems [49, 50]. Ilday et al found that even though the possible dispersion and nonlinearity of the solid-state format are considerably smaller than fiber, when a typical Ti:sapphire cavity was adjusted for large energy and net normal dispersion, weakly periodically-breathing passive self-similar behavior could be observed [49]. In contrast, Bucklew et al considered a laser with a static (no breathing) steady state evolution, consistent with the low nonlinearity, dispersion and gain per round trip [50]. They nonetheless showed this to be a novel kind of similariton laser wherein the similariton attractor is manifested over many round-trips as the laser modes lock. Hence although the amplifier similariton is important in determining the steady-state pulse, the oscillator does not feature a periodic amplifier similariton evolution in the steady state, as is the case for the fiber lasers.

Like the passive self-similar Ti:sapphire laser [49], the proposal by Bucklew et al raises the question of how exactly one should define ‘self-similar oscillator’, and whether distinctions should be drawn between parabolic pulse oscillators and oscillators characterized by the repetitive formation of similaritons. To answer this specifically for the laser proposed by Bucklew et al we note that even though the amplifier similariton attractor appears important as the laser approaches steady state, its steady state may alternatively described as dissipative soliton mode-locking. This point of view is supported by description of the laser with an average-cavity model [27]. However, it is not yet clear what the most insightful definition of an amplifier similariton laser should be. Motivated by this work, and to foreshadow the following sections, we hence suggest a working definition as follows: an amplifier similariton oscillator is one in which the steady-state pulse evolution requires for stable mode-locking the nonlinearly-attracting, asymptotic chirped parabola solution of the NLSE with gain.

This definition highlights a key difference between passive and active (amplifier similariton) self-similar oscillators. As has been noted [5, 51], passive self-similar oscillators can be described in an averaged-cavity model and there is not a clear transition between passive self-similar oscillators and dissipative soliton oscillators containing anomalous dispersion segments: the two classifications represent extremes of a continuous parameter space of cavities with stable mode-locked pulses. Pulses in the intermediate region have since been studied in work exploring Thulium-based fiber lasers with normal average dispersion [52]. This lack of a clear transition stems from the fact that, averaged over the cavity, the behavior of the passive self-similar oscillator in the steady state is reminiscent of normal dispersion dissipative soliton oscillators. In nonlinear, normal-dispersion segments the parabolic pulses effectively ‘linearize’ nonlinear phase shifts, which can then be partially cancelled by the DDL. Spectral filtering and saturable absorption are essential for restoring the pulse bandwidth each round trip. The self-similar evolution of a parabolic pulse is inseparable from the fact that the parabolic pulse effectively converts nonlinear phase to linear phase, like that accumulated in linear propagation through normal-dispersion media. However, because the round-trip pulse evolution only converges to one that meets periodic boundary conditions, the behavior of the passive self-similar oscillator is nonetheless determined by the average cavity parameters. An average cavity model should therefore describe the steady-state passive self-similar oscillator. Hence, in some respects the passive self-similar oscillator can be viewed as an average-cavity dissipative soliton oscillator.

To emphasize the significance of this last point, and the uniqueness of the amplifier similariton oscillators, we note that the steady-state pulse emitted from such a laser is largely independent of the average cavity parameters [53], and much more strongly determined only by the properties of a single segment, the normal-dispersion gain fiber. If the gain fiber could be made arbitrarily long (and the gain bandwidth made infinite) the oscillator would be completely independent of average cavity parameters. This is the due to the local nonlinear attractor: regardless of the input pulse it tends to produce the same output pulse. A continuous family of self-similar evolutions can occur in a passive fiber, and accordingly the passive self-similar oscillator has freedom to choose a self-similar evolution that most efficiently meets periodic boundary conditions. Meanwhile, the gain fiber has but a single asymptotic self-similar evolution. The important conceptual conclusion, exemplified by the definition above, is that the amplifier similariton laser is, in contrast to all other known classes of mode-locked lasers, determined by a local nonlinear attractor. As will now be described, this distinction allows for a new approach to the design of mode-locked oscillators.

7. Extensions of amplifier similariton lasers

For average-cavity soliton and dissipative soliton pulse formation, the shortest pulses are generated by lasers with net cavity dispersion near zero [54, 55]. In oscillators based on dispersion-managed solitons, the gain bandwidth (BW) becomes the main limitation to the mode-locked pulse duration. Historically, record short pulse durations of ~30 fs from mode-locked fiber lasers were achieved in dispersion-managed soliton lasers with Yb-doped fiber, which has the broadest gain BW among rare-earth doped fibers [56–58]. Amplifier similariton fiber lasers have reached pulse durations approaching those of dispersion-managed soliton fiber lasers [42, 43, 45], and so represent a promising route to relatively simple, robust lasers which generate high-energy, few-cycle pulses. A key problem that seems to immediately derail this train of thought is that the gain bandwidth limits the minimum pulse duration to ~40 fs (for Yb). However, recent work has shown that the gain bandwidth limit of the amplifier similariton in the gain fiber does not necessarily limit the bandwidth of the stable mode-locked pulse.

A mode-locked pulse with a spectrum broader than the gain BW can be generated by extending the spectral expansion beyond the limits of the amplifier similariton attractor. Figure 9 shows the schematic for a laser that implements this concept. The pulse enters a normal dispersion gain fiber and eventually evolves into an amplifier similariton. After the gain fiber, the established amplifier similariton propagates in a normal-dispersion highly-nonlinear fiber (HNLF). Due to the high nonlinearity, substantial spectral broadening occurs in the HNLF. The pulse is coupled out of the cavity when it has the largest BW. The output pulse can be compressed externally to produce a very short pulse. Again, a narrow spectral filter balances the spectral broadening while a saturable absorber initiates and stabilizes the mode-locking. The pulse fed back into the gain again evolves into an amplifier similariton. Even though the strong nonlinear spectral broadening in the HNLF constitutes a major change from the previous oscillator designs, the amplifier similariton attractor provides a measure of adaptation to the roundtrip evolution. As it effectively converts differing pulses into similar pulses, the local gain fiber attractor allows for a stable, self-consistent pulse evolution to be reached almost independently of the details of the rest of the cavity.

Figure 9.

Conceptual schematic of an amplifier similariton laser with an intracavity highly-nonlinear fiber (HNLF). From [59].

The concept discussed above was experimentally realized by Chong et al [59]. The schematic of the fiber laser and measurements of the output pulses are shown in figure 10. Small-core photonic crystal fiber (PCF) was used as a highly-nonlinear fiber. NPE was again used as a saturable absorber while a grating and collimator served as a spectral filter. Substantial spectral broadening occurred in the PCF (figure 10(a)). The mode-locked spectrum spans from ~920 nm to ~1120 nm and is clearly broader than the gain BW (roughly 40 nm centered at 1030 nm). Unfortunately, a grating pair could not compensate the residual nonlinear phase thoroughly. The rejection port of NPE is used as the output pulse, which is compressed by MIIPS to ~21 fs pulse duration. This was the first mode-locked laser with a spectrum substantially broader than the gain BW by manipulating an amplifier similariton. Pulses as short as ~20 fs at 1030 nm are attractive sources for nonlinear microscopies, and the laser successfully generated images of microspheres and biological samples by multiphoton fluorescence, second-harmonic generation (SHG) and third-harmonic generation (THG) [60].

Figure 10.

Top: schematic of the HNLF-extended amplifier similariton laser. QWP: quarter-waveplate; HWP: half-waveplate; PBS: polarizing beam-splitter. Bottom: experimental (a) spectrum after the PCF, (b) output spectrum, and (c) output autocorrelation signal after phase correction by MIIPS for a 21 fs pulse. From [59].

Although this laser demonstrated that stable pulses could be produced, a relatively complicated technique was needed to compress them to their transform limit. This is largely because the spectral broadening in the HNLF does not necessarily result in a linear frequency sweep. In general, nonlinear propagation in normal-dispersion fiber does not produce a linearly-chirped pulse, with the only exception being for chirped parabolic pulses. The linear chirp of the similariton can be removed by a simple grating or prism pair. However, the amplifier similariton spectrum cannot be broader than the gain BW. Fortunately, this limitation can be removed by inducing an evolution equivalent to the amplifier similariton evolution in a passive fiber.

In 2004, Hirooka and Nakazawa used a simple transformation to show theoretically that pulse evolution in a dispersion-decreasing fiber (DDF) with normal dispersion is mathematically equivalent to the evolution in a normal-dispersion gain fiber [61]. This amplifier-similariton-like evolution in a DDF was experimentally verified [62]. Equation (6) describes the pulse evolution in a normal dispersion DDF. Equation (6) can be transformed into equation (7) which is equivalent to pulse propagation in a normal dispersion gain fiber. Therefore, the DDF supports an evolution equivalent to the amplifier similariton. There is a significant advantage in a DDF, however: because it is a passive fiber, the gain BW limitation does not exist in a DDF.

$$\frac{\partial A}{\partial z}=-\mathrm{i}\frac{{\beta }_2\left(z\right)}{2}\frac{{\partial }^{2}A}{\partial {\tau }^2}+\mathrm{i}\gamma {\mid A\mid }^{2}A\text{where}{\beta }_2\left(z\right)=\frac{{\beta }_{20}}{1+\Gamma z}$$ (6)

$$\frac{\partial u}{\partial \xi }=\frac{\Gamma }{2}A-\mathrm{i}\frac{{\beta }_{20}}{2}\frac{{\partial }^{2}u}{\partial {\tau }^2}+\mathrm{i}\gamma {\mid A\mid }^{2}A\text{where}u=A\sqrt{1+\Gamma z},\xi =\frac{\ln (\Gamma z+1)}{\Gamma }$$ (7)

By replacing the PCF in figure 10 with a DDF, an amplifier similariton evolution in the gain fiber can be extended further in a passive DDF. A broad spectrum exceeding the gain BW can be generated due to extended spectral broadening of the amplifier similariton in a DDF. Moreover, since the amplifier similariton has a linear chirp, the output pulse should be easily compressed by a simple dispersive delay line.

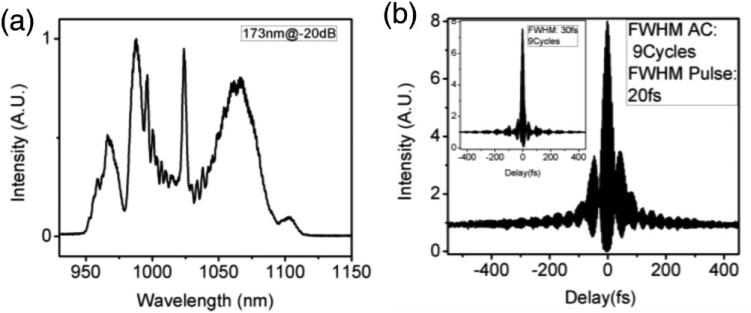
A DDF was successfully employed in a fiber laser to achieve mode-locked operation [63]. The DDF was manufactured by tapering a normal-dispersion PCF. Initial results obtained with this approach are shown in figure 11. For this laser, a grating pair was used to compress the pulse. Therefore, an extended amplifier similariton evolution in a DDF did help to keep the chirp on the pulse close to linear. However, as the pulse possessed a relatively large chirp and bandwidth, higher-order dispersion in the grating pair compressor prohibited compression to the transform limit. Work continues on this approach.

Figure 11.

Experimental results from an amplifier similariton laser with an intracavity dipersion-decreasing fiber (DDF). (a) output spectrum, and (b) output autocorrelation signal after dechirping with a grating pair. The inset in (b) shows the calculated transform-limited pulse autocorrelation. From [63].

8. Unresolved issues and future directions

Amplifier similariton lasers seem likely to complement, and may even exceed, the performance of dissipative-soliton lasers. It will be important to determine what processes limit the performance, and what the performance limits are. There is currently no systematic understanding of how to design this kind of laser or optimize the performance. Analytic results are still limited, particularly in the important regime characterized by large spectral breathing (where average cavity models likely break down). Nonetheless, it seems reasonable to expect that significant performance improvement should be possible. Perhaps the most straightforward means lies in increasing the fundamental gain bandwidth. Pumping Yb:fiber lasers at 915 nm rather than the usual 976 nm may provide one route. Use of Raman gain, or hybrid gain with rare-earth doping and Raman gain, are others.

With a fixed gain bandwidth, we are guided by our understanding of self-similar amplifiers, where much analytic theory exists [24]. This will eventually be inadequate, as it neglects the requirement of a self-consistent solution in the oscillator. The similariton is fully-defined by its duration, bandwidth, and peak power. These in turn depend on the dispersion β₂, nonlinearity γ, and gain coefficient g (gain per unit length). The self-similar evolution is disrupted if the spectrum reaches the amplifier gain bandwidth W with limiting energy $E\approx 3W^3{\beta }_2^2∕\left(\gamma g\right)$. Thus, longer fibers with lower unit gain should yield higher pulse energies [64]. For the oscillator we must also consider the self-consistency requirement, however. Since the chirp, g/(6πβ₂), is also reduced, the action of a spectral filter will produce longer and longer pulses, further from the optimal initial condition. Dispersion management is hence likely to be required in order to ensure that the long fiber lengths are not wasted on attracting distant pulses to the asymptotic solution [65]. Although short rod-like fibers may also provide significant scaling, we note that long fibers of relatively modest mode size are likely the most practical for most applications. Firstly, these fibers, such as the CCC fiber, may be coiled, may be flexible and may be simply spliced, facilitating all-fiber designs. More subtle points are (1) the peak power of the maximal self-similar pulse in a short, large-mode-area fiber may be near the self-focusing threshold [66], and (2) the relatively longer propagation length effectively translates to a greater capacity for the local nonlinear attractor to dampen fluctuations by adjusting pulses uniformly to the same output pulse, irrespective of fluctuations in the input. Many emerging fiber materials (ZBLAN and chalcogenides, e.g.) have considerably higher dispersion than fused silica at near-IR wavelengths, which may provide a means for still greater scaling of the self-similar pulse energy. As with DS pulses [67], Raman scattering is likely to eventually become an impediment to energy scaling of self-similar oscillators. Therefore, some care will be required in using longer fibers and new materials, as amplifier similariton oscillators will likely also be limited by Raman scattering.

The most promising performance from self-similar oscillators, however, may come in their capacity to generate short pulses. Without extended techniques, self-similar oscillators already provide a small advantage over dissipative soliton oscillators with typical fiber parameters. By extending the self-similar evolution and then relying on the presence of the local attractor to help make the cavity self-consistent and stable, pulses with bandwidth many times the gain bandwidth should be possible. Although it remains a distant dream, an octave-spanning mode-locked fiber laser would likely offer stability and convenience advantages over frequency comb designs that currently use bulky solid-state lasers and/or spectral broadening in ex-cavity photonic crystal fibers. Since cost, compactness and noise are of key importance in emerging applications of frequency combs, the extended self-similar oscillator represents one of the more promising platforms if frequency combs are to become commonplace tools. Initial work on amplifiersimilariton laser based frequency combs is promising [68], and several high-performing fiber frequency comb systems have started with passive similariton oscillators [69–71].

An issue that becomes especially pronounced as one imagines an octave-spanning self-similar fiber laser is that the use of a simple spectral filter is a rather inefficient means of ensuring the correct initial condition to the gain fiber. Recently the idea has been put forward to use spectral compression, whereby before entering the gain fiber the pulse passes through a significant section of anomalous dispersion, acquiring a down-chirp [72]. In subsequent nonlinear propagation in a passive fiber, the spectrum will compress as the pulse approaches a minimum, transform-limited spectral focus. A significantly greater fraction of the initial pulse energy can therefore be passed through a narrowband filter, making the cavity more efficient.

From this point of view of improved cavity efficiency, the soliton-similariton oscillator may also be attractive. However, we note that in order to reach a soliton with parameters suitable to then broaden substantially in the gain fiber, the pulse energy entering the anomalous dispersion fiber needs to be quite small. A minor point is that the soliton-similariton laser can only be realized when anomalous dispersion fiber is available. However, this implementation remains especially interesting scientifically, and some intuition suggests that two nonlinear attractors could correspond to a more stable, low-noise oscillator. Hence although we caution that oscillator designs that incorporate anomalous dispersion fiber will be energetically- and spectrally-limited, more research is required to evaluate different designs.

Regardless of the details of the pulse evolution, a valuable step will be the demonstration of all-fiber self-similar oscillators. In principle, spectral filtering or any desired dispersion management can be performed by devices developed for telecommunications applications (e.g. fiber Bragg gratings). An issue of key importance however, may be the lack of a suitable fiber-format saturable absorber. To date, all but one of the reported self-similar oscillators have used NPE, which can provide exceptionally high performance but is not environmentally stable. Initially, complete modelling of NPE appeared to be necessary to model self-similar pulse formation with a filter in a short Yb-doped fiber [42]. We have since determined that the only necessity is for a very steep saturable absorber curve (the transmission through the absorber increases very rapidly towards its peak value from zero with increasing peak power). On one hand, it seems plausible that the use of longer gain fibers may allow for more nonlinear attraction and hence greater stability, permitting lesser reliance on a saturable absorber. This hypothesis is supported by the demonstration of the low repetition rate Raman fiber laser that used a NOLM as a saturable absorber [44]. On the other hand, if this is not the case then the development of fiber-format saturable absorbers will be especially important for practical all-fiber amplifier similariton lasers.

Apart from the performance and application-oriented thinking above, self-similar oscillators provide a new test bed for nonlinear pulse dynamics that have been largely unexplored so far. Multiple bound similaritons have been observed in a fiber laser [73] and many works have shown that, in single-pass systems [74–77], there is a rich variety of similariton dynamics and interactions. Hence, many interesting phenomena are likely to be observed in similariton lasers, perhaps particularly in the soliton-similariton implementation. In our laboratory, we often observe high-energy mode-locked states which coexist with a continuous wave field. For example, this field is visible in the spectrum in figure 10 [59, 63]. The origin, and potential role of this field in the pulse behavior remains mysterious. Since the amplifier similariton oscillator is based on a fundamentally different pulse formation mechanism than the average-cavity soliton and DS oscillators (and arguably even passive self-similar oscillators), it will be interesting to investigate its starting dynamics [78, 79]. Such an investigation may provide insight into more universal features of the mode-locking transition, or indications for uniqueness of amplifier similariton oscillators.

Lastly, we wonder in particular about mode-locked pulses which are intermediate between soliton, dissipative soliton, passive similariton, dispersion-managed soliton, and amplifier similariton oscillators. These terms correspond to limiting cases that exhibit particular, clearly-defined characteristics, and variation of the cavity parameters will lead to clear bifurcations in the stable pulse behavior. However, there are nonetheless many regions of parameter space where stable mode-locked pulses are generated that defy straightforward classification. For example, consider the use of a tunable intracavity spectral filter in theoretical results by Boscolo et al [80]. In this work, stable pulses are generated with a variety of pulse shapes which have not been observed in fiber lasers with similar nonlinearity. The lasers operate in the normal dispersion regime. Clearly these pulses may be useful for applications, but how should (and in fact, can) they be categorized in terms of known mode-locking regimes? Although further work is required, our hypothesis is that such pulses fall into the broader category of average-cavity dissipative solitons. Compared to passive self-similar lasers, spectral filtering is stronger and more complex in the lasers studied by Boscolo et al However, since very little pulse evolution occurs within the gain fiber, local attraction is likely minimal and therefore the steady-state stable pulse characteristics are primarily determined by the various effects averaged over the cavity. A similar conclusion is probable for other lasers incorporating pulse-shaping, which despite cost and complexity may be a powerful technique [81]. Naturally, in an actual, heterogeneous laser implementation the intracavity pulse will evolve through the cavity, and therefore by judicious choice of where to take the output pulse, additional control is possible. Furthermore, local attraction may also play a secondary role.

This leads naturally to an important open question: how closely must a pulse match the asymptotic self-similar attractor of the gain fiber in order to benefit from the stabilizing effect of the attractor? Can we (or should we) make clear distinctions between average-cavity solitons and amplifier similaritons? Recent work yielding sub-25 fs, >2 nJ pulses is exemplary [82], as the pulse evolution and cavity design exhibits characteristics of both the dissipative soliton and amplifier similariton. Ultimately, a systematic investigation of pulses in the parameter spaces between well-established mode-locking regimes should help to provide a coherent, connective theory of mode-locked lasers—one can envision a nonlinear optical oscillator phase diagram. It seems plausible, too, that the best performance may exist in the currently unexplored transition regions.

9. Conclusion

Amplifier similariton fiber oscillators are truly unique among mode-locked lasers. The local nonlinear attractor of the amplifier similariton in active optical fiber allows exciting new fiber oscillator designs that may reach well beyond the limitations of rare-earth gain media. As the self-similar evolution of chirped parabolic pulses in passive and active fiber has no apparent nonlinear phase limit, passive and active self-similar oscillators can both exhibit extreme spectral and temporal breathing, and may be scalable to very high pulse energies. The many alternative realizations of self-similar oscillators indicates the considerable work that remains in optimizing and exploring this family of lasers, but also showcases their robustness and easily-identifiable features. Owing to the possibility for radical new designs that should permit very short pulses from a fiber platform, amplifier similariton oscillators may be valuable in future fiber-based frequency combs and medical imaging applications.