Coherent neuronal ensembles are rapidly recruited when making a look-reach decision

Summary

Selecting and planning actions recruits neurons across many areas of the brain but how ensembles of neurons work together to make decisions is unknown. Temporally-coherent neural activity may provide a mechanism by which neurons coordinate their activity in order to make decisions. If so, neurons that are part of coherent ensembles may predict movement choices before other ensembles of neurons. We recorded neuronal activity in the lateral and medial banks of the intraparietal sulcus (IPS) of the posterior parietal cortex, while monkeys made choices about where to look and reach and decoded the activity to predict the choices. Ensembles of neurons that displayed coherent patterns of spiking activity extending across the IPS, “dual coherent” ensembles, predicted movement choices substantially earlier than other neuronal ensembles. We propose that dual-coherent spike timing reflects interactions between groups of neurons that play an important role in how we make decisions.

Voluntary movements like looking and reaching are controlled by distributed networks containing millions of neurons. The brain areas associated with voluntary movements are organized into effector-specific networks specialized for the control of each movement. There is a network for controlling saccadic eye movements and a network for controlling transport movements of the arm, along with other networks that control the hand. Evidence from electrophysiological and functional neuroimaging experiments supports the idea that eye and arm movement systems are controlled by different brain networks^1–4. Effector-specific networks are widespread and extend across the frontal and parietal cortices^5–7, basal ganglia⁸, association nuclei of the thalamus⁹, and the cerebellum¹⁰.

A great deal is known about how neurons in effector-specific networks are recruited when we make decisions. In the posterior parietal cortex (PPC), neurons on the lateral bank of the intraparietal sulcus (IPS; including area LIP) tend to respond before eye movements, while neurons on the medial bank (including PRR, MIP, A5v) tend to respond before arm movements^11,12. Neural activity in PPC of macaques encodes which of multiple alternatives will be chosen, which effector will be used to make the choice and other decision-related variables^13–16. PPC neurons play a causal role in effector-specific choice. Reversibly-inactivating the PPC disrupts movement coordination, selection and decision-making, and does so in an effector-based manner^17–20. Functional neuroimaging experiments indicate that the human parietal cortex also has a similar effector-specific organization^3,4,21. Therefore, largely different networks of neurons are believed to be involved in selecting where to move the eyes and where to move the arm.

Relatively little is known about the interactions between PPC neurons and how making a look-reach decision depends on these interactions. Coherent neural activity is broadly present within the intraparietal sulcus of the PPC^22,23 and has been implicated in a wide range of cognitive processes^24,25 including decision-making^26–28, working memory^29,30, movement planning and execution^22,31,32, attention^33,34. Therefore, a relationship between coherent neural activity in PPC and effector-based decision-making is likely, and knowledge of such neuronal interactions may provide new opportunities to test models of how look-reach decisions are made.

We recorded neural activity simultaneously from electrodes in both the lateral and medial banks of the IPS while monkeys chose to make a coordinated look-and-reach to one of two locations. Coordinated movements are likely to recruit neuronal ensembles on both banks, so we used coherence to identify groups of distributed, interacting neurons. We then compared how neuronal ensembles were recruited when making a decision by estimating when the firing of neurons correctly predicted the movement choice. The results show that deciding where to look-and-reach recruits dual-coherent patterns of neuronal activity and inform models of how effector-specific networks of neurons make look-reach decisions.

Results

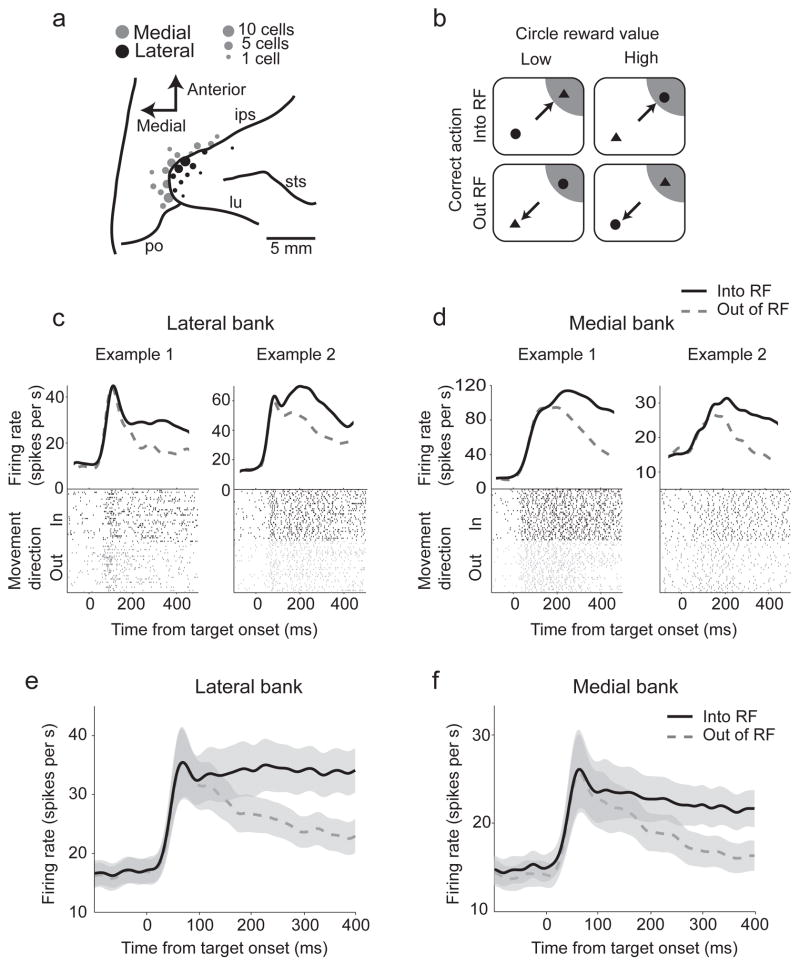
We recorded 117 neurons and LFP activity from the lateral and medial banks of the IPS in two monkeys (Fig 1a) that displayed persistent, spatially-selective responses before a reach-and-saccade movement (center-out task) as well as in a choice task that required them to choose where to look and reach (Fig 1b). We recorded 47 neurons from the lateral bank of the IPS (Monkey C: 30, Monkey R: 17) and 70 neurons from the medial bank (C: 45, R: 25). Individual neurons on both banks of the IPS (Fig 1c, d) as well as the population average (Fig 1e, f) robustly responded to the onset of the targets, and signaled the choice during an instructed delay before movement, consistent with the formation of movement plans.

Figure 1.

a) Neural recording locations on the banks of the IPS (lateral, black; medial, gray). b) Two target choice reward task. Circles and triangles were presented, each associated with a different sized juice reward. Monkeys were cued to plan a joint reach and saccade to one target. c, d) Encoding of movement choice in example neural responses from the lateral and medial banks of the IPS. The average firing rates are shown aligned to the target presentation. Solid back lines denote movements into the RF, with dashed gray lines denoting movements out of the RF. Population average firing rates: e) Lateral bank; f) Medial bank. The standard error of the mean of the firing rates (gray shaded).

Long-range and local spike-field coherence

Selection may depend on the presence of coherent patterns of neuronal activity. We first asked whether ensembles of neurons exist that are coherently-active across the IPS. To do so, we analyzed correlations between spiking and LFP activity using spike-field coherence (SFC). SFC characterizes correlations in the timing of spiking and LFP activity according to temporal frequency. SFC magnitude measures how well spike times from a particular neuron can be predicted given LFP activity, and consequently measures which neurons participate in coherent neural ensembles.

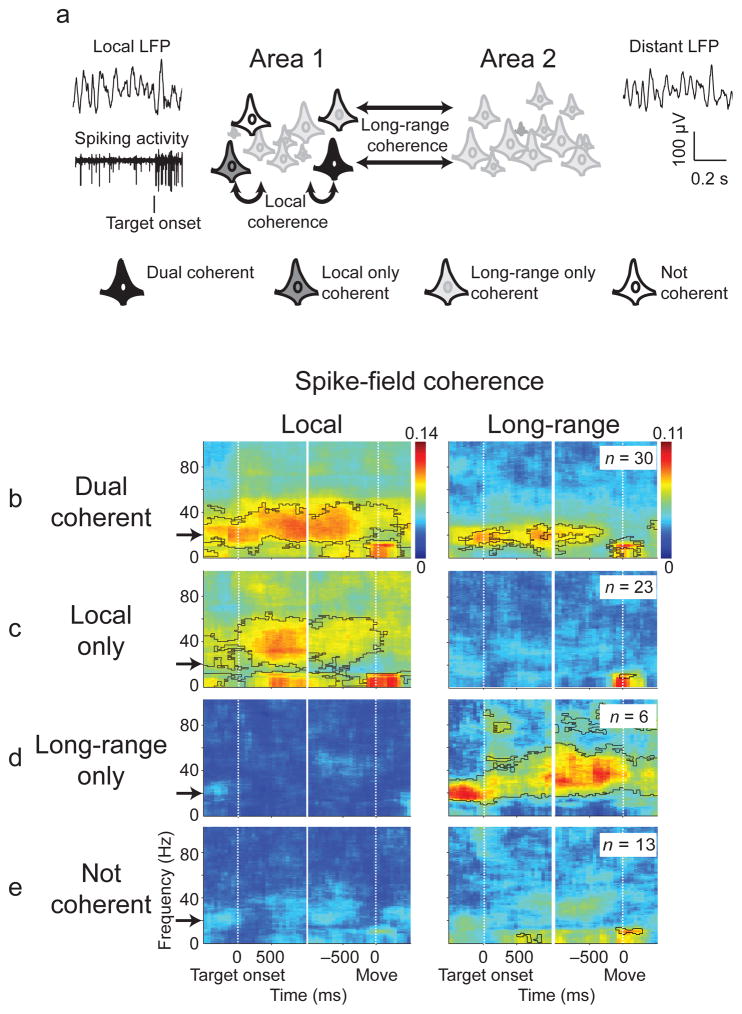
We measured SFC on the same bank (local) or on opposite banks (long-range; Fig 2a) of the IPS. We defined local-only coherent neurons as being coherent with local but not long-range LFP activity, long-range-only coherent neurons being coherent with long-range but not local LFP activity, dual coherent neurons being coherent with both long-range and local LFP activity and not coherent neurons which were not coherent with local or long-range LFPs.

Figure 2.

a) Neurons were classified based on whether its spiking activity was coherent with a local LFP, in the same area, or a distant LFP, in the adjacent area, (Permutation test, cluster corrected for multiple comparisons, p<0.05, 5 Hz smoothing). Neurons coherent with both local and long-range coherence are referred to as dual coherent (b), with only local coherence as local-only coherent (c), with only long-range as long-range only coherent (d), and without any coherence as not coherent (e). For classification SFC was tested in the beta band before the target onset cue is presented. The local and long-range coherence for each subpopulation is shown with areas of significance highlighted in black.

Seventy-two neurons in our database were recorded with LFP activity from electrodes placed both banks of the IPS (C: 53, R: 19; 144 unique spike-field pairs). Previous work has shown beta-frequency activity is specifically recruited during coordinated movements. Our initial analyses also showed that distributed coherence between the two banks of the IPS was consistent and relatively widespread in a beta, 15–25 Hz, frequency band. We, consequently, tested each neuron for significant SFC with local or long-range LFP activity at 20 Hz during the baseline epoch. Thirty neurons were dual coherent (42%; Fig 2), 23 were local-only coherent (32%), 6 were long-range-only coherent (8%), and 13 were not coherent (18%). The SFC phase between local (−38.2±20.6°) and long-range (19.4±19.5°) LFP activity differed for dual coherent neurons (p=0.01, Rank sum test) indicating that the LFP activity in the two areas differs. Finally, coherence was equally likely in each bank, with the proportion of locally coherent medial neurons not significantly different from the whole population (p = 0.11 Binomial test).

Dual coherent neurons signal choices first

Selecting a look-and-reach movement plan may involve communication between different effector-specific networks, preferentially recruiting dual coherent ensembles that extend between the banks of the IPS. If coherent ensembles are involved in selecting the plan, dual coherent neurons should start to signal movement plans earlier than other groups of neurons.

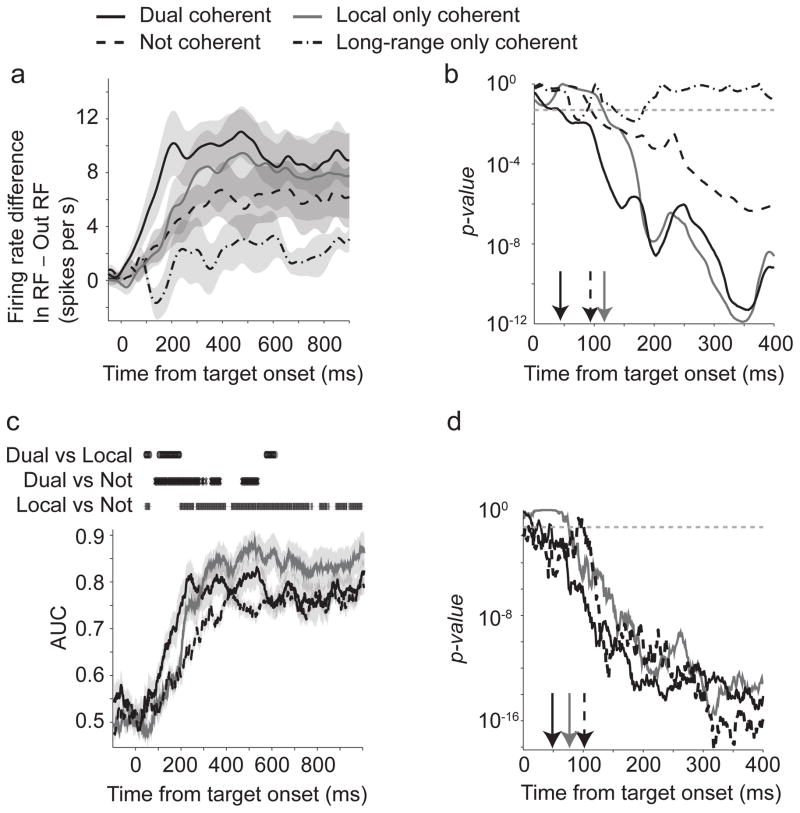
After the onset of the choice targets, firing rates of dual coherent neurons before movements into and out of the RF separated substantially earlier than the firing rates of both local-only and not coherent neurons (Dual: 45 ms; Local: 112 ms; Not: 107 ms; Fig 3a, b, Rank sum test, p<0.05). Firing rates of long-range-only coherent neurons did not become significantly different before the movement.

Figure 3.

a) Difference in firing rate for movements into and out of the RF for different groups of neurons. Mean ± S.E.M. are shown. b) P-values for a Wilcoxon rank sum test comparing firing rates into and out of the RF for each group. Arrows indicate the first point the statistical tests fell below 0.05 for three consecutive bins and remained significant. c) Area under the curve values for a ROC analysis on population average firing rates for movements into and out of the RF. Mean ± 95% confidence intervals are shown. The symbols above the AUC lines indicate significant differences between each pair of lines using a FDR corrected Wilcoxon rank sum test. d) P-values for a Wilcoxon rank sum test comparing the AUC values for each group against 0.5. Arrows indicate the first point the statistical tests fell below 0.05 for three consecutive bins and remained significant.

The separation in firing rates indicates that dual coherent neurons predict choices before the other populations. To quantify choice information moment-by-moment, we performed a receiver operating characteristic (ROC) analysis. The dual coherent neurons had a significantly higher area-under-the-curve (AUC) values than local–only and not coherent neurons (Dual: 0.55±0.01; Local: 0.51±0.01; Not: 0.51±0.01, 75 ms after target onset. Fig 3c; FDR-corrected Rank sum test. p<0.05). We performed this analysis on a population level by averaging trials from 12 randomly-selected neurons. The AUC values were also significantly different from chance (0.5) earlier for dual coherent neurons than other groups (Dual: 55 ms; Local-only: 92 ms; Not: 109 ms; Fig 3d; p<0.05, Rank sum test).

Fewer long-range-only coherent neurons were recorded so we recalculated the ROC analysis using smaller populations of neurons in order to compare all four populations (n = 5; Supplementary Fig 1a b). The properties of dual, local-only and not coherent neurons remained consistent, with long-range-only neuron firing rates separating the slowest.

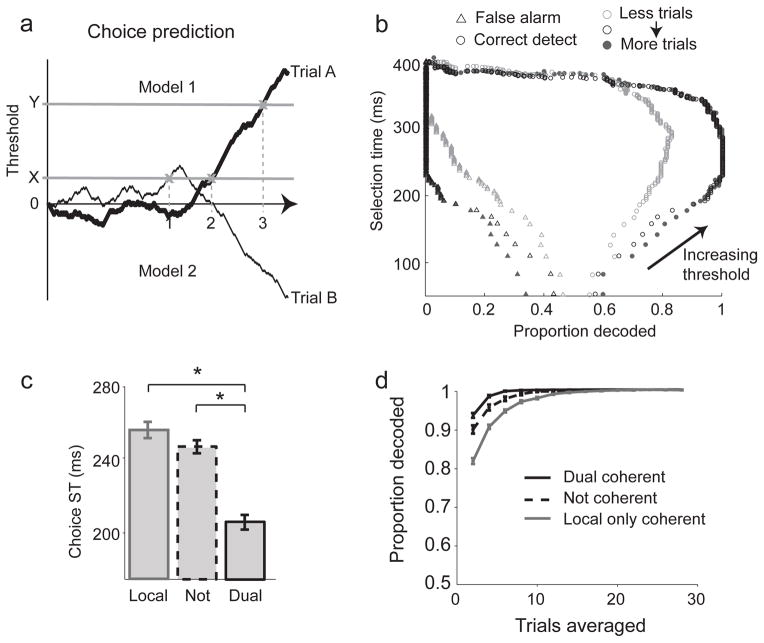
The above analyses show that dual coherent neurons are selective earlier than other groups of neurons. However, the analyses involved setting an arbitrary detection threshold. To control for this, we employed an approach from signal detection theory, the accumulated log-likelihood ratio (AccLLR) method²³, that does not employ an arbitrary detection threshold and explicitly reveals and controls for the speed-accuracy trade-off (Fig 4a, b).

Figure 4.

a) Example choice classifications of two trials, trial A which belongs to model 1 and trial B (model 2). If the threshold is set to a level X, trial A is correctly classified as belonging to model 1 however trial B is incorrectly classified resulting in false alarm. The time that the trials cross the threshold is marked as the ST (times 1 and 2). By increasing the threshold to level Y, both trial A and B are correctly classified. The ST is consequently increased as a result of the increased threshold. b) Tradeoff between ST, the correct detection rate and false alarm rate. As the threshold of detection is increased, the false alarm rate decreases while the correct detect rate increases to an optimal level. Further increases in the threshold result in trials not reaching threshold and not being classified reducing the correct detect rate. As trials used in decoding increases performance increases according until saturation is reached. c) Saturated STs for three different populations of dual coherent (solid), local-only coherent (gray solid) and not coherent (dashed) neurons. Error bars indicate standard error of the mean. Neuron–pools of size 11 were used. Stars indicate p < 0.05. d) Probability of correct classification when decoding movement choice from populations.

On each trial, neural activity for movements into or out of the RF was converted into a log-likelihood ratio that then accumulated in time. The selection time (ST) was defined by when the activity reached a threshold (Fig 4a), with the speed-accuracy trade-off set by the level of the threshold (Fig 4b). When the threshold was set to a low level, detection was fast but inaccurate. As the level of the threshold was raised, performance slowed down but was more accurate. We estimated the ST while controlling the speed-accuracy trade-off by setting the threshold to the lowest level that gave perfect classification performance (100% correct detections and 0% false alarms). To measure the ST of populations of neurons, we pooled information across neurons and trials (neuron-trials). Importantly, we found that the STs for perfect classification performance saturated and did not decrease below a certain time even when the size of the neuronal ensemble increased. The presence of saturation validated the estimate of ST and indicated it was a property of the neuronal ensemble being characterized and did not depend on the number of neurons recorded as part of the ensemble²³.

Consistent with earlier analyses, selection times were faster for dual coherent neurons than for not coherent neurons (Fig 4c, Supplementary Fig 1c; Dual: 205±4 ms; Not: 247±4 ms, p=9.6e-10, Rank sum test, mean ± s.e.m.). STs for dual coherent neurons were also faster than for local-only coherent neurons (255±5 ms, p = 1.3e-10). STs for not coherent neurons were not significantly different from local-only coherent neurons (p=0.14, Rank sum test). The results remained significant when we calculated STs using data from each monkey separately (Supplementary Fig. 1d). For the above comparisons the decoding accuracy was set to 100% (Fig 4d), however the results remained the same at an 85% decoding accuracy (Dual vs Local, p = 5e-4; Dual vs Not p = 7.4e-5, Rank sum test).

Coherent neurons may reflect processes that are not specific to decision making, such as visual selectivity. However, the timing of the visual onset was the same for coherent and not-coherent ensembles (Dual: 39±3 ms. Local: 41±5 ms. Not: 36±3 ms. All comparisons p>0.05, Rank sum test). Therefore, coherent activity was specifically associated with how quickly visual input is processed to make a choice and not associated with differences in the timing of visual input.

The above analyses pool neurons from both banks of the IPS, so to ensure that the timing of activity was similar in each area, we compared the STs for each bank separately (Supplementary Fig 2). Selection occurred at a similar time across the IPS (lateral: 205±4 ms, medial: 201±4 ms, p=0.47; Rank sum test) so neurons on both banks were recruited together during look-reach decisions. The proportions of lateral and medial bank neurons with local and long-range SFC also did not differ significantly (Supplementary Fig 3)

These results demonstrate that distributed neural ensembles in which neurons fire dual-coherently, within the lateral and medial banks of the PPC, are rapidly recruited. These dual coherent neurons predict movement choices substantially before other groups of neurons.

Neuronal ensembles defined by firing rate properties

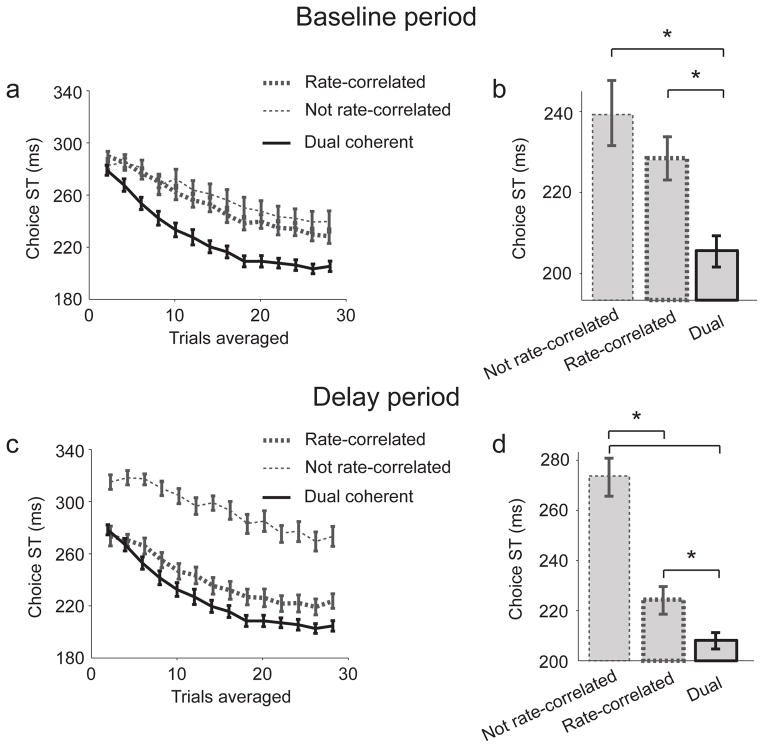
Neuronal ensembles also display correlated firing rates. Ensembles of rate-correlated neurons may be preferentially recruited for decision-making. If so groups of rate-correlated neurons should exhibit choice selectivity earlier than groups of coherent neurons. We defined a population of rate-correlated neurons (Fig 5a, b). Our database contained 60 neuron-pairs with 25 significantly rate-correlated in the baseline period (Local: 22, Long-range: 3, Unique neurons: 37), and 28 were correlated in the early delay period (Local: 23, Long-range: 5, Unique neurons: 45).

Figure 5.

STs for populations of neurons with and without rate-correlations in the a) baseline period, or c) the early delay period. b and d) Bar graph showing saturated STs. For all figures neuron–pools of size 11 were used. Stars indicate p < 0.05. Mean ± s.e.m are shown.

“Coherent” and “Rate-correlated” labels were uncorrelated across neurons suggesting separate underlying mechanisms. STs for both of the rate-correlated populations were significantly and substantially slower than for the dual coherent population (Baseline: 227±6 ms; p = 0.03, Rank sum test; Delay: 224±6 ms; p = 0.009; Fig 5). There was also no significant difference between baseline-period groupings with and without rate-correlations (No rate-correlations: 240±8 ms; p = 0.35), while Delay period rate-correlated neurons were significantly faster than those without rate-correlations (No rate-correlations: 277±4 ms; p = 7.1e-6). Therefore, rate-correlated ensembles were recruited during the early formation of movement plans, but temporally-coherent ensembles were recruited even earlier.

Choice-selectivity may be associated with neurons with higher overall levels of firing, not necessarily neurons with coherence (see Supplementary Fig 4). To address this, we measured STs for groups of neurons defined according to the level of their baseline firing rate. High baseline firing ensembles had faster STs than low baseline firing ensembles (low: 289±9 ms, high: 225±9 ms, p=9.7e-6; Rank sum test) but were slower than for dual coherent neurons (p<0.05 all comparisons). Thus, the choice-selectivity of coherent neuronal ensembles was not simply associated with groups of neurons that tend to fire more spikes (Supplementary Fig 5, 6). For the center out task, dual coherent neurons tended to have larger differences in firing rate, however this was not significant (Supplementary Fig 7).

Greater firing during choice is likely to be a feature of choice-selectivity because it allows larger differences in firing to exist for different choices. As expected, neurons with high firing rates during the delay period selected choices faster than those with low delay period firing rates (low delay ST = 288±7 ms. high delay ST = 208±4 ms, low vs high: p<1e-6; Rank sum test). Somewhat surprisingly, perhaps, STs of neuronal ensembles with high delay period firing did not differ from STs of dual-coherent neurons (high vs dual; p=0.304). Thus, coherence-related choice selectivity was similar in strength to selectivity associated with strong delay period activity.

Spike-spike coherence may also be used to define coherent ensembles, however only six neuron-pairs exhibited significant beta frequency (20 Hz) coherence at a p<0.05 significance level (Permutation test) which is expected by chance (p=0.08, Sign test). A similar lack of coherence was observed in the delay epoch (n=7). Thus, identifying coherent ensembles depended on relating the spiking of neurons to LFP activity.

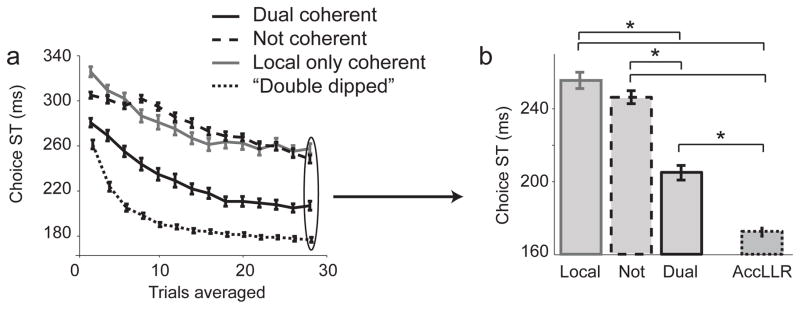
To assess how much choice information in neural firing was associated with the presence of coherence, we compared dual coherent STs with the most choice-predictive ensembles in our database. Neurons were ranked by how well they predict choices individually (AccLLR), and the most-choice-predictive neurons were grouped, effectively ‘double dipping’ to extract the most information. This method yielded STs of 174±2 ms after target onset with perfectly predicted choices (Fig 6). The most-choice-predictive ensembles were recruited significantly faster than dual coherent ensembles (p = 2.9e-7, Rank sum test), however, the dual coherent ensemble was a relatively modest 30 ms slower demonstrating that dual coherence is a good predictor of choice coding.

Figure 6.

a) STs for a neural population defined by AccLLR selectivity (“double dipped”, grey). For comparison, populations defined by coherency are also shown. b) Bar graph showing saturated STs. For all figures neuron–pools of size 11 were used. Stars indicate p < 0.05. Mean ± s.e.m are shown.

Controlling for the magnitude of coherence

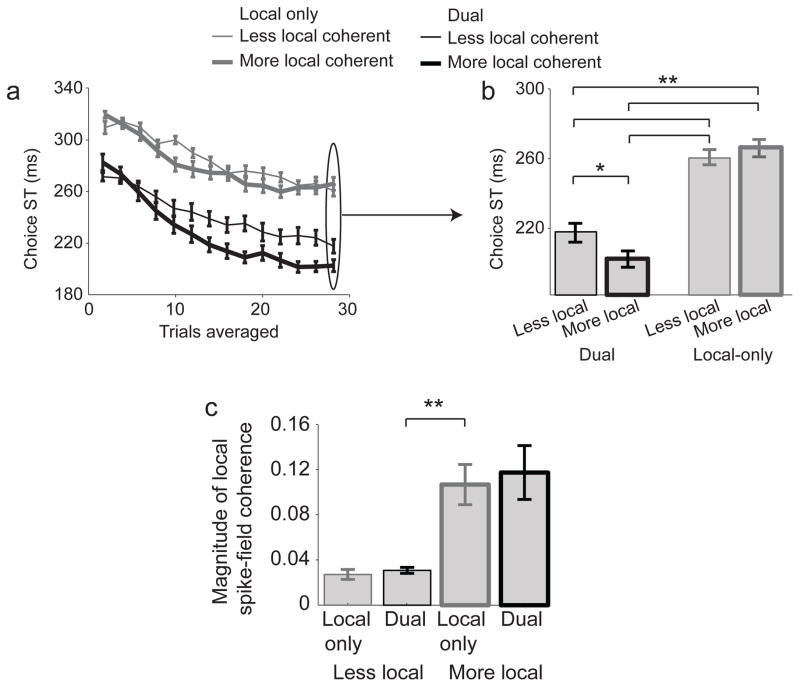
Dual coherent neurons tended to have stronger local coherence than local-only coherent neurons (see Fig 2). Fast STs in dual coherent neurons may be due to the strength of local coherence and not the presence of both local and long-range coherence. Dual coherent and local-only neurons were divided into a more-local group with high local SFC and a less-local group with low local SFC, and the STs calculated (Fig 7). The ST for the dual coherent ensemble with less-local SFC was significantly faster than the local-only ensemble with more-local SFC (p=1.2e-6; Rank sum test). Critically, local SFC magnitude for the more-local local-only coherent neurons was significantly more than for the less-local dual coherent neurons (Fig 7c, p= 0.0076; Rank sum test).

Figure 7.

a, b) STs for the local-only, and dual neurons when separated by the magnitude of local coherence power. Neuron–pools of size 8 were used. c) Average local coherence magnitude for the dual coherent and local-only coherent neurons when separated by the magnitude of local coherence. Stars indicate p < 0.01. Mean ± s.e.m are shown.

We also grouped the dual-coherent population based on the magnitude of long-range coherence. The ST for the more long-range SFC population was not significantly different from the ST for less long-range SFC (low: 202±3 ms, high: 208±7 ms; p = 0.45; Rank sum test). The role of dual-coherent ensemble in supporting fast ST was not associated with the either the magnitude of local or the long-range coherence. The early ST was associated with neurons that have both local and long-range coherence.

Controlling for errors in SFC labels

We performed analyses to demonstrate that coherence-based labels remained consistent across the trial and were not influenced by differences in firing rates across neurons. Dual coherent neurons fired at higher rates, so timing analyses were re-estimated after decimating spike trains (Supplementary Fig 4). The results remained consistent with dual coherent neuron firing rates separating (Supplementary Fig 8a–d and being more informative earlier (Supplementary Fig 8e) (vs local p=3.4e-6, vs not p=1.9e-5 Rank sum test). Dual coherent neurons from re-classified populations by decimating the firing rates before SFC estimation (Supplementary Fig 8f, 201.8 ± 5.6 ms) also remained faster than local-only coherent (p=1.5e-7 Rank sum test) and not coherent neurons (p=5.8e-7). Thus, the differences in STs were not due to the impact of differences in the overall firing rate across the populations.

Next, although SFC fluctuated in amplitude during the trial, neurons that showed coherence during the baseline, were more likely to show coherence at other times in the trial than expected by chance (79% of coherent labels remained), with the converse also being true for not coherent labels (78%). We also recalculated the SFC labels and STs as we varied the test frequency. When the frequency was above 40 Hz, only a small number of neurons had significant coherence (Fig 2b–e). For frequencies below 40 Hz there was not much change in the classifications with the ST for dual coherent neurons not changing from what we observed at 20 Hz. This indicates that the effects shown depended on detecting beta-frequency coherence. Beta-band classification is desirable as it is unlikely to be affected by false positive errors in SFC due to spike artifacts on same-electrode spike-field pairs. Same- and different-electrode SFC during the baseline (Supplementary Fig 9) were compared and although there was significantly more coherence on same-electrode pairs at frequencies above 40 Hz, the coherence at 20 Hz was identical.

Finally, the differences we observed in mean firing rates across populations of coherent neurons suggested that coherence may reflect different cell types³⁵. We recorded neurons with both broad and narrow spike widths with a dip at 500 μs (p=0.015, Hartigan’s Dip test). A heterogeneous population of neurons with broad and narrow spike widths participated in each type of coherent activity (Supplementary Fig 10), with dual coherent neurons having significantly more narrow spike widths (60%, p=0.01, Binomial test).

These results demonstrate that distributed neural ensembles in which neurons fire dual-coherently, within the lateral and medial banks of the PPC, are rapidly recruited. These dual coherent neurons predict movement choices substantially before other groups of neurons.

Discussion

The firing rates of PPC neurons with distributed neuronal coherence predict look-reach movement choices earlier than that of other groups of neurons. Dual coherent neurons, which fire spikes coherently with LFP activity on both banks of the IPS, contained a surprisingly large amount of information about the upcoming movement choice and were specific to movement selection. Furthermore, the firing rate selectivity that we observe indicates that selection may be driven by differences in the levels of firing by neurons interacting through coherent oscillatory activity. We next discuss implications of the results for models of reach-and-saccade selection before considering how coherence involves selection more broadly.

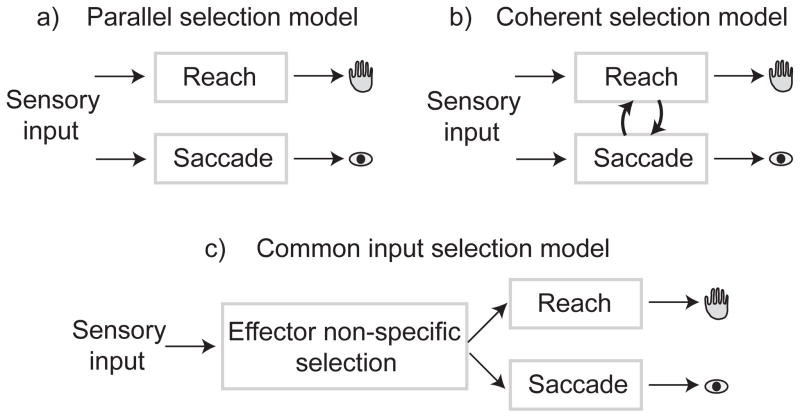
Parallel selection model

A simple model for reach and saccade target selection is the parallel selection model (Fig 8a). Here, target selection for each movement takes place in a dedicated system and the two systems operate in independently and in parallel³⁶. The essential feature of this model is that reach and saccade selection do not interact with each other and, therefore, is consistent with our ability to make decisions for one effector or the other³⁷. In the current experiments, we did not present single-effector movement choices and encouraged decisions for reaches and saccades to be made together. Choice-predictive dual coherence is evidence of functional coupling between reach and saccade selection and is not consistent with parallel selection.

Figure 8.

a) Parallel selection model where reach and saccade target selection occurs in parallel dedicated systems that do not interact with each other. b) Interacting selection model where selecting a reach-and-saccade movement depends on coordinating the activity of neurons across the reach and saccade systems. c) Common input model where target selection for reaches and saccades results from common input to the parietal reach and saccade systems from a third, effector-non-specific, selection system.

Interacting selection models

Rather than occurring in parallel, selection may involve an effectively common selection stage due to interactions between the activity of neurons in the reach system and the saccade system^38,39 (Fig 8b). These interactions could take the form of coherent patterns of neural activity. Our results support and constrain models of interacting selection and specifically support a model we term coherent selection.

The main prediction of interacting selection is that correlations in neural activity between the reach and saccade systems are associated with choice-predictive firing. Consistent with this, the most choice-predictive firing involved temporally-precise patterns of spiking across both banks of the IPS. The relationship between temporally-patterned firing and choice was present for each animal individually and survived efforts to control for variety of other confounding influences such as the level of neural firing, the strength of neural coherence, and the size of the neural ensemble used for decoding. Correlations on longer time scales in the firing rate (>100 ms) were present but were less choice-predictive. Therefore, our data supports the hypothesis that making reach-saccade decisions involves interactions between the reach and saccade systems that these interactions take the form of coherent activity.

Coherence was not simply associated with visual input into the banks of the IPS. The visual selectivity of responses occurred at the same time in coherent and not-coherent populations. Choice selectivity appeared in both banks of the IPS at the same time, within milliseconds of the other area, and the earliest choice-specific signals only occur in the coherent neurons some 10–20 ms after the onset of the visual response. These observations support a role for coherence in a choice process, not simply visual input or elevated firing, and show that selection processes in each area neither lead nor follow processes in the other.

Common input selection models

Other models of selection also involve coupling through common inputs to PPC from other potentially effector-non-specific, regions (Fig 8c). Previous work has shown that reversibly-inactivating neurons in either bank of the IPS creates spatially-specific deficits in reward-guided choice tasks²⁰. This implies that common input to the IPS alone does not select targets for both movements. However, interpreting these findings and distinguishing between common input and interacting selection involves establishing the connectivity and functional architecture of the large-scale decision network, not just the two posterior parietal regions we have studied.

Our work offers specific constraints on how common input can drive choice selective responses across the IPS. LFP activity reflects, in part, synaptic potentials near the recording electrode. If both banks of the IPS receive common input, LFP activity on each bank of the IPS is likely to reflect this. Choice-predictive dual coherence is, therefore, consistent with common input to PPC. However, choice-predictive dual coherence cannot simply result from the presence of common input to LFP activity on both banks. If inputs to the IPS are choice-specific, the magnitude of local coherence should be associated with increased choice selectivity. We find that neither the presence nor the magnitude of local coherence alone is associated with increased choice-selectivity. The patterns of choice selectivity we observe across populations of dual coherent neurons reveal a role for network interactions that must extend beyond common input alone. Additional work involving causal manipulations is needed in order to distinguish mechanisms involving common-input from those involving direct and indirect interactions.

Bottom-up and top-down selection

We presented choice targets at random spatial locations trial-by-trial; therefore, initial visual input likely drove visual-selectivity in a bottom-up manner. Likewise, blocks in which the circle or triangle targets were rewarded the most were interleaved and the resulting choices were sensitive to reward magnitudes, choice-selectivity was likely due to top-down signals. Beta-frequency band activity has been recently linked to top-down control of visual attention⁴⁰. Here, visual- and choice-selectivity offers a way to examine whether beta-coherence is associated with top-down or bottom-up processes.

Visual-selectivity occurred early and at the same time in both banks of the IPS and regardless of the presence of coherence suggesting that common bottom-up input enters the IPS but that beta-coherence is not involved with this process. Choice-selectivity was present as early as 50 ms following target onset and by ~200 ms, depending on the coherent ensemble, we could be 100% confident of predicting the choice. Behavioral work has shown that top-down influences can bias eye movement choices as early as 100 ms⁴¹. Therefore, the initial choice-selectivity appears consistent with top-down selection. Neurons from coherent and not-coherent ensembles eventually encoded the movement plan and did so with equal strength. Therefore, the relationship between distributed beta coherence was specific to the earliest period of selection, potentially at the time when the decision was being made.

Beta-activity has been a focus of computational work suggesting a role in long-range processing because it is more robust to conduction delays than higher frequency activity⁴². Experimental evidence also indicates that beta-activity may be particularly widespread across long-range neuronal circuits. Many studies indicate that beta-activity in the frontal and parietal cortices is involved with and even necessary for decision making^26–28,43. These studies and our own results indicate that the role of beta-activity in decisions reflects top-down processing and may be related to the communication demands imposed by making a decision.

Long-range-only coherence and selection

A natural hypothesis is that long-range coherence is due to interactions that reflect how the decision signal is communicated between areas. Our results, however, show that choice-selective coherence does not specifically involve long-range coherence. In fact, long-range-only coherent neurons were strikingly poor at encoding the choice, long-range-only coherent neurons were not associated with fast choice-selectivity and dual coherent neurons with more long-range coherence were not associated with faster choice-selectivity. We conclude, therefore, that selection is associated with local coherence as much as long-range coherence. One explanation is that neurons whose activity is uncorrelated with local populations are not in a position to communicate relevant information about the movement choice to the long-range population. Long-range-only coherent neurons are, in a sense, disconnected from the local component of the decision mechanism. If this is true, it could explain why long-range-only coherent neurons are even less selective than neurons with no coherence. This is consistent with the idea that if nearby neurons are not signaling together then the signals that they also send to other regions may also be less likely to correctly signal the choice. However, much larger samples of long-range-only neurons are necessary to draw strong conclusions.

Another important hypothesis is functional-anatomical and proposes that coherence involves neurons with particular anatomical properties⁴⁴. For example, local coherence may be associated with interneurons and long-range-only coherence may be associated with pyramidal projection neurons. Our analysis of spike waveforms revealed a bimodal distribution of spike widths, consistent with the presence of at least two classes of cells in our data. Dual coherent neurons fell roughly in even groups of putative interneuron (narrow) and putative pyramidal (broad) cells. This suggests that coherence is not necessarily a property of a given cell type. Particular cell types may play an important role in establishing the temporal patterning of coherent neuronal activity⁴⁵, but our data indicates that coherence is not itself restricted to particular cell types.

Caveats and concerns

We used two kinds of measures to analyze the temporal evolution of selection. Analyzing the separation in firing rate revealed when choice information was first present in the activity but did not indicate how accurately this separation could be detected. In contrast, our estimate of selection time controlled for detection accuracy and measured the time when selectivity can be detected with a given level of accuracy, ie 100%²³. By showing that the speed and accuracy of the procedure did not improve when increasing the size of ensemble, we rigorously compared ensembles that differed in their coherent properties. Both measures of timing gave consistent results and likely captured similar aspects of neural function. This is because the early selectivity present in the separation of firing rates contributed to the selection time when choices could be accurately predicted. Caveats should also be noted. First, and most importantly, the AccLLR procedure critically depended on fitting statistical models for the activity of neurons. We modeled activity with relatively-flexible time-varying Poisson processes often used to characterize neural coding but models that explicitly capture inter-trial variability may be more accurate⁴⁶. Second, AccLLR is an efficient statistical procedure but it is not intended to describe how neural activity in PPC is read-out to select actions. The AccLLR procedure detected the decision by counting the number of spikes not their timing. We chose to do this so that the signal timing results could not be due to temporal correlations. It is plausible that downstream brain areas read out the spiking activity using another algorithm, for example, one that incorporates spike timing and neural coherence.

Finally, the number of simultaneous recordings we could make limited our identification of coherent neurons. Errors in SFC classification could alter the neuronal ensembles, which could in turn alter the ST estimates. When detecting local SFC, false negatives should not be a concern because SFC is likely to be strongest when LFP activity is taken from the same electrode as spiking activity, and this very local LFP recording is always available. Our data (Supplementary Fig 9) indicate that false positives are also not an issue which is consistent with published work ⁴⁷ that reports that spike-contamination in the coherence at 20 Hz occurs only for neurons with wide spike widths, a SNR greater than 16, and a spike rate greater than 20 spikes/s. Dual coherent neurons in our database have a smaller SNR, narrower spikes and lower firing rate. False negatives in the long-range SFC cannot be ruled out, with the possibility that we have missed some dual coherent neurons. More work is needed to address this concern. Despite these caveats, we note that our comparisons are based on several convergent measures that show coherent ensembles in PPC are rapidly recruited when making decisions.

Online Methods

Experimental Preparation

Two adult male rhesus macaques (Macaca mulatta) participated in this study (Monkey C: 7.5 kg; Monkey R: 6 kg). All surgical and animal care procedures were approved by the New York University Animal Care and Use Committee and were performed in accordance with the National Institute of Health guidelines for care and use of laboratory animals. Monkeys were socially pair-housed with one other male, and kept on a 12 hour/12 hour light/dark cycle. All experimental testing was completed during the light cycle under controlled-water access. Data collection and analysis were not performed blind to the conditions of the experiment.

We surgically implanted a head-post to allow head-restraint, behavioral training and electrophysiological recordings. After training, a square recording chamber, 16 mm×16 mm inner dimension, was implanted onto the skull and a craniotomy was made to gain access to the posterior parietal cortex. In Monkey C, we targeted placement of the recording chamber and registered electrode recording locations to the cortical anatomy using a structural magnetic resonance image (MRI)-guided stereotaxic instrument (Brainsight, Rogue Research). The structural MRI was obtained with 0.5 mm isotropic voxels. MRI scans were not possible in Monkey R due to the presence of iron in the soft tissue. Therefore, the recording chamber was placed according to stereotaxic coordinates over 7 P, 13 L and recording sites were functionally-localized based on task responses and anatomically-localized based on the depth of recordings from the cortical surface as indicated by trans-dural penetration of the recording electrode and the depth at which clearly-identified action potentials were obtained.

Experimental Hardware

The start and end positions of reaches were monitored via an acoustic touch-sensitive screen (ELO Touch Systems) and eye position was constantly monitored with an infrared optical eye tracking system sampling at 120 Hz (ISCAN). Visual stimuli were presented on an LCD monitor (Dell) placed directly behind the touch screen. The visual stimuli were controlled via custom LabVIEW (National Instruments) software executed on a real-time embedded system (NI PXI-8184, National Instruments). Behavioral events were synchronized to neural recordings by placing a photodiode on the bottom corner of the monitor to detect visual stimulus events. On each experimental session, we inserted up to four glass-coated tungsten electrodes (Alpha Omega, 0.7–1.2 MΩ impedance at 1 kHz) through the dura mater into the IPS using a multielectrode motorized microdrive (NAN Instruments Ltd). Neural signals were amplified, low-pass filtered at 6 kHz and digitized at 30 kHz using 16-bits of resolution with the lowest significant bit equal to 0.1 μV (NSpike NDAQ System, Harvard Instrumentation Lab; x10 gain headstage Multichannel Systems). Recordings were referenced to the metal guide tube array resting on the dura in contact with the surface of the cortex above the recording sites.

Behavioral Tasks

We trained two monkeys to perform four tasks in which they earned fluid rewards for making reaches to green targets, saccades to red targets and coordinated reach-and-saccades to yellow targets. During each experimental session, monkeys performed a center-out task and then three variants of a two-arm-bandit choice task. They were trained to reach using the arm contralateral to the hemisphere over which recording chamber was implanted (Fig 1b).

The behavioral tasks were organized in two separate blocks of trials. In the first block of trials, 80 trials in duration, the monkeys performed a center-out task. In the second block of trials, 460±295 trials (mean±sigma trials), the monkeys performed three choice tasks on randomly interleaved trials: a reach-and-saccade choice task, a saccade-only choice task and a reach-only choice task. Fluid rewards were delivered via an electronically-controlled solenoid.

All four tasks shared the same set of initial events. The monkeys were trained to start each trial by placing their hands on two proximity sensors placed at waist height. A red and a green square were illuminated side-by-side at the center of the display (2° visual angle on a side, green on left). The monkeys then reached toward and touched the green square, and made a saccade to fixate the red square for a baseline period (500 – 800 ms, uniformly distributed).

In the center-out task, a yellow square target was then illuminated in the visual periphery (eccentricity 10° visual angle, one of eight possible locations) and the monkeys were trained to maintain fixation and touch for an instructed delay period 1,000 – 1500 ms. After this time, the initial targets were extinguished cueing the monkeys to reach and saccade to the target.

In the choice tasks, after this baseline period, two yellow targets (a triangle and circle) were presented, one placed 10° from the initial fixation and touch targets in the direction of the response field and the other placed 10° in the diametrically opposed direction. The shape of the target placed in the direction of the response field was randomly assigned each trial. The monkeys were instructed to maintain fixation and touch of the initial targets for a further 1,000 – 1,500 ms. At this point the initial fixation and touch targets were extinguished cueing the monkeys to perform a reach and saccade to one of the two targets. After target presentation, touch and fixation were maintained for 300 ms after which the monkey was given a fluid reward of volume determined by the target chosen. On a subset of trials, the yellow targets changed color to red (or green) 1,000 – 1,500 ms after the initial target onset. Each monkey maintained fixation and touch for a further 1000 – 1500 ms, after which the initial red (or green) square was extinguished, cueing the monkey to perform a saccade (or reach) to one of the two targets while maintaining touch (or fixation) of the initial green (or red) square. In this study, we analyzed data from reach-and-saccade, reach, and saccade task types together as only the neural activity immediately following target onset before the effector cue did not depend on the effector cue. We randomly interleaved reach-and-saccade, reach-only, and saccade-only choice tasks trial-by-trial with a probability of 0.24, 0.38 and 0.38, respectively. Both animals performed the same tasks and were not randomly assigned to a specific experimental grouping.

Neuronal Recordings

We recorded neuronal activity from the medial and the lateral banks of the IPS in the PPC, approx. 5 – 10 mm below the cortical surface (Fig. 1a). On each experimental session at least one electrode was lowered into each bank of the sulcus. Electrodes were positioned by a 2×2 square array of guide tubes, 2 mm on-a-side. The average separation between electrodes in the lateral bank was 1.9 ± 0.6 mm (mean ± std), and 2.1 ± 1 mm between electrodes in the medial bank. Electrodes between banks of the IPS were separated on average by 2.6 ± 0.9 mm. Recordings were referenced to the metal guide tube array resting on the dura in contact with the surface of the cortex above the recording sites.

Spike preprocessing

We extracted spike waveforms from the neural recordings by first bandpass filtering the raw neural waveforms from 0.3 – 6.6 kHz (multitaper projection filter settings, [Time duration = 0.01 s, Frequency bandwidth = 3,000 Hz, Center frequency = 3.3 kHz]), and then finding 1.6 ms duration sections of the filtered signal that crossed a threshold set at 3.5 standard deviations below the mean filtered signal. We used a robust estimate of the standard deviation. We projected spike-waveforms into a 3-D principal component feature space on a moving 100 s time window. We used the unsupervised clustering algorithm k-means to over-cluster the spike waveforms. We then manually merged clusters that displayed clear separation from the multiunit noise cloud. Only time periods during the recording in which the single unit cluster was clearly isolated from the multiunit noise cloud over the entire 100 s time window were accepted for further analysis. All clusters were verified by visually-inspected off-line.

Criterion for unit acceptance

We only entered spike recordings into the database if they displayed significant task-related differences in firing rate. Specifically, we tested for differences between the firing rate in the choice task during the baseline and the firing rate during the 100 ms interval immediately following target onset (visual response) as well as during the 500 ms period subsequent (delay response; Permutation test, p< 0.05). Statistical methods were not used to predetermine sample sizes however the sample sizes in this work are similar to those reported in previous publications.

LFP preprocessing

We obtained LFP activity by low-pass filtering the broad-band recording at 400 Hz (multitaper projection filter settings, [Time duration = 0.025 s, Frequency bandwidth = 400 Hz, Center frequency = 0 Hz]) and down-sampling the activity to 1 kHz from 30 kHz. To ensure that LFP activity was recorded from the banks of the IPS and not in between the sulci or in the white matter, we only entered LFP recordings into the database if they were made within 100 μm of a site that contained neuronal action potentials.

Response field analysis and single unit isolation

We analyzed neuronal response fields (RFs) measured during the center-out task to test whether RFs were sampled during the choice tasks with similar accuracy in the populations of dual, local-only, long-range-only and not coherent neurons. We fit the RF for each neuron by taking the firing rate during the delay period of the center-out task. We fit a Von Mises function to the response field for each cell. The Von Mises function models the response as a circular function centered about a mean angle with a width about the mean given by a concentration parameter. We measured the angular deviation between the placement of the choice targets and the center of the fitted response field and compared the deviation across each group of neurons. The angular deviation between the receptive field as mapped out by the center-out task and fit with a Von Mises distribution and the placement of the choice target, was checked to be not significantly different from 0 for all populations (Dual: p=0.67, Local-only: p=0.5, Long-range-only: p=0.21, Not: p=0.84). We also tested whether there was a significant difference in the degree of spatial tuning for each population of neurons during the instructed delay of the center-out task (Supplementary Fig 7). The single unit isolations during the recording was also controlled for to ensure that spike waveform signal-to-noise-ratio (SNR, mean waveform amplitude compared to the standard deviation of the waveform noise) were different between populations (Dual: 4.4±0.4. Local-only: 4.9±0.4. Long-range-only: 3.9±0.5. Not: 4.2±0.4. p > 0.05, all comparisons Rank sum test).

Spike-field coherence analysis

We estimated spike-field coherence (SFC) using multitaper methods with a 500 ms sliding windows with ±10 Hz frequency smoothing^48,49. To test whether spike-field pairs had significant SFC, we tested the magnitude of the SFC at 20 Hz against a null hypothesis that there was no SFC using a permutation test (at least 10,000 permutations). We generated the null distribution for no SFC by randomly permuting the order of trials for the spiking data compared to the LFP data. We tested SFC during the baseline period 250 ms before the target onset cue to maximize the number of trials. We calculated SFC for spike-field pairs on electrodes within each area (local) and between areas (long-range). We also tested SFC during the delay period centered 250 ms after target onset. For the significant regions presented in the coherograms (Fig 2b–e), we applied a cluster correction to correct for multiple comparisons⁵⁰. To divide recordings into more-local and less-local coherence groups, we ranked recordings according to decreasing magnitude of the coherence and assigned the first 50% of recordings to more-local coherence group and the last 50% to the less-local coherence group. The same procedure was used to assign recordings to more-long-range and less-long-range coherence groups. Neurons had two chances to be coherent with LFPs in each area. If the activity of a neuron was coherent with LFPs on one electrode but not another, the neuron was still classified as coherent.

Spike-spike analysis

We quantified the relationship between the spiking activity of two neurons by estimating the coherence between the two spike trains, the spike-spike coherence, and by estimating the Pearson correlation coefficient between the firing rates of the two neurons across trials, the spike-count correlations. We estimated spike-spike coherence and spike-count correlations using the same analysis parameters as we used for the SFC analysis. We also tested spike-count correlations during the delay period centered 250 ms after target onset.

Onset time analysis

We identified the onset of choice activity as the time after target onset that the firing rate of each neuron differed significantly before movement choices into and out of the RF. We did this performing a Wilcoxon rank sum test on each 50 ms time interval following the onset of the choice targets and detecting the first time when the results were significantly different at p<0.05 using a two-sided test. Since this procedure involves making multiple comparisons, we corrected the significance of the Wilcoxon rank sum tests by controlling the false discovery rate.

Receiver-Operating Characteristic analysis

We compared how movement choice information in populations of neurons evolved in time moment-by-moment. We did this by performing a Receiver-Operating Characteristic (ROC) analysis on the population average firing rate across sequential 50 ms time intervals and measuring the area under the ROC curve (AUC) at each time. We calculated the population average firing rate by averaging trials from either 12 randomly selected neurons from a population of neurons (Fig 3c, d) or by averaging 5 randomly selected neurons from a population of neurons (Supplementary Fig 1a, b). Neurons were selected without replacement. We performed statistical analyses of the moment-by-moment movement choice information by iterating the AUC calculations 20 times and constructing the EDF of the AUC. To detect the onset of movement choice information we performed a Wilcoxon rank sum test on the AUC each 50 ms time interval and detecting the first time when the results were significantly different from chance (ie AUC = 0.5; two-sided test) at p<0.05. As for the onset time analysis, we corrected the significance of the Wilcoxon rank sum tests by controlling the false discovery rate.

Accumulated Log-Likelihood Ratio Model

To quantify the timing of neural signals across neural populations more rigorously, we used an accumulated log-likelihood ratio (AccLLR) method²³ derived from the literature on sequential design. We used the AccLLR method to determine when selectivity in the neural signals for two alternatives first emerged; the selection time (ST) of a neuron. The ST was defined by when the activity reached a threshold (Fig 4a), with the speed-accuracy trade-off set by the level of the threshold (Fig 4b). When the threshold was set to a low level, detection was fast but inaccurate. As the level of the threshold was raised, performance slowed down but was more accurate. We estimated the ST while controlling the speed-accuracy trade-off by setting the threshold to the lowest level that gave perfect classification performance (100% correct detections and 0% false alarms).

In the AccLLR method, we defined a probabilistic model of the spiking activity for the two alternatives that are being tested. To determine the ST for a movement choice, the choice ST, we defined the two alternatives as movements into the RF and movements out of the RF. We also calculated visual ST by comparing the neural activity after the two peripheral targets appear to the neural activity in the baseline period.

We modeled spiking as a time-varying Poisson process for each of the two alternatives. On each trial, neural activity for movements into or out of the RF was converted into a log-likelihood ratio that then accumulated in time. We combined the activity from the different neurons by assuming independence and averaging the likelihood across neurons. We matched the detection performance across recordings from different populations explicitly by varying the position of the threshold. The probability of correct decoding increased with increasingly large ensembles of neurons, changing STs. To avoid this confound, we measured decoding accuracy and ST using neuronal ensembles large enough that the results did not change when the number of neurons in the population was increased beyond a certain size. To increase ensemble sizes, we also averaged activity from different trials with the same movement choices. We call the process of testing populations of increasing size until there is no significant change as “saturating” decoding accuracy and STs. Once decoding accuracy and STs are saturated, performance will not change with larger ensembles from the same population, and we have successfully controlled the speed-accuracy trade-off in the detection procedure.

For each of the models of spiking activity we assumed that spike times are Poisson distributed with a time varying firing rate, λ(t). For a given model at time bin Δ(t) the likelihood of spiking was given by:

$$P(N(\mathrm{\Delta }t))\mid \lambda (t))=\frac{exp(-\lambda (t)\mathrm{\Delta }t)}{N(\mathrm{\Delta }t)!}{(\lambda (t)\mathrm{\Delta }t)}^{N(\mathrm{\Delta }t)}$$

where NΔ(t) denotes the number of spikes that occurred in a short time 1 ms Δ(t) interval. The log-likelihood ratio, LLR(t), of a single spike train, belonging to the two models being tested was given by:

$$\begin{array}{ccc}\mathit{LLR}(t)& =& log\frac{P\left(\delta N(t)\mid {\lambda }_1(t)\right)}{P\left(\delta N(t)\mid {\lambda }_2(t)\right)}\\ & =& ({\lambda }_2(t)-{\lambda }_1(t))\mathrm{\Delta }t+\delta N(t)log\left(\frac{{\lambda }_1(t)}{{\lambda }_2(t)}\right)\end{array}$$

where δN(t) denotes the spiking activity for each δ(t) time interval starting at time t, with 1 representing a spike event and 0 representing no event.

The log-likelihood ratio can be calculated on a trial average basis or averaged across an ensemble of neurons. Assuming that activity on each trial or for each cell is independent, the average log-likelihood ratio was given by:

$${\mathit{LLR}}^{\mathit{ave}}(t)=\sum _{i=1}^N{\mathit{LLR}}^{(i)}(t)$$

Finally, the accumulated log-likelihood ratio was calculated by summing log-likelihoods (calculated from a single trial or multiple trials from a single or multiple cells) over time:

$$\mathit{AccLLR}(t)=\sum _{t^{\prime }=0}^t\mathit{LLR}(t^{\prime })$$

In order to test whether the ST of populations of neurons on the lateral bank differs significantly from the ST of populations of neurons on the medial bank, we measured the empirical distribution function (EDF) of the saturated STs for each population. To do this, we randomly selected, without replacement, cell ensembles of size 10, 20, 30, 40, and 47 from each population and calculated STs for trial averages ranging from 2 – 28 trials. We obtained the EDF for each ST calculation by performing 40 iterations of this procedure. We calculated the ST for each ensemble size by taking the mean ST across iterations. We tested for significant differences between STs for different groups of neurons using a Wilcoxon rank sum test. To compare STs for neural ensembles of different coherent populations, we used the same procedure but with smaller ensembles of size 8 and 11 with trial averages ranging from 2 – 28. This was due to the smaller numbers of cells available in each coherent population. To ensure that the overall firing rate did not affect the STs, we performed control analyses by decimating firing rates so that the mean baseline firing rate was the same for all the groups of neurons being compared. We set the maximum accumulation time in the AccLLR analysis to 500 ms. The results do not change when the maximum accumulation time is reduced to 400 ms.

A supplementary methods checklist is available