Bayesian hierarchical models for network meta-analysis incorporating nonignorable missingness

Abstract

Network meta-analysis expands the scope of a conventional pairwise meta-analysis to simultaneously compare multiple treatments, synthesizing both direct and indirect information and thus strengthening inference. Since most of trials only compare two treatments, a typical data set in a network meta-analysis managed as a trial-by-treatment matrix is extremely sparse, like an incomplete block structure with significant missing data. Zhang et al. proposed an arm-based method accounting for correlations among different treatments within the same trial and assuming that absent arms are missing at random. However, in randomized controlled trials, nonignorable missingness or missingness not at random may occur due to deliberate choices of treatments at the design stage. In addition, those undertaking a network metaanalysis may selectively choose treatments to include in the analysis, which may also lead to missingness not at random. In this paper, we extend our previous work to incorporate missingness not at random using selection models. The proposed method is then applied to two network meta-analyses and evaluated through extensive simulation studies. We also provide comprehensive comparisons of a commonly used contrast-based method and the arm-based method via simulations in a technical appendix under missing completely at random and missing at random.

1 Introduction

Network meta-analysis (NMA, also called mixed or multiple treatment comparisons), a metaanalytic statistical method, expands the scope of a conventional pairwise meta-analysis to simultaneously compare multiple treatments by synthesizing both direct and indirect information. NMA has two major roles. First, it enables us to obtain simultaneous inference regarding all treatments of interest, typically to select the best one or subset. With rapid growth in the number of potential treatments for a given condition, doctors and patients often want to know their population-averaged treatment-specific effects and their relative ranks in terms of safety and efficacy. Second, inference regarding the relative effect of two treatments can be strengthened by borrowing information from indirect comparisons. In the simplest case, one may be interested in comparing two treatments A and B. Direct evidence can only be obtained from randomized controlled trials (RCTs) of A versus B, while indirect evidence can be obtained from RCTs of either A or B versus a common comparator C.¹ By combining the two sources of information as a weighted average using appropriate statistical methods, more precise estimates of treatment effects than those produced by standard pairwise meta-analysis can be obtained.² In summary, NMA provides simultaneous comparisons of multiple treatments and more precise treatment effect estimates.³

Commonly, only a subset of treatments of interest (say, two or three) is compared in each trial in an NMA, so that a typical data structure expressed as a trial-by-treatment matrix is extremely sparse. For example, a recent NMA⁴ published in The Lancet comprised 117 RCTs to compare 12 new-generation antidepressants, where 114 RCTs were two-arm trials and the other 3 RCTs were three-arm trials, leading to an incomplete block structure with significant missing data. Currently, popular contrast-based (CB) NMA statistical methods^5–8 only model the observed data, while a recent arm-based (AB) method proposed by Zhang et al.⁹ assumes only a missing at random (MAR) mechanism and imputes missing components using Markov chain Monte Carlo (MCMC) algorithms. Thus, CB methods are essentially the classic “available case analysis” for missing data, which may lead to problems when the data are not missing completely at random (MCAR), or when correlations among variables are high.¹⁰ Furthermore, they can produce estimated covariance matrices that are implausible, such as estimating correlations outside of the range from −1.0 to 1.0.^10,11 The AB method does not bear such risks. In addition, simulation results in the Gaussian data context¹² and real data analyses for binary outcomes⁹ have shown that the effect size estimates by this AB method have smaller biases and narrower credible intervals (CIs) than those provided by CB methods in some cases.

In addition, the AB and CB methods involve different random effect assumptions. Shuster et al.¹³ distinguished between two random effect assumptions for meta-analysis: studies at random (SR), and effects at random (ER). SR assumes that the studies are independently chosen from a conceptual urn containing a large number of studies, while ER assumes that the effects in each study are randomly drawn from a conceptual urn, but the studies are fixed. ER makes several assumptions that are difficult to verify empirically; e.g., that the distribution of the random effects under ER is independent of study design and baseline risk (where the baseline varies across trials and can be either placebo or active treatments). The AB method requires an SR-type assumption, while the CB method instead requires the ER assumption.

Nonignorable missingness, or missingness not at random (MNAR), caused by deliberate choices of treatments at the trial design stage or selective choices during the process of systematic review and meta-analysis, is a thorny situation for NMA. For example, clinicians often select treatments that appear to be more effective based on previous RCTs or their own personal medical experience,¹⁴ which may cause a higher probability of missingness for relatively ineffective treatments. Another situation that can result in nonignorable missingness of treatments is when meta-analysts selectively choose the evidence to be synthesized. For example, some NMAs exclude placebo or no treatment groups from consideration because meta-analysts believe that placebo or no treatment trials may vary over time, or are set in favorable conditions to appease regulatory authorities.¹⁵ Other NMAs may include only treatments available in a particular location or time period, or those of perceived dose relevance, or certain specific competing treatments in the case of industry submissions to health technology assessment bodies.^15,16 In these cases, simply ignoring missingness (as the CB methods do) or considering all missing data to be MAR (as the standard AB method⁹ does) may lead to bias.¹⁰

The purpose of this paper is to develop methods to incorporate nonignorable missingness. The rest of the paper proceeds as follows. We present our proposed method in Section 2, apply it to the smoking cessation and prevention of pain on injection with Propofol data sets in Section 3, and evaluate its performance through simulation studies in Section 4. Finally, we close with a discussion of our results, several contentious issues, and a few avenues for future research in Section 5. Appendix 1 provides a comprehensive comparison of the AB method in Zhang et al.⁹ and the CB method in Lu and Ades⁸ for binary data under MCAR and MAR mechanisms.

2 Statistical method incorporating nonignorable missingness

Nonignorable missingness is inevitable when clinicians selectively include treatments in trials or meta-analysts selectively choose treatments in an NMA. Unfortunately, one can never tell from the data at hand whether the missing treatments are MAR or MNAR.¹⁰ The fundamental difficulty is that potential “lurking variables” controlling the missingness are unobserved, and thus we can never rule out MNAR. Rather than trying to test whether the missingness is MAR, we develop a novel method using sensitivity analysis to incorporate nonignorable missingness. Note that even if an assumption of MAR seems reasonable, it is worthwhile to investigate how the results may change under nonignorable missingness.

Suppose an NMA comprises I RCTs to compare K treatments of interest. Let i = 1, 2, …, I index the trials and k = 1, …, K index the treatments. Let S_i be the set of treatments that are compared in the i-th trial and C_i be its cardinality. Trials with C_i ≥ 3 are called “multi-arm” trials, in contrast to C_i = 2 for “two-arm” trials. In this paper, we only focus on the binary data case, but our method can be easily extended to other types of data. We let y_obsi = (y_ik, n_ik), k ∈ S_i and y_misi = (y_ik, n_ik), k ∉ S_i denote the observed data and missing data from the i-th trial, where n_ik is the total number of subjects and y_ik is the number of responses for the k-th treatment in the i-th trial. The corresponding probability of response is denoted by p_ik. Then we let Y_obs = (y_obs1, …, y_obsI) and Y_mis = (y_mis1, …, y_misI) denote the full collections of the observed and missing data.

Let R be a corresponding I × K indicator matrix of missingness with (i, k)-entry r_ik, where r_ik = 0 if y_ik is observed and r_ik = 1 if y_ik is missing. (Y_obs, Y_mis, R) and (Y_obs, R) denote the complete and observed data, respectively. The practical implication of MNAR is that the likelihood requires an explicit model for R. Selection models, introduced by Heckman,¹⁷ provides a way to do this. Here, we factor the joint distribution of the complete data and the missingness indicators into a marginal density for the complete data and a conditional density for the missingness indicators given the complete data, i.e., f(Y_obs, Y_mis, R|θ, α) = f(Y_obs, Y_mis|θ, α) f(R|Y_obs, Y_mis, θ, α), where θ is the set of parameters of interest and α is the set of parameters for the missingness mechanism. This factorization can usually be simplified to f(Y_obs, Y_mis, R|θ, α) = f(Y_obs, Y_mis|θ) f(R|Y_obs, Y_mis, α), if Y_obs, Y_mis|θ is conditionally independent of α, and R|Y_obs, Y_mis, α is conditionally independent of θ, which is usually reasonable in practice. We further call f(Y_obs, Y_mis|θ) the model of interest (MOI) and f(R|Y_obs, Y_mis, α) the model of missingness (MOM).¹⁸ We first separately specify MOI and MOM, and then combine them into a single joint statistical model.

2.1 Various MOIs

Following Zhang et al.,⁹ multivariate generalized linear mixed models (MGLMMs) are often used for the MOI. The number of responses y_ik is assumed to have an independent binomial distribution with probability p_ik, i.e., y_ik ~ Bin(n_ik, p_ik), while p_ik on a transformed scale, i.e., g(p_ik), is assumed to have a multivariate normal distribution. Here, g() is some appropriate link function; we prefer the probit link Φ⁻¹() because it enables a closed form for the population-averaged event rate,⁹ while the canonical logit link does not. Thus, the model is parameterized as follows

$${\mathrm{\Phi }}^{-1}(p_{ik})={\mu }_k+{\nu }_{ik},{({\nu }_{i1},\dots ,{\nu }_{iK})}^T~\mathit{MVN}(0,{\mathrm{\sum }}_k)$$ (1)

where μ_k is the fixed effect and ν_ik is the random effect for the k-th treatment in the i-th trial, and (ν_i1, … ν_iK) is a vector of all random effects in the i-th trial with covariance matrix Σ_k.

A possible factorization of Σ_K is Σ_K = diag(σ₁, …, σ_K) × Ω_K × diag(σ₁, …, σ_K), where Ω_K is a positive definite correlation matrix, and diag(σ₁, …, σ_K) is a diagonal matrix with k-th entry σ_k representing the standard deviation for the random effects ν_ik. In (1), the trial-level heterogeneity in response to treatment k is captured by σ_k, and the within-trial dependence among treatments is captured by Ω_K. Zhang et al.⁹ show the population-averaged event rate can be calculated as ${\pi }_k=E(p_{ik}\mid {\mu }_k{\sigma }_k)={\int }_{-\infty }^{\infty }\mathrm{\Phi }({\mu }_k+{\sigma }_{k}z)\varphi (z)dz=\mathrm{\Phi }({\mu }_k/\sqrt{1+{\sigma }_k^2})$, where Φ() is the cumulative density function, and ϕ() is the probability density function for the standard normal distribution. As such, marginal effect measures can then be calculated, including the relative risk, RR_kl = π;_k/π_l, risk difference, RD_kl = π_k − π_l, and odds ratio, ${\text{OR}}_{kl}=\frac{{\pi }_k/(1-{\pi }_k)}{{\pi }_l/(1-{\pi }_l)}$.

Various MOIs can be proposed according to (1). The simplest model can be specified as Φ⁻¹(p_ik) = μ_k + ν_i with ν_i ~ N(0, σ²) accounting for heterogeneity across trials. In this case, random effects for different treatments within the same trial are perfectly correlated (a correlation coefficient of 1); we refer to this model as MOI i. MOI i can be extended to allow heterogeneous variances, i.e., Φ⁻¹(p_ik) = μ_k + ν_ik with ${\nu }_{ik}~N(0,{\sigma }_k^2)$; this is MOI ii. This model assumes that random effects for different treatments within the same trial are uncorrelated. Another way to extend MOI i is Φ⁻¹(p_ik) = μ_k + ν_ik where (ν_i1, ν_i2, …, ν_iK) has an exchangeable correlation matrix with the same correlation parameter ρ and the same variance parameter σ²; we call this model MOI iii. A more general model is Φ⁻¹(p_ik) = μ_k + ν_ik with (ν_i1, ν_i2, …, ν_iK) being an exchangeable correlation matrix with the same correlation parameter ρ but different variance parameters ${\sigma }_k^2$ for different treatments; this is MOI iv. Finally, the most general model assumes an arbitrary unstructured covariance matrix Σ_K, where variances of different treatments are different, and correlations between different pairs of treatments are also different; this is model MOI v. In general, MOI i is simple but may not be practical in most cases, whereas there may not be enough information contained in the data to accurately estimate all the parameters in MOI v when the number of treatments K is large and the number of studies I is small. The exchangeable correlation models MOI iii and MOI iv appear to offer sensible yet practical alternatives.

Since improper prior distributions may lead to improper posteriors in some complex models,^19–22 we select minimally informative but proper priors. Specifically, we chose N(0, 1000) priors for μ_k in all models, Gamma(1, 1) priors for the precisions τ = 1/σ² in MOI i and ${\tau }_i=1/{\sigma }_i^2$ in MOI ii (corresponding to a 95% Bayesian CI for variance parameters ranging from 0.27 to 39.5), and U(0, 5) priors for σ and σ_k and U(0.0001,1) for ρ in MOI iii and MOI iv. A vague Wishart prior is chosen for the precision matrix in the unstructured model MOI v, i.e., ${\mathrm{\sum }}_K^{-1}~W(V^{-1},n)$, where n=K is the degrees of freedom and V is a known K×K matrix with diagonal elements equal to 0.1 and off-diagonal elements equal to 0.005. It turns out that the above prior corresponds to a 95% Bayesian CI for the variance parameters ranging from 0.02 to 98.93, and a 95% Bayesian CI for the correlation parameters ranging from −1.00 to 1.00 (i.e., fully noninformative).

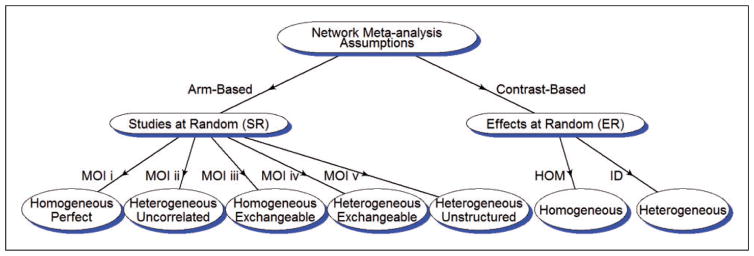
Figure 1 shows various model assumptions for MOI i to MOI v. Each model is labeled near the arrow of the line and the corresponding model assumption is shown in the ellipse. “Homogeneous” and “Heterogeneous” indicate what variances are used for random effects; and “Perfect,” “Uncorrelated,” “Exchangeable,” and “Unstructured” categorize the correlation matrices of random effects. In addition, the aforementioned SR and ER assumptions introduced in Shuster et al.¹³ are adopted for the AB and CB methods in this diagram. The HOM and ID models are two CB models from Lu and Ades⁸ that will be used in our simulation studies.

Figure 1.

Diagram of model assumptions. The arm-based method assumes studies at random (SR) while the contrast-based methods assume effects at random (ER). Homogeneous/heterogeneous refer to variances and perfect/exchangeable/unstructured refer to correlation matrices. Perfect refers to a correlation of 1 among random effects for different treatments within the same trial. Finally, HOM and ID are the homogeneous and heterogeneous models in Lu and Ades.⁸

2.2 MOM specifications

Now we introduce specifications for the MOM. If f(R|Y_obs, Y_mis, α) = f (R|α), the mechanism is MCAR; if f(R|Y_obs, Y_mis, α) = f(R|Y_obs, α), it is MAR; and if there is no simplification possible for the conditional distribution f(R|Y_obs, Y_mis, α), it is MNAR.

We assume r_ik, the missingness indicator for the k-th treatment in the i-th trial, has a Bernoulli distribution with a probability of missingness $p_{ik}^{\text{mis}}$, i.e., $r_{ik}~\mathit{Ber}(p_{ik}^{\text{mis}})$. Under the MNAR mechanism, $p_{ik}^{\text{mis}}$ depends on y_ik. A common way to realize the above is through linking $p_{ik}^{\text{mis}}$ with the estimated p_ik (which is approximately $\frac{y_{ik}}{n_{ik}}$), i.e., $h_1(p_{ik}^{\text{mis}})=h_2(p_{ik})$, where $h_1(p_{ik}^{\text{mis}})$ and h₂(p_ik) are some proper functions of $p_{ik}^{\text{mis}}$ and p_ik. We here use the canonical logit link for both h₁() and h₂(). However, we note that a probit link would work equally well; see Appendix 2 for results for the two real data sets under both the logit and probit links. Tables 9 and 10 reveal the results to be broadly similar. Specifically, our MOM is proposed as follows

Table 9.

Posterior medians and their 95% credible intervals for the population-averaged event rates of the four treatments in the smoking cessation data set with different link functions.

	logit		probit
	JM ii	JM i	JM i	JM ii
πA	0.09 (0.06,0.12)	0.09 (0.06,0.13)	0.09 (0.06,0.13)	0.09 (0.06,0.12)
πB	0.15 (0.09,0.24)	0.13 (0.07,0.22)	0.13 (0.07,0.24)	0.15 (0.09,0.24)
πC	0.18 (0.14,0.23)	0.18 (0.14,0.24)	0.18 (0.14,0.24)	0.18 (0.14,0.23)
πD	0.22 (0.14,0.34)	0.20 (0.11,0.33)	0.21 (0.11,0.34)	0.22 (0.14,0.34)
DICM	109.2	104.1	103.7	108.7
DICI	323.1	323.2	323.2	323.0

Results from JM i and JM ii are reported. π_A–D represent the event rates for Treatments A–D.

Table 10.

Posterior medians and their 95% credible intervals for the population-averaged event rates of the eight treatments in the data set about prevention of pain on injection with Propofol with different link functions.

	logit		probit
	JM i	JM ii	JM i	JM ii
πA	0.28 (0.21,0.35)	0.30 (0.24,0.37)	0.27 (0.21,0.34)	0.30 (0.24,0.36)
πB	0.49 (0.29,0.65)	0.38 (0.27,0.50)	0.50 (0.33,0.65)	0.37 (0.26,0.49)
πC	0.56 (0.40,0.71)	0.59 (0.47,0.70)	0.56 (0.40,0.71)	0.58 (0.47,0.69)
πD	0.60 (0.46,0.72)	0.63 (0.54,0.72)	0.60 (0.46,0.73)	0.63 (0.53,0.71)
πE	0.85 (0.71,0.93)	0.80 (0.66,0.90)	0.85 (0.70,0.93)	0.80 0.65,0.89
πF	0.63 (0.46,0.78)	0.62 (0.51,0.73)	0.64 (0.47,0.78)	0.62 (0.50,0.72)
πG	0.61 (0.34,0.86)	0.70 (0.52,0.85)	0.57 (0.33,0.82)	0.69 (0.50,0.84)
πH	0.46 (0.26,0.65)	0.41 (0.27,0.56)	0.47 (0.28,0.66)	0.40 (0.26,0.55)
DICM	333.3	366.7	333.8	367.6
DICI	574.0	573.5	568.5	569.3

Results from JM i and JM ii are reported. π_A–H represent the event rates for Treatments A–H.

$$\text{logit}(p_{ik}^{\text{mis}})={\alpha }_{0k}+{\alpha }_{1k}\times \text{logit}(p_{ik})$$ (2)

where α_0k is an unknown scalar parameter, and α_1k determines the missingness mechanism, i.e., nonignorable missingness if α_1k ≠ 0 and ignorable missingness if α_1k=0. In this model, the probabilities of missingness for different treatments have different parameters of missingness α_1k. We call this model MOM i. A simpler model can be specified as $\text{logit}(p_{ik}^{\text{mis}})={\alpha }_{0k}+{\alpha }_1\times \text{logit}(p_{ik})$, where all treatments share the same missingness parameter α₁. We denote this model by MOM ii.

A flat prior for α_0k with a large variance would lead to a marginal prior distribution for $p_{ik}^{\text{mis}}$ that is heavily biased towards 0 and 1. We thus specify a logistic(0, 1) prior for α_0k, which corresponds to an approximate uniform prior on (0, 1) for $p_{ik}^{\text{mis}}$.²³ In the same way, a large variance on the prior of α_1k can also lead to biased marginal priors for $p_{ik}^{\text{mis}}$. Thus, we use a weakly informative N(0,0.68) prior for α_1k, following Jackson et al.²⁴ and Mason et al.¹⁸

Finally, the joint distribution of Y_obs and R can be derived by integrating out the Y_mis as follows

$$P(Y_{\text{obs}},R)={\prod }_{i=1}^I\left\{\int \{{\prod }_{k=1}^K{(p_{ik})}^{y_{ik}}{(1-p_{ik})}^{n_{ik}-y_{ik}}\times {\prod }_{k=1}^K{(p_{ik}^{\text{mis}})}^{R_{ik}}{(1-p_{ik}^{\text{mis}})}^{1-R_{ik}}\}\mathrm{d}{Y}_{\text{mis}}\right\}$$ (3)

2.3 Model selection and construction of joint models

The Deviance Information Criterion (DIC)²⁵ was used as the model selection criterion. The deviance, up to an additive quantity not depending upon θ, is D(θ) = −2logL(θ; Data), where L(θ; Data) is the likelihood for the respective model. The DIC is given by $\overline{D(\theta )}+p_D$, where $\overline{D(\theta )}=E_{\theta \mid \text{Data}}[D(\theta )]$ is the proper mean deviance, and $p_D=\overline{D(\theta )}-D(\overline{\theta })$ is the effective number of model parameters. It rewards better fitting models through the first term and penalizes more complex models through the second term. A model with smaller overall DIC value is preferred.

All models were implemented via MCMC methods using the WinBUGS software. The convergence of MCMC chains was assessed by the Gelman-Rubin convergence statistic and by visual inspection of the chains. WinBUGS automatically generates DIC estimates for the MOIs and MOMs separately, and we call them DIC_I (DIC of interest) and DIC_M (DIC of missingness), respectively. DIC_I is generated based on the observed data likelihood; while in the construction of DIC_M, Y_mis are treated as extra parameters in the MOMs, with the MOI acting as their prior distribution. Mason et al.¹⁸ have suggested the use of DIC_M to compare the fit of different MOMs with the same MOI. We remark that use of DIC in missing data setting is controversial; see Celeux et al.²⁶

Thus, the construction of the joint models can be summarized as two steps: in the first step, the best MOI with the smallest DIC_I is chosen from MOI i to MOI v; and in the second step, MOM i and MOM ii are coupled with the best MOI as joint models, named JM i and JM ii. We will select the joint model with the smaller DIC_M as our final model.

3 Data analysis

3.1 Smoking cessation data

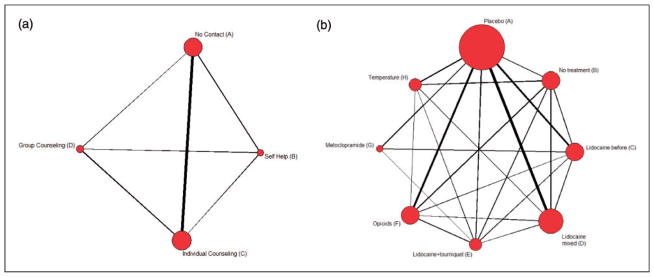
We apply our proposed method in Section 2 to a smoking cessation data set^27,28. This data set comprises 24 trials (22 two-arm and 2 three-arm) and 18,822 participants trying to quite smoking using one of the four treatments: (A) no contact, (B) self-help, (C) individual counseling, and (D) group counseling. Figure 2(a) shows an undirected graph elucidating the network of comparative relations for the four treatments, with the size of each node proportional to the frequency of that treatment, and the thickness of the link proportional to the number of trials investigating the pairwise comparison.

Figure 2.

Graphical representations for the networks of the smoking cessation and prevention of pain on injection with Propofol data sets. The size of each node is proportional to the number of trials including the respective intervention, and the thickness of the link is proportional to the numbers of trials investigating the relation.

Table 1 shows the posterior medians of population-averaged event rates (π_A, π_B, π_C, and π_D) and their 95% posterior CIs for various models. MOI iii, MOI iv, and MOI v, which assume random effects (ν_i1, ν_i2, …, ν_iK) in the same trial have a multivariate normal distribution, show smaller DIC_I than MOI i and MOI ii, which assume either perfect or no correlations. While MOI iii, MOI iv, and MOI v get similar DIC_Is, we selected MOI iii as the best MOI because it is the simplest in parameterization and easiest in implementation.

Table 1.

Posterior medians and their 95% credible intervals for the population-averaged event rates of the four treatments in the smoking cessation data set.

	MOI i	MOI ii	MOI iii	MOI iv	MOI v	JM i	JM ii
πA	0.11 (0.08,0.15)	0.10 (0.08,0.13)	0.09 (0.06,0.12)	0.08 (0.06,0.11)	0.08 (0.06,0.10)	0.09 (0.06,0.13)	0.09 (0.06,0.12)
πB	0.13 (0.09,0.18)	0.17 (0.11,0.27)	0.14 (0.09,0.22)	0.16 (0.09,0.33)	0.15 (0.09,0.24)	0.13 (0.07,0.22)	0.15 (0.09,0.24)
πC	0.18 (0.14,0.24)	0.25 (0.16,0.39)	0.18 (0.14,0.23)	0.18 (0.13,0.24)	0.17 (0.13,0.23)	0.18 (0.14,0.24)	0.18 (0.14,0.23)
πD	0.20 (0.14,0.27)	0.31 (0.18,0.50)	0.21 (0.14,0.32)	0.23 (0.13,0.45)	0.21 (0.13,0.33)	0.20 (0.11,0.33)	0.22 (0.14,0.34)
DICM	—–	—–	—–	—–	—–	104.1	109.2
DICI	545.5	374.9	323.1	325.5	324.4	323.2	323.1

π_A–D represent the event rates for Treatments A–D. The bold cells highlight the smallest DICs.

Now let us take a look at the results from the joint models. JM i comprises MOI iii and MOM i, and JM ii comprises MOI iii and MOM ii. Table 1 shows that the estimates for the population-averaged event rates π_A and π_C from JM i and JM ii are exactly the same as MOI iii, while those for π_B and π_D are slightly different from MOI iii. These subtle differences do not provide convincing evidence of nonignorable missingness. Note that DIC_M for JM i is smaller than DIC_M for JM ii, thus MOM i is more suitable for these data than MOM ii. As such, we adopt JM i for all further investigation.

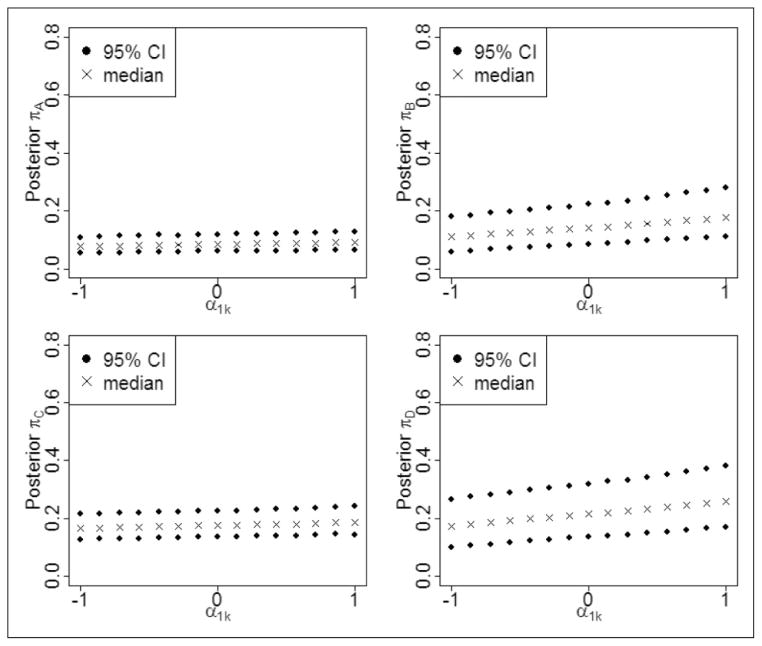
Since the values of α_1k control the degree of departure from MAR missingness, we conduct sensitivity analyses in which the changes in the estimated parameters of interest are studied for different values of the missingness parameters α_1k. In other words, we carry out a sensitivity analysis where a series of models are run with a set of fixed values for the α_1k. More specifically, we use 15 values uniformly distributed between −1 and 1, namely −1.00, −0.86, −0.71, −0.57, −0.43, −0.29, −0.14, 0.00, 0.14, 0.29, 0.43, 0.57, 0.71, 0.86, and 1.00 for α_1k. Figure 3 presents the posterior medians and their 95% CIs for the population-averaged response rates versus different values of α_1k. Note that π_A and π_C versus α_1k in the left part of Figure 3 are horizontal lines, while π_B and π_D versus α_1k in the right part of Figure 3 have slight slopes. Thus, Treatments B and D seem to be slightly dependent on the missingness parameter α_1k, but Treatments A and C are more robust to changes in α_1k here. However, we do note that in the smoking cessation data, the numbers of trials that contain Treatments A (19) and C (19) are larger than the numbers of trials containing Treatments B (6) and D (6), which explains at least part of the reason why Treatments B and D are more sensitive to the missingness parameter. In summary, neither Table 1 nor Figure 3 suggests the presence of serious nonignorable missingness.

Figure 3.

Population-averaged event rates variations with changes in α_1k. Posterior medians and their 95% credible intervals are presented for the smoking cessation data.

Table 2 presents the odds ratios comparing the four treatments estimated from JM i and JM ii. In JM i, with Treatment A as the baseline treatment, our estimates are OR_BA = 1.44 with 95% CI (0.67, 3.01), OR_CA = 2.20 with 95% CI (1.42, 3.44), and OR_DA = 2.44 with 95% CI (1.11, 5.29). Thus Treatments C (individual counseling) and D (group counseling) are significantly more effective than A (no contact) for smoking cessation, while Treatment B (self-help) is not significantly different from A. We draw the same basic conclusions regarding statistical significance from JM ii, though the magnitudes of the estimated ORs are slightly different.

Table 2.

Posterior medians of ORs estimated from JM i and JM ii with their 95% credible intervals for the smoking cessation data set.

	ORBA	ORCA	ORDA	ORCB	ORDB	ORDC
JM i	1.44 (0.67,3.01)	2.20 (1.42,3.44)	2.44 (1.11,5.29)	1.53 (0.76,3.33)	1.70 (0.71,4.26)	1.11 (0.53,2.32)
JM ii	1.83 (0.95,3.51)	2.26 (1.49,3.44)	2.98 (1.55,5.80)	1.23 (0.66,2.36)	1.63 (0.78,3.40)	1.32 (0.71,2.44)

Statistically significant results are given in bold. OR_kl represents the odds ratio of Treatments k versus l.

3.2 Prevention of pain on injection with Propofol

Picard et al.²⁹ conducted a quantitative systematic review to test the relative efficacy of analgesic interventions that had been used to prevent pain caused by Propofol injection. Veroniki et al.³⁰ further evaluated inconsistency between the direct and indirect evidence in this data set. This data set contains 43 trials and 4495 subjects to compare eight treatments: (A) Placebo, (B) No treatment, (C) Lidocaine before, (D) Lidocaine mixed, (E) Lidocaine+tourniquet, (F) Opioids, (G) Metoclopramide, and (H) Temperature. Figure 2(b) shows the graphical representation of this network, where some direct comparisons are not available.

MOI iii has the smallest DIC_I among the five MOIs, while MOM i has a smaller DIC_M and is thus the better MOM. Thus, JM i is selected as the final model for this data set. Table 3 presents the posterior medians and corresponding 95% CIs for the estimated population-averaged event rates across the eight treatments. Comparing the results of JM i and MOI iii, we find 32.43% (i.e., (0.49–0.37)/0.37=32.43%) and 15.00% (i.e., (0.46–0.40)/0.40=15.00%) relative changes for the posterior medians of π_B and π_H, respectively, which are substantial and indicate nonignorable missingness. This seems to make sense because trials without a placebo- or no treatment-arm were not included in this NMA. In other words, trials comparing solely active treatments were excluded. However, an NMA that includes only placebo/no treatment comparisons may yield different results from one that does not consider placebo/no treatment comparisons, or one that considers both types of comparisons.¹⁵ Another phenomenon we observe in Table 3 is that JM i and JM ii yield quite different results for the estimated event rates, while the results of JM ii are closer to those of MOI iii, suggesting the necessity of heterogeneous missingness parameters α_1k.

Table 3.

Posterior medians and their 95% credible intervals for the population-averaged event rates of the eight treatments in the data set about prevention of pain on injection with Propofol.

	MOI i	MOI ii	MOI iii	MOI iv	MOI v	JM i	JM ii
π A	0.31 (0.25,0.37)	0.31 (0.25,0.38)	0.30 (0.24,0.36)	0.30 (0.24,0.36)	0.30 (0.25,0.36)	0.28 (0.21,0.35)	0.30 (0.24,0.37)
πB	0.35 (0.28,0.43)	0.37 (0.30,0.46)	0.37 (0.26,0.48)	0.36 (0.28,0.47)	0.36 (0.28,0.45)	0.49 (0.29,0.65)	0.38 (0.27,0.50)
πC	0.55 (0.48,0.63)	0.54 (0.44,0.63)	0.58 (0.47,0.68)	0.57 (0.45,0.69)	0.57 (0.46,0.67)	0.56 (0.40,0.71)	0.59 (0.47,0.70)
πD	0.63 (0.56,0.69)	0.61 (0.53,0.69)	0.63 (0.54,0.71)	0.62 (0.52,0.71)	0.63 (0.54,0.71)	0.60 (0.46,0.72)	0.63 (0.54,0.72)
πE	0.82 (0.74,0.88)	0.80 (0.70,0.87)	0.80 (0.66,0.89)	0.79 (0.64,0.89)	0.82 (0.70,0.90)	0.85 (0.71,0.93)	0.80 (0.66,0.90)
πF	0.62 (0.54,0.69)	0.62 (0.54,0.70)	0.61 (0.51,0.72)	0.63 (0.53,0.71)	0.63 (0.54,0.71)	0.63 (0.46,0.78)	0.62 (0.51,0.73)
πG	0.62 (0.52,0.72)	0.61 (0.45,0.71)	0.68 (0.51,0.83)	0.62 (0.33,0.82)	0.65 (0.43,0.79)	0.61 (0.34,0.86)	0.70 (0.52,0.85)
πH	0.44 (0.34,0.53)	0.48 (0.35,0.61)	0.40 (0.27,0.54)	0.42 (0.25,0.62)	0.47 (0.30,0.64)	0.46 (0.26,0.65)	0.41 (0.27,0.56)
DICM	—–	—–	—–	—–	—–	333.3	366.7
DICI	648.0	619.6	569.1	571.3	571.3	574.0	573.5

π_A–H represent the event rates for Treatments A–H. The bold cells highlight the smallest DICs.

Sensitivity to the prior distributions was also conducted and is summarized in Table 4. S₁ and S₂ investigate more informative versions of the normal prior distributions for μ_k, namely, N(0, 100) and N(0, 10), respectively. Heavy-tailed t-distributions with degrees of freedom 2 and 5 are also employed for μ_k (models S₃ and S₄). Table 4 shows that the estimated π_A–H in S₁–S₄ are all close to those from MOI iii in Table 3 (Note that MOI i–iv use similar prior distributions; we pick MOI iii for illustration), thus MOI iii seems to be robust to these other prior distributions for the μ_k. S₅ uses a more informative Uniform (0.01, 1) prior for standard deviation parameter σ, while S₆ and S₇ employ more informative Gamma priors for the precision τ = 1/σ² with different shape and rate parameters (shape=1 and rate=0.5 in S₆, and shape=3 and rate=1 in S₇). It seems MOI iii is not particularly sensitive to the use of these prior distributions either. Next, sensitivity to the Wishart prior distribution for ${\mathrm{\sum }}_K^{-1}$ in MOI v is also explored. A W(V⁻¹, 8) is employed in S₈ and S₉, where V is a 8×8 matrix with diagonal elements equal to 0.01 and 0.005, respectively, and offdiagonal elements equal to 0.005. Comparison of results from S₈ and S₉ with those from MOI v in Table 3 reveals that more informative Wishart priors do not appear to have a substantial effect on the estimates. In addition, following Barnard et al.,³¹ we also use a Wishart (I₈, 9) prior for ${\mathrm{\sum }}_K^{-1}$ in sensitivity analysis (here K=8). Comparison of MOI v and S₁₀ reveals that the estimated event rates for Treatments A, B, C, D, and F are robust, while those for Treatments E, G, and H are a little sensitive, perhaps due to smaller sample sizes (6, 4, and 7, respectively). Sample sizes for A, B, C, D, and F are 34, 11, 12, 18, and 12, which is also reflected by the node sizes in Figure 2(b). In addition, the total numbers of patients assigned to Treatments E, G, and H are 146, 245, and 264, compared with 1315, 341, 512, 1202, and 470 for A, B, C, D, and F.

Table 4.

Prior sensitivity analysis.

	MOI iii							MOI v
	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10
πA	0.30 (0.24,0.36)	0.30 (0.24,0.36)	0.30 (0.24,0.36)	0.30 (0.24,0.36)	0.30 (0.24,0.36)	0.30 (0.24,0.36)	0.30 (0.24,0.36)	0.30 (0.24,0.36)	0.30 (0.25,0.37)	0.30 (0.24,0.37)
πB	0.37 (0.26,0.48)	0.37 (0.26,0.48)	0.37 (0.27,0.48)	0.37 (0.27,0.48)	0.37 (0.26,0.48)	0.37 (0.26,0.48)	0.36 (0.26,0.48)	0.36 (0.29,0.44)	0.35 (0.28,0.42)	0.35 (0.24,0.48)
πC	0.58 (0.47,0.68)	0.58 (0.47,0.68)	0.57 (0.46,0.68)	0.57 (0.47,0.68)	0.58 (0.47,0.68)	0.58 (0.47,0.68)	0.58 (0.46,0.68)	0.57 (0.47,0.67)	0.56 (0.48,0.65)	0.58 (0.45,0.69)
πD	0.63 (0.53,0.71)	0.63 (0.54,0.71)	0.62 (0.53,0.7)	0.62 (0.53,0.71)	0.63 (0.54,0.71)	0.63 (0.53,0.71)	0.63 (0.53,0.71)	0.63 (0.54,0.7)	0.63 (0.55,0.7)	0.62 (0.52,0.71)
πE	0.80 (0.66,0.89)	0.79 (0.66,0.89)	0.78 (0.65,0.88)	0.78 (0.65,0.88)	0.79 (0.66,0.89)	0.80 (0.66,0.89)	0.80 (0.66,0.89)	0.82 (0.72,0.9)	0.83 (0.74,0.89)	0.77 (0.59,0.88)
πF	0.61 (0.5,0.72)	0.61 (0.5,0.71)	0.61 (0.5,0.71)	0.61 (0.5,0.71)	0.61 (0.5,0.72)	0.61 (0.5,0.71)	0.61 (0.5,0.71)	0.63 (0.54,0.7)	0.62 (0.54,0.69)	0.63 (0.51,0.73)
πG	0.68 (0.5,0.83)	0.68 (0.5,0.83)	0.66 (0.49,0.81)	0.67 (0.5,0.82)	0.68 (0.5,0.83)	0.68 (0.5,0.83)	0.68 (0.5,0.83)	0.65 (0.42,0.77)	0.66 (0.53,0.75)	0.70 (0.45,0.87)
πH	0.40 (0.27,0.54)	0.40 (0.27,0.54)	0.40 (0.28,0.54)	0.40 (0.27,0.54)	0.40 (0.27,0.54)	0.40 (0.27,0.54)	0.40 (0.27,0.54)	0.46 (0.32,0.62)	0.46 (0.34,0.58)	0.41 (0.24,0.6)

S₁: μ_k ~ N(0, 100); S₂: μ_k ~ N(0, 10); S₃: μ_k ~ t-dist (0, df = 2); S₄: μ_k ~ t-dist (0, df = 5); S₅: σ ~ Uniform (0.01,1); S₆: τ ~ Gamma (1,0.5); S₇: τ ~ Gamma (3, 1); $S_8:{\mathrm{\sum }}_K^{-1}~W(V^{-1},8)$, where V is a known 8 × 8 matrix with diagonal elements equal to 0.05 and off-diagonal elements equal to 0.005; $S_9:{\mathrm{\sum }}_K^{-1}~W(V^{-1},8)$, where V is a known 8 × 8 matrix with diagonal elements equal to 0.01 and off-diagonal elements equal to 0.005; $S_{10}:{\mathrm{\sum }}_K^{-1}~W(I_8,9)$. Posterior medians and their 95% credible intervals for the population-averaged event rates are reported. π_A–H represent the event rates for Treatments A–H.

Table 5 shows the estimated ORs from JM i and JM ii. In JM i, Treatments C, D, E, F, and G are significantly better than Treatment A, and Treatment E is significantly better than Treatments B, C, D, F, and H. No other comparisons are statistically significant (i.e., all other CIs include 0). In JM ii, in addition to these significant results, Treatments C, D, F, and G are significantly better than Treatments B and H. This phenomenon seems consistent with the results in Table 3, where the estimated event rates from JM i and JM ii sometimes differ. In general, Treatment E (lidocaine+tourniquet) emerges as the most effective analgesic method, under either JM i or JM ii.

Table 5.

Posterior medians of ORs and their 95% credible intervals estimated from JM i and JM ii for the data set about prevention of pain on injection with Propofol.

	ORBA	ORCA	ORCB*	ORDA	ORDB*	ORDC	OREA
JM i	2.53 (0.94,5.21)	3.34 (1.73,6.70)	1.36 (0.52,3.93)	4.00 (2.26,6.92)	1.61 (0.65,4.57)	1.2 (0.48,2.81)	15.47 (6.32,36.96)
JM ii	1.41 (0.82,2.41)	3.32 (2.06,5.49)	2.36 (1.28,4.40)	4.05 (2.69,6.08)	2.88 (1.65,5.05)	1.22 (0.70,2.10)	9.68 (4.61,20.81)
	OREB	OREC	ORED	ORFA	ORFB*	ORFC	ORFD
JM i	6.28 (2.24,18.38)	4.62 (1.63,12.80)	3.86 (1.38,10.86)	4.56 (2.10,9.79)	1.87 (0.73,4.67)	1.37 (0.48,3.71)	1.13 (0.45,2.98)
JM ii	6.88 (3.05,15.71)	2.91 (1.30,6.53)	2.39 (1.10,5.31)	3.89 (2.36,6.43)	2.76 (1.52,5.08)	1.17 (0.64,2.12)	0.96 (0.56,1.67)
	ORFE	ORGA	ORGB*	ORGC	ORGD	ORGE	ORGF
JM i	0.30 (0.10,0.83)	4.18 (1.35,15.55)	1.71 (0.40,9.18)	1.25 (0.37,4.82)	1.04 (0.29,4.55)	0.27 (0.07,1.23)	0.92 (0.22,4.47)
JM ii	0.40 (0.18,0.89)	5.40 (2.53,13.26)	3.85 (1.60,10.19)	1.63 (0.72,4.05)	1.34 (0.59,3.40)	0.56 (0.21,1.66)	1.39 (0.60,3.57)
	ORHA	ORHB	ORHC*	ORHD*	ORHE	ORHF*	ORHG*
JM i	2.23 (0.88,5.12)	0.91 (0.35,2.18)	0.66 (0.21,1.94)	0.56 (0.20,1.47)	0.14 (0.04,0.44)	0.49 (0.16,1.37)	0.53 (0.10,2.25)
JM ii	1.61 (0.86,2.97)	1.15 (0.58,2.22)	0.49 (0.23,0.97)	0.40 (0.21,0.75)	0.17 (0.07,0.39)	0.41 (0.20,0.83)	0.30 (0.11,0.74)

Statistically significant results are given in bold. OR_kl represents the odds ratio of Treatments k versus l.

^*shows ORs statistically significant in JM ii but not in JM i.

4 Simulations

We conducted two simulation studies to evaluate the performance of our proposed method. In Simulation 1, data are generated under nonignorable missing mechanism. Models ignoring and incorporating this mechanism are compared. In Simulation 2, we explore whether our proposed method still performs well when the missingness is ignorable, and check the performance of the CB method⁸ under this ignorable missingness as well.

4.1 Simulation setups

We generate a binary-data NMA of 30 trials comparing three treatments (1, 2, and 3) for both simulations. For convenience, we assume 100 patients are assigned to each treatment arm; 1000 replicates of simulated data sets are generated. The relative bias, defined as the difference between the true value and the mean of 1000 posterior estimates divided by the true value, and the empirical mean squared error (MSE) are calculated as measures of performance.

4.1.1 Simulation 1

We first assess the performance of our proposed method under nonignorable missingness, i.e., the MNAR mechanism. Data are generated according to MOI iii, which emerged as the best MOI for both real data sets. We set the true parameters of interest as follows: treatment-specific fixed effects μ₁ = −1.4, μ₂ = −1.0, and μ₃ = −0.8, standard deviation σ = 0.4, and correlation coefficient ρ = 0.5. The probability of response for Treatment k in Trial i, p_ik, is generated according to Φ⁻¹(p_ik) = μ_k + ν_ik, where (ν_i1, ν_i2, …, ν_iK) has an exchangeable correlation matrix with the same correlation parameter ρ and variance parameter σ². Then, the artificial data y_ik are generated by y_ik ~ Bin(100, p_ik). The corresponding true odds ratios comparing three treatments are OR₂₁ = 2.00, OR₃₁ = 2.77, and OR₃₂ = 1.38.

We assume Treatments 1 and 3 are fully observed, whereas Treatment 2 is missing not at random. Therefore an NMA, with some trials comparing all three treatments of interest and the others comparing just two of them, is generated. We let the probability of missingness for Treatment 2 depend on the missing values themselves y_i2 through formula $\text{logit}(p_{i2}^{\text{mis}})=1+\text{logit}(\frac{y_{i2}}{n})$, which brings nonignorable missingness.

Our investigation is based on fitting five models (M_MAR, M_MNAR1, M_MNAR2, M_MNAR3, and M_MNAR4), as specified in Table 6. M_MAR is set to be exactly the same as MOI iii, which ignores the nonignorable missingness. M_MNAR1 uses MOI iii as the MOI and $\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+0\ast \text{logit}(p_{i2})$ as the MOM. Since the missingness parameter is set to be 0, it is actually equivalent to the M_MAR model. For M_MNAR2, both parts of the model are correctly specified, i.e., MOI iii as the MOI, and $\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+{\alpha }_1\ast \text{logit}(p_{i2})$ as the MOM (note that the estimated p_i2 is an approximation for $\frac{y_{i2}}{n}$). M_MNAR3 and M_MNAR4 have overly complex forms for missingness, i.e., $\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+{\alpha }_1\ast \text{logit}(p_{i2})+{\alpha }_2\ast p_{i2}^2$ and $\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+{\alpha }_1\ast \text{logit}(p_{i2})+{\alpha }_2\ast \text{logit}(p_{i1})$, respectively, jointly modeled with MOI iii. In general, M_MNAR2, M_MNAR3, and M_MNAR4 consider nonignorable missingness, while M_MAR and M_MNAR1 disregard nonignorable missingness.

Table 6.

Specifications of fitted models in Simulation 1.

Model name	Model of interest	Model of missingness
MMAR	MOI iii	NA
MMNAR1	MOI iii	$\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+0\ast \text{logit}(p_{i2})$
MMNAR2	MOI iii	$\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+{\alpha }_1\ast \text{logit}(p_{i2})$
MMNAR3	MOI iii	$\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+{\alpha }_1\ast \text{logit}(p_{i2})+{\alpha }_2\ast p_{i2}^2$
MMNAR4	MOI iii	$\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+{\alpha }_1\ast \text{logit}(p_{i2})+{\alpha }_2\ast \text{logit}(p_{i1})$

MOI iii: Φ⁻1(p_ik) = μ_k + ν_ik, where (ν_i1, ν_i2, …, ν_iK) has an exchangeable correlation matrix with the same correlation parameter ρ and variance parameter σ². α₀ is a scalar parameter, and α₁ is the missingness parameter.

4.1.2 Simulation 2

In this section, we choose MOI iii as the true model, and use the same parameters of interest as in Simulation 1 to generate the simulated data sets. The true odds ratio is thus the same as well. Similar incomplete block structure for the data set is generated (i.e., Treatment arms 1 and 3 are fully observed whereas Treatment arm 2 contains missing data) except that the probability of missingness for Treatment 2 is dependent on the observed data y_i1, i.e., $\text{logit}(p_{i2}^{\text{mis}})=1+\text{logit}(\frac{y_{i1}}{n})$, rather than on the missing values themselves y_i2.

We now fit four models (M_MAR, M_MNAR2, M_HOM and M_ID) and compare their performances. M_MAR and M_MNAR2 have the same specifications as Simulation 1 in Table 6. M_HOM and M_ID are the HOM and ID models proposed in Lu and Ades,⁸ namely

$$\begin{array}{l}{y}_{ik}\stackrel{\text{ind}}{\sim }\text{Bin}(n_{ik},p_{ik}),i=1,\dots ,I,k\in S_i,\\ \text{logit}(p_{ik})={\mu }_i+X_{ik}{\delta }_{\mathit{ibk}},{\delta }_{\mathit{ibk}}\stackrel{\text{ind}}{\sim }N(d_{bk},{\sigma }_{bk}^2)\end{array}$$ (4)

where μ_i is the specified baseline effect that is commonly regarded as a nuisance parameter; X_ik is the indicator for baseline, taking value 0 when k=b and 1 when k ≠ b; b(i) is the specified baseline treatment in the i-th trial, commonly denoted by b for simplicity as above; and δ_ibk represents the contrast between Treatments k and b for the i-th trial and is assumed to have a normal distribution with mean d_bk and variance ${\sigma }_{bk}^2$. This method assumes that d_hk=d_bk − d_bh. With heterogeneous variances ${\sigma }_{bk}^2$, we call this model M_ID; if the variances are set to be homogeneous at σ², we call it M_HOM.

4.2 Simulation results

We now summarize the results from the two simulation studies separately.

4.2.1 Simulation 1

Table 7 provides evidence that ignoring nonignorable missingness will lead to biases. M_MAR and M_MNAR1 produce larger relative biases and MSEs for OR₂₁ and OR₃₂ than the true M_MNAR2 and overly complex M_MNAR3 and M_MNAR4. For example, the relative bias for OR₂₁ is −0.11 from M_MAR and M_MNAR1, while it is only −0.04 from M_MNAR2 and M_MNAR3, and −0.08 from M_MNAR4; the relative bias for OR₃₂ is 0.16 from M_MAR and M_MNAR1, while it is 0.08 from M_MNAR2 and M_MNAR3, and 0.11 from M_MNAR4. Note that M_MAR and M_MNAR1 produce exactly the same results because these two models are actually the same (M_MNAR1 uses $\text{logit}(p_{i2}^{\text{mis}})={\alpha }_0+0\ast \text{logit}(p_{i2})$ as the MOM); while M_MNAR2 and M_MNAR3 also generate very similar results (the differences are only in the third decimal place thus not shown in Table 7) because the overly complex term ${\alpha }_2\ast p_{i2}^2$ is not influential to the results.

Table 7.

Performances of various models when MNAR is present.

		OR21	OR31	OR32
ReBias	MMAR	−0.11	0.01	0.16
	MMNAR1	−0.11	0.01	0.16
	MMNAR2	−0.04	0.01	0.08
	MMNAR3	−0.04	0.01	0.08
	MMNAR4	−0.08	0.01	0.11
MSE	MMAR	0.14	0.18	0.11
	MMNAR1	0.14	0.18	0.11
	MMNAR2	0.13	0.18	0.07
	MMNAR3	0.13	0.18	0.07
	MMNAR4	0.13	0.18	0.10

$\text{ReBias}=\frac{\text{Bias}}{\text{True}\text{Value}}$

The MSEs show similar results. For OR₂₁, the MSEs are 0.14 from M_MAR and M_MNAR1, 0.13 from M_MNAR2, M_MNAR3 and M_MNAR4; for OR₃₂, the MSEs are 0.11 from M_MAR and M_MNAR1, 0.07 from M_MNAR2 and M_MNAR3, and 0.10 from M_MNAR4. Thus, we conclude that joint models M_MNAR2, M_MNAR3, and M_MNAR4 incorporating nonignorable missingness do outperform M_MNAR1 and M_MAR, though misspecification of the missingness may slightly affect the model performance as is shown by M_MNAR4.

Note that the relative biases and MSEs for OR₃₁ from all models are the same because Treatments 1 and 3 are fully observed. All models perform similarly well with very small relative bias, i.e., 0.01.

4.2.2 Simulation 2

Table 8 compares the performances of M_MAR, M_MNAR2, and the CB M_HOM and M_ID models, when the missing data are generated under MAR mechanism. M_MAR is almost unbiased for all OR estimates; M_MNAR2 produces estimates with very small biases; while the CB M_HOM and M_ID models show much bigger biases. Let us take OR₂₁ as an example, the relative biases are 0.01 from M_MAR, 0.08 from M_MNAR2, 0.14 from M_HOM, and 0.15 from M_ID.

Table 8.

Performances of the proposed method and the CB method under MAR mechanism.

		OR21	OR31	OR32
ReBias	MMAR	0.01	0.00	0.01
	MMNAR2	0.08	0.00	−0.06
	MHOM	0.14	0.10	−0.02
	MID	0.15	0.11	−0.01
MSE	MMAR	0.10	0.15	0.04
	MMNAR2	0.14	0.15	0.04
	MHOM	0.23	0.31	0.06
	MID	0.27	0.34	0.06

M_HOM: Lu and Ades HOM model [8]. M_ID: Lu and Ades ID model [8]. $\text{ReBias}=\frac{\text{Bias}}{\text{True}\text{Value}}$.

The conclusions regarding these four models from the MSEs are similar. With OR₂₁ as an example again, the MSEs are 0.10 from M_MAR, 0.14 from M_MNAR2, 0.23 from M_HOM, and 0.27 from M_ID. In summary, our proposed method works well, even if missingness is ignorable. In contrast, the CB methods produce larger biases and MSEs under the MAR mechanism.

In a nutshell, our proposed method still performs well even if the missingness is at random and permits sensible results under the MNAR mechanism. When the results of models assuming MAR show big differences from models assuming MNAR, attention is needed to potential nonignorable missingness; failure to do so may lead to biased estimations.

5 Discussion

Although clinical and policy-making interest often lies in comparing active treatments, new drugs are often compared with placebo or standard treatments in order to obtain approval for drug licensing.³² In addition, it is unrealistic to expect that comparisons of all treatments of interest will be provided from any single trial, as most trials are only two or three arms. NMA, if properly applied, can serve decision making as a better tool than pairwise meta-analysis³³ by providing indirect comparison results, simultaneous inference regarding multiple treatments, and more precise estimation. Thus, it has the potential to bring tremendous changes to the practice of evidence-based medicine.

Deliberate choices of treatments by clinicians or selective choices of treatments by meta-analysts may lead to MNAR. Neither the CB methods^5–8 nor the AB method⁹ can easily handle this challenging situation. In this paper, we extended the AB method in Zhang et al.⁹ to incorporate nonignorable missingness using selection models and applied the proposed method to two real data sets. The smoking cessation data set did not show evidence of nonignorable missingness, but serious nonignorable missingness appeared in the analysis of the prevention of pain on injection with Propofol data set. Simulation studies showed that our proposed method incorporating nonignorable missingness produced less-biased estimates when nonignorable missingness was present and did not hurt if the missingness was ignorable.

A major criticism of the AB method is the assumption that the actual event rates are exchangeable across studies (i.e., exchangeability of absolute study effects), potentially allowing the control rate in one study to influence estimation of the treatment effect in another. In a meta-analysis, studies are firstly screened and collected according to some inclusion criteria, which contains characteristics of the target populations. A (usually CB) meta-analysis is then carried out under the fundamental assumption that treatment contrasts are exchangeable across studies. However, this assumption can be violated if selected studies do not represent a common target population.^12,34 In the same vein, our assumption of exchangeable event rates seems to be plausible if the studies of an NMA come from a common superpopulation. AB thinking has already been applied in traditional meta-analysis.^35,36 Senn³⁷ discussed this controversial issue, and concluded that the amount of bias arising from the AB method is likely to be low, and thus little harm is likely to be done in practice. Senn also acknowledged some advantages of the AB method in traditional meta-analysis.

One advantage of the AB method over the CB methods is that the AB method can sensibly include one-arm studies alongside comparative studies. AB methods assume missing arms to be MAR and imputes them through MCMC, and thus one-arm trials can still contribute to the likelihood function. CB methods require a baseline treatment for each study (i.e., at least two arms) and are thus unable to synthesize one-arm studies. Inclusion of one-arm studies in synthesis has been widely discussed in the literature,^38,39 and the AB method can be a nice alternative, though requires careful consideration of heterogeneity between the different designs, as well as potential bias introduced when adding one-arm studies. In addition, this is intimately related to the flexibility of the AB method. Suppose we have an NMA aiming to compare Treatments A, B, and C but only sparse information on A is available. The AB method can utilize information of A from trials of A versus D, while the CB methods cannot.

The selection model is intuitively appealing because it shows how the probabilities of missingness depend directly on the data values and also that the factorization directly specifies f (Y_obs, Y_mis|θ), which is the distribution in which analysts are usually interested. However, the selection model relies heavily on the correct specification of the model form.¹⁰ Thus, the performance of this method is model-, data-, and context-specific, as expected. Alternatively, pattern-mixture models do not require correct specification of the precise model form, albeit with their own limitations; for example, they are by construction underidentified and require identifying constraints.⁴⁰ Methods that utilize advantages of both selection and pattern-mixture models await further development.

Future work also looks toward approaches for handling inconsistency and publication bias. Inconsistency, defined as apparent discrepancy between direct and indirect comparisons of two treatments, is one of the major issues in NMA. The extensive criticism of NMA is associated with the difficulty in evaluating the assumption underlying the statistical synthesis of direct and indirect evidence. Current existing methods assessing inconsistency have their own drawbacks or are cumbersome to apply; see Hong et al.⁴¹ for a recent Bayesian alternative. Publication bias, the concern that studies with significant results are more likely to be published and published studies are more likely to be included in a meta-analysis, is another potentially serious issue⁴² in NMA. User-friendly approaches that test as well as account for inconsistency and publication bias need further effort.

Overall, many health care practitioners remain somewhat skeptical of NMA and tend to give priority to direct evidence to inform decision making because this emerging statistical technique is still somewhat imperfect. Besides the issues of inconsistency and publication bias, the assumption underlying the models, the statistical expertise required to fit them, and the lack of an interpretable and simple measure to evaluate the risk of biases all contribute to this skepticism. Future research should focus on these issues and their evaluation, interpretation, and applicability.

Appendix 1. A Simulation studies comparing AB and CB methods

In this appendix, we aim to compare the performances of the AB method proposed in Zhang et al. (2014) [9] and the CB method proposed in Lu & Ades (2009) [8], under missing completely at random (MCAR) and MAR mechanisms.

Simulation setup

A network meta-analysis containing 30 trials comparing three treatments is generated according to the unstructured heterogeneous-variance model MOI v specified in the main paper, i.e., p_ik = Φ(μ_k + ν_ik), where (ν_i1, …, ν_iK)^T ~ MVN(0,Σ_k) and Σ_k is the covariance matrix determined by correlation parameters ρ = (ρ₁₂, ρ₁₃, ρ₂₃) and standard deviation parameters σ = (σ₁, σ₂, σ₃). We let the mean parameters have values μ₁ = −1.0, μ₂ = −0.5, and μ₃ = −0.8, standard deviation parameters have values σ₁ = 0.3, σ₂ = 0.4, and σ₃ = 0.5, and correlation coefficients have values ρ₁₂ = 0.4, ρ₁₃ = 0.5, and ρ₂₃=0.6. The response rate p_ik for the k-th treatment in the i-th trial is calculated according to the above MOI v formula and specified parameters. Then the number of binary responses {y_ik} are randomly generated from a binomial distribution with n=100 and probabilities p_ik. Note that the above parameters correspond to the true population-averaged treatment-specific response rates π₁ = 0.17, π₂ = 0.32, and π₃ = 0.24, and thus the true odds ratios are OR₂₁ = 2.33, OR₃₁ = 1.53, and OR₃₂=0.66.

Let r_ik be the missingness indicator, taking value 1 when the record for the k-th treatment in the i-th trial is missing and 0 when the record is present, and $p_{ik}^{\text{mis}}$ be the corresponding probability of missingness. We consider simulated scenarios of missingness mimicking the characteristics of the real smoking cessation data, where most of the trials (22) are two-arm and only a few (2) are three-arm. Treatment 2 is assumed to be completely observed, while Treatments 1 and 3 have missing values. We let n_mis=10, 11, 12, 13, 14 trials be missing for Treatment 3, and then another n_mis trials be missing for Treatment 1 selected from the remaining 30 – n_mis, ensuring each trial contains at least two treatments (while 30 – 2n_mis have 3). For the MCAR situation, the missingness of Treatments 3 and 1 are determined by $\text{logit}(p_{i3}^{\text{mis}})=1$ and $\text{logit}(p_{i1}^{\text{mis}})=-1$ respectively. For the MAR situation, the missingness of Treatment 3 is determined by $\text{logit}(p_{i3}^{\text{mis}})=1+\text{logit}(\frac{y_{i2}}{n})$, whereas the missingness of Treatment 1 is determined by $\text{logit}(p_{i3}^{\text{mis}})=-1-\text{logit}(\frac{y_{i2}}{n})$. Note that in missing data simulations it is a common approach to generate complete data first and then randomly delete some, leaving the missing percentage unknown. We instead first decide how many trials will be deleted and then select these trials according to $p_{i3}^{\text{mis}}$ and $p_{i1}^{\text{mis}}$, until the pre-determined number of missing trials is obtained. In this way, we are able to track the model performance under various missingness percentages.

We now fit two models to the simulated data sets. One is the unstructured heterogeneity AB model proposed by Zhang et al. [9], and the other is the unstructured heterogeneity CB model proposed by Lu and Ades [8]. These two models are labeled as MOI v and ID model, respectively, in Figure 1 in the main paper.

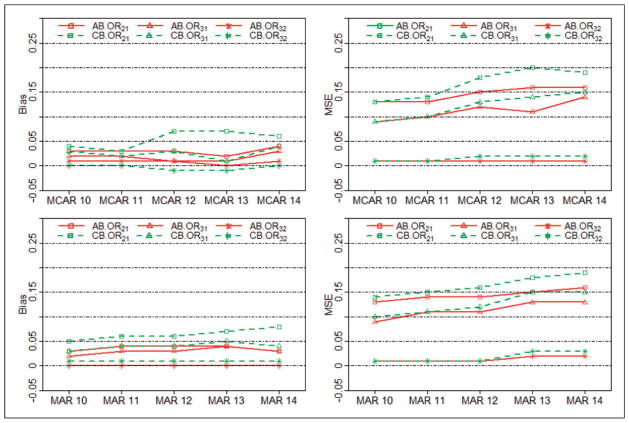
Simulation results

Figure 4 presents the biases and MSEs of ORs (OR₂₁, OR₃₁, and OR₃₂) obtained from the AB method and the CB method under both MCAR and MAR mechanisms. Bias from the AB method is consistently smaller than 0.05 for all n_mis = 10, 11, 12, 13, or 14 under both mechanisms, whereas bias from the CB method sometimes is bigger than 0.05 (see the two plots in the left column of Figure 4). Under both MCAR and MAR mechanisms, MSE from the AB method (the right column of Figure 4) is consistently smaller than from that of CB method for different n_mis values. This suggests that the AB method is less biased than the CB method. Another phenomenon observed in Figure 4 is that the difference between two methods is smaller when the number of missing trials is small, e.g. when n_mis = 10 and 11. However, when n_mis becomes bigger, e.g. 12, 13, and 14, closer to the missing situation in the real smoking cessation data, the AB method is more robust. In general, the AB method outperforms the existing CB method in terms of bias and MSE under both MCAR and MAR mechanisms.

Figure 4.

Performance comparisons for the AB⁹ and CB⁸ methods. Biases and MSEs under both MCAR and MAR mechanisms are shown.

Appendix 2. Real data analysis results with different link functions for MOMs

Table 9 compares the results using the logit link for the MOMs with those obtained using a probit link for the MOMs for the smoking cessation data. Results from both JM i and JM ii are presented. We can see that the different link functions produce similar results for both joint models. Table 10 presents corresponding results for the prevention of pain on injection with Propofol data set; again, changes are very modest. In summary, both the logit and probit link functions seem to work equally well.