Approximately independent linkage disequilibrium blocks in human populations

Abstract

Summary: We present a method to identify approximately independent blocks of linkage disequilibrium in the human genome. These blocks enable automated analysis of multiple genome-wide association studies.

Availability and implementation: code: http://bitbucket.org/nygcresearch/ldetect; data: http://bitbucket.org/nygcresearch/ldetect-data.

Contact: tberisa@nygenome.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

The genome-wide association study (GWAS) is a commonly used study design for the identification of genetic variants that influence complex traits. In this type of study, millions of genetic variants are genotyped on thousands to millions of individuals, and each variant is tested to see whether an individual’s genotype is predictive of their phenotypes. Because of linkage disequilibrium (LD) in the genome (Pritchard and Przeworski, 2001), a single genetic variant with a causal effect on the phenotype leads to multiple statistical (but non-causal) associations at nearby variants. One initial analysis goal in a GWAS is to count the number of independent association signals in the genome while accounting for LD.

The most commonly used approach to counting independent single-nucleotide polymorphisms (SNPs) that influence a trait is to count ‘peaks’ of association signals—this can be done manually when the number of peaks is small (e.g. Wellcome Trust Case Control Consortium 2007) or in a semi-automated way when the number of peaks is larger (e.g. Jostins et al. 2012). There are also fully automated methods that use LD patterns estimated from large reference panels of individuals (Yang et al., 2012). In some contexts (e.g. when performing identical analysis on multiple GWAS with the goal of comparing phenotypes), it is useful to define approximately independent LD blocks a priori rather than letting them vary across analyses performed on different phenotypes (Loh et al., 2015; Pickrell, 2014).

To define approximately independent LD blocks, Loh et al. (2015) used non-overlapping segments of 1 megabase, and Pickrell (2014) used non-overlapping segments of 5000 SNPs. The breakpoints of these segments undoubtedly sometimes fall in regions of strong LD, thus potentially splitting a single association signal over two blocks (and leading to over-counting of the number of associated variants). A better approximation could be obtained by considering the empirical patterns of LD in a reference panel (e.g. Anderson and Novembre 2003; Greenspan and Geiger 2004; Mannila et al. 2003). In the remainder of this article, we present an efficient signal processing-based heuristic for choosing approximate segment boundaries.

2 Approach and results

To estimate LD between pairs of SNPs, we use the r² metric. If a genetic variant is in LD with another genetic variant that has a causal influence on disease, then r² (times the strength of association at the causal SNP) is proportional to the association statistic at the non-causal SNP (Pritchard and Przeworski, 2001). For our purposes, we define two sets of SNPs as ‘approximately independent’ if the pairwise r² between SNPs in different sets is close to zero.

Our approach is a heuristic for choosing segment boundaries, given a mean segment size (which is the required input). Let there be n genetic variants on a chromosome. The method can be broken down into the following basic steps (see the Supplementary Material for details):

1. Calculate the n × n covariance matrix C for all pairs of SNPs using the shrinkage estimator of C from Wen and Stephens (2010).

2. Convert the covariance matrix to n × n matrix of squared Pearson product-moment correlation coefficients P.

3. Convert the matrix $P=(e_{i,j})$ to a $(2n-1)$-dimensional vector $V=(v_k)$ as follows:

$$\begin{array}{c}{v}_k={\displaystyle \sum _{i=1}^k{t}_{i,k-i+1}},t_{i,j}=\{\begin{array}{ll}{e}_{i,j},\hfill & \text{if}\hspace{0.17em}1\le i,j\le n\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array},\\ \hspace{1em}(k=1,2,\mathrm{...},2n-1)\end{array}$$

The effect of this step is representing each antidiagonal of P by the sum of its elements (Fig. 1a and b). This step has similarities to Bulik-Sullivan et al. (2015), where the authors represent each column by the sum of its elements. The method presented in this article uses the antidiagonal to differentiate between neighboring blocks of similar size.

• 4. Apply low-pass filters of increasing widths to (i.e. ‘smooth’) V until the requested number of minima is achieved.

• 5. Perform a local search in the proximity of each minimum from Step 4 to fine tune the segment boundaries.

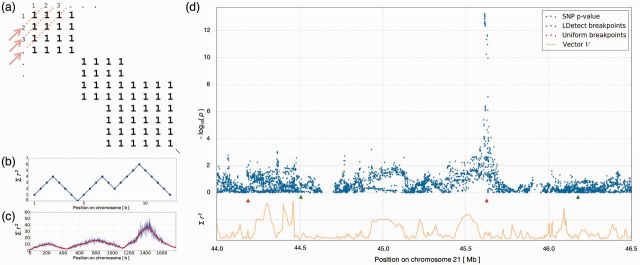
Fig. 1.

(a) and (b) Schematic of the conversion of matrix P to vector V. (c) Example data (blue) with Hann filter applied (red). (d) Example of Crohn’s disease GWAS hits with partially filtered vector V and comparison of breakpoints

In reality, matrix P turns out to be sparse, approximately banded and approximately block-diagonal, with sporadically overlapping blocks (Slatkin, 2008; Wall and Pritchard, 2003; Wen and Stephens, 2010).

To provide intuition for Step 3, Figure 1a shows a simplified example of a correlation matrix P, where two SNPs i and j are either correlated (represented by 1 in element e_ij of the matrix) or uncorrelated (represented by zero, not shown). Representing each antidiagonal of P by the sum of its elements results in the vector shown in Figure 1b and identifying segments representing blocks of LD reduces to identifying local (or more stringently, global) minima in this vector. In reality, the elements e_ij of P are continuous values from the interval $[0,1]$ and result in an extremely noisy vector V (example in blue in Fig. 1c) Therefore, to identify large-scale trends of LD and reduce high frequency components in the signal, we apply a signal processing technique dubbed low-pass filtering [utilizing a Hann window (Blackman and Tukey, 1958)] in Step 4. The result of applying a low-pass filter (with width = 100) is shown in red in Figure 1c.

Applying wider and wider filters to vector V in Step 4 allows us to focus on the large scale structure of LD blocks but also causes the approach to miss small scale variation around identified minima. To counteract this effect, Step 5 conducts a local search in the proximity of each local minimum identified in Step 4 to find the closest SNP l with $\text{min}\sum _{i<l}\sum _{j>l}{e}_{ij}$.

We applied this method to sequencing data from European, African and East Asian populations in the 1000 Genomes Phase 1 dataset. We set a mean block size of 10 000 SNPs and used the algorithm to define the block boundaries. As expected, these boundaries fall in regions with considerably higher recombination rates than the genome-wide average (Supplementary Fig. S4). In Figure 1d, we show an example from GWAS results for Crohn’s disease (Jostins et al., 2012) where using uniformly distributed breakpoints would result in double-counting of an association signal, whereas the LD-aware breakpoints avoid stretches of SNPs in LD.

To test whether this approach is useful more generally, we ran fgwas (Pickrell, 2014) on GWAS of Crohn’s disease (Jostins et al., 2012) and height (Wood et al., 2014), using both uniformly distributed breakpoints and LD-aware breakpoints. Using the LD-aware breakpoints successfully eliminated double-counting of SNPs in moderate-to-high LD and on opposite sides of uniform breakpoints (Supplementary Material Section S6).

Funding

This work was supported by the National Institutes of Health (NIH) R01 grant number MH106842 to Joseph K. Pickrell.

Conflict of Interest: none declared.