Bayesian neural adjustment of inhibitory control predicts emergence of problem stimulant use

A key goal of addiction research is to identify biomarkers that predict subsequent dependence. Harlé et al. show that in high-functioning occasional stimulant users performing an inhibitory control task, individual differences in how the brain encodes the need to stop predict the likelihood of abuse or dependence three years later.

A key goal of addiction research is to identify biomarkers that predict subsequent dependence. Harlé et al. show that in high-functioning occasional stimulant users performing an inhibitory control task, individual differences in how the brain encodes the need to stop predict the likelihood of abuse or dependence three years later.

Abstract

Bayesian ideal observer models quantify individuals’ context- and experience-dependent beliefs and expectations about their environment, which provides a powerful approach (i) to link basic behavioural mechanisms to neural processing; and (ii) to generate clinical predictors for patient populations. Here, we focus on (ii) and determine whether individual differences in the neural representation of the need to stop in an inhibitory task can predict the development of problem use (i.e. abuse or dependence) in individuals experimenting with stimulants. One hundred and fifty-seven non-dependent occasional stimulant users, aged 18–24, completed a stop-signal task while undergoing functional magnetic resonance imaging. These individuals were prospectively followed for 3 years and evaluated for stimulant use and abuse/dependence symptoms. At follow-up, 38 occasional stimulant users met criteria for a stimulant use disorder (problem stimulant users), while 50 had discontinued use (desisted stimulant users). We found that those individuals who showed greater neural responses associated with Bayesian prediction errors, i.e. the difference between actual and expected need to stop on a given trial, in right medial prefrontal cortex/anterior cingulate cortex, caudate, anterior insula, and thalamus were more likely to exhibit problem use 3 years later. Importantly, these computationally based neural predictors outperformed clinical measures and non-model based neural variables in predicting clinical status. In conclusion, young adults who show exaggerated brain processing underlying whether to ‘stop’ or to ‘go’ are more likely to develop stimulant abuse. Thus, Bayesian cognitive models provide both a computational explanation and potential predictive biomarkers of belief processing deficits in individuals at risk for stimulant addiction.

Introduction

An important goal of addiction research is to identify predictive biomarkers that can quantify the risk of future problem use for an individual subject. Occasional off-prescription use of stimulants to enhance cognitive performance has recently become an alarming trend among healthy young adults, including highly functioning university students (Herman-Stahl et al., 2006). Such experimentation with illegal stimulants (e.g. cocaine, methamphetamine) or medically prescribed stimulants to other parties (e.g. Adderall) is associated with a higher risk of developing substance dependence (Tapert et al., 2002; Elkashef and Vocci, 2003) as well as pervasive executive deficits (Yücel et al., 2007; Reske et al., 2011). The ability to identify early-on which occasional users are likely to develop a substance use disorder, or to discontinue use, is therefore a critical step to improve the efficiency of prevention efforts.

Bayesian ideal observer models can quantify individuals’ beliefs and expectations about their environment as a function of behavioural context and experienced choices and outcomes. These models provide a way to understand how the brain processes complex environments and how the breakdown of this process can contribute to clinical prediction of illness trajectory. In this approach, we infer otherwise unknown beliefs in individuals regarding upcoming events (e.g. occurrence of a particular stimulus) and how such beliefs are updated based on past events experienced by the observer. Such methods may be particularly important for prediction research in at-risk populations with very subtle or non-detectable behavioural deficits on standard neuropsychological measures, which is the case for occasional stimulant users (OSU). While significant executive deficits have been demonstrated in chronic stimulant dependence (Salo et al., 2002; Monterosso et al., 2005; Hester et al., 2007; Tabibnia et al., 2011), only subtle behavioural impairments in error monitoring and inhibitory control (i.e. ability to withhold a prepotent action) have been observed in OSU (Colzato et al., 2007; Reske et al., 2011). Here, we use Bayesian model-based analysis of event-related functional MRI data associated with baseline inhibitory function in a stop-signal task to predict OSU clinical status 3 years later. Based on previous studies showing that healthy volunteers (Ide et al., 2013) and OSU (Harlé et al., 2014) continuously alter their response strategy in this inhibitory control paradigm, we hypothesized that such computational neural variables would perform significantly better than other variables, such as non-computational task-based brain activity and clinical measures (e.g. cumulative drug use), in predicting long-term clinical status.

Although there are few neuroimaging studies of OSU, stimulant dependence has been linked to reduced functioning of dopamine transporters and abnormal metabolism in regions critical to inhibitory control, including basal ganglia, anterior cingulate cortex (ACC), and other prefrontal areas (Volkow et al., 1999; Bolla et al., 2004; London et al., 2004; Kim et al., 2009). In inhibitory control paradigms, stimulant-dependent users show altered activity in ACC and anterior insula, as well as right superior/inferior frontal gyrus (Kaufman et al., 2003; Hester and Garavan, 2004; Li et al., 2007; Nestor et al., 2011). Given recent work implicating ACC and insula in coding Bayesian prediction errors (i.e. difference between probability of stop signal and actual trial type) in healthy non-users (Ide et al., 2013) and OSU (Harlé et al., 2014), we hypothesize that abnormal neural responses associated with Bayesian prediction errors in those regions would lead to difficulties in implementing cognitive control among OSU and be particularly predictive of future problem use.

Materials and methods

Participants

The University of California, San Diego Human Subjects Review Board, approved the study protocol. Over a 5-year period, potential participants were recruited via Internet advertisements, newspapers, and flyers (Reske et al., 2011). As a result, 1025 individuals underwent detailed telephone screens, of which 184 OSU met study inclusion criteria and provided written informed consent to participate. OSU endorsed (i) 2+ off-prescription uses of cocaine or amphetamines over the past 6 months; (ii) no lifetime stimulant dependence; (iii) no lifetime stimulant use for medical reasons; and (iv) no treatment of substance-related problems. Once enrolled, participants completed three sessions: (i) a baseline interview session to evaluate clinical diagnoses and determine current patterns of drug use (n = 184); (ii) a neuroimaging session examining brain and behaviour responses during decision-making (n = 158; 86%); and (iii) a follow-up interview session 3 years later to determine changes in clinical status and patterns of drug use (n = 157/158).

Baseline interview session

Lifetime DSM-IV Axes I and II diagnoses, including substance abuse and dependence (APA, 2013), were assessed by the Semi-structured Assessment for the Genetics of Alcoholism II (SSAGA II) (Bucholz et al., 1994). Diagnoses were based on consensus meetings with a clinician specializing in substance use disorders (M.P.P; see Supplementary material for exclusion criteria). Information on current alcohol and nicotine use patterns was also collected and participants completed questionnaires indexing personality and mood variables that have previously been associated with drug use such as impulsivity, sensation seeking, and depression, including the Barratt Impulsiveness Scale (BIS-11) (Patton and Stanford, 1995), the Sensation Seeking Scale (SSS-V) (Zuckerman and Link, 1968), and the Beck Depression Inventory (BDI) (Beck et al., 1961).

Neuroimaging session

This session was completed within 2 weeks of the baseline interview session. Participants were instructed to abstain from illicit substance use ≥72 h prior to this session and abstinence was determined by urine toxicology screen. They completed six blocks of a stop-signal task while undergoing functional MRI. On ‘go’ trials (n = 216), they had to press as quickly as possible the left button when an ‘X’ appeared and the right button when an ‘O’ appeared. On ‘stop’ trials (i.e. whenever they heard a tone during a trial; n = 72), they were instructed not to press either button (Fig. 1). Prior to scanning, participants’ mean reaction time from stimuli onset was determined to compute six levels of stop signal delay (SSD), providing an individually customized range of difficulty (for more details see Matthews et al., 2005; Harlé et al., 2014).

Figure 1.

Stop signal task. At the onset of each trial, either an ‘X’ or an ‘O’ appeared on a black background back-projected to the MRI room. Participants were instructed to press, as quickly as possible, the left button when an ‘X’ appeared, and the right button when an ‘O’ appeared. They were also instructed not to press either mouse button whenever they heard a tone during a trial (stop trials). Each trial lasted 1300 ms and each trial was separated by 200-ms interstimulus intervals (blank screen). Individual response latency was used to denote the period of inhibitory processing and provided a subject-dependent jittered reference function. Participants performed six blocks of the task, each containing a total of 48 trials (12 stop and 36 non-stop trials in each block). Trial order was pseudorandomized throughout the task. Prior to scanning, participants performed the stop task in a behavioural testing session to determine their mean reaction time from ‘X’ and ‘O’ stimuli onset. Such individual measures were used to determine the stop signal delay (SSD) for the six different stop trial types. Specifically, stop signals were delivered at 0 (RT-0), 100 (RT-100), 200 (RT-200), 300 (RT-300), 400 (RT-400), or 500 (RT-500) ms less than the mean reaction time after the beginning of the trial, thus providing a range of difficulty level.

Bayesian model of probabilistic prediction

In recent work (Shenoy and Yu, 2011; Shenoy et al., 2011; Ide et al., 2013), stopping behaviour adjustments has been well captured by a Bayes optimal decision-making model. This model assumes that an individual updates the previous probability of encountering stop trials, P(stop), on a trial-by-trial basis based on trial history and adjusts decision policy as a function of P(stop), with systematic consequences for go reaction time and stop accuracy in the upcoming trial. A higher predicated P(stop) is associated with a slower go reaction time and a higher likelihood of correctly stopping on a stop trial in healthy subjects (Ide et al., 2013; Harlé et al., 2014).

To model the trial-by-trial adjustment of prior expectations, we used a Bayesian hidden Markov model adapted from the Dynamic Belief Model (DBM) (Yu and Cohen, 2009; Ide et al., 2013) (Fig. 2A). The model makes the following assumptions about subjects’ internal beliefs regarding task structure: on each trial k, there is a hidden probability r_k of observing a stop signal (s_k = 1 for stop trial) and probability 1 − r_k of observing a go trial (s_k = 0); r_k is the same as r_{k − 1} with probability α, and resampled from a prior beta distribution p₀(r) with probability 1 − α. Predictive probability of trial k being a stop trial, P_k(stop): = P(s_k = 1 | s_{k − 1}), where s_k = (s₁, … , s_k) is a vector of all past trial outcomes, 1 for stop trials and 0 go trials, can be computed as:

$$\begin{array}{c}P\left(s_k=1|{\text{S}}_{k-1}\right)={\displaystyle \int }P\left(s_k=1|r_k\right)p\left(r_k|{\text{S}}_{k-1}\right)d{r}_k\\ {\displaystyle ={\displaystyle \int r_{k}p\left(r_k|{\text{S}}_{k-1}\right)}d{r}_k=\langle r_k|{\text{S}}_{k-1}\rangle }\end{array}$$

Predictive probability of seeing a stop trial, P_k(stop), is the mean of the predictive distribution p(r_k|s_{k − 1}), which, by marginalizing over the uncertainty of whether r_k has changed from the last trial, becomes a mixture of the previous posterior distribution and a fixed prior distribution, with α and 1−α acting as the mixing coefficients, respectively:

$$p\left(r_k|{\text{S}}_{k-1}\right)=\alpha p\left(r_{k-1}|{\text{S}}_{k-1}\right)+\left(1-\alpha \right)p_0\left(r_k\right)$$

Posterior distribution over stop trial frequency is updated according to Bayes’ rule:

$$p\left(r_k|{\text{S}}_k\right)\mathrm{\propto }P\left(s_k|r_k\right)p\left(r_k|{\text{S}}_{k-1}\right)$$

Parameters for the beta distribution p₀(r) and α were kept constant across all subjects and set based on previous fits of subjects’ task expectations [i.e. Beta(2.5,7.5; mean = 0.25], and α = 0.8] (Shenoy and Yu, 2011; Ide et al., 2013; Harlé et al., 2014). Given these parameters and sequence of observed stop/go trials (pseudo-randomized, fixed across subjects), we computed the corresponding sequence of subjective P(stop) probabilities for the trial sequence participants experienced. In subsequent functional MRI analyses, the trial-by-trial estimation of P(stop) = 〈r_k〉 (i.e. representing the most up-to-date estimated likelihood of encountering a stop signal based on all previous trials) was used as a parametric regressor in functional MRI analyses. Importantly, we examined whether the model predictions would be sensitive to parameters α and the prior distribution p₀(r) at the individual level (Harlé et al., 2014) and found that produced P(stop) values were highly correlated across parameter settings and did not differ significantly between individual level or group level settings (r > 0.9; R² > 0.8). For this reason, we opted for a fixed parameter setting across individuals. We also tested for potential clinical group differences in parameter values, and found no significant difference (i.e. the fixed setting value were optimal for both groups).

Figure 2.

Stop-signal task behavioural results. (A) Bayesian hidden Markov model used, a version of the Dynamic Belief Model (Yu and Cohen, 2009), which computes trial-wise sequential predictions about the frequency of stop trials. The prior probability of encountering a stop signal on trial k, P_k(stop), is compared with the actual trial outcome (0 = go; 1 = stop) to produce a signed prediction error [SPE; i.e. outcome-P_k(stop)] or unsigned prediction error [UPE; i.e. |outcome − P_k(stop)|], which are combined with the prior to produce a new updated prior for the next trial k + 1. (B) Distribution of Go reaction time for each group (red: PSU = problem stimulant users, mean Go reaction time = 578 ms; black: DSU = desisted stimulant users, mean Go reaction time = 634 ms). (C) Error rates by stop signal delay (SSD) for each group (red: PSU; black: DSU; error bars = SEM); (D) Bayesian model prediction and behavioural data presented for each group: red/square for PSU (n = 38), black/circles for DSU (n = 50). As predicted by Bayes optimal decision-making in the stop signal task, individuals’ Go reaction times (RT) was positively correlated with trial-wise P(stop) model estimates in each group. DSU (black) and PSU (red) model lines represent best linear regression fit to mean go reaction time. Error bars = SEM.

Behavioural statistical analyses

For behavioural dependent variables with repeated measures [e.g. trial-wise reaction times and error as a function of P(stop)], we conducted hierarchical generalized mixed-effect linear models treating subject as a random factor (with varying intercepts and slopes) and other variables as fixed effects (Baayen et al., 2008). A logit link function was used for binary error data (i.e. performance accuracy section) (Jaeger, 2008). We report change in log likelihood ratio (following a chi-squared distribution) and regression coefficients (when applicable) with associated t-test and P-values. While there is currently no strong agreement on how to estimate degrees of freedom for mixed-effect generalized linear models, the reported degrees of freedom and P-values for regression coefficients of interest were estimated based on the Satterthwaite (1946) approximation. These statistics were obtained using R statistics [http://cran.r-project.org; lmerTest library, lmer()]. This method is more conservative than another common method used in standard statistical packages, which estimates degrees of freedom by subtracting the number of fixed effects from the total number of observations for each parameter (Baayen et al., 2008).

First-level functional MRI analyses

Using a fast event-related functional MRI design, six T₂*-weighted echo planar imaging functional runs were collected for each participant, along with one T₁-weighted anatomical image (see Supplementary material for image acquisition and preprocessing details).

In a first general linear model (GLM), three types of trials [Go, Stop Success (SS), and Stop Error (SE)] were convolved with a canonical haemodynamic response function. Each of these predictors were entered both as linear regressors [multiplied by the mean of the computed P(stop) values across all trials] and parametrically modulated (Büchel et al., 1998) by trial-level P(stop) estimates. Such an approach allowed us to isolate neural activations (and their potential predictive value in subsequent prediction analyses) associated with both trial type alone (i.e. categorical regressor) and P(stop). Thus, after deconvolution, this model included six task regressors [three categorical: Go, SS, SE; and three model-based parametric: GoxP_k(stop), SSxP_k(stop), SExP_k(stop)].

To assess updating processes related to P(stop), we created a second GLM with trial-wise Bayesian signed prediction error [i.e. SPE: (Outcome − P(stop)] and unsigned prediction error [i.e. UPE: |Outcome − P(stop)|] included as parametric regressors of interest. We distinguished these types of prediction errors as they may provide different types of information important for adjusting behaviour. UPE represent an overall degree of discrepancy between one’s internal model prediction and actual outcome, that is a ‘goodness of fit’ measure of one’s internal predictive model [in this case P(stop) estimation]. In contrast, SPE provide additional information on the direction of this discrepancy, which may be more relevant to orienting or motivating the individual towards specific actions (e.g. Go versus Stop). This second model also included a parametric regressor modelling trial error (0 = correct or 1 = error) to control for performance error-related activity (Ide et al., 2013). Both GLM models included a baseline regressor (consisting of intertrial intervals and instruction phases), linear drift and three motion regressors (pitch, yaw, roll) (Matthews et al., 2005), as well as Go reaction times and SSD as parametric regressors of no-interest. Images were spatially filtered (Gaussian full-width at half-maximum 4 mm) to account for individual anatomical differences. Anatomical and functional images were manually transformed into Talairach space.

Individual subjects’ per cent signal change (%SC) scaled beta weight values for five regressors/contrasts of interest from these two first level models were extracted for their use as independent measures in second level prediction analyses (see below). These included two categorical contrasts, (Stop − Go) [i.e. (SS + SE) / 2 − Go] and (SE − SS), and the three computational regressors: P(stop) [i.e. 0.5 × GoxP_k(stop) + 0.25 × SSxP_k(stop), + 0.25 × SExP_k(stop)], UPE, and SPE.

Three-year follow-up interview session

OSU who completed the neuroimaging session were contacted 3 years after their initial lab visit to complete another standardized interview (phone or in-person) examining extent of drug use in the 3-year interim period (using the SSAGA II). Two groups were identified: problem stimulant users (PSU) and desisted stimulant users (DSU). PSU (n = 38) were a priori defined by: (i) continued stimulant use since baseline interview; and (ii) endorsement of 2+ symptoms of DSM-IV amphetamine and/or cocaine abuse and/or dependence criteria occurring together 6+ contiguous months since the initial visit [M = 4.2 symptoms; standard deviation (SD) = 2.3; range: 2–9]. This classification is therefore more stringent than a DSM-IV stimulant abuse diagnosis (requiring only one symptom) and is consistent with the required criteria to meet a DSM-5 substance use disorder (APA, 2013). All PSU had at least one diagnosis of stimulant abuse or dependence, including 43% meeting criteria for DSM-IV stimulant dependence. In comparison, DSU (n = 50) endorsed: (i) no 6-month periods with 1+ stimulant uses; and (ii) no symptoms of interim stimulant abuse/dependence. Thus data from 88 subjects, from the subset of 158 OSU previously published in Harlé et al. (2014), were included in the present analyses. The remaining 69 OSU with follow-up data did not meet PSU or DSU group criteria and therefore were not included in further computations.

Clinical prediction analyses

Statistical approach

To allow for cross-validation of variables’ predictive accuracy, we adopted a split-sample approach. We first identified potential predictive neural regions by conducting voxelwise logistic regression analyses in a randomly selected ‘training’ subset of our sample (n = 88/2 = 44; using random.org). The remaining ‘test’ subset was used to assess the relative predictive power of these activation clusters identified based on the training sample. This enabled us to obtain a more parsimonious model and more conservative estimates of model coefficients and accuracy measures. Both training and test samples were stratified based on clinical status base rates to produce equivalent proportions of PSU and DSU in each sample (i.e. 50/2 = 25 randomly selected DSU and 38/2 = 19 randomly selected PSU). For each final predictive regions identified by the random forest selection, two sets of coefficients were obtained: those extracted based on the test sample (used for final cut points and accuracy estimation), and those based on the training sample (calculated as the average slope and intercept coefficients across all voxels in the brain region).

Identification of predictive neural regions: second-level functional MRI analyses with robust logistic regression

To identify brain areas with task-related activations predicting future clinical outcome, while minimizing the influence of outliers and risk of model overfitting, we conducted voxelwise robust logistic regressions with 3-year follow-up status as the dependent measure (coded 1 = PSU versus 0 = DSU). This analysis was restricted to the randomly selected training sample (n = 88/2 = 44). For each voxel (j), the log odds of this outcome for the i^th subject is modelled as a linear combination of the M predictor variables of interest with an equation of this form:

$$\mathrm{logit}(p_i)=\mathrm{lo}{g}_e\left(\frac{p_i}{1-p_i}\right)={\alpha }_j+{\displaystyle \sum _{m=1}^M{\beta }_{jm}{X}_{ijm}}$$

where p_i is the probability of PSU status at 3-year follow-up for the i^th subject, α_j and β_jm are the intercept and coefficients for the M model predictors, and X_ijm represent the standardized values for the M predictors of interest for the i^th subject. These independent variables included activation (normalized beta weight) associated with each of the five task regressors extracted from the first level GLM [i.e. Go-Stop, SE-SS, P(stop), UPE, and SPE] along with three baseline indices of drug use (lifetime uses of amphetamine, cocaine, and marijuana). We did not include baseline indices of alcohol and tobacco usage, as (i) no lifetime use measures were obtained for these drugs; and (ii) groups had very similar baseline use for both drugs (P > 0.8). This analysis was implemented by fitting a robust generalized model equation using R statistics [http://cran.r-project.org; robust library, glmrob()]. The method uses a Mallows quasi-likelihood estimator and Huber-type robust M-estimator of variance, allowing us to bound the influence of outliers (Cantoni and Ronchetti, 2006).

To obtain the resulting whole-brain statistical maps and identify significantly predictive brain regions, we corrected for multiple comparisons using a cluster threshold adjustment based on Monte Carlo simulations (AFNI’s AlphaSim), based on whole-brain voxel size and 4 mm smoothness. A minimum cluster volume of 448 µl was used, with a cluster significance of P = 0.01 corrected for multiple comparisons.

Cross-validation and variable selection: random forest analysis

Using the ‘test’ sample, average %SC from baseline was extracted for each of the significant regions associated with each task regressor of interest (i.e. regions of interest identified by robust logistic regression in training sample). To obtain a more selective predictive model, we included all these activations as well as the three baseline lifetime drug use measures as independent variables in a random forest analysis predicting 3-year clinical outcome. Random forest analysis is a robust predictive technique, outperforming other classification algorithms such as the support vector machine (Qi et al., 2006). Specifically, the combination of bagging and random feature selection in random forests minimizes threats to variable selection resulting from multicollinearity and relatively large numbers of predictors relative to sample size, both common issues in brain imaging studies (Bureau et al., 2005).

The random forest procedure involves three main steps (Breiman, 2001; Strobl et al., 2009). The first step is to construct a large number of classification trees (e.g. 2000). Each tree is based on a bootstrapped subsample of participants and a randomly selected subset of independent variables. For each tree, the random forest algorithm determines the optimal split point for each selected variable in order to correctly classify participants into PSU or DSU. In a second step, each tree classifies subjects that were not used in its original construction (i.e. out-of-bag sample). Such individual tree ‘votes’ are aggregated to provide the predicted status of each participant, and thus determine overall accuracy measures (i.e. classification accuracy, sensitivity, specificity, positive and negative likelihood ratios). In a third and final step, data from the out-of-bag sample are used to estimate variable importance and select the most predictive variables (i.e. those with highest importance scores). Such importance metric quantifies how much each variable contributes to classification accuracy and is defined as the decrease in overall accuracy when values of that variable are randomly permuted (i.e. breaking the association between predictor and outcome variable) (for more details, see Supplementary material and Strobl et al., 2009; Genuer et al., 2010; Ball et al., 2014).

The final output of the random forest process is therefore a cross-validated accuracy estimate (i.e. true positives + true negatives), which we compared to the base response rate and its confidence interval (CI) with a chi-square goodness of fit test. In the test sample, the most accurate base response rate (with no predictors in the model) was 25 / 44 = 57% (95% CI: 42–70%). In this study, we ran three random forest analyses each with a distinct set of baseline variables to compare the overall performance of (i) drug use measures; (ii) categorical functional MRI regressors; and (iii) Bayesian/computational functional MRI regressors, respectively.

Individual predictor accuracy

To further understand the relationship between task-based activation and future likelihood of stimulant abuse and/or dependence in the most reliably predictive identified regions of interest (i.e. identified with random forest analysis), we conducted bootstrapped robust logistic regressions predicting 3-year clinical outcome with each predictor individually (i.e. average region of interest activation), implemented in R statistics (http://cran.r-project.org; robust and boot libraries). As with the training sample whole-brain analyses, this robust generalized model equation used a Mallows quasi-likelihood estimator minimizing the influence of outliers. For significance test, we provide the change in likelihood ratio (relative to a baseline model), which follows a chi-squared distribution. Cut points (in zero-meaned standardized scores) corresponding to a 50% probability of PSU versus DSU classification and 10-fold cross-validated test accuracy were also estimated for these models.

Results

Participant characteristics and drug use

Groups did not differ in ethnicity [PSU/DSU: 67%/64% Caucasian, 16%/16% Asian-American, 8%/8% Hispanic, 0%/4% African-American, 8%/8% other; χ²(4) = 1.54, P = 0.82], gender [PSU: 56% female; DSU: 54% female; χ²(1) = 1.35, P = 0.71], age, education, or verbal IQ (P > 0.05; see Table 1). In addition, they did not differ in alcohol and cigarette use, attention deficit hyperactivity disorder or conduct disorder symptoms (assessed with the SSAGA-II). Although groups did not differ in baseline cocaine and marijuana use, PSU reported a higher cumulative number of amphetamine uses at baseline (P = 0.03). Consistent with their diagnoses, PSU reported significantly higher interim use of cocaine and amphetamine (P < 0.001; see Table 1), however groups did not differ in interim marijuana use. Thus, generally, PSU and DSU did not differ in terms of their demographic and psychological profile at baseline.

Table 1.

Participants’ baseline characteristics as a function of 3-year follow-up clinical outcome.

	PSU n = 38		DSU n = 50
	Mean	SD	Mean	SD	t-test
Demographics
Age	20.7	1.6	21.0	10.3	P = 0.41(0.83)
Education	14.6	1.4	14.9	10.2	P = 0.33(0.98)
Verbal IQ (WTAR)	109.8	6.1	108.6	80.6	P = 0.47(0.71)
Alcohol (typical drinks/week)	18.6	13.7	18.2	130.8	P = 0.91(0.11)
Nicotine (typical cigarettes/day)	2.3	3.7	2.9	40.5	P = 0.87(0.15)a
Attention/hyperactivity (from SSAGA II)
ADHD attention Symptoms	1.4	2.5	0.5	00.99	P = 0.26(10.13)a
ADHD hyperactivity Symptoms	1.2	2.2	0.7	10.4	P = 0.56(0.59)a
Conduct symptoms	1.5	1.7	1.6	10.5	P = 0.86(0.17)
Personality/mood
BIS	66.8	9.6	64.5	9.0	P = 0.24(10.18)
SSS	25.0	4.9	24.7	4.7	P = 0.73(0.35)
BDI	1.7	1.7	3.4	3.9	P = 0.37(0.89)a
Lifetime drug uses (baseline)
Cocaine	26.2	40.6	22.3	46.2	P = 0.27(10.10)a
Prescription Stimulants	29.1	38.7	24.7	78.0	P = 0.03(20.22)a
Cannabis	784.9	1094.6	811.4	1158.1	P = 0.52(0.64)a
Interim drug uses (baseline − follow-up)
Cocaine	279.0	605.9	5.8	18.7	P < 0.001(50.06)a
Prescription stimulants	60.6	86.6	6.5	28.2	P < 0.001(70.20)a
Marijuana	580.9	924.7	762.9	1520.0	P = 0.54(00.62)a

Q = intelligence quotient; WTAR = Wechsler Test of Adult Reading; N/A = not applicable; BIS = Baratt Impulsiveness Scale; SSS = Sensation Seeking Scale; BDI = Beck Depression Inventory.

^at-test computed using natural log transformed + 0.01 values (due to non-normal distributions) replicated results for raw data. Bold indicates statistically significant values.

Behavioural performance

Reaction times and model-based behavioural adjustment

Consistent with our model’s assumptions (Shenoy and Yu, 2011; Shenoy et al., 2011; Ide et al., 2013), a positive linear relationship between Go reaction time and P(stop) was observed in all participants [B = 272 ms, t(84) = 4.9, P < 0.05, model omnibus test: χ²(1) = 21.8, P < 0.001; mean Pearson correlation coefficient: r = 0.13]. While PSU demonstrated a tendency for faster Go reaction time relative to DSU, the group main effect on Go reaction time was not statistically significant [χ²(1) = 1.3, P = 0.25; mean reaction time: PSU = 578 ms; DSU = 634 ms; see Fig. 2B for Go reaction time distributions]. We note that DSU and PSU also did not differ in their mean reaction times during the pre-scanning stop-signal task [PSU: mean reaction time = 617 ms; DSU: mean reaction time = 606 ms; t(86) = 0.3, P = 0.75]. The Group × P(stop) interaction was marginally significant [χ²(2) = 4.8, P = 0.09], showing a trend for smaller positive slope of reaction time slowing as a function of P(stop) in DSU who also had a wider Go reaction time range. A strong linear relationship between Go reaction time and P(stop) in both groups [PSU: B = 385, t(35) = 12.0, P < 0.001; χ²(1) = 110.4, P < 0.001; DSU: B = 187, t(48) = 6.2, P < 0.001; χ²(1) = 39.1, P < 0.001]. For illustration of the linear trends, Fig. 2D shows data collapsed across all subjects for PSU and DSU separately, where Go trials were binned by P(stop) and average reaction time calculated for each bin separately.

Finally PSU and DSU did not differ in Stop Signal Reaction Time [SSRT; mean PSU = 251 ms; mean DSU = 165 ms, t(86) = 1.4, P = 0.16; see Supplementary material for SSRT computation] or post-stop slowing [i.e. reaction time difference on trials following Go versus Stop trials; t(86) = 1.2, P = 0.24].

Performance accuracy

As expected, participants had a higher likelihood of error on trials with longer SSD [χ²(5) = 2161, P < 0.0001]. However, PSU and DSU did not differ in their average stop error rates [Group main effect: χ²(1) = 1.9, P = 0.17; mean error rates: PSU = 0.47; DSU = 0.41] and no significant group by SSD interaction was observed [χ²(5) = 5.31, P = 0.38; Fig. 2C]. Moreover, as predicted by our ideal observer model (Shenoy and Yu, 2011; Shenoy et al., 2011; Ide et al., 2013) and the observed reaction time adjustment, we found a negative relationship between error likelihood and P(stop), with higher P(stop) prompting a smaller likelihood of error [odds ratio = 0.23, Wald z = −2.34, P < 0.05; omnibus test: χ²(1) = 5.37, P < 0.05]. Neither main effect of group [χ²(1) = 1.3, P = 0.24] nor Group × P(stop) interaction [χ²(2) = 2.02, P = 0.37] reached statistical significance, suggesting PSU and DSU similarly utilized higher expectancy of a encountering a stop trial to slow down and minimize commission errors.

Overall, results are consistent with our previous work (Ide et al., 2013; Harlé et al., 2014) and suggest that both PSU and DSU maintain and update an internal estimate of stop trial probability, which they use to anticipate and modulate their inhibitory control performance with systematic consequences on Go reaction time and stop error rate. That is, by slowing down as the expectation of a stop trial increases, individuals can minimize the risk of a stop error (Shenoy and Yu, 2011).

Predictive analyses

After correction for multiple comparisons, whole-brain robust logistic regression analyses in the training sample identified a total 38 regions of interest in which task-based activation (at baseline) predicted 3-year follow-up status. These included 17 clusters associated with categorical non-Bayesian model inferred contrasts (eight for Stop-Go, nine for SE-SS) and 21 clusters associated with Bayesian computational contrasts of interest [three for P(stop), six for UPE, and 12 for SPE]. The predictive power of these regions of interest, as well as baseline drug use measures, was cross-validated in the test sample using random forest analyses.

Drug use model

The full model included baseline lifetime uses of cocaine, amphetamine, and marijuana (as reported in Table 1), as predictors of 3-year follow-up clinical status (PSU versus DSU). No variable met criteria for inclusion in the final model. The full model yielded an overall accuracy of 52%, which is not statistically significantly different from the no-predictor model based on response rate alone. Sensitivity was 48%, and specificity was 56%. The positive likelihood ratio of 1.08 (95% CI: 0.56, 2.08) and the negative likelihood ratio of 0.94 (95% CI: 0.54, 1.63) were not statistically different from each other and statistically different from 1.0 (P > 0.05; see Table 2).

Table 2.

Test characteristics of cross-validated predictive models

Model	Accuracy (%)	Sensitivity (%)	Specificity (%)	Positive LR (95% CI)	Negative LR (95% CI)
Drug usea	52	48	56	1.08 (0.56, 2.08)	0.94 (0.54, 1.63)
Neural – SST categorical	64	59	67	1.76 (0.88, 3.52)	0.62 (0.33, 1.17)
Neural – SST computational	74*	62	83	3.51 (1.34, 9.21)	0.47 (0.26, 0.87)

^aNo variable was retained for inclusion in a final predictive model, thus full model accuracy are reported.

*Statistically significant difference from response rate-based accuracy 57% (95% CI: 42–70%).

SST = stop signal task; LR = likelihood ratio.

Categorical neural predictors model

Predictors in the full model included activations extracted from 17 regions of interest identified with robust logistic regressions. One variable met criteria for inclusion in the final model: (SE-SS) activation in rostral ACC [Brodmann area (BA) 25; Centre of Gravity Talairach Coordinates (CoGTC): 2,19,−4]. However, the final model yielded an overall accuracy of 64%, which is not statistically significantly different from the no-predictor model based on response rate alone. Sensitivity and specificity for this final model were 59% and 67%, respectively. The positive likelihood ratio of 1.76 (95% CI: 0.88, 3.52) and the negative likelihood ratio of 0.62 (95% CI: 0.33, 1.17) were statistically different from each other (P < 0.05), but not statistically different from 1.0 (P > 0.05; see Table 2).

Bayesian computational neural predictors model

Predictors in the full model included activations extracted from 21 regions of interest identified with robust logistic regressions, including three regions of interest for trial type-independent P(stop) activation, six regions of interest associated with Bayesian UPE [UPE: outcome − P(stop)] activation, and 12 regions of interest associated with SPE [SPE: |outcome − P(stop)|] activation. Four variables met criteria for inclusion in the final model: UPE activation in right thalamus (CoGTC: 2,−11,2), as well as SPE activation in right anterior insula/inferior frontal gyrus (IFG; CoGTC: 28,16,−10), in a cluster overlapping right superior medial prefrontal cortex (PFC) (BA9) and dorsal ACC (BA32; CoGTC: 19,37,22), and in right caudate (BA25; CoGTC:1,7,1). The final model yielded an overall accuracy of 74%, which represents a statistically significant improvement in accuracy from the model based on response rate alone. Sensitivity and specificity for this final model were 62% and 83%, respectively. The positive likelihood ratio of 3.51 (95% CI: 1.34, 9.21) and the negative likelihood ratio of 0.47 (95% CI: 0.26, 0.87) were statistically different from each other and from 1.0, P < 0.05 (Table 2 and Supplementary Fig. 1). A random forest analysis on a ‘combined’ model including all drug use, neural categorical, and neural computational predictors produced the same set of five variables meeting criteria for inclusion in the final model (i.e. SS-SE activation in rostral ACC, UPE activation in thalamus and SPE activations in medial PFC/ACC, anterior insula, and caudate). This final model yielded an overall accuracy of 76% (sensitivity: 67%; specificity: 83%), which was significantly different from base response rate model (P < 0.05) but did not differ from the computational predictor model based on McNemar’s chi-squared test [χ²(1) = 2.0, P = 0.96]. In addition, the computational predictor model accuracy was significantly different from the drug use model [χ²(1) = 8.1, P < 0.01] and only at a trend level from the categorical predictor model [χ²(1) = 3.2, P = 0.07].

Among these four regions of interest, SPE activation in medial PFC/ACC had the strongest individual contribution to model accuracy (i.e. importance score = 6.8%), followed by SPE activations in caudate (importance score = 5.8%) and anterior insula/IFG (importance score = 5.7%), and UPE activation in right thalamus (importance score = 3.7%).

Predictor accuracy and cut points

Table 3 includes bootstrapped robust logistic regression coefficients and associated statistics for each cross-validated statistically significant predictor identified by the random forest (i.e. computational model). Coefficients were plotted as logistic functions along with accuracy measures and the estimated 0.50 probability cut point typically used for logistic regression models. Finally, to ease interpretation, group mean activations by group (DSU versus PSU) are also presented for these brain regions.

Table 3.

Bootstrapped robust regression coefficient estimates for predictive regions of interest

Predictors	B	SE	P-value	exp(B)	95% CI for exp(B)	Cut point*
Right thalamus (UPE)	1.24	0.35	0.001	3.45	1.74–6.86	0.26
Right medial PFC/ACC (SPE)	0.89	0.41	0.029	2.44	1.09–5.44	0.36
Right anterior insula (SPE)	1.16	0.45	0.009	3.19	1.32–7.71	0.17
Right caudate (SPE)	1.10	0.41	0.007	3.02	1.35–6.74	0.29

*z score; all predictors represent deactivations proportional to Bayesian prediction errors; UPE = unsigned prediction error [i.e. |outcome − P(stop)|]; SPE = signed prediction error [i.e. outcome − P(stop)].

For all four computational predictors, larger neural responses negatively correlated with Bayesian prediction errors were associated with a higher likelihood to be categorized in the PSU group 3 years later. Specifically, for every standardized unit increase in UPE deactivation in right thalamus, one was about three times as likely to develop a future stimulant use disorder [odds ratio = 3.45; χ²(1) = 5.5, P < 0.05] (Table 3 and Fig. 3A and B). As shown in Fig. 3C, while average activation associated with a negative UPE was significantly different from zero in PSU, such activation was close to zero in DSU. Similarly, an individual was two to three times as likely to be categorized in the PSU group for every standardized unit increase in SPE deactivation in medial PFC/ACC [odds ratio = 2.44; χ²(1) = 5.8, P < 0.05] (Table 3 and Fig. 4B), anterior insula/IFG [odds ratio = 3.19; χ²(1) = 6.2, P < 0.05] (Table 3 and Fig. 4A), and caudate [odds ratio = 3.02; χ²(1) = 5.5, P < 0.05] (Table 3 and Fig. 4C). As can be seen in Fig. 4D, activations associated with a negative SPE in these regions was significantly different from zero in PSU (P < 0.02), but not significantly different from zero in DSU (P > 0.05). The standardized cut points associated with a 50% probability of being classified as PSU versus DSU ranged from z = 0.17 to 0.36 (Table 3 and Figs 3 and 4). The respective receiver operating characteristic (ROC) curves associated with these individual models are presented in Fig. 5.

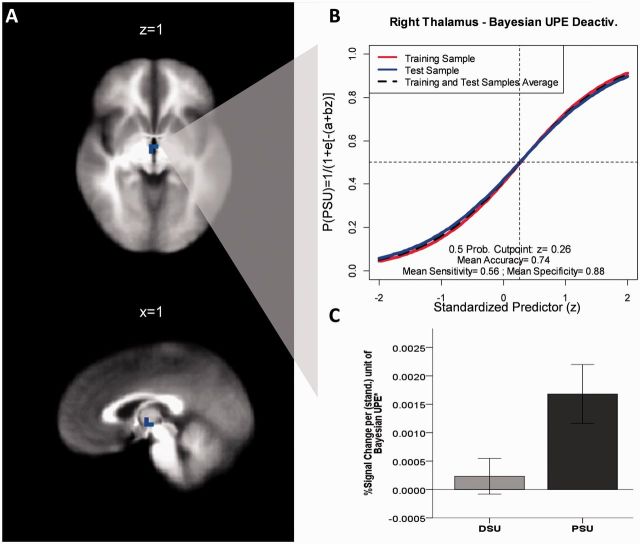
Figure 3.

Region of interest in which activation associated with a Bayesian UPE predicts 3-year clinical status (PSU versus DSU). (A) Activation in the right thalamus associated with a Bayesian UPE predicts 3-year clinical status (PSU versus DSU); (B) logistic regression curves representing long-term probability of developing stimulant abuse (PSU status) as a function of (standardized) UPE deactivation in the right thalamus; robust coefficients estimated in training (red) and test sample (green); 50–50% probability cut point and 10-fold cross-validated accuracy measures were estimated based on the test sample (green). (C) Average per cent signal change per standardized unit increase in UPE deactivation for each follow-up group (DSU: n = 50; PSU: n = 38; error bars = SEM).

Figure 4.

Regions of interest in which activation associated with a Bayesian SPE predicts 3-year clinical status (PSU versus DSU). Logistic regression curves representing long-term probability of developing stimulant abuse (PSU status) as a function of (standardized) SPE deactivation in the right anterior insula/inferior frontal gyrus (IFG) (A), the right medial prefrontal cortex (mPFC)/ACC) (B), and the right caudate (C); robust coefficients estimated in training (red) and test sample (green); 50–50% probability cut point and 10-fold cross-validated accuracy measures were estimated based on the test sample (green curves). (D) Average per cent signal change per standardized unit increase in SPE deactivation for each follow-up group (DSU: n = 50; PSU: n = 38; error bars = SEM). PSU had significantly greater SPE deactivations in the right medial PFC/ACC, t(41) = 2.1, P = 0.04, the right anterior insula, t(41) = 3.5, P = 0.001, and the caudate, t(41) = 3.0, P = 0.004. Moreover these deactivations were significantly different from 0 in PSU [medial PFC/ACC: t(18) = 2.6, P = 0.02; anterior insula: t(18) = 3.0, P = 0.008; caudate: t(18) = 3.1, P = 0.006], but not different from 0 in DSU [medial PFC/ACC: t(24) = 0.77, P = 0.45; anterior insula: t(24) = 1.6, P = 0.12; caudate: t(24) = 1.3, P = 0.20].

Figure 5.

Receiver operant characteristic curves for each of the main (computational) single predictor robust logistic regression models, representing the sensitivity (true positive rates) and specificity (true negative rates) associated with different predictor cut points.

Discussion

In this study we aimed to determine whether the combination of functional neuroimaging and computational approaches to behaviour are able to generate predictions that can help determine whether an individual will progress to problem use. We used a Bayesian ideal observer model to infer probabilistic expectations of inhibitory response in a stop-signal task among OSU collected at baseline. Cross-validated robust regression and random forest analyses showed that neural responses associated with Bayesian model-inferred prediction errors (representing the trial-wise discrepancy between expectation of a stop trial and actual trial outcome) in right ACC, anterior insula, caudate, and thalamus most robustly predicted 3-year clinical status (i.e. meeting criteria for stimulant use disorder versus desisted use status). These computational neural variables significantly contributed predictive validity above the base rate, which was not the case for other baseline predictors a priori thought to be promising, such as reported lifetime drug use or non-model based neural predictors. To our knowledge, this is the first study to apply a Bayesian cognitive model to event-related neural activity to predict long-term clinical outcome.

Greater correlation of neural activity with Bayesian model-inferred prediction errors was predictive of clinical outcome in four brain regions, including the anterior insula/IFG, medial PFC/ACC, caudate, and thalamus. Based on the evidence that PSU and DSU had similar trial-by-trial variability in reaction time and stop error rate relative to the Bayesian model-based P(stop) measures, different correlation coefficients associated with Bayesian prediction errors in these brain regions are unlikely to reflect differential adequacy of model fit between the two groups, but instead reflect differences in the underlying neural representation of processing strategies. Based on our results, it appears that those OSU who are more likely to develop stimulant abuse may already experience during their experimentation phase a stronger discrepancy between their internal model of what to expect and the actual outcomes.

The set of predictive regions identified in this study is congruent with this interpretation. Indeed, expectancy violation and prediction error signals have been consistently observed in the medial PFC, especially ACC (Somerville et al., 2006; Aarts and Roelofs, 2011; Kennerley et al., 2011), and insula (Murray et al., 2007; Preuschoff et al., 2008; d'Acremont et al., 2009; Bossaerts, 2010). Importantly, recent computational work has linked activation of both dorsal ACC (Behrens et al., 2007; Rushworth and Behrens, 2008) and anterior insula (Preuschoff et al., 2008; Singer et al., 2009; Bossaerts, 2010) to the coding of surprise and uncertainty in the environment (i.e. volatility). In addition, while ventral striatum (including ventral caudate as found here) has most often been implicated in reward learning, this region appears to encode prediction errors in a variety of learning paradigms (Menon et al., 2007; Delgado et al., 2008), and prediction error signals have also been observed in the thalamus (Ploghaus et al., 2000; Kim et al., 2006). Overall, our results suggest that a greater neural response proportional to prediction errors associated with the anticipated need to stop is associated with a higher likelihood of developing stimulant abuse or dependence 3 years later.

The hypothesis that PSU have exaggerated prediction error response and thus experience greater expectancy violation is also consistent with research suggesting neural alterations specific to trend detection and prediction in stimulant users (Aron and Paulus, 2007). These neural inefficiencies are linked to difficulties adapting to task-specific contexts and a tendency towards more stereotyped, automatic behaviour (e.g. more impulsivity and false alarms in inhibitory tasks) (Verdejo-Garcia et al., 2005; Aron and Paulus, 2007). In fact, it has been argued that persistent residual prediction errors and failure to learn may underlie the repetitive cycle of urges and maladaptive behavioural responses typically observed in addicts (Redish, 2004). Interestingly, most of our clinically predictive computational variables involved activation to signed prediction errors (observed in ACC, anterior insula, and caudate). Indeed because these signals include information on the direction of expectancy deviation, they may be particularly relevant to the selection of specific actions in the task (e.g. Go versus Stop). Thus, it is tempting to speculate that PSU may have difficulty updating stimulus-response contingencies to flexibly modulate their behaviour because of the neural processing deficits of prediction errors. As a consequence, these individuals may engage in a more rigid behavioural pattern that has also been observed in stimulant abusers. In support of this hypothesis, a recent study found that OSU, relative to healthy controls, exhibited persistent activation in the insula and striatum during a prediction task even after contingencies had been established (Stewart et al., 2013). Our previous finding that relative to healthy controls, OSU had weaker neural encoding of P(stop) and associated prediction errors may seem at odds with the present results. However, we note that such weaker signals were observed in different neural areas and were primarily associated with P(stop) and UPE encoding instead of SPE as found here. It is therefore not incompatible if OSU are less efficient in tracking the probability of stop trials [P(stop)] and its updating (UPE), that they should also experience greater discrepancy between their action expectations and actual signal, particularly at a lower level of processing (i.e. action preparedness). Thus, the altered ability to monitor and update the relationship between internal and external stimuli, and available responses, could prompt greater discrepancy between expected and actual events in individuals at high risk for developing stimulant abuse.

While we did not find evidence of significant task-related behavioural impairment in PSU relative to DSU at baseline, it is not necessarily incompatible with the presence of subtle deficits in the cognitive processes supporting action prediction at that time. At baseline, our sample of OSU was relatively high-functioning (i.e. attending school in a competitive university setting). It is likely that other compensatory cognitive mechanisms could have been implemented in those individuals. For instance, less efficient internal tracking of these stop response predictions (i.e. a more proactive type of cognitive control) may have been compensated by faster processing speed (including processing of auditory stop signals) and motor response (i.e. reactive cognitive control) (Aron, 2011; Braver, 2012). Such dissociation has been recently supported by evidence of flexible adjustments in cue-based recruitment of fronto-lateral regions (Braver et al., 2009). The present work suggests that a Bayesian modelling framework may be particularly useful in subclinical populations to discern more subtle levels of impairment not being captured by behavioural measures or coarser statistical modelling. We note, however, that the probability of encountering a stop trial in this experiment was fixed and independent of recent trial history, which limits our ability to test the predictive power of more complex belief updating mechanisms, such as the presence of statistical dependency and variability of the stop signal probability in the environment. Moreover, a limitation of this study is that, despite adequate group-level fit between behaviour (e.g. reaction times) and model inferred expectations [i.e. P(stop)], there was some variability in the degree of individual model fit, overall producing a relatively weak effect size (r = 0.13). This may be due in part to the fact that the DBM parameters were fitted based on a larger baseline sample of OSU (Harlé et al., 2014) and to the modest number of trials limiting the model in its ability to consider other systematic or random sources of reaction time variability. Future research applying this Bayesian model to more dynamically complex stop-signal designs (e.g. in which the underlying stimulus or trial outcome is probabilistically predictable, and/or wider range of stop-signal delay/difficulty) may be particularly valuable to investigate neural predictors of inhibitory behavioural dysfunction in substance abusers.

Conclusion

We showed that among young adults experimenting with stimulants, larger encoding of Bayesian prediction errors associated with inhibitory function in the insula, medial PFC/ACC, caudate, and thalamus predicts development of stimulant abuse versus abstinence 3 years later. Results are consistent with the notion that OSU vulnerable to developing a stimulant use disorder are less efficient in neurally representing when to ‘stop’ or ‘go’. Naturally, while our analytical approach is strengthened by the use of robust model fitting and bootstrapping (e.g. with random forest), replication of these results in other samples and environments is needed to demonstrate test–retest reliability. If robust to replication, these computational biomarkers may provide new avenues in the prevention of stimulant addiction.

Glossary

Abbreviations

ACC

anterior cingulate cortex

DSU

desisted stimulant users

OSU

occasional stimulant users

PFC

prefrontal cortex

PSU

problem stimulant users

SPE

signed prediction error

UPE

unsigned prediction error

Funding

This study was funded by the National Institute on Drug Abuse (NIDA) with grants R01 DA016663-01A1 (to M.P.P.) and F32DA036959 (to K.M.H.).

Supplementary material

Supplementary material is available at Brain online.