Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Jan 2;138(3):1010–1016. doi: 10.1021/jacs.5b12124

Solution Synthesis Approach to Colloidal Cesium Lead Halide Perovskite Nanoplatelets with Monolayer-Level Thickness Control

Quinten A Akkerman †,‡, Silvia Genaro Motti §,⊥, Ajay Ram Srimath Kandada §, Edoardo Mosconi #, Valerio D’Innocenzo §,⊥, Giovanni Bertoni †,∇, Sergio Marras †, Brett A Kamino ⊗, Laura Miranda ⊗, Filippo De Angelis ∥,#, Annamaria Petrozza §, Mirko Prato †,*, Liberato Manna †,*
PMCID: PMC4731826  PMID: 26726764

Abstract

graphic file with name ja-2015-12124d_0005.jpg

We report a colloidal synthesis approach to CsPbBr3 nanoplatelets (NPLs). The nucleation and growth of the platelets, which takes place at room temperature, is triggered by the injection of acetone in a mixture of precursors that would remain unreactive otherwise. The low growth temperature enables the control of the plate thickness, which can be precisely tuned from 3 to 5 monolayers. The strong two-dimensional confinement of the carriers at such small vertical sizes is responsible for a narrow PL, strong excitonic absorption, and a blue shift of the optical band gap by more than 0.47 eV compared to that of bulk CsPbBr3. We also show that the composition of the NPLs can be varied all the way to CsPbBr3 or CsPbI3 by anion exchange, with preservation of the size and shape of the starting particles. The blue fluorescent CsPbCl3 NPLs represent a new member of the scarcely populated group of blue-emitting colloidal nanocrystals. The exciton dynamics were found to be independent of the extent of 2D confinement in these platelets, and this was supported by band structure calculations.

Introduction

Ultrathin semiconductor nanosheets and nanoplatelets (NPLs) have recently come under intense scrutiny, in part due to the growing interest in two-dimensional (2D) systems triggered by research on graphene and related materials.1−4 In the time span of only a few years, a plethora of colloidal syntheses of 2D nanocrystals of various materials, including PbS, SnSe, Cu2-xS, ZrS2, MSe2 (M = Mo, W),5−9 and CdE (E = S, Se, Te),10−14 have been reported. Especially the cadmium chalcogenide platelets/sheets have received much attention due to the tight control over size and shape that could be achieved, so that their well-defined optical properties could be directly compared to those of spherical/rod-shaped CdE nanocrystals that have been studied so intensively in the previous years.15,16 Colloidal nanocrystals of lead halide-based perovskites represent the latest entries, with reliable synthesis approaches having appeared only in the past two years.17−22 These nanocrystals immediately gained huge interest due to their high quantum yields (up to 80%), their sharp emissions lines (0.12 eV line width), and the freshly discovered possibility to tune the halide composition, both during synthesis and by post-synthetic anion-exchange reactions.23−25 Furthermore, lead halide perovskite nanocrystals have already been shown capable of lasing and acting as quantum emitters.26−28

In comparison to the more mature case of inorganic semiconductors nanocrystals, the size and shape control of lead halide perovskite nanocrystals in the form of sheets/platelets is less advanced, with only a few papers dealing with this issue. Two works reported colloidal MAPbBr3 (MA = methylammonium) nanosheets with control over the sheet thickness,29,30 while in another work (C4H9NH3)2PbBr4 nanosheets were directly grown on a substrate and then detached from it.31 Yet, in order to directly correlate dimensionality with quantum confinement effects in sheets/platelets, colloidal synthesis approaches need to be refined in such a way as to reach control of the thickness down to a discrete number of monolayers, with differences in thickness from sample to sample at the level of a single monolayer. Such control would allow for disentangling quantum confinement from dielectric confinement effects. Also, colloidal free-standing particles are clear from spurious behaviors which are often overwhelming in perovskites grown on a substrate, due to their inherently deformable structure.31−33

Here, we report a synthesis approach to CsPbBr3 NPLs with precise thickness tunability in the range from 3 to 5 unit cells. This was made possible by devising a room-temperature synthesis scheme in which a mixture of chemical precursors remained unreactive unless acetone was injected into it, which initiated the nucleation and growth process. The low temperature at which the synthesis was carried out made shape control possible. Other solvents, in addition to acetone, were able to nucleate and grow the halide perovskite nanocrystals, although only acetone promoted the growth of platelets. At this small thickness, the CsPbBr3 NPLs emitted in the blue region of the spectrum, a region that is notoriously not well covered by many colloidal nanocrystal systems. Such level of control in platelet thickness could then be extended to the corresponding CsPbCl3 and CsPbI3 materials by means of anion exchange, which preserved the size and shape of the starting particles. The electronic and optical properties of the CsPbBr3 NPLs with thickness smaller than the estimated Bohr radius were compared to those of non-quantum-confined samples, the latter in the form of both polycrystalline thin films and cube-shaped nanocrystals with large edge sizes: the major conclusion from this comparison was that, while the magnitude of the band gap is clearly dependent on the extent of 2D confinement, the excitonic dynamics in lead halide perovskites is virtually independent of it (it was essentially the same in both NPLs and bulk samples) and is instead sensitive only to the presence of trap states. Both results are rationalized in terms of the DFT-calculated band structures of the investigated NPLs.

Experimental Section

Chemicals

Lead(II) bromide (PbBr2, 99.999% trace metals basis), cesium carbonate (Cs2CO3, reagentPlus, 99%), cesium bromide (CsBr, 99.9%), tetrabutylammonium chloride (TBACl, ≥97.0%), iodine (I2, 99.99%), hydrobromic acid (HBr, 48 wt% in H2O, ≥99.99%), 1-octadecene (ODE, technical grade, 90%), oleylamine (OLAM, 70%), oleic acid (OA, 90%), acetone (AcO, anhydrous, 99.8%), ethanol (EtOH, ≥99.8), 2-Propanol, (IsoP, anhydrous, 99.5%), dimethyl sulfoxide (DMSO, ACS reagent ≥99.9%), and N,N-dimethylformamide (DMF, anhydrous, 99.8%) were purchased from Sigma-Aldrich. Toluene (TOL, anhydrous, 99.8%) was bought from Carlo Erba reagents. All chemicals were used without any further purification.

Synthesis and Purification of CsPbBr3 NPLs

The CsPbBr3 NPLs were synthesized by an adaptation of the synthesis described by Schmidt et al.17 Here, the MA-Br precursor was replaced with a Cs-oleate precursor, as reported by Protesescu et al.,18 and only oleylamine and oleic acid were used as ligands. All syntheses were performed in air, at room temperature, and with unpurified/non-degassed chemicals (OA, ODE, OLAM, acetone, toluene). To a solution of 1.25 mL of ODE, 0.125 mL of OA, 0.125 mL of OLAM, a variable amount of HBr (in the 0–7.5 μL range), and 0.1 mL of Cs-OA precursor (0.1 M, 0.35 g of Cs2CO3 degassed in 20 mL of ODE and 1.25 mL of OA at 150 °C) was swiftly injected 0.2 mL of PbBr2 precursor (0.4 M, 735 mg PbBr2 in 5 mL of DMF). Within seconds, the solution turned turbid white, and after 10 s, 5 mL of acetone was swiftly added to quench the reaction (the solution turned turbid, and its color evolved slowly to green). The NPLs were precipitated by centrifugation at 3500 rpm for 5 min and then redispersed in toluene, resulting in a blue-emitting solution. The thickness of the NPLs could be controlled by tuning the amount of HBr in the mixture: the higher the amount, the thinner the NPLs.

Anion-Exchange Reactions

These were performed as described in our previous work,23 with the only difference being that all exchanges in the present experiments were carried out in air: 0.25 mL of crude CsPbBr3 NPL solution was dispersed in 1 mL of TOL, and different quantities of OLAM-I (0.5 mmol of I2 reacted with 0.250 mL of OLAM overnight and dissolved in 5.75 mL of TOL) or 0.17 M TBACl in TOL were swiftly injected.

Preparation of CsPbBr3 Thin Films

The solution for deposition was prepared by mixing 2.00 g of PbBr2 and 1.16 g of CsBr in 17.23 mL of anhydrous DMSO in an inert environment. The solution was heated at 100 °C for 16 h, or until it became optically clear. It was then filtered through a glass fiber syringe filter with an average pore size of 2 μm. Films were prepared on O2-plasma cleaned glass substrates (under inert atmosphere) and spun at 1000 rpm for 300 s. This procedure yielded clear yellow films, which were cured at 100 °C for 5 min in a forced-air convection oven under N2.

Transmission Electron Microscopy (TEM)

Conventional TEM images were acquired on a JEOL JEM-1011 microscope equipped with a thermionic gun at 100 kV accelerating voltage. High-resolution TEM (HRTEM) imaging was performed on a JEOL JEM-2200FS microscope equipped with a Schottky gun operated at an accelerating voltage of 80 kV, a CEOS spherical aberration corrector in objective lens enabling a spatial resolution of 0.9 Å, and an in-column Ω-filter. The chemical composition was determined by energy-dispersive X-ray spectroscopy (EDS) performed in high-angle annular dark-field scanning TEM (HAADF-STEM) mode with a 1.0 nm electron probe and a Bruker Quantax 400 system with a 60 mm2 XFlash 6T silicon drift detector, using the Cliff–Lorimer method for quantification of the elements. An analytical double-tilt holder equipped with a low-background beryllium tip was used in order to reduce spurious signal from the grid and holder. The samples were prepared by drop-casting diluted NPLs colloidal suspensions onto 200-mesh carbon-coated copper grids for conventional TEM imaging, and 400-mesh ultrathin carbon-coated copper grids for HRTEM imaging.

Powder X-ray Diffraction (XRD) Analysis

Accurate determination of the lattice parameter was carried out by measuring the samples on a Rigaku SmartLab X-ray diffractometer, equipped with a 9 kW Cu Kα rotating anode (operating at 40 kV and 150 mA) and D\teX Ultra 1D detector. The diffraction patterns were collected in Bragg–Brentano parafocusing geometry over a 2θ angular range of 10–100°, with a step size of 0.01°. XRD data analysis was performed using HighScore 4.1 software. The evolution of the NPLs sample after an annealing treatment at different temperatures was monitored using a PANalytical Empyrean X-ray diffractometer equipped with a 1.8 kW Cu Kα ceramic X-ray tube, PIXcel3D 2×2 area detector and operating at 45 kV and 40 mA. The diffraction patterns were collected in air at room temperature using parallel-beam geometry and symmetric reflection mode. All XRD samples were prepared by drop-casting a concentrated solution on a zero diffraction silicon wafer. The annealing was performed on drop-cast samples, heated on a hot plate in a glovebox.

Optical Absorption Spectroscopy

The spectra were taken on a Varian Cary 5000 UV–vis–NIR spectrophotometer. Samples were prepared by diluting the crude NPLs solutions in TOL (20 μL in 1 mL) in 1 cm path length quartz cuvettes.

Time-Resolved Photoluminescence (PL)

Time-resolved PL measurements were performed using a femtosecond laser source and a streak camera detection system (Hamamatsu C5680). The output of a tunable Ti:sapphire laser (Coherent Chameleon Ultra II, temporal and spectral bandwidths of ∼140 fs and ∼5 nm, respectively) was used to pump a second harmonic stage (based on BBO) to generate the pump pulses for the experiment. For the experiments with the thin films the pump wavelength was tuned to 400 nm, while for the colloidal suspensions of NPLs/nanocrystals it was tuned to 480 nm. The thin-film samples were mounted in a chamber under vacuum, and the colloidal samples were measured in toluene solution in quartz cuvettes. The PL was collected and focused onto a spectrometer coupled to the detection system and time-resolved with a linear voltage sweep module. The measurements were performed either using the original repetition rate of the laser output, 80 MHz, or at 4 MHz, obtained through the use of an acousto-optical modulating pulse picker (APE Pulse Select).

Photoluminescence Quantum Yield (PLQY)

A monochromatic laser diode centered at 405 nm was used as the pump, and it was coupled into an integrating sphere (Labsphere) where a quartz cuvette containing the sample was placed. The emitted light was then collected from the sphere with an optical fiber coupled to a spectrometer (Ocean Optics MAYA Pro 2000). PLQY was calculated according to the method described by de Mello et al.34 For evaluating the relative PLQY, the excitation was achieved using pulses of ∼100 fs duration and central wavelength of 400 nm at 250 kHz. The pulses were provided by a Ti:sapphire based regenerative amplifier (Coherent RegA 9000) operating at 250 kHz seeded by a mode-locked Ti:sapphire oscillator (Coherent Micra-18) operating at 80 MHz. The beam was focused onto a BBO crystal generating second harmonic at 400 nm and pulses of ∼100 fs duration. The PL was collected perpendicular to the excitation line and focused into a fiber coupled to a spectrometer (Ocean Optics Maya Pro 2000).

Computational Details

To simulate the CsPbBr3 perovskite NPLs, we defined a series of 2×2 periodic slabs cut from the optimized bulk cubic CsPbBr3 crystal structure, which expose CsBr-terminated surfaces. The thickness of the slabs was varied from 1 inner layer to 17 inner layers, plus two symmetric capping layers on both NPLs sides. The employed periodic cell dimensions were a = b = 11.802 Å, corresponding to twice the experimental a = b cell parameters.35 For all slabs we added ∼10 Å of vacuum along the nonperiodic c direction. The choice of using periodic slabs is justified by the large lateral dimensions of the NPLs compared to their vertical size. To lift out the possible effects due to relaxation of the smaller slabs, we built all slabs using the geometry optimized for the bulk system. All the calculations were carried out with the PWscf code, as implemented in the Quantum Espresso package along with the GGA-PBE functional at Γ point of the Brillouin zone.36,37 For all calculations, electron–ion interactions were described by ultrasoft pseudopotentials with electrons from Cs 6s; Br 4s, 4p; Pb 6s, 6p, 5d shells explicitly included in the calculations. Both scalar relativistic and spin–orbit coupling calculations were performed. Plane-wave basis set cutoffs for the smooth part of the wave functions and the augmented density were 25 and 200 Ry, respectively.

Results and Discussion

The synthesis of the CsPbBr3 NPLs, differently from previous reports, was carried out at room temperature starting from a mixture of Cs oleate, oleylamine, oleic acid, PbBr2 and HBr that remained stable unless an additional component was added to it. PL spectra of this “precursor” solution, taken in rapid succession (every 2 s, see Figure SI1A in the Supporting Information), evidenced the steady presence of a broad peak centered at around 3.2 eV that originates from the surfactants present in the flask (see Figure SI1B) and is not due to the formation of small CsPbBr3 clusters. Then, as soon as acetone was added to the precursor mixture, a narrower peak appeared at around 2.95 eV. Within seconds, this peak further red-shifted and narrowed (indicating the nucleation and growth of CsPbBr3 NPLs), and finally settled to an energy value that depended on the amount of HBr added (for example 2.83 eV, for a 7.5 μL addition of HBr, see Figure SI1B). It is likely that acetone destabilizes the complexes of Cs+ and Pb2+ ions with the various molecules in solution and therefore sets the trigger for the nucleation of the particles. This was further confirmed by a set of experiments in which different time lags between injections of the Pb precursor and acetone were tested, but all yielded NPLs with the same morphological and optical features (Figure SI2). We tested other polar solvents, for example, protic solvents like isopropanol and ethanol, but they were not as effective as acetone in shape control (Figure SI3A). The addition of ethanol, for example, led to the quick formation of large particles (20–40 nm in size, see Figure SI3B), most likely due to excessive destabilization of the initial metal complexes.

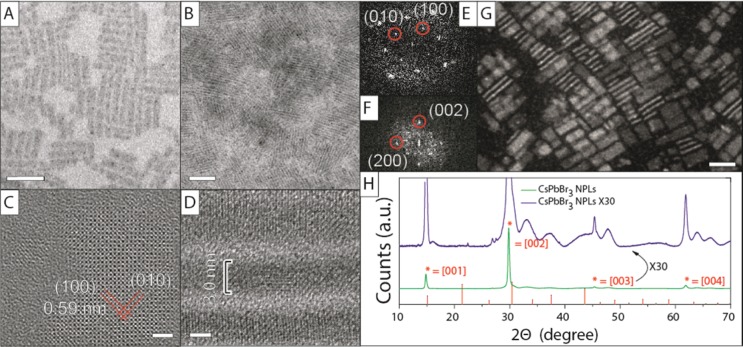
TEM and HRTEM images of a typical sample of CsPbBr3 NPLs synthesized with our approach are reported in Figure 1A–D. In grids prepared from diluted samples, the NPLs were lying flat with respect to the substrate (Figure 1A,C), whereas samples deposited from concentrated solutions were characterized by stacks of face-to-face aligned NPLs, with the particles often oriented perpendicularly with respect to the carbon support film (see Figure 1B,D). This latter arrangement enabled a precise estimation of the NPL thickness. In this specific sample obtained without HBr in the precursor solution, the NPLs had a thickness of 3.0 ± 0.4 nm (corresponding to 5 unit cells) and average lateral dimensions of 7.9 ± 1.2 nm × 40.9 ± 6.8 nm. During the exposure of the CsPbBr3 NPLs to the electron beam, metallic lead particles were formed (Figures 1A and SI4), as revealed by combined HRTEM and compositional analysis. This electron-beam-induced transformation of the sample is consistent with what already reported for large MAPbBr3 sheets.29 The platelet morphology is particularly evident from dark-field TEM analysis (Figure 1G), in which NPLs either lying flat or edge-on with respect to the support film could be seen.

Figure 1.

Figure 1

Open in a new tab

Structural analysis of CsPbBr3 NPLs emitting at 460 nm. TEM images of CsPbBr3 NPLs at (A) low concentrations and (B) high concentrations. HRTEM images of NPLs (C) in top view and (D) in stacks as well as their respective Fourier transform patterns (E,F). (G) STEM dark-field image of NPLs. (H) XRD pattern of CsPbBr3 NPLs. Reference pattern of cubic CsPbBr3, ICSD 29073. Scale bars correspond to 50 nm in A and B, 2 nm in C and D, and 20 nm in G.

XRD analysis was carried out on the platelets. At low angles, a series of diffraction peaks originating from the stacked superstructure of the NPLs were observed (see Figure SI5). The interplanar spacing of 5.1 nm corresponding to these peaks is in good agreement with the thickness of the NPLs (3.0 nm) plus 2 layers of passivating organic ligands (oleylamine/oleic acid, about 1.0 nm per layer). A conventional pattern collected on CsPbBr3 NPLs is instead reported in Figure 1H. Due to the anisotropic shape of the NPLs, the [0 0 l] (l = 1, 2, 3, 4, ...) planes parallel to the lateral dimensions exhibited narrow peaks, with a high intensity (Figure 1H, green line). The other peaks, which are related to families of planes that are actually reduced only to a few unit cells, were also present but were much broader and less intense (Figure 1H, zoom in, purple line). Also, the peaks were shifted toward lower 2θ angles with respect to those of the reported diffraction pattern of cubic CsPbBr3. Using the most intense [002] diffraction peak and considering a cubic cell, a unit cell size of 0.599 nm was calculated, which is larger than the bulk cubic CsPbBr3 cell (0.587 nm) by 0.012 nm. A possible explanation from this deviation in cell size is due to passivation of top and bottom facets of the cell by protonated oleylamine ligands, which locally would effectively mimic an alkyl ammonium lead halide type of cell. This is also in line with the Cs:Pb:Br ratios equal to 0.59:1.00:2.95 measured by elemental analysis (via STEM-EDS), which indicate a substantial cesium deficiency in the NPLs. Therefore, it is likely that Cs+ ions of the top and bottom facets are mostly replaced by oleyl ammonium ions, and this can slightly expand the overall lattice, given the extremely small thickness of the platelets. XRD patterns collected on samples heated at increasing temperatures gave peak positions that were closer to that of the bulk pattern (already at 50 °C, with an almost perfect match at 150 °C, see Figure SI6). As the intensity ratios too were closer to those of the bulk, we conclude that annealing caused partial sintering of the NPLs, with consequent desorption of part of the ligands and overall reorganization of the lattice that gets more in line with that of bulk CsPbBr3 than the initial NPLs. Also, it is interesting to note that the unit cell parameters estimated by HRTEM analysis (performed at 80 kV to minimize electron beam damage) were similar to those of the bulk, with an estimated lattice parameter around 0.59 ± 0.02 nm (Figure 1C,D). It is likely that the electron beam irradiation on these platelets has an effect similar to that observed by annealing films of NPLs.

The thickness of the NPLs was precisely controlled by dosing the amount of added HBr during the synthesis, from a minimum value of 3 monolayers (ML) when adding 7.5 μL of HBr, up to 5 ML in the absence of HBr. TEM analysis showed indeed that the NPLs thickness decreased from 3.0 nm for the 5 ML sample to 2.5 and 1.8 nm respectively for the 4 and 3 ML samples, as shown in Figures 2D,E, SI7, and SI8. Furthermore, as shown in Figure SI9, for the example of the 3 ML sample, the thinner NPLs retained the crystallinity and the lattice parameters of the 5 ML sample. Such level of control may be explained considering that the increased acidity of the solution due to the addition of HBr aids in the protonation of oleylamine, as also reported by Yuan et al.38 The protonated oleylamine can compete with Cs+ ions on the surface of the growing platelets, essentially slowing down the growth in the vertical dimension. This view is also in line with what recently observed on MAPbBr3 NPLs,29 where the thickness control was achieved by tuning the acidity of the reaction mixture by changing the concentration of OA.

Figure 2.

Figure 2

Open in a new tab

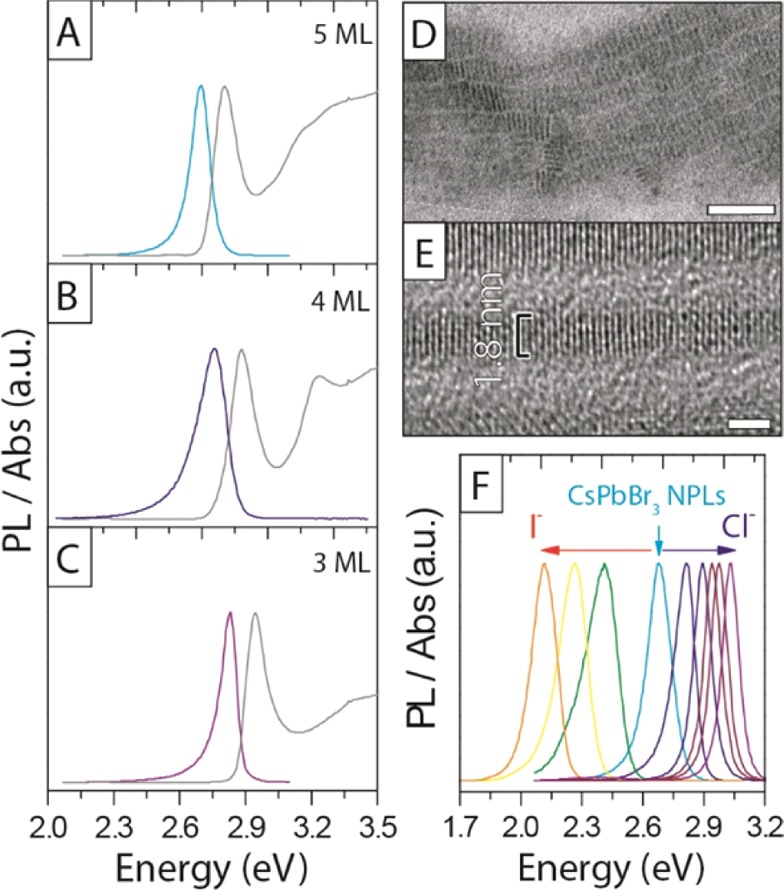
Optical and structural properties of different thicknesses of CsPbBr3 NPLs and the exchanged CsPbCl3 and CsPbI3 NPLs. (A–C) Three different thicknesses, with (A) 5 ML emitting at 2.70 eV, Stoke shift (Ss) = 0.11 eV, and fwhm = 0.11 eV; (B) 4 ML emitting at 2.76 eV, Ss = 0.12 eV, and fwhm = 0.17 eV; and (C) 3 ML emitting at 2.83 eV, Ss = 0.11 eV, and fwhm = 0.09 eV. (D,E) TEM and HRTEM image of 3 ML thick sample indicated a thickness of 1.8 nm. (F) Fine-tuning the PL of CsPbBr3 NPLs with anion-exchange reactions to CsPbCl3 and CsPbI3. Scale bar corresponds to 50 nm in D, and 2 nm in E.

The optical bandgap was remarkably sensitive to the number of layers in this 3–5 ML regime, as shown in Figure 2A–C, with a blue shift and strengthening of the excitonic transition for thinner sheets as a result of confinement effects. Although the PLQY of the 5 ML NPLs dropped to 31% from the 78% value of the cube-shaped CsPbBr3 nanocrystals,23 the yield was still comparable to that of CsPb(Br:Cl)3 nanocrystals prepared by anion exchange (as reported in our previous work) and emitting at the same energy (PLQY at 2.75 eV = 37%).23 The stability of the NPLs was related to the number of layers: the 4 ML sample, emitting at 2.75 eV, was only stable for a day, and quickly formed a 2.70 eV 5 ML emitting sample, whereas the 3 and 5 ML samples were stable for at least one month, with only the appearance of a secondary emission peak at 2.36 eV, as well as a sedimentation of a green/yellow precipitate, indicating the formation of larger nonquantum confined CsPbBr3 aggregates (see Figure SI10). The reasons for this peculiar trend in stability are presently unclear. Due to the instability of the 4 ML NPLs, as reported above, no reliable HRTEM and XRD data could be recorded for that sample.

As it was shown for cube-shaped CsPbBr3 nanocrystals,23,24 also in the present case the Br– anions in the NPLs could be easily replaced with Cl– and I– anions, delivering NPLs that were progressively richer in Cl– or in I–, as shown in Figure 2F. Here, the absorption could be finely tuned by the addition of Cl– and I– complexes (Figure SI11). As calculated by Protesescu et al.,18 the exciton Bohr radius is related to the halide composition, being 2.5 nm for CsPbCl3, 3.5 nm for CsPbBr3, and 6 nm for CsPbI3. This can also be observed for the three different samples of NPLs with different halide compositions. While the emission of the 5 ML CsPbBr3 NPLs had blue-shifted by 0.34 eV relative to the bulk (2.36 eV), the CsPbI3 NPLs prepared by anion exchange, and thus with the same thickness as the starting CsPbBr3 NPLs (apart from a variation due to the changed lattice parameter), exhibited a more pronounced confinement effect: the emission was blue-shifted by 0.36 eV compared to its bulk value of 1.77 eV. On the other hand, the emission from the CsPbCl3 NPLs was blue-shifted by only 0.08 eV from its bulk value (2.96 eV), which is in line with the smaller Bohr radius of the CsPbCl3 perovskite.

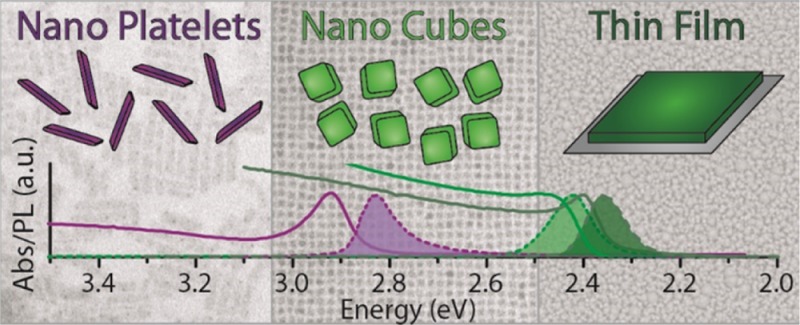
In Figure 3A we compare the absorption and emission spectra of Br-based NPLs of different thicknesses with those recorded from colloidal cube-shaped CsPbBr3 nanocrystals (as reported in our previous work, also see Figure SI12)23 and from polycrystalline thin film prepared by direct crystallization of the precursors on a glass substrate (see Experimental Section). The thin film was made of crystallites with sizes ranging within hundreds of nanometers (see Figure SI13), the cube-shaped nanocrystals had a dimension of about 8.5 nm. The cubes and the polycrystalline thin film exhibited very similar optical edges. The absence of any remarkable differences in both the absorption and emission spectra of the two samples suggests that the 8.5 nm cube-shaped particles presented only weak quantum confinement effects. This is in agreement with the fact that the exciton Bohr radius of CsPbBr3 is around 3.5 nm, as discussed earlier.18 The NPLs on the other hand, with their thickness of 3 nm or below, did experience a blue shift of the optical edge.

Figure 3.

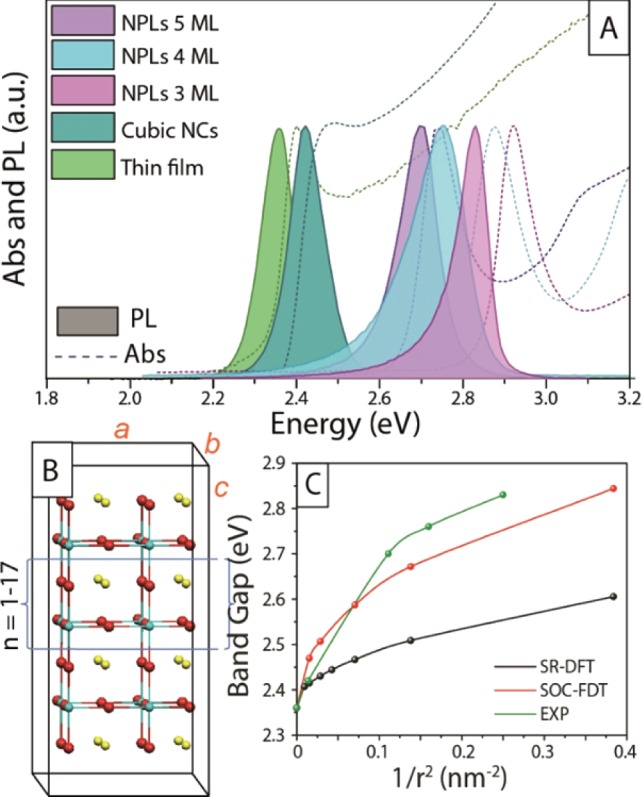
Figure 3

Open in a new tab

(A) Absorption and PL spectra of CsPbBr3 as a thin film (see Figure SI13), cube-shaped nanocrystals, and NPLs of different thicknesses. (B) Employed cubic CsPbBr3 2D slabs and unit supercell. a–b are the periodic dimensions. (C) Comparison of the experimental (green line) and SR- and SOC-DFT calculated band gaps (black line and red line, respectively) as a function of the NPLs inverse squared dimension (1/r2).

To further investigate the electronic properties of the synthesized NPLs we carried out DFT calculations on 2D periodic slabs of cubic CsPbBr3 of increasing dimensions, up to ca. 11 nm along the nonperiodic direction, see Figure 3B. DFT calculations were performed by including relativistic effects at both the scalar relativistic (SR) and spin–orbit coupling (SOC) levels. It was previously shown that SOC plays a central role in determining the electronic properties of organohalide lead perovskites.39,40 Though SOC-DFT was found to considerably underestimate the band gap of these semiconductors, with more elaborate SOC-GW calculations delivering an improved agreement, the two methods provide qualitatively similar band gap trends.41,42

Here we thus limited the level of theory to SOC-DFT since GW calculations are impracticable even on the smallest considered slab. We report the evolution of the experimental (from PL measurements) and calculated band gap in Figure 3C. SR- and SOC-DFT results have been scaled so that the bulk band gap matches the experimental 2.36 eV value. Due to the use of a 2×2 unit cell, the cubic bulk CsPbBr3 phase shows a direct band gap at the Γ point (instead than R) of the Brilluoin zone. As it can be noticed, our SOC-DFT calculations nicely reproduce the experimental band gap evolution, showing a nonlinear (approximately square-root-like) trend with 1/r2 (r being the NPLs dimension along the aperiodic c direction). SR-DFT results deliver a significantly different picture, confirming the importance of SOC effects not only in determining the electronic and optical properties of bulk organohalide lead perovskites but also in defining their quantum confinement behavior. According to the effective mass model, by plotting the band gap vs 1/r2 one should obtain a straight line. This was verified for CsPbBr3 quantum dots by Protesescu et al.18 In practice, deviations from this ideal behavior are found in ultrasmall quantum wells, like the NPLs investigated here, due to tunneling of the electron/hole wave functions outside the well boundaries, i.e., due to the lack of effectively infinite potential barriers at the NPLs border. This is precisely the case of the NPLs synthesized here, for which an almost linear behavior is found for the larger systems (down to 5 ML, ca. 3 nm, corresponding to ca. 0.1 in the scale of Figure 3C), with a significant deviation found for smaller dimensions, similar to what reported by Sichert et al.29 A variation of the dielectric properties of CsPbX3 NPLs with quantum confinement was also recently reported by Sapori et al.,43 indicating a decrease of the dielectric constant with reduced NPLs thickness.

Figure 4A reports the PL dynamics from the cube-shaped 8.5 nm nanocrystals and from the NPLs at different excitation densities. The decays were purely monoexponential and intensity independent. A monomolecular decay may be the result either of exciton decay or of carrier trapping at defects sites. The latter can be easily discarded by looking at the relative PLQY as a function of the excitation intensity, reported in Figures 4B and SI14. The PLQY is intensity independent, especially at low excitation densities (right side of the plot). This trend is not compatible with a trap-limited process, which would instead exhibit an increase of PLQY with intensity due to trap-filling (Figure SI13B and Note SI1).32 Note that bulk films of CsPbBr3, which should have a greater number of traps and thus more nonradiative losses than the ligand-passivated NPLs, are characterized by shorter PL lifetimes at low excitation densities, which we ascribe to trap induced quenching. At higher excitation densities the traps are filled, and thus their role in the excitation dynamics is reduced, and indeed the PL lifetimes increases. We can therefore conclude that in our CsPbBr3 NPLs the intensity-independent monomolecular lifetimes, along with high PLQY, are the fingerprint of a pure excitonic decay, with minimal nonradiative losses in the system. The PL dynamics is generally very sensitive to confinement effects. Greater overlap of electron and hole wave functions should lead to a larger recombination rate, thus to a reduction of the PL lifetimes.44,45 However, the behavior of NPLs did not differ much from that of cube-shaped nanocrystals. As shown in Figure 4A, in the NPLs (5 ML) a monomolecular decay with lifetime of about 3 ns (4 ns for the cube-shaped nanocrystals) could be estimated, which is intensity independent within an excitation range between 1 and 100 nJ/cm2. The 3 ML NPLs exhibited very similar lifetimes, as shown in Figure SI15.

Figure 4.

Figure 4

Open in a new tab

(A) PL dynamics of cube-shaped nanocrystals (t = 4 ns) and NPLs (t = 3 ns). (B) Relative PLQY of 5 ML NPLs.

To qualitatively explain the observed trends in lifetimes, we calculated the effective electron and hole masses for the investigated series of NPLs and for the bulk CsPbBr3 by SOC-DFT. This was done by parabolic band fitting along the Γ → M direction of cubic the Brilluoin zone. Notice that, due to the employed cubic symmetry, no Rashba–Dresselhaus k-dependent band splitting was observed in our SOC-DFT band structures.40,42 The calculated effective masses along with the corresponding exciton reduced masses, memh/(me + mh), are reported in Table 1. As expected, the calculated effective masses and the exciton reduced mass both increase with quantum confinement, with the carriers effective masses remaining very close to each other along the series, suggesting almost perfect ambipolar transport in CsPbBr3. The calculated reduced mass for the bulk (∼0.09) is consistent with available experimental estimates (0.12–0.13),46 although our value is likely underestimated, as SOC-DFT tends to underestimate the band gap. According to the Kane model,47 the interband oscillator strength is f0 ≈ m0/me, meaning the exciton oscillator strength decreases with increasing me. The exciton lifetime is inversely proportional to the radiative rate constant (kr), τ ∼ 1/kr, which is equal to the oscillator strength times the square of the emitted energy (Eg), kr ∝ Eg2f0, thus τ ∝ 1/(Eg2f0). Based on the SOC-DFT calculated quantities (with Eg scaled to match the experimental bulk value), we estimate a comparable kr for the n = 1 and n = ∞ systems, in line with the similar values of measured PL lifetimes values.

Table 1. SOC-DFT Calculated Band Gap (Eg) Electron/Hole Effective Masses and Reduced Masses, in Units of m0, Where m0 Is the Electron Mass.

n Ega (eV) mh/m0 me/m0 μ/m0
1 2.84 0.246 0.242 0.122
3 2.67 0.224 0.226 0.112
5 2.59 0.211 0.215 0.107
11 2.51 0.198 0.202 0.100
15 2.47 0.191 0.195 0.096
∞ 2.36 0.172 0.171 0.086
Open in a new tab
a

The calculated band gap values were rescaled by 2.09 eV to match the measured PL band gap for the bulk.

In summary, we have demonstrated a fast and easy synthesis method that delivers CsPbBr3 NPLs with the control over the thickness down to only 3–5 monolayers. While the optical bandgap of the 2D semiconductor was strongly sensitive to confinement effects, the emissive dynamics were insensitive to confinement, suggesting fascinating properties of such excitonic system. Furthermore, the Br– anions could be replaced with Cl– or I– anions, thereby extending shape control also to CsPbCl3 and CsPbI3 NPLs.

Acknowledgments

The research leading to these results has received funding from the European Union 7th Framework Programme under Grant Agreement No. 614897 (ERC Consolidator Grant “TRANS-NANO”) and No. 316494 (Destiny Marie Curie Network) and from Fondazione Cariplo (project GREENS No. 2013-0656). We thank Ilaria Bargigia for her help with the PL measurements. E.M. thanks the European Union 7th Framework Programme (FP7/2007%2013) under Grant Agreement No. 604032 of the MESO project. S.G.M. thanks the CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico - Brasil) for the scholarship [206502/2014-1].

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.5b12124.

  • Figures SI1–S15, showing PL and Abs measurements on precursor solutions, TEM image of nanocrystals prepared with EtOH additions, analysis of Pb dots formed under electron beam radiation, low-angle XRD pattern, XRD patterns of annealed CsPbBr3 NPLs, PL and Abs of NPLs after 1 week, PL and Abs of anion-exchanged NPLs, TEM images of 8.4 nm cube-shaped CsPbBr3 nanocrystals, SEM image and intensity-dependent PL dynamics of CsPbBr3 thin film, and relative PLQY upon dilution of NPLs, and Note S1 on excitation density (PDF)

The authors declare no competing financial interest.

During the review of our paper, a similar paper was published by Bekenstein et al.48

Supplementary Material

ja5b12124_si_001.pdf (3.3MB, pdf)

References

  1. Xu M.; Liang T.; Shi M.; Chen H. Chem. Rev. 2013, 113, 3766–3798. 10.1021/cr300263a. [DOI] [PubMed] [Google Scholar]
  2. Rao C. N. R.; Ramakrishna Matte H. S. S.; Maitra U. Angew. Chem., Int. Ed. 2013, 52, 13162–13185. 10.1002/anie.201301548. [DOI] [PubMed] [Google Scholar]
  3. Huang X.; Tan C.; Yin Z.; Zhang H. Adv. Mater. 2014, 26, 2185–2204. 10.1002/adma.201304964. [DOI] [PubMed] [Google Scholar]
  4. Butler S. Z.; Hollen S. M.; Cao L.; Cui Y.; Gupta J. A.; Gutiérrez H. R.; Heinz T. F.; Hong S. S.; Huang J.; Ismach A. F.; Johnston-Halperin E.; Kuno M.; Plashnitsa V. V.; Robinson R. D.; Ruoff R. S.; Salahuddin S.; Shan J.; Shi L.; Spencer M. G.; Terrones M.; Windl W.; Goldberger J. E. ACS Nano 2013, 7, 2898–2926. 10.1021/nn400280c. [DOI] [PubMed] [Google Scholar]
  5. Vaughn D. D.; In S.-I.; Schaak R. E. ACS Nano 2011, 5, 8852–8860. 10.1021/nn203009v. [DOI] [PubMed] [Google Scholar]
  6. Schliehe C.; Juarez B. H.; Pelletier M.; Jander S.; Greshnykh D.; Nagel M.; Meyer A.; Foerster S.; Kornowski A.; Klinke C.; Weller H. Science 2010, 329, 550–553. 10.1126/science.1188035. [DOI] [PubMed] [Google Scholar]
  7. van der Stam W.; Akkerman Q. A.; Ke X.; van Huis M. A.; Bals S.; de Mello Donega C. Chem. Mater. 2015, 27, 283–291. 10.1021/cm503929q. [DOI] [Google Scholar]
  8. Yoo D.; Kim M.; Jeong S.; Han J.; Cheon J. J. Am. Chem. Soc. 2014, 136, 14670–14673. 10.1021/ja5079943. [DOI] [PubMed] [Google Scholar]
  9. Jung W.; Lee S.; Yoo D.; Jeong S.; Miró P.; Kuc A.; Heine T.; Cheon J. J. Am. Chem. Soc. 2015, 137, 7266–7269. 10.1021/jacs.5b02772. [DOI] [PubMed] [Google Scholar]
  10. Grim J. Q.; Christodoulou S.; Di Stasio F.; Krahne R.; Cingolani R.; Manna L.; Moreels I. Nat. Nanotechnol. 2014, 9, 891–895. 10.1038/nnano.2014.213. [DOI] [PubMed] [Google Scholar]
  11. Ithurria S.; Tessier M. D.; Mahler B.; Lobo R. P. S. M.; Dubertret B.; Efros A. L. Nat. Mater. 2011, 10, 936–941. 10.1038/nmat3145. [DOI] [PubMed] [Google Scholar]
  12. Ithurria S.; Dubertret B. J. Am. Chem. Soc. 2008, 130, 16504–16505. 10.1021/ja807724e. [DOI] [PubMed] [Google Scholar]
  13. Pedetti S.; Ithurria S.; Heuclin H.; Patriarche G.; Dubertret B. J. Am. Chem. Soc. 2014, 136, 16430–16438. 10.1021/ja509307m. [DOI] [PubMed] [Google Scholar]
  14. Mahler B.; Nadal B.; Bouet C.; Patriarche G.; Dubertret B. J. Am. Chem. Soc. 2012, 134, 18591–18598. 10.1021/ja307944d. [DOI] [PubMed] [Google Scholar]
  15. Lhuillier E.; Pedetti S.; Ithurria S.; Nadal B.; Heuclin H.; Dubertret B. Acc. Chem. Res. 2015, 48, 22–30. 10.1021/ar500326c. [DOI] [PubMed] [Google Scholar]
  16. Wang F.; Wang Y.; Liu Y.-H.; Morrison P. J.; Loomis R. A.; Buhro W. E. Acc. Chem. Res. 2015, 48, 13–21. 10.1021/ar500286j. [DOI] [PubMed] [Google Scholar]
  17. Schmidt L. C.; Pertegás A.; González-Carrero S.; Malinkiewicz O.; Agouram S.; Mínguez Espallargas G.; Bolink H. J.; Galian R. E.; Pérez-Prieto J. J. Am. Chem. Soc. 2014, 136, 850–853. 10.1021/ja4109209. [DOI] [PubMed] [Google Scholar]
  18. Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Krieg F.; Caputo R.; Hendon C. H.; Yang R. X.; Walsh A.; Kovalenko M. V. Nano Lett. 2015, 15, 3692–3696. 10.1021/nl5048779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Aygüler M. F.; Weber M. D.; Puscher B. M. D.; Medina D. D.; Docampo P.; Costa R. D. J. Phys. Chem. C 2015, 119, 12047–12054. 10.1021/acs.jpcc.5b02959. [DOI] [Google Scholar]
  20. Zhang F.; Zhong H.; Chen C.; Wu X.-g.; Hu X.; Huang H.; Han J.; Zou B.; Dong Y. ACS Nano 2015, 9, 4533–4542. 10.1021/acsnano.5b01154. [DOI] [PubMed] [Google Scholar]
  21. Huang H.; Susha A. S.; Kershaw S. V.; Hung T. F.; Rogach A. L. Adv. Sci. 2015, 2, 1500194. 10.1002/advs.201500194. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Zhu F.; Men L.; Guo Y.; Zhu Q.; Bhattacharjee U.; Goodwin P. M.; Petrich J. W.; Smith E. A.; Vela J. ACS Nano 2015, 9, 2948–2959. 10.1021/nn507020s. [DOI] [PubMed] [Google Scholar]
  23. Akkerman Q. A.; D’Innocenzo V.; Accornero S.; Scarpellini A.; Petrozza A.; Prato M.; Manna L. J. Am. Chem. Soc. 2015, 137, 10276–10281. 10.1021/jacs.5b05602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Nedelcu G.; Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Grotevent M. J.; Kovalenko M. V. Nano Lett. 2015, 15, 5635–5640. 10.1021/acs.nanolett.5b02404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jang D. M.; Park K.; Kim D. H.; Park J.; Shojaei F.; Kang H. S.; Ahn J.-P.; Lee J. W.; Song J. K. Nano Lett. 2015, 15, 5191–5199. 10.1021/acs.nanolett.5b01430. [DOI] [PubMed] [Google Scholar]
  26. Park Y.-S.; Guo S.; Makarov N. S.; Klimov V. I. ACS Nano 2015, 9, 10386–10393. 10.1021/acsnano.5b04584. [DOI] [PubMed] [Google Scholar]
  27. Yakunin S.; Protesescu L.; Krieg F.; Bodnarchuk M. I.; Nedelcu G.; Humer M.; De Luca G.; Fiebig M.; Heiss W.; Kovalenko M. V. Nat. Commun. 2015, 6, 8056. 10.1038/ncomms9056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hu F.; Zhang H.; Sun C.; Yin C.; Lv B.; Zhang C.; Yu W. W.; Wang X.; Zhang Y.; Xiao M. ACS Nano 2015, 9, 12410–12416. 10.1021/acsnano.5b05769. [DOI] [PubMed] [Google Scholar]
  29. Sichert J. A.; Tong Y.; Mutz N.; Vollmer M.; Fischer S.; Milowska K. Z.; García Cortadella R.; Nickel B.; Cardenas-Daw C.; Stolarczyk J. K.; Urban A. S.; Feldmann J. Nano Lett. 2015, 15, 6521–6527. 10.1021/acs.nanolett.5b02985. [DOI] [PubMed] [Google Scholar]
  30. Tyagi P.; Arveson S. M.; Tisdale W. A. J. Phys. Chem. Lett. 2015, 6, 1911–1916. 10.1021/acs.jpclett.5b00664. [DOI] [PubMed] [Google Scholar]
  31. Dou L.; Wong A. B.; Yu Y.; Lai M.; Kornienko N.; Eaton S. W.; Fu A.; Bischak C. G.; Ma J.; Ding T.; Ginsberg N. S.; Wang L.-W.; Alivisatos A. P.; Yang P. Science 2015, 349, 1518–1521. 10.1126/science.aac7660. [DOI] [PubMed] [Google Scholar]
  32. D’Innocenzo V.; Srimath Kandada A. R.; De Bastiani M.; Gandini M.; Petrozza A. J. Am. Chem. Soc. 2014, 136, 17730–17733. 10.1021/ja511198f. [DOI] [PubMed] [Google Scholar]
  33. Grancini G.; Marras S.; Prato M.; Giannini C.; Quarti C.; De Angelis F.; De Bastiani M.; Eperon G. E.; Snaith H. J.; Manna L.; Petrozza A. J. Phys. Chem. Lett. 2014, 5, 3836–3842. 10.1021/jz501877h. [DOI] [PubMed] [Google Scholar]
  34. de Mello J. C.; Wittmann H. F.; Friend R. H. Adv. Mater. 1997, 9, 230–232. 10.1002/adma.19970090308. [DOI] [Google Scholar]
  35. Poglitsch A.; Weber D. J. Chem. Phys. 1987, 87, 6373–6378. 10.1063/1.453467. [DOI] [Google Scholar]
  36. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; Dal Corso A.; de Gironcoli S.; Fabris S.; Fratesi G.; Gebauer R.; Gerstmann U.; Gougoussis C.; Kokalj A.; Lazzeri M.; Martin-Samos L.; Marzari N.; Mauri F.; Mazzarello R.; Paolini S.; Pasquarello A.; Paulatto L.; Sbraccia C.; Scandolo S.; Sclauzero G.; Seitsonen A. P.; Smogunov A.; Umari P.; Wentzcovitch R. J. Phys.: Condens. Matter 2009, 21, 395502. 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  37. Perdew J. P.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  38. Yuan Z.; Shu Y.; Tian Y.; Xin Y.; Ma B. Chem. Commun. 2015, 51, 16385–16388. 10.1039/C5CC06750B. [DOI] [PubMed] [Google Scholar]
  39. Mosconi E.; Amat A.; Nazeeruddin M. K.; Grätzel M.; De Angelis F. J. Phys. Chem. C 2013, 117, 13902–13913. 10.1021/jp4048659. [DOI] [Google Scholar]
  40. Even J.; Pedesseau L.; Jancu J.-M.; Katan C. J. Phys. Chem. Lett. 2013, 4, 2999–3005. 10.1021/jz401532q. [DOI] [Google Scholar]
  41. Umari P.; Mosconi E.; De Angelis F. Sci. Rep. 2014, 4, 4467. 10.1038/srep04467. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Amat A.; Mosconi E.; Ronca E.; Quarti C.; Umari P.; Nazeeruddin M. K.; Grätzel M.; De Angelis F. Nano Lett. 2014, 14, 3608–3616. 10.1021/nl5012992. [DOI] [PubMed] [Google Scholar]
  43. Sapori D.; Kepenekian M.; Pedesseau L.; Katan C.; Even J. Nanoscale 2015, 10.1039/C5NR07175E. [DOI] [PubMed] [Google Scholar]
  44. Niquet Y. M.; Allan G.; Delerue C.; Lannoo M. Appl. Phys. Lett. 2000, 77, 1182–1184. 10.1063/1.1289659. [DOI] [Google Scholar]
  45. Heitmann J.; Müller F.; Yi L.; Zacharias M.; Kovalev D.; Eichhorn F. Phys. Rev. B: Condens. Matter Mater. Phys. 2004, 69, 195309. 10.1103/PhysRevB.69.195309. [DOI] [Google Scholar]
  46. Tanaka K.; Takahashi T.; Ban T.; Kondo T.; Uchida K.; Miura N. Solid State Commun. 2003, 127, 619–623. 10.1016/S0038-1098(03)00566-0. [DOI] [Google Scholar]
  47. Kane E. O. J. Phys. Chem. Solids 1957, 1, 249–261. 10.1016/0022-3697(57)90013-6. [DOI] [Google Scholar]
  48. Bekenstein Y.; Koscher B. A.; Eaton S. W.; Yang P.; Alivisatos A. P. J. Am. Chem. Soc. 2015, 137, 16008–16011. 10.1021/jacs.5b11199. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja5b12124_si_001.pdf (3.3MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES