Combining anatomical, diffusion, and resting state functional magnetic resonance imaging for individual classification of mild and moderate Alzheimer's disease

Abstract

Magnetic resonance imaging (MRI) is sensitive to structural and functional changes in the brain caused by Alzheimer's disease (AD), and can therefore be used to help in diagnosing the disease. Improving classification of AD patients based on MRI scans might help to identify AD earlier in the disease's progress, which may be key in developing treatments for AD. In this study we used an elastic net classifier based on several measures derived from the MRI scans of mild to moderate AD patients (N = 77) from the prospective registry on dementia study and controls (N = 173) from the Austrian Stroke Prevention Family Study. We based our classification on measures from anatomical MRI, diffusion weighted MRI and resting state functional MRI. Our unimodal classification performance ranged from an area under the curve (AUC) of 0.760 (full correlations between functional networks) to 0.909 (grey matter density). When combining measures from multiple modalities in a stepwise manner, the classification performance improved to an AUC of 0.952. This optimal combination consisted of grey matter density, white matter density, fractional anisotropy, mean diffusivity, and sparse partial correlations between functional networks. Classification performance for mild AD as well as moderate AD also improved when using this multimodal combination. We conclude that different MRI modalities provide complementary information for classifying AD. Moreover, combining multiple modalities can substantially improve classification performance over unimodal classification.

Highlights

• •We use machine learning classification to classify Alzheimer's disease.
• •For classification we use anatomical MRI, diffusion MRI, and resting state fMRI.
• •Grey matter density is most successful for single modality classification.
• •Combining multiple modalities improves classification of Alzheimer's disease.

1. Introduction

Early diagnosis is key to the development of treatments for Alzheimer's disease (AD) (Prince et al., 2011). In this respect it is well recognised that magnetic resonance imaging (MRI) might be highly useful as an early AD biomarker (Jack et al., 2010). Several MRI techniques have been applied successfully to study average group differences between AD patients and controls in voxel based grey matter (Ferreira et al., 2011), white matter (Li et al., 2012), diffusion measures (Douaud et al., 2011), and functional connectivity (Gour et al., 2014, Binnewijzend et al., 2012).

In addition to average group difference in case control studies, similar MRI measures have also been used to predict or classify the disease class (i.e., patient or control) of individuals. This classification based on MRI scans could be helpful in making a reliable diagnosis of AD in the future. Machine learning classification is a suited candidate to make such individual predictions, because it is well equipped to handle high-dimensional data such as those from MRI. Reliable individual classification of AD and controls has already been achieved with MRI measures of grey matter atrophy (Klöppel et al., 2008, Plant et al., 2010, Cuingnet et al., 2011), white matter integrity (Nir et al., 2014), and brain activity (Lee et al., 2013, Koch et al., 2012).

Some studies suggest that classification of Alzheimer's disease may further improve when combining several MRI modalities (Mesrob et al., 2012, Sui et al., 2013), while another recent study found better classification by using a single MRI modality (Dyrba et al., 2015). It is not yet clear which MRI modality or combination of modalities provide the best classification performance of AD patients.

The goal of this study is to perform individual classification of mild to moderate AD from healthy controls, and to combine information from several modalities to improve this individual classification. We compare classification performance for typical measures of grey matter atrophy, white matter integrity, and functional connectivity. Then we investigate whether combining modalities improves classification performance. We test how this multimodal classification model is able to separate patients with mild AD and patients with moderate AD from healthy controls.

2. Materials and methods

2.1. Data sample

2.1.1. Participants

Our dataset was collected as a part of the prospective registry on dementia (PRODEM; see also Seiler et al., 2012). Our sample only contained subjects scanned at the Medical University of Graz. The inclusion criteria are: dementia diagnosis according to DSM-IV criteria (American Psychiatric Association, 2000), non-institutionalisation and no need for 24-h care, and availability of a caregiver who agrees to provide information on the patients' and his or her own condition. Patients were excluded from the study if they were unable to sign a written informed consent or if co-morbidities were likely to preclude termination of the study. We conducted our study with the baseline scans from the PRODEM study, and included only patients diagnosed with AD in according the NINCDS-ADRDA Criteria (McKhann et al., 1984), for which anatomical MRI, diffusion MRI, and resting state functional MRI scans were present. Amyloid imaging for additional confirmation of the diagnosis was unavailable in our sample.

The healthy controls were drawn from the Austrian Stroke Prevention Family Study, which is a prospective single-centre community-based follow-up study with the goal of examining the frequency of vascular risk factors and their effects on cerebral morphology and function in the healthy elderly. On the basis of structured clinical interview and a physical and a neurological examination, participants had to be free of overt neurologic or psychiatric findings and had to have no history of a neuropsychiatric disease, including cerebrovascular attacks and dementia. The study protocol was approved by the ethics committee of the Medical University of Graz, Austria, and written informed consent was obtained from all subjects.

This resulted in a dataset of 77 AD patients between ages 47 and 83, of which 39 had mild AD (MMSE > 20), and 38 had moderate AD (MMSE ≤ 20) (Perneczky et al., 2006), and 173 healthy controls between ages 47 and 83 (see Table 1).

Table 1.

Demographics for the study population.

Demographics	Controls	Mild AD	Moderate AD
Age	66.1 ± 8.71	70.3 ± 7.85	66.9 ± 9.06
Gender, ♂/♀	74/99 (57%♀)	17/22 (56%♀)	14/ 24 (63%♀)
Education (years)	11.5 ± 2.76	11.6 ± 3.45	10.0 ± 2.79
Disease duration (months)	0.00 ± 0.00	22.6 ± 15.5	30.9 ± 30.7
MMSE	26.7 ± 5.80	24.2 ± 2.07	16.6 ± 2.73
CDR	–	0.72 ± 0.25	0.92 ± 0.39
GDS	2.11 ± 2.15	2.54 ± 2.09	2.74 ± 3.02

Data is represented as mean ± standard deviation. MMSE = mini mental state exam, CDR = clinical dementia rating, GDS = geriatric depression scale.

2.1.2. MR acquisition

Each participant was scanned on a Siemens Magnetom TrioTim 3 T MRI scanner. Anatomical T1-weighted images were acquired with TR = 1900 ms, TE = 2.19 ms, flip angle = 9, isotropic voxel size of 1 mm. Diffusion images were acquired along 12 non-collinear directions, scanning each direction 4 times with TR = 6700 ms, TE = 95 ms, 50 axial slices, voxel size = 2.0 × 2.0 × 2.5 mm. Resting-state fMRI series of 150 volumes were obtained with TR = 3000 ms, TE = 30 ms, flip angle = 90°, 40 axial slices, with an isotropic voxel size of 3 mm. We instructed participants to lie still with their eyes closed, and to stay awake.

2.2. Software

The MRI data were preprocessed using FMRIB Software Library (FSL, version 5.0) (Smith et al., 2004, Jenkinson et al., 2012). For all further data analyses we used MATLAB and Statistics Toolbox Release 2015b.

2.3. MRI preprocessing

The preprocessing of the anatomical MRI included brain extraction, bias field correction, and non-linear registration to standard MNI152 (Grabner et al., 2006). The preprocessing of the diffusion MRI included brain extraction and correction of eddy currents. For the fMRI data the preprocessing included brain extraction, motion correction (Jenkinson et al., 2002), a temporal high pass filter with a cutoff point of 100 s, and 3 mm FWHM spatial smoothing. Additionally, we used the FMRIB's ICA-based Xnoiseifier (FIX, version 1.06), with the included standard training data to automatically identify and remove noise components from the fMRI time course (Salimi-Khorshidi et al., 2014).

2.4. Anatomical atlases

In order to compare properties across subjects we used two anatomical atlases (Fig. 1) included in FSL. For grey matter regions we used the Harvard–Oxford probabilistic anatomical brain atlas (Desikan et al., 2006). Each brain region in this atlas consist of a probability map, where each voxel is assigned a probability of being part of each region. We split the 48 cortical regions of the Harvard–Oxford atlas into left and right hemisphere regions, resulting in 96 cortical regions. The cortical regions were combined with the 14 brain regions from the subcortical atlas, excluding the brain stem because it was not fully scanned for each participant. This resulted in a total of 110 grey matter anatomical regions. For the white matter regions we defined 20 white matter regions using the probabilistic JHU white-matter tractography atlas (Hua et al., 2008). All voxels under 25% probability per region were removed from each of the 110 grey matter, and each of the 20 white matter regions. For the analyses we used the voxel-wise probabilities that survived the thresholding for each region.

Fig. 1.

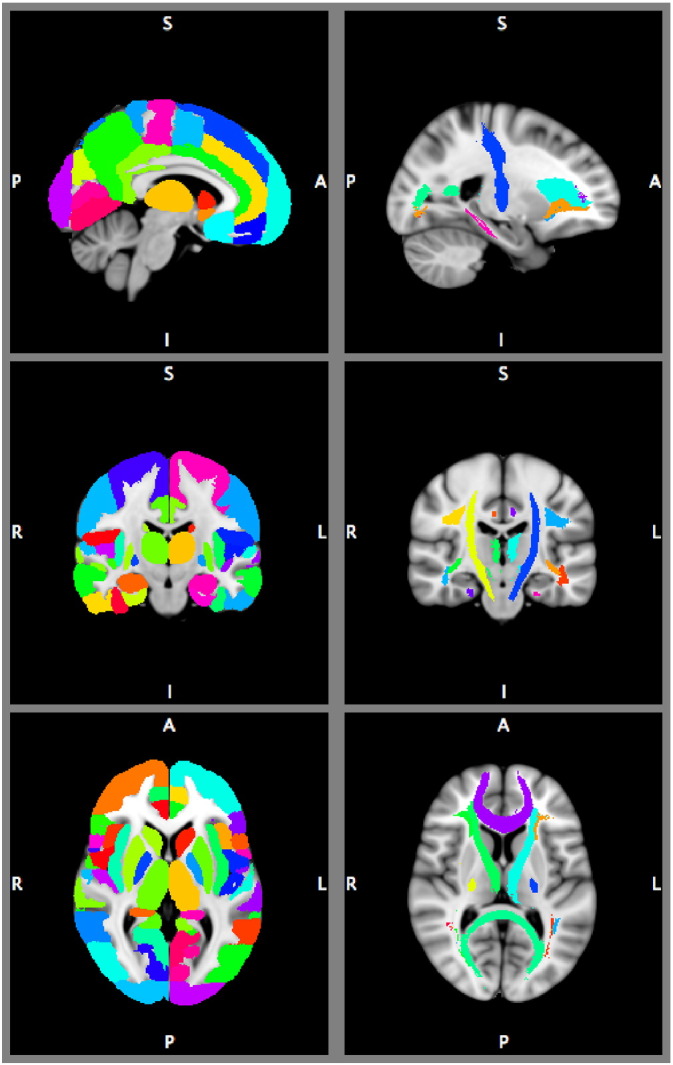
Anatomical atlases overlaid on MNI brain template. Left part shows the Harvard–Oxford cortical and subcortical areas. Right part shows the JHU white-matter tractography atlas. The images are thresholded at 25%, and showing the area with the maximum probability for displaying purposes, but the atlases were treated as probabilistic in our analyses.

2.5. Anatomical features

We identified anatomical features by calculating the grey matter density (GMD), and white matter density (WMD) for each brain voxel (Zhang et al., 2001). For the GMD, we averaged the voxel-wise values for each of the 110 grey matter regions weighted by the voxel-wise region probability. This provided a measure of brain atrophy within grey matter regions. For the WMD, we averaged the voxel-wise values across each of the 20 white matter regions, weighted by voxel-wise region probability. This resulted in a feature vector of 110 average GMDs per subject, and a feature vector of 20 average WMDs per subject.

2.6. Diffusion features

We calculated the fractional anisotropy (FA) and mean diffusivity (MD) values for each voxel with dtifit (Basser et al., 1994). Then we averaged those values for each of the 20 white matter regions, weighted by the region probability, and partial volume corrected with the WMD, resulting in feature vectors of 20 mean FA and MD values per subject.

2.7. Functional connectivity features

We performed temporal concatenation independent component analysis (ICA) (Beckmann and Smith, 2004) with a relatively high dimensionality fixed at 70 components in order to get a more refined division of functionally coherent areas than with low dimensional ICA (Beckmann, 2012, Smith et al., 2013). We used an ICA threshold of 0.99, meaning that each voxel included in the ICA map was 99 times more likely to be part of the component than to be caused by the Gaussian background noise. Then we calculated the mean time courses for each component for each subject, weighted by the ICA weight map, and partial volume corrected with GMD.

For each component we determined the functional connectivity with every other component. We defined the functional connectivity as the full correlations (FC) or as a sparse L1-regularised partial correlations (PC) between the components' time courses. We calculated the PC using the graphical lasso algorithm (Friedman et al., 2008), with λ = 100 (Smith et al., 2011). Both functional connectivity measures resulted in a feature vector of $\frac{70\times 69}{2}=2415$ (partial) correlations.

2.8. Elastic net classification with nested cross validation

We used the aforementioned six feature vectors from the three modalities with a logistic elastic net regression for classification (Zou and Hastie, 2005, Friedman et al., 2010). We used 10-fold cross validation to determine the generalisation performance of an elastic net regression models. For each subject this produced a predicted value between 0 and 1, where 0 represents a control subject and 1 represents an AD patient.

The elastic net regression procedure estimates a sparse regression model by imposing a penalty for including features and for the weight of each feature, so that only a subset of the features are included. To determine the parameters for the optimal size of this penalty without overestimating the classification performance we used an additional nested cross validation loop (Varma and Simon, 2006, Kriegeskorte et al., 2009). In the outer loop we performed 10-fold cross validation, where 9/10th of the total dataset served as training set, and 1/10th as test set. Then we performed a nested, 10-fold cross validation on the training set over a grid of parameters to determine the penalty. We used the penalty parameters that resulted in the lowest binomial deviance in the nested loop to train the model on the original training set. This model was used to make predictions for each participant in the test set. This procedure was repeated 10 times so that each participant was part of the test set once. By using this approach we did not use the test set to estimate the model, nor the penalty parameters that we used to train the model. We also included age and sex to the model without any penalty, so that all estimated regression coefficients for the feature weights were conditional on the age and sex of the subject.

To reduce the variability in the classification outcome resulting from the random partitioning in training and test folds we repeated the entire classification procedure 50 times. This allowed us to average out this variability, and report the range of observed outcomes under different train and test set partitioning.

2.9. Measuring classification performance

To assess the classification performance we performed receiver operating characteristic (ROC) analyses on the estimated outcomes between 0 and 1 from the elastic net regression. We calculated the ROC curve by shifting the threshold for classifying an individual as AD from 0 to 1, and plotted the true positive rate (sensitivity) versus the false positive rate (1 — specificity) for each intermediate point. The area under this ROC curve (AUC) is a measure of classification performance that is insensitive to the distribution between controls and AD patients (Fawcett, 2006), so that we can take full advantage of the larger number of controls than AD patients in our dataset. We also reported the sensitivity, and specificity values corresponding to the optimal point in the ROC curve, given an equal penalty for a false positive and a false negative prediction, and the class distribution equal to that in our sample. Because we repeated the procedure 50 times, the reported AUCs, sensitivity, and specificity values are the average over the 50 repetitions of the cross validation procedure.

Additionally, we investigated how well the predicted outcomes were able to separate mild AD from controls, and moderate AD from controls. For this purpose we also assessed the ROC curves for the mild and moderate subgroups versus controls separately.

2.10. Combining modalities

After assessing the performance for each individual modality we combined different modalities in order to study possible improvements in classification performance. We took a forward stepwise approach using feature concatenation to combine information from different modalities. We started with the best performing single modality feature. For each step we added each of the remaining modalities to the winning combination from the previous step. We assessed the classification performance for the combined modalities by determining the AUC. We continued the procedure until each of the modalities that we considered had been added.

3. Results and discussion

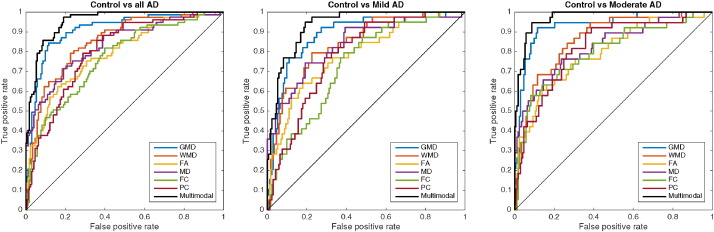
The classification results are summarised in Table 2, Table 3 for the unimodal and stepwise multimodal procedures respectively. The AUC curves for the unimodal results and the best performing step of the multimodal procedure is depicted in Fig. 2.

Table 2.

Alzheimer's patients versus controls classification. The mean, minimum and maximum area under the ROC curve over 50 repetitions are reported, as well as the sensitivity, specificity, and classification accuracy for the optimal point in the ROC. Results are shown for grey matter density (GMD), white matter density (WMD), fractional anisotropy (FA), mean diffusivity (MD), full correlations between ICA components (FC), and regularised partial correlations between ICA components (PC). Multimodal represents the best combination from step 5 of our stepwise multimodal procedure (GMD, WMD, FA, MD, and SPC).

Modality	AUC	Min–max	Sensitivity	Specificity	Accuracy
GMD	0.909	(0.901–0.915)	0.818	0.899	0.874
WMD	0.850	(0.845–0.858)	0.623	0.902	0.816
FA	0.789	(0.784–0.796)	0.547	0.885	0.781
MD	0.832	(0.823–0.840)	0.537	0.941	0.816
FC	0.760	(0.743–0.772)	0.422	0.921	0.767
PC	0.791	(0.778–0.803)	0.529	0.859	0.758
Multimodal	0.952	(0.946–0.959)	0.826	0.927	0.896

Table 3.

Multimodal classification performance for the stepwise concatenation procedure. Each step combines the best combination from the previous step with the remaining modalities. The best result occurs with the combination of GMD, FA, WMD, PC, and MD in step 5.

Step\combined with:	GMD	FA	WMD	PC	MD	FC
1: –	0.909	0.789	0.850	0.791	0.832	0.760
2: GMD	–	0.933	0.930	0.926	0.932	0.922
3: GMD + FA	–	–	0.949	0.927	0.934	0.930
4: GMD + FA + WMD	–	–	–	0.951	0.941	0.938
5: GMD + FA + WMD + PC	–	–	–	–	0.952	0.939
6: GMD + FA + WMD + PC + MD	–	–	–	–	–	0.930

Fig. 2.

Receiver operating characteristic plot for all Alzheimer's disease patients, mild AD, and moderate AD versus control for elastic net classification with nested cross validation, for grey matter density (GMD), white matter density (WMD), fractional anisotropy (FA), mean diffusivity (MD), full correlation between independent components (FC), and regularised partial correlation between independent components (PC). Multimodal represents the best combination from step 5 of our stepwise multimodal procedure (GMD, WMD, FA, MD, and PC). The diagonal line represents random classification performance.

3.1. Anatomical MRI

The measures derived from the anatomical MRI scan, grey matter density average of Harvard–Oxford regions, and white matter density of JHU tractography regions resulted in an excellent AUC of 0.909 and 0.850 respectively (Table 2). The good classification performance for GMD was expected, as AD has traditionally been seen as a grey matter atrophy disease (Frisoni et al., 2010). The classification performance with GMD that we found compares favourably to a recent similar study by Dyrba et al. (2015), who found an AUC of 0.86. While our methods were very similar, we used the Harvard–Oxford atlas to segment our data, and Dyrba et al. (2015) used the AAL atlas. The difference in atlases for segmentation, and our larger sample size might explain the difference in classification performance.

3.2. Diffusion weighted MRI

The measures derived from diffusion weighted MRI, fractional anisotropy and mean diffusivity of JHU tractography regions performed very reasonable with an AUC of 0.789 and 0.832 respectively (Table 2). This performance was much higher than the AUC between 0.652 and 0.720 that Mesrob et al. (2012) found with combined FA and MD measures, but lower than the 0.86 that Dyrba et al. (2015) found. While Mesrob et al. (2012) examined the DTI measures in grey matter areas, Dyrba et al. (2015) and our study examined the DTI measures in white matter regions, which possibly explains the differences in classification performance.

3.3. Functional connectivity

The measures derived from resting state functional MRI resulted in an AUC of 0.760 and 0.791 for full correlations and regularised partial correlations between ICA components respectively (Table 2). The higher performance of the regularised partial correlations compared to the full correlations is in line with the simulation study by Smith et al. (2011). Still, this classification performance was relatively poor compared to 0.848 found by Koch et al. (2012), and 0.80 found by Dyrba et al. (2015). Koch et al. (2012) found their result by examining the correlation between ICA components that resulted in the highest discriminative power. Because selecting this best performing correlation was not part of the cross-validation loop, their finding is likely an overestimation of the out-of-sample generalisability. Dyrba et al. (2015) used predefined components to study the correlations between functional regions, while we used ICA on our own dataset to acquire the components, which might partly explain differences from our findings.

3.4. Multimodal

The stepwise procedure that we used to concatenate features from different modalities resulted in an AUC of up to 0.952 (Table 3). This result was achieved by starting the procedure with the best performing single modality, GMD. Classification performance improved the most when adding FA (from 0.909 to 0.933 AUC). After that, the best improvement resulted from adding WMD (0.933 to 0.949 AUC). Then, adding PC further improved classification performance marginally (0.949 to 0.951 AUC), which was subsequently improved marginally again by adding MD (from 0.951 to 0.952). Adding the FC to the previous combination decreased the classification performance compared to the previous step (from 0.952 to 0.930 AUC). The resulting best multimodal model containing GMD, FA, WMD, PC, and MD performed well above any of the modalities separately (Fig. 2).

Our findings are in contrast with the study of Dyrba et al. (2015), who did not find any improved performance by combining similar measures derived from the same MRI modalities. This difference is possibly explained by our larger sample size, allowing many more training examples in each cross validation fold. Additionally, they used a multi-kernel support vector machine to combine information from different modalities, while we used feature concatenation. Apparently the elastic net classifier that we used in this study is suited to select relevant predictors, even when the feature space increases through concatenation. Still, more advanced methods to combine information from multiple modalities, such as linked ICA Groves et al. (2011), may benefit even more from the additional information from multiple modalities.

3.5. Mild Alzheimer's disease and moderate Alzheimer's disease classification

To investigate the results of our classification methods further we assessed the classification performance for mild AD and moderate AD separately. The classification results for mild AD versus controls and moderate AD versus  controls can be found in Table 4, Table 5 respectively.

Table 4.

Mild AD versus controls classification. Multimodal represents the best combination from step 5 of our stepwise multimodal procedure (GMD, FA, WMD, PC, and MD).

Modality	AUC	min–max	Sensitivity	Specificity	Accuracy
GMD	0.886	(0.878–0.897)	0.665	0.920	0.873
WMD	0.841	(0.829–0.851)	0.564	0.926	0.859
FA	0.783	(0.779–0.790)	0.287	0.974	0.848
MD	0.838	(0.832–0.844)	0.369	0.993	0.878
COR	0.728	(0.706–0.751)	0.183	0.966	0.822
SPC	0.770	(0.737–0.796)	0.176	0.969	0.823
Multimodal	0.934	(0.927–0.944)	0.721	0.935	0.896

Table 5.

Moderate AD versus controls classification. Multimodal represents the best combination from step 5 of our stepwise multimodal procedure (GMD, FA, WMD, PC, and MD).

Modality	AUC	Min–max	Sensitivity	Specificity	Accuracy
GMD	0.933	(0.924–0.942)	0.777	0.941	0.912
WMD	0.860	(0.853–0.866)	0.515	0.936	0.860
FA	0.794	(0.787–0.804)	0.361	0.978	0.867
MD	0.826	(0.811–0.839)	0.447	0.974	0.879
COR	0.793	(0.769–0.823)	0.465	0.944	0.858
SPC	0.812	(0.795–0.829)	0.349	0.956	0.847
Multimodal	0.971	(0.964–0.975)	0.813	0.956	0.930

The single modality classification performance for moderate AD (up to 0.933 for GMD) is substantially higher than it is for mild AD (up to 0.886 for GMD). The combination of GMD, FA, WMD, PC, and MD improves the classification performance for both mild AD (from 0.886 for GMD to 0.934 for multimodal) and moderate AD (from 0.933 for GMD to 0.971 for multimodal). This improvement is mainly due to an improved sensitivity, from 0.665 to 0.721 in mild AD, and from 0.777 to 0.813 in moderate AD. At the same time the specificity also marginally improves from 0.920 to 0.935 in mild AD, and from 0.941 to 0.956 in moderate AD.

3.6. General discussion

In our method we took much care in the generalisability of our findings by employing a nested cross validation approach. This approach assured that the class outcomes of the predicted subject was not required to be known when training the model, nor to estimate the model's penalty parameters. Furthermore, none of the feature reduction that we performed relied on observed class difference in our sample, which would result in overestimation of classification performance. Instead we reduced dimensionality by relying on anatomical atlases for the anatomical and diffusion features, and on data-driven unsupervised learning of independent components for the functional features. Further feature reduction was conducted in the model training phase by the elastic net classifier. Again the feature reduction in this phase did not rely on class differences in the test subjects, but only in the training subjects. Additionally, because of the relatively large sample size that we used the results were very reliable over different iterations of the cross validation procedure, increasing our confidence that the results of the procedure generalise well.

Interestingly, the multimodal procedure resulted in the best classification performance when all modalities were combined, except for the full correlation between ICA components. The partial correlations, which were based off of the same components' time-courses, were part of the best multimodal combination. Apparently, the full correlations did not add information to the classification model over what the partial correlations did.

The improvement in classification performance in the multimodal case over the best single modality measure was substantial, especially given the relatively good performance for grey matter density. We found this multimodal improvement in both the mild AD as well as the moderate AD group. Therefore we are optimistic that these findings will apply to even earlier stages of dementia as well.

3.7. Limitations

While we expect that our cross validation procedure ensured good generalisability of the classification performance, the models that were trained to predict each subject rely heavily on both random and non-random class differences in the training sample. Therefore we cannot reliably differentiate between real and random class differences in the trained models, which is the reason that we have refrained from biological interpretation of model parameters.

Furthermore, even though the general trend in our multimodal procedure suggests that there is added information gained from combining multiple modalities, it is sometimes difficult to draw hard conclusions about which modality improves the classification the most. For example, the improvement from adding FA to GMD resulted in an AUC of 0.933, but adding MD instead resulted in an AUC of 0.932. It would be naive to conclude that the combination of GMD and FA performs better than the combination of GMD and MD. Still, the general finding is that combining modalities with decent individual classification performance improves the classification. More findings from similar research should shed light on what measures result in the most powerful combination to classify AD. Overall the elastic net classification model is very well suitable to build a good model when many features from different modalities are added, which is why the combination of all features, except full correlations, resulted in optimal classification.

In our procedure we have made some choices that could affect the results. We chose the Harvard Oxford atlas to parcellate GMD, and the JHU tracts to parcellate WMD and diffusion measures. Different atlases for parcellation might have produced slightly different results. The 70-dimensionality ICA from which we derived areas for functional connectivity was chosen because they produce a more fine grained representation of functional areas than lower dimensionality ICA. However, the dimensionality of the ICA is a trade-off between detail in the functional areas and the number of correlations, and it is not known what dimensionality is optimal in this trade-off.

The question remains how well our results generalise to cases where the patients' symptoms are less severe, such as in mild cognitive impairment, as well as to early AD diagnosis. The procedures used in this research could serve as a starting point to answer these questions.

4. Conclusion

In our study we found that combining information from anatomical MRI, diffusion weighted MRI, and resting state functional MRI can improve AD classification performance for both mild AD and moderate AD. The best combination in our study consisted of the average grey matter density over anatomical regions, fractional anisotropy, mean diffusivity, and white matter density over white matter tracts, and regularised partial correlations between ICA components. When only a single modality can be considered for classification, grey matter density consistently results in the best classification performance. However, when available there is a clear benefit from incorporating anatomical MRI, diffusion weighted MRI, and resting state functional MRI for diagnostic purposes. Therefore, we recommend that MRI scanning protocols designed for diagnosis of Alzheimer's disease collect structural, diffusion, and functional MRI. Furthermore, we found that an elastic net classifier is well suited to estimate a predictive model when features from different modalities are combined by simple concatenation.