The Composition and Structure of the Inorganic Core of Relaxed Intermediate X(Y122F) of E. coli Ribonucleotide Reductase

Abstract

Activation of the diferrous center of the β₂ (R2) subunit of the class 1a Escherichia coli ribonucleotide reductases (RNR) by reaction with O₂ followed by one-electron reduction yields a spin-coupled, paramagnetic Fe(III)/Fe(IV) intermediate, denoted X, whose identity has been sought by multiple investigators for over a quarter century. To determine the composition and structure of X, the present study has applied ⁵⁷Fe, ^14,15N, ¹⁷O and ¹H ENDOR measurements combined with quantitative measurements of ¹⁷O and ¹H EPR line broadening studies to WT X, which is very short-lived, and to X prepared with the Y122F mutant, which has a lifetime of many seconds. Previous studies have established that over several seconds X(Y122F) relaxes to an equilibrium structure. The present report focuses on the relaxed structure. It establishes the following conclusions. (i) The ⁵⁷Fe and ¹⁴N ENDOR spectra of X(WT) quenched at 42 ms, and X(Y122F) quenched at 8 ms and 4 s all are identical, indicating that the properties of the [Fe₂, His₂] coordination center of X is unchanged by the Y122F mutation, and is invariant during relaxation as the quench delay increases. (ii) ¹⁷O ENDOR and quantitative EPR from X enriched separately with H₂¹⁷O and ¹⁷O₂(g), along with ^1,2H ENDOR shows that relaxed X contains an Fe(III)-bound hydroxide oxygen derived from solvent and an oxo-bridge derived from O₂ gas. (iii) The loss of hyperfine coupling to the second ¹⁷O from the ¹⁷O₂ molecule during the relaxation process, and the absence of a bridging ¹⁷O from solvent, together indicate that the inorganic core of relaxed X has the composition, [(OH⁻)Fe(III)-O-Fe(IV)]: there is no second inorganic oxygenic bridge, neither oxo nor hydroxo. (iv) The geometric analysis of the ¹⁴N ENDOR data, together with recent EXAFS measurements (Dassama, L. M. et al.; J. Am. Chem. Soc. 2013, 135, 16758) of the Fe-Fe distance, support the view that X contains a ‘diamond-core’ Fe(III)/Fe(IV) center, with the irons bridged by two ligands. (v) One bridging ligand of the core of X is the oxo-bridge (O_Br) derived from O₂ gas. Given the absence of a second inorganic oxygenic bridge (point iii), the second bridging ligand must be protein derived, and is most plausibly assigned as a carboxyl oxygen from E238.

Introduction

The β2 (R2) subunit of the class 1a Escherichia coli ribonucleotide reductases (RNR) is one of the class of diferrous non-heme iron proteins that carry out a broad range of reactions, ranging from reversible O₂ binding to fatty acid desaturation and methane oxidation.^1–4 The RNRs catalyze the conversion of nucleoside diphosphates to deoxynucleoside diphosphates in reactions involving complex free radical chemistry.^5–7 The β2 subunits in their oxidized forms/states contain a non-heme diferric center adjacent to a tyrosyl radical (Y•)^8,9 that initiates the reduction process. The active diferric-Y• cofactor in vitro is generated from the diferrous-Y center in a reaction with O₂ and an external reductant. This process has been studied by a number of time-resolved biophysical methods, including stopped flow spectroscopy and rapid freeze-quench (RFQ) EPR, ENDOR, Mössbauer, MCD and EXAFS spectroscopies.^10–16 A paramagnetic diiron intermediate designated X has been observed by all of these methods. X is one-electron oxidized relative to the resting diferric state of β2 and is catalytically competent to oxidize tyrosine 122 to Y122•.^17,18 RFQ Q-band ⁵⁷Fe ENDOR spectroscopy¹⁹ established that the diiron center of X has an antiferromagnetically spin-coupled [Fe(III), S = 5/2]/[Fe(IV), S = 2] core with an S = ½ ground state. As X is both the first high-valent intermediate of a diiron center to be trapped, and can be readily trapped in high yield, it has been the paradigm for such reactive states for over a quarter century. Nonetheless, to date no consensus has been reached as to the composition and structure of X.

Studies of many diiron proteins, in different oxidation states, indicate that the observed antiferromagnetic exchange-coupling between the Fe ions of X requires the presence of one or more oxo and/or hydroxo bridges. Some time ago we used a combination of ¹H and ²H, ¹⁷O CW and pulsed-ENDOR protocols to identify the inorganic core of X: the number of oxo bridges and the types of protonated oxygen (OH_x) species and their disposition relative to the ferric and ferryl ions of X.^12,14,20 These studies led us to conclude that the [(H_xO)Fe(III)-O-Fe(IV)] fragment forms the complete inorganic core of X, with the possibility that additional bridging ligand(s) supplied by the protein complete the core structure.

This interpretation was subsequently questioned by computational studies whose efforts were driven by the EXAFS measurement of an Fe-Fe distance of 2.51 Ź¹ which was viewed as being too short to be compatible with our proposal. One of these studies proposed that the core of X has a μ-oxo/μ-hydroxo Fe^III/Fe^IV core, but did not address the existence of terminal (H_xO),¹⁰ and the other study^21,22 concluded that X possesses a di-μ–oxo Fe^III/Fe^IV core plus a terminal (H₂O) bound to Fe(III) ion.²² Thus, each of the two studies includes features that differ from our proposed structure, but they do not agree between themselves. As a first step towards resolving the issue, we took advantage of improvements in 35 GHz pulsed-ENDOR performance to reexamine the protonation state of the oxygenic ligands of the inorganic core of X by directly probing the exchangeable proton(s) with ²H pulsed-ENDOR spectroscopy. This study confirmed (i) that X contains a terminal OH_x ligand to Fe(III) ion, and (ii) does not contain a μ–hydroxo bridge.²³ A very recent EXAFS study of X has proposed a greater Fe-Fe distance, 2.78 Å but nonetheless suggested the present of a di-μ–oxo Fe(III)/Fe(IV) core.²⁴

In the present report we definitively answer the question of the number of ¹⁷O atoms from ¹⁷O₂ incorporated in X by combining Q-band pulsed ENDOR measurements of the ¹⁷O hyperfine couplings with quantitative measurements of ¹⁷O EPR linebroadening that utilizes the couplings. We further establish that the solvent -derived OH_x aqua ligand of Fe(III) is an hydroxo (x = 1) derived from solvent, and determine that a second atom of ¹⁷O is not incorporated from solvent. These finding complete the assignment of the inorganic core of X.

In carrying out this effort we explicitly address issues associated with the nature of the RNR samples used by us and others in spectroscopic studies. Firstly, X in WT RNR is formed so rapidly that tyrosyl radical is generated even at the earliest time points, and this interferes with the analyses, so measurements are generally made with the stable X of the Y122F-β2 variant. Secondly, ¹⁷O hyperfine EPR broadening and ENDOR of X(Y122F) reveal that the second atom of ¹⁷O₂ is lost as the RFQ delay time is extended from 8 ms until several seconds and X relaxes to its equilibrium structure.¹⁴ We here use ⁵⁷Fe, ^14,15N Q-band pulsed ENDOR measurements to show that the [Fe₂, His₂] coordination center of X is unchanged by the Y122F mutation and is invariant with quench delay time, despite the relaxation process, and that the OH⁻ ligand is fully occupied throughout the process. We further report minor perturbations to the H_xO coordinated to Fe(III) ion caused by the loss of a putative H-bond with the Y122 hydroxyl mediated by D84. Finally, as the conclusion to a quarter century of studies by many investigators, the measurements of ¹⁷O ENDOR and EPR linebroadening definitively yield the composition and give a most-probable structure for the inorganic core of X(Y122F) that has relaxed to its final, equilibrium structure.

Materials and Methods

Samples

X in WT and Y122F β2 in D₂O buffer was prepared by RFQ methods as reported,¹⁴ and stored in liquid nitrogen since then. 35 GHz EPR and ENDOR spectroscopy demonstrate that the signals are unchanged by this storage.

ENDOR Spectroscopy

The 35 GHz pulsed-ENDOR spectrometer²⁵ employed in this study has been described.²⁶ As discussed in detail,^27–29 for a frozen solution sample, the determination of the full hyperfine tensor (and quadrupole tensor) of an interacting nucleus is achieved by obtaining a 2-D set of orientation-selective ENDOR spectra collected at multiple fields across the EPR envelope and comparing this set with simulated 2-D patterns. The ENDOR simulations were performed with the program Endorsim an enhanced version of the simulation program GENDOR.²⁷ The Davies and Mims response factors have a major influence on the observed ENDOR response, and are incorporated into Endorsim.²⁷

Results and Discussion

A. Spin Coupling and the Spin Hamiltonian Parameters of X

The EPR spectra taken of X prepared with WT, and mutant (Y122F) RNR preloaded with Fe(II), mixed with O₂-saturated buffer, and freeze-quenched in isopentane¹⁴ 42 ms after mixing, as well as relaxed X(Y122F) quenched at 4 s all have the same g-tensor, whose values we find to be, g = [2.006, 1.998, 1.993]. This g-tensor is almost perfectly rhombic, but the deviations from this limit leaves g₁ as the unique magnetic direction. The g-tensor of an antiferromagnetically spin-coupled [Fe(III), S = 5/2]/[Fe(IV), S = 2] diiron center such as X is described by Eq 1,³⁰

$$\mathbf{g}=\mathrm{K}(\text{III})\times \mathbf{gFe}(\text{III})+\mathrm{K}(\text{IV})\times \text{gFe}(\text{IV});\mathrm{K}(\text{III})=7/3;\mathrm{K}(\text{IV})=-4/3$$ (1)

where the K(i) are vector-coupling projection coefficients arising from the exchange-coupling.

The Fe(III) ion g-tensor gFe(III) is essentially isotropic, so the anisotropy of g is determined by that of the Fe(IV) ion g-tensor, gFe(IV). In general, the unique direction of this single-ion g-tensor, and thus g for the coupled center, corresponds to the direction of the axial component of the zero-field splitting tensor associated with the S = 2 Fe(IV) ion. This in turn is oriented along the direction of the strongest rhombic ligand-field component, which corresponds to the strongest bond to Fe(IV) ion. We interpret the invariant g-values as evidence that the ligand field at Fe(IV), and thus the coordination sphere of this ion is not perturbed by the Y122F mutation, and does not change significantly at 4 seconds after formation. We return to this issue below through ENDOR measurements of the hyperfine couplings to the ⁵⁷Fe(i) and coordinated ligands, in particular histidyl ¹⁴N nitrogens.

For use below, we further note that the hyperfine coupling tensor observed for a nucleus (n), A(n), of a ligand bound to one of the Fe ions, Fe(i), i = III or IV, equals the product of its single-ion hyperfine coupling, A(n,i) as determined by the bonding to Fe(i), multiplied by the Fe(i) vector coupling projection coefficient,

$$\mathbf{A}(\mathrm{n})=\mathrm{K}(\mathrm{i})\times \mathbf{A}(\mathrm{n},\mathrm{i})$$ (2, A)

When the ligand interacts with both Fe ions, as would for example occur for an atom associated with a bridge, its observed hyperfine tensor is given by the sum of the intrinsic couplings to each iron, as weighted by the corresponding vector coupling projection coefficient,

$$\mathbf{A}(\mathbf{n})=\mathrm{K}(\text{III})\times \mathbf{A}(\mathrm{n},\text{III})+\mathrm{K}(\text{IV})\times \mathbf{A}(\mathrm{n},\text{IV})=7/3\times \mathbf{A}(\mathrm{n},\text{III})-4/3\times \mathbf{A}(\mathrm{n},\text{IV})$$ (2, B)

B. ⁵⁷Fe and ¹⁴N ENDOR Spectra of X(WT/Y122F)

In this section we use a variety of double resonance/magnetic resonance techniques to characterize the ⁵⁷Fe ions of X and their histidyl ¹⁴N ligands. We show that their magnetic properties are unchanged by the Y122F mutation and invariant to the delay time before the samples are freeze-quenched after mixing with O₂-saturated buffer.

⁵⁷Fe Davies ENDOR

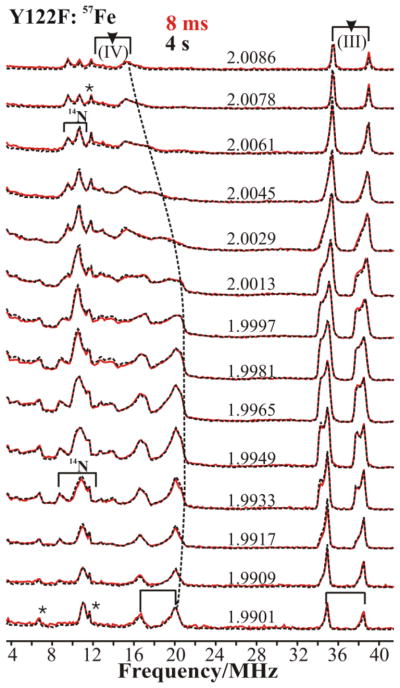
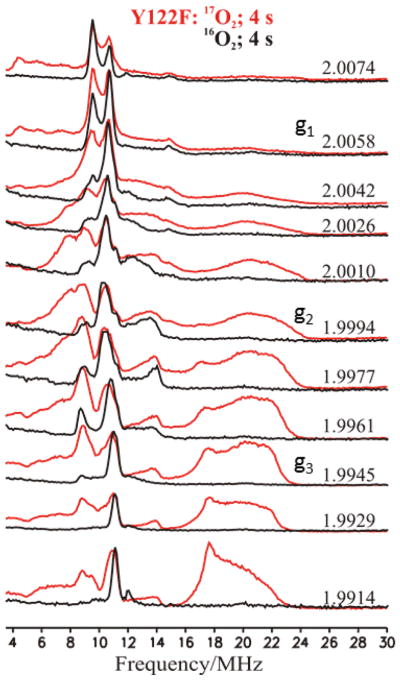
Fig 1 compares the 2-D field-frequency patterns of Davies ENDOR spectra collected across the EPR envelope of ⁵⁷Fe-enriched X(Y122F) freeze-quenched at 8 ms and 4 s delay time after mixing, and Fig S1A compares patterns for X(WT) and X(Y122F) freeze-quenched at 42 ms(WT)/8 ms(Y122F) after mixing. Comparison of the three patterns with spectra from unenriched samples shows well-defined ⁵⁷Fe signals in the 34–40 MHz and 14–22 MHz ranges, the former associated with ⁵⁷Fe(III) ion, the latter with ⁵⁷Fe(IV) ion. The 2-D field-frequency patterns of Fig S1B show that the mutation causes no changes in the properties of either of the Fe ions of X. Correspondingly, Fig 1 shows that both the Fe(III) and Fe(IV) ENDOR signals are identical at early and late quench time, likewise indicating that the coordination spheres of both Fe ions are invariant with the quench-delay after mixing.

Figure 1.

2-D field-frequency plot of Davies ⁵⁷Fe-ENDOR spectra of X(Y122F) prepared with ⁵⁷Fe and freeze quenched at 8 ms (red lines) and 4 s (black dotted lines) after mixing. Note: the indicated precision of the g-values reflects the precision of the differences in g-values, which is determined by differences in magnetic fields (10.0 G steps). Conditions: π pulse length = 80 ns, τ = 600 ns, repetition time = 50 ms, average microwave frequency = 34.95GHz, T = 2 K. The asterisk marks indicate the 3^rd Harmonics of ⁵⁷Fe(III) and ⁵⁷Fe(IV) ENDOR signals. (g-values represent relative precision of 5 SF, not absolute accuracy)

The 2-D ⁵⁷Fe(III) and ⁵⁷Fe(IV) patterns all are extremely well simulated (Fig S1B) with a hyperfine tensor for ⁵⁷Fe(III) that is nearly isotropic, a_iso(⁵⁷Fe(III)) = −73.5 MHz, while that for Fe(IV) is substantially anisotropic and has an isotropic component roughly half that of Fe(III), a_iso(⁵⁷Fe(IV)) = +33.9 MHz. The tensor values for both Fe ions (Table 1) are in good agreement with those reported previously for X(Y122F).¹⁹ The signs of the isotropic couplings for the two Fe ions were obtained by RD-PESTRE measurements (Fig S2).³¹ They reflect the signs of the vector coupling projection coefficients for the spin-coupled di-iron center as described in eq 2,A.

Table 1.

Hyperfine Interactions of Relaxed RNR-Intermediate X

Hyperfine Coupling/MHz	RNR-X
	17Ow		17OBr	57Fe(IV)	57Fe(III)	14N(III)Cb		14N(III)Rc	14N(IV)Cc
	A	P	A	A	A	A	P	A	A
A1	−34.1	0.07	[5]a	+26.3	−74.8	+12.8	−0.40	0.58
A2	−23.6	−0.38	−21.4	+38.4	−72.0	+11.8	−0.73	1.04
A3	−18.6	0.51	−21.4	+37.1	−73.7	+17.1	+1.13	0.66
aiso	−25.4		− [12.6] a	+33.9	−73.5	+13.9	-	0.76	~ 1.4

^aEstimated.

^bTensors coaxial; Euler angles [α=0°, β=6°, γ=51°], as previously defined.^36,37

^cCalculated from parameters for ¹⁵N isotopomer by scaling with ratio of nuclear g-factors.

Both the g-tensor and the orientation of the ⁵⁷Fe(IV) hyperfine tensor are determined by the zero-field tensor at ⁵⁷Fe(IV). As reported previously for the Y122F mutant quenched at 600 ms,¹⁹ within error, the A of ⁵⁷Fe(IV) and g tensor are coaxial. As would thus be expected, the unique value of the Fe(IV) hyperfine tensor is associated with the unique g-value, g₁, both being assignable to the direction of the principal component of the zero-field splitting tensor.

¹⁴N Davies ENDOR

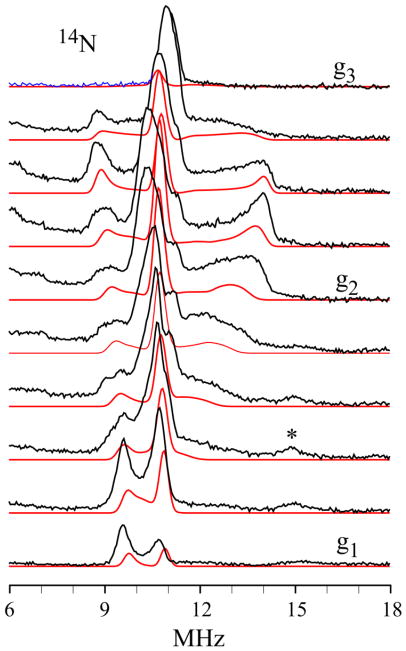
The ¹⁴N Davies ENDOR responses from the histidyl ¹⁴N coordinated to Fe(III) (denoted, ¹⁴N(III)_C) of X appear in the 6–14 MHz region of Fig 1 and in Figs 2 and S1. As is the case with the ⁵⁷Fe ENDOR spectra, the ¹⁴N Davies ENDOR spectra of X(WT) and X(Y122F) collected at 42ms (WT)/8 ms(Y122F) and of X(Y122F) at 8 ms and 4 s are identical, Fig 1 and Fig. S1A. Analysis of the 2-D field-frequency pattern of ¹⁴N Davies ENDOR spectra (Fig 2) gives the modestly anisotropic ¹⁴N(III)_C coupling tensor, A(¹⁴N(III) _C) = [12.8, 11.8, 17.1] MHz, a_iso(¹⁴N(III)_C) = 13.9 MHz, and a quadrupole interaction tensor typical of Fe-bound histidine ¹⁴N, P =[−0.40, −0.73, +1.13] MHz. The positive sign of the hyperfine coupling for ¹⁴N(III)_C was obtained by RD-PESTRE measurements (Fig S2). The two tensors are coaxial, with the A₁ and P₁ = P_x directions (defined by |P_x| < |P_y| < |P_z|) closely parallel with g₁ (Table 1). Numerous studies of high-spin Fe-bound ¹⁴N of histidine show that this maximum hyperfine and nuclear-quadrupole interactions lie along the ¹⁴N-Fe(III) bond vector, whereas the minimum quadrupole interaction (P_x) is normal to the imidazole plane.³² Therefore, the measurements show that g₁ lies roughly normal to the plane of the imidazole bound to Fe(III) ion.

Figure 2.

(Black) Davies ENDOR spectra of the ¹⁴N_Im coordinated to the Fe(III) ion for RNR-X taken at 10.0 G intervals across the EPR envelope of X(Y122F). (*) The feature in the vicinity of 15 MHz that appears as g approaches g₁, is a proton harmonic. (Red) Simulations using hyperfine and quadrupole parameters given in Table 1.

^14/15N Mims ENDOR

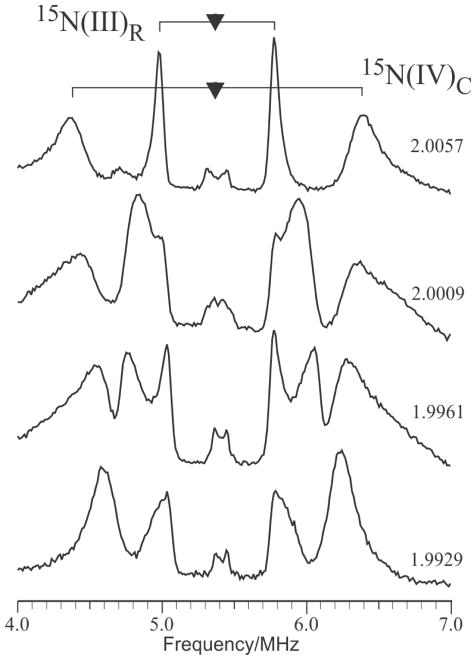
Mims ENDOR spectra of ¹⁴N associated with the more weakly-coupled histidine bound to Fe(IV) (denoted ¹⁴N(IV)_C) are poorly resolved (Not shown). However, Fig 3, shows the well-resolved ¹⁵N Mims ENDOR response of ¹⁴N(IV)_C, as well as a signal from the remote ¹⁵N of the histidine bound to Fe(III) (denoted ¹⁵N(III)_R). Both ¹⁵N nuclei have HFI dominated by an isotropic components, but the signals from ¹⁵N(IV)_C is relatively broad (around 0.3 MHz full-width/half-maximum) when compared to the hyperfine interaction (around 2 MHz). Typically ¹⁵N linewidths scale with the isotropic coupling, but the linewidths of the coordinated Fe(IV) His, ¹⁵N(IV)c is approximately the same as that associated with ¹⁵N(III)c, whose isotropic coupling is approximately 10x larger. This suggests that coordination geometry of ^14,15N(IV)c is not sharply defined. Indeed, the anisotropy of this hyperfine interaction is less than the linewidth, making detailed analysis impossible.

Figure 3.

Mims ENDOR spectra of weakly-coupled ¹⁵N nuclei in globally-labelled ¹⁵N X(Y122F) freeze-quenched at 620 ms after mixing. Two patterns from distinct sites are apparent. The broader outer peaks are assigned to the coordinated N_δ–His on the Fe(IV) ion; it is characterized by a predominantly isotropic HFI with a_iso(¹⁵N) ~ 2.0 MHz. The narrower inner peaks are associated with the remote ¹⁵N of the histidine imidazole coordinated to the Fe(III) ion. Conditions: microwave frequency 35.04 GHz; τ = 250 ns; T_RF = 40 us; T = 2 K. (g-values represent relative precision of 5 SF, not absolute accuracy)

In contrast to these broad lines, the narrow features (ca. 0.070 MHz) associated ¹⁵N(III)_R allow for a straightforward analysis of its tensor components with |A(¹⁵N(III)_R)| = (0.81, 1.45, 0.92) MHz.

Conclusions from ⁵⁷Fe and ¹⁴N ENDOR

The ⁵⁷Fe ENDOR spectra of X(WT) quenched at 42 ms and X(Y122F) quenched at 8 ms and 4 s all are identical. The same is true for the ¹⁴N ENDOR spectra. In particular, the hyperfine and quadrupole interactions of the histidine bound to Fe(III) ion are invariant.

The unique value of the Fe(IV) hyperfine tensor is oriented along the unique g-value, g₁, which corresponds to the principal direction of the zero-field splitting tensor. The orientation of the hyperfine and quadrupole tensors of the ¹⁴N(III)_C shows that the Fe(III)-N bond lies in the g₂–g₃ plane, perpendicular g₁, and that the normal to the plane of the histidine imidazole is closely parallel to g₁.

C. Fe(III)-bound-¹⁷O_wH_x

In this section we recall the results of recent ^1,2H ENDOR studies of X and describe the present use of quantitative EPR measurements of X in H₂O/D₂O to determine the protonation state, ‘x’, of a Fe(III)-bound OH_x. We further report the present use of multiple magnetic resonance/double resonance techniques to characterize the solvent-derived ¹⁷OH_x ligand. In this one instance we compare the properties of the oxygen of this ligand, denoted ¹⁷O_w, in WT enzyme quenched at 42 ms with that of the mutant enzyme quenched at 42 ms and 4 s, to test our previous suggestion that the ¹⁷OH_x ligand changes its occupancy over the quenching delay period, 8 ms - 4 s.

^1,2H ENDOR, EPR, and characterization of the Protonated Oxygenic Ligands of X

We recall the following definitive results of our recent study of the protonation state of oxygenic ligands of the inorganic core of X.²³ By directly probing the exchangeable proton(s) with ²H pulsed ENDOR spectroscopy these measurements confirmed that X contains an Fe(III)-bound terminal aqua ligand (H_xO), and does not contain a μ-hydroxo bridge. The ²H ENDOR measurements further demonstrated that this conclusion is applicable to both wild type and the β2 Y122F mutant; in fact we detected no difference between the properties of protons on the terminal oxygens in the two variants.

The ²H ENDOR spectra collected from the OH_x aqua ligand were accurately simulated with a single ²H bound to the ligand with a single orientation, and thus are most plausibly assigned to a terminal hydroxyl (OD⁻). The only way the ^1,2H ENDOR results would be consistent with a water ligand, x = 2, would be if the two protons were related by a symmetry element, a 2-fold axis running along the Fe-O vector, or a mirror plane with Fe-O lying in that plane. Given the unsymmetric environment of the aqua ligand on Fe1, this seems highly unlikely.

To test this proposal, that is that x = 1, we have now compared the X-band EPR spectra of RNR-X(Y122F) quenched in H₂O and D₂O at 4 s to see if this could confirm the presence of a hydroxide ligand (x = 1 proton), rather than a water ligand (x = 2) to Fe(III) ion. As shown in Fig S3, only x = 1 gives a satisfactory description of the broadening of the EPR envelope of X in H₂O buffer relative to the envelope of the intermediate in D₂O-buffer. Thus, the ENDOR and EPR hyperfine-broadening measurements agree that the solvent-derived OH_x ligand on Fe(III) in X is an hydroxo ligand: x = 1.

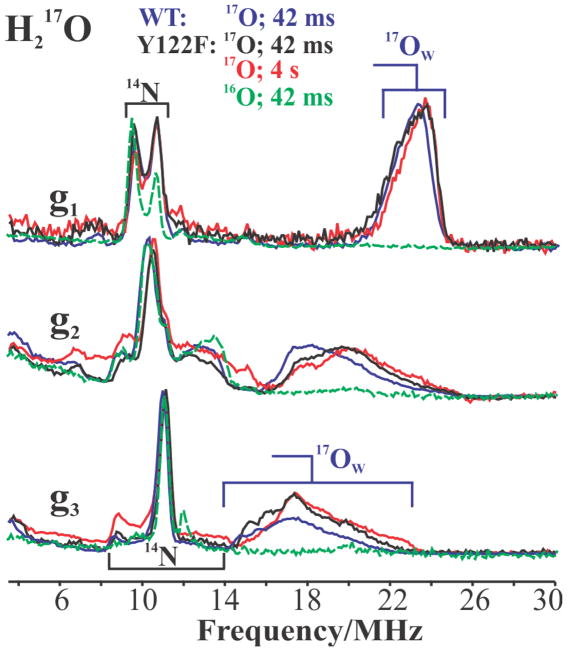
¹⁷O_w at 42 ms

Fig 4 presents 35 GHz Davies ¹⁷O-ENDOR spectra recorded at the three canonical g-values for X(WT) and X(Y122F) prepared with H₂¹⁷O and quenched at 42 ms, and also at 4 s for Y122F. In addition to the strong ¹⁴N ENDOR responses in the 6–16 MHz range (described above), the spectrum of X(WT) prepared in H₂¹⁷O buffer and collected at g₁ displays an additional intense feature assigned as the ν₊ branch of the solvent-derived oxygen associated with the core of X, denoted ¹⁷O_w and previously assigned as an ¹⁷O_wH ligand bound to Fe(III) of X. The peak is centered at ν₊ = A(¹⁷O_w)/2 + ν(¹⁷O) ~ 24 MHz, corresponding to a hyperfine coupling of A(¹⁷O_w) ~ 34 MHz, and is broadened by a small, unresolved quadrupole interaction, 12P₁ ~ 4–5 MHz (Fig 4). As the field is increased towards g₂ and g₃, the ¹⁷O ENDOR response shifts to lower frequency, at g₃ becoming a broad feature centered at ν₊ ~ 18 MHz (A(¹⁷O_w) ~ 19 MHz) and exhibiting a large unresolved quadrupole splitting, 12P₃ ~ 7–8 MHz.

Figure 4.

Davies pulsed ENDOR spectra of ¹⁷O_w in X at the three canonical g-values, prepared with ¹⁷OH₂ buffer: Y122F freeze quenched at 42 ms (black) and 4 s (red) after mixing; WT freeze-quenched at 42 ms (blue). As baseline a spectrum is included for abundance X(Y122F, green) (42 ms) prepared in natural-abundance buffer solution. Conditions: π pulse length = 80 ns, τ = 600 ns, repetition time = 50 ms, 34.971 GHz (Y122F), 34.93 GHz (WT), T = 2 K.

The entire 2-D pattern of Davies pulsed ¹⁷O_w-ENDOR spectra collected over the EPR envelope is shown in Fig S4, and is in excellent agreement with the CW ENDOR measurements reported earlier for X(Y122F).¹⁴ As illustrated in the spectra taken at the canonical g-values, g₁, g₂, g₃ shown in Fig 4, the ¹⁷O_w-ENDOR responses are so alike that they correspond to essentially identical couplings for X(WT) (blue), relaxed X(Y122F) (red), and even X(Y122F) collected at early time (black). The spectra in Fig 4 show only subtle differences in the shapes at g₂ and g₃ of ¹⁷O_w-ENDOR spectra of X(WT) from those of the two X(Y122F) preparations, best resolved at the g₃ single-crystal-like field. This difference is likely due to the loss of H-bonding interaction between the [¹⁷O_wH]⁻ ligand and the OH of Y122 through the D84 ligand to the Fe(III) ion and its absence in the mutant, but as discussed immediately below, the hyperfine tensor for ¹⁷O_w (Y122F) is the same as that of ¹⁷O_w (WT) within error (Table 1).

The experimental patterns of Davies pulsed ¹⁷O_w-ENDOR spectra for X(Y122F) and X(WT) were both well simulated (not shown) by assuming a single contributing ¹⁷O_w with the hyperfine tensor, A(¹⁷O_w) = −[34, 24, 19] MHz, dominated by an isotropic coupling of a_iso(¹⁷O_w) = −25.4 MHz (see Table 1 for other parameters). In the absence of a successful direct measurement of the sign of the coupling to ¹⁷O_w, the signs of the HFI were assigned by assuming positive spin density on ¹⁷O_w derived from direct delocalization from the Fe(III) ion; as g_N < 0 for ¹⁷O and we assume ρ(O_w) ~ (A/g_N) > 0, then A(¹⁷O_w) < 0. The derived couplings match the values reported for ¹⁷O_w (Y122F) by Burdi et al, within error.¹⁴

¹⁷O_w ENDOR, 4 s vs 42 ms

Comparison of the 35 GHz 2-D field-frequency Davies pulsed ENDOR patterns for X(Y122F) samples prepared in H₂¹⁷O buffer and quenched early (42 ms; black) and late (4 s; red), Fig 4, clearly shows the frequencies of ¹⁷O_w ENDOR features observed at short and long quenching times are identical, and thus the properties of ¹⁷O_w as indicated by its spin Hamiltonian parameters do not change during delay before quenching. Of particular significance, normalization of each of the current Davies ENDOR spectrum to its ¹⁴N signal as an internal reference, and comparison of the intensities of the normalized spectra from X quenched at 42 ms and 4 s shows that the intensity of the ¹⁷O_w signal does not change as the quench-time is lengthened from 42 ms to 4 s, Fig 4. This observation corrects the interpretation of our earlier measurements,¹⁴ that the intensity of the signal from ¹⁷O_w does exhibit a change, with ¹⁷O_w ‘exchanging in’ from solvent over time. Re-examination of the earlier data¹⁴ shows that the apparent change in intensity with time reflects subtle baseline uncertainties in the CW ENDOR measurements then employed, which are absent in the Davies pulsed ENDOR measurements.

As confirmation of the invariance of the occupancy of H_x¹⁷O_w with quench time, Fig S5 shows ¹H ENDOR measurements that also indicate that by the earliest quench times, 8–42 ms, X contains an H_xO ligand that is equilibrated with solvent, and that its occupancy, properties, and isotopic composition are invariant with quench time.

EPR quantitation of ¹⁷O_w

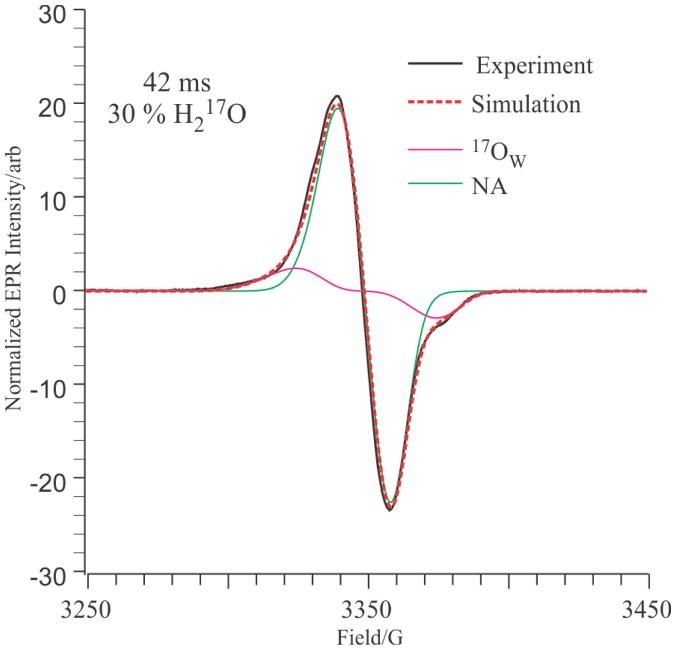
To confirm the invariant ¹⁷O_w site occupancy we used the refined ¹⁷O_w tensor values obtained here to simulate the EPR spectrum of X prepared in 30 % H₂¹⁷O sample and quenched at 42 ms as the sum of the individual contributions of ¹⁷O and ¹⁶O isotopologs. In the EPR simulations, the only adjustable parameter was the percentage occupancy of ¹⁷O_w; the g-values and ¹⁷O and ⁵⁷Fe hyperfine tensors were fixed, and the linewidths were fixed to those derived through simulation of the spectrum of X prepared in H₂¹⁶O. The resulting one-parameter least-squares fit yielded the EPR simulation, shown in Fig 5, in which the occupancy of ¹⁷O_w is 30(2) %, equal to the ¹⁷O_w percentage in the solvent. This result incidentally shows that there is no scrambling of the oxygen of the OH ligand to the Fe(III) ion with O-atoms derived from O₂(g) during assembly of the X-intermediate state.

Figure 5.

Normalized EPR spectrum (black solid line) and simulation (red dotted line) of X(Y122F) quenched at 42 ms in the presence of 30 % H₂¹⁷O. The simulation is the sum of 69.2 % natural abundance (green) and 30.8 % H₂¹⁷O (magenta) X(Y122F). Experimental parameters: temperature 35.0 K; microwave power 10.0 mW; microwave frequency 9.375 GHz; modulation amplitude, 4.0 G; time constant 32 ms; scan time 60 seconds, average of 40 scans. Simulation parameters: g = (2.0058, 2.0005, 1.9955); LW = (14, 10, 10) G; A(¹⁴N) = (12, 12, 17) MHz; A(¹H) = (20, −10, −10) MHz; A(⁵⁷Fe(III)) = (75, 75, 75) MHz, weight 2.0 %, A(⁵⁷Fe(IV)) = (26, 38, 38) MHz, weight 2.0 %; A(¹⁷O) = (30, 20, 20) MHz, weight = 30.0 %.

The sensitivity of these simulations to isotopic composition is highlighted by the finding that to achieve an adequate simulation required the inclusion of contributions from natural-abundance ⁵⁷Fe (2.15%) isotopologs for both the Fe(III) and Fe(IV) sites. The fit without ⁵⁷Fe inclusion resulted in a 2 % increase in the predicted occupancy of the ¹⁷O_w.

D. Geometric Analysis of the ⁵⁷Fe(IV), ¹⁴N, and ^1,2H₂¹⁷O_w interaction tensors

It is typically folly to attempt to analyze the spin-Hamiltonian ENDOR parameters of a spin-coupled center like X in terms of geometric structure without independent constraints. The magnitudes of hyperfine interactions as well as their relative signs are dependent on the spin-coupling parameters. Any atom that lies in the region between the two paramagnetic centers experiences dipolar coupling that arises from both centers and can be extremely difficult to decompose into single-ion effects in the absence of information on spin coupling. However, with X, we have hyperfine information for three well-defined sites that is related only to the properties of a single Fe ion: the protons (HFI) and oxygen (HFI, NQI) of (^1,2H¹⁷O_w)⁻ bound to the Fe(III) ion; the ¹⁴N of histidine bound to the Fe(III) (¹⁴N(III)_C; HFI, NQI); and the ⁵⁷Fe of Fe(IV) (HFI). The ⁵⁷Fe HFI tensor of Fe(III) is equally well-defined, but is essentially isotropic and offers no geometric information.

We begin by assembling the directional information implicit in the ENDOR-derived nuclear interaction tensors. (i) Both the ¹⁷O_w and ^1,2H of (^1,2HO_w)⁻ exhibit axial HFI with the Fe(III) ion of X, and these necessarily maximize roughly along the Fe(III)-O_w direction. According to the experiments, this direction corresponds to the direction of g₁. (ii) Previous studies show that the HFI and NQI interactions of ¹⁴N(III)_C bound to Fe(III) maximize in a direction along the Fe(III)-N(III)_C bond. Experimentally that direction lies in the g₂–g₃ plane, and thus the Fe(III)-N(III)_C bond is roughly perpendicular to the Fe(III)-OH bond vector.

A geometric interpretation of the orientations of the interaction tensors relative to the molecular framework of X is informed through use of the crystal structure of the Fe(III)-Fe(III) resting-state cluster as a guide, through the reliable assumption that there is little reorganization around the Fe(III) site of X when the partner Fe(IV) site of X is reduced by one electron to form the diferric resting state, and thus, the relative orientations of the histidine and water at the Fe(III) of X are essentially the same as in the crystallographically characterized diferric enzyme.^33,34 Figure 6 shows the relevant portion of the diferric structure.

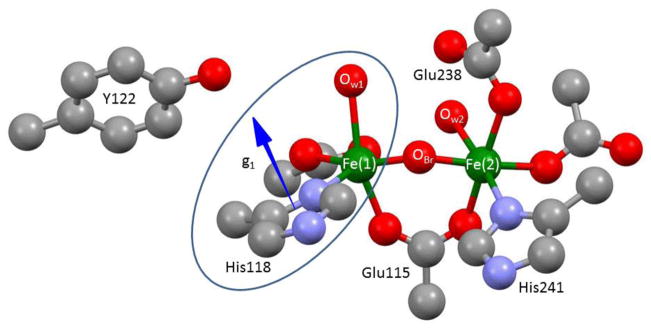
Figure 6.

Structure of diferric site from PDB # 1MXR crystal structure.^33,34 Ellipse encloses the portion of this center assumed to be a good representation of the corresponding structure of the Fe(III) site of X. Arrow indicates the proposed orientation of g₁. Although the g-tensor is fixed by the properties of the Fe(IV) ion of X, assigned as Fe(2), it is translated to His118 for visualization of the relative orientation of the Fe(1)-O bond.

In the diferric state of RNR, both Fe centers have coordinated aqua ligands shown in Fig. 6 whereas in X, only the ferric ion has an aqua ligand. Examination of the relative geometries of the N_His-Fe-O_w coordination for the two Fe ions in the diferric state, shows that for Fe(1), the His and H₂O ligands adopt a cis arrangement (~ 90° angle between Fe-O(1) and Fe-N(III)_C bonds), while for Fe(2), the His and H₂O ligands are in a trans geometry (~ 180° angle between bonds). The experimental finding that the Fe(III)-N(III)_C bond is roughly perpendicular to the Fe(III)-OH bond are only consistent with the assignment of the Fe(1) site in the diferric state to the Fe(III) ion in X, and therefore the assignment of ¹⁴N(III)_C to N_δ-His118. This assignment of Fe(III) to Fe(1) confirms earlier suggestions.

It is further shown above that the normal to the plane of the His118 imidazole ligand to Fe(III) in X is essentially parallel to g₁ (the Fe(1)-O_w axis), and this geometry also is essentially preserved in the diferric structure at Fe(1). The fact that the relative geometries of the water and imidazole ligands of the ferric ion in X are maintained through the reduction of X to the Fe(III)-Fe(III) state is a strong indication that we can use these relationships as a guide when looking at other interactions, most notably, the ⁵⁷Fe(IV) HFI tensor. Now consider the present finding that the unique axis of the HFI of Fe(IV) of X lies roughly along g₁. If we project the predicted g₁ direction onto the coordination sphere of the Fe(2) site in the diferric structure, we find that this direction is normal to the Fe-O-Fe plane of the diferric structure and roughly perpendicular to the Fe(2)-O direction, rather than being contained within the Fe-O-Fe plane. Previous studies by Solomon and coworkers¹⁰ suggest that this arises because there is a second ligand bridging the Fe ions, with g₁ normal to the ‘diamond core’³⁵ thus formed, Chart 1. One of these bridges of course is O_Br; the next section discusses the identity of the second bridging ligand.

E. ¹⁷O₂-Derived Ligands

In this section we use pulsed ENDOR and quantitative treatment of ¹⁷O hyperfine broadening to deduce the characteristics and number of ¹⁷O ligands from ¹⁷O₂ that are associated with X(Y122F) quenched at 4 s after mixing, leading to a most-probable structure for relaxed X

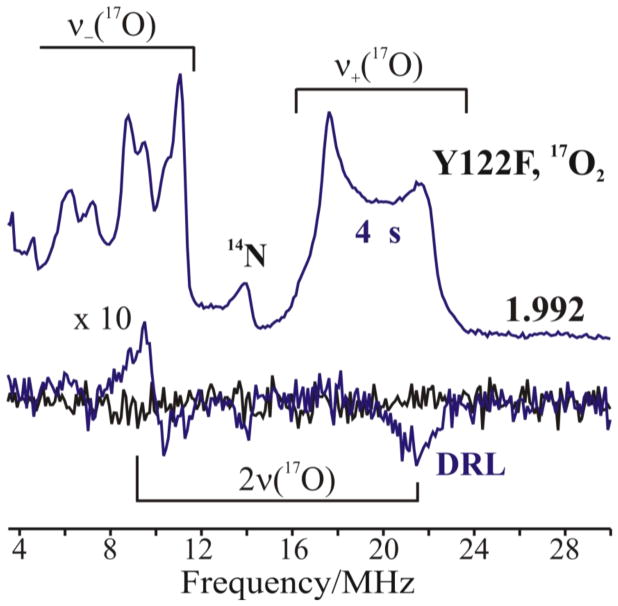
X Quenched at 4 s; ENDOR Measurements of ¹⁷O_Br

Davies ENDOR

In our previous report a 2-D field-frequency ENDOR pattern of ¹⁷O ENDOR measurements on X prepared with 89 % ¹⁷O₂ was generated by combining CW-ENDOR spectra at high g-values with Davies ENDOR spectra at low g-values, and was interpreted as arising from a single bridging ¹⁷O ligand. The improved sensitivity of the current spectrometer yielded a complete, high-quality 2-D pattern of Davies spectra, Fig 7. The spectra collected from g₃ to g₂ show a ν₊(¹⁷O) feature centered at ~ 18 MHz and broadened by unresolved ¹⁷O quadrupole splittings. As the g value is raised above g₂ this feature shifts to lower frequency while broadening and losing intensity, until near g₁ it is barely detectable as an apparent ‘rise’ in the baseline. This 2-D pattern is indeed described in terms of a single ¹⁷O, denoted ¹⁷O_Br with A_|| = A₁ ≪ A_⊥ ≈ A₂ ≈ A₃ ≈ +21.4 MHz. The negative sign of the coupling has been derived from RD-PESTRE measurements obtained near g₃ (Fig 8), which show that A/g_N > 0. As g_N < 0 for ¹⁷O, the hyperfine sign follows; this result implies that the spin density on ¹⁷O_Br is positive. Optimized values of the hyperfine and quadrupole tensor components are given in Table 1; these are in excellent agreement to those previously reported.

Figure 7.

2-D field-frequency plot of Davies ENDOR of X(Y122F) prepared with natural abundance (black solid lines) and 89 % ¹⁷O₂ quenched at 4 s (red solid lines). Conditions: π pulse length = 80 ns, τ = 600 ns, repetition time = 50 ms, T_rf = 40 μs, average microwave frequency = 34.96 GHz, T = 2 K.

Figure 8.

Top: Davies pulsed ¹⁷O-ENDOR spectra recorded at g₃ = 1.992 for X(Y122F) prepared with ¹⁷O₂ gas and freeze quenched at 4 s (blue lines). Bottom: Corresponding ¹⁷O RD-PESTRE traces (blue trace) with null trace (black). The intensity of the RD-PESTRE spectrum is multiplied 10-fold relative to the ENDOR traces. The goalposts defined the υ₊/υ₋ branches of the ¹⁷O-signal. Conditions: See Fig 7.

Site Occupancy of ¹⁷O₂-Derived Ligands deduced from X-Band EPR Linebroadening of Y122F(¹⁷O₂)

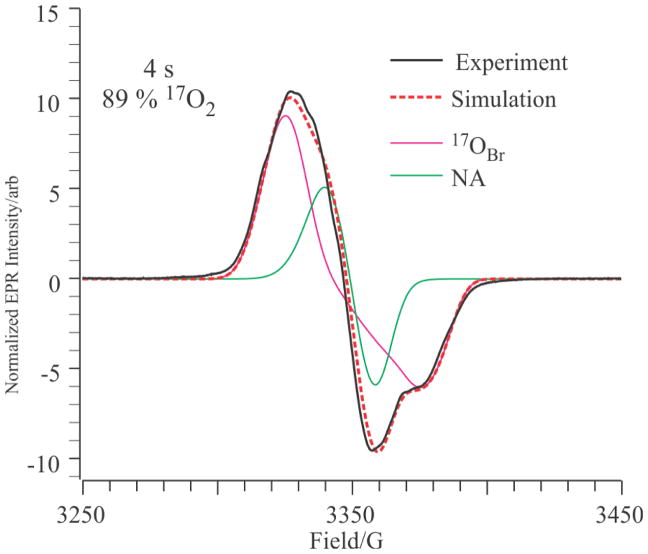
Using the ENDOR-derived HFI values for ¹⁷O_Br as a guide, we have simulated the X-band EPR spectrum of the X(Y122F) quenched at 4 s after formation with 89 % ¹⁷O₂(g). The values of A₂ and A₃ were fixed at 25 MHz, the values of A₁ and the ¹⁷O occupancy were allowed to vary, and all other parameters were fixed as above. The best fit at 4 s, Fig. 9 was obtained with 82 % labeling of a single O_Br that has |A₁| ~ 11. Relaxing the constraint, A₂ = A₃ improved the fit slightly, but without significant change in occupancy. This confirms that relaxed X(Y122F) contains only the single ¹⁷O_Br atom from ¹⁷O₂(g) with essentially complete conversion of one ¹⁷O atom of the diatomic to the bridging oxo ligand. This O₂-gas derived site has been identified as an oxo bridge, ¹⁷O_Br in the RNR-X site [Fe(III)-O_Br-Fe(IV)].¹⁴

Figure 9.

Normalized X-band EPR (black solid line) simulation (red dotted line) of X (Y122F) quenched at 4 s in 89 % ¹⁷O₂(g). The simulation is a simple sum of the green and magenta spectra, which show the decomposition into 18.0 % natural abundance (green) and 82 % ¹⁷O_Br. Experimental parameters: as in Fig 6. Simulation parameters: g = (2.0058, 2.0005, 1.9955); LW = (14, 10, 10) G; A(¹⁴N) = (12, 17, 12) MHz; A(¹H) = (20, −10, −10) MHz; A(¹⁷O) = (11, 25, 25) MHz, weight = 82 %.

Composition and Structure of Relaxed X

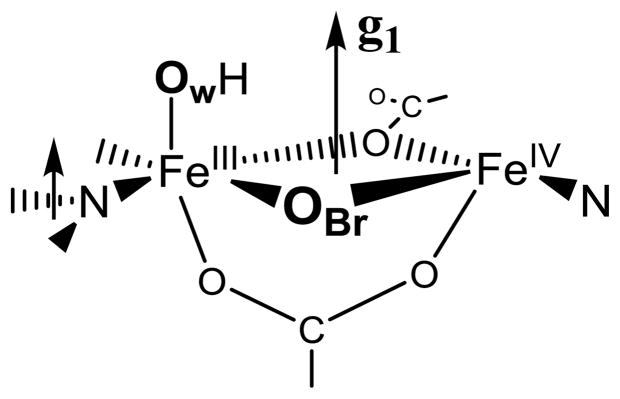
The results of the present experiments establish that relaxed X contains one oxygen atom derived from O₂, present as oxo-bridge, identifying one bridging atom (Y) of Chart 1 as O_Br. In addition, it contains one oxygen atom derived from solvent in the form of the hydroxyl bound to Fe(III) ion. Thus, the composition of the inorganic core of relaxed X is shown to be, [(OH⁻)Fe(III)-O-Fe(IV)]. As our measurements concur with the recent EXAFS study in implying that X exhibits the ‘diamond core’ of Chart 1, this in turn requires that the second bridging atom (Z) of Chart 1 is protein-derived. This bridge is most plausibly assigned as a carboxyl oxygen; as has been discussed previously,²² this would involve E238. With retention of the bridging carboxylate of Glu 115, this yields as the core of relaxed X the structure shown in Chart 2.

The same composition of the inorganic core of relaxed X (although without identification of the aqua ligand as an hydroxyl) was in fact first proposed by us in 1998. However, this conclusion was generally rejected, without addressing the evidence on which it was based, because it was thought to imply an Fe-Fe distance longer than the accepted value for the Fe-Fe distance, 2.51 Å. The recent revision of that distance to 2.78 Ų⁴ alleviates such concerns, although the basis for the difference between the earlier and latter EXAFs data still remains unclear.

Conclusions: The Structure of relaxed X

The suite of advanced paramagnetic resonance techniques applied to X freeze-quenched at 4 s thus confirm the previously proposed composition of the inorganic core of X, and provides new insights into its structure. The present measurements have established the following conclusions.

1. The ⁵⁷Fe and ¹⁴N ENDOR spectra of X(WT) quenched at 42 ms and X(Y122F) quenched at 8–42 ms and 4 s all are identical, indicating that the properties of the [Fe₂, His₂] coordination center of X is unchanged by the Y122F mutation, and is invariant during relaxation as the quench delay increases.

2. ¹⁷O ENDOR and quantitative EPR from X enriched separately with H₂¹⁷O and ¹⁷O₂(g), along with ^1,2H ENDOR shows that relaxed X contains one Fe(III)-bound hydroxide oxygen (¹⁷O_W) derived from solvent and one oxo-bridge derived from O₂ gas (¹⁷O_Br).

3. The hyperfine coupling to the second ¹⁷O from ¹⁷O₂ is lost during the relaxation process, and there is no bridging ¹⁷O from enriched solvent. Thus, the inorganic core of relaxed X does not have a second inorganic oxygenic bridge, neither oxo nor hydroxo: its composition is [(OH⁻)Fe^III-O-Fe^IV].

4. The geometric analysis of the ¹⁴N ENDOR data, together with EXAFS measurements of the Fe-Fe distance, support the view that X contains a ‘diamond-core’³⁵ Fe(III)/Fe(IV) center, Chart 1.

5. One bridging ligand of the core of X (Chart 1, atom Y) is the oxo-bridge (O_Br) derived from O₂ gas. Given the absence of a second inorganic oxygenic bridge (point iii), the second bridging ligand, Z, must be protein derived, and is most plausibly assigned as a carboxyl oxygen from E238, yielding as the core of relaxed X the structure shown in Chart 2.

Chart 1.

Chart 2.