Abstract
We report a method for achieving advanced photon diagnostics of x-ray free-electron lasers (XFELs) under a quasi-noninvasive condition by using a beam-splitting scheme. Here, we used a transmission grating to generate multiple branches of x-ray beams. One of the two primary diffracted branches (+1st-order) is utilized for spectral measurement in a dispersive scheme, while the other (−1st-order) is dedicated for arrival timing diagnostics between the XFEL and the optical laser pulses. The transmitted x-ray beam (0th-order) is guided to an experimental station. To confirm the validity of this timing-monitoring scheme, we measured the correlation between the arrival timings of the −1st and 0th branches. The observed error was as small as 7.0 fs in root-mean-square. Our result showed the applicability of the beam branching scheme to advanced photon diagnostics, which will further enhance experimental capabilities of XFEL.
I. INTRODUCTION
X-ray free-electron lasers (XFELs)1–3 have promoted researches in a variety of scientific fields such as chemistry, material science, physics, and biology. Coherent x-ray pulses with an unprecedented peak power (>10 GW) and an ultrashort temporal duration (<10 fs) have opened novel opportunities to observe the electronic and structural dynamics of matter with an ångström and femtosecond spatio-temporal resolution. Owing to these unique properties of XFEL sources, notable scientific progresses have been reported in studies on capturing unstable short-lived species in light-induced chemical reactions,4–6 elucidating atomic displacements in phonon oscillations,7,8 creating exotic states of matter with high energy densities,9–13 and determining damage-free structures of crystallized proteins.14–16
Most of the current XFEL sources operate on the basis of a self-amplified spontaneous emission (SASE) scheme,17,18 which causes shot-to-shot variations in radiation properties such as a pulse energy, a temporal duration, a spatial profile, a wavefront, and a spectrum. Detailed knowledge of these stochastic fluctuations is critical for conducting accurate data analysis. A transmissive beam monitor, which consists of a nanocrystal diamond film and photodiodes,19 for example, has provided the pulse energy and the center-of-mass position of XFEL light, which are highly useful for normalization of signals.
Furthermore, diagnostics on arrival timings between an XFEL and an optical laser pulses is indispensable to improve the temporal resolution in ultrafast experiments, because an intrinsic temporal resolution that is determined by the temporal duration of x-ray or optical pulse can be significantly deteriorated by a possible timing jitter between these pulses. To solve this issue, X-ray/optical cross-correlators20–29 have been developed at the free-electron laser in Hamburg (FLASH)28,29 and the Linac Coherent Light Source (LCLS).21–27 Intense x-ray irradiation induces an ultrafast change of the electronic states in semiconductor materials; a rapid increase of free-carrier density, resulting from photoabsorption and subsequent electron-electron (electron-phonon) scattering processes, modifies the complex refractive index (). This perturbation is probed by a transient modulation of the optical transmittance or reflectivity. Harmand et al.22 have applied this scheme to determine the relative arrival timing in the hard x-ray regime and achieved an accuracy of sub-10 fs in root-mean-square (RMS).
Recently, Sato et al.20 have successfully reduced the pulse energy required for arrival timing diagnostics from the sub-millijoule order22 to 12 μJ at 12 keV by combining line-shaped focused x-rays with a target comprising high-Z materials that have a small penetration depth of x-rays. Although this method is highly efficient even for short-wavelength x-rays, it does not work as a shot-to-shot monitoring tool for pump-probe experiments owing to its photon-destructive nature. Also, Inubushi et al.30 have developed a dispersive spectrometer with a high resolution of 14 meV, while being in a destructive manner.
If one could perform these photon-destructive diagnostics simultaneously with experiments, one would expect to design advanced experiments with greater flexibilities. In this paper, we propose a scheme using a transmission grating to split an x-ray beam into a main branch and several sub-branches, which are dedicated for experiments and diagnostics, respectively. Similar approaches have been used for building a split-and-delay line7 as well as for spectral monitoring31,32 combined with a thin bent analyzer crystal.33 Here, we utilized the +1st-order and −1st-order branches for measuring the spectrum and the arrival timing jitter, respectively (see Fig. 1(a)), while the 0th-order branch is used for experiments. In Section II, we give a design concept of the optical system implemented at a hard x-ray beamline, BL3,34 of SPring-8 Angstrom Compact Free Electron Laser (SACLA2). In Section III, we describe the results and discussion of proof-of-principle experiments for investigating the performance. Finally, we give a summary and discuss future perspectives in Section IV.
FIG. 1.
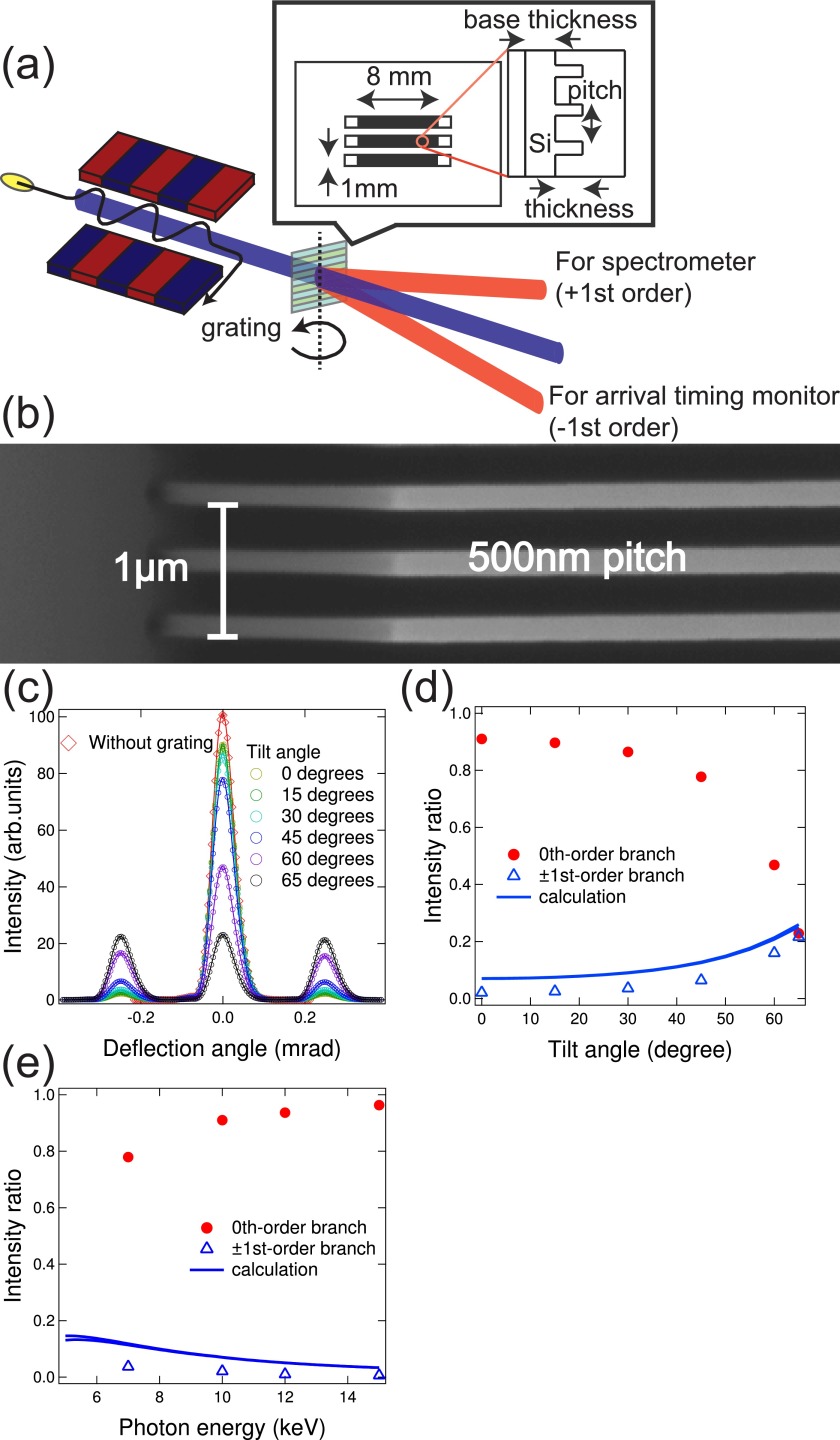
(a) Schematic of the one-dimensional transmission grating working as a beam splitter. The incident x-ray beam from the source is introduced into the grating, which generates multiple branches in the vertical direction. The inset in (a) illustrates the grating shape. (b) Scanning electron microscopy image of the grating with a 500 nm period. (c) Intensities of the split branches for different tilt angles, measured at a photon energy of 10 keV. (d) Diffraction efficiency with respect to the tilt angle (blue triangles). (e) Photon energy dependence of the diffraction efficiency with the tilt angle of 0° (blue triangles). The blue lines in (d) and (e) were obtained by calculation using Eq. (1). The red circles in (d) and (e) are the 0th-order intensities.
II. DESIGN CONCEPT OF OPTICAL SYSTEM
A. Transmission grating beam splitter
As key optics devices in this scheme, we employ one-dimensional transmission gratings with high aspect ratios, which diffract a small fraction of the incoming x-ray beam into multiple branches (Fig. 1(a)). The design parameters of the three gratings are listed in Table I. They were fabricated from thin silicon membranes coated with a 20-nm-thick chromium layer and a 200-nm-thick poly-methylmethacrylate (PMMA) resist layer. The grating lines were defined by electron-beam lithography. After exposure and development, the line patterns were transferred into the chromium layer using chlorine-based dry etching. The chromium layer served as a hard mask for the reactive ion etching into the silicon membranes. These gratings were prepared to cover a wide range of photon energy, although the 500-nm-period grating was used in the present study (Fig. 1(b)). The +1st-order and −1st-order branches propagate in the vertical plane with the deflection angle given by , where is the wavelength and d is the period. At 10 keV ( = 1.24 Å), the period d = 500 nm gives = 0.248 mrad. To control a diffraction efficiency, the grating can be tilted along the vertical axis so as to change its effective thickness (see Fig. 1(a)).35 A large horizontal acceptance of 8 mm allows us to set a tilt angle up to 65°, corresponding to an increase in an effective aspect ratio by a factor of 2.37. For the present diffractive structures with rectangular profiles and a duty cycle of 0.5 (Table I), the first-order diffraction efficiency DE is given by35,36
| (1) |
where z is the effective thickness, is the wavelength, and and are the imaginary and real parts of the complex refractive index, respectively. Figures 1(c) and 1(d) show the angular dependence of DE measured using synchrotron radiation. We obtained DE in the range of 2.1%–21.6% (91.0%–22.8% in the transmitted 0th order) for the tilt angle range of 0°–65°. We observed that the values of DE were slightly smaller than those calculated using Eq. (1), which may be caused by a misalignment of the tilt axis from the ideal orientation perpendicular to both the grating structure and the incoming radiation.
TABLE I.
Design parameters of the transmission gratings.
| No. | 1 | 2 | 3 |
|---|---|---|---|
| Period (nm) | 700 | 500 | 300 |
| Duty cycle | 0.5 | 0.5 | 0.5 |
| Thickness (μm) | 3.8 | 3.8 | 2.8 |
| Base thickness (μm) | 8–10 | 8–10 | 15–20 |
| Spatial acceptance (H × V mm2) | 8 × 1 | 8 × 1 | 8 × 1 |
| Material | Si | Si | Si |
| Profile | Rectangular | Rectangular | Rectangular |
For arrival timing and spectral diagnostics, the tilt angle of 0° is routinely used. We evaluated an intensity loss of the 0th-order main beam by the grating for various photon energies, as shown in Fig. 1(e). The x-ray transmittance was measured to be 78.0%–96.4% (3.70%–0.62% in DE) for the photon energy range of 7–15 keV. Also, we confirmed that the beam profile and the focusing performance of the main beam were unchanged even with the presence of the grating at a tilt angle range below 45°.
B. Arrival timing monitor
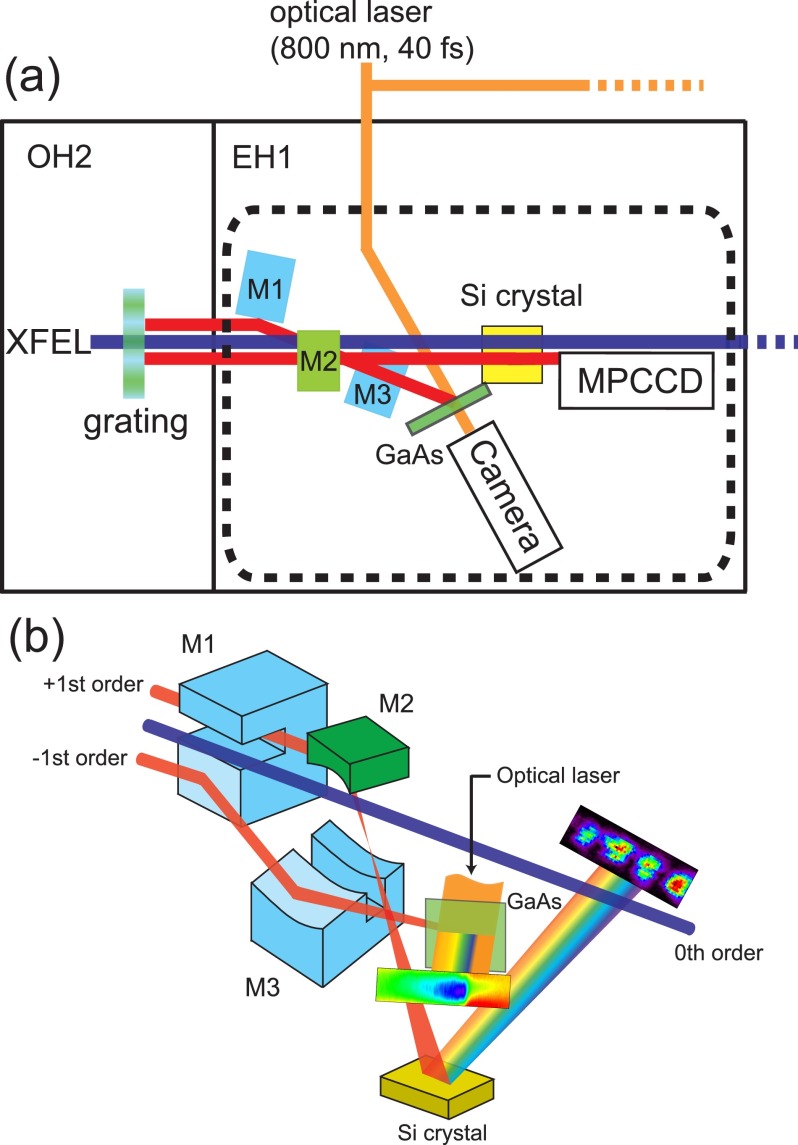
A schematic of the arrival timing monitor is presented in Fig. 2. The x-ray beam in the −1st-order branch is delivered to a flat mirror (M1) located 8.085 m from the grating, which is used for enlarging lateral separation from the 0th-order beam, as shown in Fig. 2(b). Note that M1 has a groove with a cross section of 10 × 5 mm2 so as to avoid interference with other branches. After the horizontal reflection, an elliptical mirror (M3), set at a distance of 0.7 m from M1, is utilized to focus the −1st-order branch vertically on a sample surface with an incident angle of 45°. The footprint on the sample surface is 1500 (H) × 30 (V) μm2. The specifications of the mirrors are listed in Table II.
FIG. 2.
(a) Top-view diagram of the optical system installed at BL3 of SACLA. The grating was installed in the Optics Hutch (OH). The x-ray mirrors (M1–M3), the GaAs wafer, the OPAL camera, the Si analyzer crystal, and the MPCCD detector were placed in Experimental Hutch 1 (EH1). (b) Schematic of the dotted area in (a). The distances among the optics are as follows: grating to M1, 8.085 m; M1 to M2, 0.35 m; M2 to M3, 0.35 m; M3 to GaAs crystal, 2.12 m; M2 to Si crystal, 2.58 m; Si crystal to MPCCD, 0.35 m.
TABLE II.
Specifications of the x-ray mirrors.
| Diagnostics | Arrival timing monitor | Dispersive spectrometer | |
|---|---|---|---|
| X-ray branch | −1st order | +1st order | |
| Reflection geometry | Horizontal | Vertical | Vertical |
| Abbreviation | M1 | M3 | M2 |
| Surface profile | Flat | Elliptical cylinder | Elliptical cylinder |
| Substrate material | Si | SiO2 | SiO2 |
| Surface coating | Rh | Rh | |
| Effective length (mm) | 390 | 408 | 90 |
| Substrate size (mm3) | 400 × 50 × 50 | 420 × 50 × 50 | 100 × 50 × 15 |
| Glancing angle (mrad) | 3 | 1.55 | 2.7 |
| Spatial acceptance (mm) | 1.17 | 0.63 | 0.243 |
| Focal length (m) | 2 | 0.085 | |
| Groove size (mm3) (L × W × D) | 400 × 10 × 5 | 420 × 10 × 5 |
As targets, we use 5-μm-thick gallium arsenide (GaAs) single crystals glued on 500-μm-thick sapphire substrates. As a probe, a synchronized Ti:sapphire laser pulse with a duration of 40 fs and a central wavelength of 800 nm is focused on the sample using a cylindrical lens with a normal incident angle. The full-width at half-maximum (FWHM) spot size is 3500 (H) × 75 (V) μm2. The spatial modulation of the optical transmittance is recorded using a CCD detector (Adimec OPAL 2000D/c) with imaging lenses. The spatial resolution is measured to be 1.1 μm/pixel, which is converted to 2.6 fs/pixel using the optical geometry of the spatial encoding.20
C. Dispersive spectrometer
The +1st-order branch is introduced into a dispersive x-ray spectrometer,30,37 which consists of an elliptical mirror (M2) set at a distance of 8.435 m from the grating, a flat Si analyzer crystal, and a multiport charge-coupled device (MPCCD) detector38 (see Fig. 2). The mirror M2 enlarges the divergence () of the +1st-order branch to 2.5 mrad. The analyzer crystal diffracts x-rays with the wavelength satisfying the Bragg law when the divergent x-rays impinge with different incident angles. The dispersed spectrum is recorded as a spatial intensity distribution on the MPCCD, which has a pixel size of 50 × 50 μm2. The spectral resolution is given by
| (2) |
where , , L, , E, and p are the Bragg angle, the source size, the distance from the source to the detector, the FWHM width of the Darwin curve, the photon energy, and the pixel size of the MPCCD detector, respectively. The spectral range is given by
| (3) |
We prepared Si (111) and Si (220) analyzer crystals to vary the resolution and the spectral range (see Table III) with a range of 10°–80°. This tunability is useful for conducting various types of experiments39,40 as well as for optimizing machine parameters.
TABLE III.
Theoretical parameters of the dispersive spectrometer at 10 keV.
| Index of Si analyzer crystal | Bragg angle (deg) | Resolution (meV) | Spectral range (eV) |
|---|---|---|---|
| 111 | 11.404 | 1567 | 123.9 |
| 220 | 18.838 | 758 | 73.3 |
| 333 | 36.384 | 246 | 33.9 |
| 444 | 52.272 | 140 | 19.3 |
| 660 | 75.623 | 49 | 6.4 |
III. PROOF-OF-PRINCIPLE EXPERIMENTS
To evaluate performance of the system implemented in the beamline, we measured a correlation by performing an independent measurement using the 0th-order branch, which was located at ∼3 m from the system. The central photon energy, the average pulse energy, and the temporal duration of the XFEL pulses were 10 keV, 360 μJ, and ∼5 fs, respectively. DE for the grating was 2.1%, corresponding to an average pulse energy of 7.6 μJ in the ±1st-order branches. The 0th-order beam was attenuated to 7.8 μJ with a 0.5-mm-thick Si attenuator.
A. Arrival timing diagnostics
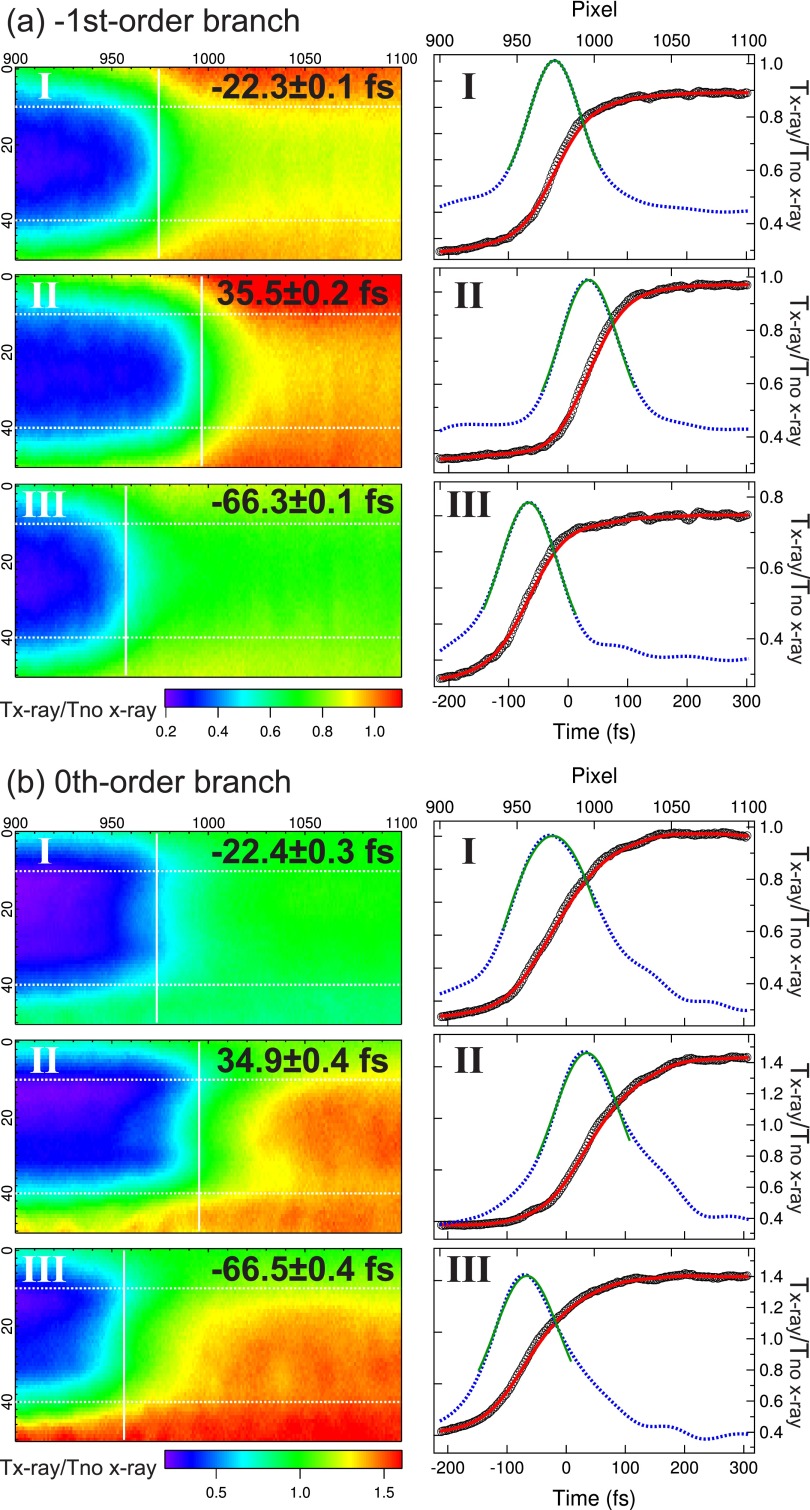
Figure 3 shows background-subtracted images of three consecutive single shots recorded using the −1st-order and the 0th-order branches. A background image was built from an average of 100 shots taken with optical lasers (without x-rays) and was used as a reference for normalization. The temporal overlaps were projected to the horizontal axes of the images. We integrated the intensities of the pixels between the two white dotted lines in each image along the vertical axis and extracted the projection shown as black circles on the right of the images. The upper and the lower axes represent the pixel number and the relative time, respectively. The positive direction in the relative time indicates the earlier irradiation of x-rays with respect to the optical lasers. The vertical axis is the optical transmittance normalized by that without x-ray illumination. Although the normalization process could not eliminate a considerable deviation from unity in the unexcited region owing to fluctuation of the optical intensity and pointing, we observed a sharp change in transmittance of over 50% after x-ray excitation. To analyze the correlation between the two independent measurements, edge positions were retrieved by the following procedure. The projections were smoothed by a low-path filter to remove the noise, which are shown as red lines in Fig. 3. We then obtained the blue dotted lines by differentiating the smoothed red lines and fitted the regions around the peaks with Gaussian functions. The resultant fitted curves are shown as green lines. We defined the Gaussian centers obtained as the relative timing values. Note that we determined the conversion coefficient from the pixels to the timings by mapping the average peak positions while scanning the optical delay. The conversion coefficient was determined to be 2.6 fs/pixel, which agreed with a value expected from the optical geometry. The arrival timings, shown as vertical white lines in the images, exhibit shot-to-shot variation because of the intrinsic temporal jitter. We observed an excellent agreement between the two sets of arrival timing values presented in the images. The average error bars of the Gaussian centers in the fitting procedure were 0.14 fs and 0.35 fs for the −1st-order and 0th-order branches, respectively. The temporal width of the change in transmittance, which is the FWHM of the Gaussian profile, was typically ∼100 fs. This length corresponds to the convolution of the temporal durations of the XFEL and optical laser pulses, and inherent electronic responses of the sample with respect to x-ray excitation.
FIG. 3.
Single-shot images and projections recorded using the −1st-order (a) and the 0th-order (b) branches. Roman numerals (I, II, and III) are used to identify each pulse in both (a) and (b). The Gaussian fitting range was 60 pixels around the maximum point of the first derivatives. The resultant Gaussian centers are shown as the vertical white lines in the images.
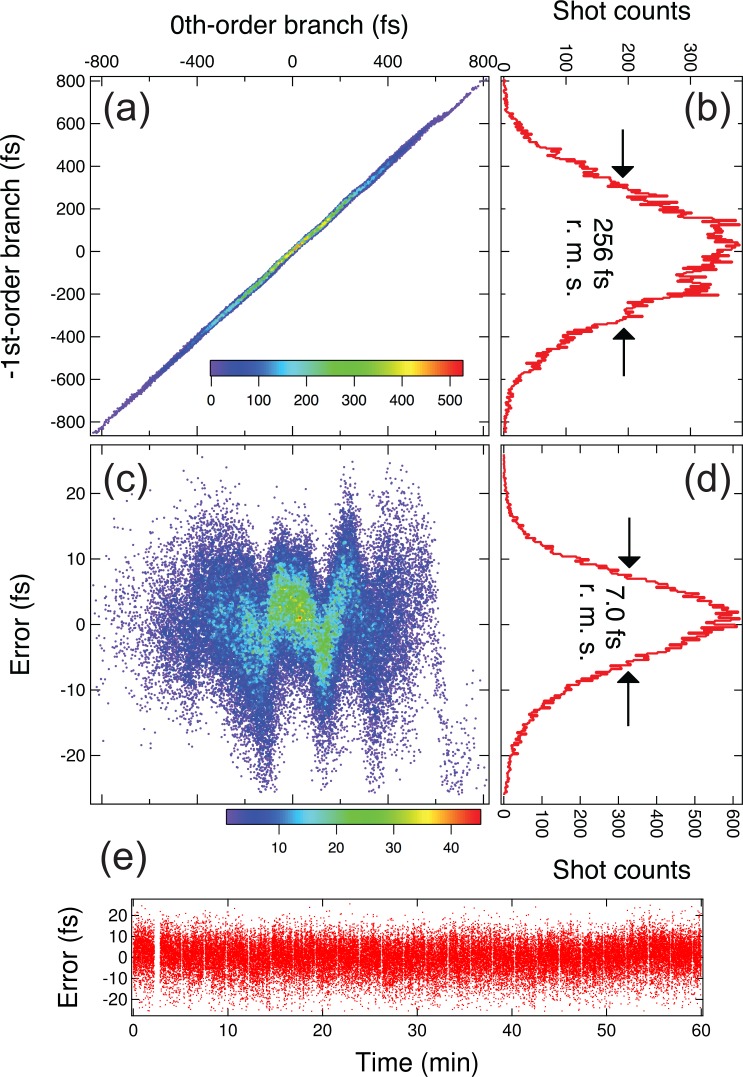
On the basis of this analysis, we collected 47 220 images and determined the arrival timing for each shot. The scatter plot in Fig. 4(a) presents the correlation between the arrival timings of the −1st-order and 0th-order branches. The temporal jitter can be seen in the top right histogram (Fig. 4(b)), where the RMS width was 256 fs (FWHM = 603 fs). The correlation between the two diagnostics was obtained by linear least squares fitting. The residual error of the fitting, which is defined as the overall accuracy, is plotted in Fig. 4(c). The systematic error may have originated from mechanical vibrations of the optics and the samples, optical pointing fluctuations, and imperfection of the sample flatness. We note that further correction of this systematic error may be achieved by applying a nonlinear pixel-to-time calibration, as performed in Ref. 22. The error histogram in Fig. 4(d) has the RMS width of 7.0 fs (FWHM = 16.5 fs). This sub-10 fs accuracy should allow the temporal resolution to be improved down to the femtosecond regime, which is mainly governed by the temporal duration of the optical lasers after re-sorting the data to remove the jitter. Moreover, the error variation was stable over 1 h (Fig. 4(e)), assuring a long-term reliable operation of arrival timing diagnostics.
FIG. 4.
(a) Scatter plot colored by density showing the correlation between the arrival timings of the two monitors. (b) Histogram showing the temporal jitter. The bin width was 5 fs. (c) Residual errors after the linear fitting of the scatter plot. (d) Histogram corresponding to (c) with a bin width of 0.2 fs. (e) Time dependence of the residual errors.
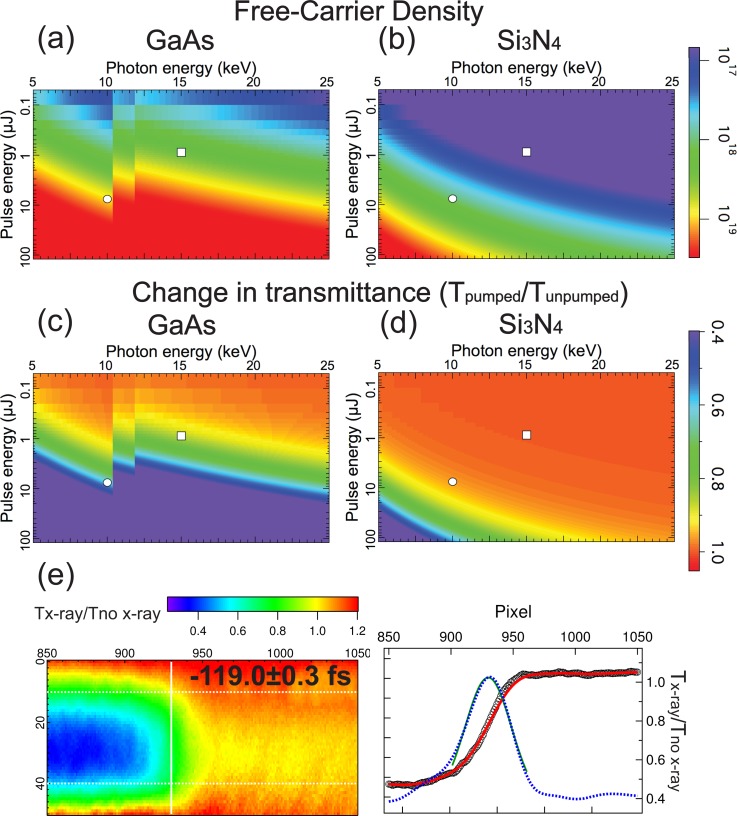
Next, we investigated an applicable range of the photon energy. For this purpose, we simulated the expected signal using the Drude model41,42 and the Fresnel formula. First, the free-carrier density (N) created in bulk matter was estimated (see Figs. 5(a) and 5(b)). Assuming a uniform distribution of hot carriers (electron and hole pairs) in the medium, the free-carrier density is given by
| (4) |
where E0, Eb, , A, l, and are the incoming pulse energy, the band gap of the target material, the incident angle of the x-ray beam, the footprint size, the sample thickness, and the penetration depth, respectively. Under our experimental conditions, the carrier density in the GaAs crystal was calculated to be 9.3 × 1018 cm−3 (white circle in Fig. 5(a)), which is about one order of magnitude higher than that of a silicon nitride (Si3N4) membrane with the same thickness (see Fig. 5(b)). The steep edges at 10.367 keV and 11.867 keV in Fig. 5(a) originate from the Ga and As K edge, respectively. Using the free-carrier density, the complex dielectric function in the excited state is given by
| (5) |
| (6) |
| (7) |
where is the dielectric function in the un-pumped ground state, we and wh are the plasma frequencies of electrons and holes, and me(mh), , (), e, and w are the effective mass of electrons (holes), the vacuum permittivity, the damping factors of electrons (holes), the elementary charge, and the angular momentum of the probe light, respectively. Using the Fresnel formula and dielectric function, the transmittance of the optical laser T(w) at normal incidence is given by
| (8) |
where t1, t2, , and are Fresnel coefficients, and c is the speed of light. By integrating Eq. (8) over the spectral range of the probe (the FWHM bandwidth was 47 nm and the central wavelength was 800 nm), we estimated the transmittance modulation of GaAs as shown in Fig. 5(c). The expected change in the optical transmission was 0.59, which well agreed with the observation. We emphasize that such a significantly high response of the optical transmission (>30%) is simply predicted over a wide photon energy range (5–25 keV) with a pulse energy of less than 10 μJ. For the Si3N4 membrane with the same thickness, a change of 3%–4% was calculated (Fig. 5(d)). A higher photon energy leads to further reduction of the signal intensity. Experimentally, we confirmed an applicability of GaAs to short-wavelength measurements by performing a similar measurement at a photon energy of 15 keV (Fig. 5(e)), which showed a high optical response over 50%.
FIG. 5.
Carrier densities ((a) and (b)) and transmittance modulation ((c) and (d)) simulated for GaAs ((a) and (c)) and Si3N4 ((b) and (d)). The thickness was assumed to be 5 μm for both the GaAs crystal and the Si3N4 membrane. The horizontal and vertical axes are the photon energy and pulse energy of the XFEL, respectively. The white circles correspond to the pulse energy at 10 keV. We used parameters me, mh, , and of 0.065, 0.45, 0.5, and 0.5 for GaAs and 0.3, 0.3, 0.5, and 0.5 for Si3N4, respectively. (e) Single-shot image and projection of the −1st-order branch with a photon energy of 15 keV. The white squares in (a)-(d) correspond to the pulse energy (0.97 μJ in the total 157 μJ) at 15 keV.
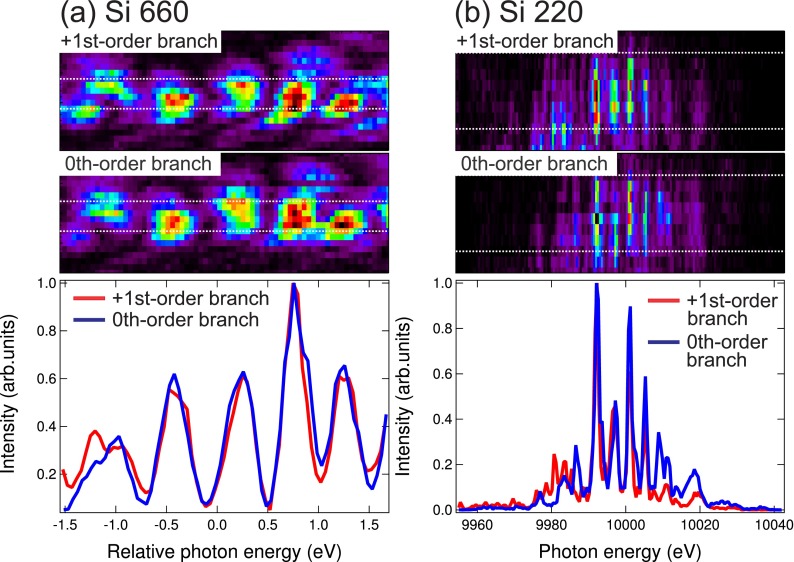
B. High resolution spectral measurement
Figure 6 presents the single-shot spectra of the +1st-order and 0th-order branches. Using a Si (660) reflecting plane, the spike features of SASE radiation were completely resolved (Fig. 6(a)). The spectral range of these two spectrometers was 6.4 eV in Table III, while we showed spectra only in an overlap area (∼3 eV) between them in Fig. 6(a). We found reasonable agreement in both an energy dispersion (horizontal) and a spatial chirp (vertical) direction between the spectra. These results indicated that the chromatic dispersion effect induced by the diffraction at the grating was negligible in the +1st-order branch. The average spike width was determined to be 470 meV. Note that we can easily switch the reflecting plane to a lower index of Si (220), for example, in order to cover a wider bandwidth, as shown in Fig. 6(b).
FIG. 6.
(a) Single-shot spectra measured with Si (660) analyzer crystals using the +1st-order (red line) and the 0th-order (blue line) branches. The center of the relative photon energy corresponds to 9999.75 eV. (b) Wide-range single-shot spectra measured with the Si (220) analyzer crystal. The white dotted lines in (a) and (b) represent the area of integration used to extract the spectra.
IV. SUMMARY
We have developed a beam branching method for enabling advanced photon diagnostics with small perturbation using a grating beam splitter. The 0th-order transmission branch, which keeps over 90% of the original intensity at 10 keV, is provided for a diverse range of applications. By measuring the correlation between the arrival timings of the −1st-order and 0th-order branches, we found that the RMS error in the arrival timing diagnostics was below 10 fs. The calculation verified the applicability of GaAs for higher photon energies of up to 25 keV with a pulse energy of less than 10 μJ. Further improvement of the temporal resolution will be explored by implementation of an optical laser with a shorter temporal duration.
The spectral property of SASE-XFEL light was characterized using the +1st-order branch with tunability of a spectral range and a resolution. This scheme will play an important role in a broad range of experiments with the SASE and the self-seeding43 operations.
ACKNOWLEDGMENTS
We are grateful to the supporting members of SACLA. We appreciate Dr. Yoshiki Kohmura for the help in evaluation of the grating performance at BL29XU of SPring-8. We also thank Dr. Muneaki Hase of the University of Tsukuba for the fruitful discussion. The experiments were performed with the approval of Japan Synchrotron Radiation Research Institute (JASRI, proposal Nos. 2014B8071, 2014A8053, and 2013B8072).
References
- 1. Emma P., Akre R., Arthur J., Bionta R., Bostedt C., Bozek J., Brachmann A., Bucksbaum P., Coffee R., Decker F. J., Ding Y., Dowell D., Edstrom S., Fisher A., Frisch J., Gilevich S., Hastings J., Hays G., Hering P., Huang Z., Iverson R., Loos H., Messerschmidt M., Miahnahri A., Moeller S., Nuhn H. D., Pile G., Ratner D., Rzepiela J., Schultz D., Smith T., Stefan P., Tompkins H., Turner J., Welch J., White W., Wu J., Yocky G., and Galayda J., “ First lasing and operation of an ångstrom-wavelength free-electron laser,” Nat. Photonics 4, 641–647 (2010). 10.1038/nphoton.2010.176 [DOI] [Google Scholar]
- 2. Ishikawa T., Aoyagi H., Asaka T., Asano Y., Azumi N., Bizen T., Ego H., Fukami K., Fukui T., Furukawa Y., Goto S., Hanaki H., Hara T., Hasegawa T., Hatsui T., Higashiya A., Hirono T., Hosoda N., Ishii M., Inagaki T., Inubushi Y., Itoga T., Joti Y., Kago M., Kameshima T., Kimura H., Kirihara Y., Kiyomichi A., Kobayashi T., Kondo C., Kudo T., Maesaka H., Marechal X. M., Masuda T., Matsubara S., Matsumoto T., Matsushita T., Matsui S., Nagasono M., Nariyama N., Ohashi H., Ohata T., Ohshima T., Ono S., Otake Y., Saji C., Sakurai T., Sato T., Sawada K., Seike T., Shirasawa K., Sugimoto T., Suzuki S., Takahashi S., Takebe H., Takeshita K., Tamasaku K., Tanaka H., Tanaka R., Tanaka T., Togashi T., Togawa K., Tokuhisa A., Tomizawa H., Tono K., Wu S. K., Yabashi M., Yamaga M., Yamashita A., Yanagida K., Zhang C., Shintake T., Kitamura H., and Kumagai N., “ A compact X-ray free-electron laser emitting in the sub-ångström region,” Nat. Photonics 6, 540–544 (2012). 10.1038/nphoton.2012.141 [DOI] [Google Scholar]
- 3. McNeil B. W. J. and Thompson N. R., “ X-ray free-electron lasers,” Nat. Photonics 4, 814–821 (2010). 10.1038/nphoton.2010.239 [DOI] [Google Scholar]
- 4. Kim K. H., Kim J. G., Nozawa S., Sato T., Oang K. Y., Kim T. W., Ki H., Jo J., Park S., Song C., Sato T., Ogawa K., Togashi T., Tono K., Yabashi M., Ishikawa T., Kim J., Ryoo R., Kim J., Ihee H., and Adachi S., “ Direct observation of bond formation in solution with femtosecond X-ray scattering,” Nature 518, 385–389 (2015). 10.1038/nature14163 [DOI] [PubMed] [Google Scholar]
- 5. Wernet Ph., Kunnus K., Josefsson I., Rajkovic I., Quevedo W., Beye M., Schreck S., Grübel S., Scholz M., Nordlund D., Zhang W., Hartsock R. W., Schlotter W. F., Turner J. J., Kennedy B., Hennies F., de Groot F. M. F., Gaffney K. J., Techert S., Odelius M., and Föhlisch A., “ Orbital-specific mapping of the ligand exchange dynamics of Fe(CO)5 in solution,” Nature 520, 78–81 (2015). 10.1038/nature14296 [DOI] [PubMed] [Google Scholar]
- 6. Ogi Y., Obara Y., Katayama T., Suzuki Y.-I., Liu S. Y., Bartlett N. C.-M., Kurahashi N., Karashima S., Togashi T., Inubushi Y., Ogawa K., Owada S., Rubešová M., Yabashi M., Misawa K., Slavíček P., and Suzuki T., “ Ultraviolet photochemical reaction of [Fe(III)(C2O4)3]3− in aqueous solutions studied by femtosecond time-resolved X-ray absorption spectroscopy using an X-ray free electron laser,” Struct. Dyn. 2, 034901 (2015). 10.1063/1.4918803 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. David C., Karvinen P., Sikorski M., Song S., Vartiainen I., Milne C. J., Mozzanica A., Kayser Y., Diaz A., Mohacsi I., Carini G. A., Herrmann S., Färm E., Ritala M., Fritz D. M., and Robert A., “ Following the dynamics of matter with femtosecond precision using the X-ray streaking method,” Sci. Rep. 5, 7644 (2015). 10.1038/srep07644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Trigo M., Fuchs M., Chen J., Jiang M. P., Cammarata M., Fahy S., Fritz D. M., Gaffney K., Ghimire S., Higginbotham A., Johnson S. L., Kozina M. E., Larsson J., Lemke H., Lindenberg A. M., Ndabashimiye G., Quirin F., Sokolowski-Tinten K., Uher C., Wang G., Wark J. S., Zhu D., and Reis D. A., “ Fourier-transform inelastic X-ray scattering from time- and momentum-dependent phonon-phonon correlations,” Nat. Phys. 9, 790–794 (2013). 10.1038/nphys2788 [DOI] [Google Scholar]
- 9. Tamasaku K., Shigemasa E., Inubushi Y., Katayama T., Sawada K., Yumoto H., Ohashi H., Mimura H., Yabashi M., Yamauchi K., and Ishikawa T., “ X-ray two-photon absorption competing against single and sequential multiphoton processes,” Nat. Photonics 8, 313–316 (2014). 10.1038/nphoton.2014.10 [DOI] [Google Scholar]
- 10. Yoneda H., Inubushi Y., Yabashi M., Katayama T., Ishikawa T., Ohashi H., Yumoto H., Yamauchi K., Mimura H., and Kitamura H., “ Saturable absorption of intense hard X-rays in iron,” Nat. Commun. 5, 5080 (2014). 10.1038/ncomms6080 [DOI] [PubMed] [Google Scholar]
- 11. Yoneda H., Inubushi Y., Nagamine K., Michine Y., Ohashi H., Yumoto H., Yamauchi K., Mimura H., Kitamura H., Katayama T., Ishikawa T., and Yabashi M., “ Atomic inner-shell laser at 1.5-ångström wavelength pumped by an X-ray free-electron laser,” Nature 524, 446–449 (2015). 10.1038/nature14894 [DOI] [PubMed] [Google Scholar]
- 12. Beye M., Schreck S., Sorgenfrei F., Trabant C., Pontius N., Schüßler-Langeheine C., Wurth W., and Föhlisch A., “ Stimulated X-ray emission for materials science,” Nature 501, 191–194 (2013). 10.1038/nature12449 [DOI] [PubMed] [Google Scholar]
- 13. Rohringer N., Ryan D., London R. A., Purvis M., Albert F., Dunn J., Bozek J. D., Bostedt C., Graf A., Hill R., Hau-Riege S. P., and Rocca J. J., “ Atomic inner-shell x-ray laser at 1.46 nanometres pumped by an X-ray free-electron laser,” Nature 481, 488–491 (2012). 10.1038/nature10721 [DOI] [PubMed] [Google Scholar]
- 14. Suga M., Akita F., Hirata K., Ueno G., Murakami H., Nakajima Y., Shimizu T., Yamashita K., Yamamoto M., Ago H., and Shen J. R., “ Native structure of photosystem II at 1.95 Å resolution viewed by femtosecond X-ray pulses,” Nature 517, 99–103 (2015). 10.1038/nature13991 [DOI] [PubMed] [Google Scholar]
- 15. Hirata K., Shinzawa-Itoh K., Yano N., Takemura S., Kato K., Hatanaka M., Muramoto K., Kawahara T., Tsukihara T., Yamashita E., Tono K., Ueno G., Hikima T., Murakami H., Inubushi Y., Yabashi M., Ishikawa T., Yamamoto M., Ogura T., Sugimoto H., Shen J. R., Yoshikawa S., and Ago H., “ Determination of damage-free crystal structure of an X-ray-sensitive protein using an XFEL,” Nat. Methods 11, 734–736 (2014). 10.1038/nmeth.2962 [DOI] [PubMed] [Google Scholar]
- 16. Chapman H. N., Fromme P., Barty A., White T. A., Kirian R. A., Aquila A., Hunter M. S., Schulz J., DePonte D. P., Weierstall U., Doak R. B., Maria F. R. N. C., Martin A. V., Schlichting I., Lomb L., Coppola N., Shoeman R. L., Epp S. W., Hartmann R., Rolles D., Rudenko A., Foucar L., Kimmel N., Weidenspointner G., Holl P., Liang M., Barthelmess M., Caleman C., Boutet S., Bogan M. J., Krzywinski J., Bostedt C., Bajt S., Gumprecht L., Rudek B., Erk B., Schmidt C., Hömke A., Reich C., Pietschner D., Strüder L., Hauser G., Gorke H., Ullrich J., Herrmann S., Schaller G., Schopper F., Soltau H., Kühnel K. U., Messerschmidt M., Bozek J. D., Hau-Riege S. P., Frank M., Hampton C. Y., Sierra R. G., Starodub D., Williams G. J., Hajdu J., Timneanu N., Seibert M. M., Andreasson J., Rocker A., Jönsson O., Svenda M., Stern S., Nass K., Andritschke R., Schröter C. D., Krasniqi F., Bott M., Schmidt K. E., Wang X., Grotjohann I., Holton J. M., Barends T. R. M., Neutze R., Marchesini S., Fromme R., Schorb S., Rupp D., Adolph M., Gorkhover T., Andersson I., Hirsemann H., Potdevin G., Graafsma H., Nilsson B., and Spence J. C. H., “ Femtosecond X-ray protein nanocrystallography,” Nature 470, 73–77 (2011). 10.1038/nature09750 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Saldin E. L., Schneidmiller E. A., Shvyd'ko Y. V., and Yurkov M. V., “ X-ray FEL with a meV bandwidth,” Nucl. Instrum. Methods Phys. Res. A 475, 357–362 (2001). 10.1016/S0168-9002(01)01539-X [DOI] [Google Scholar]
- 18. Saldin E. L., Schneidmiller E. A., and Yurkov M. V., “ Statistical and coherence properties of radiation from x-ray free-electron lasers,” New J. Phys. 12, 035010 (2010). 10.1088/1367-2630/12/3/035010 [DOI] [Google Scholar]
- 19. Tono K., Kudo T., Yabashi M., Tachibana T., Feng Y., Fritz D., Hastings J., and Ishikawa T., “ Single-shot beam-position monitor for x-ray free electron laser,” Rev. Sci. Instrum. 82, 023108 (2011). 10.1063/1.3549133 [DOI] [PubMed] [Google Scholar]
- 20. Sato T., Togashi T., Ogawa K., Katayama T., Inubushi Y., Tono K., and Yabashi M., “ Highly efficient arrival timing diagnostics for femtosecond X-ray and optical laser pulses,” Appl. Phys. Express 8, 012702 (2015). 10.7567/APEX.8.012702 [DOI] [Google Scholar]
- 21. Hartmann N., Helml W., Galler A., Bionta M. R., Grünert J., Molodtsov S. L., Ferguson K. R., Schorb S., Swiggers M. L., Carron S., Bostedt C., Castagna J.-C., Bozek J., Glownia J. M., Kane D. J., Fry A. R., White W. E., Hauri C. P., Feurer T., and Coffee R. N., “ Sub-femtosecond precision measurement of relative X-ray arrival time for free-electron lasers,” Nat. Photonics 8, 706–709 (2014). 10.1038/nphoton.2014.164 [DOI] [Google Scholar]
- 22. Harmand M., Coffee R., Bionta M. R., Chollet M., French D., Zhu D., Fritz D. M., Lemke H. T., Medvedev N., Ziaja B., Toleikis S., and Cammarata M., “ Achieving few-femtosecond time-sorting at hard X-ray free-electron lasers,” Nat. Photonics 7, 215–218 (2013). 10.1038/nphoton.2013.11 [DOI] [Google Scholar]
- 23. Bionta M. R., Hartmann N., Weaver M., French D., Nicholson D. J., Cryan J. P., Glownia J. M., Baker K., Bostedt C., Chollet M., Ding Y., Fritz D. M., Schorb S., Zhu D., White W. E., and Coffee R. N., “ Spectral encoding method for measuring the relative arrival time between x-ray/optical pulses,” Rev. Sci. Instrum. 85, 083116 (2014). 10.1063/1.4893657 [DOI] [PubMed] [Google Scholar]
- 24. Schorb S., Gorkhover T., Cryan J. P., Glownia J. M., Bionta M. R., Coffee R. N., Erk B., Boll R., Schmidt C., Rolles D., Rudenko A., Rouzee A., Swiggers M., Carron S., Castagna J.-C., Bozek J. D., Messerschmidt M., Schlotter W. F., and Bostedt C., “ X-ray-optical cross-correlator for gas-phase experiments at the Linac coherent light source free-electron laser,” Appl. Phys. Lett. 100, 121107 (2012). 10.1063/1.3695163 [DOI] [Google Scholar]
- 25. Beye M., Krupin O., Hays G., Reid A. H., Rupp D., de Jong S., Lee S., Lee W.-S., Chuang Y.-D., Coffee R., Cryan J. P., Glownia J. M., Föhlisch A., Holmes M. R., Fry A. R., White W. E., Bostedt C., Scherz A. O., Durr H. A., and Schlotter W. F., “ X-ray pulse preserving single-shot optical cross-correlation method for improved experimental temporal resolution,” Appl. Phys. Lett. 100, 121108 (2012). 10.1063/1.3695164 [DOI] [Google Scholar]
- 26. Krupin O., Trigo M., Schlotter W. F., Beye M., Sorgenfrei F., Turner J. J., Reis D. A., Gerken N., Lee S., Lee W. S., Hays G., Acremann Y., Abbey B., Coffee R., Messerschmidt M., Hau-Riege S. P., Lapertot G., Lüning J., Heimann P., Soufli R., Fernández-Perea M., Rowen M., Holmes M., Molodtsov S. L., Föhlisch A., and Wurth W., “ Temporal cross-correlation of x-ray free electron and optical lasers using soft x-ray pulse induced transient reflectivity,” Opt. Express 20, 11396–11406 (2012). 10.1364/OE.20.011396 [DOI] [PubMed] [Google Scholar]
- 27. Bionta M. R., Lemke H. T., Cryan J. P., Glownia J. M., Bostedt C., Cammarata M., Castagna J.-C., Ding Y., Fritz D. M., Fry A. R., Krzywinski J., Messerschmidt M., Schorb S., Swiggers M. L., and Coffee R. N., “ Spectral encoding of x-ray/optical relative delay,” Opt. Express 19, 21855–21865 (2011). 10.1364/OE.19.021855 [DOI] [PubMed] [Google Scholar]
- 28. Gahl C., Azima A., Beye M., Deppe M., Döbrich K., Hasslinger U., Hennies F., Melnikov A., Nagasono M., Pietzsch A., Wolf M., Wurth W., and Föhlisch A., “ A femtosecond X-ray/optical cross-correlator,” Nat. Photonics 2, 165–169 (2008). 10.1038/nphoton.2007.298 [DOI] [Google Scholar]
- 29. Maltezopoulos T., Cunovic S., Wieland M., Beye M., Azima A., Redlin H., Krikunova M., Kalms R., Frühling U., Budzyn F., Wurth W., Föhlisch A., and Drescher M., “ Single-shot timing measurement of extreme-ultraviolet free-electron laser pulses,” New J. Phys. 10, 033026 (2008). 10.1088/1367-2630/10/3/033026 [DOI] [Google Scholar]
- 30. Inubushi Y., Tono K., Togashi T., Sato T., Hatsui T., Kameshima T., Togawa K., Hara T., Tanaka T., Tanaka H., Ishikawa T., and Yabashi M., “ Determination of the pulse duration of an X-ray free electron laser using highly resolved single-shot spectra,” Phys. Rev. Lett. 109, 144801 (2012). 10.1103/PhysRevLett.109.144801 [DOI] [PubMed] [Google Scholar]
- 31. Karvinen P., Rutishauser S., Mozzanica A., Greiffenberg D., Juranić P. N., Menzel A., Lutman A., Krzywinski J., Fritz D. M., Lemke H. T., Cammarata M., and David C., “ Single-shot analysis of hard x-ray laser radiation using a noninvasive grating spectrometer,” Opt. Lett. 37, 5073–5075 (2012). 10.1364/OL.37.005073 [DOI] [PubMed] [Google Scholar]
- 32. Makita M., Karvinen P., Zhu D., Juranic P. N., Grünert J., Cartier S., Jungmann-Smith J. H., Lemke H. T., Mozzanica A., Nelson S., Patthey L., Sikorski M., Song S., Feng Y., and David C., “ High-resolution single-shot spectral monitoring of hard x-ray free-electron laser radiation,” Optica 2, 912–916 (2015). 10.1364/OPTICA.2.000912 [DOI] [Google Scholar]
- 33. Zhu D., Cammarata M., Feldkamp J. M., Fritz D. M., Hastings J. B., Lee S., Lemke H. T., Robert A., Turner J. L., and Feng Y., “ A single-shot transmissive spectrometer for hard x-ray free electron lasers,” Appl. Phys. Lett. 101, 034103 (2012). 10.1063/1.4736725 [DOI] [Google Scholar]
- 34. Tono K., Togashi T., Inubushi Y., Sato T., Katayama T., Ogawa K., Ohashi H., Kimura H., Takahashi S., Takeshita K., Tomizawa H., Goto S., Ishikawa T., and Yabashi M., “ Beamline, experimental stations and photon beam diagnostics for the hard x-ray free electron laser of SACLA,” New J. Phys. 15, 083035 (2013). 10.1088/1367-2630/15/8/083035 [DOI] [Google Scholar]
- 35. David C., Nöhammer B., and Ziegler E., “ Wavelength tunable diffractive transmission lens for hard x rays,” Appl. Phys. Lett. 79, 1088–1090 (2001). 10.1063/1.1379364 [DOI] [Google Scholar]
- 36. Schnopper H. W., Van Speybroeck L. P., Delvaille J. P., Epstein A., Källne E., Bachrach R. Z., Dijkstra J., and Lantward L., “ Diffraction grating transmission efficiencies for XUV and soft x rays,” Appl. Opt. 16, 1088–1091 (1977). 10.1364/AO.16.001088 [DOI] [PubMed] [Google Scholar]
- 37. Yabashi M., Hastings J. B., Zolotorev M. S., Mimura H., Yumoto H., Matsuyama S., Yamauchi K., and Ishikawa T., “ Single-shot spectrometry for X-ray free-electron lasers,” Phys. Rev. Lett. 97, 084802 (2006). 10.1103/PhysRevLett.97.084802 [DOI] [PubMed] [Google Scholar]
- 38. Kameshima T., Ono S., Kudo T., Ozaki K., Kirihara Y., Kobayashi K., Inubushi Y., Yabashi M., Horigome T., Holland A., Holland K., Burt D., Murao H., and Hatsui T., “ Development of an X-ray pixel detector with multi-port charge-coupled device for X-ray free-electron laser experiments,” Rev. Sci. Instrum. 85, 033110 (2014). 10.1063/1.4867668 [DOI] [PubMed] [Google Scholar]
- 39. Katayama T., Inubushi Y., Obara Y., Sato T., Togashi T., Tono K., Hatsui T., Kameshima T., Bhattacharya A., Ogi Y., Kurahashi N., Misawa K., Suzuki T., and Yabashi M., “ Femtosecond x-ray absorption spectroscopy with hard x-ray free electron laser,” Appl. Phys. Lett. 103, 131105 (2013). 10.1063/1.4821108 [DOI] [Google Scholar]
- 40. Obara Y., Katayama T., Ogi Y., Suzuki T., Kurahashi N., Karashima S., Chiba Y., Isokawa Y., Togashi T., Inubushi Y., Yabashi M., Suzuki T., and Misawa K., “ Femtosecond time-resolved X-ray absorption spectroscopy of liquid using a hard X-ray free electron laser in a dual-beam dispersive detection method,” Opt. Express 22, 1105–1113 (2014). 10.1364/OE.22.001105 [DOI] [PubMed] [Google Scholar]
- 41. Ashcroft N. W. and Mermin N. D., Solid State Physics ( Brooks/Cole, 1976). [Google Scholar]
- 42. Mao S. S., Quéré F., Guizard S., Mao X., Russo R. E., Petite G., and Martin P., “ Dynamics of femtosecond laser interactions with dielectrics,” Appl. Phys. A 79, 1695–1709 (2004). 10.1007/s00339-004-2684-0 [DOI] [Google Scholar]
- 43. Amann J., Berg W., Blank V., Decker F.-J., Ding Y., Emma P., Feng Y., Frisch J., Fritz D., Hastings J., Huang Z., Krzywinski J., Lindberg R., Loos H., Lutman A., Nuhn H.-D., Ratner D., Rzepiela J., Shu D., Shvyd'ko Y., Spampinati S., Stoupin S., Terentyev S., Trakhtenberg E., Walz D., Welch J., Wu J., Zholents A., and Zhu D., “ Demonstration of self-seeding in a hard-X-ray free-electron laser,” Nat. Photonics 6, 693–698 (2012). 10.1038/nphoton.2012.180 [DOI] [Google Scholar]