Abstract
Purpose:
To deliver high quality intensity modulated radiotherapy (IMRT) using a novel generalized sparse orthogonal collimators (SOCs), the authors introduce a novel direct aperture optimization (DAO) approach based on discrete rectangular representation.
Methods:
A total of seven patients—two glioblastoma multiforme, three head & neck (including one with three prescription doses), and two lung—were included. 20 noncoplanar beams were selected using a column generation and pricing optimization method. The SOC is a generalized conventional orthogonal collimators with N leaves in each collimator bank, where N = 1, 2, or 4. SOC degenerates to conventional jaws when N = 1. For SOC-based IMRT, rectangular aperture optimization (RAO) was performed to optimize the fluence maps using rectangular representation, producing fluence maps that can be directly converted into a set of deliverable rectangular apertures. In order to optimize the dose distribution and minimize the number of apertures used, the overall objective was formulated to incorporate an L2 penalty reflecting the difference between the prescription and the projected doses, and an L1 sparsity regularization term to encourage a low number of nonzero rectangular basis coefficients. The optimization problem was solved using the Chambolle–Pock algorithm, a first-order primal–dual algorithm. Performance of RAO was compared to conventional two-step IMRT optimization including fluence map optimization and direct stratification for multileaf collimator (MLC) segmentation (DMS) using the same number of segments. For the RAO plans, segment travel time for SOC delivery was evaluated for the N = 1, N = 2, and N = 4 SOC designs to characterize the improvement in delivery efficiency as a function of N.
Results:
Comparable PTV dose homogeneity and coverage were observed between the RAO and the DMS plans. The RAO plans were slightly superior to the DMS plans in sparing critical structures. On average, the maximum and mean critical organ doses were reduced by 1.94% and 1.44% of the prescription dose. The average number of delivery segments was 12.68 segments per beam for both the RAO and DMS plans. The N = 2 and N = 4 SOC designs were, on average, 1.56 and 1.80 times more efficient than the N = 1 SOC design to deliver. The mean aperture size produced by the RAO plans was 3.9 times larger than that of the DMS plans.
Conclusions:
The DAO and dose domain optimization approach enabled high quality IMRT plans using a low-complexity collimator setup. The dosimetric quality is comparable or slightly superior to conventional MLC-based IMRT plans using the same number of delivery segments. The SOC IMRT delivery efficiency can be significantly improved by increasing the leaf numbers, but the number is still significantly lower than the number of leaves in a typical MLC.
Keywords: sparse orthogonal collimator, rectangular representation, direct aperture optimization, IMRT
1. INTRODUCTION
Intensity modulated radiation therapy (IMRT) is a cornerstone of modern radiation therapy physics. By modulating the incident x-ray intensities, IMRT has provided unprecedented control over x-ray dose distributions to target tumors and spare normal tissues. IMRT was afforded by the development of inverse optimization algorithms and enabling hardware. With a few exceptions, such as the compensator based IMRT,1–5 the multileaf collimator (MLC) that consists of a large number of thin moving tungsten leaves has been the dedicated device to modulate the x-ray fluence. Due to considerations including the mechanical complexity, cost, accessibility and reliability of early MLCs, attempts have been made to use only the orthogonal jaws on conventional Linacs for IMRT.6–8 Jaws-only IMRT requires the entire IMRT plan to be delivered using exclusively rectangular apertures. Different methods were reported to generate these apertures, including fluence stripping9 and direct aperture optimization (DAO).7 In the former method, a fluence optimization was first performed and the resulting fluence was subsequently stripped to rectangles for jaws-only delivery. The method inevitably suffered from dosimetric quality compromise and low delivery efficiency due to sequential simplification of the fluence maps. To address these difficulties, additional collimator devices such as masks8 and rotational and dynamic jaws10 have been theorized. The DAO approach was incorporated into a commercial planning system.7 This approach utilized a simulated annealing process to search and select rectangular apertures that minimized an objective function. It was shown that for simple cases, the jaws-only IMRT can achieve superior plan quality to 3D conformal plans.11 In a follow up study, Mu and Xia showed that even for more complex head and neck IMRT plans, the jaws-only approach can result in acceptable dosimetry, at a cost of longer delivery time.6
With the maturation of MLC technology, the problems that plagued early MLC devices, such as reliability and cost, have been mitigated. However, there is still a need to miniaturize the dose modulator for purposes including small animal irradiator, robotic Linac, and high resolution dose modulation where reducing the leaf thickness for the application is no longer feasible, or the reduction requires significant compromise in field size, reliability, and interleaf leakage. For these applications, the jaws-only IMRT may still be viable but its viability clearly depends on whether its limitations in dosimetry quality and delivery efficiency can be overcome by new algorithms, hardware development, and the presence of proper applications. Recently, we described a formulation of the inverse optimization problem that consists of an L2 fidelity terms and an L1 regularization term.12 The solution algorithm based on the first-order primal–dual approach gave remarkable freedom to modify and simplify the optimized fluence maps. Because the optimization was performed in the dose domain, substantial modification and simplification of the fluence maps are possible without degrading the dosimetric quality. This development paves the path to a new algorithm that optimally implements the jaws-only IMRT concept on a generalized collimator.
2. MATERIALS AND METHODS
2.A. Sparse orthogonal collimators (SOCs)
The SOC design consists of two orthogonally oriented collimator systems with N number of leaves in each collimator bank, where N is a small number. The term “sparse” was chosen in contrast to the “dense” leaf arrangement in a conventional MLC. For this study, we estimated the delivery efficiency of SOC having N = 1, N = 2, and N = 4 leaves in each bank, shown in Fig. 1. Evidently, jaws-only is a special case of SOC when N = 1. In theory, the intensity modulation resolution of SOC is determined by the leaf step size instead of the leaf width.
FIG. 1.
Schematic of the SOC design with N = 1 (A), N = 2 (B), and N = 4 (C). Gray regions are the collimator leaves. Matching colored regions indicate areas where the fluence field can be delivered in parallel.
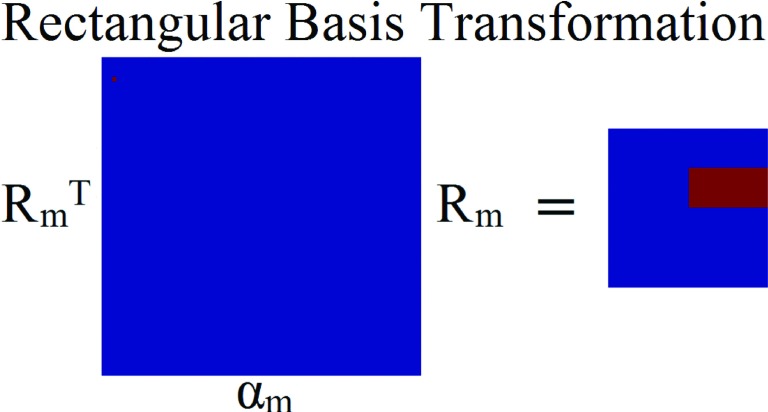
2.B. Rectangular basis transform
Same as jaws-only IMRT, the apertures deliverable by SOC are rectangular. As such, development of a rectangular basis to solve the optimization was necessary. We developed a scaling function for rectangular representation, Rm. This scaling function has two main appealing properties. First, it produces a single region that is rectangular and contains one value. Second, the value of the coefficient in the rectangular basis is equal to the value of the rectangle that is produced from the coefficient when it is transformed, making easy to breakdown the final fluence to its constituent rectangles. Rm uses a coefficient set, notated as αm. For a 2n × 2n fluence matrix, the coefficient matrix αm has dimensions , and Rm has dimensions . For example, if the fluence matrix is a 4 × 4 matrix, then the rectangular basis transform is
| (1) |
As shown in Fig. 2, the fluence can be constructed from the basis coefficients via the equation
| (2) |
FIG. 2.
Schematic of the rectangular basis transform used in this study.
In order to prepare for optimization, the coefficient matrix αm and fluence map fm were vectorized, denoted as αv and fv, respectively. To handle the vectorized notation, a special transform matrix, Rv, that incorporates both the vertical and horizontal operations produced by and Rm, was created. An expression to relate these variables together is
| (3) |
where vec(X) is the vectorization operator.
2.C. Optimization formulation and Chambolle–Pock algorithm
The optimization based on rectangular representation is as follows:
| (4) |
where is the optimization variable. Rv is the rectangular transform matrix for the coefficient vector αv. W is a weighting factor for the structures of interest, A is the fluence to dose transformation matrix, and d0 is the desired dose, which is set to the prescription dose for the PTV and zero for the OARs. The fluence to dose transformation matrix is calculated using a convolution/superposition code using a 6 MV x-ray polyenergetic kernel.
The L2-norm data fidelity term penalizes any deviations in the dose from d0, and the L1-norm sparsity term encourages a low number of nonzero coefficients. The definition of norm, for some vector x of length n, is . The number of nonzero coefficients is exactly equal to the number of fluence segments for delivery. The weighting parameter λ is used to regulate the number of nonzero coefficients by weighting the importance of the L1-norm in the cost function.
Constraining αv to stay positive is possible since the rectangular transform was constructed such that the value of the coefficients equals the value of the fluence rectangle.
The optimization problem was solved utilizing the Chambolle–Pock algorithm, a first-order primal–dual algorithm,13 where Eq. (4) is rewritten in the form
| (5) |
where . F and G are convex, lower semicontinuous functions and, for our particular problem, are defined as
| (6) |
where
| (7) |
This formulation can be solved using the over-relaxed Chambolle–Pock algorithm presented by Condat,14 which uses the iteration
| (8) |
where
| (9) |
As a primal–dual algorithm, the Chambolle–Pock algorithm solves both the primal problem, shown as Eq. (5), and its corresponding dual problem simultaneously by the iteration shown in Eq. (8). Here, z is a variable in the dual formulation and is optimized alongside the primal variable av. The proximal mapping function or “prox operator” is defined as , and and are simplified into simple low cost calculations shown in Eq. (9). The over-relaxation parameter is 0 < p < 2, and the algorithm is equivalent to the original Chambolle–Pock algorithm when p = 1. The step sizes τ and σ must satisfy the constraint for guaranteed convergence, and, in our experiments, are chosen as to satisfy . The norm of K is computed using the power iteration method.15 Further details on this algorithm are described previously.12
Due the convex nature of the optimization problem, the starting values and z0 can be set as anything within the boundary constraints. For this study, and z0 = 0.
2.D. Expanding the rectangular basis for optimal delivery efficiency
It is recognized that the current formulation of Rv does not contain every possible rectangle for the matrix. The affect the dosimetry result is minimal since the current rectangular basis is overcomplete, and every possible rectangle can be expressed as a linear combination of the existing basis rectangles. However, this can affect the delivery efficiency, causing a longer delivery time with more apertures. The increased computational cost of including every possible rectangle is enormous. A 64 × 64 fluence grid would have 86 528 000 variables to solve for 20 beams, which is much larger than the 322 580 variables found with the reduced basis. To address this issue with minimal increase in computational cost, a method for including new and more efficient rectangles to the current rectangle basis is introduced. This method allows for the selection of rectangles that do not currently exist in the original rectangular basis, while keeping increases to computational to a minimum by only adding in new rectangles that are probable to be to chosen. The method is as follows:
-
(1)
Start with original rectangular basis Rv.
-
(2)
Optimize Eq. (4) with Chambolle–Pock algorithm.
-
(3)
Find new rectangular apertures based on the selected apertures from step
-
a.Take every pairwise combination of selected apertures,
-
b.for each pair, perform a union of the aperture shapes to generate a new aperture,
-
c.new aperture passes if it fits 2 criteria:
-
i.New aperture is rectangular,
-
ii.new aperture is unique to current library of apertures.
-
i.
-
a.
-
(4)
Update Rv for all new apertures that pass in part 3.
-
(5)
Repeat steps 2–4 until no new rectangular apertures are found in step 3.
Due to the fact that the original rectangular basis was already overcomplete and had access to the individual beamlets, adding the new step will not affect the dosimetry, but instead it will reduce the number of selected apertures for delivery and increase delivery efficiency.
2.E. Evaluation
2.E.1. Patient studies
Seven previously treated patients consisting of 2 glioblastoma multiforme (GBM) patients, 3 head & neck (H&N) patients, including 2 SBRT patients and 1 conventional fractionated patient with 3 PTVs (H&N3PTV), and 2 lung (LNG) patients were included in the study. The prescription doses and PTV volumes are shown in Table I. The patients were first planned on the 4π radiotherapy platform to optimize both beam orientation and fluence maps using previously described column generation and pricing approach.16,17 During optimization, a 5 cm ring structure was added around the PTV to penalize the dose spillage to normal tissue. The platform has been shown to achieve superior dosimetry to coplanar volumetric modulated arc therapy (VMAT).18–20 As a result of the optimization, 20 noncoplanar beams were selected from a candidate pool of 1162 equally spaced noncoplanar beams for each patient.
TABLE I.
Prescription doses and PTV volumes for each of the cases.
| Prescription dose (Gy) | PTV volume (cm3) | |
|---|---|---|
| GBM #1 | 25 | 6.23 |
| GBM #2 | 30 | 57.77 |
| H&N #1 | 40 | 23.76 |
| H&N #2 | 40 | 18.86 |
| Lung #1 | 50 | 138.75 |
| Lung #2 | 50 | 47.78 |
| H&N3PTV | 54.00 | 197.54 |
| 59.40 | 432.56 | |
| 69.96 | 254.98 |
The dose distributions were compared after generating deliverable segments on the two different platforms: (1) the rectangular aperture optimization (RAO) method and (2) the direct MLC segmentation (DMS) method.
For the RAO plans, the optimized fluences from the 4π radiotherapy plan were not used while adopting the optimized beam angles. Rectangular apertures were calculated using Eq. (4) and the Chambolle–Pock algorithm. λ was varied until the average number of segments per beam for each case was roughly 15.
For the DMS method, the raw fluence from the 4π radiotherapy plan was stratified and a MLC segmentation algorithm was applied to calculate the deliverable MLC segments. The MLC segmentation algorithm was based on a reduction level method by Xia and Verhey,21 described previously in detail.12 The stratification step size was adjusted through a bisection algorithm so that the number of calculated MLC segments in DMS equaled to that of RAO, and the MLC segments were calculated to be deliverable along the direction of leaf motion without any collimator rotations.
For all of the cases except the H&N3PTV RAO plan, the beamlet resolution was 0.5 cm2 and the dose matrix resolution was 0.25 cm3. Due to computational complexities of the optimization, the H&N3PTV RAO plan was evaluated with a beamlet resolution of 1 cm2 and dose matrix resolution of 0.5 cm3.
All treatment plans were normalized such that the prescription dose was delivered to 95% of the PTV. As dosimetric endpoints for comparison, R50 and PTV homogeneity, D98, D99, and Dmax, as well as OAR mean and max doses, were evaluated. R50 is a measure of high dose spillage and is defined as the 50% isodose volume divided by the PTV volume. Homogeneity is defined as D95/D5, and maximum dose is defined from ICRU-83,22 where Dmax is defined as D2, the dose to 2% of the structure’s volume.
Aperture size, reported as number of bixels, is evaluated and compared between the RAO and DMS methods for all seven cases. A bixel is a basic square unit on an IMRT fluence map, and aperture continuity is defined as the four directly neighboring bixels. The RAO method, by design, is limited to 1 aperture per delivery segment, while the DMS method can have multiple apertures per segment.
2.E.2. Sparse orthogonal collimator travel time estimation
In order to evaluate the potential delivery time for using SOCs with N = 1, N = 2, and N = 4 leaves per bank, the delivery order of the segments must first be optimized. The problem was formulated as a modified form of the open traveling salesman problem (TSP), and then solved using a basic genetic algorithm, an open source matlab code provided by Kirk.23
The general TSP attempts to find the shortest path through a set of points in space, traveling to each point only once. The open variation of the problem allows for the end point to be different than the start point, rather than forming a closed loop. As a genetic algorithm, the open source code solves the TSP by first generating random populations, which are different potential routes that visit all points exactly once. The genetic algorithm then groups the paths into random groups of 4. For each group, it takes the population with the shortest route, randomly selects two of the points along the route, and performs three types of mutations on the subroute between the two points: (1) Swap: The order of the two points is swapped along the subroute (2) Flip: The subroute existing between the two selected points is reversed (3) Slide: All points between and including the two selected points are shifted by one, with the first point becoming the last point on the subroute. These three mutations replace the three worst solutions of the group of four. This is performed for every grouping and repeated for a set number of iterations, selecting a different random grouping of four each time. After a set number of iterations, an optimal or near-optimal solution is found.
For our problem, each rectangular segment can be defined as four numbers describing the location of the collimator edge. In a sense, each rectangular segment can be mathematically described as a 4D point. Subtracting two of these points tells us how far each collimator has to travel from one segment to another. The open source code by Kirk can solve the TSP in any number of dimensions by finding the Euclidean norm distance between two points. Since the limiting factor in travel time between two segments is defined by the one collimator leaf that has to travel the furthest, the code was modified such that instead of using the Euclidean distance between two points, it used the single largest distance a collimator leaf had to travel for calculation.
In this study, 100 populations and 10 000 iterations were used in the genetic algorithm to solve the TSP.
Once the order of the segments is solved, the collimator travel time was calculated with an estimated jaw acceleration of 5 cm/s2 and maximal speed of 2 cm/s, which is typical for a C-arm Linac.
The N = 2 and N = 4 SOC designs have color coded regions shown in Fig. 1 that can be delivered in parallel. To account for this, the segments are grouped into regions and an individual collimator travel time for each region is optimized and calculated separately. Between regions that can be simultaneously delivered, the longest travel time is recorded. When using SOC with N > 1 to deliver a larger aperture, adjacent leaves move together as a single leaf.
The same aperture ordering scheme and time calculation, using the same jaw acceleration and maximal speed, was performed for DMS as well, with each aperture described as the location of every MLC location.
The total travel time for delivery and efficiency is evaluated for the seven patients and compared between DMS and RAO with the N = 1, N = 2, and N = 4 leaf collimator designs.
3. RESULTS
3.A. Fluence map evaluation
Figure 3 is a schematic of the fluences from the same beam angle and the MLC segmentation steps needed to create deliverable fluences. The DMS method requires extra postoptimization processing to stratify the fluence, which changes the optimized fluence and degrades the dosimetry. The RAO method, on the other hand, creates rectangles that can be delivered without any further processing of the fluence. Despite delivery from the same beam angle, the fluence patterns from the two methods are substantially different for most beam angles. This difference can be explained by the fact that RAO is a direct aperture regularization approach centered on the dose domain optimization. It utilizes the sparsity term to limit the total number of coefficients, and therefore, limit the total number of apertures. RAO plans included the aperture constraints during the optimization stage while DMS incorporate the MLC constraints after the optimization.
FIG. 3.
Schematic of fluence maps produced by RAO and DMS method for the same beam angle.
Figure 4(A) illustrates the transform from rectangular basis coefficients, our optimization variable, to the fluence domain, and Fig. 4(B) shows the breakdown of the fluence map into its deliverable rectangles, which correspond directly to the coefficients. On average, approximately 16 delivery segments per beam were used.
FIG. 4.
Schematic of an optimized fluence and the breakdown into its deliverable rectangular apertures.
3.B. Patient results
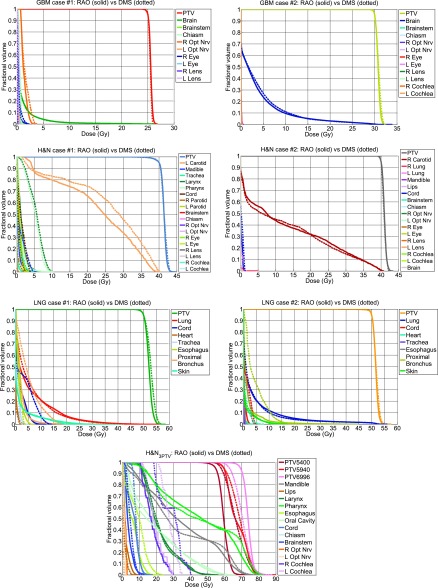
Figure 5 shows the DVHs for all cases. The PTV and OAR dose statistics are tabulated in Tables II and III, respectively. The average difference (RAO − DMS) of D98, D99, and Dmax for the PTV between all cases, using only the 59.4 Gy PTV from the H&N3PTV case, was −0.149%, −0.264%, and −0.834%, respectively, as a percent of the prescription dose, indicating equivalent PTV coverage. The PTV homogeneity, on average, is 0.025 higher with RAO than with DMS. On the other hand, RAO increased R50 by 0.489, indicating a slightly increased high dose spillage to the body.
FIG. 5.
DVH comparisons of the GBM, H&N, LNG, and H&N3PTV cases.
TABLE II.
Comparison of PTV homogeneity, D98, D99, and Dmax as well as R50 and average number of delivery segments. Total average includes the PTVs from the six single target cases and the 59.4 Gy PTV from the H&N3PTV case. R50 from the H&N3PTV case is calculated based on the 59.4 Gy prescription dose and the total PTV volume contributed by all three.
| PTV statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Homogeneity | D98 | D99 | Dmax | R50 | |||||
| Patient case | Average number of segments per beam | RAO | DMS | RAO − DMS (Gy) | RAO | DMS | |||
| GBM #1 | 13.55 | 0.959 | 0.968 | −0.072 | −0.029 | +0.309 | 3.418 | 3.505 | |
| GBM #2 | 12.70 | 0.952 | 0.944 | −0.029 | −0.100 | −0.223 | 2.636 | 2.517 | |
| H&N #1 | 12.45 | 0.942 | 0.935 | −0.219 | −0.083 | −0.167 | 3.857 | 3.088 | |
| H&N #2 | 10.90 | 0.954 | 0.955 | −0.119 | −0.235 | +0.213 | 3.961 | 3.549 | |
| Lung #1 | 11.85 | 0.921 | 0.904 | −0.053 | −0.309 | −1.041 | 4.192 | 3.466 | |
| Lung #2 | 8.35 | 0.940 | 0.933 | −0.100 | −0.060 | −0.272 | 3.961 | 3.381 | |
| Average excluding H&N3PTV | 11.63 | 0.945 | 0.940 | −0.099 | −0.136 | −0.197 | 3.671 | 3.251 | |
| H&N3PTV | 54.00 | 18.95 | 0.848 | 0.754 | −3.832 | −4.665 | −13.309 | 10.699 | 9.798 |
| 59.40 | 0.778 | 0.763 | +0.294 | +0.079 | −2.270 | ||||
| 69.96 | 0.891 | 0.804 | +6.662 | +6.077 | −1.436 | ||||
| Total average | 12.68 | 0.909 | 0.884 | +0.281 | +0.075 | −2.022 | 4.675 | 4.186 | |
TABLE III.
Largest and smallest values found for (RAO − DMS) dose differences for the Dmax and Dmean. The average value of the dose differences between OARs for each case is included. OARs that received 0 Gy in both the RAO and DMS cases are excluded in the evaluation.
| Dmax | Dmean | |||||
|---|---|---|---|---|---|---|
| Dose difference RAO − DMS (Gy) | Largest value | Smallest value | Average value | Largest value | Smallest value | Average value |
| GBM #1 | +0.123 L opt nrv | −0.609 R opt nrv | −0.216 | +0.023 L opt nrv | −0.245 R opt nrv | −0.080 |
| GBM #2 | +0.200 R eye | −0.005 brainstem | +0.051 | +0.023 R eye | +0.0002 L opt nrv | +0.006 |
| H&N #1 | +0.546 L paroid | −4.325 larynx | −1.570 | +0.368 L parotid | −3.959 larynx | −1.197 |
| H&N #2 | +0.070 brain | −1.097 L lung | −0.288 | +0.364 R carotid | −0.189 spinal cord | −0.002 |
| Lung #1 | +2.698 skin | −7.737 ProxBronch | −0.695 | +0.489 trachea | −3.117 ProxBronch | −0.640 |
| Lung #2 | +1.188 lung | −3.208 heart | −1.360 | +0.076 lung | −2.681 ProxBronch | −0.687 |
| H&N3PTV | +1.992 lips | −11.150 R cochlea | −1.486 | +1.801 mandible | −10.8611 R cochlea | −1.475 |
The H&N3PTV case had severe dose degradation in the DMS case after MLC segmentation. Before this postprocessing step, the plan was able to achieve a D95 of 55.3, 59.4, and 68.8 Gy for the 54, 59.4, and 69.96 Gy PTV, respectively. However, segmenting the large fluence maps into a relatively small number of deliverable segments caused the dose to degrade, and after normalization to the 59.4 Gy PTV, the D95 changed to 57.8, 59.4, and 62.6 Gy, respectively. The higher prescription level PTVs had large dose degradation, and the dose normalization caused overdosing to the 54 Gy PTV by an extra 3.8 Gy.
Due to the unacceptable dosimetry to the target volumes of the H&N3PTV caused by the DMS method, another plan, termed the dose domain regularized (DDR) plan,12 was included for comparison. DDR piecewise smooths the fluence using an anisotropic total variation regularization term while penalizing deviations from the optimal dose calculated from the 4π radiotherapy plan but before any postprocessing from the DMS plan. The DDR plan then underwent the same stratification and segmentation steps as the DMS plan. Even though the DDR plans and the DMS plans originated from the same exact 4π optimized plan, the DDR plan suffers much less from the stratification and segmentation steps, allowing for better dose coverage and homogeneity to the 69.96 Gy PTV than the RAO plan. A DVH comparison between RAO and DDR is shown in Fig. 6.
FIG. 6.
DVH comparison between RAO and DDR methods for H&N3PTV case.
This average difference for maximum and mean dose for all OARs between all plans, excluding structures that received zero dose from both plans, are −1.94% and −1.44%, respectively, as a percent of the prescription dose, meaning that for typical radiotherapy plans that have a prescription dose ranging from 30 to 60 Gy, we can expect to spare from 0.582 to 1.164 Gy of max dose and from 0.432 to 0.864 Gy of mean dose to OARs.
Figure 7 shows the dose color washes for 7 patient cases. Both methods achieved high dose conformality with comparable PTV coverage and slightly different normal organ dose distributions.
FIG. 7.
Dose color washes of (A) GBM, (B) H&N, (C) LNG, (D) H&N3PTV patients. The dose cutoff for viewing was chosen to be 10% of the prescription dose.
Figure 8 show the histogram comparison of aperture sizes for RAO and DMS methods. Limited to one aperture per delivery segment, the RAO plan produced far fewer apertures than the DMS method, which had, on average, about three apertures per segment. The mean aperture size for RAO is roughly 3.9 times larger than the mean aperture size for DMS. The maximum aperture size is about 15 bixels larger using RAO comparing to DMS. The aperture statistics are shown in Table IV.
FIG. 8.
Histograms comparing the aperture sizes of the RAO and DMS method for each of the seven cases.
TABLE IV.
Aperture statistics for the RAO and DMS methods for the seven cases.
| Total number of apertures | Mean aperture size (number of bixels) | Max aperture size (number of bixels) | ||||
|---|---|---|---|---|---|---|
| RAO | DMS | RAO | DMS | RAO | DMS | |
| GBM #1 | 271 | 587 | 2.79 | 1.86 | 8 | 13 |
| GBM #2 | 254 | 643 | 9.37 | 2.45 | 32 | 23 |
| H&N #1 | 249 | 743 | 5.06 | 2.06 | 24 | 22 |
| H&N #2 | 218 | 650 | 5.88 | 2.22 | 32 | 21 |
| LNG #1 | 237 | 619 | 22.52 | 3.96 | 96 | 48 |
| LNG #2 | 167 | 525 | 14.29 | 2.71 | 32 | 25 |
| H&N3PTV | 379 | 1144 | 12.96 | 3.24 | 96 | 64 |
| Average | 253.57 | 701.57 | 10.41 | 2.64 | 45.71 | 30.86 |
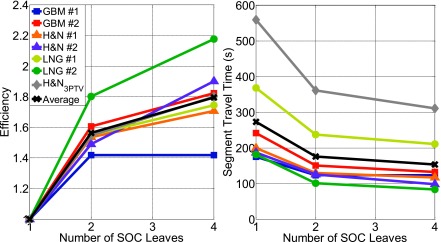
Figure 9 show the total segment travel time for all 20 beams for each patient case. The average efficiency for the N = 1, N = 2, and N = 4 leaf SOC designs is 1 (by definition), 1.56, and 1.80, respectively, and the average time is 273.20, 175.61, and 153.77 s, respectively. The largest gain in efficiency was observed when the SOC design was changed from N = 1 to N = 2. The N = 4 design does further increases the efficiency, but a trend of diminishing returns is apparent. The average segment travel time between all patients for the DMS case was estimated to be 278.11 s, which is approximately equal to the N = 1 SOC design. The individual travel times are shown in Table V. Overall, the total leaf travel times are consistent with 20 field step-and-shoot IMRT delivery.
FIG. 9.
Plots of efficiency and segment travel time against the number of SOC leaves. Efficiency = 1 leaf SOC delivery time/x leaf SOC delivery time.
TABLE V.
Comparison of the segment travel time between DMS and RAO with the various SOC designs.
| Segment travel time comparison (s) | ||||
|---|---|---|---|---|
| DMS | RAO N = 1 | RAO N = 2 | RAO N = 4 | |
| GBM #1 | 173.95 | 175.30 | 123.62 | 123.62 |
| GBM #2 | 235.11 | 241.83 | 150.51 | 132.59 |
| H&N #1 | 168.10 | 199.44 | 129.89 | 116.80 |
| H&N #2 | 175.68 | 187.13 | 125.60 | 98.42 |
| LNG #1 | 346.60 | 368.08 | 237.56 | 210.92 |
| LNG #2 | 218.13 | 181.68 | 100.79 | 83.43 |
| H&N3PTV | 629.22 | 558.97 | 361.30 | 310.60 |
| Average | 278.11 | 273.20 | 175.61 | 153.77 |
4. DISCUSSION
In the study, we presented a novel method to generate rectangular apertures for SOC IMRT delivery. This method is based on regularization of the rectangular basis coefficient in the dose domain to minimize the number of apertures while maintaining the dosimetric quality. Compared to the MLC-based plans, despite the remarkable simplification of fluence maps into deliverable rectangles, the direct aperture optimization nature allows RAO to stay competitive. Our study was based on a noncoplanar beam orientation optimization platform that we previously showed to be superior to coplanar arc plans. However, the same RAO method is readily applicable to coplanar IMRT without modification.
Although the Chambolle–Pock algorithm is remarkably efficient in solving the dose domain optimization problem, the computational cost of RAO plans remains substantial, particularly for larger PTVs. The length and width of the fluence grid are discretized to be a power of two to work properly. For instance, using our beamlet size of 0.5 cm2, any plan with a PTV larger than 4 cm but smaller than 8 cm in diameter must uses a 16 × 16 fluence grid, even if it is just slightly larger than 4 cm. The H&N3PTV plan had the largest PTV dimension measuring approximately 20 cm. If RAO was performed using the regular beamlet size, this plan would have required a 64 × 64 fluence grid for each beam. Our coefficient space then has a resolution of 127 × 127 pixels, making the optimizer solve 322 580 variables simultaneously for all 20 beams. The inclusion of a dose domain transformation matrix, which contains tens of millions of nonzero entries, in the optimization further increases the computational complexity. The amount of data that must be handled simultaneously in the memory would exceed the available 512GB RAM on our workstation for larger PTVs and high dose calculation resolution. Therefore, the RAO method for the H&N3PTV plan was recalculated at half the dose matrix resolution and half of the beamlet resolution to achieve a reasonable cost optimization although superior dosimetric quality is expected had the higher dose resolution been used.
The scaling function Rm is neither orthogonal nor invertible. However, this does not affect plan optimality because sufficient basis were used to cover the entire aperture. We then added a second step to capture all those bases that were not included in the initial optimization but are more efficient to deliver. Moreoever, the optimization method only requires a one way transform from the coefficient space, αm, to the fluence domain, fm, and does not ever need to decompose the fluence back to the rectangular wavelet domain. Therefore, orthogonality and invertibility are irrelevant in this problem.
Jaws-only IMRT was initially developed as an alternative method to MLC based IMRT, which was costly and unreliable in its early stage. However, with the maturation of MLC technology, the need has considerably declined for general purpose IMRT on state of the art C-arm machines. The SOC IMRT, however, is appealing in several unique aspects. First, the delivery time and dosimetric quality do not need to be compromised because of the new hardware design and optimization algorithm. Second, even for N = 4, the SOC system still has far fewer and thicker moving leaves than the conventional MLC, allowing it to be further miniaturized to for compact Linac head designs24 and small animal irradiators. An effective way to reduce the Linac head size is by moving the beam intensity modulator closer to the X-ray source. Moving the MLC closer to the x-ray source while maintaining the same intensity modulation resolution is increasingly difficult since a shorter source-to-collimator distance would require reduction of the already thin MLC leaf width, making fabrication more challenging, reducing mechanical reliability and increasing the interleaf leakage from the loss of the tongue and groove. In comparison, the resolution of SOC IMRT is not dependent on the leaf width, but rather on the motor accuracy capable of being in the micron range. For the same reason, the undesirable trade-off between large field size and high resolution MLCs can be avoided with SOC. Third, as shown in the aperture size comparison, the SOC plan apertures are on average 3.9 times larger than those of the MLC plans. This would allow a significantly shorter beam-on time, reduced leakage dose, and potentially improved IMRT QA results.
The dosimetric improvement was driven by the novel RAO algorithm. To overcome the other major deficiency of jaw-only IMRT, the SOC utilizing increasing number of leaves per bank can significantly improve delivery efficiency. The number of leaves in the proposed SOC is still far fewer than the typical number of leaves in a MLC, thus maintaining the ability to miniaturize and achieve a higher modulation resolution. Based on our estimation, increasing N beyond four may still increase the delivery efficiency, but the returns start to diminish. Although the same colored areas can be delivered in parallel, these areas are smaller and more fragmented with increasing N. Multiple leaves need to move in synchrony to deliver x-rays in the rest of the area, reducing the return for more leaves per bank. Considering the increasing mechanical complexity, an N = 2 to N = 4 leaf/bank design may be an optimal balance between complexity and delivery efficiency.
In this study, the potential dosimetric advantages of using higher achievable resolution were not explored, limited by the finite beamlet calculation resolution, the discretized nature of the rectangular representation, and available computer resources. To explore this potential, we will investigate an adaptive grid and multiresolution approach in future research.
5. CONCLUSION
The IMRT problem was formulated into a direct aperture optimization problem minimizing the dose error while solving for the fluences using rectangular representation. This resulted in rectangular apertures that can be directly delivered with jaws only. The delivery efficiency may further be enhanced using modified SOCs utilizing 2–4 leaves per collimator bank. The potential gains from the greater resolution capabilities of jaws and SOCs have yet to be fully explored because of current computational limits in handling the number of discretized beamlets.
ACKNOWLEDGMENTS
This research is supported by Varian Medical Systems, Inc., and NIH Grant Nos. R43CA183390 and R01CA188300.
REFERENCES
- 1.Chang S. X., Cullip T. J., Deschesne K. M., Miller E. P., and Rosenman J. G., “Compensators: An alternative IMRT delivery technique,” J. Appl. Clin. Med. Phys. 5(3), 15–36 (2004). 10.1120/jacmp.2021.25274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tajima Y., Nakayama H., Itonaga T., Shiraishi S., Okubo M., Mikami R., Sugahara S., and Tokuuye K., “Dosimetric evaluation of compensator intensity modulation-based stereotactic body radiotherapy for stage I non-small cell lung cancer,” Br. J. Radiol. 88, 20150122 (2015). 10.1259/bjr.20150122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Waghorn B. J., Staton R. J., Rineer J. M., Meeks S. L., and Langen K., “A comparison of the dosimetric effects of intrafraction motion on step-and-shoot, compensator, and helical tomotherapy-based IMRT,” J. Appl. Clin. Med. Phys. 14(3), 121–132 (2013). 10.1120/jacmp.v14i3.4210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Robinson J., Opp D., Zhang G., Cashon K., Kozelka J., Hunt D., Walker L., Hoffe S., Shridhar R., and Feygelman V., “Evaluating dosimetric accuracy of flattening filter free compensator-based IMRT: Measurements with diode arrays,” Med. Phys. 39(1), 342–352 (2012). 10.1118/1.3671936 [DOI] [PubMed] [Google Scholar]
- 5.Nangia S., Chufal K. S., Arivazhagan V., Srinivas P., Tyagi A., and Ghosh D., “Compensator-based intensity-modulated radiotherapy in head and neck cancer: Our experience in achieving dosimetric parameters and their clinical correlation,” Clin. Oncol. 18(6), 485–492 (2006). 10.1016/j.clon.2006.03.018 [DOI] [PubMed] [Google Scholar]
- 6.Mu G. and Xia P., “A feasibility study of using conventional jaws to deliver complex IMRT plans for head and neck cancer,” Phys. Med. Biol. 54(18), 5613–5623 (2009). 10.1088/0031-9155/54/18/017 [DOI] [PubMed] [Google Scholar]
- 7.Earl M. A., Afghan M. K., Yu C. X., Jiang Z., and Shepard D. M., “Jaws-only IMRT using direct aperture optimization,” Med. Phys. 34(1), 307–314 (2007). 10.1118/1.2403966 [DOI] [PubMed] [Google Scholar]
- 8.Webb S., “Intensity-modulated radiation therapy using only jaws and a mask,” Phys. Med. Biol. 47(2), 257–275 (2002). 10.1088/0031-9155/47/2/306 [DOI] [PubMed] [Google Scholar]
- 9.Dai J. R. and Hu Y. M., “Intensity-modulation radiotherapy using independent collimators: An algorithm study,” Med. Phys. 26(12), 2562–2570 (1999). 10.1118/1.598794 [DOI] [PubMed] [Google Scholar]
- 10.Webb S. and Poludniowski G., “Intensity-modulated radiation therapy (IMRT) by a dynamic-jaws-only (DJO) technique in rotate-translate mode,” Phys. Med. Biol. 55(21), N495–N506 (2010). 10.1088/0031-9155/55/21/N01 [DOI] [PubMed] [Google Scholar]
- 11.Kim Y., Verhey L. J., and Xia P., “A feasibility study of using conventional jaws to deliver IMRT plans in the treatment of prostate cancer,” Phys. Med. Biol. 52(8), 2147–2156 (2007). 10.1088/0031-9155/52/8/007 [DOI] [PubMed] [Google Scholar]
- 12.Nguyen D., O’Connor D., Yu V. Y., Ruan D., Cao M., Low D. A., and Sheng K., “Dose domain regularization of MLC leaf patterns for highly complex IMRT plans,” Med. Phys. 42(4), 1858–1870 (2015). 10.1118/1.4915286 [DOI] [PubMed] [Google Scholar]
- 13.Chambolle A. and Pock T., “A first-order primal–dual algorithm for convex problems with applications to imaging,” J. Math. Imaging Vision 40(1), 120–145 (2011). 10.1007/s10851-010-0251-1 [DOI] [Google Scholar]
- 14.Condat L., “A primal–dual splitting method for convex optimization involving lipschitzian, proximable and linear composite terms,” J. Optim. Theory Appl. 158(2), 460–479 (2013). 10.1007/s10957-012-0245-9 [DOI] [Google Scholar]
- 15.Golub G. H. and Van Loan C. F., Matrix Computations, 4th ed., Johns Hopkins Studies in the Mathematical Sciences (The Johns Hopkins University Press, Baltimore, MD, 2013), Vol. XXI, p. 756. [Google Scholar]
- 16.Romeijn H. E., Ahuja R. K., Dempsey J. F., Kumar A., and Li J. G., “A novel linear programming approach to fluence map optimization for intensity modulated radiation therapy treatment planning,” Phys. Med. Biol. 48(21), 3521–3542 (2003). 10.1088/0031-9155/48/21/005 [DOI] [PubMed] [Google Scholar]
- 17.Romeijn H. E., Ahuja R. K., Dempsey J. F., and Kumar A., “A column generation approach to radiation therapy treatment planning using aperture modulation,” SIAM J. Optim. 15(3), 838–862 (2005). 10.1137/040606612 [DOI] [Google Scholar]
- 18.Dong P., Lee P., Ruan D., Long T., Romeijn E., Low D. A., Kupelian P., Abraham J., Yang Y., and Sheng K., “4pi noncoplanar stereotactic body radiation therapy for centrally located or larger lung tumors,” Int. J. Radiat. Oncol., Biol., Phys. 86(3), 407–413 (2013). 10.1016/j.ijrobp.2013.02.002 [DOI] [PubMed] [Google Scholar]
- 19.Dong P., Lee P., Ruan D., Long T., Romeijn E., Yang Y., Low D., Kupelian P., and Sheng K., “4pi non-coplanar liver SBRT: A novel delivery technique,” Int. J. Radiat. Oncol., Biol., Phys. 85(5), 1360–1366 (2013). 10.1016/j.ijrobp.2012.09.028 [DOI] [PubMed] [Google Scholar]
- 20.Dong P., Nguyen D., Ruan D., King C., Long T., Romeijn E., Low D. A., Kupelian P., Steinberg M., Yang Y., and Sheng K., “Feasibility of prostate robotic radiation therapy on conventional C-arm Linacs,” Pract. Radiat. Oncol. 4(4), 254–260 (2014). 10.1016/j.prro.2013.10.009 [DOI] [PubMed] [Google Scholar]
- 21.Xia P. and Verhey L. J., “Multileaf collimator leaf sequencing algorithm for intensity modulated beams with multiple static segments,” Med. Phys. 25(8), 1424–1434 (1998). 10.1118/1.598315 [DOI] [PubMed] [Google Scholar]
- 22.Grégoire V. and Mackie T. R., “State of the art on dose prescription, reporting and recording in intensity-modulated radiation therapy (ICRU report No. 83),” Cancer/Radiothérapie 15(6–7), 555–559 (2011). 10.1016/j.canrad.2011.04.003 [DOI] [PubMed] [Google Scholar]
- 23.Kirk J., Open traveling salesman problem–genetic algorithm,matlab, 2008, available at http://www.mathworks.com/matlabcentral/fileexchange/21196-open-traveling-salesman-problem-genetic-algorithm.
- 24.Dong P., Yu V., Nguyen D., Demarco J., Woods K., Boucher S., Low D. A., and Sheng K., “Feasibility of using intermediate x-ray energies for highly conformal extracranial radiotherapy,” Med. Phys. 41(4), 041709 (10pp.) (2014). 10.1118/1.4868464 [DOI] [PubMed] [Google Scholar]