Abstract
We explored the phenomenon of unintentional movements of a multi-joint effector produced by multiple transient changes in the external force. The subjects performed a position-holding task against a constant bias force produced by a robot and were instructed not to intervene voluntarily with arm movements produced by changes in the robot force. The robot produced a smooth force increase leading to hand movement from the trunk, followed by a dwell time. Then, the force dropped to its initial value leading to hand movement toward the initial position but with an undershot. Such perturbation episodes were repeated four times in a row. The accumulated perturbation and undershoot distances kept increasing without saturation within the sequence of four perturbation episode. The limb apparent stiffness before dwell time increased over sequential perturbations while apparent stiffness after dwell time decreased. We interpret the results as consequences of a drift of the hand referent coordinate (RC) caused by a hypothesized RC-back-coupling mechanism and a coupled drift of the apparent stiffness. The results show that RC-back-coupling continues to lead to unintentional movements over repeated perturbations and is accompanied by a relatively slow re-setting process.
Keywords: equifinality, unintentional movement, referent configuration hypothesis, back-coupling, apparent stiffness
INTRODUCTION
The hypothesis of movement control with referent body coordinates (RC-hypothesis, Feldman 2009, 2015) assumes that the central nervous system (CNS) uses neural variables that translate into referent spatial values for a few task-specific salient variables (RCTASK). Further, these values result in referent length values for all the muscles of the body corresponding to a body configuration at which all the muscles would be at the threshold of activation via the stretch reflex. Typically, this body configuration is not achievable due to external and anatomical constraints, and the body comes to a state with non-zero muscle activations and forces exerted on the environment.
According to the RC-hypothesis, transient perturbations are not expected to lead to discrepancy between the initial equilibrium state and the final state assuming that the person does not change neural commands during the application and removal of the perturbation. This phenomenon has been addressed as equifinality. Indeed, equifinality has been documented in several studies (Bizzi et al. 1976; Kelso and Holt 1980; Schmidt and McGown 1980; Latash and Gottlieb 1990). A number of studies, however, reported violations of equifinality during movements performed in unusual situation, such as rotation in the centrifuge or moving in an artificial force field with negative damping (Lackner and DiZio 1994; DiZio and Lackner 1995; Hinder and Milner 2003). These results have been interpreted as reflecting unintentional changes in the neural control signals, i.e., in RCTASK (Feldman and Latash 2005).
Recent studies (Zhou et al. 2014, 2015b) reported violation of equifinality during multi-joint positional tasks under long-lasting transient perturbations and the “do not intervene voluntarily” instruction. When a force change (perturbation) was applied and then removed, the hand stopped short of the initial position if there was a dwell time between the perturbation application and removal. These violations of equifinality have been interpreted as unintentional movements (Zhou et al. 2015b): Indeed, in the initial and final states, the external force was the same but the limb was in a different position. Somewhat similar phenomena of hysteresis were reported earlier (Feldman 1979; Gottlieb and Agarwal 1988; see also Archambault et al. 2005) in studies of joint reactions to loading-unloading sequences. These effects were, however, relatively small in magnitude and were observed in experiments without a dwell time between the loading and unloading phases.
Unintentional movements have been discussed as examples of a process referred to as RC-back-coupling (cf. Ambike et al. 2014, 2015; Reschechtko et al. 2014). According to this idea, even when the subject tries not to react to external force change, a drift in RCTASK towards actual values of the salient variables is triggered by a perturbation. The drift has been modeled as an exponential time process with the time constant of about 1 s (Zhou et al. 2015b).
The magnitude of violations of equifinality, the undershoot distance, seen under single transient perturbations (a perturbation is applied and removed only once) saturated with dwell times over 2 s (Zhou et al. 2015b). If another transient perturbation is applied following the first one, its consequences are expected to depend on ability of the system to re-set. If the hypothetical RC-back-coupling process has saturated, no further increase in the accumulated undershoot distance is expected (Hypothesis 1). We tested this hypothesis using sequences of four transient perturbations with the dwell times of 3 s within each sequence of force application and removal. Violations of equifinality were expected during the first episode of perturbation application-removal, while further transient perturbation episodes were not expected to lead to further drift in the hand position when the force returned to the bias magnitude.
An earlier study (Zhou et al. 2015a) has shown that the subjects co-adjust the apparent stiffness (k; see Latash and Zatsiorsky 1993) of the limb with the RC drift to keep the hand motionless during the dwell time. Here we define k as a scalar constant relating the hand force to the discrepancy between its actual and referent coordinates. In particular, the pre-dwell k was smaller than the post-dwell k, which showed an exponential increase with the dwell time saturating in about 2 s. If no violations of equifinality are observed in response to perturbation episodes following the first one (as in Hypothesis 1), k before and after those perturbation episodes should be the same (Hypothesis 2).
Another manipulation explored ability of the system to reset to the pre-perturbation state given different rest intervals between successive episodes of perturbation application-removal. We compared the responses to the second transient perturbation following the first one after the rest intervals of 3 s and 10 s. To avoid fatigue, only two perturbation episodes were used with the 10-s rest interval. This was an exploratory aim.
METHODS
Participants
Eight self-reported right-handed male subjects took part in this study (age: 27.5 ± 0.8 years, height: 1.73 ± 0.07 m, and mass: 67.3 ± 5.4 kg; mean ± SE). All subjects were healthy and had no history of hand injury. All subjects provided informed consent in accordance with the procedures approved by the Office for Research Protection of the Pennsylvania State University.
Apparatus
The HapticMaster (Moog, The Netherlands), an admittance-controlled robot with an arm that possesses three degrees of freedom (DOFs), was used to apply external forces to a handle. The handle with three kinematic DOFs - pitch, roll and yaw - was attached to the end of the robot arm. The robot arm was used to generate both baseline force (FBIAS) and perturbation force (FPERT) (details in Procedures). During the experiment, subjects sat upright in the chair and held the handle attached to the robot arm with the right hand; gravity forces acting on the hand/arm were not compensated. Note that the robot was used in the force-control mode: It produced specified force changes, while the hand was free to stop at any position where its force balanced the robot force. The hand force changed during the robot-induced motion due to the well-known length dependence of muscle force due to both peripheral and reflex mechanisms. We performed two calibration procedures for the robot. One of them used the robot in a position-control mode and applied various external loads within the range used in our study. The other used the robot in the force-control mode, attached its handle to a spring and applied a baseline force of 20 N. Then the robot applied a transient 20 N perturbation with a dwell time (similar to those described later). In both cases, in the final state, the deviations of the robot handle from the initial state were on the order of 1-2 mm, which is an order of magnitude lower than the deviations observed in our study.
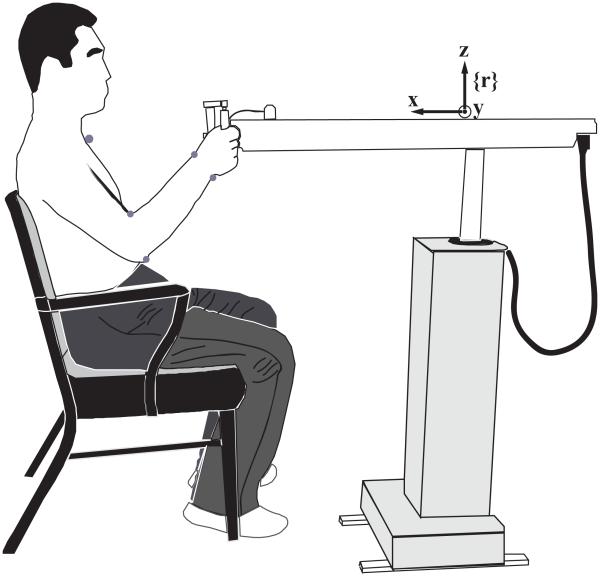
Reflective markers (1.85 cm in diameters) were placed on the suprasternal notch (SN), and medial/lateral epicondyles of the humerus, and ulnar/radial styloid processes (Figure 1). A ProReflex MCU240 infrared light-emitting camera was used to guide the subject to the initial joint configuration in all trials -- marker locations of the initial joint configuration from the camera were drawn on a transparent sheet attached to a 20-inch monitor placed 0.8 m in front of subjects. The data from the robot, rather than the marker information, were used at the data processing stage.
Figure 1.
The side view of experimental setup. The subject sat on a chair and grasped comfortably the handle of the robot arm with the right hand. Several markers (grey dots) were attached on the body for regulation of the initial joint configuration.
The initial position of the handle was set as the origin of robot coordinate system {r}. The x-axis was a horizontal axis in a sagittal plane pointing in the posterior direction, the y-axis was a horizontal axis in a frontal plane pointing to right side of the subject, and the z-axis pointed vertically upward. The robot arm was aligned such that the subject’s hand moved primarily in a parasagittal plane. Subjects selected a comfortable hand position where the hand could move at least 30 cm freely along negative (x–) direction. The robot coordinate system and the initial joint configuration of the subject are illustrated in Figure 1.
Experimental procedure
The subject sat in the chair holding the handle before each trial started. The robot generated a constant baseline force (FBIAS = 20 N) along the x-axis; as a result, the subject had to produce a 20 N force towards the trunk to resist FBIAS and maintain the initial posture (Figure 1).
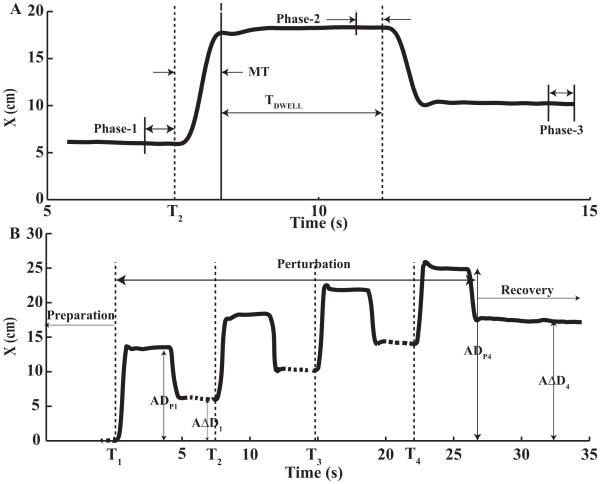
Each trial consisted of three parts. The first part, Preparation, was a steady state lasting 2–4 s until a change in FBIAS was initiated (perturbation force, FPERT starting at time T1, Figure 2A shows the second perturbation episode, while Figure 2B shows a sequence of four episodes). The second part, Perturbation, was comprised of either two or four transient perturbation episodes. The condition with two perturbation episodes separated by a 10-s steady-state rest interval between consecutive episodes is referred to as Double-Perturbation. The condition with four perturbation episodes separated by 3-s steady-state rest intervals between consecutive episodes is referred to as Quad-Perturbation (Figure 2B). For each perturbation episode (FPERT, acting in the same direction as FBIAS, increased in magnitude over 0.5 s, reached a peak value (see below), was kept at that value for 3 s, and then decreased smoothly over 0.5 s. The Perturbation Number (Ni, from 1 to 4) refers to the location of a perturbation episode within a trial. Figure 2 shows the initiation times of the four perturbation episodes as T1, T2, T3, and T4. During the final part, Recovery, the robot force stayed at FBIAS. Note that all robot force changes were smooth to avoid the so-called triggered responses (known also as long-latency reflexes, pre-programmed reactions, and M2-3; Hammond 1955; Tatton et al. 1978; reviewed in Shemmel et al. 2010). A recent study of the EMG patterns in arm muscles using similar perturbations (Falaki et al. 2014) showed no visible phasic muscle reactions that would resemble triggered responses.
Figure 2.
A: The hand trajectory during the second perturbation episode within a Quad-Perturbation trial. The data are for a typical trial performed by a representative subject. Three Phases are shown where the data were extracted. B: A typical hand trajectory along the x-axis showing all four perturbation episodes within a Quad-Perturbation trial. ADPi and AΔDi are the accumulated perturbation distance and undershoot distance after the ith perturbation. The dashed part of the trajectory is the rest between two successive perturbation episodes.
Before the experiment, the subject performed practice trials. During these trials, a magnitude of FPERT was selected, such that the handle stopped about 10 cm from the starting position for the first perturbation. As a result, the first handle excursion was approximately matched across subjects (see Results) while FPERT magnitude varied from subject to subject. For each subject, the magnitude of FPERT was the same for all perturbation episodes.
During the Perturbation and Recovery parts, the subject was instructed not to interfere voluntarily (“allow the robot to move your arm, do not relax and do not resist”; Feldman 1966; Latash 1994). The subjects received an explanation that they were not required to keep the same hand position but not to correct hand deviations produced by changes in the robot force over successive perturbation episodes throughout the trial. The subjects got extensive practice, up to 10 min, to get used to this instruction. Practice was considered successful when a change in the robot force produced a smooth movement of the hand without reversals. FPERT pulled the subject’s hand away from its initial position. The hand stopped at a new position where its force balanced the sum of FBIAS and FPERT. During this phase, peak velocity (VPEAK) of the handle was computed on-line. Movement time was defined as the time interval between T1 and the time when the handle velocity dropped under 10% VPEAK. After movement time, the robot kept its force unchanged for 3 s (dwell time, TDWELL). Then, the robot force returned smoothly to FBIAS and, as a result, the subject’s hand moved towards the initial position, typically with an undershoot (see Figure 2 and Results). After 3 s, the next perturbation episode was administered. Each trial lasted for 35 s and 6 trials were conducted in a row. Short rest intervals were offered between trials (about 10 s).
To explore the effect of rest interval between two consecutive episodes, we compared the hand excursions in response to the second perturbation episode under the Double-Perturbation (10-s rest interval) and Quad-Perturbation (3-s rest interval) conditions. Within each condition, six trials were performed in a row with 10-s rest intervals between successive trials. Trials within each condition were blocked, while conditions were randomized.
Data Processing
The recorded data were analyzed offline using a customized Matlab-based program. Three time intervals were extracted from each episode for further analysis (Figure 2A): 1) The 0.5-s time interval prior to the initiation of a perturbation episode (Ti; i = 1, …, 4) was defined as Phase-1; 2) Phase-2 was defined as the final 0.5 s of the dwell time. 3) Phase-3 was defined as the last 0.5 s for a perturbation episode prior to the initiation of the next one. Thus, Phase-3 for one episode was Phase-1 for the next episode (Figure 2A,B). For each episode, the perturbation distance (DPi, where i refers to the number of perturbation episode) was defined as the difference between Phase-2 and Phase-1 along the x-axis while the undershoot distance (ΔDi) was defined as the distance between Phase-3 and Phase-1 along the x-axis. The relative undershoot for one perturbation episode was computed as ΔDi/DPi. The accumulated perturbation distance over the i-th perturbation episode, ADPi was defined as the distance between Phase-2 within a perturbation episode and the initial state before the first perturbation along the x-axis. Similarly, the accumulated undershoot distance, AΔDi, was defined as the distance between Phase-3 of a perturbation and the initial state before T1 along the x-axis (Figure 2B).
The hand apparent stiffness in response to force increase (before dwell time), ki,UP and in response to force decrease (after the dwell time), ki,DN was calculated for each episode i = 1, 2, 3, 4. By definition, ki,UP = FPERT/DPi within a perturbation episode i, while ki,DN = FPERT/(DPi–ΔDi).
Statistics
All descriptive statistics are reported in the text and figures as means and standard errors unless stated otherwise. Two-way, repeated-measures ANOVAs were used to test effect of Perturbation Number (Ni, i = 1, 2, 3, 4) and Phase (pre- and post-dwell) in Quad-Perturbation on the accumulated deviations (ADPi and AΔDi) and apparent stiffness (k). A t-test was used to test effects of Delay (3 s and 10 s) on the apparent stiffness during the FPERT application for the second perturbation episode in the Quad-Perturbation and Double-Perturbation conditions. To fulfill the assumption of normality, dependent variables were log-transformed when needed. Pairwise comparisons with Bonferroni corrections were used to explore significant effects. The statistical tests were performed with SPSS 20.0 (IBM Corporation, USA) and Matlab (Mathworks Inc, MA, USA).
RESULTS
Each transient perturbation episode led to movement of the hand from the body in response to the application of FPERT, then the hand was nearly motionless during the dwell time (its velocity was at all times under 5% of the peak value observed in response to the perturbation), and then it moved towards the body when FPERT was removed. A typical trial for a sequence of four perturbations is shown in Figure 2B. Note that the return movement of the hand towards the body undershot the initial position. This was true for each of the perturbation episodes. As a result, there was accumulation of the overall undershoot during the trial. The accumulated deviation from the initial position induced by a sequence of four perturbation episodes, averaged across subjects, was 24.5 ± 2.1 cm. The averaged across subjects magnitude of FPERT was 21.3 ± 1.8 N. Note the large magnitude of the distance from the initial to the final steady state (undershoot) following each sequence of FPERT application and removal, which was obvious to experimenters as well as to the subjects (reported at the end of the experiment).
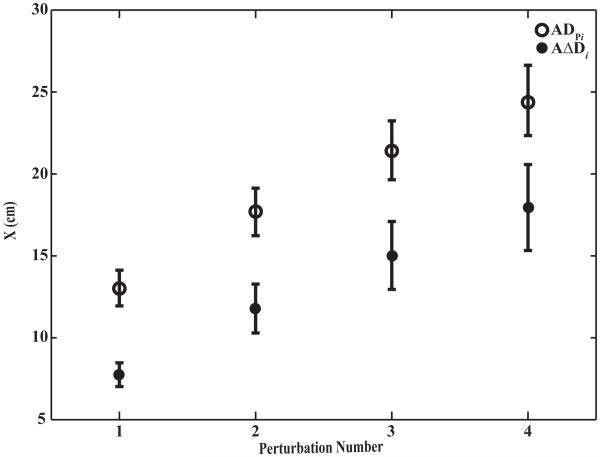
The accumulated hand deviation (ADPi) produced by a sequence of FPERT applications increased gradually with Ni (Figure 3) and a similar pattern was also observed for the accumulated undershoot (AΔDi). Specifically, the magnitude of ADPi was 13.0 ± 1.1 cm for N1, 17.7 ± 1.5 cm for N2, 21.4 ± 1.8 cm for N3 and 24.5 ± 2.1 cm for N4. AΔDi was: 7.8 ± 0.7 cm for N1, 11.8 ± 1.5 cm for N2, 15.0 ± 2.1 cm for N3 and 18.0 ± 2.6 cm for N4. Two-way ANOVAs with repeated measures on hand displacement, using factors Phase (two levels, pre- and post-dwell) and Ni (four levels, i = 1, 2, 3, 4), showed significant effects of both Phase, F(1, 7) = 21.23, p < 0.01, and Ni, F(1.06, 7.4) = 27.64, p < 0.001. Pairwise contrasts with Bonferroni corrections confirmed that both variables at all four levels of Ni were significantly different from one another. There was a significant Phase × Ni interaction, F(1.26, 8.79) = 11.46, p < 0.01. The interaction reflected that the difference between ADPi and AΔDi became larger from episode 1 to episode 4. Hence, within each episode of FPERT application and removal, hand undershoot was observed across all perturbation episodes.
Figure 3.
Accumulated perturbation distance (ADPi) and undershoot distance (A?Di) averaged across subjects with standard error bars. Perturbation Number (Ni) refers to the number of perturbation episode within one Quad Perturbation trial. Ni is an integer ranging from 1 to 4.
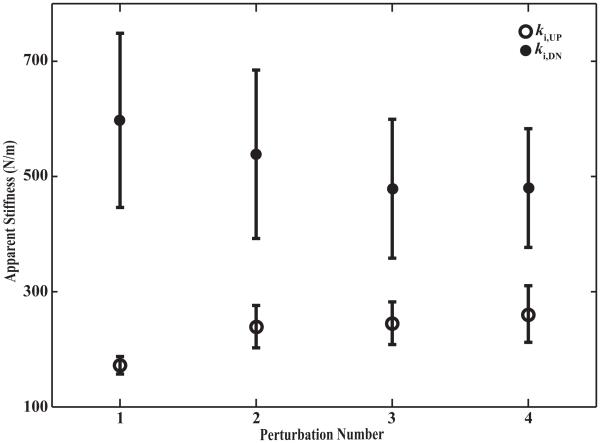
The apparent stiffness measured during the application, ki,UP, and during the removal, ki,DN, of FPERT also changed consistently with Ni. The averaged across subjects values are presented in Figure 4. Specifically, the magnitude of ki,UP was 172 ± 15 N/m for N1, 239 ± 37 N/m for N2, 245 ± 37 N/m for N3 and 261 ± 49 N/m for N4. Apparent stiffness measured at the end of the dwell time, ki,DN, was consistently much larger than ki,UP: 597 ± 151 N/m for N1, 539 ± 146 N/m for N2, 478 ± 121 N/m for N3 and 480 ± 103 N/m for N4. A two-way ANOVA with repeated measures on k, using factors Phase and Ni, showed a significant effect of Phase, F(1, 7) = 13.23, p < 0.01 reflecting significantly smaller k before the dwell time (230 ± 18 N/m) as compared k after the dwell time (553 ± 63 N/m). There was a significant Phase × Ni interaction, F(1.52, 10.65) = 18.71, p < 0.001. The interaction reflected the fact that ki,UP increased while ki,DN decreased with Ni. Pairwise contrasts with Bonferroni corrections confirmed that k1,UP was significantly smaller than any other ki,UP, while k1,DN was significantly larger than any other ki,DN. There was no main effect of Ni.
Figure 4.
Apparent hand stiffness before dwell time, ki,UP and after dwell time, ki,DN averaged across subjects with standard error bars. Perturbation Number (Ni) refers to the number of perturbation episode within one Quad Perturbation trial. Ni is an integer ranging from 1 to 4.
The second perturbation episode came after the first one with different delays, 3 s and 10 s, in the Quad-Pertutbation and Double-Perturbation trials, respectively. The longer rest period prior to the second perturbation episode resulted in a lower pre-dwell k value seen during the FPERT application in the second perturbation episode, 196 ± 23 N/m in the Double-Perturbation trials vs. 239 ± 37 N/m in the Quad-Perturbation trials; t(7) = 8.92, p < 0.05.
DISCUSSION
The results of the experiments falsified both specific hypotheses. The first hypothesis predicted that sequential perturbations would lead to saturation of the accumulated undershoot distance. In fact, the accumulated perturbation distance (ADPi) and undershoot distance (AΔDi) kept increasing, and no clear signs of saturation were seen within the sequence of four perturbation episodes (Figure 3). It looked that the drift would continue until the hand reached the limit of its anatomically possible distance from the trunk. The behavior of the apparent stiffness (k) indices falsified the main prediction of the second hypothesis. In particular, k observed in response to the FPERT application increased over sequential perturbations after the first one. In contrast, k measured during the removal of FPERT decreased over sequential perturbations. As a result, the difference between the k values over the two phases of a single perturbation episode dropped (Figure 4). Longer time delay before an upcoming perturbation episode resulted in smaller pre-dwell k values suggesting slow adjustments in the task-related control variables during the steady-state interval between two successive perturbations.
Violation of equifinality under sequential perturbations
The phenomenon of equifinality has frequently been viewed as a strong prediction of the RC hypothesis and its predecessor, the equilibrium-point hypothesis (Feldman 1966, 1986; Feldman and Levin 1995). However, several studies documented violations of equifinality in unusual conditions such as rotation in a centrifuge (Lackner and DiZio 1994) and movements performed in a simulated force field with negative damping (Hinder and Milner 2003). In addition, earlier series of studies using transient perturbations have presented examples of violations of equifinality across tasks and systems of analysis: Multi-finger prehension and force production (Ambike et al. 2014; Reschechtko et al. 2015), and multi-joint positional tasks analyzed within the space of joint configurations (Zhou et al. 2014; 2015b) and muscle activations (Falaki et al. 2014). All the mentioned studies observed violations in equifinality and suggested the same explanation: A perturbation taking a task-specific salient variable away from its RC triggers a drift of the RC towards the actual value of that variable. We termed this hypothetical mechanism RC-back-coupling.
Specifically, an exponential drift (exponent time constant about 1 s) of the hand final position with dwell time was observed in response to a loading-unloading transient perturbation with dwell time applied while the subjects performed a position-holding task similar to the one in the current study (Zhou et al. 2015b). However, a similar unloading-loading perturbation led to no consistent positional errors (Qiao et al. 2015). Thus, violations of equifinality were seen only when a perturbation increased the initial difference between the actual and referent coordinates. This conclusion is consistent with earlier studies suggesting that humans can keep RC unchanged during perturbations leading to unloading of active muscles while loading (stretching) active muscles could lead to an inability to keep the RC (Archambault et al. 2005; see also Feldman and Levin 1995).
In the current study, we observed violations of equifinality in all four perturbation episodes – the hand always stopped short of the pre-perturbation position after each loading-unloading episode. This result suggests that RC-back-coupling does not saturate, at least not within the studied range of times and perturbation magnitudes.
While the neurophysiological mechanisms of RC-back-coupling remain unknown, its physical meaning allows relatively straightforward interpretation (cf. Ambike et al. 2015). Note that active force production by an effector reflects the difference between RC and actual coordinate of a salient variable. As a result, a drift of RC towards the actual coordinate of that variable reduces the difference between the two and leads to a drop in active force generation. In other words, it moves the system towards a minimum of its potential energy, which is a natural property of physical systems.
Changes in the apparent stiffness with the RC drift
The idea of control with referent spatial trajectories makes apparent stiffness (k) of moving effectors highly important in defining the forces that emerge due to the discrepancies between the actual and referent coordinates. Indeed, the same combination of actual and referent coordinates may lead to different forces (and, consequently, different movements) depending on k, which links spatial deviations to force generation in a linear approximation. Decades ago, studies on hand apparent stiffness ellipses supported the idea of control with equilibrium trajectories (Mussa-Ivaldi et al. 1985; Flash 1987, 1989). Moreover, the notion of apparent stiffness ellipse has been incorporated into the idea of impedance control during limb movements (Hogan et al. 1987).
In a previous study (Zhou et al. 2015a), the stiffness ellipse in a similar initial condition had its major principal axis close to the x-axis, the direction of FBIAS application (the angle between the two axes was within 10°). Following a perturbation, the apparent stiffness in that study increased significantly during the dwell time, and this increase was more than two-fold. We also observed a large increase in k from the FPERT application segment to the FPERT removal segment within the first perturbation episode. The difference between the two k values remained large throughout the four episodes although it did show a decrease after the first episode; the difference became significant by episode 4.
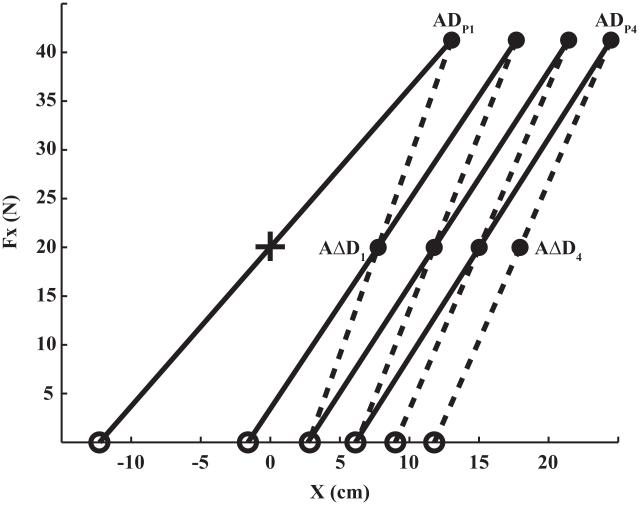
The above observations are summarized in Figure 5. The initial equilibrium position of the hand is shown as a cross on the Fx–x plane. The application of FPERT during the first episode led to the hand motion away from the trunk to a new coordinate; the slope of the trajectory on the Fx–x plane represents the pre-dwell k. After the dwell time, the force returned to FBIAS, the hand moved toward the trunk but stopped short of its initial value; the slope of that trajectory represents the post-dwell k. Further perturbation episodes led to similar pairs of hand trajectories but, as can be seen in Fig. 5, while the force oscillated between the same magnitudes, the hand moved further and further away from the trunk as reflected in the accumulated distance, AΔD1 to AΔD4. While the process did not saturate, it did show a trend towards smaller differences between the k values within each perturbation episode, which is expected to reflect a drop in ΔD increments from the first to the fourth episode. This is also reflected in the largest drifts of the RC induced by the first episode compared to the later episodes (see the open circles in Fig. 5).
Figure 5.
The equilibrium positions of the hand are shown on the force-coordinate (Fx vs. x) plane. The initial equilibrium position of the hand is shown with the cross. Black dots represent mean equilibrium positions averaged across subjects while the referent hand positions are shown as open circles. An increase in force led to the hand motion to a new coordinate, ADPi (i = 1, 2, 3, 4). After the dwell time, the force returned back to its initial value, and the hand moved to a new, intermediate position, AΔDi. The slope of the straight lines represents the apparent stiffness of the arm. The solid lines represent the apparent stiffness before dwell time while the dashed lines the apparent stiffness after dwell time. After the dwell time, the apparent stiffness increases as shown by the steeper lines. The referent hand coordinate drifts towards the trunk during the rest period between two perturbation episodes.
One of the non-trivial observations is the lack of hand drift during the dwell time and during the rest intervals between the successive perturbation episodes. This was possible only if the drifts in RC and k were perfectly coupled. Note that this phenomenon did not happen in isometric tasks with positional perturbations (Wilhelm et al. 2013; Reschechtko et al. 2014); in those studies, a perturbation applied to a finger was followed by a quick drop in the finger force during the dwell time reflecting the RC drift (as predicted by the RC-back-coupling idea), but without a corresponding k adjustment. As the current study shows, the co-adjustments of RC and k persist during repetitive transient perturbations. They could reflect an unintended by-product of the instruction “allow the robot to move your arm”, which could be interpreted by the subjects as “when the robot force does not change, keep the hand position”.
It is also possible that changes in the peripheral force-generating muscle properties contributed to the observed violations of equifinality. However, we are unaware of any peripheral mechanisms of muscle force depression/facilitation (De Ruiter et al. 1998; De Ruiter et al. 2000; Zatsiorsky and Prilutsky 2012) or muscle reflexes (reviewed in Partridge and Partridge 1993) that would show opposite trends during hand loading and unloading. Note that during the rest intervals between two successive perturbation episodes RC drifted back toward its initial value and k dropped, i.e. the system re-set itself, at least partly. The comparison of the two magnitudes of the rest interval, 3 s and 10 s in the Quad-Perturbation and Double-Perturbation conditions, showed a continuing change in k that was obviously coupled with a drift of RC (since the hand did not move during any of the rest intervals, its velocity was always under 5% of the peak value observed in response to the perturbation). Mechanisms of RC re-setting remain unknown and waiting for further exploration. This process seems to be much slower than the RC drift during the dwell time, which saturates after 2 s (Zhou et al. 20915 a,b).
To summarize, taken together, this experiment provides a strong argument in favor of the hypothesis that an unintentional drift in the RC of an effector can be produced by a perturbation driving the actual configuration away from the referent one (RC-back-coupling hypothesis). It shows that this phenomenon is persistent over multiple sequential applications of perturbations and is accompanied by a slower process of RC re-setting.
Highlights.
Transient perturbations with dwell time lead to violations of equifinality;
Sequential transient perturbations lead to accumulation of the effects;
There are parallel changes in the arm apparent stiffness during dwell time;
Unintentional drift of hand referent coordinate is the likely mechanism of these effects.;
There is a slower process of re-setting referent coordinate after the perturbation.
Acknowledgments
The present work was supported by NIH Grants NS-035032 and AR-048563.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Ambike S, Paclet F, Zatsiorsky VM, Latash ML. Factors affecting grip force: anatomy, mechanics, and referent configurations. Experimental Brain Research. 2014;232:1219–1231. doi: 10.1007/s00221-014-3838-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ambike S, Zatsiorsky VM, Latash ML. Processes underlying unintentional finger-force changes in the absence of visual feedback. Experimental Brain Research. 2015;233:711–721. doi: 10.1007/s00221-014-4148-x. [DOI] [PubMed] [Google Scholar]
- Archambault PS, Mihaltchev P, Levin MF, Feldman AG. Basic elements of arm postural control analyzed by unloading. Experimental Brain Research. 2005;164:225–241. doi: 10.1007/s00221-005-2245-6. [DOI] [PubMed] [Google Scholar]
- Bizzi E, Polit A, Morasso P. Mechanisms underlying achievement of final head position. Journal of Neurophysiology. 1976;39:435–444. doi: 10.1152/jn.1976.39.2.435. [DOI] [PubMed] [Google Scholar]
- De Ruiter CJ, De Haan A, Jones DA, Sargeant AJ. Shortening induced force depression in human adductor pollicis muscle. Journal of Physiology. 1998;507:583–591. doi: 10.1111/j.1469-7793.1998.583bt.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Ruiter CJ, Didden DA, Jones DA, Haan AD. The force velocity relationship of human adductor pollicis muscle during stretch and the effects of fatigue. Journal of Physiology. 2000;526:671–681. doi: 10.1111/j.1469-7793.2000.00671.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dizio P, Lackner JR. Motor adaptation to Coriolis force perturbations of reaching movements: endpoint but not trajectory adaptation transfers to the nonexposed arm. Journal of Neurophysiology. 1995;74:1787–1792. doi: 10.1152/jn.1995.74.4.1787. [DOI] [PubMed] [Google Scholar]
- Falaki A, Towhidkhah F, Zhou T, Latash ML. Task-specific stability in muscle activation space during unintentional movements. Experimental Brain Research. 2014;232:3645–3658. doi: 10.1007/s00221-014-4048-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman AG. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. II. Controllable parameters of the muscle. Biophysics. 1966;11:565–578. [Google Scholar]
- Feldman AG. Central and Reflex Mechanisms of Motor Control. Nauka; Moscow: 1979. (in Russian) [Google Scholar]
- Feldman AG. Once more on the equilibrium-point hypothesis (λ-model) for motor control. Journal of Motor Behavior. 1986;18:17–54. doi: 10.1080/00222895.1986.10735369. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Origin and advances of the equilibrium-point hypothesis. Advances in Experimental and Medical Biology. 2009;629:637–643. doi: 10.1007/978-0-387-77064-2_34. [DOI] [PubMed] [Google Scholar]
- Feldman AG. Referent Control of Action and Perception: Challenging Conventional Theories in Behavioral Neuroscience. Springer; New York, NY: 2015. [Google Scholar]
- Feldman AG, Latash ML. Testing hypotheses and the advancement of science: recent attempts to falsify the equilibrium point hypothesis. Experimental Brain Research. 2005;161:91–103. doi: 10.1007/s00221-004-2049-0. [DOI] [PubMed] [Google Scholar]
- Feldman AG, Levin MF. Positional frames of reference in motor control: their origin and use. Behavioral and Brain Sciences. 1995;18:723–806. [Google Scholar]
- Flash T. The control of hand equilibrium trajectories in multi-joint arm movements. Biological Cybernetics. 1987;57:257–274. doi: 10.1007/BF00338819. [DOI] [PubMed] [Google Scholar]
- Flash T. Generation of reaching movements: plausibility and implications of the equilibrium trajectory hypothesis. Brain Behavior and Evolution. 1989;33:63–68. doi: 10.1159/000115901. [DOI] [PubMed] [Google Scholar]
- Gottlieb GL, Agarwal GC. Compliance of single joints: Elastic and plastic characteristics. Journal of Neurophysiology. 1988;59:937–951. doi: 10.1152/jn.1988.59.3.937. [DOI] [PubMed] [Google Scholar]
- Hammond PH. Involuntary activity in biceps following the sudden application of velocity to the abducted forearm. Journal of Physiology. 1955;127:23P–25P. [PMC free article] [PubMed] [Google Scholar]
- Hinder MR, Milner TE. The case for an internal dynamics model versus equilibrium point control in human movement. Journal of Physiology. 2003;549:953–963. doi: 10.1113/jphysiol.2002.033845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogan N, Bizzi E, Mussa-Ivaldi FA, Flash T. Controlling multijoint motor behavior. Exercise and Sport Science Reviews. 1987;15:153–190. [PubMed] [Google Scholar]
- Kelso JAS, Holt KG. Exploring a vibratory systems analysis of human movement production. Journal of Neurophysiology. 1980;43:1183–1196. doi: 10.1152/jn.1980.43.5.1183. [DOI] [PubMed] [Google Scholar]
- Lackner JR, DiZio P. Rapid adaptation to Coriolis force perturbations of arm trajectory. Journal of Neurophysiology. 1994;72:299–313. doi: 10.1152/jn.1994.72.1.299. [DOI] [PubMed] [Google Scholar]
- Latash ML. Reconstruction of equilibrium trajectories and joint stiffness patterns during single-joint voluntary movements under different instructions. Biological Cybernetics. 1994;71:441–450. doi: 10.1007/BF00198920. [DOI] [PubMed] [Google Scholar]
- Latash ML, Gottlieb GL. Compliant characteristics of single joints: preservation of equifinality with phasic reactions. Biological Cybernetics. 1990;62:331–336. doi: 10.1007/BF00201447. [DOI] [PubMed] [Google Scholar]
- Latash ML, Zatsiorsky VM. Joint stiffness: Myth or reality? Hum Move Sci. 1993;12:653–692. [Google Scholar]
- Mussa-Ivaldi FA, Hogan N, Bizzi E. Neural, mechanical, and geometric factors subserving arm posture in humans. Journal of Neuroscience. 1985;5:2732–2743. doi: 10.1523/JNEUROSCI.05-10-02732.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Partridge LD, Partridge LD. The Nervous System: Its Function and Interaction with the World. The MIT Press; 1993. Cambridge pp. [Google Scholar]
- Qiao M, Zhou T, Latash ML. Positional errors introduced by transient perturbations applied to a multi-joint limb. Neuroscience Letters. 2015;595:104–107. doi: 10.1016/j.neulet.2015.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reschechtko S, Zatsiorsky VM, Latash ML. Stability of multi-finger action in different spaces. Journal of Neurophysiology. 2014;112:3209–3218. doi: 10.1152/jn.00395.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reschechtko S, Zatsiorsky VM, Latash ML. Task-specific stability of multifinger steady-state action. Journal of Motor Behavior. 2015;47:365–377. doi: 10.1080/00222895.2014.996281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt RA, McGown C. Terminal accuracy of unexpected loaded rapid movements: Evidence for a mass-spring mechanism in programming. Journal of Motor Behavior. 1980;12:149–161. doi: 10.1080/00222895.1980.10735215. [DOI] [PubMed] [Google Scholar]
- Shemmell J, Krutky MA, Perreault EJ. Stretch sensitive reflexes as an adaptive mechanism for maintaining limb stability. Clinical Neurophysiology. 2010;121:1680–1689. doi: 10.1016/j.clinph.2010.02.166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tatton WG, Bawa P, Bruce IC, Lee RG. Long loop reflexes in monkeys: an interpretive base for human reflexes. Progress in Clinical Neurophysiology. 1978;4:229–245. [Google Scholar]
- Wilhelm L, Zatsiorsky VM, Latash ML. Equifinality and its violations in a redundant system: Multi-finger accurate force production. Journal of Neurophysiology. 2013;110:1965–1973. doi: 10.1152/jn.00461.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Prilutsky BI. Biomechanics of Skeletal Muscles. Human Kinetics: Champaign IL. 2012 [Google Scholar]
- Zhou T, Solnik S, Wu Y-H, Latash ML. Unintentional movements produced by back-coupling between the actual and referent body configurations: violations of equifinality in multi-joint positional tasks. Experimental Brain Research. 2014;232:3847–3859. doi: 10.1007/s00221-014-4059-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Zatsiorsky VM, Latash ML. Unintentional changes in the apparent stiffness of the multi-joint limb. Experimental Brain Research. 2015a;233:2989–3004. doi: 10.1007/s00221-015-4369-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Zhang L, Latash ML. Characteristics of unintentional movements by a multijoint effector. Journal of Motor Behavior. 2015b;47:352–361. doi: 10.1080/00222895.2014.986045. [DOI] [PMC free article] [PubMed] [Google Scholar]