Test for Rare Variants by Environment Interactions in Sequencing Association Studies

Summary

We consider in this paper testing rare variants by environment interactions in sequencing association studies. Current methods for studying the association of rare variants with traits cannot be readily applied for testing for rare variants by environment interactions, as these methods do not effectively control for the main effects of rare variants, leading to unstable results and/or inflated Type 1 error rates. We will first analytically study the bias of the use of conventional burden based tests for rare variants by environment interactions, and show the tests can often be invalid and result in inflated Type 1 error rates. To overcome these difficulties, we develop the interaction sequence kernel association test (iSKAT) for assessing rare variants by environment interactions. The proposed test iSKAT is optimal in a class of variance component tests and is powerful and robust to the proportion of variants in a gene that interact with environment and the signs of the effects. This test properly controls for the main effects of the rare variants using weighted ridge regression while adjusting for covariates. We demonstrate the performance of iSKAT using simulation studies and illustrate its application by analysis of a candidate gene sequencing study of plasma adiponectin levels.

1. Introduction

The advent of high-throughput next-generation sequencing technology has made a massive amount of genetic data available. A challenge for analyzing sequencing association studies is the presence of rare variants which are defined here as genetic variants with minor allele frequency (MAF) less than 5%. Due to the low frequencies of rare variants, classical single marker tests commonly used in genome-wide association studies (GWAS) for studying common variants effects are not applicable. Numerous statistical methods have been developed for testing for association with rare variants effects, where gene-level analysis is often performed to jointly study the effects of the rare variants in a gene. See Lee et al. (2014) for a review. However little work has been done for testing for gene and environment interactions in the presence of rare variants. This paper aims at filling this gap.

This work is motivated by an investigation of the interaction effects between rare genetic variants and alcohol use on plasma adiponectin levels. The dataset is from the Cohorte Lausannoise (CoLaus) study, a population-based study in Lausanne, Switzerland (Warren et al., 2012). Information on plasma adiponectin levels, alcohol usage and other covariates are available. The genotypes of 11 rare genetic variants from sequencing the adiponectin encoding gene ADIPOQ are also obtained. Earlier analysis reported two rare genetic variants within the ADIPOQ gene that are independently associated with adiponectin levels (Warren et al., 2012). A question of interest is to study whether the association of rare genetic variants in the ADIPOQ gene with adiponectin levels is modified by alcohol usage.

To date, statistical methods for analyzing rare genetic variants have focused on assessing the association between rare variants and traits. In view of the lack of power of single marker analysis of rare variants, these methods are typically region-based tests where one tests for the cumulative effects of the rare variants in a region. These region-based methods can be broadly classified into three classes: burden tests, non-burden tests and hybrid of the two. The key difference between burden and non-burden tests is how the cumulative effects of the rare variants are combined for association testing. For the commonly used simple burden tests, one summarizes the rare variants within a region as a single summary genetic burden variable, e.g. the total number of rare variants in a region, and tests its association with a trait. Many variations of burden tests have been developed (Li and Leal, 2008; Madsen and Browning, 2009; Price et al., 2010; Morris and Zeggini, 2010). Burden tests implicitly assume all the rare variants in the region under consideration are causal and are associated with the phenotype in the same direction and magnitude. Hence, they all share the limitation of substantial power loss when there are many non-causal genetic variants in a region and/or when there are both protective and harmful variants (Basu and Pan, 2011).

Several region-based non-burden tests have been proposed by aggregating marginal test statistics (Neale et al., 2011; Basu and Pan, 2011; Lin and Tang, 2011). One such test is the sequence kernel association test (SKAT) (Wu et al., 2011), where one summarizes the rare variants in the region using a kernel function, and then test for association with the trait of interest using a variance component score test. SKAT is robust to the signs and magnitudes of the associations of rare variants with a trait. It is more powerful than the burden tests when the effects are in different directions or the majority of variants in a region are null, but is less powerful than burden tests when most variants in a region are causal and the effects are in the same direction. Several hybrids of the two methods have been proposed to improve test power and robustness (Lee et al., 2012; Derkach et al., 2013; Sun et al., 2013).

The tests discussed above are designed to assess the association of the main effects of rare variants with traits and cannot be readily adapted to assess the interactions between rare variants and environmental factors. A naive approach to assess rare variants by environment interactions is to extend the burden test by fitting a model with both the summary genetic burden variable, environment, and their interaction, and performing a one degree of freedom test for the interaction. However, as we will show in this paper, when there are multiple causal variants with their main effects having different magnitudes and/or signs, such a burden rare variant by environment test fails, and may lead to inflated Type 1 error rates. This is because adjusting for the main effects of the multiple causal variants using a single summary genetic burden variable is inappropriate. Likewise, a naive approach to assess rare variants by environment interactions using SKAT by including the main effects of rare variants as part of covariates and applying SKAT to the interaction terms is problematic. This is because SKAT only allows adjustment of a small number of covariates and cannot handle the presence of a large number of rare variants in a region. Furthermore since the rare variants are observed in low frequency, a model with all the rare variants as main effects will be highly unstable and may not even converge.

Existing methods for assessing common variants by environment interactions such as Gene-Environment Set Association Test (GESAT) (Lin et al., 2013) have several limitations when applied for rare variants. GESAT estimates the main effects of the common variants by applying a L₂ penalty on the genotypes scaled to unit variance; this assumes that the main effects of the scaled genotypes are comparable in magnitudes, which may not hold in the case of rare variants. GESAT also assumes that the regression coefficients of the rare variants by environment interactions are independent of each other, and suffers from power loss when most rare variants in a gene interact with the environmental factor and the interaction effects have the same direction.

In this paper, we consider testing for rare variants by environment interactions in sequencing association studies. First, we investigate the analytic bias of burden tests in testing for rare variants by environment interactions and show that it is generally biased. Our bias analysis provides insight for studying gene-environment (GE) interaction effects in sequencing association studies. Second, to overcome the limitations of aforementioned tests in testing for rare variants by environment interactions, we propose a novel optimal test called interaction sequence kernel association test (iSKAT) for assessing the rare variants by environment association with traits. The proposed test iSKAT is optimal within a class of tests and is powerful and robust to the proportion of causal variants in a gene and the signs and magnitudes of the rare variants by environment interactions, and properly controls for the main effects of the rare variants. We demonstrate iSKAT via simulation studies and analysis of the sequencing data from the CoLaus study.

2. The Model

Assume n unrelated subjects are sequenced in a region with p variants. For ease of presentation, we consider a single environmental factor, in which we are interested in studying the rare variants by environment interactions. The method extends easily to the case where there is more than one environmental factor. Let Y_i, G_i = (G_i1,···,G_ip)^⊺, E_i, X_i = (X_i1,···,X_iq)^⊺ be the phenotype, genotypes for the p variants in a region, environmental factor and q covariates for the i^th sample respectively, for i = 1,···, n. The q covariates might include variables like age, gender or principal components derived from common genetic variants to correct for population stratification (Price et al., 2006). Let S_i = (E_iG_i1,···,E_iG_ip)^⊺, which is a vector of rare variants by environment interaction terms for the i^th individual. We further define an n × 1 phenotype vector Y = (Y₁,···, Y_n)^⊺, an n × 1 environmental factor vector E = (E₁,···,E_n)^⊺, an n × q covariate matrix X = [X₁ . . .X_n]^⊺, an n × p rare variant genotype matrix G = [G₁ . . .G_n]^⊺ and an n × p GE interactions matrix S = [S₁···S_n]^⊺.

To present the model for both continuous and binary phenotypes concisely, we assume a generalized linear model framework. Let f (Y_i) = exp [(Y_iθ_i − b(θ_i)/{a_i (ϕ)} + c(Y_i, ϕ)] be the density of Y_i, for some functions a (·), b (·), and c (·). θ_i and ϕ are the canonical parameter and dispersion parameter respectively. Without loss of generality, we assume a_i (ϕ) is the same for all i = 1,···,n. Let g (·) be a canonical link function. The mean $({\mu }_i=\mathcal{E}(Y_i\mid {\mathit{X}}_i,E_i,{\mathit{G}}_i))$ of the phenotype (Y_i) is related to X_i, E_i, G_i and S_i by:

$$g\left({\mu }_i\right)={\mathit{X}}_i^{⊺}{\alpha }_1+E_i{\alpha }_2+{\mathit{G}}_i^{⊺}{\alpha }_3+{\mathit{S}}_i^{⊺}\beta ={\tilde{\mathit{X}}}_i^{⊺}\alpha +{\mathit{S}}_i^{⊺}\beta ,$$ (1)

where $\alpha ={({\alpha }_1^{⊺},{\alpha }_2,{\alpha }_3^{⊺})}^{⊺}$ and ${\tilde{\mathit{X}}}_i={({\mathit{X}}_i^{⊺},E_i,{\mathit{G}}_i^{⊺})}^{⊺}$. We are interested in testing if there are any GE interactions, i.e. the null hypothesis H₀ : β = 0. This test is challenged by the fact that the dimension of rare variants in a region might not be small and estimation of the regression coefficients α involving rare variants by directly fitting (1) is diffcult.

3. Bias Analysis of Burden Tests

In view of the difficulty in estimating regression coefficients of rare variants, burden tests are typically used for analyzing the association of rare variants with traits by summarizing rare variants in a region by a summary genotype score. In this section, we study the bias of using conventional burden tests for GE interactions in the presence of rare variants, and show that using burden tests for analyzing rare variants by environment interactions can often be invalid and result in inflated Type 1 error rates. Without loss of generality, we focus on a commonly used burden test that summarizes rare variants in a region by the total number of rare variants. Results for other burden tests follow analogously.

For simplicity we assume that there are no covariates present. We assume that data are generated from the following simplified model of (1):

$$g\left[\mathcal{E}(Y_i\mid E_i,{\mathit{G}}_i)\right]={\alpha }_1+{\alpha }_2{E}_i+\sum _{j=1}^p{G}_{ij}{\alpha }_{3j}+\sum _{j=1}^p{G}_{ij}{E}_i{\beta }_j.$$ (2)

Define the summary genetic variable in the burden test to be $G_i^{\ast }={\sum }_{j=1}^p{G}_{ij}$, which is the total number of rare variants in a region. To assess rare variants by environment interactions, one fits the burden GE regression model as:

$$g\left[\mathcal{E}(Y_i\mid E_i,G_i^{\ast })\right]={\alpha }_1^{\ast }+{\alpha }_2^{\ast }{E}_i+{\alpha }_3^{\ast }{G}_i^{\ast }+{\beta }^{\ast }{G}_i^{\ast }{E}_i.$$ (3)

A comparison of (2) and (3) shows that the burden GE model (3) generally mis-specifies the true model (2) in both the genetic main effects and interaction effects. Testing the null hypothesis of no rare variants by environment interactions using burden test model (3) corresponds to testing H₀ : β* = 0. In order for burden test model (3) to be valid, we will at least require β* = 0 when the null hypothesis H₀ : β = 0 holds.

In general, under the null hypothesis of no rare variants by environment interactions H₀ : β = 0 in the true model (2), β* in burden test model (3) will not be zero. As a consequence, the burden based test for rare variants GE interactions is generally biased and can have an inflated Type 1 error rate. For example, if the asymptotic limit of the MLE of β* by fitting (3) is a function of ${\left\{{\alpha }_{3j}\right\}}_{j=1}^p$, β* will be capturing the main effects instead of the interaction effects. This implies that the Type 1 error is generally wrong and the results can be misleading. In Web Appendix 1.3., we consider the scenario when G and E are dependent and show that the asymptotic limit of the MLE of β* can be a function of the main rare variants effects ${\left\{{\alpha }_{3j}\right\}}_{j=1}^p$ and is thus generally biased, and the bias generally worsens with increasing G – E dependence and main effects. Below we discuss the special case of G – E independence for linear regression and logistic regression when disease prevalence is low.

3.1 Bias analysis of β* under G – E independence for linear and logistic regressions (rare disease)

It is of interest to identify cases when β* = 0 under the null hypothesis H₀ : β = 0 when (2) is the true model. Burden test model (3) imposes a model on $\mathcal{E}(Y_i\mid E_i,G_i^{\ast })$. Based on the true model (2), we can calculate $\mathcal{E}(Y_i\mid E_i,G_i^{\ast })$. We show in Web Appendix 1 that $\mathcal{E}(Y_i\mid E_i,G_i^{\ast })$ from the true model (2) can be approximated by:

$$g\left[\mathcal{E}(Y_i\mid E_i,G_i^{\ast })\right]\approx {\alpha }_1+{\alpha }_2{E}_i+\sum _{j=1}^p\mathcal{E}(G_{ij}\mid E_i,G_i^{\ast }){\alpha }_{3j}+\sum _{j=1}^p\mathcal{E}(G_{ij}\mid E_i,G_i^{\ast })E_i{\beta }_j.$$ (4)

Note that equation (4) is exact for linear regression, but holds only approximately for logistic regression under the rare disease assumption.

When G and E are independent, we show in Web Appendix 1 that (4) simplifies to:

$$g\left[\mathcal{E}(Y_i\mid E_i,G_i^{\ast })\right]\approx {\alpha }_1+{\alpha }_2{E}_i+\left(\sum _{j=1}^p{a}_j{\alpha }_{3j}\right)G_i^{\ast }+\left(\sum _{j=1}^p{a}_j{\beta }_j\right)G_i^{\ast }{E}_i,$$ (5)

where $a_j={\mathrm{MAF}}_j∕{\sum }_{k=1}^p{\mathrm{MAF}}_k$ for j = 1,···p and MAF_j is the MAF of the jth variant. Comparing (5) and burden test model (3), we can express the parameters in the mis-specified burden test model (3) in terms of the parameters in the true model (2) as:

$${\alpha }_1^{\ast }={\alpha }_1,{\alpha }_2^{\ast }={\alpha }_2,{\alpha }_3^{\ast }=\sum _{j=1}^p{a}_j{\alpha }_{3j},{\beta }^{\ast }=\sum _{j=1}^p{a}_j{\beta }_j.$$

It follows that when G and E are independent, β* in the mis-specified burden test model (3) is a weighted average of the interaction effects in the true model β₁,···, β_p. Hence for both linear and logistic regressions under the rare disease assumption, we have that β* = 0 approximately when the null hypothesis H₀ : β = 0 holds and (2) is the true model.

3.2 Var(Y|E, G*) under G – E independence for linear and logistic regressions (rare disease)

Even if β* = 0 when the null hypothesis H₀ : β = 0 holds, inference based on the burden test model (3) can still be wrong, as $\mathrm{Var}(Y_i\mid E_i,G_i^{\ast })$ might be mis-specified. Specifically, from the true model (2), we can calculate the true $\mathrm{Var}(Y_i\mid E_i,G_i^{\ast })$. For linear regression, we have:

$$\mathrm{Var}(Y_i\mid E_i,G_i^{\ast })={\sigma }^2+\mathrm{Var}\left[\left\{\sum _{j=1}^p{G}_{ij}{\alpha }_{3j}+\sum _{j=1}^p{G}_{ij}{E}_i{\beta }_j\right\}\mid E_i,G_i^{\ast }\right]\equiv {\sigma }_i^2,$$

where σ² = Var (Y_i|E_i, G_i). Since $\mathrm{Var}(Y_i\mid E_i,G_i^{\ast })$ depends on $G_i^{\ast }$ which differs for each individual, the homoscedasticity assumption is violated for the mis-specified burden test linear regression model (3). When we have a continuous outcome, the burden test linear regression model will generally be biased and cannot be used for testing for GE interactions even when G and E are independent unless a sandwich estimator for the variance is used.

For logistic regression with rare disease assumption, some calculations show that:

$$\mathrm{Var}(Y_i\mid E_i,G_i^{\ast })\approx \mathcal{E}(Y_i\mid E_i,G_i^{\ast }),$$

which is what the burden test logistic regression model (rare disease) assumes. Consequently the burden test logistic regression model (rare disease) can provide approximate correct testing for rare variants by environment interactions when G and E are independent.

4. Testing for Rare Variants by Environment Interactions using interaction Sequence Kernel Association Test (iSKAT)

To overcome the difficulties of burden tests in testing for rare variants by environment interactions, we develop the interaction sequence kernel association test (iSKAT). In general the test for H₀ : β = 0 can proceed using a p degrees of freedom test. However since p might be large, such an approach might suffer from considerable power loss. Let W₁ = diag(w₁₁,···,w_1p) be a p × p matrix of weights. Assume that the β_j's (j = 1,···,p) have mean zero and variance $w_{1j}^2\tau$, and an exchangeable correlation ρ. The exchangeable correlation assumption is only imposed on the regression coefficients of the interaction effects, no assumption is imposed on the correlation between the genetic variants. This extends the SKAT-O test (Lee et al., 2012) for rare variant main effects to test for rare variants by environment interactions in the GE interaction model. The null hypothesis H₀ : β = 0 thus reduces to testing for H₀ : τ = 0.

If ρ = 1, the β_j's are perfectly correlated. The interaction term aggregates rare variants into a summary variable as ${\sum }_{j=1}^p{\beta }_j{G}_{ij}{E}_i=\beta \left({\sum }_{j=1}^p{w}_{1j}{G}_{ij}{E}_i\right)$, in the same spirit as burden tests, and one would expect it is more powerful when there are many rare variants by environment interactions and the interaction effects are in the same direction. Note that this model becomes $g\left({\mu }_i\right)={\mathit{X}}_i^{⊺}{\alpha }_1+E_i{\alpha }_2+{\mathit{G}}_i^{⊺}{\alpha }_3+\left({\sum }_{j=1}^p{w}_{1j}{G}_{ij}{E}_i\right)\beta$, which differs from the naive burden test model (3) in that the main effects are correctly. If ρ = 0, the β_j's are assumed to be independent in the same spirit as SKAT, and one would expect that it is more powerful when the effects of rare variants by environment interactions are in different direction or most variants have no interaction effects.

For a fixed ρ, a score test statistic for testing the variance component H₀ : τ = 0 is:

$$Q_{\rho }={[\mathit{Y}-\mu \left(\widehat{\alpha }\right)]}^{⊺}{\mathit{SW}}_1{\mathit{R}}_{\rho }{\mathit{W}}_1{\mathit{S}}^{⊺}[\mathit{Y}-\mu \left(\widehat{\alpha }\right)],$$ (6)

where R_ρ = (1 − ρ)I + ρ11^⊺, and $\widehat{\alpha }$ is estimated under the null model:

$$g\left(\mu \right)=\mathit{X}{\alpha }_1+E{\alpha }_2+\mathit{G}{\alpha }_3=\tilde{\mathit{X}}\alpha .$$ (7)

We use weighted ridge regression to estimate α in null model (7), imposing a penalty on α₃, where the penalty on α_3j depends on the weights w_2j (Web Appendix 2.1.). For fixed ρ, if $\widehat{\lambda }=o\left(\sqrt{n}\right)$, Q_ρ asymptotically follows a mixture of chi-squares distribution and a p-value can be obtained using characteristic function inversion (Web Appendix 2.2.).

As ρ is unknown in practice, we construct an optimal test, iSKAT, that minimizes the p-values of Q_ρ over the range of ρ (0 ≤ ρ ≤ 1). Specifically, we consider the test statistic:

$$Q_{\mathrm{iSKAT}}=\underset{0\le \rho \le 1}{\min }{p}_{\rho },$$ (8)

where p_ρ is the p-value computed based on Q_ρ. In practice, a grid search over ρ ∈ [0,1] is used, for example in the simulations and data application we used a grid search at intervals of 0.1. Note that the optimal ρ depends on the proportion of non-zero β coefficients and the proportion of β coefficients that are positive (Lee et al., 2012). We describe how a p-value for Q_iSKAT is obtained using one-dimensional integration in Web Appendix 2.3.

5. Simulation Studies

We conduct numerical studies to (a) evaluate the performance of iSKAT for assessing rare variants by environment interactions and (b) demonstrate that using burden tests for testing rare variants by environment interactions can have inflated Type 1 error rates. We examine the performance of five methods. The first method is iSKAT with weights w_1j = w_2j = Beta(MAF_j; 1,25), the beta distribution density function with parameters 1 and 25 evaluated at the sample MAF, which is the recommended weights for SKAT when there is no prior information (Wu et al., 2011). The second and third methods are special cases of iSKAT with ρ = 0 and ρ = 1 respectively. The last two methods are burden tests in which we summarize the genetic variants in a region using a single summary variable and then test for association of this summary genetic variable with the environmental factor after adjusting for the main effect of this summary genetic variable. Specifically, the fourth method (CAST) is an extension of the cohort allelic sum test (Morgenthaler and Thilly, 2007), where the summary genetic variable is an indicator function of whether or not there is any rare variant within the region. For the fifth method (Counting), the summary genetic variable is the weighted counts (with weights w_j = Beta(MAF_j; 1,25)) of the total number of rare variants alleles in the region.

We note that when G_j and G_jE are perfectly collinear for the j^th rare variant, the main and interaction effects of the j^th rare variant in model (1) are not identifiable. Due to the low observed MAF of the rare variants, such high collinearity is common. For example, for singletons, G_j and G_jE are always perfectly collinear. For identifiability, for all five methods, we only include the j^th rare variant in the interaction terms if G_j and G_jE are not perfectly collinear, while still accounting for its main effect. For iSKAT, we include the j^th rare variant in the G matrix, but exclude it from the S matrix in model (1) if G_j and G_jE are perfectly collinear. The burden tests are modified to have two “collapsed” main effects: the first “collapsed ” main effect collapses over the G_j's that are not perfectly collinear with G_jE, and the second “collapsed ” main effect collapses over the G_j's that are perfectly collinear with G_jE. In the simulations, the two burden tests include both “collapsed” main effects, but only test the first “collapsed” variable for interaction effects.

For all methods, we restrict testing to rare variants with MAF < 0.05. We generate datasets by sampling the genotypes and covariates (including the environmental variable) jointly with replacement from the CoLaus dataset in Section 6. The environmental factor is binary. We consider n = 1945 and n = 4000:

$$Y_i={\mathit{X}}_i^{⊺}{\alpha }_1+E_i{\alpha }_2+{\mathit{G}}_i^{⊺}{\alpha }_3+E_i{\mathit{G}}_i^{⊺}\beta +{∊}_i,$$ (9)

where α₁ = (3.6, −0.030, −1.4, 8.3, −4.1, 2.2, 0.005, −0.015, −0.0056, 0.0069, −0.033, 0.15)^⊺, α₂ = 0.015 and ε_i ~ N(0, 0.27). α₁, α₂ and ε are chosen to mimic the CoLaus dataset in Section 6. For each scenario, we evaluate the Type 1 error and power using 10⁵ and 500 simulations respectively.

To evaluate the empirical Type 1 error rates, phenotypes are generated under the null model i.e. β = 0. We consider two scenarios, when there are (a) main effects α₃ = (−0.218, 0, 0, −0.476, 0, 0, −0.151, −0.845, 0.0945, 0, −0.133)^⊺ and (b) no main effects β₃ = 0. The value of α₃ in scenario (a) is chosen to mimic the CoLaus dataset. The empirical Type 1 error rates are shown in Table 1. When there are (a) main effects α₃ ≠ 0, iSKAT gives a correct Type 1 error rate but burden tests can have inflated Type 1 error rates (top two panels of Table 1). When there are (b) no main effects α₃ = 0, all five methods have correct Type 1 error rates (bottom two panels of Table 1). There is some evidence to suggest that G and E are dependent in the CoLaus dataset (Section 6). Since the genotypes and covariates are sampled jointly from the CoLaus dataset, this preserves the association between the rare variants and environmental factor. Thus the observed Type 1 error inflation of burden tests could be due to a mis-specification of the mean model, e.g. when G and E are dependent, and/or a mis-specification of the variance model, which occurs even when G and E are independent.

Table 1.

Empirical Type 1 error rates for continuous outcomes in the presence of main effects (top two panels) and in the absence of main effects (bottom two panels) for n = 1945 and n = 4000 respectively. When there are main effects for rare variants (top two panels), iSKAT gives correct Type 1 error rates but burden tests can have inflated Type 1 error rates. When there are no main effects for rare variants (bottom two panels), all five methods have correct Type 1 error rates. Simulated datasets were generated by sampling the genotypes and covariates jointly with replacement from the CoLaus dataset to preserve the association between G and E. The p-value for the dependence between G and E in the the CoLaus dataset was 0.042, which suggests G – E dependence.

With Main Effects
	α-level	iSKAT	iSKAT (ρ = 0)	iSKAT (ρ = 1)	CAST	Counting
n = 1945	1e-02	1.11e-02	9.98e-03	9.76e-03	1.02e-01	8.51e-02
	1e-03	9.80e-04	9.20e-04	1.00e-03	2.73e-02	2.10e-02
	1e-04	1.20e-04	1.10e-04	1.20e-04	6.39e-03	4.70e-03

	α-level	iSKAT	iSKAT (ρ = 0)	iSKAT (ρ = 1)	CAST	Counting
n = 4000	1e-02	1.06e-02	9.77e-03	1.02e-02	2.26e-01	1.96e-01
	1e-03	1.15e-03	1.02e-03	1.12e-03	7.96e-02	6.35e-02
	1e-04	1.60e-04	1.10e-04	1.50e-04	2.55e-02	1.85e-02

Without Main Effects
	α-level	iSKAT	iSKAT (ρ = 0)	iSKAT (ρ = 1)	CAST	Counting
n = 1945	1e-02	1.11e-02	9.97e-03	9.71e-03	1.01e-02	9.91e-03
	1e-03	9.70e-04	9.10e-04	9.90e-04	1.11e-03	8.80e-04
	1e-04	1.20e-04	1.10e-04	1.20e-04	1.10e-04	1.10e-04

	α-level	iSKAT	iSKAT (ρ = 0)	iSKAT (ρ = 1)	CAST	Counting
n = 4000	1e-02	1.06e-02	9.74e-03	1.02e-02	1.03e-02	1.01e-02
	1e-03	1.14e-03	1.02e-03	1.12e-03	1.04e-03	1.08e-03
	1e-04	1.60e-04	1.10e-04	1.50e-04	1.80e-04	1.50e-04

To evaluate empirical power, phenotypes are generated under the alternative. We only compare the power of iSKAT and burden tests for scenario (b) no main effects α₃ = 0, since the burden tests have correct Type 1 error in this scenario. We vary the number of non-zero β_j's, proportion of non-zero β_j's that are positive and the magnitudes of the non-zero β_j's. We set the magnitudes of the non-zero β_j's as |β_j| = c, and increased c from zero until 0.475.

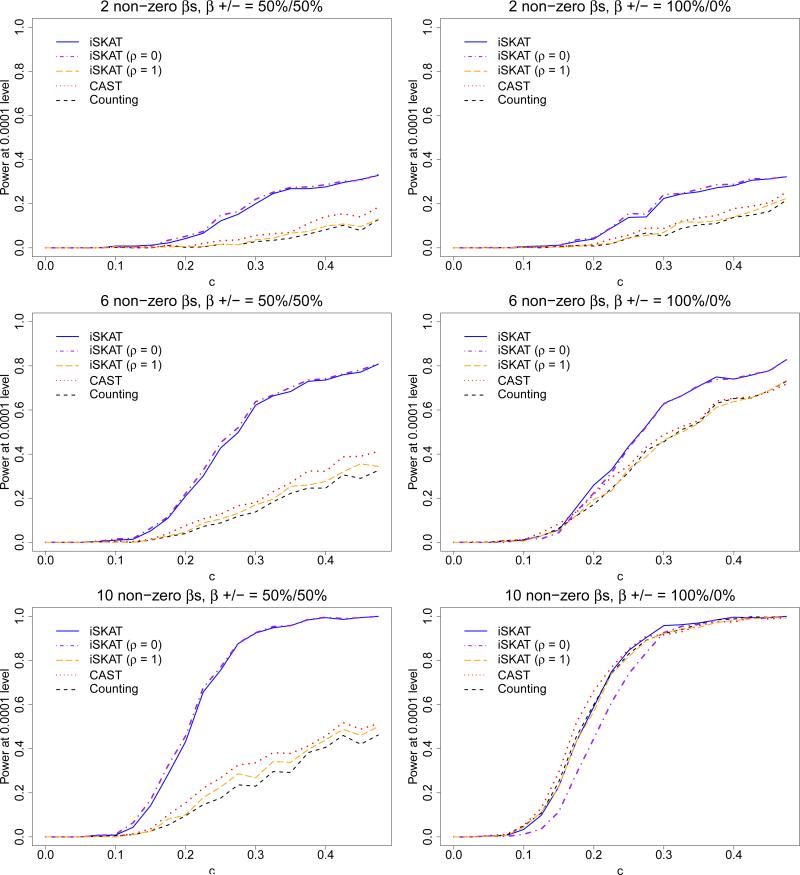
The results for n = 1945 are given in Figure 1. Similar results for n = 4000 are given in Web Figure 6. The top, middle and bottom panels of Figure 1 give the three scenarios when there are 2, 6 and 10 non-zero β_j's respectively. The left and right panels of Figure 1 give the two cases when 50% of the β_j's are positive and 100% of the β_j's are positive respectively. For each plot, we vary c, the magnitude of the non-zero β_j's. As shown in Figure 1, iSKAT generally outperforms the burden tests in terms of power, except for the case when almost all variants interact with environment, in which case the two methods have similar performance.

Figure 1.

Empirical power curves for n = 1945 at α = 0.0001 level of significance for testing rare variant GE interaction effects on a continuous outcome when there are no main effects - iSKAT (solid line), iSKAT with ρ = 0 (dashed-and-dotted line), iSKAT with ρ = 1 (long dashed line), CAST (dotted line) and Counting (short dashed line). Top panel - 2 non-zero β_j's; Middle panel - 6 non-zero β_j's; Bottom panel - 10 non-zero β_j's. Left panel - 50% of β_j's are positive; Right panel -100% of β_j's are positive. In each plot, we set the magnitudes of the non-zero β_j's as |β_j| = c, and increased c from zero until 0.475. Datasets were generated by sampling the genotypes and covariates jointly with replacement from the CoLaus dataset to preserve the association between G and E. Note that the p-value for the association between G and E in the CoLaus dataset was 0.042, which suggests plausible G – E dependence.

In all the plots except the bottom right plot, iSKAT has power similar to iSKAT with ρ = 0. However, in the bottom right plot, iSKAT has power similar to iSKAT with ρ = 1, which is what we would expect since this is the case when virtually all rare variants have interaction effects and the interactions all have the same sign. This is because iSKAT with ρ = 0 does not make any assumption on the GE interaction coefficients and performs well in a range of situations, e.g. when the GE interaction coefficients have different magnitude and signs. In the extreme case where all of rare variants interacts with E and have the same magnitude and sign, iSKAT with ρ = 1 will have optimal power. These results also show that iSKAT has an omnibus performance for different scenarios.

Additional simulation results on the CoLaus dataset are in Web Appendix 3. We demonstrate that the rare variants main effects estimated using weighted ridge regression ${\widehat{\alpha }}_3$ are similar to the true rare variants main effects α₃ (Web Appendix 3.1.) and that the asymptotic and empirical p-values are similar (Web Appendix 3.2. and 3.3.). Web Appendix 4 provides simulation results when genotypes are generated from a coalescent model. The empirical Type 1 error rates confirm the conclusions of the bias analysis presented in Section 3. When there are no main effects of the rare variants (α₃ = 0), burden tests have correct Type 1 error rates for both continuous and binary outcomes (Web Figures 7-8, 17-18, Web Table 2-3). When there are main effects of the rare variants (α₃ ≠ 0), for a continuous outcome, burden tests can have inflated Type 1 error rates, under both G – E independence (Web Figures 9-10) and G – E dependence (Web Figures 11-12). For a binary outcome, where there are main effects of the rare variants, Type 1 error rates are inflated under G – E dependence (Web Figures 21-22), but not under G – E independence (Web Figures 19-20). For both continuous and binary outcomes, the bias generally worsens with increasing G – E dependence (Web Figures 15-16, 25-26) and increasing main effect sizes (Web Figures 13-14, 23-24). The simulations also demonstrate that iSKAT has power that outperforms or is comparable to the burden tests (Web Figures 27-30).

6. Data Analysis

Low circulating levels of adiponectin are associated with multiple clinical conditions such as obesity, hypertension and metabolic abnormalities. Family studies have demonstrated that adiponectin levels are highly inheritable. Furthermore rare genetic variants within the adiponectin coding gene ADIPOQ have been reported to be associated with adiponectin levels - Warren et al. (2012) reported two uncommon genetic variants, rs17366743 (chr3:188054783) and rs17366653 (chr3:188053510), each with MAF of about 2%, that are independently associated with adiponectin levels. Alcohol usage has been found to be associated with both adiponectin levels and ADIPOQ expression levels (Sierksma et al., 2004; Joosten et al., 2008). Our dataset is from the Cohorte Lausannoise (CoLaus) study, which is a population-based study in Lausanne, Switzerland. Information on plasma adiponectin levels, alcohol usage and rare genetic variants in the exon region of the ADIPOQ gene are available (Warren et al., 2012). The goal of this analysis of the CoLaus resequencing dataset is to study whether the association of adiponectin levels with rare genetic variants of the ADIPOQ gene is modified by alcohol usage.

Our analysis used individuals who passed quality control filtering and had complete information on phenotype (plasma adiponectin levels) and covariates (age, sex, waist circumference, hip circumference, body mass index, smoking usage and alcohol usage (yes/no)). A log10 transformation was applied to the plasma adiponectin levels and extreme values of adiponectin levels (six observations exceeding lower 0.1% or upper 99.9% percentile) were set to the boundary value (value at 0.1% or 99.9%), to improve normality and lessen the impact of outliers (Web Figure 31). The data analysis used 1945 study subjects and 11 rare variants within the exon region of the ADIPOQ gene.

We first restricted the analysis to the 11 rare variants (MAF < 0.05). Web Table 6 provides the MAF and missing rates of each of these 11 rare variants. Of the 11 rare variants, 6 are singletons and of the 5 non-singletons, 2 have MAF from 0.02-0.05, 2 have MAF from 0.001 to 0.02 and 1 has MAF less than 0.001. Missing rates ranged from 0.051% to 2.06%. Missing genotypes were imputed with the homozygote of the major allele, in view of the variants being rare. Association analysis results (Web Table 12) were similar when missing genotypes were imputed with the mean. We first applied SKAT-O (Lee et al., 2012) with Beta(MAF_j; 1,25) weights to test for the main effects of the rare variants on adiponectin levels. We considered a linear regression of plasma adiponectin levels on the 11 rare variants in the ADIPOQ gene while adjusting for alcohol usage, age, sex, waist circumference, hip circumference, body mass index, smoking usage and population stratification using the first five components from multi-dimensional scaling (derived from GWAS data). Similar to iSKAT, SKAT-O assumes the correlation of the main effects of the rare variants is ρ, and uses the minimum p-value from different ρ values as the test statistic. In Web Table 7, we report SKAT-O p-values corresponding to each ρ value. Using a grid search of ρ ∈ [0, 1] at intervals of 0.1, SKAT-O gave a p-value of 1.8 × 10⁻¹⁴ (Table 2), confirming the strong association of rare variants in the exon region of the ADIPOQ gene with adiponectin levels. Next, to examine the G – E independence assumption, we applied SKAT-O to investigate if rare variants in the exon region of the ADIPOQ gene are associated with alcohol usage. SKAT-O gave a p-value of 0.042 (Table 2), suggesting that rare variants in the exon region of the ADIPOQ gene are associated with alcohol usage.

Table 2.

Summary of association analysis results of the CoLaus resequencing dataset. The SKAT-O test (Lee et al., 2012) was used to test for the main rare variant effects on adiponectin levels (first row) and their effects on alcohol usage (second row). The iSKAT test was used to test for interaction effects between ADIPOQ gene and alcohol use on adiponectin levels (third-fifth rows).

Analysis	p-value
Main effects of rare variants of ADIPOQ gene on adiponectin levels	1.8e-14
Main effects of rare variants of ADIPOQ gene on alcohol usage	4.2e-02
Interaction effects of rare variants of ADIPOQ gene *alcohol on adiponectin levels	3.7e-02
Interaction effects of rare variants of ADIPOQ gene*alcohol on adiponectin levels, adjusting for effects of common variant chr3:188053586 and chr3:188053586*alcohol	6.1e-02
Interaction effects of ADIPOQ gene*alcohol (chr3:188053586*alcohol and rare variants*alcohol) on adiponectin levels	4.0e-02

Finally we applied iSKAT to investigate ADIPOQ-alcohol interaction effects on plasma adiponectin levels. We did not apply the burden tests since as demonstrated in the simulation studies in Section 5, the burden tests can have inflated Type 1 error. We considered a linear regression of adiponectin levels on the main effects of 11 rare variants in the ADIPOQ gene, alcohol usage, ADIPOQ-alcohol interactions and the aforementioned covariates. We note that even though the analysis adjusted for the main effects of all 11 rare variants, including the 6 singletons, these 6 singletons were not assessed for interaction effects due to collinearity (Section 5). Analysis adjusting only for the main effects of the 5 non-singletons gave similar results (Web Table 13). We used a grid search over ρ ∈ [0, 1] at intervals of 0.1. In Web Table 8, we report iSKAT p-values corresponding to each fixed ρ value. The iSKAT test statistic (Equation (8)) is the minimum of these 11 p-values, which was 0.022 and attained at ρ = 1 (Web Table 8). iSKAT gave a p-value of 0.037 (Table 2) for the GE interaction terms, suggesting a potential ADIPOQ gene and alcohol interaction effect on plasma adiponectin levels. For comparison, iSKAT with ρ = 0 gave a p-value of 0.23, while the other ρ values gave p-values between 0.022 and 0.23 (Web Table 8). iSKAT estimates the rare variants main effects ${\widehat{\alpha }}_3$ in the null model from ridge regression (Web Appendix 2.1.) and these are reported in Web Table 9.

For comparison, in Web Table 10, we report the estimated rare variants main effects from unpenalized linear regression (ridge regression with ridge parameter λ = 0). Both sets of estimates are similar in the CoLaus resequencing dataset. In addition, if unpenalized linear regression was used to estimate the rare variants main effects instead of weighted ridge regression, iSKAT would give the same p-value of 0.037 for ADIPOQ-alcohol interaction effects. This is consistent with the simulations presented in Web Appendix 4.3., where we find that both procedures of fitting the null model had similar performance when the null model without penalization converged. However, the null model without penalization did not converge for 71% of the simulations.

The p-value from iSKAT (p-value_iSKAT = 0.037) is bigger than that for iSKAT with ρ = 1 (p-value_{iSKAT with ρ=1} = 0.022), even though the minimum p-value was indeed attained at ρ = 1. This is because the p-value of iSKAT accounts for searching over a set of ρ values that is done through a grid search. The p-value from iSKAT controls the Type 1 error rate for a single region/test. If multiple regions are tested, i.e. in a whole-exome study, multiple testing correction can proceed via any method that controls the family-wise error rate. To illustrate, if a Bonferroni correction is used and 20,000 region-sets are tested, the threshold for significance for each of the 20,0000 region-sets (where each of the 20,000 p-values are from iSKAT) will be 0.05/20, 000, in order to have a family-wise Type 1 error rate of 0.05.

The CoLaus resequencing dataset had one common variant chr3:188053586 (rs2241766, MAF = 0.138) within the exon region of the ADIPOQ gene, and in Web Table 11, we report linkage disequilibrium (LD) measures between chr3:188053586 and the remainder 11 rare variants, suggesting a weak correlation between the common variant and the rare variants. In an individual marker analysis, both the main effect of chr3:188053586 (p-value = 0.045) and its interaction with alcohol usage (p-value = 0.014) were significantly associated with adiponectin levels. When both chr3:188053586 and rare variants of ADIPOQ were tested jointly for their interaction effects with alcohol use on plasma adiponectin levels, i.e. by including chr3:188053586 in X and its interaction with alcohol in S in model (1), in addition to rare variant terms, iSKAT gave a p-value of 0.040 (Table 2). To further investigate rare variants interaction effects with alcohol use on plasma adiponectin levels after accounting for the common variant, we performed iSKAT using rare variants after adjusting additionally for both the main effect of chr3:188053586 and its interaction with alcohol usage by including both variables in X in model (1). This iSKAT analysis interrogating only rare variants interaction effects, after adjusting for interaction effect of common variant chr3:188053586, gave a p-value of 0.061 (fourth row of Table 2). This is slightly larger than the p-value interrogating only rare variants interaction effects without adjusting for the common variant (p-value = 0.037, third row of Table 2), providing suggestive evidence of interaction effects between rare variants in APIPOQ and alcohol usage on plasma adiponectin levels that are not due to the common variant.

7. Discussions

We have developed an omnibus test, iSKAT, for assessing rare variants by environment interactions. The test is optimal within a class of tests. Our proposed approach is robust to the signs and magnitudes of the rare variants by environment effects, while effectively controlling for the main effects of rare variants. The proposed test iSKAT has various practical advantages: it is computationally efficient as no permutation is needed and p-values are obtained analytically; it allows for prior biological information to be incorporated by using flexible weights, and allows for adjustment of covariates. We note that iSKAT is an association test and the results should be interpreted from an association analysis standpoint. Much stronger conditions are required in order to interpret the interactions as being causal.

We have considered a particular class of kernels for modeling the rare variants by environment interaction effects, where each kernel within the class has kernel matrix SW₁R_ρW₁S^⊺. We constructed iSKAT to be a test that is optimal within this class. Other kernels can be used to model the GE interaction effects. To construct a test that is optimal within a set of candidate kernels, an approach similar to that utilized by Wu et al. (2013) can be used.

There are three classes of unified region-based association tests, corresponding to three different null hypotheses, that might be of interest in a rare variants association study. The first test is a test of main rare variants effects, see Lee et al. (2014) for an overview. The second test is a joint test of main rare variants effects and rare variants by environment effects; this test examines the effects of rare variants in the presence of plausible GE interactions. The third test is a test of rare variants by environment effects only after accounting for main rare variants effects. In the data application, we have illustrated how the first and third hypotheses can be tested using SKAT-O (Lee et al., 2012) and iSKAT respectively. It will be of future research interest to develop a joint test of the second class, by extending the work of Ionita-Laza et al. (2013) to the rare variant GE interaction context.