A General Design Approach and Practical Realization of Decoupling Matrices for Parallel Transmission Coils

Abstract

Purpose

In a coupled parallel transmit (pTx) array, the power delivered to a channel is partially distributed to other channels because of coupling. This power is dissipated in circulators resulting in a significant reduction in power efficiency. In this paper, a technique for designing robust decoupling matrices interfaced between the RF amplifiers and the coils is proposed. The decoupling matrices ensure that most forward power is delivered to the load without loss of encoding capabilities of the pTx array.

Theory and Methods

The decoupling condition requires that the impedance matrix seen by the power amplifiers is a diagonal matrix whose entries match the characteristic impedance of the power amplifiers. In this work, the impedance matrix of the coupled coils is diagonalized by a successive multiplication by its eigenvectors. A general design procedure and software are developed to generate automatically the hardware that implements diagonalization using passive components.

Results

The general design method is demonstrated by decoupling two example parallel transmit arrays. Our decoupling matrices achieve better than −20dB decoupling in both cases.

Conclusion

A robust framework for designing decoupling matrices for pTx arrays is presented and validated. The proposed decoupling strategy theoretically scales to any arbitrary number of channels.

Introduction

The additional degrees-of-freedom (DOF) introduced by parallel transmit (pTx) coils allow mitigation of the non-uniform B1+ profile at high fields i.e., 3T and higher, as well as reduction of the specific absorption rate (1–20). Recently, we have shown that increasing the number of independent Tx channels can dramatically improve the capability of the pTx pulse design to create uniform flip-angle excitations at much reduced local and global Specific Absorption Rate (SAR) compared to birdcage coil excitations (11,17). This is in agreement with studies by other groups that have observed important performance improvement in terms of flip-angle uniformity when increasing the Tx channel count (21,22). However, in our simulation work (17), we have found that the B1+ and SAR performance improvement when increasing the channel count was accompanied with an important increase in power consumption. Although it may appear counter-intuitive that the reduction of SAR requires additional radiofrequency (RF) power, this is simply due to the fact that the traditional metric for RF power is proportional to the square of the absolute value of the RF waveforms applied to different Tx channels. This definition of RF power is independent of the phase of the power amplifiers (RFPA) and does not take into account power that may be reflected or transmitted from one RF power amplifier to another due to coupling. However this metric is still useful because it determines the total power output of the RF power amplifier. In other words, this result simply means that to create highly uniform flip-angle distributions at low SAR requires more powerful RF amplifiers.

This problem of increased power consumption of pTx arrays with many channels is made dramatically worse if there is significant coupling between the Tx channels (17). Indeed, in a coupled pTx array the power delivered to a channel is partially transmitted to other channels. This “coupled” power is dissipated in the circulators and is not used for excitation, resulting in very low efficiency of the array as a whole (23). Furthermore, coupling between the Tx channels increases the overlap between their B1+ maps, thus reducing the effective number of degrees of freedom of the array available for sculpting the flip-angle map (2,7,24–27).

Several methods have been proposed to decouple antenna arrays and magnetic resonance imaging coil arrays (28). Conventional decoupling techniques such as partial overlap of Tx loops (29) and capacitive and inductive decoupling (30–33) are well suited to small arrays but may fail for coils with many Tx elements (i.e., >8). This is because these approaches only allow decoupling of nearest-neighbor loops, while in large pTx arrays the most important coupling often occurs between next and third-neighbor elements (34). In order to decouple distant neighbor channels, capacitive ladder networks have been proposed (35). However such networks are difficult to build and are not robust to variation in the load as they are highly sensitive to the specific tuning and matching of the array.

Note that pre-correction of the digital waveforms by the inverse of the coupling matrix (36,37) does not solve the lost power problem as it does not prevent power from going upstream to the Tx chain and into the circulators where it is simply dissipated into heat. Recently, (38) and (39) proposed to use active elements in a feedback loop to decouple coil arrays by impedance synthesis. However the power dissipated in the active elements may reduce the overall power efficiency.

It was shown in (40–43) that a passive network can be connected between an antenna array and its driving power amplifiers to achieve decoupling between array elements. Such techniques have only been applied outside of MR, such as in antenna systems for telecommunications, and have not been extended to the problem of matching and decoupling of multichannel arrays used for parallel transmission in magnetic resonance imaging. A similar approach was proposed in (44) for MRI receive coils. However, (44) focuses only on a restrictive class of degenerate solutions to the decoupling equation that may not be suitable for MRI transmit arrays.

There is clearly a need for a robust and scalable decoupling strategy of parallel transmission arrays. In this paper, we propose a general approach for the design and realization of a high-power decoupling matrix, inserted between the power amplifiers and a coupled parallel transmit array as shown in Figure 1. The decoupling matrix decouples all array elements, minimizes the power lost in the circulators and ensures maximum power transfer to the load. Our strategy robustly diagonalizes (in hardware) the impedance matrix of the coils using hybrid coupler networks connected in series. This is a known technique in the antenna design community (42). In this work we improve on the standard lumped-element realization (which is composed of a very large number of lumped elements) by using a distributed element realization which is architecturally similar to a Butler matrix (45,46). However, while a Butler matrix utilizes an array of identical hybrid ring couplers to implement the Discrete Fourier Transform (DFT) operation primarily used for beamforming, our decoupling matrix utilizes custom, non-identical hybrid couplers to implement arbitrary unitary operations.

Figure 1.

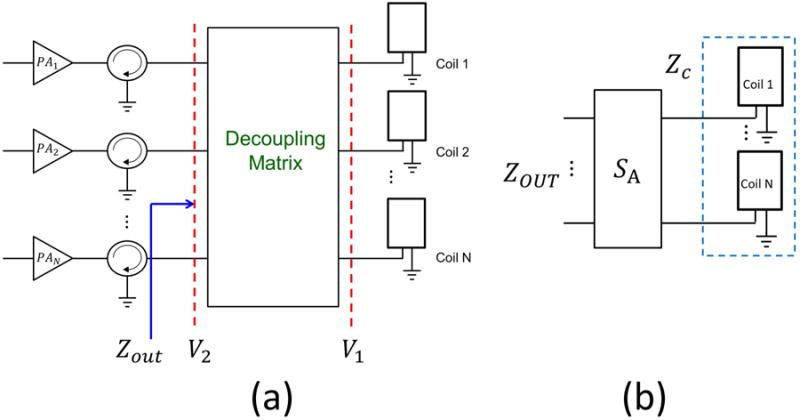
(a) Block diagram of a parallel transmission RF array. A decoupling matrix is connected between the power amplifiers and the array. V₁ and V₂ are the voltage vectors at the array and the power amplifiers respectively. Z_out is the impedance matrix of the load seen by the power amplifiers. Perfect decoupling and matching is obtained when Z_out is a diagonal matrix with diagonal entries equal to the characteristic impedance of the power amplifiers. (b) Interconnection of two circuit blocks. Z_C and Z_OUT are the impedance matrices at the coils and the output respectively. S_A is the diagonalizing block.

We have previously shown in (47) and (48) that theoretically our decoupling matrix can achieve near-perfect decoupling between all channels. In this work we demonstrate our general design procedure by designing and fabricating decoupling matrices for 2-channel and 4-channel coupled arrays used for parallel transmission in magnetic resonance imaging. These designs are provided as examples of the application of the general design procedure and as a proof of concept. The general design procedure presented in this paper could theoretically be applied to any arbitrary number of channels and can be readily applied to other coupled systems such as receive coil arrays. Furthermore, our design procedure is not geometry-dependent, and most importantly it could also be used in conjunction with other decoupling methods such as partial overlap of Tx loops or capacitive decoupling in order to decouple the challenging elements of the coupling matrix.

We summarize below the main contributions of this work:

• We propose a general design procedure to decouple array elements in arbitrary parallel transmit coils using a decoupling matrix

• Our strategy is independent of geometrical configuration of the coils and the number of array channels, and could be used in conjunction with other decoupling methods.

• The performance of the decoupling matrices produced by our procedure is robust to load and component variations

• Our general design procedure is implemented in a software tool that can generate the hardware implementing the decoupling with minimal to no intervention from designers. A Matlab-based open source implementation of the algorithm will be available at (49).

• The decoupling matrices generated by our procedure are comprised only of reactive elements and distributed transmission line components. This implies a low insertion loss.

• Our procedure guarantees that the generated decoupling matrices retain all the original degrees of freedom of the coupled array for transmit pulse design.

Theory

Decoupling Conditions

The impedance matrix of a coupled N – channel array is described by a dense symmetric complex matrix Z_C = R_C + jX_C ∈ ℂ^N×N. The off-diagonal elements of Z_C, z_ij(i≠j) indicate the coupling between the elements i and j of the array. Since all sources are typically independent, the source impedance matrix is typically diagonal, with the output impedances of the corresponding power amplifiers as the diagonal elements (typically 50Ω).

The mathematical condition for achieving full decoupling requires that the impedance matrix of the load (Z_out, shown in Figure 1 (a)) seen by the power amplifiers is a diagonal matrix with matched (typically 50Ω) impedance values to those of the RF power amplifiers. For a 50Ω system, the desired Z_out is given by Eq. (1).

$$Z_{\mathit{\text{out}}}=\left[\begin{array}{ccc}50& & \\ & \ddots & \\ & & 50\end{array}\right]$$ (1)

Furthermore, in order to have the ability to drive array elements individually, it is required that the voltage transformation introduced by the decoupling matrix is full rank. Let V₁ and V₂ be the voltage vectors at the array and the power amplifiers respectively then, V₂ = TV₁, where T is a full rank matrix.

Interconnection of Circuit Blocks

Consider the interconnection of two circuit blocks as shown in Figure 1(b). Let S_C and Z_C(=R_C + jX_C) describe the scattering and impedance matrices of the coupled array (on the right) respectively. Let S_A ∈ ℂ^2N×2N describe the S-parameter matrix of the block S_A at the operating frequency. We wish to diagonalize the coil array impedance matrix Z_C. We do this by first diagonalizing the reactance matrix X_C. We diagonalize X_C by a multiplication with its eigenvectors.

$$D_X=A{X}_C{A}^T,$$

here D_X is a diagonal matrix composed of the eigenvalues of X_C, and A is a matrix composed of the eigenvectors of X_C. Since, X_C is the reactance matrix of a passive reciprocal network it is symmetric. This implies that A is composed of orthonormal eigenvectors.

Suppose that we have a network such that its S-parameter matrix S_A has the following block form:

$$S_A=\left[\begin{array}{cc}0& A\\ A^T& 0\end{array}\right],$$ (2)

where A ∈ ℝ^N×N When S_A and S_C are connected as shown in Figure 1(b) then according to Theorem 1 in (42),

$$S_{\mathit{\text{OUT}}}=A{S}_C{A}^T$$

Where S_OUT is the S-parameter matrix at the left side of the block S_A. Furthermore from (40,42,50), if A is composed of orthonormal set of real vectors, then the corresponding impedance matrices are related by

$$S_{\mathit{\text{OUT}}}=A{S}_C{A}^T.$$

Therefore S_A implemented via (2) successfully diagonalizes the reactive matrix X_C (i.e., X_OUT = AX_CA^T = AA^TD_XAA^T = D_X).

Methods

The decoupling condition described in theory requires diagonalization of a fully dense complex matrix. In this work, we diagonalize the impedance matrix of a coupled array by a multiplication with its eigen-vectors implemented via hybrid couplers.

Figure 2 shows the schematic of the proposed decoupling matrix. The coupled array is described by a fully dense symmetric complex impedance matrix, Z_C = R_C + jX_C. In the decoupling matrix, the first block S_A diagonalizes the imaginary part of the complex impedance (X_C). This results into a diagonal reactance matrix which is eliminated by a series connection with opposite reactive elements. This yields a dense real matrix which is diagonalized by the block S_B. Finally, we can use single port matching networks (such as quarter wavelength transformers) to match the diagonal resistance values to the impedance of the power amplifiers. Such a decoupling framework can be divided into four stages. The following section provides details on each of these stages.

Figure 2. Block diagram of the decoupling matrix.

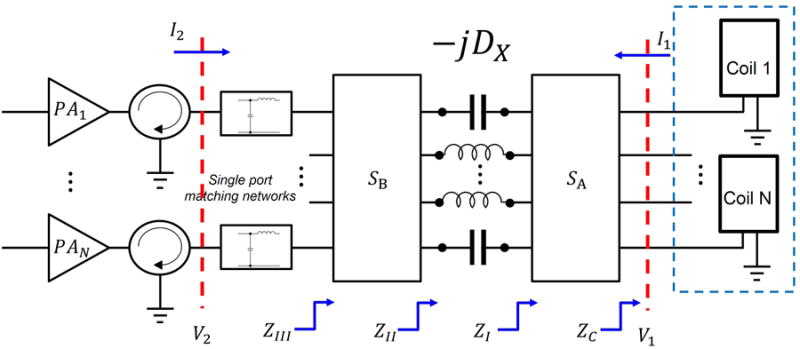
The Four Stages of Decoupling Matrix

Stage 1

The first stage constitutes the S_A block. We design S_A, such that the columns of the orthogonal matrix A are the eigen-vectors of X_C. Consequently, this block diagonalizes the imaginary part, X_C. Let us denote the intermediate impedance matrix at the output of stage 1 as Z_I as shown in Figure 2, then

$$Z_I=A(Z_C)A^T=R_I+j{D}_X$$ (3)

Where R_I = AR_CA^T and D_X is a diagonal matrix with the eigen values of X_C.

Stage 2

Stage 2 eliminates the diagonal matrix D_X. We can achieve this simply by a series connection of reactive elements of opposite signs at the operating frequency (the Larmor frequency). Let us denote the output impedance of stage 2 as Z_II, then

$$Z_{II}=R_I+j{D}_X-j{D}_X=R_I.$$ (4)

Stage 3

The impedance presented at the input of the stage 3 is a symmetric dense real matrix R_I. Similar to Stage 1, we design a block S_B whose S-parameter matrix at the operating frequency is given by

$$S_B=\left[\begin{array}{cc}0& B\\ B^T& 0\end{array}\right],$$

such that the columns of the orthogonal matrix B ∈ ℝ^N×N are the eigenvectors of R_I. As a result, this block diagonalizes R_I. Let us denote the intermediate impedance at the output of stage 3 as Z_III, then

$$Z_{III}=B(R_I)B^T=D_R.$$ (5)

Here D_R is a diagonal matrix with the eigen values of R_I.

Stage 4

The impedance matrix presented at input to stage 4 is a diagonal ‘resistance’ matrix. At this point the coils are completely decoupled, however they are not matched. The task for stage 4 is to match this diagonal matrix to the impedance of power amplifiers Z₀ (typically Z₀ = 50Ω).

To accomplish this task, we can use any standard and well-established single port matching technique to individually match each of the diagonal entries in R_I to the output impedance of the corresponding power amplifier. In our realization, we used an L-match network for each port. In an L-match network, an inductor and capacitor are inserted between the source and load resistances. At the resonance frequency of the network, the imaginary part of the network's impedance is zero. Then, the input impedance is resistive, but has a value different from the corresponding element of R_I. By choosing appropriate inductor and capacitor values, this resistance can be made equal to Z₀ = 50Ω at our operation frequency of 297.2MHz (51,52).

Full Rank Transformation

Theorem 1

The voltage transformation introduced by our decoupling matrix is full rank.

Proof

A detailed proof is given in the Appendix.

We can show that V₂ = BAV₁. Here A and B are the off-diagonal block matrices of the S-parameter matrices S_A and S_B respectively. Since A and B are orthogonal by construction, T = BA defines a full rank transformation.

Realization of the S_A/B Blocks

We observe that the S-parameter matrix of a 2-channel (4-ports) 180-degree hybrid coupler with unequal divide ratio has the same form required to implement the blocks S_A/B in Eq. (2) (The −j being multiplied by the matrix in Eq. (6) can be removed by a series connection of transmission lines with length equal to 270 degrees at the input ports). Note that this is a rotation matrix. A series of such rotations matrices, known as Givens rotations (53), are computed as part of a standard algorithm to diagonalize (i.e. computing its singular value decomposition) matrices (53).

$$S_{180-\mathit{\text{hybrid}}}(\theta )=-j\left[\begin{array}{cccc}0& 0& \mathit{cos}\theta & \mathit{sin}\theta \\ 0& 0& -\mathit{sin}\theta & \mathit{cos}\theta \\ \mathit{cos}\theta & -\mathit{sin}\theta & 0& 0\\ \mathit{sin}\theta & \mathit{cos}\theta & 0& 0\end{array}\right]$$ (6)

$$\text{where},A(\mathit{\text{or}}B)=\left[\begin{array}{cc}\mathit{cos}\theta & \mathit{sin}\theta \\ -\mathit{sin}\theta & \mathit{cos}\theta \end{array}\right],$$

Here the angle θ indicates the rotation angle and is computed from the standard singular value decomposition algorithm via Givens rotations (53). This rotation is implemented by the ratio of the impedances of the hybrid coupler. The impedances (Z_0A, Z_0B) of various sections of a hybrid coupler are shown in Figure 3 (a) and are related by the following expressions.

Figure 3.

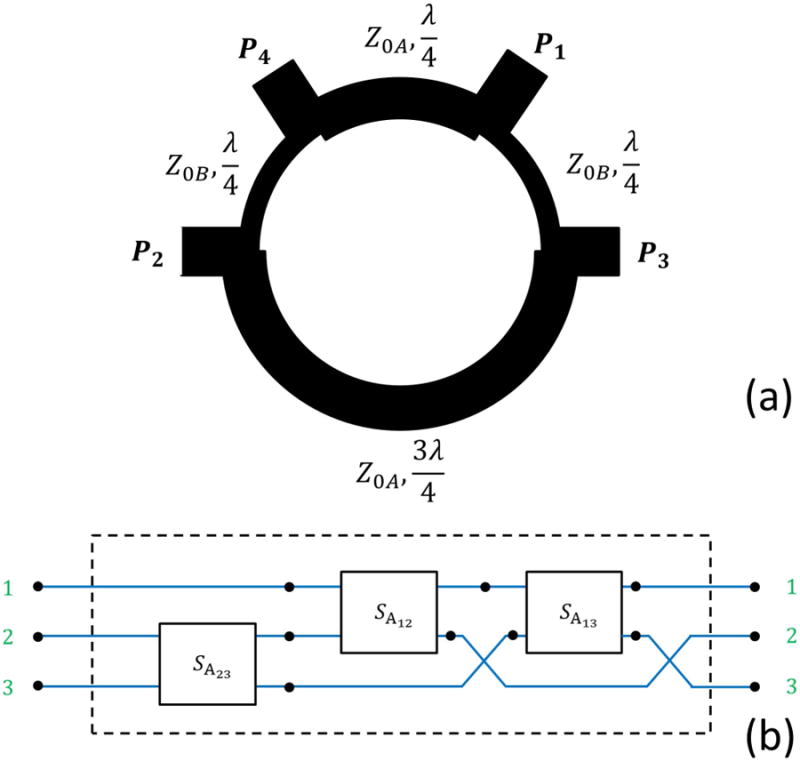
(a) Layout of an unequal divide 180-degrees hybrid coupler. P₁, P₂ and P₃, P₄ are input and output ports respectively. (b) Interconnection of three 2-channel hybrid couplers to realize a 3-channel S_A block.

$$\begin{array}{c}{Z}_{0A}=Z_0\sqrt{\frac{1+\gamma }{\gamma }}\\ Z_{0B}=Z_0\sqrt{1+\gamma }\\ \gamma ={\left(\frac{\mathit{sin}\theta }{\mathit{cos}\theta }\right)}^2\end{array}$$ (7)

Figure 4 shows the layout of a 2 × 2 180 degree hybrid coupler (4 ports). Note that a single 2 × 2 coupler can implement only a 2-channel S_A/B block. In order to realize S_A/B blocks with N-channels, 0.5N(N − 1) of these 2 × 2 couplers can be interconnected, as dictated by the Givens rotations (53). For example for N = 3, we require three (0.5N(N − 1)=3) 2 × 2 couplers. The connections are shown in Figure 3 (b).

Figure 4.

(a) Bore simulator/RF shield with lab bench setup (b) Configuration of loading phantom and pTx coil within bore simulator (c) Back view of physical decoupling matrix (d) Individual hybrid coupler constructed in 59mil Rogers 3003 substrate

For small rotation angles, the matrix A(or B) tends to the identity matrix. We also note that removing a hybrid coupler is equivalent to replacing the hybrid's equivalent rotation matrix by the identity matrix. In a small-rotation case, the corresponding hybrid coupler will make minimal changes to the impedance matrix. This occurs when two channels are already decoupled. In such cases, we can then set a threshold for a minimum rotation angle θ to account for such pairs of channels. In a practical realization, this threshold may allow us to use fewer than N(N − 1) hybrid couplers, simplifying the design. In such cases, the minimum rotation threshold can be adjusted to trade between performance and complexity.

Robustness Analysis

In this section we show that the decoupling matrix is robust to variations in the load and in the values of lumped components. We show that a small bounded perturbation (ΔZ_C) in the load (Z_C) will result in a small bounded perturbation (ΔZ_OUT) in the output (Z_OUT). Let ‖ΔZ_C‖₂ < ε, we show that ‖ΔZ_OUT‖₂ < ε. Mathematically our decoupling matrix can be expressed as:

$$Z_{\mathit{\text{OUT}}}=B(A{Z}_C{A}^T-j{D}_X)B^T$$

Then

$$\begin{array}{c}{Z}_{\mathit{\text{OUT}}}+\mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}=B(A(Z_C+\mathrm{\Delta }{Z}_C)A^T-j{D}_X)B^T\\ \Rightarrow \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}=BA\mathrm{\Delta }{Z}_C{A}^T{B}^T\\ {\Vert \mathrm{\Delta }{Z}_C\Vert }_2<\epsilon \Rightarrow {\Vert \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}\Vert }_2<\epsilon \end{array}$$

This is because both A and B are unitary matrices and the two-norm (or the spectral-norm) of a matrix is unitarily invariant. Following similar reasoning we can show that

$${\Vert \mathrm{\Delta }{D}_X\Vert }_2<\epsilon \Rightarrow {\Vert \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}\Vert }_2<\epsilon ,$$

where ΔD_X is a matrix describing perturbation in the lumped component values. A similar procedure may be followed to check sensitivity to variations in the A and B matrices which are implemented via hybrid couplers.

As an example, we demonstrate rubustness to variations in A. We show that a small bounded perturbation (ΔA) in the A matrix, such that ‖ΔA‖₂ < ε, results into ‖ΔZ_OUT‖₂ < γε. Mathematically:

$$\begin{array}{c}{Z}_{\mathit{\text{OUT}}}+\mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}=B((A+\mathrm{\Delta }A)(Z_C){(A+\mathrm{\Delta }A)}^T-j{D}_X)B^T\\ \Rightarrow \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}=B\mathrm{\Delta }A{Z}_C{A}^T{B}^T+BA{Z}_C\mathrm{\Delta }{A}^T{B}^T+B\mathrm{\Delta }A{Z}_C\mathrm{\Delta }{A}^T{B}^T\end{array}$$

Ignoring the quadratic term (BΔAZ_CΔA^TB^T) and applying norm operator, we get:

$$\Rightarrow {\Vert \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}\Vert }_2\le {\Vert B\mathrm{\Delta }A{Z}_C{A}^T{B}^T\Vert }_2+{\Vert BA{Z}_C\mathrm{\Delta }{A}^T{B}^T\Vert }_2$$

Since A and B are unitary matrices

$$\begin{array}{c}\Rightarrow {\Vert \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}\Vert }_2\le {\Vert \mathrm{\Delta }A{Z}_C{A}^T\Vert }_2+{\Vert A{Z}_C\mathrm{\Delta }{A}^T\Vert }_2\\ \Rightarrow {\Vert \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}\Vert }_2\le 2{\Vert \mathrm{\Delta }A\Vert }_2{\Vert Z_C\Vert }_2{\Vert A\Vert }_2\\ \Rightarrow {\Vert \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}\Vert }_2\le 2{\Vert Z_C\Vert }_2{\Vert \mathrm{\Delta }A\Vert }_2\end{array}$$

Hence for ${\Vert Z_C\Vert }_2=\frac{\gamma }{2}$ we get,

$${\Vert \mathrm{\Delta }A\Vert }_2<\epsilon \Rightarrow {\Vert \mathrm{\Delta }{Z}_{\mathit{\text{OUT}}}\Vert }_2<\gamma \epsilon .$$

This shows that the decoupling matrix is robust to variations in loading conditions and component values.

Sensitivity Analysis for Component Value Variations

The reactance cancellation matrix D_X is implemented with discrete components. These have a manufacturer-provided variability in their values, typically ±5%. To test the sensitivity of a decoupling matrix to these variations, we design a decoupling matrix for a given load Z_C and then simulate its performance to a ±5% variation in the value of each discrete reactive component. This test illustrates the expected worst-case performance due to discrete component variations.

Required Components

In order to design a decoupling matrix to decouple an N – channel array, we need

• N(N − 1) unequal divide hybrid couplers. Note that this number may be reducible for a relaxed decoupling requirement – e.g. in a case where two elements in the array are already sufficiently decoupled we do not need to introduce a coupler between them to meet a particular performance specification

• N reactive elements

• N single port matching networks

Measurement Set-up

We demonstrate our decoupling framework by designing and fabricating a decoupling matrix for a 2-channel and a 4-channel array, shown in Supporting Figure S1 (a) and Figure 4 (b) respectively. The coil elements were individually tuned to 297.2MHz. The S-parameter matrix of the 2-channel array (without a decoupling matrix) shows significant coupling between the elements as illustrated in Figure S2(a) and (b). The S-parameter matrix of the 4-channel array also shows significant coupling between individual elements, illustrated in Figure 5 (a) and (b). Further in this case, the S₁₃ and S₂₄ parameters are comparable to other coupling parameters. This implies that this coil array has significant next-nearest-neighbor coupling which cannot easily be solved by nearest-neighbor capacitive cancelling or by overlapping the Tx loops.

Figure 5.

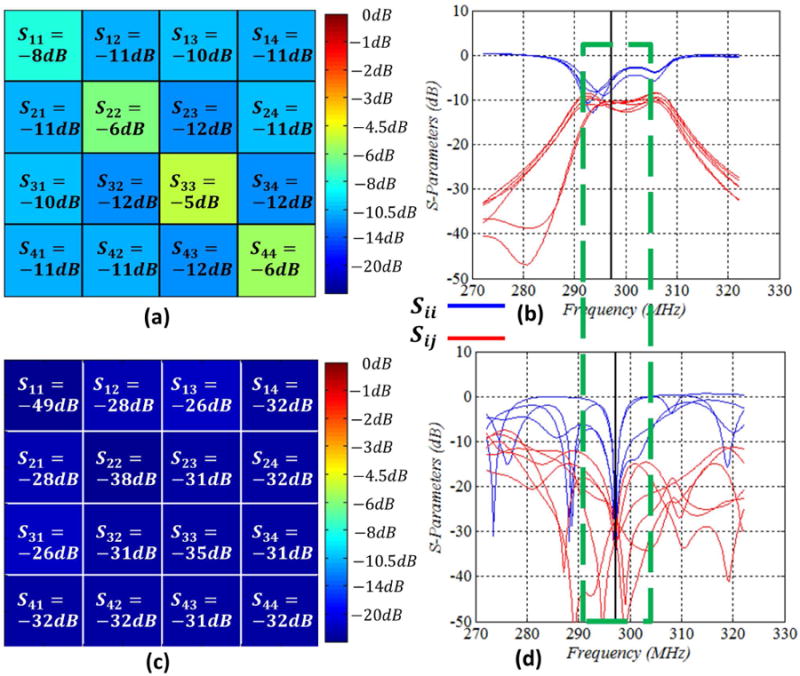
(a) S-parameter matrix of the coupled array at the operating frequency. (b) Frequency dependence of the S-parameters of the coupled array. Blue curves indicate the diagonal, while red curves indicate off-diagonal elements. (c) S-parameter matrix of the decoupled array at the operating frequency using our decoupling matrix. (d) Frequency dependence of the S-parameters of the decoupled array. The green dotted box highlights the band around the Larmor frequency and shows the improvement in terms of the S-parameters.

Results

A 2-channel example (hardware implementation)

As the first example, we implemented a decoupling matrix to decouple a 2-channel array using the hybrid coupler shown in Supporting Figure S1 (b), available online. The hybrid coupler was designed at 297.2MHz and fabricated on FR-4 substrate. The insertion loss introduced by the decoupling matrix was less than −0.3dB per channel. The level of coupling and matching achieved by our decoupling matrix was less than −40dB, as shown in Supporting Figure S2 (c) and (d).

We tested the performance of our decoupling matrix with three difference head phantoms as shown in Supporting Figure S3. The measurements show that when using loading phantoms with circumferences varying from 37.5cm to 61.5cm (Supporting Figure S3 (a)), the worst case coupling was still below −28dB.

A 4-channel example (hardware implementation)

For a second example, we implemented our decoupling matrix to decouple the elements of a 4-channel pTx coil (Figure 4). The hybrid couplers were fabricated with a PCB router on Rogers 3003 substrate and were designed for 297.2MHz operation. The S-parameters for the coil array are shown in Figure 5 (a) and (b) and show coupling of −10dB to −12dB for both nearest-neighbor and next-nearest-neighbor coil elements. With the decoupling matrix, all S-parameters for the network were lowered below −26dB, as shown in Figure 5 (c) and (d). All tests were done with the coil located inside a bore simulator for RF shielding Figure 4 (a).

To test the performance of our decoupling matrix with different loads, we recorded the system's S-parameters when loaded with three differently-sized phantoms, shown in Figure 6 (a). The phantoms were a 1600mL, a 2000mL and a 2800mL sphere, all filled with a 0.9% NaCl/0.09% Magnevist gadopentetate dimeglumine solution. As shown in Figure 6 (b-d), all S-parameters of the system are under −22dB for the smaller two phantoms, and all are under −18dB for all load conditions. For all individual hybrid couplers, the insertion loss was −0.25dB to −0.33dB, including connecting cables. Considering only the PCB and its connectors, the insertion loss was between −0.057dB and −0.072dB per hybrid coupler. The Givens rotation angles implemented by all hybrid couplers matched the designed rotation angles to within one degree of angle.

Figure 6.

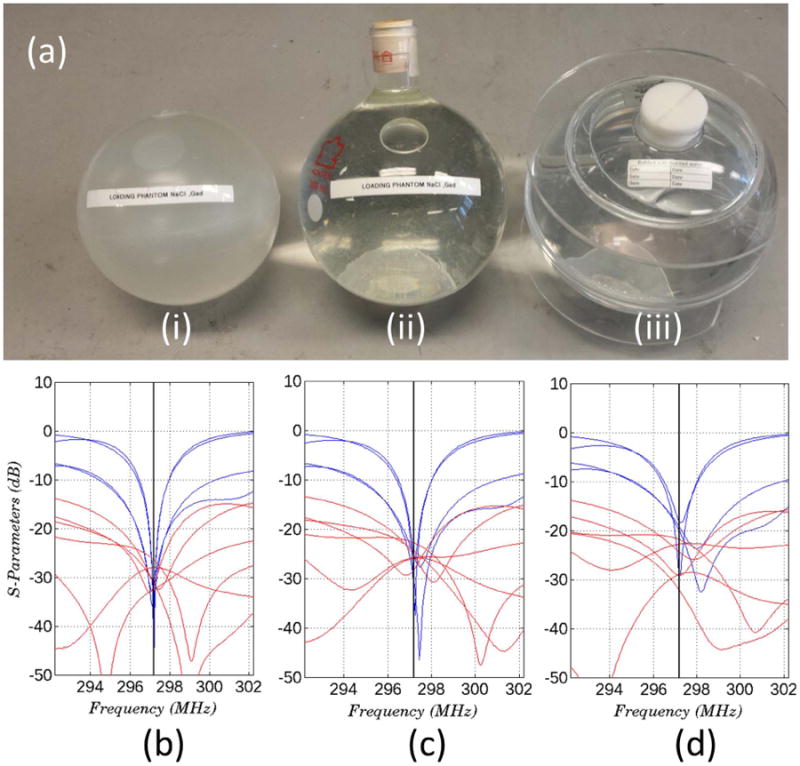
Frequency dependent S-parameters of the 4-channel array with decoupling matrix loaded with phantoms of different sizes. (a) Phantoms are spheres filled with a 0.9% NaCl and 0.09% Magnevist gadopentetate dimeglumine solution. (i) Volume=1600mL (ii) Volume=2000mL (iii) Volume=2800mL (b) Phantom (i), all S-parameters are below -26dB (c) Phantom (ii), all S-parameters are below -22dB (d) Phantom (iii), all S-parameters are below -18dB. Only S₂₂ and S₃₃ are above -20dB

This realization used only 9 of the possible 12 = N(N–1) hybrid couplers in its implementation, as not all were necessary to lower coupling between all channels to below −20dB. However, due to manufacturing process limitations, hybrid couplers that implemented Givens rotations below 15 degrees were constructed as two hybrid couplers on a single board. In these cases, the first hybrid applied a positive rotation of angle ϕ₁, and the second applied a negative rotation of angle −ϕ₂, such that the net transformation was a rotation of angle ϕ₁ – ϕ₂. By making ϕ₁ and ϕ₂ close in magnitude, an arbitrarily small rotation angle could be implemented. The insertion loss from a double-hybrid board, including cables, was −0.395dB to −0.405dB and, excluding cables, was −0.084dB to −0.11dB.

A 4-channel example with sensitivity analysis (simulation)

In this example we designed a decoupling matrix to decouple a 4-channel transmit array. The performance was tested in simulations only. In this example, we used only 8 couplers instead of 12 = N(N – 1) and still had worst case decoupling better than −25dB. Figure 7 (a) and (b) shows the frequency dependent S-parameter matrix of the array without and with a decoupling matrix at the operating Larmor frequency of 297.2MHz. Figure 7 (c) shows the results of a sensitivity analysis. We varied the values of the lumped components used in the design within ±5% of the nominal component values, and found that the worst case decoupling level was still within an acceptable range of −25dB.

Figure 7.

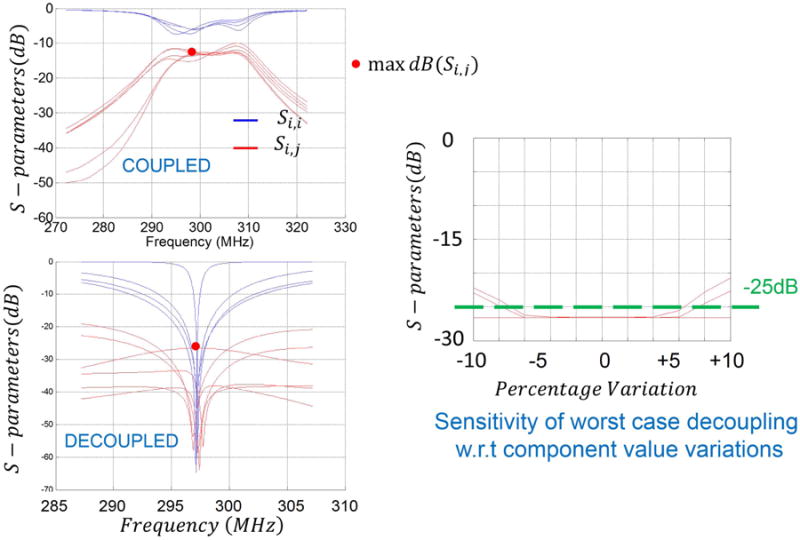
Simulated plots for a 4-channel example. The design used only 8 hybrid couplers instead of 12 (a) S-parameter matrix of the coupled array at the operating frequency. (b) Frequency dependence of the S-parameters of the decoupled array. (c) Sensitivity of the worst case decoupling with respect to lumped component variations (each line corresponds to the worst case decoupling variations by varying values of individual lumped elements).

Discussion

We have presented a framework using design automation principles to design decoupling and matching networks - decoupling matrices - for parallel transmit arrays operating at high frequencies. To our knowledge, this is the first presentation of a general procedure that decouples pTx arrays with an arbitrary number of transmit channels. Key advantages of our proposed framework are that it is generic, easily implemented and scalable. This means that the proposed decoupling strategy is independent of the array's geometrical configuration and the number of channels. Such a matrix could be used to decouple pTx coils with many channels (i.e., >16), which are difficult to decouple properly using existing methods but have been shown to be beneficial for SAR reduction and manipulation of the transverse magnetization signal.

When using a decoupling matrix during scans, it is proposed to place it near the pTx array and away from the RF power amplifiers. This is principally to reduce standing wave loss in the transmission lines connecting the decoupling matrix to the pTx coil. This transmission line is implemented using 50Ω cable, but is terminated by different effective impedances at both ends. This can lead to a high voltage standing wave ratio (VSWR) and large insertion loss in the cables. It is thus proposed to make the cables connecting the decoupling matrix to the pTx array as short as possible. This placement of the decoupling matrix introduces the need for an MR-safe, compact implementation. Prior work with Butler matrices at 7T has shown that architecturally similar devices can meet these specifications (54). Directional couplers used to measure power for control of the RF power amplifiers are to be placed between the RF amplifiers and the decoupling matrix so they measure RF amplifier power output.

The decoupling is achieved at the cost of only a small insertion loss. This insertion loss is implementation dependent. A distributed element approach is more suited for higher frequencies (for MRI at 7T or higher) where the hybrid couplers can easily be implemented via transmission lines. The insertion loss in this case will depend on the operating frequency and the dielectric loss tangent of the substrate of the transmission line. Since our decoupling matrix is similar to a Butler matrix in construction, it can be expected to have similar insertion loss. Butler matrices for 7T MRI applications are well studied and have been implemented with microstrip transmission lines (54). A possible downside of using a distributed element realization is the physical size of the matrix. As mentioned before, our strategy requires a worst-case N(N – 1) unequal divide hybrid couplers, and as a result, the size of the decoupling matrix could be large. A lumped element based realization is also possible (55), however since it requires a large number of lumped elements to realize a hybrid coupler, the insertion loss may increase. In our 4-channel realization, the insertion loss from the hybrid coupler itself was −0.057dB to −0.072dB, while the loss of the hybrid with the necessary interconnect cables was −0.25dB to −0.33dB. Thus, most of the insertion loss in our realization was due to series loss in the cables and impedance mismatches at the cable/connector interfaces. If this network were implemented in a single printed circuit board, with all interconnects done on the substrate, we would expect substantially reduced insertion loss. This claim is supported by the measured insertion loss of the two-hybrid boards. Each of these boards contained two hybrid couplers in series, but the insertion loss (−0.085dB to −0.11dB) was less than double that of a single-hybrid board.

The insertion loss of an individual hybrid coupler leads to scalability limitations of this method. For example, implementing a full 32-channel decoupling matrix would require each channel to individually pass through 2(N – 1)=62 hybrid couplers. Even in the best case of −0.057dB loss per hybrid, this is a total loss of −3.54dB – over half the input power. For an 8-channel pTx array, full decoupling would imply an insertion loss of −0.8dB i.e., 83% power delivery. However, some 8-channel pTx coils only show greater than −20dB of coupling between nearest-neighbor elements. This would imply a necessary insertion loss of under −0.3dB per channel. For an improved 4-channel realization, the expected insertion loss would be −0.34dB to −0.44dB. This is a power delivery of 90.5% to 92.5%. The off-diagonal terms of the coil's S-matrix are between −10dB and −12dB, meaning that between 22% and 26% of input power on one port is scattered back on the other three ports, and under 78% is delivered to the load. Thus, we would expect a decoupling matrix implemented entirely in PCB to significantly improve the power efficiency of this 4-channel pTx array. However, insertion loss of a decoupling matrix is only prohibitively high if it is greater than the efficiency gained by having a fully matched network. Whether or not a decoupling matrix meets this constraint must be determined on a coil-by-coil basis.

A decoupling strategy is useful if its performance is robust to load and component variations. We have shown both theoretically and experimentally that the decoupling matrix is robust to load variations, and have shown theoretically that it is robust to component variations. As shown in the results section, we have tested our implemented decoupling matrix under different loading conditions and found that its performance is satisfactory with load variations. Similarly, we performed a sensitivity analysis by varying the values of the lumped components used in the design within ±5% of the nominal component values, and found that the worst case decoupling level was with in an acceptable range of −25dB. We did observe in our 4-channel decoupling matrix that loading the coil with a significantly larger phantom than was designed for raised S₂₂ and S₃₃ to −18dB and −19dB, respectively. We expect, however, that using lower-Q matching networks (eg, Pi- or T-match) might reduce the dependence of S_ii parameters on load conditions.

Finally, our decoupling matrix creates orthogonal modes of excitations of the Tx channels that, although different from the coil natural basis, retain the degrees of freedom for pulse design. This is supported by the fact that the voltage transformation introduced by the decoupling matrix is full rank (i.e., no loss of Tx degrees of freedom). Thus, pulse design subject to B1 uniformity or SAR constraints can be easily done with our decoupling matrix by accounting for this full-rank transformation between the coil and RF amplifier bases.

In the future, we plan on extending the implementation to an 8-channel pTx system. Further work will involve measuring B1 maps with and without a decoupling matrix to further validate this method. Since the mathematical principals of decoupling are similar for receive coils, we would like to explore how such a decoupling matrix can be used to decouple receive coil arrays.

Appendix

Proof that the voltage transformation by our decoupling matrix is full rank

We compute the voltage transformation relation between the voltages V₁ and V₂ and show that the transformation is indeed full rank. We note that the above blocks are connected in cascade, i.e. the output of one block is connected to the input of the next. For such a connection the best choice to represent the blocks is via the ABCD-parameters, given in (8).

$$\left[\begin{array}{c}{V}_2\\ I_2\end{array}\right]=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{c}{V}_1\\ -I_1\end{array}\right],$$ (8)

This is because we can compute the ABCD-parameters of the entire chain simply by multiplication of the ABCD -parameter matrices of the individual blocks. Substituting the individual ABCD -parameter matrices in (8).

$$\left[\begin{array}{c}{V}_2\\ I_2\end{array}\right]=\left[\begin{array}{cc}I& j{D}_1\\ j{D}_2& I\end{array}\right]\left[\begin{array}{cc}B& 0\\ 0& B\end{array}\right]\left[\begin{array}{cc}I& -j{D}_X\\ 0& I\end{array}\right]\left[\begin{array}{cc}A& 0\\ 0& A\end{array}\right]\left[\begin{array}{c}{V}_1\\ -I_1\end{array}\right],$$ (9)

$$\left[\begin{array}{c}{V}_2\\ I_2\end{array}\right]=\left[\begin{array}{cc}BA& -jB{D}_{X}A+j{D}_{1}BA\\ j{D}_{2}BA& D_{2}B{D}_{X}A+BA\end{array}\right]\left[\begin{array}{c}{V}_1\\ -I_1\end{array}\right],$$ (10)

Where D₁ and D₂ are diagonal matrices. Under no load condition, I₁ = 0, this implies

$$V_2=BA{V}_1=T{V}_1$$

Since both B and A matrices are orthogonal by construction, T is a full-rank matrix. Hence the voltage transformation introduced by the decoupling matrix is full rank.