Summary
Humans explore static visual scenes by alternating rapid eye movements (saccades) with periods of slow and incessant eye drifts [1–3]. These drifts are commonly believed to be the consequence of physiological limits in maintaining steady gaze, resulting in Brownian-like trajectories [4–7], which are almost independent in the two eyes [8–10]. However, because of the technical difficulty of recording minute eye movements, most knowledge on ocular drift comes from artificial laboratory conditions, in which the head of the observer is strictly immobilized. Little is known about eye drift during natural head-free fixation, when microscopic head movements are also continually present [11–13]. We have recently observed that the power spectrum of the visual input to the retina during ocular drift is largely unaffected by fixational head movements [14]. Here we elucidate the mechanism responsible for this invariance. We show that, contrary to common assumption, ocular drift does not move the eyes randomly, but compensates for microscopic head movements, thereby yielding highly correlated movements in the two eyes. This compensatory behavior is extremely fast, persists with one eye patched, and results in image motion trajectories that are only partially correlated on the two retinas. These findings challenge established views of how humans acquire visual information. They show that ocular drift is precisely controlled, as long speculated [15], and imply the existence of neural mechanisms that integrate minute multimodal signals.
Keywords: Eye movements, head movements, visual acuity, retina, vestibulo-ocular reflex, microsaccades, ocular drift
Results and Discussion
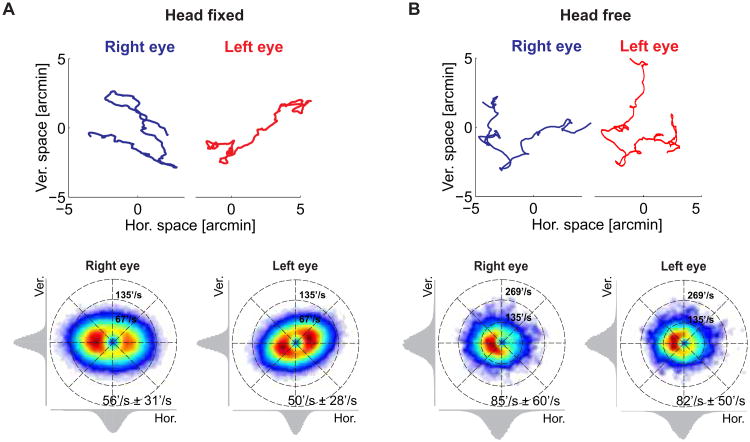
How do the eyes move in the periods between voluntary gaze shifts? Figure 1A summarizes current textbook knowledge on ocular drift, the slow wandering of the eye that incessantly occurs during fixation on a stationary object. Ocular drift resembles a random walk: it changes direction frequently, in a seemingly erratic manner, yielding relatively small overall displacements of the retinal image over the course of a typical fixation [4–7]. However, at each instant in time, the velocity of ocular drift is not negligible. Its mean instantaneous speed is close to 1 deg/s [7, 16], resulting in motion signals on the retina that would be immediately visible had they originated from objects in the scene rather than from eye movements. Drifts also appear to be little correlated in the two eyes, with each eye following its own trajectory almost independent from that of the other eye [8–10].
Figure 1. Ocular drift characteristics.
The eyes move incessantly during visual fixation. (A) Eye movements measured under strict head immobilization, a common condition in oculomotor experiments. The subject maintained fixation on a small marker while head movements were prevented by means of a bite bar and head rest. (B) Eye movements (rotations of the eyes within the head) acquired during normal head-free fixation (see Supplementary Experimental Procedures and Figure S1). In both A and B:(Top) Examples of ocular drift traces in the two eyes. (Bottom) Probability distributions of ocular drift velocities. The two panels show data from the right and left eye for one observer. Marginal distributions for the vertical and horizontal velocity components are shown on the corresponding axes. Numbers represent means and standard deviations of the instantaneous speed.
As customary in studies of microscopic eye movements, the data in Figure 1A were collected by means of a high-resolution eye-tracker while the subject's head was carefully immobilized. For comparison, Figure 1B shows the distributions of drift velocities in the two eyes measured for one observer during natural head-free fixation. In this case, eye movements were recorded by means of the Maryland Revolving Field Monitor (MRFM), a custom device specifically designed to give precise measurements without requiring immobilization of the head [17]. These data illustrate two important points. First, as previously reported [11], ocular drift tends to be faster during normal head-free fixation than under the standard laboratory condition of head immobilization. All participants exhibited considerably higher instantaneous speeds of ocular drift than those typically measured under head-fixed conditions (averages across all eyes: 94′/s vs. 51′/s; p <0.0001, two-tailed unpaired t-test). Second, a striking similarity appears in the shape of the distributions of drift velocities in the two eyes. On average, the binocular difference in the instantaneous drift velocity was of 27′/s in amplitude and 27° in direction. These differences are much smaller than those that would result from two independent random walks, each matched to the drift speed of the corresponding eye (p <0.001, paired two-tailed t-test). Thus, the eyes appeared to drift in a similar manner during natural head-free fixation.
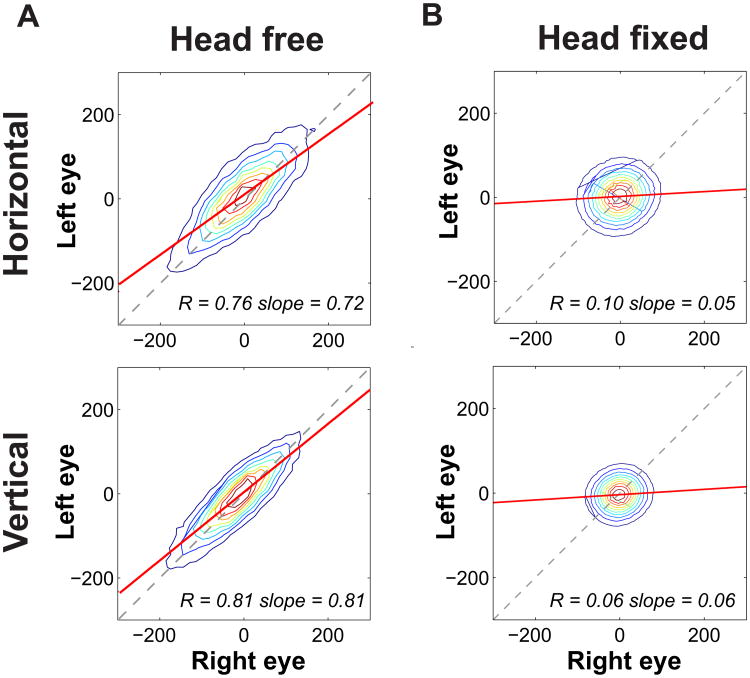
To investigate the similarity between drifts in the two eyes, we compared their instantaneous velocities while subjects normally fixated on nearby point-light sources without any head restraints. Only the periods of steady-state fixation, long after the completion of the previous saccade and long before the occurrence of the next one, were considered in this study (see Figure S1). As shown in Figure 2A, eye velocities were highly correlated on both the horizontal and the vertical axis, and the slope of the linear regression between left and right eye measurements was close to one. Correlation values differed significantly from zero for all subjects on both axes (p < 0.001, two-tailed t-test) and were also much higher than the spurious correlation levels that could be expected from common measurement noise in head and eye signals (p < 0.05, two-tailed bootstrap t-test; see Supplementary Experimental procedures).
Figure 2. Binocular drift coordination.
Joint probability distributions for the instantaneous velocities of ocular drift in the two eyes. Colored lines represent iso-probability contours. The two columns refer to different conditions: (A) Natural head-free binocular viewing. (B) Head-fixed binocular viewing. In this latter condition, the subject's head was firmly immobilized by a bite-bar and a head-rest. The two rows show horizontal and vertical velocity components. In all panels, the solid and dashed lines represent the linear regression and the 45° diagonal, respectively. Average correlation and slope of the linear regression are reported in each panel. Data represent averages across N=4 observers. See Figure S2 for the results of similar analysis under monocular viewing.
The similarity between the drifts in the two eyes was also confirmed by the strong frequency coherence for both horizontal and vertical velocities (average and std: 0.90 ± 0.07). These levels of correlation were significantly higher than those measured from the same subjects when resting on a bite bar during eye-tracker calibration—a condition in which microscopic head movements still occurred (average correlation: 0.12 ± 0.07; p < 0.003, paired two-tailed t-test)—and much larger than the values typically measured under the standard laboratory condition of strict head immobilization (0.08 ± 0.05; p <0.0001, unpaired two-tailed t-test). In this latter condition, drifts in the two eyes were virtually uncorrelated on both axes (Figure 2B). These results reveal that that the common notion that the two eyes drift independently during fixation is a consequence of the artificial conditions of standard experiments. Under natural viewing conditions, binocular coordination applies not only to saccades and smooth pursuits, but also to the much finer scale of fixational eye movements.
Given that the two eyes drift in a similar manner, it becomes important to understand what controls their fixational motion. Figure S2A shows the results of a similar analysis when the task was repeated under monocular viewing. In this case, one eye was patched to prevent visual stimulation, while its movements continued to be recorded during otherwise normal head-free fixation. Levels of correlation between drifts in the two eyes remained far above chance (p < 0.001, two-tailed t-test) and did not differ statistically from those measured during binocular viewing (p >0.11, paired two-tailed t-test). Thus, absence of retinal stimulation in one eye had little consequence on the degree of binocular drift coordination.
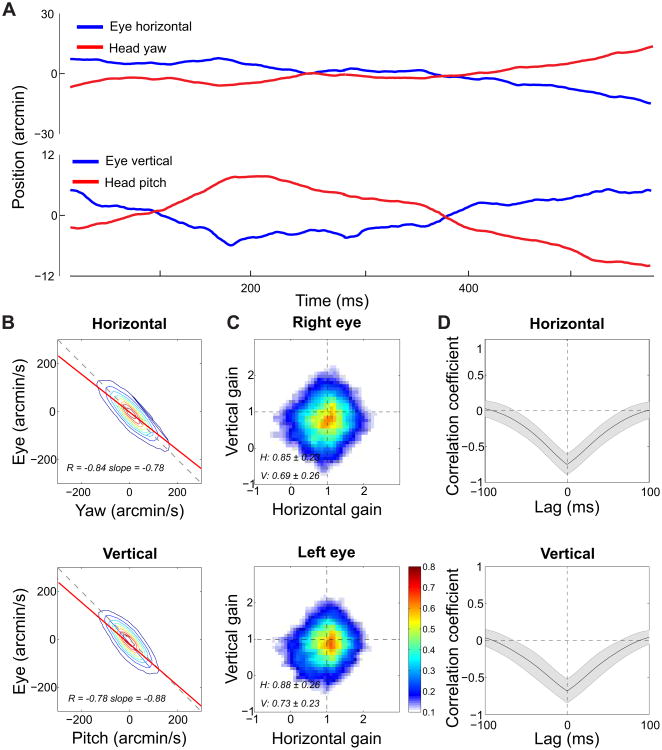
To investigate the origins and functions of the binocular drift coordination, we examined the relation between fixational head and eye movements. Small involuntary head movements are always present during natural fixation [11–13]. In our experiments, the subjects' head continually translated with average instantaneous linear speed of 6 mm/s and rotated with angular speeds of 49′/s (yaw) and 41′/s (pitch; see example in Figure 3A).
Figure 3. Fixational head-eye coordination.
(A) An example of head and eye traces during steady fixation. Note the very small scale of the movements on the y axis. (B) Comparison between the velocities of head and eye rotations. The horizontal and vertical components of ocular drift velocity are plotted as a function of the angular speeds of head yaw and pitch, respectively. Solid and dashed lines represent the linear regressions and the 45° diagonal. (C) Head/eye compensation gain. Distributions of the instantaneous gain between fixational head and eye movements. On each axis, gain equal one corresponds to perfect compensation (the fixated target remains immobile on the retina). Larger and smaller gain values represent over- and under-compensation, respectively. (D) Head/eye compensation delay. Mean cross-correlation functions between head and eye rotations. Shaded areas represent one standard deviation. Data are averages across all the recorded eyes during normal binocular viewing. See Figure S2 for the results of similar analysis under monocular viewing.
Figure 3B compares the horizontal and vertical components of the instantaneous drift velocity to the angular speeds of yaw and pitch head rotations, respectively. Head and eye rotations were strongly anticorrelated on both axes of motion, a phenomenon that was slightly more pronounced on the horizontal axis (p <0.05, two-tailed paired t-test). On both axes, correlation values were far above the levels that one would expect from common noise in the measurements (p <0.001, two-tailed bootstrap t-test) and also much larger than the correlation obtained by randomly pairing head and eye movement traces (p <0.001, two-tailed t-test). Strong anticorrelations persisted when one eye was patched (p <0.005, two-tailed paired t-test; Figure S2B) and did not change significantly from those measured during normal binocular viewing (p =0.32, paired two-tailed t-test). Thus, under both viewing conditions, ocular drift rotated the eyes with similar velocity to the head but in the opposite direction, as shown in the example trace in Figure 3A.
Since the targets were not at optical infinity, both head rotations and translations contributed to the motion of the retinal image. Therefore, we estimated the gain of the fixational head-eye coordination by examining the consequences of head and eye movements on the projection of the fixated target on the retina. We reconstructed retinal image motion by means of a standard eye model [18] and compared instantaneous drift velocity to the ideal eye velocity that would keep the fixated target immobile on the retina (Figure 3C). Ocular drift well compensated for head instability, yielding an average gain of 0.76 (p < 0.04, two-tailed t-test; gain one represents perfect compensation). Compensation was more accurate on the horizontal axis than on the vertical one (p <0.007, two-tailed paired t-test) and continued to operate efficiently during monocular viewing (average monocular gain: 0.79; p <0.003, two-tailed paired t-test). These gains are not far from those normally measured for much larger voluntary head oscillations [19, 20]. They are remarkably high considering the scale of fixational head and eye movements.
To operate efficiently, a fixational head/eye compensation mechanism needs not only to be accurate, but also to act quickly. Figure 3D shows the average cross-correlation functions between head and eye rotations on both the horizontal and vertical axes. Based on the sampling rate of the recordings (488 Hz) the smallest delay we can reliably measure is ∼2 ms, a temporal resolution sufficient to quantify the fast delays of the vestibulo-ocular reflex (VOR), generally between 10 and 15 ms [19–22]. These data show that the fixational compensatory mechanism was, on average, very fast: the cross-correlation function possessed a broad envelope that peaked around 0 ms. A similar shape in the cross-correlation function was also observed when directly analyzing the consequence of head and eye movements on the retinal image and during monocular viewing. Thus, ocular drift not only corrected for previous head movements but also frequently anticipated them, suggesting a joint control of fixational head and eye movements.
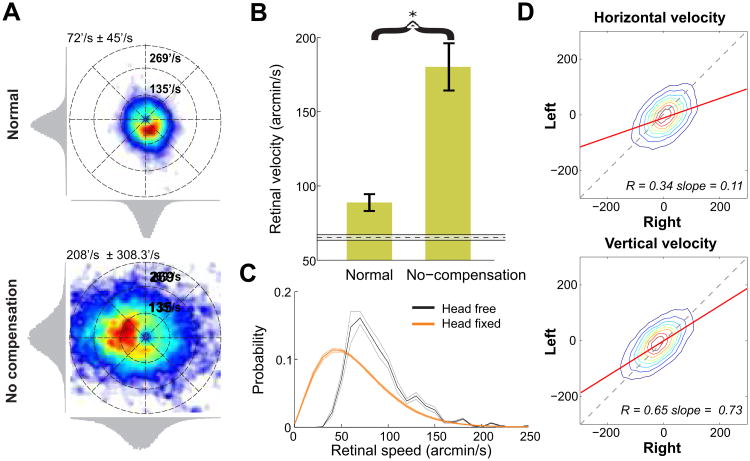
How does the compensation of fixational head and eye movements affect the stimulus on the retina? To investigate this question, we examined the speed of the retinal projection of the fixated target. Because of the separation between the eye's center of rotation and the optical nodal points, Gullstrand's eye model amplifies the velocity of the retinal image by a factor of approximately 40% relative to the velocity of ocular drift. Taking this amplification into account, the mean instantaneous speed of the fixated target on the retina during fixation was 90′/s. This value is much closer to the speed measured with the head immobilized (65′/s) than one would expect by considering head and eye movements independently (Figure 4A, C). For comparison, Figure 4 also shows the velocity of retinal motion obtained by decoupling fixational head and eye movements. In this analysis, ocular traces were reversed in time so to maintain their statistical properties, but eliminate the synchronization with head movements. This manipulation led to much higher speeds of the retinal image (179′/s; p < 0.005, two-tailed paired t-test). At this speed, the stimulus' projection would move far from the preferred retinal locus during the course of fixation. Thus, despite the faster ocular drift and the presence of head movements during natural fixation, head/eye compensation maintained retinal image motion within levels close to those experienced with the head immobilized.
Figure 4. Retinal image motion.
(A) Examples of probability distributions of the velocity of the fixated target on the retina. (Top) Normal head-free fixation. (Bottom) No head-eye coordination. Compensation was disrupted by decoupling head and eye traces. (B) Average speeds of the retinal projection of the fixated target for the two conditions in A. For comparison, the dashed line shows the average retinal speed measured in standard experiments with head immobilization, when subjects freely observed natural scenes. Error bars and the shaded region represent one standard deviation. The asterisk marks statistical significance at p < 0.005 (two-tailed paired t-test). (C) Retinal speed distributions in the sequential looking task under head-free and head-fixed conditions. Error bars represent s.e.m. (D) Binocular correlation in retinal image motion. Joint probability distributions of the velocity components in the projections of the fixated target in the two retinas. Different rows compare horizontal and vertical velocities (arcmin/s). In B-D, data represent averages across all recorded eyes.
Given the precision of the fixational head/eye compensation and the strong binocular correlation, one may intuitively assume that motion signals in the two retinas were also strongly correlated. However, this was not the case. Because head/eye compensation was not complete and the movements of the two eyes did not match perfectly, the resulting retinal motion was only partly correlated (Figure 4D). The measured correlation values were significantly lower than those obtained for eye drift (p < 0.0009, two-tailed paired t-test), particularly on the horizontal axis. On average, the instantaneous retinal velocities of the fixated target in the two eyes differed by 47′/s in amplitude and 40° in direction. Therefore, motion signals in the two eyes continue to differ considerably during natural fixation.
The results of Figures 1-3 show that the standard textbook description of how the eyes move during inter-saccadic fixation is not correct. The widespread notion that the two eyes drift randomly and independently with almost uncorrelated Brownian trajectories [4–7] only applies to the artificial laboratory condition in which the head of the observer is strictly immobilized. Outside the laboratory, fixational eye movements compensate for the microscopic head movements that continually occur during natural fixation. This compensation is remarkably fast and precise. Thus, rather than an uncontrolled random process resulting from noise at the neural and/or muscular levels, the smooth fixational motion of the eye represents a form of slow control aimed at maintaining ideal visual conditions [15].
How is the fixational head/eye compensation generated? One possibility is that ocular drift is the outcome of smooth pursuit on a stationary target, as previously speculated [23]. Although the target remains immobile in space, its projection moves on the retina because of fixational head movements. The resulting retinal velocities are well above the thresholds necessary for triggering pursuit eye movements [24, 25]. However, the characteristics of this motion, notably its speed, high gain, and the observation that head/eye compensation continues to operate in a visually-deprived eye, are all reminiscent of the vestibulo-ocular reflex (VOR). The VOR is well known for its velocity, with response latencies to actively generated or imposed head rotations typically in the 5-15 ms range [19–22]. Zero delays similar to those observed in our study have also been reported in the presence of self-generated head movements [26, 27]. Such anticipatory behavior presumably relies on the integration of vestibular signals with corollary discharges associated with head movements, an operation consistent with VOR physiology [28, 29] and which could be accomplished by known multimodal integration mechanisms [29–31]. With the exception of isolated pioneering efforts [11], the difficulty of precisely recording very small eye movements during natural head-free fixation has prevented study of the limits of the VOR, and it is not known whether vestibular neurons respond to such small head rotations. Our results indicate that VOR functions extend to a very fine scale and are normally responsible for the smooth component of fixational eye movements.
Irrespective of the specific mechanisms responsible for the fixational head/eye compensation, ocular drift assumes a very different character in the presence of normal head movements. This finding, however, does not automatically imply that standard oculomotor experiments with the head immobilized should be abandoned. In contrast with the changes in eye movements, the motion of the retinal image is little affected by freeing the head: it preserves its Brownian-like characteristics and maintains similar speed, therefore accounting for the robustness of the frequency content of visual input signals [14]. Head-fixed experiments continue to represent a valid approach for studying the characteristics of the retinal input, and drift remains a useful concept to describe the motion of the retinal image, but this notion needs to replace that of ocular drift as a separate category of eye movements.
In sum, our results suggest that the smooth fixational motion of the retinal image is the residual of a stabilization mechanism that operates to preserve the characteristics of retinal stimulation [32, 33]. Whether this residual motion is the consequence of physiological limits in head/eye compensation or represents instead a visuomotor strategy conserved for its perceptual benefits is as yet unclear. In either case, however, the resulting retinal image motion bears functional consequences. Previous work has shown that this motion reformats the mostly static visual image into a spatiotemporal signal with specific characteristics [34, 35]. This transformation not only prevents the reduction in contrast experienced under retinal stabilization, but also redistributes the spatial power of the external stimulus in the space-time domain in a way that counterbalances the structure of natural scenes [7] and enhances sensitivity to high spatial frequencies [36]. Without the fixational head/eye compensation, this redistribution would be altered, retinal image motion would be too fast for high-acuity vision [37–39], and the fixated target would quickly leave the small foveal locus of optimal sensitivity [40]. Thus, the oculomotor behavior described in this study appears to be critical for vision of fine spatial detail.
An interesting hypothesis now emerges. The nature of the spatiomporal reformatting of visual input signals—and, consequently, the range of spatial frequencies transmitted to the brain—depends on the characteristics of retinal image motion. This phenomenon is well captured by a Brownian model of retinal drift, in which lower diffusion constants lead to transmission of a wider equalized range of spatial frequencies, but with a lower gain. The current work raises the possibility that this trade-off can be regulated by controlling the fixational head/eye compensation: a more precise compensation would lead to a decrease in the diffusion constant and vice-versa. Further work is necessary to investigate whether humans use this mechanism to tune retinal image motion to the task demands.
Experimental Procedures
Subjects and Task
Seated subjects (20 in total; age range 30-70) were instructed to look sequentially at a series of fixation markers. Four observers took part in the head-free experiments conducted at the University of Maryland, and 16 subjects participated in the head-fixed experiments conducted at Boston University (4 subjects in binocular and 12 in monocular recordings). All experiments followed the ethical procedures approved by the University of Maryland and the Charles River Campus Institutional Review Board at Boston University.
Apparatus
In the head-free experiments head and eye rotations were measured and sampled at 488 Hz by means of the MRFM, a 2D coil system specifically developed to maintain resolution higher than 1′ even in the presence of considerable head and body motion [41]. Head-fixed data were recorded by means of a Dual Purkinje Image eye-tracker and sampled at 1 Khz. A custom dental-imprint bite-bar and a head rest were used to prevent head movements.
Data analysis
Only the very steady periods of fixation were considered in this study. These were the periods of binocular convergence on the fixation marker in which, for each individual subject, the velocities of both eyes remained within the 95th percentiles of the distributions measured at steady-state fixation (the distributions measured at least 300 ms after saccade end; see Supplementary Experimental Procedures). Only periods longer than 150 ms were included in the analysis. Results were extremely robust and changed little with fixation selection criteria.
Head and eye rotations were computed from the coil data following standard geometrical transformations [42]. Since estimation of eye movements relied on signals from both the eye and head coils, Monte Carlo simulations of the experiments were conducted to rule out possible noise influences in the analyses of Figures 2 and 3.
In Figures 3 and 4, we reconstructed the trajectory of the retinal projection of the fixated target by means of Gullstrand eye model with accommodation, which was properly positioned on the basis of the recorded head and eye movements data. The instantaneous gain of head/eye compensation was estimated on the basis of two velocity vectors on the retina: the ideal velocity νH necessary to counteract the effect of head movements and maintain the fixated target immobile on the retina, and the velocity νE resulting from eye movements alone. On each axis, the gain was defined as the ratio of the corresponding components of νE and νH.
Supplementary Material
Highlights.
Textbook descriptions of eye movements do not apply to natural head-free fixation
Fixational eye drifts continually compensate for microscopic head movements
Ocular drifts are coordinated in the two eyes and often anticipate head movements
The resulting motion signals on the retina differ considerably in the two eyes
Acknowledgments
This work was supported by National Institutes of Health grant EY18363 and National Science Foundation grants BCS-1127216 and 1420212. We thank Robert M. Steinman for making data collected with the Maryland Revolving Field Monitor, which was supported by the Air Force Office of Scientific Research, available for analysis and Jonathan D. Victor for many helpful comments and suggestions.
Footnotes
Author contributions: MP and MR conceived and designed the project and wrote the article. MP collected and analyzed data. MA helped with data analysis. MR supervised the work.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Steinman RM, Haddad GM, Skavenski AA, Wyman D. Miniature eye movement. Science. 1973;181:810–819. doi: 10.1126/science.181.4102.810. [DOI] [PubMed] [Google Scholar]
- 2.Kowler E. Eye movements: The past 25 years. Vision Res. 2011;51:1457–1483. doi: 10.1016/j.visres.2010.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rucci M, Victor JD. The unsteady eye: An information-processing stage, not a bug. Trends Neurosci. 2015;38:195–206. doi: 10.1016/j.tins.2015.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nachmias J. Two-dimensional motion of the retinal image during monocular fixation. J Opt Soc Am. 1959;49:901–908. doi: 10.1364/josa.49.000901. [DOI] [PubMed] [Google Scholar]
- 5.Burak Y, Rokni U, Meister M, Sompolinsky H. Bayesian model of dynamic image stabilization in the visual system. Proc Natl Acad Sci USA. 2010;107:19525–19530. doi: 10.1073/pnas.1006076107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Engbert R, Mergenthaler K, Sinn P, Pikovsky A. An integrated model of fixational eye movements and microsaccades. Proc Natl Acad Sci USA. 2011;108:765–770. doi: 10.1073/pnas.1102730108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kuang X, Poletti M, Victor JD, Rucci M. Temporal encoding of spatial information during active visual fixation. Curr Biol. 2012;20:510–514. doi: 10.1016/j.cub.2012.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ditchburn RW, Ginsborg BL. Involuntary eye movements during fixation. J Physiol. 1953;119:1–17. doi: 10.1113/jphysiol.1953.sp004824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cornsweet TN. Determination of the stimuli for involuntary drifts and saccadic eye movements. J Opt Soc Am. 1956;46:987–993. doi: 10.1364/josa.46.000987. [DOI] [PubMed] [Google Scholar]
- 10.Krauskopf J, Cornsweet TN, Riggs LA. Analysis of eye movements during monocular and binocular fixation. J Opt Soc Am. 1960;50:572–578. doi: 10.1364/josa.50.000572. [DOI] [PubMed] [Google Scholar]
- 11.Skavenski AA, Hansen RM, Steinman RM, Winterson BJ. Quality of retinal image stabilization during small natural and artificial body rotations in man. Vision Res. 1979;19:675–683. doi: 10.1016/0042-6989(79)90243-8. [DOI] [PubMed] [Google Scholar]
- 12.Crane BT, Demer JL. Human gaze stabilization during natural activities: Translation, rotation, magnification, and target distance effects. J Neurophysiol. 1997;78:2129–2144. doi: 10.1152/jn.1997.78.4.2129. [DOI] [PubMed] [Google Scholar]
- 13.Aytekin M, Rucci M. Motion parallax from microscopic head movements during visual fixation. Vision Res. 2012;70:7–17. doi: 10.1016/j.visres.2012.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Aytekin M, Victor JD, Rucci M. The visual input to the retina during natural head-free fixation. J Neurosci. 2014;34:12701–12715. doi: 10.1523/JNEUROSCI.0229-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Epelboim J, Kowler E. Slow control with eccentric targets: Evidence against a position-corrective model. Vision Res. 1993;33:361–380. doi: 10.1016/0042-6989(93)90092-b. [DOI] [PubMed] [Google Scholar]
- 16.Cherici C, Kuang X, Poletti M, Rucci M. Precision of sustained fixation in trained and untrained observers. J Vis. 2012;12:1–16. doi: 10.1167/12.6.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Epelboim J, et al. Gaze-shift dynamics in two kinds of sequential looking tasks. Vision Res. 1997;37:2597–2607. doi: 10.1016/s0042-6989(97)00075-8. [DOI] [PubMed] [Google Scholar]
- 18.Gullstrand A. Appendix II. In: von Helmholtz H, Southall JPC, editors. Helmholtz's treatise on physiological optics. Rochester, NY: Dover; 1924. pp. 351–352. [Google Scholar]
- 19.Collewijn H, Smeets JB. Early components of the human vestibulo-ocular response to head rotation: Latency and gain. J Neurophysiol. 2000;84:376–389. doi: 10.1152/jn.2000.84.1.376. [DOI] [PubMed] [Google Scholar]
- 20.Goldberg JM, et al. The Vestibular System: A Sixth Sense. Oxford University Press; USA: 2012. [Google Scholar]
- 21.Tabak S, Collewijn H, Boumans LJ, van der Steen J. Gain and delay of human vestibulo-ocular reflexes to oscillation and steps of the head by a reactive torque helmet. I. Normal subjects. Acta Otolaryngol. 1997;117:785–795. doi: 10.3109/00016489709114203. [DOI] [PubMed] [Google Scholar]
- 22.Angelaki DE, McHenry MQ. Short-latency primate vestibuloocular responses during translation. J Neurophysiol. 1999;82:1651–1654. doi: 10.1152/jn.1999.82.3.1651. [DOI] [PubMed] [Google Scholar]
- 23.Steinman RM, Kowler E, Collewijn H. New directions for oculomotor research. Vision Res. 1990;30:1845–1864. doi: 10.1016/0042-6989(90)90163-f. [DOI] [PubMed] [Google Scholar]
- 24.Mack A, Fendrich R, Wong E. Is perceived motion a stimulus for smooth pursuit. Vision Res. 1982;22:77–88. doi: 10.1016/0042-6989(82)90169-9. [DOI] [PubMed] [Google Scholar]
- 25.Poletti M, Listorti C, Rucci M. Stability of the visual world during eye drift. J Neurosci. 2010;30:11143–11150. doi: 10.1523/JNEUROSCI.1925-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.King WM, Shanidze N. Anticipatory eye movements stabilize gaze during self-generated head movements. Ann NY Acad Sci. 2011;1233:219–225. doi: 10.1111/j.1749-6632.2011.06165.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.King WM. Getting ahead of oneself: Anticipation and the vestibulo-ocular reflex. Neuro-science. 2013;236:210–219. doi: 10.1016/j.neuroscience.2012.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cullen KE. The neural encoding of self-motion. Curr Opin Neurobiol. 2011;21:587–595. doi: 10.1016/j.conb.2011.05.022. [DOI] [PubMed] [Google Scholar]
- 29.Carriot J, Brooks JX, Cullen KE. Multimodal integration of self-motion cues in the vestibular system: Active versus passive translations. J Neurosci. 2013;33:19555–19566. doi: 10.1523/JNEUROSCI.3051-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ernst MO, Bu¨lthoff HH. Merging the senses into a robust percept. Trends Cogn Sci. 2004;8:162–169. doi: 10.1016/j.tics.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 31.Fetsch CR, Pouget A, DeAngelis GC, Angelaki DE. Neural correlates of reliability-based cue weighting during multisensory integration. Nat Neurosci. 2012;15:146–154. doi: 10.1038/nn.2983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Steinman RM. Moveo ergo video: Natural retinal image motion and its effect on vision. In: Landy MS, Maloney LT, Pavel M, editors. Exploratory vision: The active eye. New York: Springer; 1995. pp. 3–50. [Google Scholar]
- 33.Liao K, et al. A reinterpretation of the purpose of the translational vestibulo-ocular reflex in human subjects. Prog Brain Res. 2008;171:295–302. doi: 10.1016/S0079-6123(08)00643-2. [DOI] [PubMed] [Google Scholar]
- 34.Rucci M, Casile A. Decorrelation of neural activity during fixational instability: Possible implications for the refinement of V1 receptive fields. Visual Neurosci. 2004;21:725–738. doi: 10.1017/S0952523804215073. [DOI] [PubMed] [Google Scholar]
- 35.Rucci M. Fixational eye movements, natural image statistics, and fine spatial vision. Network: Computation in Neural Systems. 2008;19:253–285. doi: 10.1080/09548980802520992. [DOI] [PubMed] [Google Scholar]
- 36.Rucci M, Iovin R, Poletti M, Santini F. Miniature eye movements enhance fine spatial detail. Nature. 2007;447:851–854. doi: 10.1038/nature05866. [DOI] [PubMed] [Google Scholar]
- 37.Westheimer G, McKee SP. Visual acuity in the presence of retinal-image motion. J Opt Soc Am. 1975;65:847–850. doi: 10.1364/josa.65.000847. [DOI] [PubMed] [Google Scholar]
- 38.Steinman RM, Levinson JZ, Collewijn H, van der Steen JV. Vision in the presence of known natural retinal image motion. J Opt Soc Am A. 2007;2:226–233. doi: 10.1364/josaa.2.000226. [DOI] [PubMed] [Google Scholar]
- 39.Flipse JP, van der Wildt GJ, Rodenburg M, Keemink CJ, Knol PG. Vontrast sensitivity for oscillating sine wave gratings during ocular fixation and pursuit. Vision Res. 1988;28:819–826. doi: 10.1016/0042-6989(88)90029-6. [DOI] [PubMed] [Google Scholar]
- 40.Poletti M, Listorti C, Rucci M. Microscopic eye movements compensate for nonhomogeneous vision within the fovea. Curr Biol. 2013;23:1691–1695. doi: 10.1016/j.cub.2013.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rubens SM. Cube-surface coil for producing a uniform magnetic field. Rev Sci Instrum. 1945;16:243–245. [Google Scholar]
- 42.Haslwanter T. Mathematics of three-dimensional eye rotations. Vision Res. 1995;35:1727–1739. doi: 10.1016/0042-6989(94)00257-m. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.