A Method to Estimate the Size and Characteristics of HIV-positive Populations Using an Individual-based Stochastic Simulation Model

Supplemental Digital Content is available in the text.

Abstract

It is important not only to collect epidemiologic data on HIV but to also fully utilize such information to understand the epidemic over time and to help inform and monitor the impact of policies and interventions. We describe and apply a novel method to estimate the size and characteristics of HIV-positive populations. The method was applied to data on men who have sex with men living in the UK and to a pseudo dataset to assess performance for different data availability. The individual-based simulation model was calibrated using an approximate Bayesian computation-based approach. In 2013, 48,310 (90% plausibility range: 39,900–45,560) men who have sex with men were estimated to be living with HIV in the UK, of whom 10,400 (6,160–17,350) were undiagnosed. There were an estimated 3,210 (1,730–5,350) infections per year on average between 2010 and 2013. Sixty-two percent of the total HIV-positive population are thought to have viral load <500 copies/ml. In the pseudo-epidemic example, HIV estimates have narrower plausibility ranges and are closer to the true number, the greater the data availability to calibrate the model. We demonstrate that our method can be applied to settings with less data, however plausibility ranges for estimates will be wider to reflect greater uncertainty of the data used to fit the model.

Despite the introduction of effective antiretroviral therapy (ART), HIV remains a key public health issue in most parts of the world, including Europe. UNAIDS estimates suggest that there were 2.2 million people living with HIV in the European region in 2012.¹

To understand an HIV epidemic in detail, a range of epidemiological data is required. Such data will help inform and monitor the impact of policies and interventions to tackle issues of prevention, diagnosis, and treatment of HIV. UNAIDS have launched a new target, “90-90-90,” which refers to three key steps to improve healthcare outcomes for HIV-positive people and to limit new infections: 90% of HIV-positive people to know their status, 90% of all diagnosed people to receive ART, and 90% of all people receiving ART to have viral suppression. There has also been increased interest in estimating the HIV care cascade^2,3 as an additional tool to understand and monitor linkage and retention in care.

It is desirable to have some estimates, regardless of the availability of surveillance data, to be able to consider future healthcare needs and to understand the importance of improved surveillance systems. A number of methods already exist to estimate the number of people living with HIV, which are based on fitting to prevalence survey data or performing back-calculations to reconstruct the historical HIV incidence curve.^4–6 However, there are relatively few countries in Europe where these methods are currently applied, due to lack of available data or resources, or concerns over their applicability for concentrated epidemics.⁷ Even in settings where such methods have been applied, few have provided a breakdown of the characteristics of HIV-positive populations, including size of the undiagnosed population, CD4 count and viral load distribution of the total population and the undiagnosed population, and number of people with triple class drug failure and resistance.

The objective of the Stochastic Simulation of Outcomes of People with HIV In Europe project in EuroCoord (EuroCoord-SSOPHIE project) is to generate such HIV estimates for European countries by developing a calibration method using an individual-based model of HIV. We present here the method we have developed which first calibrates such a model to the range of surveillance data available, and then uses the parameter sets which calibrate well to estimate and characterise the status of HIV-positive populations. The method is applied to data on men who have sex with men (MSM) in the UK and to pseudodata to assess the impact of different levels of availability of data.

METHODS

In brief, the calibration method presented here is a set of procedures that uses existing methodology (approximate Bayesian computation [ABC] methods) to calibrate a simulation model of HIV, to make inference about the populations simulated using parameter sets which calibrate well to the available data (includes both routinely collected case-report data and observational data). The method is first applied to generate HIV estimates for MSM in the UK for 2013. Surveillance data used to calibrate the model were obtained from Public Health England databases. Behavioural and other clinical data were obtained from a range of sources, described in references.^8,9 We chose the MSM epidemic in the UK as it has been studied extensively using other methods and there are other estimates with which we can compare our results.^10,11 We assume that the first infections occurred in 1980. Diagnosis of HIV was possible from 1984 onwards.¹² ART use was based on information from clinical cohorts.¹³ This modelling study was exempt from the need for review by the institutional review board as only aggregate data published in the public domain were used.

The Model

The method uses an updated version of an individual-based stochastic simulation model of HIV progression and the effect of ART (HIV Synthesis progression model).^9,14,15 The model is programmed in SAS software, Version 9.3 (SAS Institute Inc., Cary, NC). Model assumptions and parameters are based on data from observational cohort studies and clinical trials. The model aims to reconstruct the HIV-positive population of interest by simulating data on individual people from infection and following them over time. Variables such as CD4 count, viral load, use of specific antiretrovirals, treatment interruptions, presence of resistance mutations, and adherence levels are updated every 3 months. The risk of loss to follow-up, AIDS events, AIDS deaths, and non-AIDS deaths are also modeled. Note that in this model, we do not follow HIV-negative individuals as transmission of HIV is not modeled. Further details of the model have been described previously,^8,9 and additional updates are included in the eAppendix (Section 2; http://links.lww.com/EDE/A994).

There are multiple parameter values describing various elements of the underlying progression of HIV and the effect of ART. We have previously shown that the model output mimics empirical data on such processes well.^8,14 Therefore, for the purpose of calibrating the model parameters to a given HIV-positive population, we hold parameter values reflecting the intrinsic effects of HIV and ART fixed. In other words, this assumes that these parameter values are the same regardless of the population under consideration and are effectively part of the model structure.

Parameter Values Sampled Per Simulation

To calibrate the model to a particular population, the parameters which are sampled are those thought to potentially differ between populations or which have a large degree of uncertainty. We chose to focus only on one population (MSM) because the HIV incidence and diagnosis rate curves will typically differ by transmission route.

The two main sets of parameters for which values are sampled per simulation are those which parameterize the HIV incidence (number of new infections per year) and diagnosis rate. As all individuals in our progression model are HIV positive, the latter is the probability of diagnosis in an undiagnosed, asymptomatic individual in any 3-month period. The incidence and diagnosis rate curves between 1980 and 2013 are parameterized using seven and four parameters, respectively. These parameters inform two independent piecewise constant curves, i.e., the incidence and diagnosis rate are modeled to be constant over 5- and 8-year periods, respectively. We use such crude parameterization to limit the number of parameters and because the aim is not to estimate these curves per se, but to find sets of parameter values which generate a modeled population with characteristics similar to that of the surveillance and/or observational data.

There are a number of other parameter values that are likely to be specific for a given population and which are also varied across simulations: proportion of people resistant to testing, probability of not being linked to care soon after diagnosis, rate of loss to follow-up while ART-naïve, rate of treatment interruption, rate of restarting ART after interruption, rate of loss to follow-up while interrupting ART, rate of re-entry into care, probability of starting ART when eligible, rate of emigration and the population distribution of adherence levels. The prior distributions of these parameters are derived from observational studies carried out in the setting of interest or from other European studies. We sampled these parameters per simulation to reflect the uncertainty conveyed by the prior distributions used.

How the Model Is Calibrated to Country Data

The model is calibrated using ABC methods.¹⁶ The model naturally lends itself to working in a Bayesian framework to account for multiple parameter combinations providing outputs which fit well to the observed data (instead of converging to a single set of parameter values as would be the case in maximum likelihood estimation). ABC methods are suitable for calibrating simulation models to multiple datasets within tolerance bounds and have the advantage of accounting for parameter uncertainty and correlations. They are ideal for our purpose because we wish to explore a wide parameter space and consider as many parameter sets as possible that are consistent with the data.

ABC involves running the model multiple times where each run of the model is considered one simulation. In each simulation, unknown parameters are sampled from prior distributions, thereby constructing a different HIV-positive population. For each simulation, outputs of the model are compared with a range of surveillance data (in settings with incomplete surveillance systems, observational data may be used additionally or instead). Hereafter, we refer to each type of data (e.g., number of HIV diagnoses) as a “data item.” We quantify how well the model outputs match the surveillance data (i.e., assessing the goodness-of-fit) by calculating the “calibration score.” If the calibration score is within the tolerance threshold, then the set of parameter values used for that simulation are accepted. This process is repeated over multiple simulations. Further details of this calibration procedure are included in the eAppendix (Section 3; http://links.lww.com/EDE/A994).

For any single simulation, the calibration score is calculated as the weighted average of the deviances of the modeled outputs from the observed data. Therefore, the lower the calibration score, the better the model fits to the data. Weights for each data item are chosen a priori to reflect perceived data quality and completeness. Examples of data items which may be used to calibrate the model include: number of HIV diagnoses, number of first AIDS diagnoses, number of deaths, median CD4 count at diagnosis, number of new diagnoses which are recent infections, number seen in care and number on ART. The calibration process is continued until at least 100 sets of parameter values are within the tolerance threshold. In this particular application of the method, we have specified that the threshold should be a calibration score <0.2 (i.e., average deviation from the observed data across all data items is <20%). Further simulations are then performed using the accepted parameter sets to account for stochastic variability (i.e., variability in model outputs between simulation runs when using the same parameter set). The median, 5th and 95th percentiles of the distribution of these model outputs at each calendar year are considered the point estimate and plausibility range limits, respectively. The primary model outputs of interest are the number of people living with HIV, broken down by diagnosis status, ART-use, viral load, and CD4 count strata.

To apply this method to the HIV epidemic among MSM in the UK, the model is calibrated to a wide range of surveillance data available until 2012. As it is an individual-based model, we simulate a random 10% sample of the total infections to make the simulations more manageable, then multiply our outputs up. The data items and corresponding weights used to calibrate the model are shown in the Table.

TABLE.

Data Items and the Range of Calendar Years for Which Data Were Used to Calibrate the Model (Weights Used in Calibration Score Given in Brackets)

We also apply the calibration method to pseudodata to assess how well our method works for different availability of data items. The pseudodata was simulated also using the HIV Synthesis progression model, for a given incidence and diagnosis rate (all other parameters are fixed). The simulated outputs are used as if they are real data and the method is applied to model the hypothetical epidemic. Various data for the epidemic can then be assumed to be “unknown,” which then allows us to use the method described above to see how well it is able to reconstruct the true epidemic in different data availability scenarios. We conceived three scenarios of data availability: high, medium, and low (Table). The method was applied under each scenario and the resulting HIV estimates compared. Although this approach is somewhat circular in that the same model is used to generate and analyse the epidemic, it provides a useful means of being able to compare our calibration method with differing levels of data availability. Full details are given in the eAppendix (Section 5; http://links.lww.com/EDE/A994).

RESULTS

Calibration to Data on MSM in the UK and Resulting Estimates for 2013

Twenty-thousand simulations of the epidemic were generated, of which 294 were within the 0.2 calibration score tolerance threshold. A further 1,000 simulations were performed by resampling these 294 parameter sets. The following results presented are those generated using the 742 parameter sets where the calibration score was <0.2 (median: 0.178, min: 0.107, max: 0.199) among the 1,000 resampled simulations. Figure 1 shows that the model largely calibrates to the surveillance data. The surveillance data in 2012 compared with the median across the simulations, respectively, were number of HIV diagnoses (3,230 vs. 2,840), number of AIDS diagnoses (140 vs. 360), number of deaths (160 vs. 290), proportion of diagnoses with CD4 <350 cells/mm³ (34% vs. 39%), number seen for care (33,970 vs. 35,310) and number seen for care and currently on ART (28,530 vs. 30,215).

FIGURE 1.

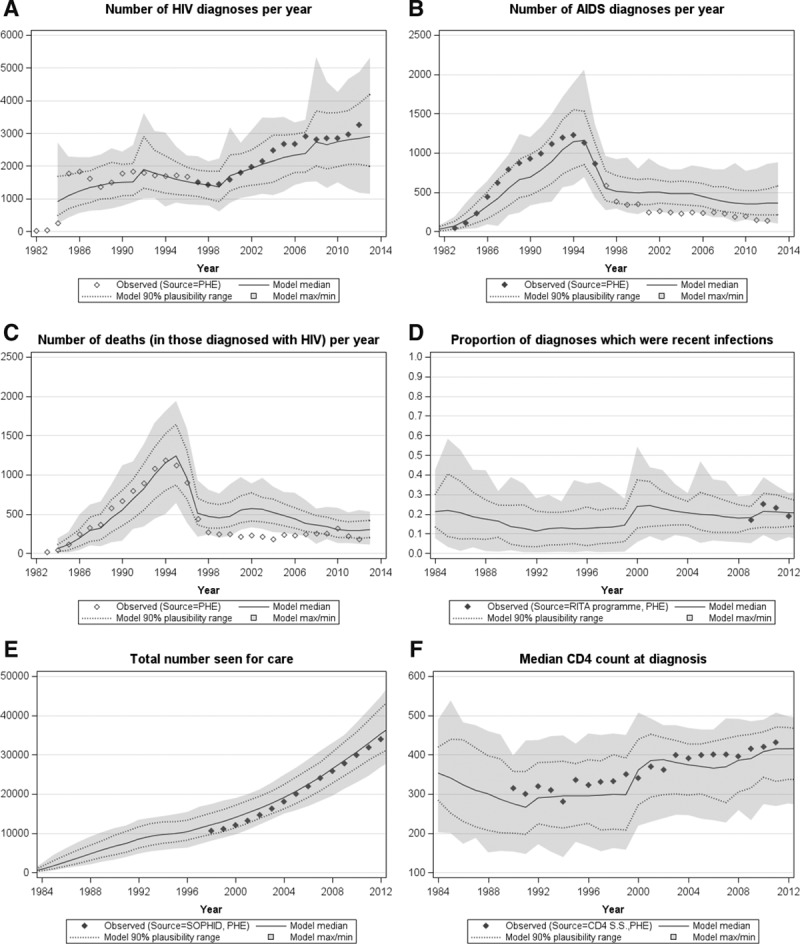
Calibrating the model to data on MSM in the UK. A, Number of HIV diagnoses, (B) number of AIDS diagnoses, (C) number of deaths, (D) proportion of diagnoses which were recent infections (defined here as an infection which took place within six months of an HIV diagnosis), (E) total number seen for care, (F) Median CD4 count at diagnosis. Diamonds represent surveillance data until 2012 supplied by Public Health England (PHE). Filled diamonds show data used to calibrate the model; open diamonds show data not used to calibrate the model. Model median (solid line), model 90% plausibility range (dotted lines) and model range (light grey band) also shown. RITA indicates recent infection testing algorithm; SOPHID, survey of prevalent HIV infections diagnosed; CD4 SS, CD4 surveillance scheme.

The distribution of incidence and diagnosis rate parameters are shown in Figure 2. This shows a steady increase in incidence from 1980, followed by a slightly lower level in the early 1990s and then a gradual increase again from then onwards. An estimated 3,210 (90% plausibility range:1,730–5,350) infections per year on average are thought to have occurred since 2010. The cumulative number of HIV infections that is thought to have occurred by end of 2012 totalled 67,720 (56,470–78,800). The diagnosis rate in asymptomatic individuals has steadily increased over time, but still remains low at an estimated rate of 0.042 (0.025–0.069) per 3 months in recent years.

FIGURE 2.

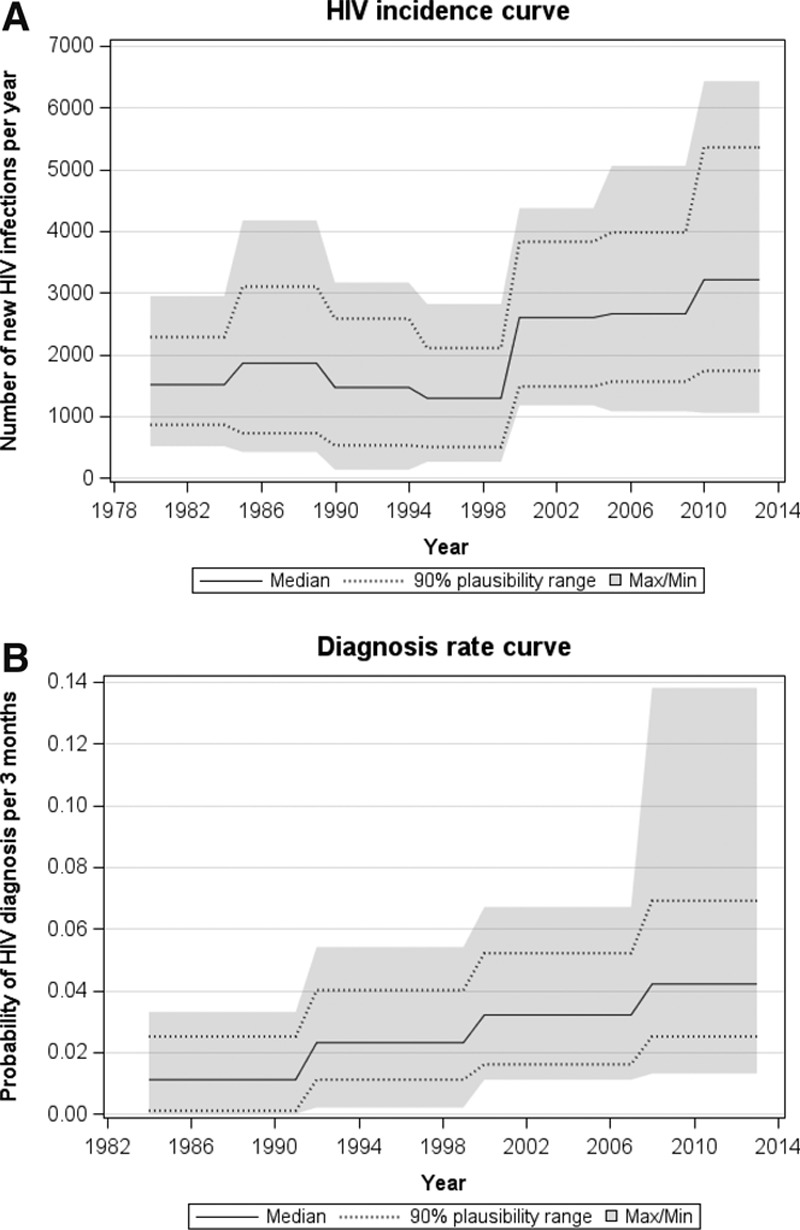
A, Estimated incidence (number of new HIV infections in a year) and the (B) estimated diagnosis rate (probability of being diagnosed in any given 3-month period) among MSM in the UK.

By 2013, an estimated 48,310 (90% plausibility range: 39,900–45,560) MSM were living with HIV in the UK (Figure 3), and 2,300, 5,500, 11,830, and 28,680 individuals had CD4 count ≤200, 201–350, 351–500, and >500 cells/mm³ respectively. It is thought that 10,400 (6,160–17,350) MSM were living with undiagnosed HIV, which means the undiagnosed proportion is 22% (13%–36%, Figure 3). In this undiagnosed population, an estimated 710, 1,930, 3,040, and 4,720 individuals had CD4 count ≤200, 201–350, 351–500, and >500 cells/mm³, respectively.

FIGURE 3.

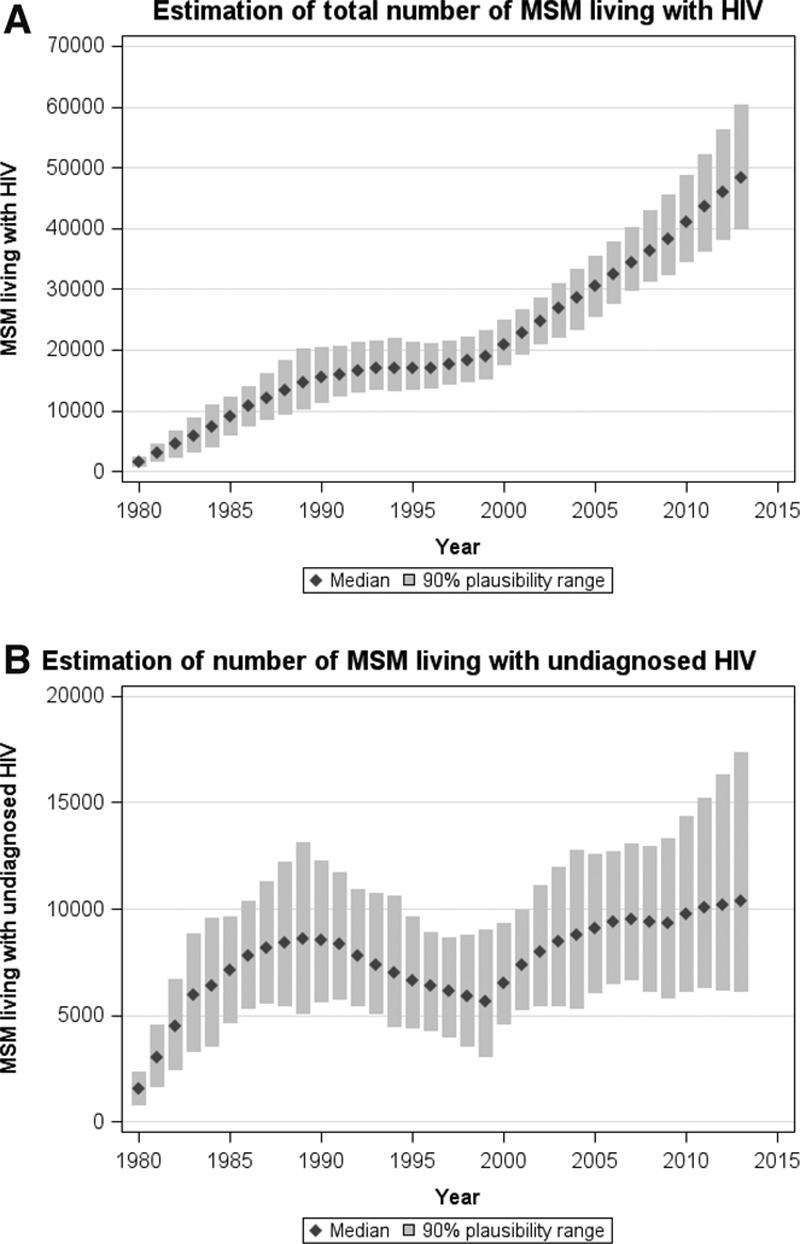
Estimates of the (A) total number of MSM living with HIV in the UK and (B) total number of MSM living with undiagnosed HIV, by calendar year. Columns and error bars: Modeled median and 90% plausibility range.

Figure 4A shows the estimated HIV care cascade in 2013. According to the model outputs, of all MSM living with HIV in 2013, 22% were undiagnosed, 23% were not in care, and 66% were receiving ART (current UK guidelines recommend ART to be initiated once the CD4 count drops below 350 cells/mm³). More than half (62%) of all HIV-positive MSM are thought to have suppressed viral load (<500 copies/ml). Of the 40,530 MSM in need of treatment (defined as people on ART and people ART-naïve with CD4 count <500 cells/mm³), 80% were estimated to be actually receiving it. Figure 4B shows a detailed breakdown of the population characteristics in terms of diagnosis status, treatment status, viral load distribution, CD4 count distribution, and resistance development.

FIGURE 4.

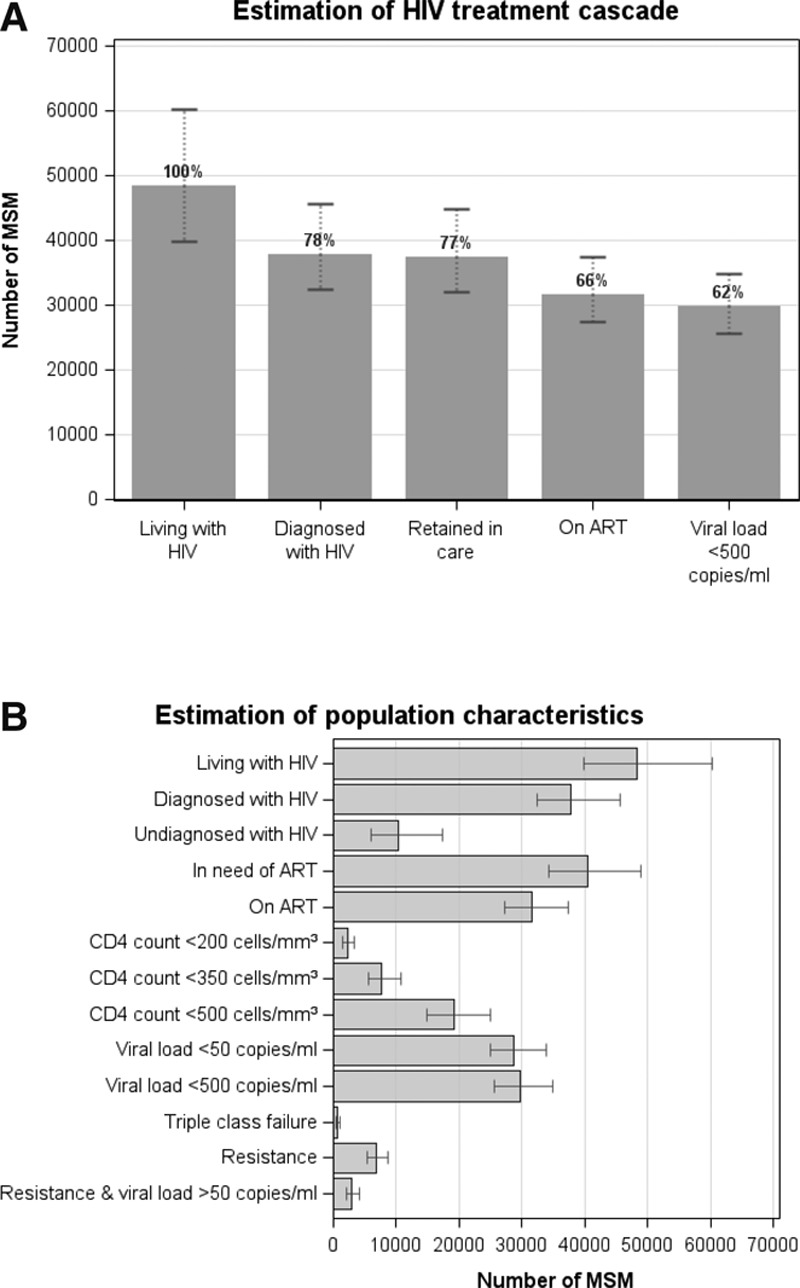
Estimated (A) treatment cascade and (B) population characteristics of all MSM living with HIV in the UK in 2013. Columns and error bars: Modeled median and 90% plausibility range. ART indicates antiretroviral therapy. “Resistance” is defined as at least one resistance mutation in majority virus. “In need of ART” includes people who are on ART and those who are ART-naïve with CD4 count <500 cells/mm³. ART indicates antiretroviral therapy.

Validation on Pseudodata to Assess Impact of Various Degrees of Data Availability

The results that follow are based on 100 simulations which had calibration score <0.2 for each of the three data availability scenarios. Where there were more than 100 simulations with calibration score <0.2, the 100 parameter sets leading to the 100 smallest calibration scores were used. The smallest calibration score achieved among these 100 simulations were 0.153, 0.138, and 0.001, respectively, for “high,” “medium,” and “low” data availability.

Figure 5 shows the estimated number of people living with HIV and living with undiagnosed HIV in 2013 by data availability. The category, “based on prior distributions,” refers to the median and 90% plausibility range of the estimates based on the full parameter distributions, including the outputs which did not get accepted based on the tolerance threshold; the plausibility range for this category therefore shows how wide it could have been if there were no data to calibrate the model to, compared with the other three scenarios). Although the smallest minimum calibration score was achieved with the “low” data availability scenario, the plausibility range is also the widest as the model was calibrated only to two data points.

FIGURE 5.

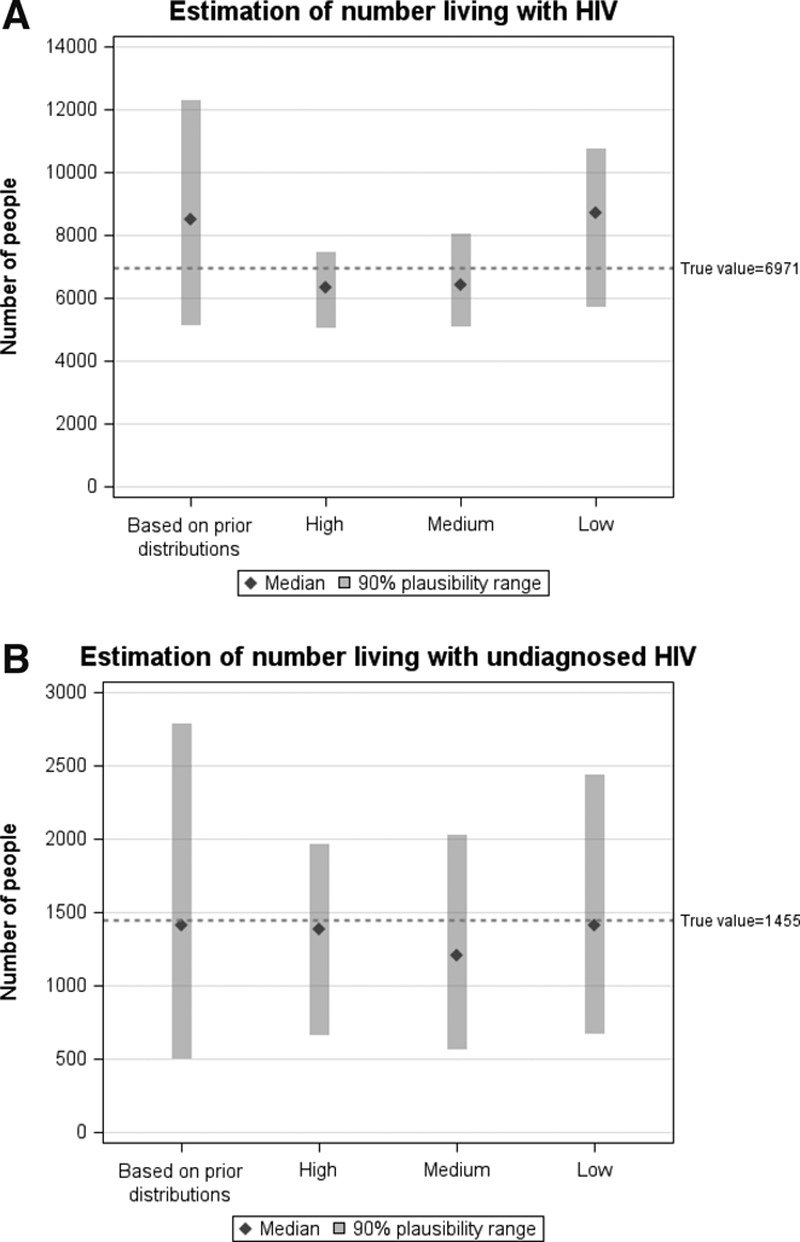
Estimate of the (A) number of people living with HIV and (B) number of people living with undiagnosed HIV in a hypothetical epidemic by data availability (high, medium, and low; see Table). Columns and error bars: modeled median and 90% plausibility range. “Based on prior distributions” refers to the outputs when all parameter sets are considered (none excluded by calibration-score criteria). The reference line (dotted) refers to the actual number of people living with HIV in the hypothetical epidemic.

Figure 6 depicts how well each data availability scenario was able to recapture the “true” incidence and diagnosis rate curves. Comparing with the incidence curve firstly, only the “high” scenario was able to obtain the approximate trend of an initial rise in incidence, followed by a dip, then a gradual increase subsequently, although some of the observations are outside the 90% plausibility range. All three scenarios estimate approximately the same number of infections which took place from 2010 onward, although the widths of the plausibility range differ greatly. Comparing with the diagnosis rate curve, all three scenarios were able to obtain a diagnosis rate of approximately 0.06 per 3 months in the most recent years of the epidemic. The differences, however, lie in the widths of the plausibility range, especially in the early years of the epidemic.

FIGURE 6.

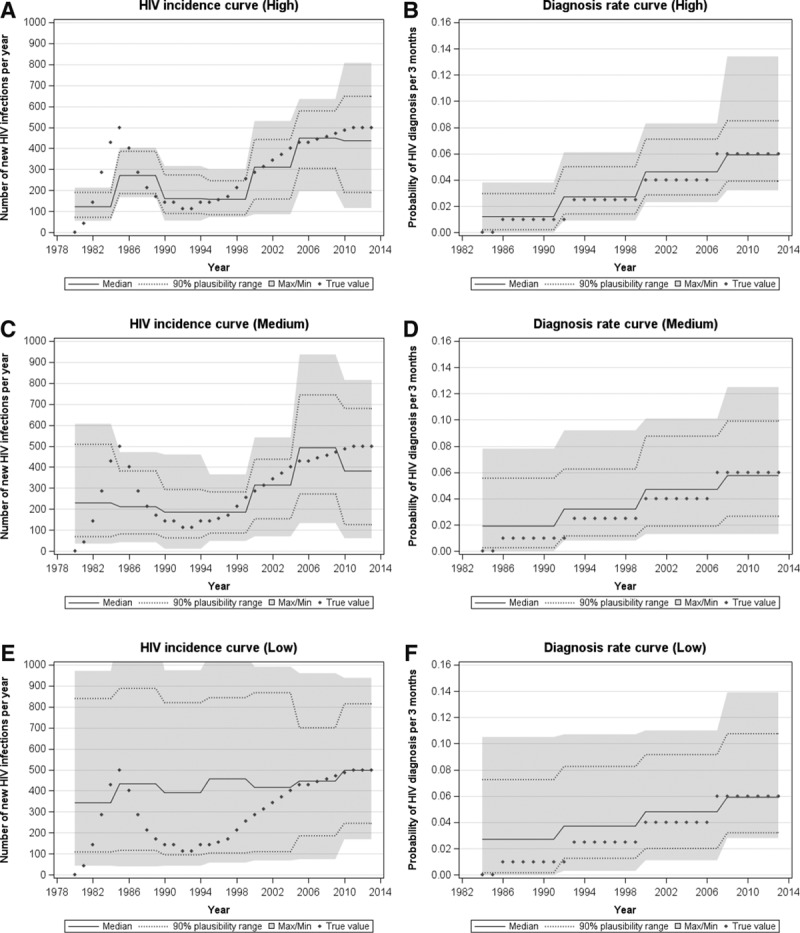
The resulting incidence curves and diagnosis rate curves as determined using our calibration method to the (A) and (B) high, (C) and (D) medium, and (E) and (F) low data availability scenario, respectively, with the “true” values as in the hypothetical epidemic represented by diamonds.

DISCUSSION

We have demonstrated an approach to estimate the size and characteristics of HIV-positive populations using a stochastic computer simulation model of HIV progression and the effects of ART. As the model reconstructs the population characteristics at a level corresponding to data collected as part of clinical care, it provides an approach to describe and understand HIV-positive populations in detail. We have shown that it is possible to generate estimates of numbers of people living with HIV and their characteristics, albeit with different levels of uncertainty, depending on the quality and availability of surveillance data. Together with other available information, epidemiologic and clinical estimates generated using our method could be used to further inform decisions and policies.^17,18 Although the HIV care cascade can be ascertained using alternative estimates of the undiagnosed proportion together with available surveilance data about the diagnosed population, we have also demonstrated (Figure 4) that it is possible to estimate the full cascade using this approach.

The number of MSM living with HIV in the UK is now estimated to be 48,310 for 2013. We estimated that there were approximately 3,210 new infections per year between 2010 and 2013, which was higher than the average for 2005–2009. However, the total number of undiagnosed HIV infections is thought to have remained reasonably stable over the past 5 to 7 years at around 10,000. The estimates and plausibility ranges generated using our method are based on the assumptions within the HIV Synthesis progression model and the prior distributions chosen. Our results were consistent with other UK estimates of the number of MSM living with HIV, living with undiagnosed HIV, and their CD4 count distribution.¹⁰

Results from our pseudodata example, which compared estimates when calibrating the model with varying amounts of data availability, show the difference in estimates and ranges for three different scenarios. Our results indicate that more reliable estimates are made with a wide range of surveillance data, and that having historical data also helps. The width of the plausibility range increases with less data available to calibrate the model. The differences between the three different scenarios showed that having data about the current population in care, such as data on the numbers of people on ART and case-report data on the number of diagnoses in a year, vastly help inform estimates of the total numbers living with HIV.

Our method has a number of advantages. The HIV Synthesis progression model simulates each individual’s life course and therefore reconstructs detailed characteristics of individuals which compose the HIV-positive population.¹⁹ The model can therefore be calibrated to a wide range of observational data (data items) simultaneously, which is beneficial because for some countries there may not be much HIV case-report data while data on the numbers of people on ART might be very accurate. It is possible to calibrate the model to less data; however, the plausibility ranges will be wider due to greater uncertainty. It is thus a very flexible approach which can utilise the data that is available, including but not limited to case-report data. We consider that our method is particularly useful when there are various sources of data available, as it also provides a framework for triangulation to assess overall coherence and consistency of data from various sources. The method in principle becomes very similar to other existing back-calculation methods when it uses only data that are used in those methods for calibration.

Using an individual-based model means that it is possible to estimate not only the size of the undiagnosed population but also we can simultaneously describe the population in terms of whether they are in care, ART coverage, immunological status, and population viral load. The model is also able to take account of specific drug use if data on regimens used are available, and hence can output estimates of drug resistance mutations and drug side effects, which may further help to inform national recommendations and policies.

By extending the duration of the simulated epidemic and projecting into the future, the method can also potentially be used for making short-term projections. Such projections, however, will be based heavily on the assumptions made regarding the incidence and diagnosis rate in the future and all resulting estimates will only be as reliable as the information put into the model.

A limitation of any modelling approach is that the validity of model estimates is highly dependent on the quality of available data used to calibrate the model. This means that the more reliable and accurate the data used to calibrate the model, the more likely estimates will be useful. In particular, it is essential to know the characteristics of the data and the mechanisms of surveillance systems so that these can inform the model calibration process. For instance, most countries will know about data problems such as under-ascertainment, double-counting, and misclassification bias, so efforts to reduce these errors or otherwise adjust the surveillance data accordingly is of importance. In our UK MSM example specifically, we think that the discrepancy between the observed data and modeled outputs on AIDS case reports (Figure 1) is due to known substantial under-reporting of such data in the UK in the era of effective ART.²⁰ For this reason, the model was not calibrated to data on AIDS case reports in those years (Table).

There are also a number of other limitations specific to our approach. First, even though our simulations are run on a computing cluster, as we use an individual-based model, our method is time consuming. However, once the plausible range of the historic incidence and diagnosis rate curves have been estimated, updating the estimates in future years will not require the same intensive fitting process to find parameter sets which calibrate well. Another limitation is the choice to use piecewise constant curves to parameterize the incidence and diagnosis rate. Other back-calculation studies on MSM epidemics in Western Europe have found a peak in incidence in the early to mid-1980s^21–23; however, due to the parameterization used, we cannot observe such a peak using this method. Although this means that the resulting incidence curve may not be an accurate reflection of infections in the past, estimates are unlikely to be severely biased, as the modeled incidence is just an average over a given time period. We investigate and discuss this further in the eAppendix (Section 4; http://links.lww.com/EDE/A994). One other limitation is that the definition of a “good” calibration score is somewhat arbitrary. The method simultaneously tries to fit to multiple data items, which may have their own biases, over a large number of years. Although we expect the data items to be complementary with one another, they will nevertheless have under- or over-counting nuances so we would not expect the calibration score to be zero. The results from applying the method to pseudodata illustrated that the more data there are to calibrate the model, the less likely it is to find a small calibration score.²⁴

The EuroCoord-SSOPHIE project aims to build on a previous effort to generate HIV estimates for Europe.²⁵ The development of methods to produce various HIV estimates and projections remains an important area within HIV epidemiology.^{10,22,26–28} Our method provides an alternative and complementary approach to existing methods because a more extensive range of data sources can be incorporated, if available. Having different methods that use different data and assumptions enables us to see whether the various approaches give comparable estimates, which provide support for the various estimates. The method presented here also provides a way to estimate key indicators such as the total number of people living with HIV, which helps to put targets such as the UNAIDS “90-90-90” into context. An adaptation of the method will be required to model epidemics among risk groups with a high proportion of migrants, such as people who acquired HIV in sub-Saharan Africa, as it is assumed that infections are mainly acquired in the setting of interest.

We have shown here an approach using an individual-based simulation model of HIV, which describes the size and characteristics of HIV-positive populations. This novel method allows us to also naturally produce plausibility ranges for these estimates, which describe the uncertainty surrounding the estimates, based on the data to which the model was calibrated.

ACKNOWLEDGMENTS

The authors acknowledge the Public Health England (PHE) HIV surveillance team and the use of UCL Legion High Performance Computing Facility (Legion@UCL) in the completion of this work. SSOPHIE project working group in EuroCoord: Fumiyo Nakagawa, Alioum Ahmadou, Andrew Amato-Gauci, Alison Brown, Jan Albert, Daniela Bezemer, Valentina Cambiano, Colin Campbell, Jordi Casabona, Daniel Commenges, Mario Cortina Borja, Dominique Costagliola, Daniela de Angelis, Valerie Delpech, Andrea de Luca, Martin Donoghoe, Deborah Ford, Geoff Garnett, Peter Ghys, Tim Hallett, Jesper Kjaer, Roger Kouyos, Rebecca Lodwick, Jens Lundgren, Nikos Pantazis, Santi Perez-Hoyos, Patrizio Pezzotti, Anastasia Pharris, Chantal Quinten, Mika Salminen, Colette Smit, Colette Smith, Jonathan Sterne, Virginie Supervie, Rodolphe Thiebaut, Claire Thorne, Pat Tookey, Giota Touloumi, Ard van Sighem, Andrew Phillips. EuroCoord Executive Board: Fiona Burns, University College London, UK; Geneviève Chêne, University of Bordeaux, France; Dominique Costagliola (Scientific Coordinator), Institut National de la Santé et de la Recherche Médicale, France; Carlo Giaquinto, Fondazione PENTA, Italy; Jesper Grarup, Region Hovedstaden, Denmark; Ole Kirk, Region Hovedstaden, Denmark; Laurence Meyer, Institut National de la Santé et de la Recherche Médicale, France; Heather Bailey, University College London, UK; Alain Volny Anne, European AIDS Treatment Group, France; Alex Panteleev, St. Petersburg City AIDS Centre, Russian Federation; Andrew Phillips, University College London, UK, Kholoud Porter, University College London, UK; Claire Thorne, University College London, UK. EuroCoord Council of Partners: Jean-Pierre Aboulker, Institut National de la Santé et de la Recherche Médicale, France; Jan Albert, Karolinska Institute, Sweden; Silvia Asandi, Romanian Angel Appeal Foundation, Romania; Geneviève Chêne, University of Bordeaux, France; Dominique Costagliola (chair), INSERM, France; Antonella d’Arminio Monforte, ICoNA Foundation, Italy; Stéphane De Wit, St. Pierre University Hospital, Belgium; Peter Reiss, Stichting HIV Monitoring, Netherlands; Julia Del Amo, Instituto de Salud Carlos III, Spain; José Gatell, Fundació Privada Clínic per a la Recerca Bíomèdica, Spain; Carlo Giaquinto, Fondazione PENTA, Italy; Osamah Hamouda, Robert Koch Institut, Germany; Igor Karpov, University of Minsk, Belarus; Bruno Ledergerber, University of Zurich, Switzerland; Jens Lundgren, Region Hovedstaden, Denmark; Ruslan Malyuta, Perinatal Prevention of AIDS Initiative, Ukraine; Claus Møller, Cadpeople A/S, Denmark; Kholoud Porter, University College London, United Kingdom; Maria Prins, Academic Medical Centre, Netherlands; Aza Rakhmanova, St. Petersburg City AIDS Centre, Russian Federation; Jürgen Rockstroh, University of Bonn, Germany; Magda Rosinska, National Institute of Public Health, National Institute of Hygiene, Poland; Manjinder Sandhu, Genome Research Limited; Claire Thorne, University College London, UK; Giota Touloumi, National and Kapodistrian University of Athens, Greece; Alain Volny Anne, European AIDS Treatment Group, France. EuroCoord External Advisory Board: David Cooper, University of New South Wales, Australia; Nikos Dedes, Positive Voice, Greece; Kevin Fenton, Public Health England, USA; David Pizzuti, Gilead Sciences, USA; Marco Vitoria, World Health Organisation, Switzerland. EuroCoord Secretariat: Silvia Faggion, Fondazione PENTA, Italy; Lorraine Fradette, University College London, UK; Richard Frost, University College London, UK; Andrea Cartier, University College London, UK; Dorthe Raben, Region Hovedstaden, Denmark; Christine Schwimmer, University of Bordeaux, France; Martin Scott, UCL European Research & Innovation Office, UK.

Supplementary Material

ede-27-247-s001.docx ^{(47KB, docx)}