Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Jan 12;120(3):433–439. doi: 10.1021/acs.jpcb.5b11157

Phase Space Bottlenecks in Enzymatic Reactions

Dimitri Antoniou 1, Steven D Schwartz 1,*
PMCID: PMC4734068  NIHMSID: NIHMS756916  PMID: 26756622

Abstract

graphic file with name jp-2015-11157e_0009.jpg

The definition of a transition state on an individual reactive trajectory is made via a committor analysis. In the past, the bottleneck definition has often been applied in configuration space. This is an approximation, and in order to expand this definition, we are revisiting an enzyme in which we had identified a fast subpicosecond motion that makes the reaction possible. First we used a time-series analysis method to identify the exact time when this motion initiates donor–acceptor compression. Then we modified the standard committor analysis of transition path sampling to identify events in phase space and found that there is a dividing surface in phase space significantly earlier than the configurationally defined transition-state crossing.

1. Introduction

Studying the passage over a transition state in enzymatic reactions remains a formidable task. There are two main approaches, one that employs variational transition state theory (VTST),1 with the main focus on calculating the free energy to reaction, and transition path sampling (TPS),2,3 with the main focus on analyzing ensembles of reactive trajectories and extracting important dynamical details. Despite the sometimes heated discussion about the merits of the two approaches they complement each other, VTST is often used by groups who are more focused in calculating reaction rates and kinetic isotope effects, while TPS is often used by groups who are more focused in identifying mechanistic details at the atomic level. In earlier work, we proposed that in some enzymes there may exist short time scale motions near the active site that help create the conditions for the chemical event.4 We have used TPS in these studies and found that the biggest difficulty is to identify methods that can successfully analyze the ensemble of reactive trajectories. In this work, we start from the formulation of the problem in the Grote–Hynes framework of reactions, which we then use to formulate a new method for analyzing TPS-generated ensembles of reactive trajectories. This analysis applied to a specific enzymatic reaction will show that there may be a bottleneck in phase space that has to be passed through to create the conditions for the reaction, and that this bottleneck may be distinct from the configurational bottleneck in geometry and positions in time. Very often (but not always5), it is assumed that the enzymatic transition state can be defined in configurational space.

We will summarize briefly the standard conceptual framework for reactions in condensed phases. The emphasis will be on the limits where a solution is possible within this framework, because we want to show that the effect we want to study lies in a lacuna of this framework. There are two flavors of the standard framework, the Grote–Hynes theory (GH)6 and the variational transition state theory,1 which are equivalent in certain limits.7−9 Insight into dynamics is more natural if one starts from GH and derives VTST as a limit, which is the path we will follow here. Let us assume that the barrier-crossing event for the reaction coordinate s is described by the generalized Langevin equation

1. 1

where V(s) is the mean-field barrier to reaction. Grote and Hynes6 solved eq 1 for the case of a parabolic barrier V(s) and found rich dynamic behavior. First, the direction of the unstable frequency at the barrier crossing is not that of the uncoupled coordinate s, but it is rotated because s is coupled to the environment mode which cannot adjust adiabatically to the motion of s. This rotation is the same one that is captured by VTST. In fact, for a harmonic environment coupled bilinearly to the reaction coordinate it can be shown that the GH theory and VTST are identical.9 Second, the time scale of the reaction is determined by the Laplace frequency component of γ(t) at the frequency of the unstable mode. Finally, one can find the behavior of the solution in several limits discussed below.10

The first limit is when the dynamics of the environment is much faster than that of the reaction coordinate (equilibrium solvation): the environment can adjust adiabatically to the motion of s and provide the equilibrium solvation that was assumed for V(s) in eq 1. Then, only the short-time behavior at time-scales 1/ωb (inverse barrier curvature) near the TS crossing matters. Staying in the above equilibrium solvation limit if the coupling of s to the environment is strong, the passage over the barrier is diffusion-controlled, the transmission coefficient is <1, and the full frequency dependence of the friction is required. This result is what is referred to when one reads that “recrossing identifies dynamical effects”, which is correct as long as one understands that the dynamical effect that is identified is diffusion-controlled barrier-crossing at strong friction. Another important limit is when the motion s is much faster than the environment and the friction is sufficiently strong: we are in the nonadiabatic solvation limit and the value of friction that matters is γ(t = 0) . In this case, instead of the solvated barrier it is the nonadiabatic (i.e., bare) potential that is relevant.

This brief discussion shows how the GH theory extends the VTST framework because it can illuminate dynamic details that are missing from it. The GH/VTST framework has been extremely successful, in fact it provides the concepts and vocabulary for describing reactive events (there is also an alternative view that combines VTST with information extracted from individual trajectories, the ensemble-averaged VTST11,12). Relevant to the following discussion are two dynamical details of reaction events that are included in GH: the coupling of the reaction coordinate to the environment during TS crossing is captured by rotation of the TS dividing surface and the interplay of time scale separations can lead to qualitatively different regimes. However, there is a limiting case were no results were derived, when some environment motions have the same time scale as the crossing of the barrier. We will now argue that a rate-promoting enzyme motion we have proposed is an example of exactly this limit and that GH theory can be generalized to accommodate it.

In a study of proton transfer in enzymatic reactions Borgis and Hynes13 suggested the possibility that a motion that modulates the donor–acceptor distance may be critical, since it affects the transfer probability for the proton, and they derived a solution in the deep-tunneling limit. In this limit, there is time scale separation between tunneling and protein motions. A few years ago, we extended this idea for enzymatic proton-transfer reactions14,15 in cases where the barrier height is moderate. TPS analysis showed that the motion q that modulates the chemical barrier height and width has time scale similar to the time scale of barrier crossing. This motion cannot be part of the environment modes of the GH theory since it is neither much faster nor much slower than barrier crossing. In addition, as we will find later, their main influence is felt far from the TS, so their effect cannot be captured through a rotation of the TS dividing surface. A simple model that can describe such a motion q that modulates the width and height of a barrier is to assume that q is harmonic and is coupled to s through a term s2q. In earlier work we had generalized and solved the GLE for this simple model and found that the friction kernel was equal to16

1. 2

where γ0 is the friction kernel of eq 1. When the frequency ωq is large, the influence of the fast oscillatory term cos[ωq(t – t′)] cancels out, and we arrive back to the equilibrium solvation limit. But when the time scales of q and barrier crossing are similar, we get behavior that cannot be described within the GH framework: the friction kernel is now position-dependent and the second term in eq 2 (which multiplies ṡ in eq 1) may mean that q is coupled to the velocity of the reaction coordinate s far from TS (interestingly, the original Grote–Hynes paper6 examined a case with oscillatory friction kernel, but there was no position dependence). One may think that even if q prepares the system for reaction away from the TS, what affects the rate are events near the TS crossing, but we have shown in a previous paper17 that the rate of a system that obeys eq 2 depends on the frequency of the q.

We should point out that the well-known studies by Hynes on proton-transfer in solution that describe a similar rate-promoting motion by a thermodynamic average of the tunneling matrix element18 concern a situation with separation of time scales and correspond to ωq much smaller than the barrier-crossing time scale. On the other hand, the case we examine here with the time scale of ωq similar to barrier crossing, cannot be captured by an average. Finally, the dynamics that is captured by the mode q is completely unrelated to the dynamics captured by the recrossing factor, since q is effective away from the equilibrium solvation limit and has nothing to do with strong friction and diffusion-controlled barrier crossing. Of course eq 2 is a toy model, and by itself, it cannot explain realistic enzymatic reactions; for that, one needs atomistic simulations like those that are the output of TPS. As we already mentioned, it is often difficult to devise methods for analyzing TPS-generated trajectories, and for that reason, simple models, like the above, can point to fruitful directions for TPS postanalysis.

In the rest of the paper, we will argue that in a particular enzymatic system there is coupling between a nonreactive motion and the bond-breaking and bond-forming distances, that they have similar time scales and the coupling happens away from the TS; we will finally show that the velocities of the nonreactive motions must have specific values, therefore the dividing surface to reaction not only is defined in coordinates but also has a component in phase space.

2. Dynamical Coupling of the Reaction Coordinate

The enzyme we studied was lactate dehydrogenase (LDH), in which we have identified a rate-promoting motion in a series of papers.19−22 We should point out that this motion is not present in other enzymes.23 Details about the crystal structure used and preparation for the simulation can be found in our earlier work,22 The quantum region (QM) consists of the substrate pyruvate, the NAD cofactor and part of His169 which donates the proton to pyruvate during oxidation.24 The QM region was described with the AM1 semiemprical method and the generalized hybrid orbital method was used to treat the two covalent bonds which divide the QM and classical regions. We have argued that a motion that originates in the protein matrix and is directed along the axis that connects donor and acceptor facilitates catalysis. In Figure 1 we show part of the active site of LDH and the residues along this axis of the motion that may facilitate catalysis. We do not show residues (Glu102, Glu192, Asp194, Thr248) that are important for binding and substrate recognition, since this is not the focus of this work.

Figure 1.

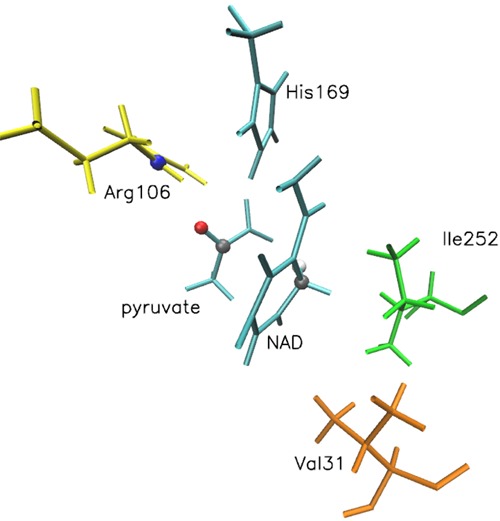
Figure 1

Open in a new tab

Active site of LDH: substrate (pyruvate) and cofactor (NAD) in cyan. Also shown are three residues along the axis that connects donor and acceptor. Two atoms that are in close proximity are highlighted: a nitrogen in Arg106 and an oxygen in pyruvate. The hydride donor and acceptor atoms are marked with gray.

On the donor side, Ile252 lies right behind the nicotinamide ring of NAD, and Val31 is next to it. On the acceptor side, Arg106 lies very close to the pyruvate (substrate). Arg106 polarizes the substrate carbonyl and is considered crucial for catalysis. Ile252 stabilizes the neutral (NADH) coenzyme form25 and is also known to be evolutionary conserved in the LDH family.26 Val31 is also along the donor–acceptor axis, and in previous work, we considered it as a candidate for initiating their compression. To be fair, this enzyme is an ideal candidate for the effect we are studying in this paper: Ile252 lies right next to the nicotinamide ring of NAD and can easily push it, while two electronegative atoms, in Arg106 and in pyruvate, are in close proximity allowing Arg106 to easily push the small pyruvate molecule.

Using TPS we generated 100 reactive trajectories. Details from a typical reactive trajectory are shown in Figure 2 where we plot distances between certain pairs of atoms during the chemical event. As is common with hydride transfer reactions, the chemical event is preceded by a compression of the donor–acceptor distance. In Figure 2 we see a shortening of distances between 252–donor, 31–donor and 106–acceptor just before the donor–acceptor compression. Of course, correlation alone between distances does not imply causation; e.g., it is conceivable that the donor–acceptor distance is freely oscillating without any interaction with the nearby residues and what we see in Figure 2 is just the donor periodically approaching immobile residues behind the NAD ring. Then, its distance from Ile252 and Val31 would also exhibit the behavior shown in Figure 2. In the rest of this section we will show that this is not the case and there is dynamic coupling between the motions of these residues and the donor and acceptor atoms.

Figure 2.

Figure 2

Open in a new tab

Distances between donor–acceptor, Ile252–donor, 106–acceptor, and 31–donor during the chemical barrier crossing.

To identify collision events, the study of changes of velocities is a better diagnostic than changes in distances. The simplest method would be to calculate velocity cross-correlations, but this has to be rejected since it is known from time series theory27 that cross-correlations (unlike autocorrelations) have arbitrary normalization for zero time lag. Therefore, this method would not be capable of size estimates of effects. Another method that is often used to study protein motions is principal component analysis,28 but it uses averages of motions; therefore, it is more suitable for the study of long time scale motions. Since the dominant trend of the time evolution of these distance is oscillatory, it is natural to use a method that is able to identify changes in the oscillatory behavior at specific times along the trajectory. A Fourier transform analysis is not appropriate for this since it is localized in frequency space and lacks any information in time. However, there is a method that has been developed for exactly this situation, the empirical mode decomposition (EMD),29 which has become a standard tool for the analysis of nonstationary signals. EMD can be considered as a time-dependent generalization of Fourier transforms: the signal x(t) is decomposed in a Fourier-like series

2. 3

with time-dependent frequency ωj(t) and amplitude of oscillation aj(t).

A central concept in EMD are the instantaneous modes (IM), which are oscillatory signals found by a sifting procedure (this procedure is summarized graphically in Figure 3): one finds functions that envelop the signal from above and below; the first IM is the average of these two envelops; the IM is subtracted from the signal, which results in a new signal; the method is iterated starting with the new signal. The output is a set of IMs, which have different time scales for their oscillatory behavior, and whose sum is the original signal:

2. 4

Then one takes the Hilbert transform 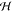Inline graphic of each instantaneous mode, which is the principal value integral

2. 5

Then one forms the complex signal

2. 6

which gives the time-dependent amplitude a(t) of eq 3 while the instantaneous frequency ω(t) that appears in eq 3 is given by

2. 7

Alternatively, one could have found this time-dependent frequency spectrum using wavelet analysis. Experience has shown that EMD and wavelet analysis lead to similar results.

Figure 3.

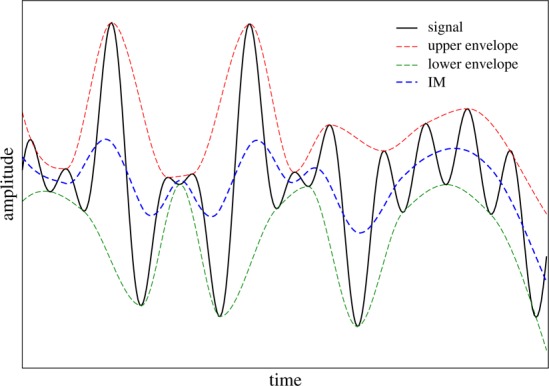
Figure 3

Open in a new tab

Construction of an instantaneous mode for EMD analysis: one forms envelopes that bound the signal from above and below and takes their average, which is an IM. This IM is subtracted from the signal to form a new signal, and the process is then repeated.

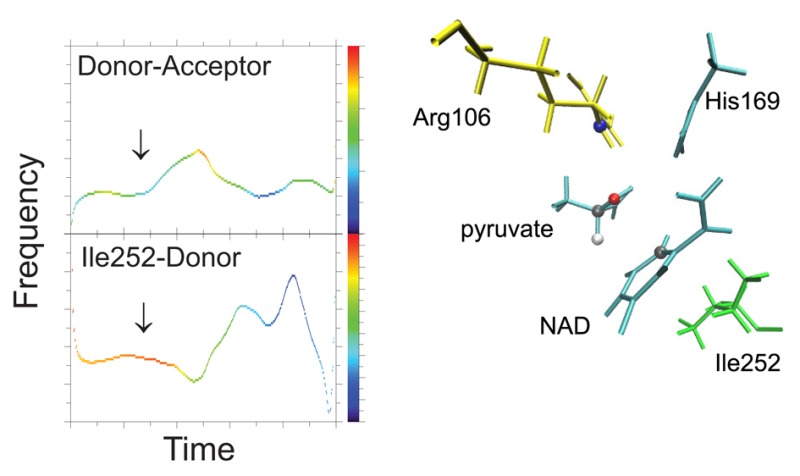
We have performed an EMD analysis of the time series shown in Figure 2. These calculations were done with the statistical software R.30 In Figure 4, we show time-dependent frequency plots of the distance time-series shown in Figure 2. For the donor–acceptor and the Ile252–donor time series there was one dominant instantaneous mode, whose Hilbert spectrum is plotted, while for the other two time series there was no dominant IM and we plotted the one with frequency most similar to the first two. First, we note that just before the start of the compression of the donor–acceptor distance there is an increase in its frequency, at 100 fs. We note that at the same time the donor–acceptor frequency event starts, there is a change in frequency of the Ile252–donor distance, in the opposite direction, suggesting a transfer of energy between the two motions. This shows that the donor–acceptor distance does not oscillate independently of the motion of Ile252, but the donor scatters off Ile252 just before the donor–acceptor compression starts. As we stressed in the introduction, this is an effect that cannot be captured by a thermodynamic average. On the other hand, Arg106 and Val31 do not seem to play a role in compressing donor–acceptor in this particular trajectory. Interestingly, Figure 4 shows that the frequency in which these events take place is about 150 cm–1, which is the frequency of an equilibrium density fluctuation of this protein that we had calculated in an earlier work.20

Figure 4.

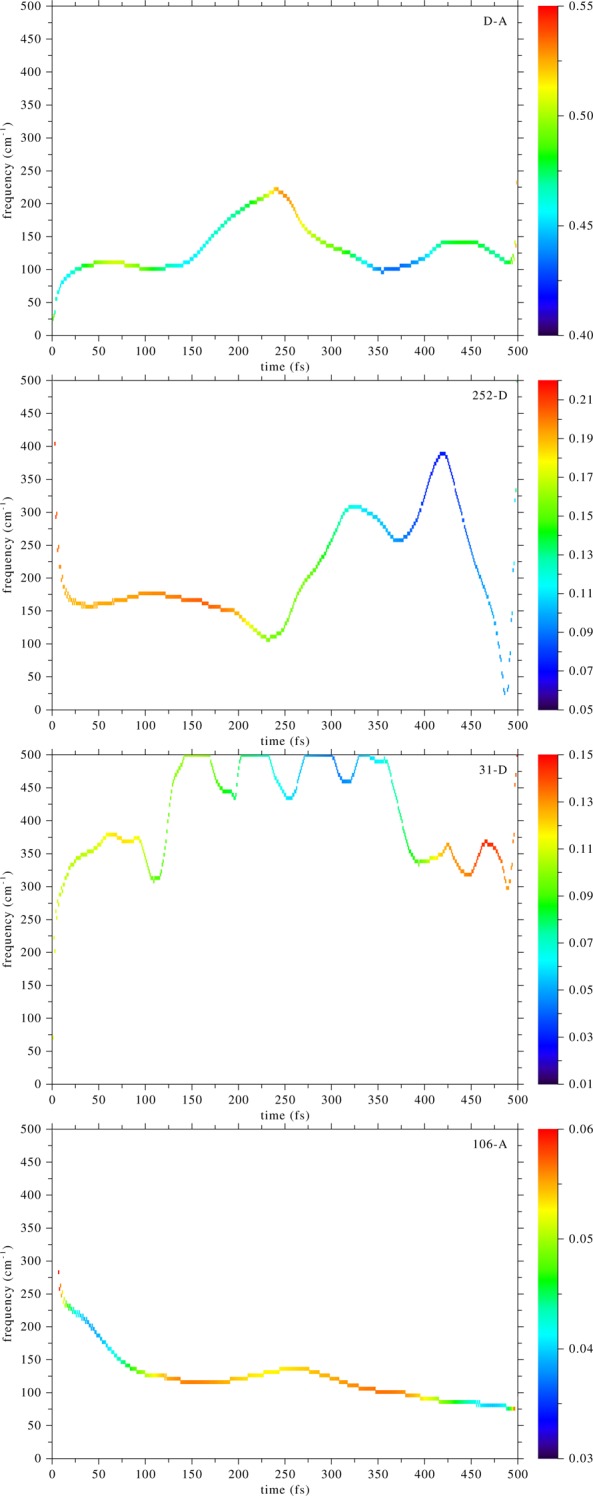
Figure 4

Open in a new tab

Empirical mode decomposition of the time series of Figure 2. These are plots of the frequency component (vertical axis) vs time (horizontal axis), while the color indicates the power density of the signal. From top to bottom: donor–acceptor, Ile252–donor, 31–donor, and 106–acceptor. The donor–acceptor distance compression in Figure 2 started at ∼120 fs. The Ile252–donor distance seems to be dynamically coupled to the donor–acceptor motion; note the change in frequencies of these two motions at 100 fs.

We saw this pattern (pushing of the donor by Ile252) in other trajectories of the TPS ensemble as well, but another class of trajectories showed a different pattern. All trajectories of the ensemble belong to one of these two classes. A typical example of the alternate pattern is shown in Figure 5, which to the naked eye does not look different than that of Figure 2. For the donor–acceptor and the Arg106–acceptor time series there was one dominant instantaneous mode, whose Hilbert spectrum is plotted, while for the other two time series there was no dominant IM, and we plotted the one with frequency most similar to the first two. In Figure 6, we show an EMD analysis of the time series of Figure 5: the start of the change of frequency of the donor–acceptor distance is accompanied by an opposite change in frequency of the Arg106 motion. In this trajectory Arg106, and possibly Ile252 and Val31, are coupled dynamically to the donor–acceptor motion.

Figure 5.

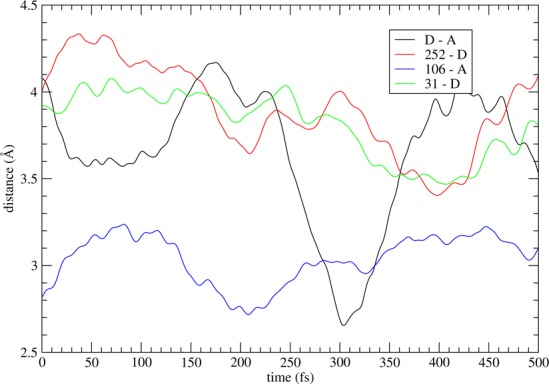
Figure 5

Open in a new tab

Same distances as in Figure 2, for a different trajectory.

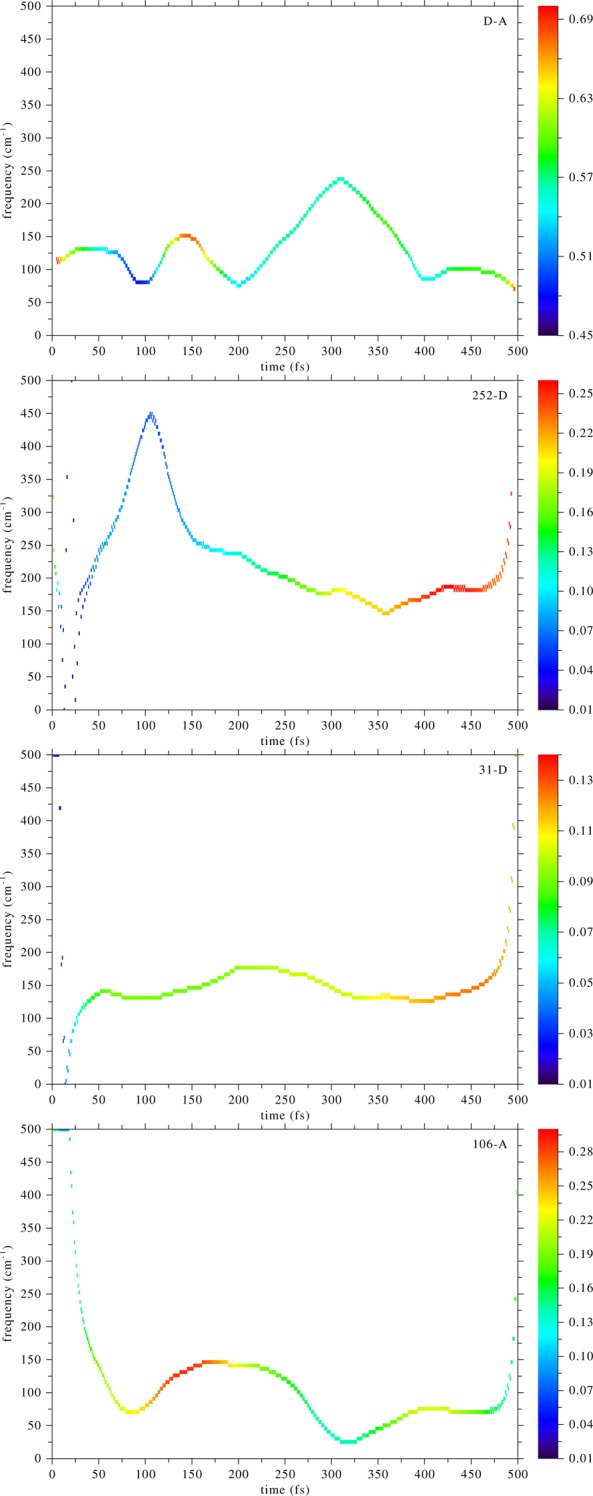
Figure 6.

Figure 6

Open in a new tab

Empirical mode decomposition of the time series of Figure 5. These are plots of the frequency component (vertical axis) vs time (horizontal axis), while the color indicates the power density of the signal. From top to bottom: donor–acceptor, Ile252–donor, 31–donor, and 106–acceptor. The donor–acceptor distance compression in Figure 5 started at ∼200 fs. The Arg106–acceptor distance seems to be dynamically coupled to the donor–acceptor motion; note the change in frequencies of these two motions at 200 fs.

In this section we showed that the donor–acceptor compression is not an independent event, but it is coupled dynamically to the motion of Ile252 and Arg106, and the coupling happens away from the TS. These results are consistent with the extension to the GLE we discussed in the introduction, where we used a toy model to capture the effect of motions that compress the donor–acceptor distance in the same time scale as the barrier crossing event. This dynamic coupling alone is not guaranteed to be related with the chemical event in the enzyme. One needs to perform some committor analysis of the TPS ensemble that outputs a relation of this dynamic coupling with the reaction. The standard committor analysis cannot capture these events because it is performed in coordinate space,2 but the results of this section showed us the direction for extending the committor test, as we will show in the next section.

3. Extended Committor Analysis

Once an ensemble of reactive trajectories has been generated by TPS a standard postproduction procedure is to perform a committor analysis and find the surface in coordinate space with the property that trajectories initiated from it have equal probability to reach reactants or products. This surface is called the separatrix and is usually taken as the rigorous definition of the transition state. In all committor analyses we are aware of, the separatrix was identified in coordinate space. The previous section showed that there are important events in momentum space and we will now examine if they are related to the reactive event. It is known that the separatrix is completely defined in coordinate space only if the reactive paths can be defined exclusively in coordinate space.31 We have modified the standard committor calculation procedure to accommodate for the possibility that specific values of selected atom momenta are necessary at specific times for the reaction to happen. Instead of fixing all atomic coordinates and drawing all atomic momenta from a Boltzmann distribution, we fixed in addition the momenta of selected atoms and drew randomly momenta for the remaining atoms. The shooting move has not been drawn from a true Boltzmann distribution since some atoms kept their original momenta, but because the proportion of these atoms is very small compared to the overall system the resulting shooting has to a very good approximation the correct distribution.

The results shown in Figure 7 were produced by fixing the momenta of the following: the QM atoms; the QM and Ile252 atoms; the QM, Ile252, and Arg106 atoms. One expects that when the velocities of the QM atoms are fixed remotely from the TS calculated in coordinate space, the new separatrix will be shifted with respect to the coordinate space separatrix, since close to the TS the active site is already organized optimally and the remaining requirement, the donor–acceptor compression that allows the hydride transfer to happen, has already started. This effect is seen in Figure 7, where the separatrix calculated with the QM atoms fixed (blue dots) is significantly earlier than the coordinate space separatrix (black dots).

Figure 7.

Figure 7

Open in a new tab

Committor functions generated by fixing momenta of selected atoms (in addition to fixing the coordinates of all atoms) before performing the committor analysis. The location of the committor function calculated in coordinate space alone is marked with black dots. Blue dots mark the committor when the momenta of the QM atoms are fixed before calculated the committor. Fixing the momenta of atoms of nearby residues results in the committors indicated with red and green dots.

The panels in Figure 7 correspond to the two trajectories that were examined in the previous Section. The left panel corresponds to the trajectory analyzed in Figures 2 and 4, which had identified residue Ile252 as responsible for initiating the donor–acceptor compression. Fixing the velocities of Ile252 and performing committor analysis moves the separatrix 10 fs earlier than its location when only the momenta of the QM atoms were fixed. This shows that the motion of Ile252 is not only dynamically coupled to the donor–acceptor motion, it is also involved in the reaction itself, even though its action happens far from the coordinate defined TS.

Similarly, the right panel of Figure 7 examines the trajectory analyzed in Figures 5 and 6. There we found that it is the motion of Arg106 that initiates the donor–acceptor compression, with a possible small contribution from the motion of Ile252. Repeating the procedure of fixing momenta of selected atoms and then calculating the committor function shows results consistent with the time-series analysis. Ile252 has a small effect in pushing the separatrix toward earlier times, while the effect of Arg106 is larger.

4. Conclusions

Using the empirical mode decomposition method, we have shown that in lactate dehydrogenase there is a motion that is dynamically coupled to the donor–acceptor compression and identified the exact time of this event. We then generalized committor analysis and showed that the velocity of this motion defines a dividing surface that separates reactants and products and that this surface is earlier than the transition state. We should emphasize that the focus was not in proving that dynamical effects are important, or what is the proper definition of dynamics, or whether the events we described are just part of a preorganization of the active site. Rather, we are interested in describing the reactive event in atomistic detail and drawing conclusions that can be useful in further investigations. For example, work is already under way in using these results for devising mutations that will alter the properties of this enzyme.

Acknowledgments

The authors acknowledge the support of the National Institutes of Health, Grant GM068036.

The authors declare no competing financial interest.

References

  1. Garrett B.; Truhlar D. In Theory and Applications of Computational Chemistry: the first forty years; Dykstra C., Frenking G., Kim K., Scuseria G., Eds.; Elsevier: 2005. [Google Scholar]
  2. Dellago C.; Bolhuis P.; Geissler P. Transition path sampling. Adv. Chem. Phys. 2002, 123, 1–86. 10.1002/0471231509.ch1. [DOI] [PubMed] [Google Scholar]
  3. Bolhuis P.; Dellago C. Practical and conceptual path sampling issues. Eur. Phys. J.: Spec. Top. 2015, 224, 2409–2427. 10.1140/epjst/e2015-02419-6. [DOI] [Google Scholar]
  4. Schwartz S. D.; Schramm V. L. Enzymatic transition states and dynamic motion in barrier crossing. Nat. Chem. Biol. 2009, 5, 551–558. 10.1038/nchembio.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gertner B. J.; Bergsma J. P.; Wilson K. R.; lee S.; Hynes J. T. Nonadiabatic solvation model for SN2 reactions in polar solvents. J. Chem. Phys. 1987, 86, 1377. 10.1063/1.452225. [DOI] [Google Scholar]
  6. Grote R. F.; Hynes J. T. The stable states picture of chemical reactions. II. Rate constants for condensed and gas phase reaction models. J. Chem. Phys. 1980, 73, 2715. 10.1063/1.440485. [DOI] [Google Scholar]
  7. McRae R.; Schenter G.; Garrett B.; Svetlicic Z.; Truhlar D. G. Variational transition state theory evaluation of the rate constant for proton transfer in a polar solvent. J. Chem. Phys. 2001, 115, 8460–8480. 10.1063/1.1409953. [DOI] [Google Scholar]
  8. Tunon I.; Laage D.; Hynes J. Are there dynamical effects in enzyme catalysis? Some thoughts concerning the enzymatic chemical step. Arch. Biochem. Biophys. 2015, 582, 42–55. 10.1016/j.abb.2015.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Pollak E. Theory of activated rate processes: a new derivation of Kramers’ expression. J. Chem. Phys. 1986, 85, 865. 10.1063/1.451294. [DOI] [Google Scholar]
  10. Hynes J. T. Chemical reaction dynamics in solution. Annu. Rev. Phys. Chem. 1985, 36, 573. 10.1146/annurev.pc.36.100185.003041. [DOI] [Google Scholar]
  11. Truhlar D. G.; Gao J.; Garcia-Viloca M.; Alhambra C.; Corchado J.; Luz Sanchez M.; Poulsen T. D. Ensemble-averaged variational transition state theory with optimized multidimensional tunneling for enzyme kinetics and other condensed-phase reactions. Int. J. Quantum Chem. 2004, 100, 1136–1152. 10.1002/qua.20205. [DOI] [Google Scholar]
  12. Masgrau L.; Truhlar D. The importance of ensemble averaging in enzyme kinetics. Acc. Chem. Res. 2015, 48, 431–438. 10.1021/ar500319e. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Borgis D.; Hynes J. T. In The enzyme catalysis process; Cooper A., Houben J., Chien L., Eds.; Plenum: New York, 1989; p 293. [Google Scholar]
  14. Antoniou D.; Schwartz S. D. Proton transfer in benzoic acid crystals: another look using quantum operator theory. J. Chem. Phys. 1998, 109, 2287. 10.1063/1.476796. [DOI] [Google Scholar]
  15. Pineda J.; Schwartz S. Protein dynamics and catalysis: the problems of transition state theory and the subtlety of dynamic control. Philos. Trans. R. Soc., B 2006, 361, 1433–1438. 10.1098/rstb.2006.1877. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Caratzoulas S.; Schwartz S. D. A computational method to discover the existence of promoting vibrations for chemical reactions in condensed phases. J. Chem. Phys. 2001, 114, 2910–2918. 10.1063/1.1342817. [DOI] [Google Scholar]
  17. Antoniou D.; Abolfath M. R.; Schwartz S. D. Transition path sampling study of classical rate-promoting vibrations. J. Chem. Phys. 2004, 121, 6442–6447. 10.1063/1.1782813. [DOI] [PubMed] [Google Scholar]
  18. Kiefer P.; Hynes J. Kinetic isotope effects for nonadiabatic proton transfer reactions in a polar environment: 1. Interpretation of tunneling kinetic isotopic effects. J. Phys. Chem. A 2004, 108, 11793–11808. 10.1021/jp040497p. [DOI] [Google Scholar]
  19. Basner J. E.; Schwartz S. D. How enzyme dynamics helps catalyze a reaction, in atomic detail: a transition path sampling study. J. Am. Chem. Soc. 2005, 127, 13822–13831. 10.1021/ja043320h. [DOI] [PubMed] [Google Scholar]
  20. Davarifar A.; Antoniou D.; Schwartz S. The promoting vibration in LDH is a preferred vibrational channel. J. Phys. Chem. B 2011, 115, 15439–15444. 10.1021/jp210347h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Quaytman S.; Schwartz S. Reaction coordinates of an enzymatic reaction revealed by transition path sampling. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 12253–12258. 10.1073/pnas.0704304104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Masterson J. E.; Schwartz S. D. Changes in protein architecture and subpicosecond protein dynamics impact the REaction catalyzed by lactate dehydrogenase. J. Phys. Chem. A 2013, 117, 7107–7113. 10.1021/jp400376h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Dametto M.; Antoniou D.; Schwartz S. Barrier crossing in DHFR does not involve a rate-promoting vibration. Mol. Phys. 2012, 110, 531–536. 10.1080/00268976.2012.655337. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Fersht A.Structure and mechanism in protein sciences: a guide to enzyme catalysis and protein folding; W. H. Freeman: New York, 1998. [Google Scholar]
  25. Dunn C.; Wilks H.; Halsall D.; Atkinson T.; Clarke A.; Muirhead H.; Holbrook J. Design and synthesis of new enzyme based on the lactate dehydrogenase framework. Philos. Trans. R. Soc., B 1991, 332, 177–184. 10.1098/rstb.1991.0047. [DOI] [PubMed] [Google Scholar]
  26. Madern D. Molecular evolution within the L-malate and L-lactate dehydrogenase super-family. J. Mol. Evol. 2002, 54, 825–840. 10.1007/s00239-001-0088-8. [DOI] [PubMed] [Google Scholar]
  27. Chatfield C.The analysis of time series, 6th ed.; Chapman and Hall/CRC: 2003. [Google Scholar]
  28. Núñez S.; Wing C.; Antoniou D.; Schramm V. L.; Schwartz S. D. Insight into catalytically relevant correlated motions in human purine nucleoside phosphorylase. J. Phys. Chem. A 2006, 110, 463–476. 10.1021/jp051277u. [DOI] [PubMed] [Google Scholar]
  29. Huang N.; Shen Z.; Long S.; Wu M.; Shih H.; Zheng Q.; Yen N.; Tung C.; Liu H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London, Ser. A 1998, 454, 903–995. 10.1098/rspa.1998.0193. [DOI] [Google Scholar]
  30. Kim D.; Oh H. EMD: a package for empirical mode decomposition and Hilbert spectrum. R J. 2009, 1, 40–46. [Google Scholar]
  31. E W.; Ren W.; Vanden-Eijnden E. Transition pathways in complex systems: Reaction coordinates, isocommittor surfaces, and transition tubes. Chem. Phys. Lett. 2005, 413, 242–247. 10.1016/j.cplett.2005.07.084. [DOI] [Google Scholar]

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES