Explicit modeling of ancestry improves polygenic risk scores and BLUP prediction

Abstract

Polygenic prediction using genome-wide SNPs can provide high prediction accuracy for complex traits. Here, we investigate the question of how to account for genetic ancestry when conducting polygenic prediction. We show that the accuracy of polygenic prediction in structured populations may be partly due to genetic ancestry. However, we hypothesized that explicitly modeling ancestry could improve polygenic prediction accuracy. We analyzed three GWAS of hair color, tanning ability and basal cell carcinoma (BCC) in European Americans (sample size from 7,440 to 9,822) and considered two widely used polygenic prediction approaches: polygenic risk scores (PRS) and Best Linear Unbiased Prediction (BLUP). We compared polygenic prediction without correction for ancestry to polygenic prediction with ancestry as a separate component in the model. In 10-fold cross-validation using the PRS approach, the R² for hair color increased by 66% (0.0456 to 0.0755; p<10⁻¹⁶), the R² for tanning ability increased by 123% (0.0154 to 0.0344; p<10⁻¹⁶) and the liability-scale R² for BCC increased by 68% (0.0138 to 0.0232; p<10⁻¹⁶) when explicitly modeling ancestry, which prevents ancestry effects from entering into each SNP effect and being over-weighted. Surprisingly, explicitly modeling ancestry produces a similar improvement when using the BLUP approach, which fits all SNPs simultaneously in a single variance component and causes ancestry to be underweighted. We validate our findings via simulations, which show that the differences in prediction accuracy will increase in magnitude as sample sizes increase. In summary, our results show that explicitly modeling ancestry can be important in both PRS and BLUP prediction.

Introduction

Genome-wide association studies (GWAS) have identified many single nucleotide polymorphisms (SNPs) associated with complex traits [Visscher et al. 2012]. Genetic prediction based on genome-wide significant SNPs from GWAS provides some predictive ability [Wray et al. 2007; Meigs et al. 2008; Kraft and Hunter 2009; So et al. 2011], but polygenic prediction, using genetic variants that do not achieve genome-wide significance, can improve prediction accuracy [de los Campos et al. 2010; Chatterjee et al. 2013; Dudbridge 2013]. Polygenic prediction has been applied to many complex traits, such as schizophrenia and height [Evans et al. 2009; Purcell et al. 2009; Wei et al. 2009; Bush et al. 2010; Lango Allen et al. 2010; Machiela et al. 2011; Makowsky et al. 2011; Stahl et al. 2012; Vazquez et al. 2012; Wei et al. 2013; Smoller et al. 2013; Rietveld et al. 2013; Ripke et al. 2014; Wood et al. 2014].

Polygenic prediction accuracy may be partly due to genetic ancestry, especially for complex traits that are known to be associated with ancestry. For example, differences in height between Northern Europeans and Southern Europeans (e.g. due to natural selection) explain 5% of the variance of height in European Americans from the Framingham Heart Study, accounting for most of the polygenic prediction accuracy in 1,997 unrelated individuals from this sample [Makowsky et al. 2011; Wray et al. 2013; Turchin et al. 2012]. Other traits that are well-known to be associated with ancestry in European-ancestry populations include hair color, eye color, skin pigmentation, skin cancer, multiple sclerosis, rheumatoid arthritis, type 1 diabetes, Crohn’s disease, Alzheimer’s disease, coagulation factor VII (FVII) plasma level, hemoglobin disorders, and educational attainment [Candille et al. 2012; Nan et al. 2009a; Rosati 2001; Cimmino et al. 1998; Patterson et al. 2009; Kenny et al. 2012; Panza et al. 2003; Bernardi et al. 1997; Angastiniotis and Modell 1998; Borjas 1994]. Thus, it is possible that polygenic prediction studies of these traits may likewise owe some of their accuracy to genetic ancestry [Evans et al. 2009; Wei et al. 2009; Bush et al. 2010; Makowsky et al. 2011; Stahl et al. 2012; Vazquez et al. 2012; Wei et al. 2013; Rietveld et al. 2013]. In genetic association studies, ancestry is a confounder that may cause false positive associations with no biological significance [Price et al. 2010]. On the other hand, if the ultimate goal is to conduct prediction in the same population, polygenic predictions that are partly due to ancestry may be useful. However, it is important to understand how much of polygenic prediction accuracy is due to ancestry, as this will affect prediction accuracy in other populations.

An open question is how to make use of ancestry information in polygenic prediction. Most studies of polygenic prediction ignore ancestry information, but this may not be optimal. We propose to correct for ancestry in the polygenic model using principal components, while incorporating associations between ancestry and the trait as a separate component in the prediction model. We hypothesize that explicit modeling of ancestry in this fashion can improve polygenic prediction accuracy, by preventing ancestry from entering into each SNP effect and being overweighted. In this study, we investigated the impact of explicit modeling of genetic ancestry on polygenic prediction accuracy by analyzing GWAS samples of European Americans for three pigmentation-related traits, including natural hair color (HC), childhood and adolescent tanning ability (TA), and basal cell carcinoma (BCC). We employed cross-validation schemes to ensure that improvements in prediction accuracy were not caused by over-fitting. We determined that explicitly modeling ancestry can significantly improve prediction accuracy across different polygenic prediction approaches, such as polygenic risk scores and best linear unbiased predictors. We note that although polygenic risk scores may not be the optimal prediction method when raw genotypes are available, we have chosen to include them as one of the main focuses of our analyses, because they are currently the most widely used approach for polygenic risk prediction in humans.

Materials and Methods

GWAS data

We performed analyses of 3 genome-wide association studies (GWAS) of hair color (HC), tanning ability (TA), and basal cell carcinoma (BCC) nested in the Nurses’ Health Study (NHS) and the Health Professionals Follow-up Study (HPFS). The sample collection, genotyping and quality control for each GWAS were described previously [Hunter et al. 2007; Nan et al. 2011; Qi et al. 2010; Rimm et al. 1991; Curhan and Taylor 2008; Taylor et al. 2005]. All samples are self-reported European Americans. We included only SNPs genotyped with call rate >99% and minor allele frequency >1% and excluded A/T and C/G SNPs to avoid strand ambiguity. The missing genotypes were mean-imputed in the subsequent analyses. We extracted samples with complete phenotype and self-reported ancestry information into 3 GWAS sets. We obtained 7,440 samples with HC, 9,822 samples with TA, and 2,086 BCC cases and 6,173 controls. We applied LD pruning by genomic position with a R² threshold of 0.2 to obtain 71,557, 71,549 and 71,575 independent SNPs for HC, TA, and BCC, respectively.

In addition to the genotyped SNPs, we obtained imputed genotypes for variants that showed genome-wide significant association with HC, TA and BCC. This included 12 SNPs and one two-SNP haplotype associated with each of HC, TA and BCC and 6 additional SNPs associated with BCC only (Table S1) [Gerstenblith et al. 2010]. Note that some of these genome-wide significant SNPs were identified in the samples analyzed here, especially for TA; therefore, higher prediction accuracy based these genome-wide significant SNPs is expected [Han et al. 2008; Nan et al. 2009a; Nan et al. 2009b]. The imputation was done with using BEAGLE (for phasing) and MaCH using the 1000 Genomes Project Interim Phase I release as the reference panel [The 1000 Genomes Project Consortium 2012; Li et al. 2010; Browning and Browning 2007].

Phenotype definitions

The phenotype information was collected from prospective questionnaires. The natural hair color at 20 years of age was collected in 4 levels: blonde, light brown, dark brown, and black. We excluded samples with red hair color, which is a distinct trait from other hair colors and is mainly determined by the MC1R gene [Han et al. 2008]. The childhood and adolescent tanning ability with more than 2 hours of sun light exposure was collected in 4 levels: practically none, light tan, average tan, and deep tan. A previous study showed that deeper tan denotes a better response to sun light exposure and is associated with lower risk of skin cancer [Nan et al. 2009a]. Both hair color and tanning ability were analyzed as quantitative traits. The BCC cases were identified through biennial self-report; the validation rate of BCC self-reports was 90% in NHS and HPFS [Han et al. 2006; Hunter et al. 1990].

Self-reported ancestry

The participants were assigned to 1 of the 4 self-reported ancestry groups: Scandinavian, Southern European, Ashkenazi Jewish, and Other European (which includes samples with no self-reported European sub-population ancestry information). We calculated the mean and standard deviation for each trait by self-reported ancestry groups. We also tested for association between self-reported ancestry and each trait with a Wald test for HC and TA and a χ² test and odds ratios with 95% confidence intervals for BCC.

Inference of genetic ancestry

To infer genetic ancestry, we performed principal component analysis (PCA) with EIGENSTRAT software to obtain principal components as measure of genetic ancestry [Price et al. 2006; Patterson et al. 2006]. We performed PCA on the 3 GWAS and obtained the top 10 PCs specific to each GWAS. These PCs were used in all primary analyses. We also performed additional analyses in which we derived the top PCs independently for training and validation sets with an external European American reference panel (see Discussion). We plotted PC1 and PC2 to show the structure of these GWAS samples with color-coding by self-reported ancestry. To further investigate population structure, we projected the samples from Eastern European countries in the Population Reference Sample (POPRES) to the PC space derived from the TA GWAS samples, which contained most of our merged GWAS samples. The collections and methods for the Population Reference Sample (POPRES) are described by Nelson et al. (2008). The datasets used for the analyses described in this manuscript were obtained from dbGaP at http://www.ncbi.nlm.nih.gov/projects/gap/cgibin/study.cgistudy_id=phs000145.v1.p1 through dbGaP accession number phs000145.v1.p1. The PC projection was done by applying the SNP weights, which were calculated with principal components and eigenvalues derived from the TA GWAS samples, to the POPRES samples [Chen et al. 2013]. To compare the structure of POPRES samples and our GWAS samples, we plotted the projected PC1 and PC2 of POPRES samples with the PC1 and PC2 of the TA GWAS samples.

Prediction using genetic and self-reported ancestry

We demonstrated the prediction ability of ancestry by building prediction models with 1) self-reported ancestry, 2) PC1 and PC2, 3) the top 5 PCs, and 4) the top 5 PCs plus self-reported ancestry in all samples. To control for over-fitting, we also employed 10-fold cross-validation: we built prediction models by estimating model coefficients with the training set which includes 90% of the total sample size and applied the estimated model coefficients to the validation set, which includes 10% of the total sample size excluded from the training set, and calculated predicted phenotypes for the validation samples. A predicted phenotype was calculated for each validation sample as $\widehat{Y}={\sum }_{k=1}^K{\beta }_k{x}_k$ where k indexes the predictors, including PCs and/or self-reported ancestry, β_k is the regression coefficient estimated in the training set and x_k is the covariate value for the validation set. We repeated this process 10 times and pooled the validation samples with predicted phenotypes to calculate out-of-sample R² between predicted and true phenotypes. We note that the PCs used in all primary analyses were derived with all samples together.

R² was calculated for each model and a likelihood ratio test (LRT) was used to compare models. We used R² on the observed scale for HC and TA and R² on the liability scale for BCC. The R² on the observed scale were obtained by fitting linear regression models with HC and TA as continuous outcomes and with self-reported ancestry and PCs as predictors. To obtain the R² on liability scale for BCC, we first obtained R² on the observed scale for BCC by treating the BCC case-control status as a continuous outcome where all BCC cases take value 1 and controls take value 0 and fitted linear regression models with the continuous BCC outcome and the predictors. We then transformed the R² on the observed scale for BCC to the R² on the liability scale by applying the method based on the liability threshold model described in Lee et al. 2012. The transformation of observed scale R² to liability scale R² assumes a disease liability that follows the standard normal distribution and assumes all disease cases have disease liability exceeding a certain threshold value. We determined the threshold based on the population prevalence of the disease estimated in previous studies [Lear and Smith 1997; Lee et al. 2012]. The transformation is $R_{\mathit{liability}}^2=R_{\mathit{observed}}^{2}C/(1+R_{\mathit{observed}}^2\theta C)$ where $C=\frac{K(1-K)}{Z^2}\frac{K(1-K)}{P(1-P)}$ and $\theta =m\frac{P-K}{1-K}(m\frac{P-K}{1-K}-t)$. K is the population prevalence of BCC (0.3); t is the threshold according to K (0.52); Z is the height of a normal density at the threshold (0.35); m is the mean liability for BCC cases (1.16); P is the proportion of BCC cases in the case-control sample (0.25). In all analyses, the observed scale and liability scale R² were obtained using the same method. To obtain the LRT p-values, we used linear regression for HC and TA and logistic regression for BCC.

Prediction using Genetic Risk Scores (GRS) based on genome-wide significant SNPs

We built prediction models based on genetic risk scores (GRS) using genome-wide significant SNPs associated to HC, TA and BCC and compared GRS models to models based on both GRS and ancestry. We considered prediction models including 1) GRS_unadj, 2) GRS_adj, 3) GRS_adj and the top 5 PCs, and 4) GRS_adj and the top 5 PCs and self-reported ancestry (described in detail below). We employed both 10-fold cross-validation, which gives in-sample R², and 10×9-fold nested cross-validation which gives out-of-sample R² that accounts for model over-fitting.

For 10-fold cross-validation, we estimated effect sizes of the known associated SNPs in the training sets by fitting the following models in the 90% training samples:

$$Y={\beta }_0+{\beta }_1\mathit{GWAS}+{\beta }_{\mathit{unadj},j}{\mathit{SNP}}_j+\epsilon \text{for}\text{HC}\text{and}\text{TA}$$ (1)

or

$$\mathit{logit}[P(Y=1)]={\beta }_0+{\beta }_1\mathit{GWAS}+{\beta }_{\mathit{unadj},j}{\mathit{SNP}}_j\text{for}\text{BCC}$$ (2)

where SNP_j is the genotype of genome-wide significant SNP j and GWAS is a 6×1 vector of 6 indicator variables indicating which of the 7 individual GWAS the sample is from. We then applied the effect size estimates to the validation samples to construct GRS_unadj. We calculated GRS_unadj for the 10% validation samples by

$${\mathit{GRS}}_{\mathit{unadj},i}={\sum }_{j=1}^M{\widehat{\mathrm{\beta }}}_{\mathit{unadj},j}{\mathit{SNP}}_{i,j}{\text{GRS}}_{\mathrm{i}}=\sum _{\mathrm{j}=1}^{\mathrm{M}}{\widehat{\mathrm{\beta }}}_{1,\mathrm{j}}{\text{SNP}}_{\mathrm{i},\mathrm{j}}{\text{GRS}}_{\mathrm{i}}={\sum }_{\mathrm{j}=1}^{\mathrm{M}}{\widehat{\beta }}_{1,\mathrm{j}}{\text{SNP}}_{\mathrm{i},\mathrm{j}}$$ (3)

where β̂_{unadj, j} is the estimated regression coefficient using the training samples from model (1) and (2) and SNP_i,j is the genotype of validation sample i at SNP j. We also calculated GRS_adj by fitting models:

$$Y={\beta }_0+{\beta }_1\mathit{GWAS}+{\beta }_{2}PC+{\beta }_{\mathit{unadj},j}{\mathit{SNP}}_j+\epsilon \text{for}\text{HC}\text{and}\text{TA}$$ (4)

or

$$\mathit{logit}\left[P(Y=1)\right]={\beta }_0+{\beta }_1\mathit{GWAS}+{\beta }_{2}PC+{\beta }_{\mathit{unadj},j}{\mathit{SNP}}_j.\text{for}\text{BCC}$$ (5)

where SNP_j and GWAS are as previously defined and PC is a 5×1 vector of the top 5 PCs. The GRS_adj was then calculated as

$${\mathit{GRS}}_{\mathit{adj},i}=\sum _{j=1}^M{\widehat{\beta }}_{\mathit{adj},j}{\mathit{SNP}}_{i,j}$$ (6)

where β̂_{adj, j} were estimated from model (4) and (5). We then pooled the samples from 10 mutually exclusive validation sets with GRS_unadj and GRS_adj constructed with estimates from their corresponding training samples and fitted models. In-sample R² and LRT p-values were calculated in the validation set for these models, where GRS and other predictors (PCs/self-reported ancestry) we treated as univariate predictors.

For the 10×9-fold nested cross-validation, the GWAS samples were split into 2 parts with 90% of the total samples as the training set and 10% of the total samples as validation set in each fold of the nested cross-validation. For the 90% training set, we further split the samples into 2 training sets. The first training set had 80% of the total samples and the second training set had 10% of the total samples. We used the first training set to estimate effect sizes of the genome-wide significant SNPs and used those effect sizes to construct the GRS for the second training set as well as the validation set. We then fit prediction models that include GRS (and PCs/self-reported ancestry) in the second training set. The predicted phenotype was calculated for each validation sample as $\widehat{Y}={\displaystyle \sum _{k=1}^K}{\beta }_k{x}_k$ where k index the predictors, including GRS and/or PCs/self-reported ancestry, β_k is the regression coefficient estimated in the second training set and x_k is the covariate value for the validation sample. For each of the 10 folds of validation samples, we repeated this model building process for each of the 9 folds of first and second training sets and averaged the predicted phenotypes of validation samples across the 9 folds. With the pooled validation samples from the 10×9-fold nested cross-validation, we calculated out-of-sample R² between true phenotypes and predicted phenotypes. The out-of-sample R² were always calculated between a single predicted phenotype (Ŷ) and the true phenotype of validation samples and the potential inflation of R² due to increased number of predictors was eliminated. We note that the PCs used in all primary analyses were derived with all samples together.

Polygenic prediction using Polygenic Risk Scores (PRS) based on genome-wide SNPs

For the polygenic model with explicit modeling of ancestry, we adjusted for the top 5 PCs when constructing the PRS and added the top 5 PCs to the polygenic model as additional covariates. We compared prediction models constructed with 1) PRS_unadj, 2) PRS_adj, 3) PRS_adj and the top 5 PCs, and 4) PRS_adj and the top 5 PCs and self-reported ancestry. We first did the analyses with 10-fold cross-validation using R² and likelihood ratio test as figures of merit and then repeated the analyses in 10×9-fold nested cross-validation. Both 10-fold cross-validation and 10×9-fold nested cross-validation were performed in a similar fashion as described above for GRS model comparisons.

We adopted the polygenic risk score method to build polygenic prediction models [Evans et al. 2009; Purcell et al. 2009]. We used around 72,000 LD-pruned, independent genome-wide SNPs in PRS. To construct PRS without ancestry correction (PRS_unadj), we fitted regression models (1) and (2) for each of the independent genome-wide SNPs individually using the 90% training samples. To construct PRS with ancestry correction (PRS_adj), we fitted models (4) and (5) for each independent genome-wide SNP individually. The β̂_{unadj, j} and β̂_{adj, j} were used as weights to construct PRS_unadj and PRS_adj, respectively. Models (3) and (6) were used to construct PRS, except that we included all independent genome-wide SNPs in the PRS. We also constructed PRS_unadj and PRS_adj using different numbers of genome-wide SNPs determined by the association p-value (calculated for each training set) for the SNP and the target phenotype: 5×10⁻⁸, 1×10⁻⁷, 1×10⁻⁶, 1×10⁻⁵, 1×10⁻⁴, 0.001, 0.01, 0.05, 0.1, 0.5, and 1.0. For BCC, we did not construct PRS with p-value threshold smaller than 1×10⁻⁵ because no SNP showed association p-value smaller than 1×10⁻⁵ for BCC in our data.

We further extended the polygenic models above to include 1) both GRS_unadj and PRS_unadj,-gs, 2) both GRS_adj and PRS_adj,-gs, 3) both GRS_adj and PRS_adj,-gs plus the top 5 PCs, and 4) both GRS_unadj and PRS_unadj,-gs plus the top 5 PCs. Here, PRS_unadj,-gs and PRS_adj,-gs are PRS that excluded SNPs with genome-wide significant association for the target trait in previous GWAS (which are included in GRS), and SNPs in LD with those genome-wide significant SNPs (pairwise R² > 0.2). The GRS and PRS were combined in the prediction model by either summing the GRS and PRS to make one score or including GRS and PRS as two separate components of the model.

We used in-sample R² and LRT to compare these models in the validation set in the 10-fold cross-validation, where all predictors were treated as univariate predictors in the model. We calculated out-of-sample R² in the 10×9-fold nested cross-validation, where the predicted phenotypes for each validation sample were calculated as $\widehat{Y}={\displaystyle \sum _{k=1}^K}{\beta }_k{x}_k$ where k index the predictors, including PRS and/or PCs/self-reported ancestry, β_k is the regression coefficient estimated in the second training set and x_k is the covariate value for the validation sample. We note that the PCs used in all primary analyses were derived with all samples together.

Polygenic prediction using Best Linear Unbiased Predictors (BLUP) based on genome-wide SNPs

In addition to PRS, we performed polygenic prediction based on BLUP by fitting linear mixed models to estimate genome-wide SNP effect sizes simultaneously [Yang et al. 2010]. We compared prediction models based on 1) BLUP_unadj, 2) BLUP_adj, 3) BLUP_adj plus the top 5 PCs, 4) BLUP_unadj,-gs, 4) BLUP_adj,-gs, and 5) BLUP_adj,-gs plus the top 5 PCs, where –gs denotes excluding genome-wide significant SNPs from the random effects of linear mixed model and entered the model as fixed effects. We note that the PCs used in all primary analyses were derived with all samples together. We adopted 10-fold cross-validation to fit linear mixed models in the 90% training samples and output the random effects and fixed effects estimates with GCTA. The linear mixed model we used to obtain effect size estimates takes the general form:

$$Y=X\beta +g+\epsilon \text{with}\mathit{Var}(Y)=A{\sigma }_g^2+I{\sigma }_{\epsilon }^2$$ (7)

where β is a vector of fixed effects, g is the total genetic effects of the training samples with $g~N(0,A{\sigma }_g^2)$, A is the genetic relationship matrix derived from SNP genotypes, ε is the residual with $\epsilon ~N(0,I{\sigma }_{\epsilon }^2)$ [Yang et al. 2010]. In our case, the fixed effects included individual GWAS study indicator, PCs, and/or genome-wide significant SNPs. The effect sizes of SNPs used to calculate PRS were calculated as $\left({\sigma }_g^2/m\right){XV}^{-1}Y$ where V⁻¹ is the inverse of the phenotypic covariance matrix of the training samples and m is the number of SNPs used to calculated the genetic relationship matrix. We then apply the effect estimates to the 10% validation samples to construct PRS, GRS, and PCs. The calculation of PRS in the validation samples is the same as models (3) and (6). We used in-sample R² and LRT to compare these models in the 10-fold cross-validation with the pooled validation samples, where all predictors were treated as univariate predictors in the model.

Simulations comparing polygenic prediction using polygenic risk scores

It is widely known that polygenic prediction accuracy is predominantly determined by the training sample size. In our analysis using real GWAS samples, the training sample size is fixed. To examine the performance of different PRS approaches under different training sample sizes, we performed the following simulation study. We simulated a quantitative trait with 100,000 independent SNPs, where all SNPs were causal and the proportion of phenotypic variance explained by these SNPs was 0.5. We simulated sets of 1,000, 5,000, 10,000, 50,000, 100,000, 500,000, 1,000,000 training samples and 10,000 validation samples. Training samples and validation samples were each drawn from two subpopulations POP1 and POP2, with minor allele frequency equal to 0.50 in POP1 and drawn from a normal distribution with mean 0.50 and standard deviation 0.05 in POP2, so that the fixation index F_ST(POP1, POP2)=0.005. The signs of marker effect sizes were flipped so that with probability 0.51, the allele with higher frequency in POP2 had positive effect, with the result that POP2 had systematically higher trait mean and subpopulation ancestry had an R² of 0.044 with the trait. We compared three approaches: PRS_unadj, PRS_adj, and PRS_adj + ancestry, which is equivalent to PRS_adj + top PC except that ancestry is assumed to be inferred with perfect accuracy. (We did not consider additional PCs because the data was simulated to contain only one dimension of population structure.) Results were averaged across 100 simulations. We compared the simulation results to the results from our PRS analysis using real GWAS samples.

Results

Inference of genetic ancestry

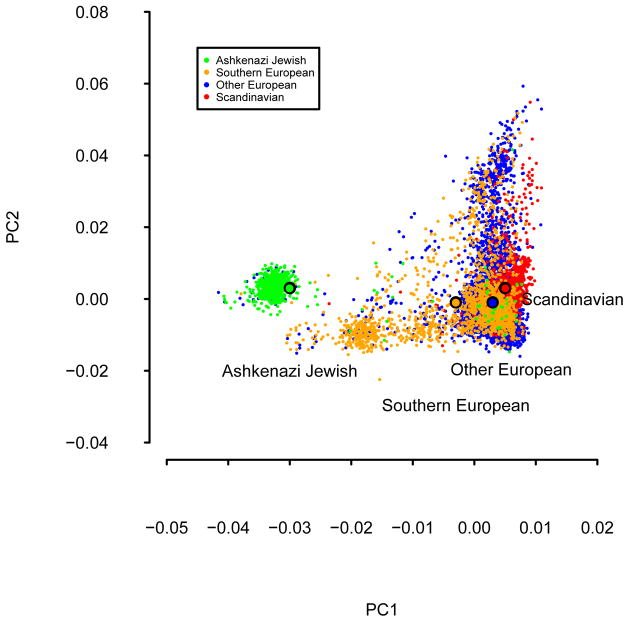
We performed analyses in three genome-wide association studies (GWAS) of hair color (HC), tanning ability (TA), and basal cell carcinoma (BCC) with samples from the Nurses’ Health Study (NHS) and the Health Professionals Follow-up Study (HPFS). We investigated the population structure in our GWAS samples using principal component analysis (PCA) [Price et al. 2006; Patterson et al. 2006], and compared the top principal components (PCs) to self-reported European ancestry. We first plotted PC1 and PC2 to investigate the population structure in the three GWAS (Figure 1). The PCA plot was color-coded with self-reported European ancestry, which has four categories: Scandinavian, Southern European, Ashkenazi Jewish, and Other European. We found that samples of self-reported Southern European ancestry had relatively lower PC1 values than samples of self-reported Scandinavian ancestry, while self-reported Ashkenazi Jewish samples had the lowest PC1 on average. In addition, the average PC1 and PC2 of Other European samples are close to the average PC1 and PC2 of Scandinavian samples, suggesting that Other European samples are predominantly of Northern European ancestry. The structure we identified in our GWAS sample is different from the canonical PC1 and PC2 in European American samples shown in Price et al. (2008) perhaps because the current data set has more samples of Eastern European ancestry than the samples analyzed in that paper. By projecting POPRES samples onto PC1 and PC2, we determined that samples with high PC2 value represent Eastern European ancestry (Figure S1) [Nelson et al. 2008]. This result suggests that lower PCs may capture additional structure. In the prediction analyses below, we include either PC1 and PC2 or the top 5 PCs; including more than 5 PCs (up to 10 PCs) did not change any of the results.

Figure 1. PCA plots for tanning ability GWAS samples, color-coded with self-reported ancestry.

Black circles with color-coded interior denote average PC values for each self-reported ancestry. The tanning ability GWAS had the largest samples size among the 3 GWAS analyzed. Results for hair color and basal cell carcinoma GWAS samples, which are largely overlapped with the tanning ability GWAS samples, were extremely similar.

Prediction using genetic and self-reported ancestry

Pigmentation-related traits are associated with ancestry, due to positive selection on lighter pigmentation in populations in regions of higher latitude [Sulem et al. 2007]. Indeed, our data showed that HC, TA and BCC are strongly associated with genome-wide ancestry and self-reported ancestry (Table 1). Compared with self-reported Scandinavian samples, Southern European samples on average have darker hair color (2.60 in Southern European vs. 2.08 in Scandinavian), increased tanning ability (2.67 in Southern European vs. 2.36 in Scandinavian), which corresponds to better protection against ultraviolet radiation, and lower risk of BCC (odds ratio [OR] for Scandinavian vs. Southern European (ref) = 1.075, 95% confidence interval [CI]: 1.036, 1.116). Ashkenazi Jewish samples on average had the darkest hair color (2.76), which is consistent with their lower PC1 value vs. South Europeans, but also had the lowest tanning ability (2.30) and highest risk of BCC among 4 self-reported ancestry groups (OR = 1.123, 95% CI: 1.074, 1.174), which are not consistent with their lower PC1 value vs. South Europeans. The Scandinavian samples had similar but slightly more extreme phenotypes than the Other European samples, consistent with the similar but slightly higher average PC1 for Scandinavian vs. Other European samples.

Table 1.

Average PCs and phenotype values for self-reported ancestry groups in GWASs on hair color, tanning ability, and basal cell carcinoma

	Average PCs (SD)a		Hair color		Tanning ability		Basal cell carcinoma
Self-reported European ancestry	1	2	N	Average	N	Average	Cases	Control	OR (95% CI)
Ashkenazi Jewish	−0.030 (0.009)	0.003 (0.004)	425	2.76 (0.73)	579	2.30 (0.87)	338	155	1.123 (1.074, 1.174)
Southern European	−0.003 (0.010)	−0.001 (0.011)	1325	2.60 (0.74)	1700	2.67 (0.90)	1151	285	Reference
Other Europeanb	0.003 (0.005)	−0.001 (0.010)	4963	2.39 (0.75)	6559	2.54 (0.91)	4074	1419	1.062 (1.035, 1.089)
Scandinavian	0.005 (0.003)	0.003 (0.009)	727	2.08 (0.80)	984	2.36 (0.91)	610	227	1.075 (1.036, 1.116)
Total			7440		9822		6173	2086

^aAverage PCs are derived from tanning ability GWAS samples, which has the largest sample size among the 3 GWAS analyzed here. Samples of the 3 GWAS are largely overlapped.

^bOther European refers to European American samples without self-reported European sub-population ancestry information.

Motivated by these observations, we fitted prediction models based on ancestry. We first examined models based on self-reported ancestry only, where the in-sample R² was 0.0397 for HC, 0.0081 for TA, and 0.0072 for BCC (Table 2). We then examined prediction models based on PCs only. The model based on top 5 PCs achieved R² of 0.0724 for HC, 0.0350 for TA, and 0.0202 for BCC in the in-sample analysis (Table 2). We also showed that adding PC3 to PC5 in addition to PC1 and PC2 improved model prediction accuracy significantly for all 3 phenotypes (p < 10⁻¹⁶ for HC and TA; 1.93×10⁻¹⁵ for BCC). This suggests that including the subtle structure captured by later PCs provided additional value in predicting these phenotypes. However, including more than 5 PCs did not change any of the results. The R² obtained by using self-reported ancestry are lower than the R² obtained by using the top 5 PCs. Interestingly, we found including self-reported ancestry in the models in addition to the top 5 PCs further improved prediction accuracy (Table 2). The improvement was significant for HC (p = 1.32×10⁻⁹) and TA (p = 5.70×10⁻³) but not for BCC (p = 0.18) in the in-sample analysis. In addition, we showed that the added information in self-reported ancestry for HC (where this effect is strongest) is primarily due to self-reported Scandinavian ancestry, which is not completely captured by the Northwest-Southeast European cline of PC1 (Table S2). We also performed out-of-sample analyses using 10-fold cross-validation and obtained similar results (Table S3). Overall, we showed that both PCs and self-reported ancestry explained part of the phenotypic variation and can be used to build prediction models for these pigmentation-related traits. Furthermore, while models based on PCs have higher prediction accuracy than models based on self-reported ancestry, self-reported ancestry can still improve prediction accuracy over PCs.

Table 2.

R² and p-values from likelihood ratio test for prediction models using PCs and self-reported European ancestry in in-sample analysis using all samples

		Hair color		Tanning ability		Basal cell carcinomaa
Model		R2	P-valueb	R2	P-valueb	R2	P-valueb
1	Self-reported ancestry	0.0397	<10−16	0.0081	<10−16	0.0072	9.19 × 10−7
2	PC1 + PC2	0.0468	<10−16	0.0146	<10−16	0.0036	5.01 × 10−4
3	PC1 + … + PC5	0.0724	<10−16	0.0350	<10−16	0.0202	1.93 × 10−15
4	PC1 + … + PC5 + self-reported ancestry	0.0779	1.32 × 10−9	0.0363	5.70 × 10−3	0.0213	1.81 × 10−1

^aR² on liability scale

^bP-values are from likelihood ratio tests comparing model 1 and 2 to the null model, model 3 to model 2, and model 4 to model 3.

Prediction using Genetic Risk Scores (GRS) based on genome-wide significant SNPs

To investigate the potential improvement of genetic risk prediction models by incorporating ancestry information, we compared genetic risk prediction models based on genetic risk scores (GRS) [Meigs et al. 2008]. We used imputed genotypes of SNPs shown to be genome-wide significant in previous GWAS to create GRS for each of the 3 phenotypes (Table S1). The models we compared included GRS without ancestry correction (GRS_unadj), GRS with ancestry correction (adjusted for the top 5 PCs) (GRS_adj), and GRS with explicit modeling of ancestry (GRS_adj+PCs). In 10-fold cross-validation, GRS_unadj attained an R² of 0.2236 for HC (p < 10⁻¹⁶), 0.1311 for TA (p < 10⁻¹⁶), and 0.0266 (p < 10⁻¹⁶) for BCC (Table 3). The R² of GRS_adj were lower than the R² of GRS_unadj for HC and BCC, but slightly higher for TA (R² = 0.1324). In 10×9-fold nested cross-validation, the R² of GRS_adj were consistently lower than R² of GRS_unadj for all 3 phenotypes (Table S3). The R² of GRS_unadj and GRS_adj were much higher than the models based on ancestry. However, we showed that the prediction accuracy was improved (relative to either GRS_unadj or GRS_adj) by including PCs in the GRS_adj model (Table 3). We repeated the GRS_unadj, GRS_adj and GRS_adj+PCs model comparison by fitting all known genome-wide significant SNPs in one model simultaneously to obtain effect size estimates for constructing GRS (Table S4). The results showed similar patterns to the results from fitting genome-wide significant SNPs individually (Table 3). The improvement also remains for the out-of-sample R² from 10×9-fold nested cross-validation (Table S3). We also calculated the R² between the top 5 PCs and the predicted phenotypes based on GRS_unadj and GRS_adj (Table S5). We found that the R² between PCs and GRS_adj were only slightly lower than the R² between PCs and GRS_unadj, which suggests that the genome-wide significant SNPs used to calculate GRS have systematically different allele frequencies across European subpopulations, e.g. due to natural selection [Turchin et al. 2012]. In addition to PCs, we also showed that including self-reported ancestry further improved prediction accuracy on top of GRS_adj + PCs for HC (R² from 0.2378 to 0.2423; p = 1.24×10⁻⁹) and TA (R² from 0.1384 to 0.1397; p = 2.73×10⁻³), but not BCC (R² from 0.0372 to 0.0385; p = 0.108) (Table S6).

Table 3.

R² and p-values from likelihood ratio test for prediction models using GWAS identified SNPs and PCs in 10-fold cross-validation

		Hair color		Tanning ability		Basal cell carcinomaa
Model		R2	P-valueb	R2	P-valueb	R2	P-valueb
1	GRSunadj	0.2236	<10−16	0.1311	<10−16	0.0266	<10−16
2	GRSadj	0.2227	<10−16	0.1324	<10−16	0.0234	<10−16
3	GRSadj + PC1 + … + PC5	0.2378	<10−16	0.1384	1.93 × 10−13	0.0372	6.82 × 10−13

^aR² on liability scale

^bP-values are from likelihood ratio tests comparing model 1 and 2 to the null model, and model 3 to model 2.

Polygenic prediction using Polygenic Risk Scores (PRS) based on genome-wide SNPs

We investigated the impact of explicitly modeling ancestry on polygenic prediction by comparing 3 polygenic models: 1) the polygenic risk score (PRS) without ancestry correction (PRS_unadj), 2) a polygenic risk score with correction for ancestry (PRS_adj), and 3) a polygenic model with explicit modeling of ancestry, where we corrected for ancestry but added a separate ancestry component (PRS_adj+PCs) [Purcell et al. 2009; Evans et al. 2009]. We compared PRS models with PRS that included all available SNPs across the genome after LD pruning. Results are displayed in Table 4. Comparing PRS_adj+PCs to PRS_unadj, the R² improved 67% (from 0.0473 to 0.0789) for hair color, 114% (from 0.0162 to 0.0347) for tanning ability and 62% (from 0.0145 to 0.0235) for BCC. The model improvements were significant with p-value < 10⁻¹⁶. We found that PRS_adj attained a lower R² than the other models (0.0055 for HC; 0.0003 for TA; 0.0029 for BCC). Notably, the improvement in R² of PRS_adj+PCs over PRS_adj was much larger than the R² of PRS_unadj in each case, suggesting that PRS_unadj suffered from a mis-specified weighting of ancestry effects, which enter into each SNP effect in the unadjusted model. The low R² of PRS_adj is consistent with the relatively small sample size in our analyses [Chatterjee et al. 2013; Dudbridge 2013], and indicates that the prediction accuracy of PRS_unadj was largely due to ancestry. Indeed, we observed R² as large as 0.9250 between PC1 and PRS_unadj (Table S5). This is consistent with our simulations, in which the prediction R² for PRS_unadj was consistently biased toward the same number, 0.044, which is the R² between ancestry and the target trait. However, the prediction R² of PRS_adj increased from 0.003 to 0.439 as the training sample size increased from 1,000 to 1,000,000, and PRS_adj+ancestry consistently outperformed both PRS_unadj and PRS_adj (Table 5). Results for PRS_adj were close to the values predicted by theory in the absence of ancestry effects (see Equation (1) of Wray et al. 2013 Nat Rev Genet) [Wray et al. 2013]. These simulations show that explicit modeling of genetic ancestry can improve polygenic prediction accuracy, and that the magnitude of this improvement can become extremely large as sample sizes grow.

Table 4.

R² and p-values from likelihood ratio test for polygenic prediction using PRS, GRS and PCs in 10-fold cross-validation

(a) PRS included all SNPs available from genome-wide SNP chip after LD-pruning
		Hair color		Tanning ability		Basal cell carcinomaa
Model		R2	P-valueb	R2	P-valueb	R2	P-valueb
1	PRSunadj	0.0473	<10−16	0.0162	<10−16	0.0145	3.34 × 10−15
2	PRSadj	0.0055	1.65 × 10−10	0.0003	7.67 × 10−2	0.0029	5.90 × 10−4
3	PRSadj + PC1 + … + PC5	0.0789	<10−16	0.0347	<10−16	0.0235	<10−16
4	PRSunadj + PC1 + … + PC5	0.0745	<10−16	0.0344	<10−16	0.0226	1.36 × 10−6

(b) GRS included known genome-wide significant SNPs; PRS excluded SNPs in LD with known genome-wide significant SNPs but included all other SNPs
		Hair color		Tanning ability		Basal cell carcinomaa
Model		R2	P-valueb	R2	P-valueb	R2	P-valueb
5	PRSunadj,-gs + GRSunadjc	0.2280	8.82 × 10−11	0.1312	0.1776	0.0333	1.44 × 10−8
6	PRSadj,-gs + GRSadj	0.2235	7.43 × 10−3	0.1326	0.1820	0.0259	6.23 × 10−4
7	PRSadj,-gs + GRSadj + PC1 + … + PC5	0.2388	<10−16	0.1386	2.45 × 10−13	0.0397	5.46 × 10−13
8	PRSunadj,-gs + GRSunadj + PC1 + … + PC5	0.2376	<10−16	0.1378	1.39 × 10−14	0.0398	6.00 × 10−6

^aR² on liability scale

^bP-values are from likelihood ratio tests comparing model 1 and 2 to the null model, model 3 to model 2, model 4 to model 1, model 5 and 6 to the corresponding models with only GRS, and model 7 to model 6, and model 8 to model 5.

^cThe R² for PRS_unadj,-gs + GRS_adj were 0.2284, 0.1327 and 0.0308 for hair color, tanning ability, basal cell carcinoma.

_-gs denotes excluding genome-wide significant SNPs.

Table 5.

Comparison between prediction R² of PRS_unadj, PRS_adj, and PRS_adj + ancestry in simulations with different training sample sizes

The fluctuations in R² of PRS_unadj are not statistically significant based on the number of simulations performed.

	R2
Training sample size (N)	PRSunadj (SE)	PRSadj (SE)	PRSadj + ancestry (SE)
1,000	0.041 (0.0016)	0.003 (0.0002)	0.042 (0.0016)
5,000	0.041 (0.0020)	0.014 (0.0004)	0.051 (0.0019)
10,000	0.043 (0.0019)	0.027 (0.0005)	0.064 (0.0018)
50,000	0.045 (0.0020)	0.111 (0.011)	0.139 (0.0019)
100,000	0.044 (0.0020)	0.182 (0.0011)	0.201 (0.0017)
500,000	0.042 (0.0020)	0.380 (0.0015)	0.384 (0.0016)
1,000,000	0.042 (0.0018)	0.439 (0.0012)	0.440 (0.0013)

SE: standard error

We also compared the 3 types of polygenic models with GRS_unadj or GRS_adj included as a component separate from PRS_unadj or PRS_adj in the model (PRS_unadj + GRS_unadj, PRS_adj + GRS_adj, and PRS_adj + GRS_adj + PCs). We excluded genome-wide significant SNPs (and SNPs in LD with known associated SNPs) from PRS_unadj and PRS_adj, since GRS based on genome-wide significant SNPs were included in the model as a separate component. Comparing the models with both PRS + GRS to the models with PRS only, the R² in general improved and the improvements were consistent with the R² from the GRS models (Table 4). The improvement in R² due to explicit modeling of ancestry remained but with a smaller magnitude, similar to the analysis using GRS only (Table 3); similar relative results were obtained when using GRS_adj in each model. For the PRS + GRS analyses, we also constructed GRS by fitting all known genome-wide significant SNPs in one model simultaneously to obtain effect size estimates (Table S7). The results showed similar patterns to the results from fitting genome-wide significant SNPs individually (Table 4). We also performed out-of-sample analyses using 10×9-fold nested cross-validation and obtained similar results (Table S3).

In addition to the 3 polygenic models described above, we evaluated the models of PRS_unadj+PCs and PRS_unadj+GRS_unadj+PCs and found that these models attained lower R² than PRS_adj + PCs and PRS_adj+GRS_adj+PCs (Table 4). This result may be caused by the fact that PRS_unadj and PCs are correlated due to ancestry information in both, which is not optimally modeled. Finally, we considered models including self-reported ancestry in addition to PCs as ancestry measures. The polygenic models with explicit modeling of ancestry were further improved by self-reported ancestry for HC and TA, but not BCC (Table S6), consistent with predictions using ancestry only (Table 2).

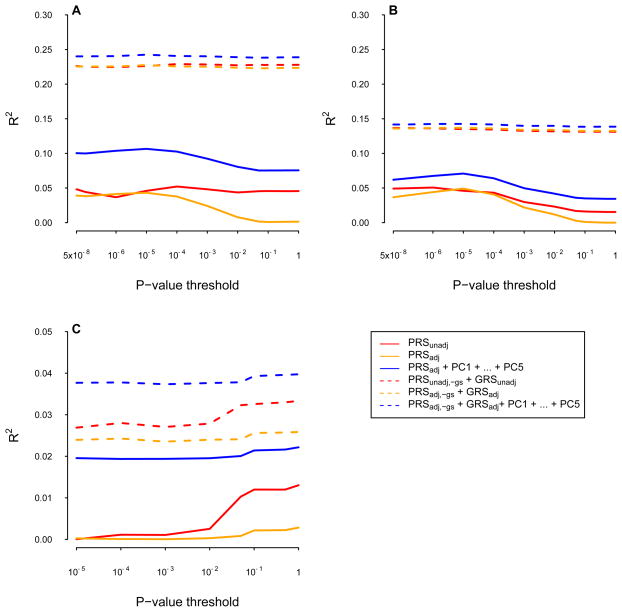
In addition to using all independent SNPs across the genome to construct PRS, we applied a p-value threshold based on association tests between individual SNPs and corresponding phenotypes to select SNPs entering PRS. We used p-value thresholds from 5×10⁻⁸ to 1 and constructed PRS corresponding to each p-value threshold [Evans et al. 2009; Purcell et al. 2009]. We fitted the 3 types of polygenic models with PRS only and the 3 types of polygenic models with both PRS and GRS, using PRS subject to different p-value thresholds (Figure 2). The prediction accuracy for the polygenic models varied with p-value thresholds and showed different patterns for the 3 traits. The R² of PRS_adj+PCs model for HC and TA increased with more stringent p-value threshold, while R² of PRS_adj+PCs model for BCC remained stable. Overall, polygenic models with explicit modeling of ancestry had higher R² than models without ancestry correction across all p-value thresholds applied to PRS. In addition, the difference between R² from the model with explicit modeling of ancestry and the model without ancestry correction remained constant across p-value thresholds. For the PRS only models, the R² changed with the p-value threshold for PRS but the magnitude of change was relatively small. For the models with both PRS and GRS components, the R² were still improved with a smaller magnitude by explicitly modeling ancestry, compared with PRS only models. We also repeated the analyses in 10×9-fold nested cross-validation and the results were similar to 10-fold simple cross-validation (Figure S2). Overall, we showed that explicit modeling of genetic ancestry improves polygenic prediction accuracy, and that this pattern persists when including known associated SNPs via a GRS, and when using p-value thresholds.

Figure 2. R² for polygenic prediction using PRS with different association p-value thresholds, GRS and PCs in 10-fold cross-validation.

(A): Hair color (B): Tanning ability (C): Basal cell carcinoma

Polygenic prediction using Best Linear Unbiased Predictors (BLUP) based on genome-wide SNPs

As a comparison to PRS, which use SNP effect sizes obtained by fitting models for each SNP individually, we compared the 3 types of polygenic models based on best linear unbiased predictors (BLUP), which use SNP effect sizes obtained by fitting all SNPs using a linear mixed model [Henderson 1975; Haile-Mariam et al. 2013; de los Campos et al. 2013; Habier et al. 2013; Bolormaa et al. 2013]. We created 3 polygenic models: BLUP without ancestry correction (BLUP_unadj); BLUP with ancestry correction (BLUP_adj); and BLUP with explicit modeling of ancestry (BLUP_adj+PCs); in BLUP_adj and BLUP_adj+PCs, ancestry was modeled using fixed effects (see Methods). In general, the R² of BLUP exhibited similar patterns as the R² of PRS (Table 6). In particular, BLUP_adj+PCs substantially outperformed BLUP_unadj. As with PRS, the improvement in R² of BLUP_adj+PCs over BLUP_adj was much larger than the R² of BLUP_unadj in each case, suggesting that BLUP_unadj suffered from a mis-specified weighting of ancestry effects; although BLUP fits all SNPs simultaneously, it does not allow for different weights for different ancestry effects (e.g. PCs). BLUP_adj had low R² due to small sample size, indicating that the prediction accuracy of BLUP_unadj was largely due to ancestry (Table S5). In models with BLUP and GRS as 2 separate components (where genome-wide significant SNPs were included in the GRS but not in BLUP), BLUP_adj+GRS_adj+PCs had significantly higher R² than BLUP_unadj+GRS_unadj (Table 6). Adding self-reported ancestry in the BLUP_adj+GRS_adj+PCs and the BLUP_adj+PCs models improves the prediction accuracy significantly for HC and TA, but not BCC (Table S6).

Table 6.

R² and p-values from likelihood ratio test for polygenic prediction using BLUP, GRS and PCs in 10-fold cross-validation

(a) BLUP included all SNPs available from genome-wide SNP chip after LD-pruning
		Hair color		Tanning ability		Basal cell carcinomaa
Model		R2	P-valueb	R2	P-valueb	R2	P-valueb
1	BLUPunadj	0.0588	<10−16	0.0131	<10−16	0.0125	2.93 × 10−13
2	BLUPadj	0.0045	5.86 × 10−9	0.0001	0.385	0.0013	0.0112
3	BLUPadj + PC1 + … + PC5	0.0781	<10−16	0.0345	<10−16	0.0218	<10−16

(b) GRS including genome-wide significant SNPs; BLUP excluded SNPs in LD with genome-wide significant SNPs but all other SNPs
		Hair color		Tanning ability		Basal cell carcinomaa
Model		R2	P-valueb	R2	P-valueb	R2	P-valueb
4	BLUPunadj,-gs + GRSunadj	0.2350	<10−16	0.1221	8.07 × 10−1	0.0275	6.49 × 10−7
5	BLUPadj,-gs + GRSadj	0.2258	8.10 × 10−3	0.1233	2.97 × 10−6	0.0208	5.52 × 10−2
6	BLUPadj,-gs + GRSadj + PC1 + … + PC5	0.2413	<10−16	0.1308	<10−16	0.0359	3.83 × 10−15

^aR² on liability scale

^bP-values are from likelihood ratio tests comparing model 1 and 2 to the null model, model 3 to model 2, model 4 and 5 to the corresponding models with only GRS, and model 6 to model 5.

_-gs denotes excluding genome-wide significant SNPs.

Discussion

Polygenic prediction using genome-wide SNPs has been widely applied to many complex traits. The most widely used polygenic prediction method is to construct a polygenic risk score (PRS), which is the sum of allele counts weighted by effect sizes estimated individually for each SNP, optionally restricting to SNPs with association p-value below a certain threshold [Chatterjee et al. 2013; Dudbridge 2013]. (It has previously been noted (Chatterjee et al. 2013) that other model selection and shrinkage methods, such as least absolute shrinkage and selection operator (LASSO)-type threshold methods that analyze all SNPs simultaneously, may modestly outperform the standard polygenic prediction approach). In previous studies using PRS, some of them adjusted for ancestry (PRS_adj) [Purcell et al. 2009; Stahl et al. 2012; Smoller et al. 2013; Rietveld et al. 2013, PGC 2014 Nature], and some of them did not (PRS_unadj) [Evans et al. 2009; Bush et al. 2010; Lango Allen et al. 2010; Machiela et al. 2011; Wood et al. 2014 Nat Genet]. However, a separate point is that modeling genetic ancestry as a separate component (PRS_adj+PCs) can improve polygenic prediction accuracy relative to either PRS_unadj or PRS_adj, as we showed for HC, TA and BCC; the same result is expected to hold for other traits associated to ancestry in subtly structured populations; this could explain why recent GWAS of height, which have reported that their association results may be impacted by very subtle population stratification [Lango Allen et al. 2010; Wood et al. 2014 Nat Genet], have attained prediction R2 using PRS that are lower than predicted by theory [Daetwyler et al. 2008 PLoS ONE]. In addition, the result still holds when including known associated SNPs via a genetic risk score (GRS), and when using p-value thresholds. In the European American data we analyzed, using 5 PCs to model ancestry improved our results relative to using 2 PCs. Surprisingly, including self-reported ancestry in addition to 5 PCs improved results further, as self-reported ancestry contains information about Scandinavian ancestry that is not well-captured by the PCs. Thus, PCs are not guaranteed to capture all ancestry information in subtly structured populations.

When applying methods that do not model genetic ancestry as a separate component (e.g. PRS_unadj or PRS_adj), it is still of interest to understand how much of polygenic prediction accuracy is due to ancestry, as this will affect prediction accuracy in other populations. For example, Rietveld et al. reported a polygenic prediction R² of 0.02 (p < 10⁻¹⁶) in an analysis of unrelated samples but a polygenic prediction R² of only 0.003 (p = 0.001) in a within-family analysis immune to ancestry effects (see Table S25 of Rietveld et al.) [Rietveld et al. 2013]. Unmodeled population structure provides one plausible explanation for this discrepancy. We note that although Rietveld et al. adjusted for 4 PCs in their analyses (PRS_adj), there is no guarantee that PCs capture all ancestry information in subtly structure populations. In addition, it is possible that PRS_adj+PCs might attain a higher prediction R² than PRS_adj in unrelated samples in the Rietveld et al. data, as we showed for HC, TA and BCC.

A previous study analyzed GWAS data from the Framingham Heart Study to compare prediction models for skin cancer risk using either pedigree information, or PCs, or polygenic prediction using Bayesian Lasso [Vazquez et al. 2012]. This study reported that polygenic prediction attained the highest prediction accuracy, PCs attained the next highest prediction accuracy, and pedigree information attained the lowest prediction accuracy. However this study did not explicitly model ancestry in the polygenic prediction model. Based on our results, it is possible that polygenic prediction with explicit modeling of ancestry might attain higher accuracy than the polygenic prediction approach employed by ref. [Vazquez et al. 2012]. It is also possible that combining pedigree information with polygenic predictions might improve prediction accuracy, although we have not explored that approach here [Haile-Mariam et al. 2013].

Alternatives to the widely used PRS approach for polygenic prediction include Best Linear Unbiased Prediction (BLUP) and its Bayesian extensions, which fit all markers simultaneously [de los Campos et al. 2013; Habier et al. 2013; Zhou et al. 2013; Bolormaa et al. 2013]. The potential benefits of explicitly modeling ancestry in this context may depend on the prior distribution of effect sizes that is assumed. Under an infinitesimal (Gaussian) prior, fitting all marker effects simultaneously may implicitly capture the effects of ancestry. However, our results showed that BLUP still showed an improvement in prediction accuracy when explicitly modeling ancestry. Although previous work has argued against including PCs as separate fixed effects in a mixed model when estimating components of heritability [Janss et al. 2012], and has shown that including PCs as separate fixed effects is generally not necessary when using standard mixed model methods for association [Yang et al. 2014], those studies did not consider prediction accuracy. Our recommendations for prediction are different from those recommendations for heritability estimation and association.

A limitation of our study is that the increased accuracy of PRS_adj+PCs (relative to PRS_adj) is contingent on validation samples having the same population structure as the training samples, as was the case in our cross-validation experiments. If validation samples do not have the same population structure then prediction accuracy will be lower, although PRS_adj+PCs is still an appropriate strategy. (For example, if validation samples are from a homogeneous population, then PRS_adj+PCs will produce predictions virtually identical to PRS_adj.) Another potential limitation of our study is that it may not be feasible to compute PCs by running PCA on raw genotypes from the union of training and validation samples, as was done here; for example, this will not be feasible if only summary statistics are available for training samples. However, in this case, the top PCs for validation samples can be computed using weights derived from external reference panels (as projected PCs), as we have described previously [Chen et al. 2013]. We repeated the main analyses with top projected PCs derived for both training and validation samples using an external European American reference panel and obtained similar results to the results using PCs derived from raw genotypes of training and validation samples (Tables S8–S12). (We note that our main analyses use only training sample genotypes and phenotypes and validation sample genotypes to predict validation sample phenotypes, which is appropriate.)

We conclude by emphasizing the dependence of polygenic prediction accuracy on sample size. Both PRS_adj (with or without P-value thresholding to impose model selection) and BLUP_adj attained low R2 in our analyses at modest sample sizes (<10,000), consistent with theoretical derivations [Daetwyler et al. 2008; Wray et al. 2013] and simulations suggesting that very large training sample sizes (100,000 or more) are needed to achieve high prediction accuracy [Chatterjee et al. 2013; Dudbridge 2013]. This limitation is in no way specific to the PRS approach. At larger sample sizes, it is likely that polygenic prediction will have significant clinical ramifications [Chatterjee et al. 2013; Dudbridge 2013]; indeed, prediction R2 has improved in recent very large studies [Ripke et al. 2014]. Notably, our simulations specifically show that the impact of explicit modeling of genetic ancestry will become extremely large as sample sizes grow.