Atrial-selective targeting of arrhythmogenic phase-3 early afterdepolarizations in human myocytes

Abstract

Background

We have previously shown that non-equilibrium Na⁺ current (I_Na) reactivation drives isoproterenol-induced phase-3 early afterdepolarizations (EADs) in mouse ventricular myocytes. In these cells, EAD initiation occurs secondary to potentiated sarcoplasmic reticulum Ca²⁺ release and enhanced Na⁺/Ca²⁺ exchange (NCX). This can be abolished by tetrodotoxin-blockade of I_Na, but not ranolazine, which selectively inhibits ventricular late I_Na.

Aim

Since repolarization of human atrial myocytes is similar to mouse ventricular myocytes in that it is relatively rapid and potently modulated by Ca²⁺, we investigated whether similar mechanisms can evoke EADs in human atrium. Indeed, phase-3 EADs have been shown to re-initiate atrial fibrillation (AF) during autonomic stimulation, which is a well-recognized initiator of AF.

Methods

We integrated a Markov model of I_Na gating in our human atrial myocyte model. To simulate experimental results, we rapidly paced this cell model at 10 Hz in the presence of 0.1 µM acetylcholine and 1 µM isoproterenol, and assessed EAD occurrence upon return to sinus rhythm (1 Hz).

Results

Cellular Ca²⁺ loading during fast pacing results in a transient period of hypercontractility after return to sinus rhythm. Here, fast repolarization and enhanced NCX facilitate I_Na reactivation via the canonical gating mode (i.e., not late I_Na burst mode), which drives EAD initiation. Simulating ranolazine administration reduces atrial peak I_Na and leads to faster repolarization, during which I_Na fails to reactivate and EADs are prevented.

Conclusions

Non-equilibrium I_Na reactivation can critically contribute to arrhythmias, specifically in human atrial myocytes. Ranolazine might be beneficial in this context by blocking peak (not late) atrial I_Na.

Graphical abstract

INTRODUCTION

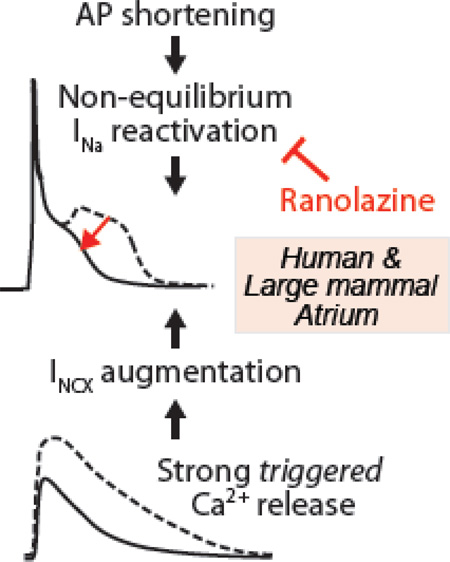
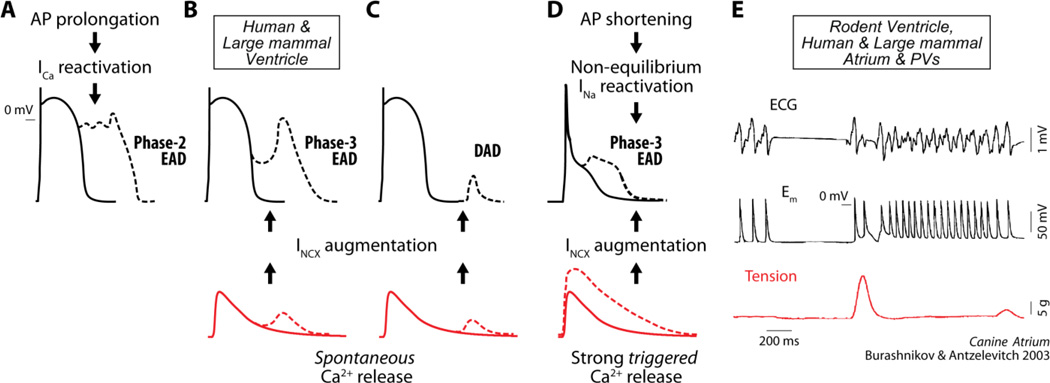
Early afterdepolarizations (EADs) are abnormal depolarizations of cardiac myocyte membrane potential (E_m) occurring during phase-2 or phase-3 of the action potential (AP). EADs have been implicated as primary mechanisms promoting ventricular arrhythmias, including Torsades des Pointes, polymorphic ventricular tachycardia and ventricular fibrillation [1]. In ventricular cells from large mammals EADs generally occur in conditions of prolonged AP duration (APD) or reduced repolarization reserve, due either to an increase in inward currents or decrease in outward currents, which promotes L-type Ca²⁺ current (I_Ca) recovery from inactivation and subsequent reactivation, forming the EAD upstroke (Fig. 7A). The imbalance between inward and outward currents can be caused by direct changes in sarcolemmal ion transport, or by discoordinated Ca²⁺ handling, leading to spontaneous sarcoplasmic reticulum (SR) Ca²⁺ release and subsequent increase in inward Na⁺/Ca²⁺ exchange (NCX) current (I_NCX), as in delayed afterdepolarizations (DADs, see Fig. 7B–C). Either way, I_Ca eventually carries the majority of inward charge contributing to the afterdepolarization upstroke [1].

Figure 7. Mechanisms of afterdepolarization formation in cardiomyocytes.

In ventricular myocytes from large mammals, phase-2 EADs are associated with I_Ca recovery from inactivation and reactivation during prolonged APs (A). Spontaneous SR Ca²⁺ release, which increases Ca²⁺ extrusion via NCX (inward current), can lead to phase-3 EADs (B) or DADs (C) when occurring during or after E_m repolarization respectively. In murine ventricle, phase-3 EADs are favored by potentiated (triggered) Ca²⁺ transient and AP shortening (D). The former causes I_NCX augmentation and AP plateau prolongation (at negative E_m), during which non-equilibrium I_Na reactivation (permitted by rapid I_Na recovery during fast repolarization) can occur. This, which is shown here to be relevant in the human atrium, could be a universal mechanism underlying EAD formation in both atria (especially PVs) and ventricles ([26]) of large mammals. Indeed, phase-3 EADs mediate re-initiation of atrial (and ventricular) fibrillation. ECG, E_m and tension recorded in canine atrium (E, reproduced with permission from [5]) show phase-3 EADs occurring after termination of fast atrial pacing, which are accompanied by increased contractile force.

Recently, we described a novel and unique mechanism underlying phase-3 EADs (Fig. 7D) in ventricular myocytes from arrhythmia-susceptible mice overexpressing Ca²⁺/calmodulin-dependent protein kinase II (CaMKII) [2]. EADs appearing during β-adrenergic stimulation in these mouse myocytes initiated at membrane potentials negative to −45 mV, and were thus incompatible with reactivation of I_Ca. These events also required intact SR Ca²⁺ release but generally occurred prior to or at the same time as the peak of the triggered Ca²⁺ transient, and thus were not driven by secondary spontaneous SR Ca²⁺ release during repolarization [2]. Computational modeling revealed that these EADs were initiated by non-equilibrium reactivation of fast Na⁺ current (I_Na), not late I_Na, and were secondary to enhanced SR Ca²⁺ release and augmented I_NCX that held voltage at a negative late plateau [2]. This was confirmed experimentally by the observation that 10 µM ranolazine, which selectively inhibits late I_Na in ventricles, did not prevent EAD initiation, whereas tetrodotoxin eliminated EADs [2] at a dose (1 µM) sufficient for approximately half inhibition of peak I_Na and 30% inhibition of late I_Na. By imposing different voltage waveforms on the Na⁺ channel model, we confirmed that specific E_m dynamics (e.g., rapidly repolarizing ramps) permit non-equilibrium reactivation, as opposed to an equilibrium component (e.g., window current) that would emerge after holding the voltage for a prolonged time [2].

This mechanism involving Ca²⁺-driven non-equilibrium I_Na reactivation is permitted by two key characteristics of the murine AP: a triangular repolarization trajectory with short and negative plateau phase (which hastens I_Na recovery from inactivation), and a repolarization phase that is strongly modulated by SR Ca²⁺ release and inward I_NCX. Thus, phase-3 EADs driven by non-equilibrium I_Na gating may constitute a novel mechanism of triggered arrhythmia in cardiac cell types known to exhibit these characteristics, including human atrial myocytes. Indeed, a mechanism involving phase-3 EADs driven by SR Ca²⁺ release and I_NCX has been shown to initiate triggered activity and re-induce atrial fibrillation (AF) in isolated canine atria (see Fig. 7E) and pulmonary vein (PV) sleeves during combined sympathetic and parasympathetic stimulation [3–5]. An interaction of both sympathetic and parasympathetic systems is thought to underlie the initiation of clinical AF in humans [6–8] and dogs [9, 10].

Here we sought to determine whether these dynamics may be relevant to the human atrium, where the relatively brief atrial AP and negative AP plateau may permit I_Na reactivation events. Indeed, without any parameter adjustment, we replicated phase-3 EADs in silico using our established human atrial cell model with updated I_Na description (see Methods). Further, we tested the hypothesis that ranolazine, which blocks both peak and late I_Na in atria (as opposed to the late I_Na selectivity in ventricles) [11–13] and suppresses AF by prolonging the effective refractory period [14], can also prevent phase-3 EAD-mediated triggered activity.

METHODS

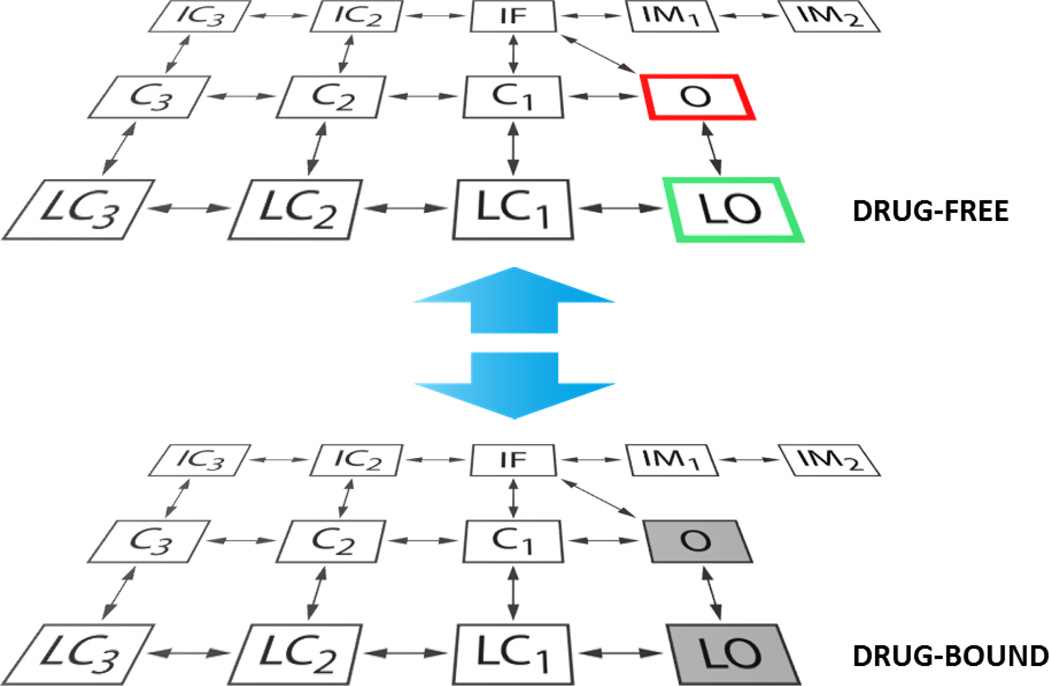
We integrated a Markov formulation of I_Na [15, 16] into our model of human atrial myocyte electrophysiology and Ca²⁺ cycling [17]. We further expanded the I_Na Markov model to describe the interaction of the Na⁺ channel with ranolazine, using the approach introduced by the Clancy group [18, 19]. Based on the assumption that the channel can reside in any state in drug-free or drug-bound conditions, the new model structure is characterized by drug-free and drug-bound layers, as shown in Fig. 1. Transitions between layers were initially modeled as done by Moreno et al [19], and transitions within the drug-bound layer were modified relative to the drug-free layer as in [19]. Several voltage-clamp protocols were simulated for parameterization of the ranolazine-I_Na model at room temperature: activation, steady-state inactivation, recovery from inactivation, tonic block of peak and late I_Na, use-dependent block (UDB), and recovery from UDB. A detailed description of the parameter identification process can be found in [19]. In our implementation, minor parameter adjustments were required to account for the different inactivation scheme in our Markov model vs. that used in [19]. Specifically, we modified the transitions between states IF and IM₁ in the drug-bound layer to match the frequency-dependence of UDB observed in experiments. The ranolazine-dependent tonic block of the delayed rectifier K⁺ current (I_Kr) was also integrated as in [19]. Current-clamp experiments were simulated at 37°C (the Q₁₀ for scaling I_Na kinetics was 2.1 [20]) to assess the occurrence of EADs with or without ranolazine in the presence of isoproterenol (ISO) and/or acetylcholine (ACh), modeled using the methods of Grandi et al [17]. All simulations were performed in MATLAB (The MathWorks, Natick, MA, USA) using the stiff ordinary differential equation solver ode15s. The model code is available for download at the following webpage: somapp.ucdmc.ucdavis.edu/Pharmacology/bers.

Figure 1. I_Na Markov model schematic.

When no drug is applied, I_Na is modeled with a 13-state Markov scheme [15, 16] accounting for both canonical and burst gating modes (see drug-free layer in figure). O and LO are respectively the conducting open states for normal and burst mode, and C₁-C₃ and LC₁-LC₃ are the corresponding closed states. IF is the fast inactivation state, IM₁-IM₂ represent intermediate inactivation, and IC₂-IC₃ are the deeply inactivated states. To model ranolazine interaction with the Na⁺ channel, we used the extended scheme shown here, assuming that the channel can reside in any state in drug-free or drug-bound conditions (as done in [18, 19]). Transitions between layers are E_m- and dose-dependent, and can occur between analogous states only. Ranolazine binding is facilitated when the channel resides in the open states. The drug unbinds rapidly from the closed states, but stays trapped in the inactivated states. O and LO in the drug-bound layer are not conducting states.

RESULTS

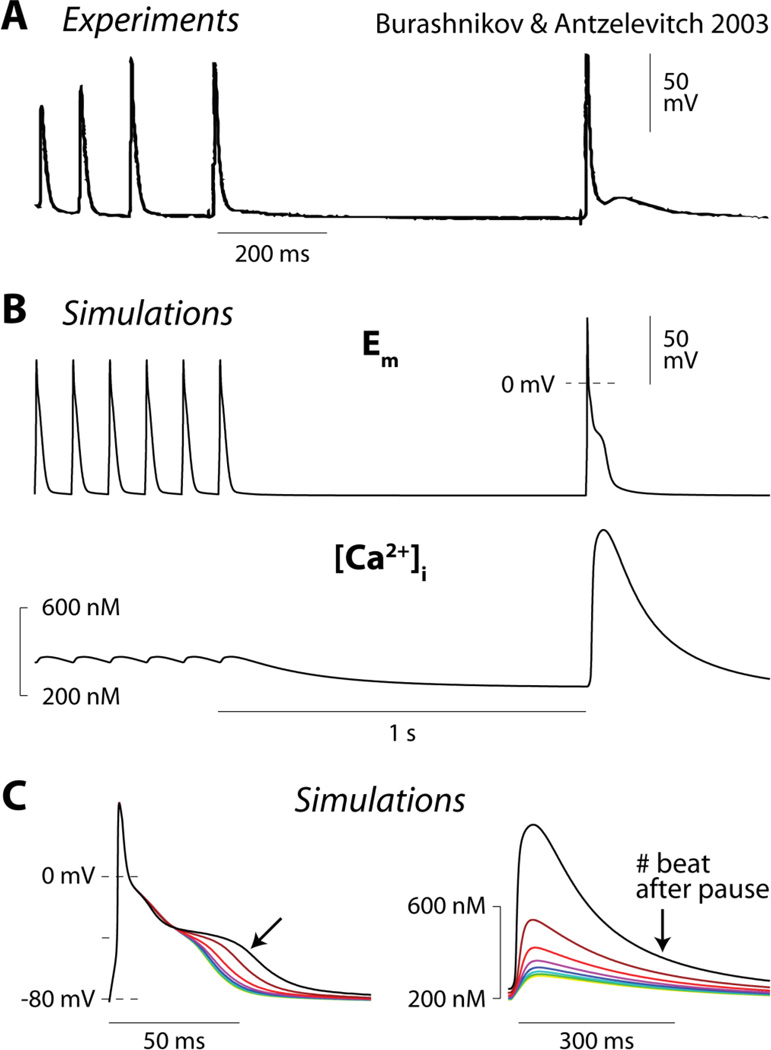
Burashnikov and Antzelevitch [5] observed the development of phase-3 EADs after spontaneous termination of AF in canine atrial tissue (Fig. 2A). Under similar conditions (ACh-abbreviated AP, in absence of sympathetic stimulation), our model exhibited a similar slowing of phase-3 repolarization (Fig. 2B, top panel) upon returning from rapid pacing (10 Hz) to sinus rhythm (1 Hz). This effect is due to pause-induced increase in SR Ca²⁺ release and, consequently, enhanced inward I_NCX. In fact, Ca²⁺ accumulation in the cell during the fast pacing interval resulted in a transient period of hypercontractility immediately after return to normal sinus rhythm (Fig. 2B, bottom). Increased Ca²⁺ extrusion via NCX contributes to generating the inward current responsible for AP plateau prolongation, i.e., as observed in mouse [2]. Beat by beat, SR Ca²⁺ load decreased, leading to a gradual reduction of the Ca²⁺ transient amplitude (Fig. 2C, right) and I_NCX, which caused progressive AP shortening (Fig. 2C, left).

Figure 2. Atrial AP plateau is potently modulated by I_NCX.

A) A phase-3 EAD is recorded immediately after (first beat after pause) spontaneous termination of AF in isolated canine atrium (reproduced with permission from [5]). B) The above experiment is simulated with our human atrial myocyte model. The cell is paced rapidly (10 Hz) for 20 s and then returned to sinus rhythm (1 Hz) in the presence of 1 µM ACh. Time courses of E_m (top) and intracellular Ca²⁺ concentration ([Ca²⁺]_i, bottom) are shown. C) Sequence of simulated beats after returning to normal sinus rhythm. AP progressively shortens (left) due to SR unloading, and diminishes Ca²⁺ transient (right) and I_NCX.

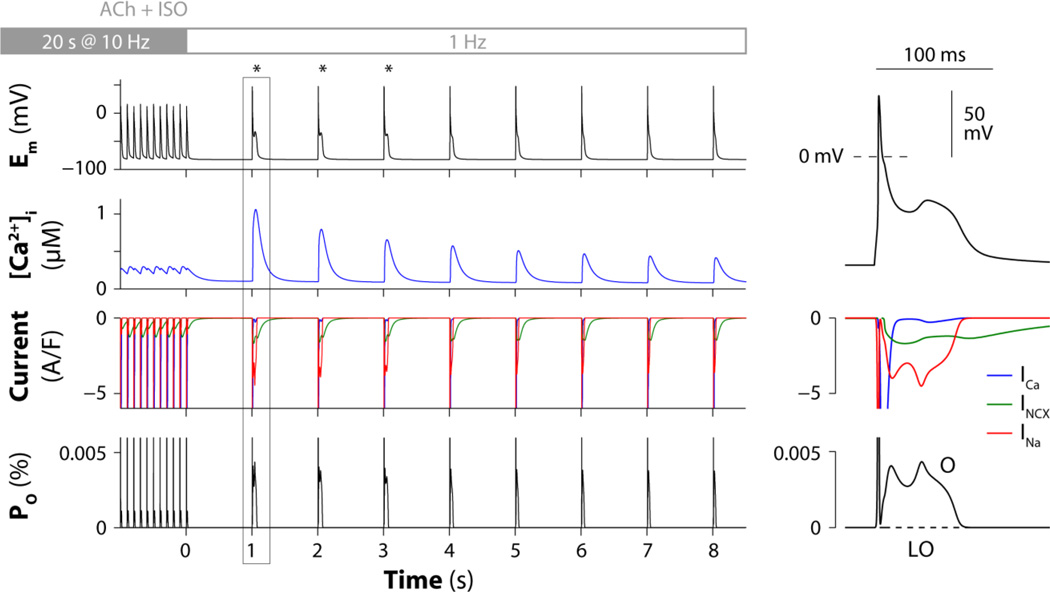
Heart rate variability analysis in human patients [6–8] and nerve activity recordings in ambulatory dogs [9, 10] indicated that the onset of AF is associated with simultaneous discharge of both sympathetic and para-sympathetic limbs, rather than by either vagal or sympathetic activity alone. Consistently, experimental studies involving autonomic nerve stimulation [4], or exogenous agonists [3], suggest that combined sympathetic and parasympathetic challenge is capable of eliciting phase-3 EADs and triggered activity. To emulate experimental protocols, we paced our atrial cell model rapidly (10 Hz), while simulating combined administration of ACh (0.1 µM) and ISO (1 µM). Again, simulations predicted a transient increase in Ca²⁺ transient amplitude after return to sinus rhythm (1 Hz pacing) due to augmented SR Ca²⁺ loading and release (Fig. 3). This enhances I_NCX, which favors AP prolongation and recruits non-equilibrium I_Na reactivation via the canonical gating mode (O), thus leading to the development of phase-3 EADs (Fig. 3, asterisks). In Fig. S1 we confirmed that during rapid repolarization ramps total I_Na (Fig. S1B, black/red traces) is carried mainly by a non-equilibrium component, because this is already substantial at E_m (and times) where the theoretically maximal equilibrium (window) current of I_Na is virtually absent (Fig. S1C, black/red traces). These results extend our observations in murine ventricles [2], and confirm that non-equilibrium I_Na reactivation is a likely arrhythmia mechanism in human atrial cells.

Figure 3. Non-equilibrium I_Na reactivation underlies phase-3 EADs in human atrial cells.

The digital human atrial myocyte is paced rapidly (10 Hz) for 20 s and then returned to sinus rhythm (1 Hz) in the presence of 0.1 µM ACh and 1 µM ISO. Left panels show the predicted time courses of E_m, [Ca²⁺]_i, I_Ca, I_NCX, I_Na, and occupancies of the I_Na model open states (O and LO). A transient period of hypercontractility occurs immediately after return to normal sinus rhythm (second row) because of augmented SR Ca²⁺ loading and release. Enhanced I_NCX facilitates I_Na reactivation (third row) via the canonical gating mode (bottom). Right panels show magnified traces for the first beat after returning to normal sinus rhythm.

We performed additional simulations to assess the likelihood of these EADs to occur and determine the factors that most markedly affect EAD formation. We varied ion channel conductances and maximal transport rates by +/- 3–5% and assessed the occurrence of EADs using the protocol in Fig. 3 (Table S1). As expected, we found EAD initiation to be especially sensitive to I_Na conductance. Changes in ACh (analyzed in 5-nM increments) or ISO doses, duration of rapid pacing (1-s increments) duration of the pause (50-ms decrements), also affect EAD occurrence by modulating the repolarization rate or I_Na availability. Specifically, starting from the original base-case parameter configuration, [ACh] higher than 135 nM, rapid pacing protocols longer than 23 s, or pauses shorter than 800 ms prevent EADs in the model, primarily by increasing repolarization rate, reducing I_Na availability, or both affecting Ca²⁺ loading and I_Na, respectively. While ISO effects in this model are simulated as static on/off switches, rather than graded dose-dependent responses, we expect lower [ISO] to result in reduced Ca²⁺ loading, and hence reduced EAD propensity.

We also attempted to replicate this EAD mechanism by another established atrial cell model, and repeated some of the simulations with the Koivumäki et al model [21]. We were unable to recapitulate frank EADs as seen in experiments and in our model, and reasoned that this may be due to fundamental differences in model construction. For example, a large difference in stability of intracellular Na⁺ markedly diminishes the potential for Ca²⁺ overload to generate “plateau” inward I_NCX in the Koivumäki et al model. Specifically, we could reproduce data similar to our simulations in Fig. 2 when reducing intracellular Na⁺, including our Markov I_Na model, and using the Grandi et al NCX formulation (not shown).

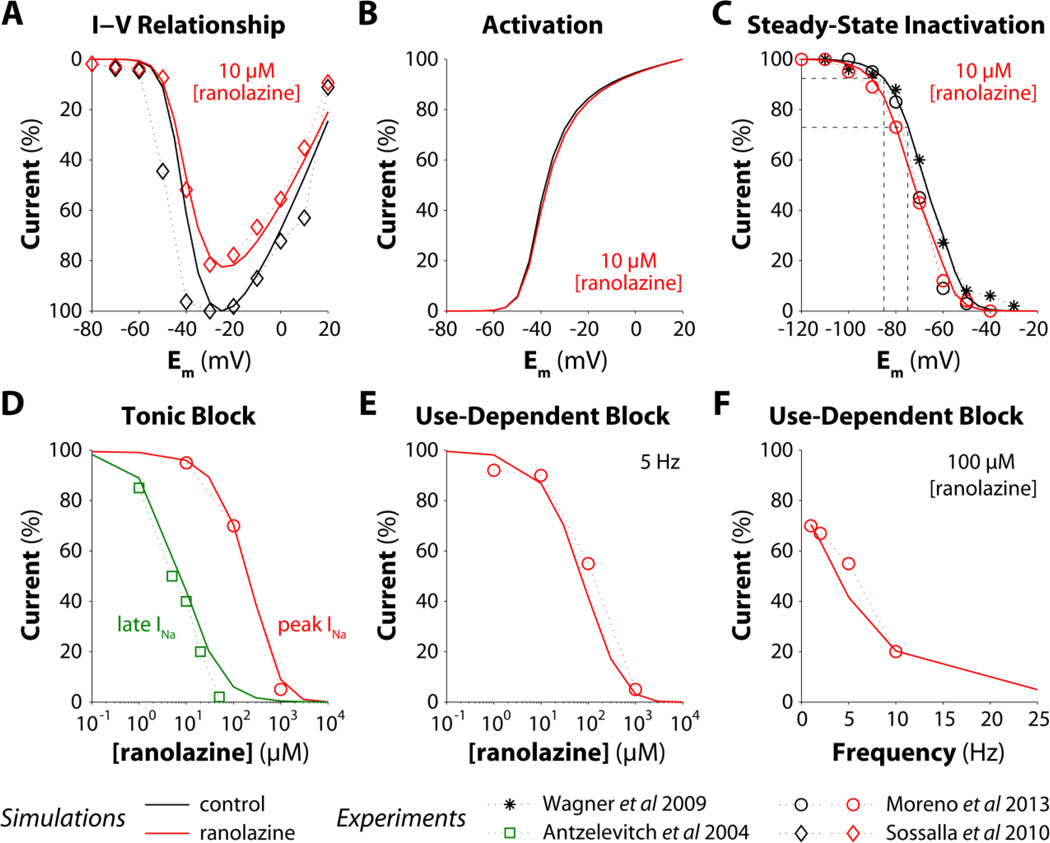
Our previous study showed that tetrodotoxin blockade of peak I_Na prevented this pro-arrhythmic I_Na reactivation in mouse ventricular cardiomyocytes [2], whereas specific block of late I_Na by ranolazine failed to prevent EAD initiation [2] though APD was shortened. Ranolazine is an open-state Na⁺ blocker that unbinds rapidly from the closed state, but stays trapped and cannot unbind from inactivated Na⁺ channels. The more depolarized resting E_m of atrial compared with ventricular myocytes (~10 mV more positive) is responsible for a larger fraction of inactivated Na⁺ channels in atrial vs. ventricular cells (e.g., the fraction of inactivated states increases about 3.5-fold from −85 to −75 mV, dashed lines in Fig. 4C), which makes ranolazine an atrial-selective blocker of peak I_Na [12, 13]. Thus, we sought to test whether ranolazine can prevent arrhythmogenic non-equilibrium I_Na reactivation in atrium. To pursue this goal, we extended our I_Na model to reproduce the experimentally observed consequences of ranolazine-Na⁺ channel interaction [15, 19, 22–24]. Ranolazine (10 µM) reduced atrial peak current (Fig. 4A) without altering the voltage-dependence of I_Na activation (Fig. 4B), negatively shifted steady-state inactivation (Fig. 4C), and slowed recovery from inactivation (not shown) [24]. Ranolazine-induced tonic block is higher for late vs. peak I_Na: simulated IC₅₀ values of 7 and 200 µM for late and peak components, respectively, were in good agreement with experimental data (Fig. 4D). In response to repetitive depolarizations, ranolazine caused UDB of peak I_Na, which increased with both drug dose (Fig. 4E) and stimulation frequency (Fig. 4F). Recovery from UDB was also slowed by ranolazine administration (not shown) [19].

Figure 4. Effects of ranolazine on I_Na biophysical properties and properties of block.

I_Na model parameters are optimized to match simulation outputs (lines) with experiments (symbols, from [15, 19, 22, 23]). A–C) Peak I_Na-E_m relationship (normalized to maximal peak current in drug-free condition), activation, and steady-state inactivation with or without 10 µM ranolazine. D) Dose-dependence of tonic block for peak and late I_Na evoked by a 200-ms depolarizing pulse from −100 to −10 mV. Current amplitude in the presence of ranolazine is normalized to the current amplitude in the absence of drug. E–F) Dose- and frequency-dependence of UDB from a train of 300 25-ms long pulses (from −100 to −10 mV). I_Na amplitude in the presence of ranolazine at the last pulse is normalized to I_Na amplitude in drug-free condition.

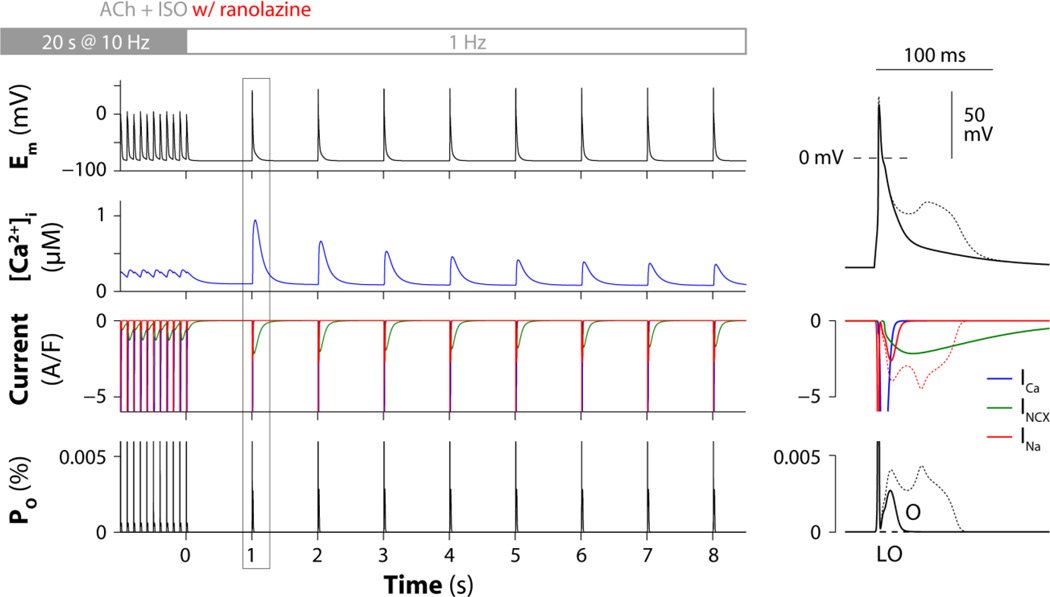
To test whether ranolazine can prevent phase-3 EAD occurrence in our atrial model, we repeated the simulation shown in Fig. 3 with the addition of various concentrations of the drug. Model outputs were qualitatively similar when simulating ranolazine doses within the therapeutic range (1–10 µM): despite Ca²⁺ overload and enhanced I_NCX, ranolazine administration prevented non-equilibrium I_Na reactivation and phase-3 EADs were suppressed. Results obtained with 5 µM ranolazine are reported in Fig. 5.

Figure 5. Ranolazine inhibits arrhythmogenic non-equilibrium I_Na reactivation.

The digital human atrial myocyte is paced rapidly (10 Hz) for 20 s and then returned to sinus rhythm (1 Hz) in the presence of 0.1 µM ACh and 1 µM ISO (as in Fig. 3) and administration of 5 µM ranolazine. Left panels show the predicted time courses of E_m, [Ca²⁺]_i, I_Ca, I_NCX, I_Na, and occupancies of the I_Na model open states (O and LO). A transient period of hypercontractility occurs immediately after return to normal sinus rhythm (second row) because of augmented SR Ca²⁺ loading and release. Despite enhanced I_NCX (third row), I_Na reactivation via the canonical gating mode (bottom) is prevented by ranolazine and EADs are suppressed. Right panels show magnified traces for the first beat after returning to normal sinus rhythm. E_m, I_Na and O traces in the absence of ranolazine (from Fig. 3) are reported for comparison (superimposed thin dotted lines).

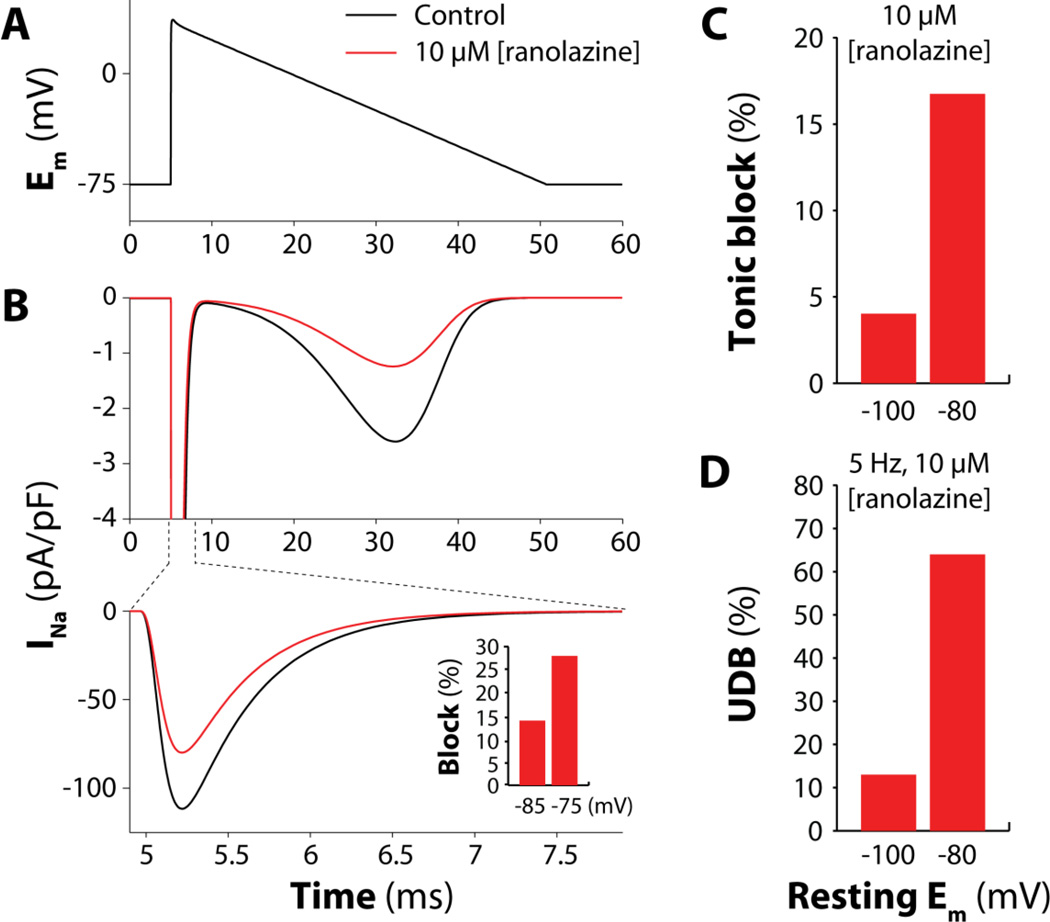
Our results confirm the hypothesis that ranolazine administration can prevent non-equilibrium I_Na reactivation because it blocks peak I_Na in atrial (but not in ventricular) myocytes. This atrioventricular difference in pharmacological outcome is due to the property of this drug to stay trapped to inactivated Na⁺ channels. Since atrial cells are more depolarized at resting E_m (vs. ventricular myocytes), more Na⁺ channels are inactivated in atrial vs. ventricular cells, leading to stronger peak I_Na block [11–13]. To quantify this, we applied a triangular (“atrial-like”) voltage command (Fig. 6A) to our human atrial model. Administration of 10 µM ranolazine caused a 28% reduction of peak I_Na (Fig. 6B) if the cell was held at the typical atrial resting E_m of −75 mV. When holding the resting potential more negative (−85 mV), as in ventricular myocytes, this I_Na block was much less (14%). Analogously, both tonic (Fig. 6C) and UDB (Fig. 6D) induced by 10 µM ranolazine were enhanced by about 4-fold when simulating a depolarized resting E_m (−80 mV vs. −100 mV in Fig. 4). Thus, it is not surprising that ranolazine exerts its anti-arrhythmic effect at relative low concentrations (1–5 µM). These observations confirm that the more depolarized resting E_m in atrial vs. ventricular myocytes plays a pivotal role in determining the ranolazine effect on I_Na peak in the two different cardiac tissues.

Figure 6. Depolarized resting E_m enhances ranolazine-induced block of peak I_Na.

A) A triangular voltage command is applied to the digital human atrial myocyte. Resting E_m is −75 mV. B) Evoked I_Na traces in drug-free condition (control) or in presence of 10 µM ranolazine. Ranolazine reduces peak I_Na by 28%, and the current reactivating during the repolarizing ramp by 52%. The more depolarized the resting E_m the larger the peak current block (inset). C) Resting E_m-dependence of tonic block for peak I_Na with 10 µM ranolazine (obtained replicating the same protocol as Fig. 4D). D) Resting E_m-dependence of UDB for peak I_Na with 10 µM ranolazine (protocol as Fig. 4E).

DISCUSSION

A mechanism for phase-3 EADs involving Ca²⁺-driven non-equilibrium I_Na reactivation is shown here to be relevant in human atrial myocytes, which exhibit an AP morphology that is intermediate to the ventricular APs of the mouse and large mammals. The mechanisms of EAD takeoff at these negative E_m are independent of I_Ca reactivation and result from enhanced triggered (not spontaneous) Ca²⁺ release, which subsequently drives NCX-induced prolongation of the (negative) AP plateau after rapid early repolarization (Fig. 7D).

In healthy ventricular myocytes of large mammals, arrhythmogenic non-equilibrium I_Na reactivation is hindered by the higher AP plateau and the increased APD, which cause accumulation of channels in the slow-recovering inactive states. However, we speculate that it might become relevant in those pathological conditions in which these AP features are drastically altered. An example may be ischemia-induced remodeling, where resting E_m is depolarized and APD is shortened. In a pacing-induced rabbit heart failure model, post-shock APD shortening and Ca²⁺ elevation induced recurrent ventricular fibrillation by promoting phase-3 EADs and triggered activity [25]. Post-shock phase-3 EADs were also obtained in Langendorff-perfused hypokalemic rabbit ventricles, when ventricular fibrillation was induced during sympathetic activation [26].

In canine atrial preparations, Burashnikov and Antzelevitch have shown that phase-3 EADs arise after AF termination, and are the trigger for re-induction of fibrillation [5] (Fig. 7E). Analogous triggered phenomena have been described in canine PVs with autonomic nerve stimulation [3], or combined ACh and epinephrine challenge [4]. These protocols mimic simultaneous sympathovagal discharges that commonly precede AF onset [6–10, 27]. Our atrial simulations are consistent with the results of these studies, and capture both the relatively subtle EADs accompanying rapid pacing and ACh (Fig. 2), and the more pronounced depolarizations observed with additional β-adrenergic challenge (Fig. 3). This graded induction from AP prolongation through to clear EADs is a feature of the progressive Ca²⁺ loading accompanying these stimuli [4], and as in our murine experiments [2], results from exaggerated SR Ca²⁺ release and I_NCX [4, 5]. Nevertheless, some variability in shape and take-off potential and timing exists in experimentally measured EADs. Figure S2A illustrates the development of ACh- and high Ca²⁺-induced late phase-3 EADs in PV [28] and superior vena cava [29] sleeve preparations. Late phase-3 EADs are observed at slow rates in beats immediately after rapid pacing and occur at variable take-off potentials (ranging from ~−70 to −45 mV). Our simulated EADs initiate at the depolarized end of this range. By performing sensitivity analysis (Table S1), we also found that relatively small changes in I_Ca conductance could uniquely produce relatively large variations in EAD morphology (take-off potential and timing, Fig. S2B). We did not see EADs originating at more negative E_m, although these are also consistent with reactivation of I_Na. EAD timing is not markedly different between the model and experiments, and in both it generally occurs at the time of greatest triangulation in trajectory, when I_Na is most apt to reactivate i.e. the phase-2/phase-3 transition. Nevertheless, small discrepancies in experimental vs. simulated EAD timing might have technical or physiological explanations. Technically, it is possible that in some recordings the microelectrodes are slightly spatially removed from the site of earliest EAD reactivation, and therefore there is some slight delay due to conduction. Physiologically, the temporal offset could be explained by slowing of repolarization due to intracellular Ca²⁺ waves, as occurs in ventricular myocytes during specific conditions of Ca²⁺ overload [30]. Whether it is this or conventional systolic Ca²⁺ release that is responsible for delaying repolarization here, importantly our simulations suggest the novel interpretation that induction of non-equilibrium I_Na dynamics is the critical end point of this EAD mechanism, and is therefore responsible for reinitiating AF in these models. In line with this contention, AP-clamp experiments in pig atrial myocytes confirmed that an EAD-shaped voltage command elicited a lidocaine-sensitive (20–200 µM) inward current compatible with simulated I_Na dynamics (not shown), similar to results in murine ventricles [2]. An important qualifier for this interpretation is that the experimental protocols involving ACh challenge also facilitate I_Na reactivation by shortening the AP. However, AP shortening and EADs of this type can also be induced by autonomic nerve stimulation without exogenous agonists [3], and it is known that simultaneous parasympathetic and sympathetic activation may precede AF onset [27]. Note that ACh will tend to cause E_m hyperpolarization (from ~−76 mV to ~−82 mV with 1 µM ACh in our simulations).

Our local sensitivity analysis involved modest perturbations in ionic conductances to support the concept that EADs are not especially sensitive to parameters other than I_Na while limiting the influence on overall model behavior (e.g., maintaining AP and Ca²⁺ transient properties close to the original base-case model). Future studies could exploit more informative techniques for parameter sensitivity analysis (and larger variations), which have been recently applied in computational electrophysiological and Ca²⁺ handling models [31–35].

PVs play a particularly important role in paroxysmal AF (pAF) patients [36], and there is evidence that PV cardiomyocytes possess properties predisposing to both Ca²⁺-driven focal activity and reentry. While it is possible that both DADs and EADs contribute to PV ectopy, based on data from models of acute AF, and data describing the early electrophysiological changes in AF [37], we contend that EADs are a likely source of ectopy early in disease progression. Specifically, we speculate that the short PV AP, and late AP plateau (at negative E_m) induced by autonomic challenge, can facilitate non-equilibrium I_Na reactivation at negative plateau E_m, late during repolarization, as we have shown in our computational human atrial myocytes (Fig. 3) and in mouse ventricular myocytes [2]. In an arrhythmia-susceptible canine model, Ca²⁺ transient amplitude and kinetics were similar in myocytes from both PVs and atrium [38], which supports the contention that what we have seen in the human atrial model might also hold true in PVs.

If our proposed mechanism proves to be an important initiator of atrial and PV ectopy, it may assist development of more effective pharmacotherapeutics, e.g., evaluating the efficacy and safety of class 1C antiarrhythmic drugs for treatment of pAF treatment. Indeed, flecainide (a potent I_Na blocker and effective anti-AF drug) is contraindicated in patients with heart failure, because of a high risk of induction of ventricular arrhythmia [39]. By revealing the mechanisms of drug efficacy and atrial selectivity, our computational approach might facilitate more specific drug development pipelines [40, 41]. In a recent study, a computational modeling approach informed and validated by experimental data has been developed to simulate the interaction kinetics of the antiarrhythmic drugs flecainide and lidocaine with cardiac Na⁺ channels (Fig. 1, [18]). More recently, this framework has been extended to simulate the novel Na⁺ channel blocker ranolazine, which preferentially blocks late vs. peak I_Na in ventricles, but also blocks hERG current I_Kr with therapeutic concentrations resulting in QTc prolongation. Ranolazine is contraindicated for patients with preexisting QT prolongation, but we have examined its effectiveness in diverse arrhythmia-provoking contexts characterized by enhancement of late I_Na [19]. Ranolazine cannot unbind from inactivated Na⁺ channels. The fraction of inactivated channels is greater in atrial vs. ventricular myocytes, as a result of the more negative Na⁺ channel steady-state inactivation curve (in some species) and the more depolarized resting E_m. This confers ranolazine atrial selectivity (compared with ventricles) for peak I_Na block [11–13]. Accordingly, our computational analysis showed that a depolarized resting E_m enhances the ranolazine-induced tonic block of peak I_Na (Fig. 6A–C). Moreover, because much of the recovery from Na⁺ channel block occurs from non-inactivated states of the channel, atrial cells show a greater accumulation of use-dependent Na⁺ channel block (Fig. 6D). Notably, ranolazine suppresses AF by prolonging the effective refractory period via an increase in post-repolarization refractoriness [14], and has been shown to suppress experimentally measured phase-3 EADs in PV sleeves, via its actions to reduce [Ca²⁺]_i secondary to changes in I_Na and late I_Ca [28]. Here, we show that ranolazine can also suppress EAD-mediated ectopic activity in atrial myocytes by significantly reducing non-equilibrium I_Na reactivation (Fig. 5). This is achieved in our model simply due to a depolarized atrial resting E_m, as differences in I_Na availability have been ruled out in human atrial vs. ventricular myocytes [42]. We speculate that ranolazine may be even more efficacious and selective for PV myocytes, given their even more depolarized resting E_m [43].

It is well known that ranolazine targets multiple mechanisms in cardiac cells. As done previously [19], our Markov I_Na model accounts for both the fast and the late I_Na (and so does the drug model). I_Kr block is incorporated as well, although it was shown to not appreciably affect atrial APD ([17], confirmed by experiments by Wettwer et al [44]), or even greatly potentiate atrial-selective I_Na block [14]. It has also been reported that ranolazine directly influences ryanodine receptor (RyR) open probability and desensitizes Ca²⁺-dependent RyR activation [45]. However, we did not see any significant effect of ranolazine (10 µM) on myocytes Ca²⁺ sparks and SR Ca²⁺ load in permeabilized mouse ventricular myocytes (not shown). In addition to direct ranolazine effects on these channels, which warrant further investigation, our previous modeling work supports the notion that ranolazine may act to desensitize RyRs indirectly by normalizing intracellular Na⁺ loading and decreasing CaMKII-dependent RyR phosphorylation [46]. In fact, reduction of late I_Na by ranolazine and GS-458967, a more selective and potent inhibitor of late I_Na, also reduces the incidence of DADs in experimental studies of PV and superior vena cava sleeves [29, 47] potentially by reducing Na⁺ and hence Ca²⁺ loading. Importantly, simulations of other Na⁺ channel blockers (flecainide, lidocaine, which does not inhibit I_Kr, and GS-458967) may help define the necessary E_m- and time-dependent characteristics of Na⁺ channel block that ensure atrial selectivity of peak I_Na blockade, as well as the consequences of off-target effects.

CONCLUSIONS

Our study unveils non-equilibrium I_Na reactivation as a novel arrhythmia mechanism in human atrial myocytes, as previously observed in mouse ventricular cells [2]. These cardiac cell types are both characterized by a triangular repolarization trajectory with short and negative plateau, and a late phase of repolarization strongly dependent on SR Ca²⁺ release and inward I_NCX. The negative AP plateau hastens I_Na recovery from inactivation, which can then reactivate when the AP is prolonged by increased Ca²⁺ extrusion via NCX, leading to phase-3 EAD initiation. We showed that pharmacological inhibition of peak I_Na can prevent this pro-arrhythmic mechanism in both atrial and ventricular cells. The more depolarized resting E_m in atrial (vs. ventricular) myocytes confers atrial selectivity for peak I_Na block to the Na⁺ channel blocker ranolazine [11–13], which prevents the arrhythmogenic reactivation of I_Na in atrial cells but not in ventricular myocytes. Our findings suggest that this pro-arrhythmic mechanism may be relevant also in human PVs, where the more depolarized resting E_m (vs. atrial free-wall cells) may further increase the efficacy of ranolazine treatment. Taken together, these observations corroborate the concept of atrial-selective inhibition of peak I_Na as a promising therapeutic strategy for the management of AF [11, 14, 41].

Highlights.

• Combined ISO and ACh cause phase-3 EADs in human atrial myocyte simulations

• Phase-3 EADs are favored by increased Ca²⁺ transients and rapid E_m repolarization

• NCX-mediated long AP plateaus recruit non-equilibrium I_Na reactivation to favor EAD

• Ranolazine prevents phase-3 EADs in an atrial selective manner

Abbreviations

ACh

acetylcholine

AF

atrial fibrillation

AP

action potential

APD

action potential duration

[Ca²⁺]_i

intracellular Ca²⁺ concentration

CaMKII

Ca²⁺/calmodulin-dependent protein kinase II

DAD

delayed afterdepolarization

EAD

early afterdepolarization

E_m

membrane potential

I_Ca

L-type Ca²⁺ current

I_Na

Na⁺ current

I_Kr

delayed rectifier K⁺ current

I_NCX

Na⁺/Ca²⁺ exchanger current

ISO

isoproterenol

NCX

Na⁺/Ca²⁺ exchanger

pAF

paroxysmal atrial fibrillation

PV

pulmonary vein

RyR

ryanodine receptor

SR

sarcoplasmic reticulum

UDB

use-dependent block