An Inverted Dielectrophoretic Device for Analysis of Attached Single Cell Mechanics

Abstract

Dielectrophoresis (DEP), the force induced on a polarizable body by a non-uniform electric field, has been widely used to manipulate single cells in suspension and analyze their stiffness. However, most cell types do not naturally exist in suspension but instead require attachment to the tissue extracellular matrix in vivo. Cells alter their cytoskeletal structure when they attach to a substrate, which impacts cell stiffness. It is therefore critical to be able to measure mechanical properties of cells attached to a substrate. We present a novel inverted quadrupole dielectrophoretic device capable of measuring changes in the mechanics of single cells attached to a micropatterned polyacrylamide gel. The device is positioned over a cell of defined size, a directed DEP pushing force is applied, and cell centroid displacement is dynamically measured by optical microscopy. Using this device, single endothelial cells showed greater centroid displacement in response to applied DEP pushing force following actin cytoskeleton disruption by cytochalasin D. In addition, transformed mammary epithelial cell (MCF10A-NeuT) showed greater centroid displacement in response to applied DEP pushing force compared to untransformed cells (MCF10A). DEP device measurements were confirmed by showing that the cells with greater centroid displacement also had a lower elastic modulus by atomic force microscopy. The current study demonstrates that an inverted DEP device can determine changes in single attached cell mechanics on varied substrates.

Introduction

Cell mechanical properties, such as stiffness, play a critical role in healthy cell and tissue function. For example, endothelial cell stiffness increases as the vascular wall stiffens and inversely correlates with nitric oxide production, an essential function of healthy endothelium.^1–3 Decreased epithelial cancer cell stiffness corresponds to increased metastatic potential and may play a role in drug resistance.^{4, 5} Cell stiffness is mediated by a combination of external (e.g., extracellular matrix) and internal (e.g., actin fiber) stimuli, and it alters signal transduction pathways, gene expression, and differentiation.⁶ While cell mechanical properties are increasingly recognized as important, we have yet to fully understand how properties such as cell stiffness can both predict and impact biological processes.

A wide variety of methods exist to test cell mechanical properties. Through techniques such as micropipette aspiration,^{7, 8} optical tweezers,^{9, 10} and the optical stretcher^{11, 12}, forces can be applied across the entire cell to enable measurement of whole cell stiffness. Alternatively, magnetic bead microrheometry,¹³ magnetic twisting cytometry,^{14, 15} and atomic force microscopy^{16, 17} apply forces to specific cell locations to measure the stiffness of precise cellular regions. However, these existing technologies are either inherently low throughput, incapable of testing attached cells, or require interaction with membrane proteins, which could result in unwanted signalling pathway activation.

We hypothesized that dielectrophoresis (DEP) could be used as a non-contact method to compare whole cell stiffness for cells attached to a substrate. DEP is the force induced on a polarizable particle in a spatially non-uniform electric field.^18–20 When a polarizable object is placed in an electric field, charges distribute unevenly across the body to create a dipole. In a uniform electric field, this dipole experiences no net force. However, in a non-uniform electric field, the forces exerted on each dipole end are unequal, leading to a net force on the dipole. The force direction is determined by competition between the induced polarization in the cell and the medium. If the cell is less polarizable than the medium, the overall effective dipole draws the particle towards the field minimum (negative DEP).

DEP was first used to manipulate individual yeast cells in 1974; single cell manipulation by DEP then became an area of intense study in the early 1990’s.^{21, 22} Since that time, DEP has been effectively used for many biological applications involving bioparticles. DEP traps immobilized micron sized particles, beads and cells, as well as submicron sized viruses into large arrays using both positive and negative DEP.^22–26 In addition, DEP can induce levitation and electrorotation of single cells in suspension.²⁷ DEP can separate different cell populations based on their dielectric properties. Breast cancer cells have been detected in blood,²⁸ and CD34+ stem cells were enriched from a larger stem cell pool.²⁹ Additionally, DEP has been used to pattern cells on uncoated substrates,³⁰ on microprinted adhesive regions,³¹ or within a three-dimensional hydrogel.³²

DEP has also been used to study the morphology and mechanics of suspended cells. In early studies, high frequency electric fields were used to stretch erythrocytes and determine shear elastic modulus and membrane viscosity.^{33, 34} Changes in T cell membrane architecture, either during stimulation or apoptosis, were measured by DEP.^{35, 36} High DEP forces stretched cell membranes to the point of failure, leading to either cell fission in sea urchin eggs or plasma membrane leakage in erythrocytes.^{37, 38} In recent years, the mechanical properties of suspended cells, including Chinese hamster ovarian cells, U937 human promonocytes, cancerous (MCF-7) and noncancerous (MCF-10A) breast epithelial cells, and cervical cancer cells (SiHa and ME180) were measured using DEP devices.^39–41 More recently, electro-deformation was used to show variation in the mechanical properties of four different cell types in suspension, which depended on cortical actin thickness.⁴² DEP was also used to measure the effect of drug treatment on leukemia NB4 cell elastic modulus.⁴³ While some of these experiments were performed on adherent cells shortly after they were detached from a substrate, to our knowledge DEP forces have not been used to study global mechanical properties of cells attached to a substrate at the time of measurement.

Both quadrupole and octopole devices have been successfully used to manipulate particles through DEP.¹⁹ For example, an extruded quadrupole electrode array was used to trap and hold single beads and cells subjected to fluid flow.^{25, 44} Octopole cages, formed by two sets of quadrupole electrodes, trapped individual pollen grains, beads, and hybridoma cells.⁴⁵ While equal voltage applied to opposing electrodes can be used to trap particles in the DEP device center, unequal applied voltage can be used to manipulate particles within the device. In one application, quadrupole electrodes with equal applied voltages were first used to trap a single cell, and then unequal voltages were applied to move the single cells into a DEP microwell.⁴⁶ Applying unequal voltages to octopole electrodes enabled beads to be manipulated into single groups of varied shapes or multiple groups within the device.⁴⁵ While unequal voltages have been used in limited applications to manipulate beads and cells, unequal voltages have not been used to study attached cell mechanics.

The objective of this study was to create a DEP device that could measure the stiffness of a single cell attached to a controlled substrate via relative electro-deformation. An extruded gold quadrupole device was microfabricated and electroplated, then inverted over a cell attached to a micropatterned hydrogel substrate. Directed pushing DEP forces of increasing magnitude were applied by applying different voltages to opposing electrodes, and subsequent cell centroid displacement was quantified by image analysis. Our data show that this DEP device provides an inexpensive, non-contact tool to measure global attached cell stiffness via electro-deformation. The inverted configuration and unequal voltages are novel compared to previous cell-manipulating DEP devices.

Materials and methods

Electric and force field modelling

A quadrupole electrode configuration was simulated using the three-dimensional AC/DC module of COMSOL Multiphysics software (version 4.3a). The quadrupole electrode device was designed as four opposing electrodes (40 μm diameter) with a central space (60 μm diameter) large enough to enable the electrodes to be lowered over a single attached cell. Since the device is symmetrical, half was modelled in COMSOL. Voltages and ground were set as shown in Figure 1a. A range of voltages was simulated using the root mean square voltage corresponding to each peak-to-peak voltage (V_pp) in Table 1.⁴⁷ Frequency was set to 1 MHz. Distributed impedance boundary conditions were set along the sides and top of the modelled electrode, and the bottom surface was set as an electrically insulating boundary. The DEP force was defined as ²⁰:

$$F_{\mathit{DEP}}=2\pi {\epsilon }_m{r}^{3}Re[CM(\omega )]\nabla {\mid E\mid }^2$$ (1)

where ε_m, r, ω, and E are relative medium permittivity, cell radius, angular frequency, and electric field strength, respectively. For a spherical particle, the Clausius-Mossotti factor (CM) was defined as:

$$CM=\frac{{\epsilon }_p^{\ast }-{\epsilon }_m^{\ast }}{{\epsilon }_p^{\ast }+2{\epsilon }_m^{\ast }}$$ (2)

where ε_p* and ε_m* are the complex permittivities of the particle and the medium, respectively. The complex permittivity of the medium was calculated as:

$${\epsilon }_m^{\ast }={\epsilon }_m+\frac{{\sigma }_m}{j\omega }$$ (3)

where is σ_m the conductivity of the medium ³⁰. The complex permittivity of the cell was determined using the spherical shell model:

$${\epsilon }_p^{\ast }={\epsilon }_s^{\ast }\left[\frac{{\left(\frac{r}{r-d}\right)}^3+2\left(\frac{{\epsilon }_{\mathit{int}}^{\ast }-{\epsilon }_s^{\ast }}{{\epsilon }_{\mathit{int}}^{\ast }+2{\epsilon }_s^{\ast }}\right)}{{\left(\frac{r}{r-d}\right)}^3-\left(\frac{{\epsilon }_{\mathit{int}}^{\ast }-{\epsilon }_s^{\ast }}{{\epsilon }_{\mathit{int}}^{\ast }+2{\epsilon }_s^{\ast }}\right)}\right]$$ (4)

where ε_s* and ε_int* are the complex permittivities of the cell shell (membrane) and cell interior, respectively, and d is the width of the cell membrane. As derived in ⁴⁸, this equation simplifies to:

$${\epsilon }_p^{\ast }=r\left[C_{\mathit{spec}}-\frac{j{G}_{\mathit{spec}}}{\omega }\right]$$ (5)

where C _spec and G _spec indicate the specific membrane capacitance and the specific membrane conductance, respectively. The dielectric properties of mammalian cells, specifically HL-60 cells, have been published in the literature.^{41, 49} In our model, specific membrane capacitance and specific membrane conductance were set to 0.016 F/m² and 2200 S/m², respectively.⁵⁰ Cell culture medium conductivity (σ_m) and permittivity (ε_m) were defined as 1.5 S/m and 80, respectively, based on our measurements and the literature.⁵¹ The cell conductivity and permittivity were defined as 0.75 S/m and 75.⁴⁴ Cell radius was set as 10 μm.

Fig. 1.

COMSOL simulation predicted negative DEP, with a directed DEP pushing force in the center of an inverted quadrupole device when different voltages were applied to Electrodes 1 and 2. (a) Half of an inverted quadrupole DEP device was modelled, taking advantage of the device symmetry. Voltage at Electrode 1 was held constant while voltage at Electrode 2 was varied. The asterisk (*) indicates the approximate cell position in relation to the electrodes, 10 μm beneath the inverted device. (b) Predicted electric field strength. Arrows indicate the relative magnitude and direction of the electric field in the central xz-plane between Electrodes 1 and 2. (c) Predicted cell polarization within the applied electric field. The approximate cell border is indicated in the device center, (d) Predicted DEP force. The DEP force magnitude in the x-direction predicted for a cell at each location in the device central xz-plane. Positive values indicate net force toward the right, while negative values indicate net force toward the left at each location. Cell radius was 10 μm. (d) DEP force in the x-direction along the x axis was evaluated at increasing distances below the device.

Table 1.

Applied DEP force for varied voltages across opposing electrodes. The voltage at Electrode 2 was lowered by applying increasing levels of resistance (shown in the first column) between the power source and the electrode.

Resistance (Ω)	Voltage at Electrode 1	Voltage at Electrode 2	Predicted DEP force (nN)
100	21	20.7	0.02
200	21	20.5	0.03
300	21	20.3	0.04
400	21	19.8	0.07
1000	21	17.8	0.17
2000	21	13.6	0.35
3000	21	10.7	0.44
4000	21	8.3	0.51

Device design and fabrication

The quadrupole DEP device was manufactured using standard microfabrication techniques. Square glass substrates (2″ × 2″) were selected for the device base to allow for cell observation using an inverted microscope. The device photomask was designed in AutoCAD and printed at high resolution onto a transparent film (JD Photo-Tools). A 4″ × 4″ chrome plate pre-coated with negative SU-8 photo resist (Telic) was exposed to ultraviolet light through the transparency mask, baked, and developed to produce the patterned chrome mask. The chrome mask was then used to create the electrodes by sequential deposition of titanium and gold, where titanium was used to enhance gold adhesion to glass.^{30, 44} NR9-1000PY (Futurrex) was chosen since the photoresist undercut was conducive to the lift-off process. Titanium and gold were then sequentially deposited by physical vapor deposition in a thermal evaporator (Thermionics VE 90) at 20 nm and 200 nm thickness, respectively. Photoresist and excess metal were removed using RDG developer.

Electrical leads were created by soldering copper wire strands onto electrode connector pads. The soldered pads were strengthened and sealed from the cell medium by curing a thin layer of polydimethlysiloxane (PDMS, Sylgard, Dow Corning) over the connector pads. Electrode thickness was then increased by gold electroplating. The device was submerged in non-cyanide gold electroplating solution (Technigold 25E RTU, Technic) maintained between 60–70°C with constant stirring. Gold was deposited by pulse plating (500 mVpp) with a 10% duty cycle using a function generator (BK Precision 4010) at a deposition rate of approximately 0.013 μm/minute. Final electrode thickness following electroplating was confirmed by optical profilometry (Zygo NewView 6000).

Polyacrylamide gel micropatterning

PDMS stamps for microcontact printing were fabricated using standard soft photolithography methods. Transparency film photomasks with a 25 μm diameter circle array were printed (JD Photo-Tools). SU-8 2025 (Microchem) was spin-coated on a glass substrate, soft baked, exposed for 3 minutes using a UV lamp (NuArc 26-1K Mercury Exposure System), post-exposure baked, developed in SU-8 developer and then hard baked. To ease PDMS release, the SU-8 mold was coated with (tridecafluoro-1,1,2,2-tetrahydro octyl)-1-trichlorosilane (UCT) by vapor deposition. PDMS was mixed using a 10:1 ratio of base to curing agent, degassed, poured onto the mold and cured at 70°C for at least three hours.

Micropatterned polyacrylamide (PA) gels were made by indirect microcontact printing.⁵² A top coverslip was patterned with fibronectin using a PDMS stamp. Stamps were incubated with a mixture of biotinylated tetramethylrhodamine-bovine serum albumin (TMR-BSA, 5 μg/mL, Invitrogen) for pattern visualization and biotinylated human plasma fibronectin (50 μg/mL, Gibco) for 40 minutes. The protein solution was then removed from the stamps, which were dried and immediately placed onto plasma-cleaned glass coverslips (5 mm for DEP device samples or 12 mm for AFM samples) for 5 minutes. A streptavidin polyacrylamide (PA) gel solution was created by adding 0.1 mg/mL streptavidin-acrylamide (Invitrogen) to a PA solution of 10% acrylamide (BioRad), 0.3% bis-acrylamide (BioRad), 1% ammonium persulfate (BioRad), and 0.3% TEMED (BioRad). A bottom coverslip was activated by sequential incubation in 0.1 M NaOH (Sigma Aldrich), (3-aminopropyl)trimethoxysilane (Sigma Aldrich), and 0.5% glutaradehyde (Polysciences) for 30 minutes. The streptavidin-PA solution was added to the bottom coverslip, after which the micropatterned top coverslip was quickly inverted over the polymerizing gel. Polymerization was completed in a 37°C, 5% CO₂ incubator for 15 minutes, after which the top coverslip was removed. The micropatterned PA gel was then rinsed thoroughly and stored in phosphate buffered saline (PBS) at 4°C for a maximum of 2 days prior to use.

Cell culture

Primary porcine aortic endothelial cells (PAEC) were isolated by the collagenase dispersion method and cultured in low glucose Dulbecco’s Modified Eagle’s medium (DMEM) (Corning) supplemented with 5% fetal bovine serum (Hyclone), 1% glutamine, and 1% penicillin-streptomycin (Invitrogen). Cells were used up to passage 8. Mammary epithelial cells (MCF-10A) and transformed mammary epithelial cells (MCF-10A NeuT) were a gift from Dr. Adrian Shieh. Cells were maintained in DMEM/F12 (Corning) supplemented with 5% horse serum (Atlanta Biologicals), 20 ng/mL epidermal growth factor (Peprotech), 500 ng/mL hydrocortisone (Sigma), 10 ng/mL cholera toxin (Enzo Lifesciences), 10 μg/mL insulin (Sigma), and 1% penicillin-streptomycin (Invitrogen). Cells were released from tissue culture dishes with trypsin, seeded onto micropatterned PA gels, and allowed to attach for 30 minutes. Unattached cells were then removed by replacing the medium. Cells were incubated on the micropatterned PA gels for 16–24 hours prior to mechanical testing. For both AFM and DEP device testing, cells were transferred into serum-free CO₂-independent medium (Invitrogen). In some samples, the actin cytoskeleton was disrupted with 200 nM cytochalasin D (Sigma Aldrich) for 15 minutes at room temperature in serum-free CO₂-independent medium.

Immunofluorescence

Endothelial cells attached to a micropatterned PA gel were fixed using 4% paraformaldehyde (Sigma Aldrich), permeabilized using 0.1% Triton X-100 (EMD Millipore) and rinsed using PBS. To prevent non-specific binding, samples were blocked with 1% bovine serum albumin (BSA) in PBS. Cells were labelled for vinculin using a primary mouse anti-vinculin antibody (1:100, Sigma), followed by an AlexaFluor 488 anti-mouse secondary antibody (1:100, Invitrogen). Actin and nuclei were labelled using rhodamine phalloidin (16.5 nM, Invitrogen) and bisbenzimide (0.2 μg/mL, Invitrogen), respectively. Images were taken using an Olympus Fluoview 1000 confocal microscope.

Atomic force microscopy

Atomic force microscopy (AFM, Veeco Bioscope) was used to validate DEP device cell relative stiffness measurements (elastic modulus). A silicon nitride cantilever with 1 μm spherical tip (196 μm long, 23 μm wide, 600 nm thick, spring constant 0.06 N/m, Novascan) was used to indent each measured cell at three distinct locations. Relative stiffness was estimated by fitting the first 200 nm of the indentation curves to the Hertz model as previously described.⁵³ Three measurements per cell were averaged and defined as the cell stiffness.

Sequential application of DEP “pushing” and “centering” forces

First, a micropatterned single cell array on a PA gel was mounted on an inverted Olympus IX81 fluorescent microscope. The extruded quadrupole DEP device was attached to a micromanipulator (Eppendorf), and the electrodes were lowered over a single cell. The cell was positioned in the device center with the electrodes approximately 10 μm above the cell.

A directed DEP “pushing” force, created by applying unequal voltages to two opposing electrodes, was used to deform the cell in a specified direction. Electrical potential was applied using a function generator (BK Precision 3011B) set to 21 V_pp, 1 MHz; the other two electrodes were grounded. The function generator positive lead was diverted into two separate lines, each going to a resistance decade box before connecting to diagonally opposing device electrodes. With no extra resistance applied, opposing electrodes received the same voltage. As resistance between the function generator and one of the electrodes was increased using the resistance decade box, unequal voltages were applied to opposing electrodes which created the directed DEP pushing force. Thus, increasing resistance to one electrode controlled pushing force magnitude and direction. A DEP “centering” force, created by applying equal voltage to two opposing electrodes, was used to return the cell to its original position in the device center.

The directed DEP pushing force was applied to a cell for 15 seconds. The decade box resistance was then returned to zero for the next 15 seconds to apply the DEP centering force. For each test sequence, 15 seconds of directed pushing force was followed by 15 seconds of centering force.

Image processing

During test sequences, brightfield images were taken every 0.5 seconds. Image processing was completed using Matlab’s Image Processing Toolbox (Mathworks). Image sequences were cropped to include the area immediately surrounding the cell. Each cropped frame in the image sequence was then binarized to isolate the cell body as a single connected component. The threshold for binarization was determined by Otsu’s method using the “greythresh” function.⁵⁴ If needed, a multiplier was used to adjust the threshold for a sequence to prevent any debris in the vicinity from being counted as part of the cell. The two-dimensional cell centroid was determined for each frame using Matlab’s “regionprops” function. Cell centroid displacement was quantified by measuring the distance between the cell centroid and the lower left corner of the cropped image. The lower left corner of the cropped image was chosen because directed DEP pushing force was consistently applied towards the upper right corner of the image; thus, when the cell deformed, the distance between the cell centroid and the lower left corner of the image increased. All measurements were then normalized relative to the initial cell position at the beginning of the test sequence.

Statistical analysis

Statistical analyses were conducted using Matlab’s statistics toolbox. Data are shown as mean ± standard deviation. Experiments were performed in duplicate, and the number of cells per experiment is indicated in the figure caption. For data shown in Figure 5c and 6c, Student’s t-test was used to compare two groups. Comparison of multiple groups in Figures 5b and 6b was completed using two-way ANOVA with a Tukey-Kramer post-test. Statistical significance is indicated by # p < 0.05, * p < 0.01, or ** p < 0.001.

Results and discussion

DEP device modelling

The extruded quadrupole DEP device was modelled in three dimensions in COMSOL to simulate DEP forces (Figure 1a). The voltage set in Table 1 was evaluated, corresponding to the increasing resistance applied between the power source and Electrode 2. The simulation predicted that a cell in the device center would experience negative DEP, toward the lower voltage Electrode 2, as is expected for cells in highly conductive media.⁵⁵ As an example, the simulation results for 2000Ω are given in Figure 1b-e. The electric field strength was highest near the higher voltage Electrode 1 (Figure 1b). Cell polarization in the non-uniform electric field is shown in Figure 1c, in which the semi-circular boundary in the device center indicates the approximate location of the cell boundary. Figure 1d indicates the predicted DEP force in the x-direction that would be experienced by a cell centered at each location within the device. DEP force in the x-direction is toward the right near Electrode 1 and toward the left near Electrode 2 (Figure 1d). For a cell positioned in the device center (indicated by the asterisk), DEP force is directed toward Electrode 2 because the higher voltage at Electrode 1 moves the location of zero force towards Electrode 2.We refer to this force at the device center with unequal applied voltages as the directed DEP “pushing” force.

Directed DEP pushing force was plotted as a function of position along the x axis connecting Electrodes 1 and 2 at increasing distances from the device surface. Figure 1e shows the predicted DEP forces for 2000Ω, when 21 V_pp (7.42 V_rms) was applied to Electrode 1 and 13.6 V_pp (4.81 V_rms) was applied to Electrode 2. As expected, the DEP force magnitude was greatest near the high voltage Electrode 1 and closest to the device surface (2 μm). However at the device center where the cell is positioned (x=0), directed DEP pushing force remained approximately 0.35 nN in the x-direction from 2–10 μm below the device surface, at this applied voltage. The model therefore predicts that small deviations in the device z position would have little effect on the DEP force experienced by the cell.

Table 1 summarizes the predicted directed DEP pushing forces experienced by the cell in the device center, 10 μm below the device surface. Predicted directed DEP pushing forces ranged from 0.02 to 0.51 nN. These forces are similar to those generated in other single cell mechanics devices. For example, single suspended fibroblast deformation was achieved using 0.2 to 0.5 nN in an optical stretching device.⁴ Red blood cells were stretched with optical tweezers by applying forces of up to 0.056 nN to opposite sides of each cell.⁹ Micropipette aspiration applies between 10 pN and 1 nN depending on the cell type.⁵⁶ Magnetic tweezers can also apply forces within the same range, from 10 pN to more than 1 nN.⁵⁷ Atomic force microscopy using large 25 μm spherical tips has also been used to evaluate whole cell stiffness by applying nN-magnitude forces.⁵⁸

DEP device microfabrication and experimental set-up

The fabricated DEP device consisted of a quadrupole electrode configuration on a single glass microscope slide (Figure 2a). The electrodes increased in width as they extended outward from the quadrupole at a 45° angle, finally attaching to a 2 mm square electrode pad for connecting wires to function generators. The final electroplated device had well-defined rounded electrode tips of 1.1 μm height, as measured by optical profilometry (Figure 2b). The DEP device was connected to a function generator using 2 resistance decade boxes so that voltage could be modulated across opposing electrodes while maintaining the electrodes in phase (Figure 2c). The device was then attached to a micromanipulator arm, which was assembled on a microscope stage. The micromanipulator was used to center and lower the DEP device over a single micropatterned cell, using the microscope for optical guidance (Figure 2d).

Fig. 2.

Microfabricated DEP device and experimental set-up, including initial testing with a polystyrene bead. (a) Microfabricated DEP device showing one set of quadrupole electrodes with wire connection pads (each demarcation on the ruler represents 1/16″), (b) optical profilometer image of the ~1.1 μm height extruded gold electrodes. (c) Electrical connections diagram. Opposing electrodes were connected to a single function generator using two resistance decade boxes to modulate applied voltage without altering phase. (d) Device schematic, with gold electrodes on glass substrate inverted over single cell array on PA gel. (e) Three-dimensional representation of the device inverted over a single suspended polystyrene bead. (f) A single suspended bead was first trapped (left) then pushed (right). Scale bar is 25 μm.

The inverted DEP device was first tested by placing the device over a single 10 μm polystyrene bead in suspension (Figure 2e). When 10 V_pp was applied to Electrodes 1 and 2, the bead was trapped in the device center where DEP force was zero (Figure 2f, left). When the resistance to Electrode 2 (upper right) was increased to 400 kΩ, the voltage to that electrode was decreased to 1.2 V_pp and the bead moved toward the lower voltage electrode (Figure 2f, right). Initially, the bead was pushed out of the device center by the directed DEP pushing force. The bead then became trapped in the zero DEP force location, which in this voltage configuration was displaced 14 μm towards the low voltage electrode.

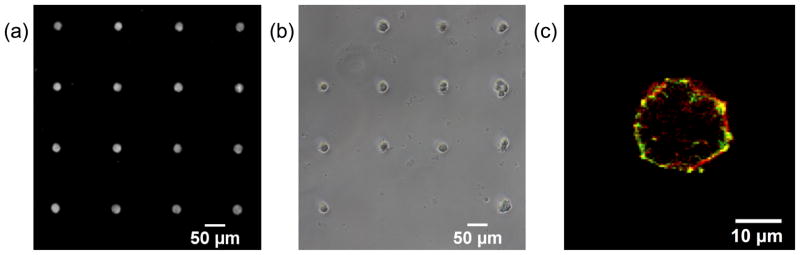
Single cells of defined spread area were created using micropatterned PA gels (Figure 3). An indirect micropatterning technique produced an array of 25 μm diameter fibronectin circles, with TMR-BSA added to the fibronectin to enable fluorescent imaging (Figure 3a). The average spot diameter on a typical patterned PA gel was 24.9 ± 3.1 μm. Cells were seeded on the micropatterned PA gels and incubated overnight, resulting in single cell arrays (Figure 3b). Cell adhesion was confirmed by labelling cells for vinculin and actin and imaging samples by confocal microscopy at the cell base. Punctate vinculin colocalized with peripheral actin fibers suggested that single cells on micropatterned PA gels formed focal adhesions by 16 hours (Figure 3c).

Fig 3.

Porcine aortic endothelial cells were micropatterned onto 25 μm fibronectin circles to control spread area while allowing cell attachment. (a) Fibronectin (with TMR-BSA to enable fluorescent imaging) circles were patterned onto a PA gel by an indirect micropatterning technique. (b) Cells adhered and spread on fibronectin circles following overnight incubation. Only circles with a single attached cell were used for analysis. (c) A single cell attached to the micropatterned PA gel exhibited punctate focal adhesions (vinculin antibody, green) colocalized with peripheral actin fibers (rhodamine phalloidin, red).

DEP device validation

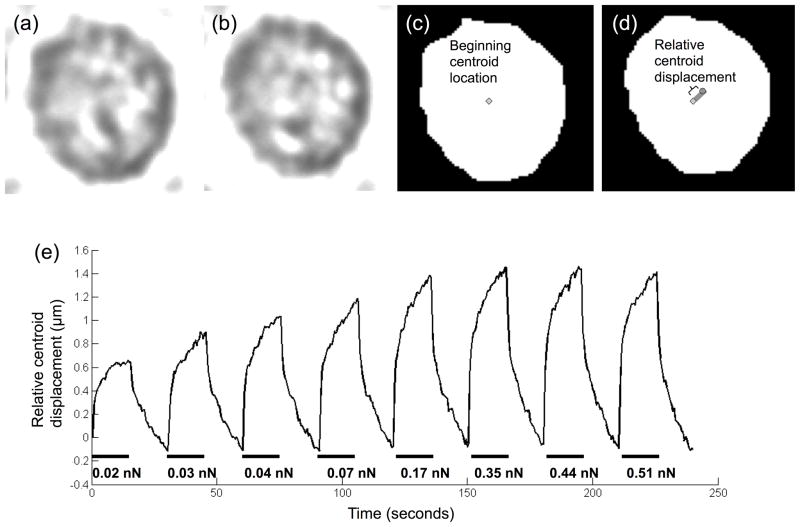
A single adhered porcine aortic endothelial cell was sequentially deformed using increasing DEP pushing forces (increasing ΔV across opposing electrodes). The extent of cell centroid displacement was quantified by image analysis. Figures 4a and 4b show representative pre-processed cell images before and during the directed pushing force, respectively. The corresponding binarized images, which were used to find the cell centroid displacement at each time frame, are shown in Figure 4c and 4d.

Fig 4.

Cell centroid displacement increased with applied directed DEP pushing force, up to a maximum displacement level. Increasing directed DEP pushing force (different voltage on opposing electrodes) were applied to deform a single cell for 15 seconds each, with 15 seconds of restoring centering force (same voltage on opposing electrodes) applied between pushes. Brightfield images were taken every 0.5 seconds. Representative brightfield images are shown before (a) and during (b) the pushing force application. Images were converted to binary in Matlab (c and d). The cell centroid was defined in each image, represented by a diamond in (c) and a circle in (d). Cell centroid displacement was quantified as the change in distance between the cell centroid and a defined point outside the cell. (e) Directed DEP pushing forces of increasing magnitude were sequentially applied to a single micropatterned porcine aortic endothelial cell.

When voltage to Electrode 2 was lowered to apply a pushing force, the cell centroid moved toward the low voltage electrode (in the predicted DEP force direction). When the same voltage was restored to both electrodes to apply a centering force, the cell centroid recovered towards its original position. As the voltage was lowered further on Electrode 2, and therefore the applied directed DEP pushing force increased, cell centroid movement also increased. For 0.3 ΔV (predicted force 0.02 nN), the cell centroid moved 0.64 μm, whereas at 12.7 ΔV (predicted force 0.51 nN), the cell centroid moved 1.5 μm (Figure 4e). Cell centroid movement plateaued at 7.4 ΔV (predicted force 0.35 nN). From these data, 0.5, 1.2, and 7.4 ΔV (predicted forces 0.03, 0.07, and 0.35 nN) were selected for future experiments since they were within the linear range (Figure 4e).

Porcine aortic endothelial cells were treated with cytochalasin D to determine if the DEP device could measure stiffness via electro-deformation changes among cells through a change in cell centroid displacement. Cytochalasin D inhibits actin polymerization and is known to decrease cell stiffness.⁵⁹ Untreated endothelial cells showed average centroid displacements of 0.47, 0.62, and 0.88 μm with predicted DEP forces of 0.03, 0.07 and 0.35 nN (Figure 5b). Centroid displacement increased 58 – 64% in cytochalasin treated cells. Interestingly, cell centroid restoration to the center position was slower in cytochalasin treated cells (Figure 5a). This observation supports the role of the actin cytoskeleton in cell elasticity, while the cytosol exhibits viscous properties.⁶⁰ In fact, treatment of adherent endothelial cells treated with 0.1 μg/mL (~2 μM) cytochalasin D has been shown to decrease stiffness while having little effect on cell viscosity by magnetic twisting cytometry.⁶¹ AFM confirmed that cytochalasin treatment decreased micropatterned cell stiffness. The calculated cell elastic modulus in cytochalasin treated cells was 6-fold lower than untreated cells (0.3 vs. 1.8 kPa, Figure 5c).

Fig 5.

When the actin cytoskeleton was disrupted with cytochalasin D, cell centroid displacement in response to applied DEP force increased as compared to untreated cells. (a) Porcine aortic endothelial cells were incubated on micropatterned PA gels overnight, and then treated with 200 nM cytochalasin D for 15 minutes at room temperature. Single untreated and treated cells were subjected to six sequential pushing forces (three DEP force magnitudes, two pushes per force magnitude) for 15 seconds each. Representative data for one untreated and one treated cell. (b) Cell centroid displacement was quantified at each predicted DEP force. Data are mean ± standard deviation (n = 3 cells per condition, 2 tests per cell at each force level). #p < 0.05, *p < 0.01, **p < 0.001 compared to untreated values at each force level, unless brackets indicate otherwise (Tukey’s test). (c) Identically treated cells were indented by AFM using a silicon nitride cantilever with 1 μm spherical tip to measure cell elastic modulus. Cell modulus was estimated by fitting the first 200 nm of the indentation curve to the Hertz model (* p < 0.01, n = 6 cells per condition).

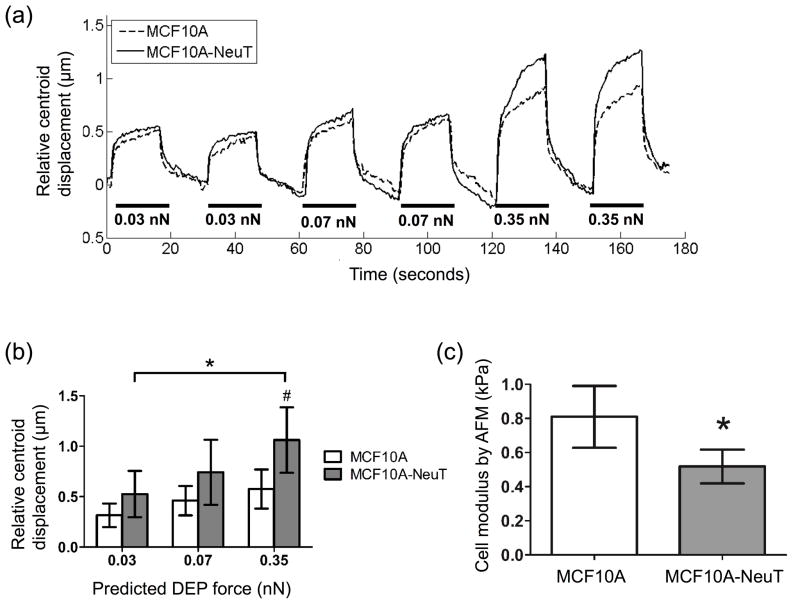
Finally, the DEP device was used to measure changes in cell centroid displacement between normal (MCF10A) and cancerous (MCF10A-NeuT) breast epithelial cells. MCF10A-NeuT cell centroid displacement was 61–84% higher than MCF10A cells, with larger differences at higher applied DEP forces (Figure 6a, b), suggesting that MCF10A-NeuT cells have lower stiffness. Similarly, the elastic modulus for transformed MCF10A-NeuT cells determined by atomic force microscopy was 1.6-fold less than normal MCF10A cells (Figure 6C, 0.52 vs. 0.81 kPa, respectively). These data confirm that the DEP device can detect cell stiffness changes via electro-deformation differences by measuring changes in cell centroid displacement among different cell types. The DEP device could detect electro-deformation differences greater than around 40%. A power analysis was performed to determine the number of cells required to detect an electro-deformation change of 20% and thereby characterize device sensitivity. Based on the variability observed for untreated PAECs, the number of cells tested would need to be increased from three to seven to detect a 20% electro-deformation difference at a power of 0.9 and significance level of 0.05.

Fig 6.

MCF10A-NeuT cells showed greater cell centroid displacement than MCF10A cells by DEP, as well as lower cell modulus by AFM. (a) Micropatterned MCF10A and MCF10A-NeuT cells were incubated on micropatterned PA gels overnight. Single cells of each type were subjected to six sequential pushing forces (three DEP force magnitudes, two pushes per force magnitude) for 15 seconds each. Representative data for one MCF10A and MCF10A-NeuT cell. (b) Cell centroid displacement was quantified at each predicted DEP force. Data are mean ± standard deviation (n = 3 cells per condition, 2 tests per cell at each force level). #p < 0.05, *p < 0.01, comparing cell types at each force level, unless brackets indicate otherwise (Tukey’s test). (c) A second set of cells were indented by AFM using a silicon nitride cantilever with 1 μm spherical tip to measure cell elastic modulus. Cell modulus was estimated by fitting the first 200 nm of the indentation curve to the Hertz model (* p < 0.01, n = 7 cells per cell type).

To validate that the device could detect changes in attached cell mechanical properties, DEP cell electro-deformation was compared to AFM cell stiffness measurements. These methods apply forces in different ways: the DEP device applies shear force to the entire cell while AFM applies local compression. However, if we approximate a cell shear modulus from our DEP device data as the applied shear stress (from DEP force at the cell edge divided by cell cross-sectional area) divided by the resultant shear strain (from centroid displacement divided by cell diameter), we get shear moduli ranging from 0.01–0.20 kPa. The shear moduli approximated using DEP device results are an order of magnitude lower than the Young’s moduli determined by AFM (0.2–2 kPa), even after accounting for the approximate 3-fold difference between shear modulus and Young’s modulus. However, cell moduli determined by magnetic twisting cytometry, which creates a more similar applied force to our DEP device, generally range from 0.01–0.25 kPa.^{62, 63} While DEP device and AFM data cannot be directly linked since these two instruments do not deform the cell in the same way, they both show changes in attached cell mechanical properties with cytochalasin treatment or between different cell types.

Applications

These data demonstrate for the first time how an inverted DEP device can determine changes in the stiffness of a material placed underneath the device, in our case a single attached cell, by measuring relative centroid displacement via electro-deformation. The inverted device configuration is an innovative feature that significantly increases device capabilities. First, it enables analysis of attached cells while not necessitating that the cells be attached to the device surface. Thus, within a single experiment the same DEP device can analyze multiple cells in series simply by changing the device position using the micromanipulator arm. The DEP device could even be lowered over a cell attached to a tissue, for example an extravasating monocyte, to measure its stiffness.

Furthermore, the DEP device can analyze cells attached to substrates with different parameters, such as stiffness or ECM coating. The micropatterned substrate eliminates the confounding variables of cell shape and spread area, which change with substrate stiffness and ECM ligand density for nearly all attached cell types.^64–72 The PA gel further prevents non-specific protein adhesion, so the effect of a particular ECM ligand can be studied. The ability to study cell stiffness on varied substrates is important, as published studies support the role of substrate stiffness and ECM protein in a variety of attached cell functions related to cytoskeletal structure.^73–75 For example, cell stiffness increases with substrate stiffening in multiple differentiated cell types.^76–78 Cell-type specific functions of circulating progenitor cells and myoblasts are also modulated by substrate stiffness.^{79, 80} In addition, substrate stiffness regulates human mesenchymal stem cell (hMSC) differentiation through RhoA/ROCK signalling.^{81, 82} This DEP device can measure cell stiffness changes in real time either as the substrate stiffness is changed, for example using dynamic photodegradable hydrogel substrates, or as cells respond to a biochemical stimulus on varied substrates.⁸³

The DEP device can also be used to detect changes in cell functions, which often relate to cell stiffness. Stiffer endothelial cells produce less nitric oxide, which is critical to vasodilation.^{1, 2} Endothelial and epithelial stiffening creates stiffer substrates for migrating immune cells, which has been proposed as a determinant of leukocyte transendothelial migration.^{3, 84–88} In cancer, decreased cell stiffness correlates with increased metastatic potential; increased cell deformability may contribute to enhanced migration through the small pores of the extracellular matrix.⁸⁹ Combined experimental (optical tweezers) and computational (actin cytoskeletal model) approaches were further used to show how the mechanical properties of normal and leukemia cells varied depending on cell type, drug treatment, and drug resistance. These data support the importance of the actin cytoskeleton in determining cancer cell stiffness and function.^{90, 91} In stem cells, cell stiffness is emerging as a “mechanical biomarker” of hMSC differentiation and adipose-derived stem cell (ASC) differentiation potential.^{92, 93} Cell stiffness also constitutes part of a panel of biophysical characteristics that indicate hMSC pluripotency.⁹⁴ Thus, this device could be used in the lab or at the bedside to measure cell functions ranging from inflammation to metastasis to differentiation.

The DEP device design also enables studying cells within a flow chamber, since the device does not need to physically contact the cells. Thus cell electro-deformation could be measured as a biochemical stimulus is applied to the cell, increasing our understanding of the kinetics of cell mechanics. In addition, cell response to fluid flow could be studied in relevant cell types such as endothelial cells. Applied fluid shear stress induces endothelial cell stiffening, as previously measured by AFM and micropipette aspiration.^95–98 Endothelial cell stiffening through actin fiber formation decreases nitric oxide production and can thereby impacts cell function.^{1, 2, 99, 100} While custom set-ups have been created that enable simultaneous AFM cell stiffness measurements and sample perfusion, this device provides a simpler, more accessible solution.^{2, 101} By inverting the DEP device, we can take advantage of the forces induced beneath inverted DEP electrodes and thus create even greater functionality and flexibility for lab-on-a-chip microdevices.

Beyond pushing single attached cells to analyze relative cell stiffness via electro-deformation, an inverted quadrupole DEP device could be used to trap and pattern cells or other particles in suspension. Recently dielectophoretic tweezers or single electrodes attached to micromanipulators have been used to capture and release cells in suspension.^{102, 103} This inverted DEP device could be used in a similar matter to trap, move, and release cells at desired locations through device movement using a micromanipulator. Furthermore, by varying the voltages applied to opposing electrodes, a suspended, trapped cell could be shifted out of the device center (e.g., towards the lower voltage electrode) to increase device resolution. As has been suggested for DEP tweezers, this inverted quadrupole DEP device could enhance the establishment of stably transfected cell lines through quickly and selectively isolating individual fluorescent protein expressing cells.¹⁰⁴ In addition, such cell manipulation capability could be useful in sorting cells into microwell arrays, ensuring single cell occupancy and enabling single cell assays.¹⁰⁵

While the DEP device has significant advantages over other techniques, the current configuration has limited throughput. The inverted DEP device can only measure one cell at a time due to the limiting step of detecting and quantifying cell centroid displacement by microscopy and image analysis, respectively. In this study, three cells were analysed per condition due to the time required to reposition the device over each cell of interest. Device throughput could be increased by creating a microarray of inverted quadrupole electrodes and using a non-optical system to detect cell electro-deformation. For example, cell position can be detected via electrical impedance.¹⁰⁶ Recently, impedance sensors were integrated into DEP cell trapping device to replace optical determination of trapping efficiency.¹⁰⁷ With single attached cell centroid displacement quantified through an impedance sensor, device throughput would only be limited by the practical size of the electrode microarray.

While using the DEP device to measure cell electro-deformation on substrates of varied stiffness has significant advantages, soft substrates may also deform under the DEP force. In our experiments, we did observe some PA gel translation with applied DEP force. However, gel translation was always significantly less than cell translation and never affected the electro-deformation difference between varied samples. We also used a 29 kPa gel, which is stiffer than the cell, to minimize gel deformation as compared to cell deformation. If softer substrates were to be used in a future study, gel deformation should be considered in the analysis.

The current device can only measure relative changes in cell electro-deformation due to limitations in quantifying the applied force. The device relies on simulation to estimate the force applied to each cell. Force estimation in the simulation depends on published mammalian cell dielectric properties that are not expected to change under the conditions tested. Should the device be used to study non-mammalian cells, or any other materials, dielectric properties would need to be adjusted in the model. In the future, the device could be calibrated to better determine the applied force. For example, hydrogel microspheres of known size, conductivity, permittivity, and stiffness could be covalently linked to a substrate, subjected to electro-deformation, and thus serve as a calibration tool.¹⁰⁸

Conclusions

In this paper, we present the simulation, microfabrication, and testing of a novel inverted DEP device that can be used to measure relative cell stiffness via electro-deformation. Unlike previous DEP devices, this device can measure changes in attached cell stiffness since it is positioned over the cell. Thus cell stiffness can be compared for varied cell types, and changes in cell stiffness can be compared with different biochemical or biomechanical stimuli. This device could also be used to manipulate cells or other micron-sized objects. This novel application of DEP expands the mechanics toolbox, specifically enabling non-contact stiffness comparisons of cells or other small material samples.