Abstract
First-principles calculations have been carried out to study the structural, electric, and magnetic properties of Ni3TeO6-type A2FeMoO6 compounds (A = Sc, Lu). Their electric and magnetic properties behave like room-temperature ferrielectric and ferrimagnetic insulators where polarization comes from the un-cancelled antiparallel dipoles of (A(1), Fe3+) and (A(2), Mo3+) ion groups, and magnetization from un-cancelled antiparallel moments of Fe3+
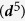 and Mo3+
and Mo3+
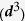 ions. The net polarization increases with A’s ionic radius and is 7.1 and 8.7 μCcm−2 for Sc2FeMoO6 and Lu2FeMoO6, respectively. The net magnetic moment is 2 μB per formula unit. The magnetic transition temperature is estimated well above room-temperature due to the strong antiferromagnetic superexchange coupling among Fe3+ and Mo3+ spins. The estimated paraelectric to ferrielectric transition temperature is also well above room-temperature. Moreover, strong magnetoelectric coupling is also anticipated because the magnetic ions are involved both in polarization and magnetization. The fully relaxed Ni3TeO6-type A2FeMoO6 structures are free from soft-phonon modes and correspond to stable structures. As a result, Ni3TeO6-type A2FeMoO6 compounds are possible candidates for room-temperature multiferroics with large magnetization and polarization.
ions. The net polarization increases with A’s ionic radius and is 7.1 and 8.7 μCcm−2 for Sc2FeMoO6 and Lu2FeMoO6, respectively. The net magnetic moment is 2 μB per formula unit. The magnetic transition temperature is estimated well above room-temperature due to the strong antiferromagnetic superexchange coupling among Fe3+ and Mo3+ spins. The estimated paraelectric to ferrielectric transition temperature is also well above room-temperature. Moreover, strong magnetoelectric coupling is also anticipated because the magnetic ions are involved both in polarization and magnetization. The fully relaxed Ni3TeO6-type A2FeMoO6 structures are free from soft-phonon modes and correspond to stable structures. As a result, Ni3TeO6-type A2FeMoO6 compounds are possible candidates for room-temperature multiferroics with large magnetization and polarization.
Single phase polar materials with ferromagnetic (ferrimagnetic) properties have drawn much attention1,2,3 recently due to their applications in developing spintronic devices for nonvolatile memories and in achieving electric-field control of magnetization in realistic information storage4,5,6,7. Therefore, searching for multiferroic materials becomes an important research direction in material physics. Up to now, various mechanisms have been proposed to explain the electric polarization in magnetic compounds. Among others, the off-center displacement of lone-pairs 6s electrons8,9, the chiral spin-density-wave driven polarization10,11,12, the charge ordering13,14,15, and the strain-induced polarization are mechanisms being discussed most16,17,18,19. Although great progresses have been made in developing single phase multiferroic materials, many important issues remain unsolved. For example, compounds with both large magnetization and polarization are still rare; the ferro(ferri)magnetic transition temperatures are usually below room temperature and restricted their applications; even if the requirements of large magnetization and polarization are fulfilled, enhancing magnetoelectric coupling is still a big challenge.
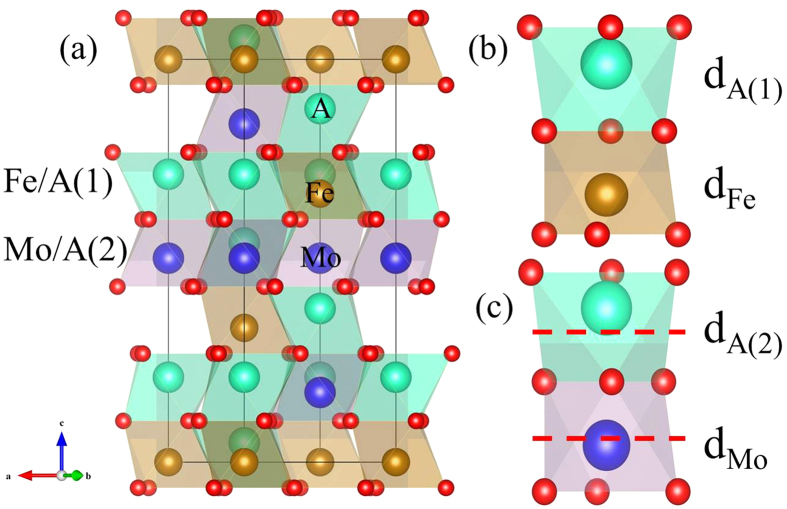
In order to meet these crucial requirements, searching for the multiferroics which have magnetic ions contributing simultaneously to electric polarization can be a good choice. Thus in this report, we have analyzed the structural, electric, and magnetic properties of two corundum-derived oxides A2FeMoO6 (A = Sc, Lu). All of them are found to be multiferroic materials and have the same polar structure as Ni3TeO63, ZnTiO320, and FeTiO321. The general crystal structure displayed in Fig. 1(a) is described by a chemical formula 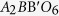
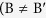 for Ni3TeO6 type;
for Ni3TeO6 type; 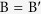 for LiNbO3 or FeTiO3 type). The structural advantage is its ability to incorporate different magnetic transition-metal ions on all cation sites for realizing magnetoelectric coupling. The common feature of the structures is the small A-site cation in six oxygen coordination, such as Sc3+ (0.69 Å) and Lu3+ (0.745 Å), in comparison with the large alkaline earth cation in twelve oxygen coordination, such as Ca2+ (1.34 Å), Sr2+ (1.44 Å), and Ba2+ (1.61 Å). The distortion of the structure can be estimated by a similar tolerance factor defined for a perovskite compound,
for LiNbO3 or FeTiO3 type). The structural advantage is its ability to incorporate different magnetic transition-metal ions on all cation sites for realizing magnetoelectric coupling. The common feature of the structures is the small A-site cation in six oxygen coordination, such as Sc3+ (0.69 Å) and Lu3+ (0.745 Å), in comparison with the large alkaline earth cation in twelve oxygen coordination, such as Ca2+ (1.34 Å), Sr2+ (1.44 Å), and Ba2+ (1.61 Å). The distortion of the structure can be estimated by a similar tolerance factor defined for a perovskite compound, 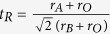 , where
, where 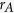 ,
, 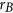 , and
, and 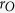 are the ionic radii of A-site ion, B-site ion (in
are the ionic radii of A-site ion, B-site ion (in 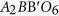 ,
,  is an averaged radius of B- and B′-site ions)22, and O ions, respectively. As found in most systems, for
is an averaged radius of B- and B′-site ions)22, and O ions, respectively. As found in most systems, for 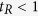 , the cubic perovskite changes its symmetry by the BO6 octahedral rotation or tilting or Jahn-Teller distortion. Good examples are the Ni3TeO6 (Ni2NiTeO6) compound with nonhysteretic colossal magnetoelectricity3, ScFeO3 (Fe takes both the B- and B′-sites)23,24 and Mn2FeMO6 (M = Nb, Ta, Mo, and W)25,26,27 compounds with polar structure and antiferromagnetic or ferrimagnetic structure. Due to the strong antiferromagnetic superexchange coupling between nearest neighbors Fe3+
, the cubic perovskite changes its symmetry by the BO6 octahedral rotation or tilting or Jahn-Teller distortion. Good examples are the Ni3TeO6 (Ni2NiTeO6) compound with nonhysteretic colossal magnetoelectricity3, ScFeO3 (Fe takes both the B- and B′-sites)23,24 and Mn2FeMO6 (M = Nb, Ta, Mo, and W)25,26,27 compounds with polar structure and antiferromagnetic or ferrimagnetic structure. Due to the strong antiferromagnetic superexchange coupling between nearest neighbors Fe3+
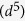 in ScFeO3, the Néel temperature is well above room-temperature (545 K). To improve the net magnetization of ScFeO3, constructing ferrimagnetic structure by replacing one of the B-site Fe3+ by a dn (n < 5) ion is a possible way, which was done in the synthesized Bi2FeCrO6 (Cr3+: d3 compound28,29).
in ScFeO3, the Néel temperature is well above room-temperature (545 K). To improve the net magnetization of ScFeO3, constructing ferrimagnetic structure by replacing one of the B-site Fe3+ by a dn (n < 5) ion is a possible way, which was done in the synthesized Bi2FeCrO6 (Cr3+: d3 compound28,29).
Figure 1. The crystal structure of Ni3TeO6-type A2FeMoO6 with R3 space group.
(a) Structure viewed along 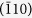 direction. (b) face-sharing A(1)O6/FeO6 octahedral pair. (c) face-sharing A(2)O6/MoO6 octahedral pairs. The dashed lines refer to the neutral plane of oxygen octahedron along c-axis and d denotes the displacement for various transition metal ions. The spheres for different ions are also indicated.
direction. (b) face-sharing A(1)O6/FeO6 octahedral pair. (c) face-sharing A(2)O6/MoO6 octahedral pairs. The dashed lines refer to the neutral plane of oxygen octahedron along c-axis and d denotes the displacement for various transition metal ions. The spheres for different ions are also indicated.
Results
To accomplish this goal, we have carried out comprehensive first-principles study on Ni3TeO6–type A2FeMoO6 compounds (A = Sc, Lu) where one of the B-site Fe3+ is replaced by Mo3+
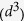 . The structural, electric, and magnetic properties of Ni3TeO6–type A2FeMoO6 have been systematically analyzed as a function of A-site cation radius. We found that the ferrimagnetic state is indeed the ground-state with net magnetic moment of 2 μB/f.u. forming between the antiparallel Fe3+ (5 μB) and Mo3+ (3 μB) ions. The polarization increases with A’s ionic radius and is 7.1 and 8.7 μCcm−2 for Sc2FeMoO6 and Lu2FeMoO6, respectively. Moreover, strong magnetoelectric coupling is achieved since the electric polarization comes partly from the same magnetic ions. The robust antiferromagnetic coupling is sustained, ensuring a Néel temperature well above room temperature. The structural analyses suggest that Ni3TeO6–type A2FeMoO6 compounds are free from soft-phonon modes and correspond to stable structures.
. The structural, electric, and magnetic properties of Ni3TeO6–type A2FeMoO6 have been systematically analyzed as a function of A-site cation radius. We found that the ferrimagnetic state is indeed the ground-state with net magnetic moment of 2 μB/f.u. forming between the antiparallel Fe3+ (5 μB) and Mo3+ (3 μB) ions. The polarization increases with A’s ionic radius and is 7.1 and 8.7 μCcm−2 for Sc2FeMoO6 and Lu2FeMoO6, respectively. Moreover, strong magnetoelectric coupling is achieved since the electric polarization comes partly from the same magnetic ions. The robust antiferromagnetic coupling is sustained, ensuring a Néel temperature well above room temperature. The structural analyses suggest that Ni3TeO6–type A2FeMoO6 compounds are free from soft-phonon modes and correspond to stable structures.
Discussion
Let us start with the Ni3TeO6-type structures of A2FeMoO6 compounds as shown in Fig. 1(a). The structures are obtained after the full relaxation of lattice parameters and atomic positions with effective on-site Coulomb repulsion 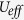 = 4.0, 1.0, and 5.0 eV for Fe-3d, Mo-4d and Lu-5f electrons, respectively. The structures can be constructed in two steps: (1) (A(1)O6, FeO6) (Fig. 1(b)) and (A(2)O6, MoO6) (Fig. 1(c)) octahedral pairs form face-sharing structures along c-axis; (2) the two face-sharing structures then form zigzag chains by edge-sharing A(1)O6/FeO6 and A(2)O6/MoO6 octahedral pairs in the ab-plane. Due to the strong electrostatic repulsion among the neighboring cations in the centers of the face-shared octahedral pairs, large antiferro-polar displacements take place along c-axis for (A(1), Fe), and (A(2), Mo) ion pairs (see Fig. 1(b,c)). Thus, antiparallel electric moments are formed for each face-sharing A(1)O6/FeO6 and A(2)O6/MoO6 octahedral pairs, and ferrielectric polarization is generated along c-axis. The fully optimized structural parameters and atomic positions of ferrimagnetic Ni3TeO6-type A2FeMoO6 are listed in Table 1 together with those of antiferromagnetic ScFeO3 as a reference. In Table 1, the lattice parameters, atomic positions, and bond angles are highly accurate. A relative error less than 1% is achieved between our calculated data and the available experimental data23,24. The spontaneous polarization was computed using the Berry phase method30. The total polarization of ScFeO3 is 2.0 and 1.6 μCcm−2 for theoretically optimized and the experimentally measured structures, respectively. These results are close to the value 1.4 μCcm−2 observed experimentally23. The computed polarization is 7.1 and 8.7 μCcm−2 for ferrimagnetic Sc2FeMoO6 and Lu2FeMoO6, respectively. The polarization increases with A’s ionic radius. Larger radius, probably, strengthens the repulsive force between neighboring ions in the centers of face-sharing A(1)O6/FeO6 and A(2)O6/MoO6 octahedral pairs. Our study shows that the ferrimagnetic structures not only greatly improved the magnetization property, but also significantly enhanced the polarization of A2FeMoO6 regarding the reference compound ScFeO3. The incompatibility between ferroelectricity and ferromagnetism gets nicely reconciled in the ferrielectric and ferrimagnetic A2FeMoO631. In addition, strong magnetoelectric coupling between the polarization and magnetization is also intrinsically embedded in the structures.
= 4.0, 1.0, and 5.0 eV for Fe-3d, Mo-4d and Lu-5f electrons, respectively. The structures can be constructed in two steps: (1) (A(1)O6, FeO6) (Fig. 1(b)) and (A(2)O6, MoO6) (Fig. 1(c)) octahedral pairs form face-sharing structures along c-axis; (2) the two face-sharing structures then form zigzag chains by edge-sharing A(1)O6/FeO6 and A(2)O6/MoO6 octahedral pairs in the ab-plane. Due to the strong electrostatic repulsion among the neighboring cations in the centers of the face-shared octahedral pairs, large antiferro-polar displacements take place along c-axis for (A(1), Fe), and (A(2), Mo) ion pairs (see Fig. 1(b,c)). Thus, antiparallel electric moments are formed for each face-sharing A(1)O6/FeO6 and A(2)O6/MoO6 octahedral pairs, and ferrielectric polarization is generated along c-axis. The fully optimized structural parameters and atomic positions of ferrimagnetic Ni3TeO6-type A2FeMoO6 are listed in Table 1 together with those of antiferromagnetic ScFeO3 as a reference. In Table 1, the lattice parameters, atomic positions, and bond angles are highly accurate. A relative error less than 1% is achieved between our calculated data and the available experimental data23,24. The spontaneous polarization was computed using the Berry phase method30. The total polarization of ScFeO3 is 2.0 and 1.6 μCcm−2 for theoretically optimized and the experimentally measured structures, respectively. These results are close to the value 1.4 μCcm−2 observed experimentally23. The computed polarization is 7.1 and 8.7 μCcm−2 for ferrimagnetic Sc2FeMoO6 and Lu2FeMoO6, respectively. The polarization increases with A’s ionic radius. Larger radius, probably, strengthens the repulsive force between neighboring ions in the centers of face-sharing A(1)O6/FeO6 and A(2)O6/MoO6 octahedral pairs. Our study shows that the ferrimagnetic structures not only greatly improved the magnetization property, but also significantly enhanced the polarization of A2FeMoO6 regarding the reference compound ScFeO3. The incompatibility between ferroelectricity and ferromagnetism gets nicely reconciled in the ferrielectric and ferrimagnetic A2FeMoO631. In addition, strong magnetoelectric coupling between the polarization and magnetization is also intrinsically embedded in the structures.
Table 1. The structural parameters and atomic positions for the ferrimagnetic state of Ni3TeO6-type A2FeMoO6 (space group: R3) and the antiferromagnetic state of ScFeO3 (space group: R3c) calculated with
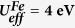 ,
,
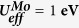 , and
, and
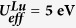 .
.
| Sc2FeMoO6(Theory) | Lu2FeMoO6(Theory) | ScFeO3(Theory) | ScFeO3 (Experiment) | |
|---|---|---|---|---|
| a/Å | 5.053 | 5.391 | 5.219 | 5.197 |
| c/Å | 13.511 | 14.330 | 14.027 | 13.936 |
| zA1 | 0.1258 | 0.1220 | 0.1216 | 0.1228 |
| zA2 | 0.2887 | 0.2853 | 0.2882 | 0.2895 |
| zFe | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| zMo | 0.1595 | 0.1604 | 0.1664 | 0.1667 |
| xO1 | 0.3217 | 0.3073 | 0.3169 | 0.3172 |
| yO1 | 0.3562 | 0.3534 | 0.3581 | 0.3555 |
| zO1 | 0.0629 | 0.0638 | 0.0627 | 0.0622 |
| xO2 | 0.3692 | 0.3805 | 0.3745 | 0.3716 |
| yO2 | 0.0288 | 0.0262 | 0.0247 | 0.0221 |
| zO2 | 0.2301 | 0.2309 | 0.2293 | 0.2288 |
| Fe-O-Mo/° | 135.17 | 137.82 | 135.71 | 135.13 |
| dA1/Å | 0.348 | 0.411 | 0.315 | 0.336 |
| dA2/Å | 0.294 | 0.357 | 0.315 | 0.336 |
| dFe/Å | 0.276 | 0.277 | 0.261 | 0.314 |
| dMo/Å | 0.183 | 0.187 | 0.261 | 0.314 |
The last column lists the available experimental data. a and c are the lattice constants in the hexagonal setting, whereas, x, y, and z are the reduced internal atomic positions of A(1) (0, 0, z), A(2) (0, 0, z), Fe (0, 0, z), Mo (0, 0, z), and O (x, y, z). Fe-O-Mo is the Fe-O-Mo angle. dA(1), dA(2), dFe, and dMo refer to the atomic displacements with respect to neutral planes in Fig. 1(b,c).
Having investigated the structural and electric properties of Ni3TeO6-type A2FeMoO6 compounds, we are now in position to discuss their electronic and magnetic properties. For Ni3TeO6-type A2FeMoO6, the orbital configurations of 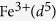 and
and 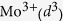 are similar to those of La2FeCrO6 according to previous study32. The schematic diagram for the relevant atomic energy levels is illustrated in Fig. 2. The spin-up and spin-down d-orbitals are separated by spin exchange energy ΔS, d(eg) and d(t2g) orbitals are separated by a crystal-field-splitting energy 10Dq. The nature of the superexchange coupling between
are similar to those of La2FeCrO6 according to previous study32. The schematic diagram for the relevant atomic energy levels is illustrated in Fig. 2. The spin-up and spin-down d-orbitals are separated by spin exchange energy ΔS, d(eg) and d(t2g) orbitals are separated by a crystal-field-splitting energy 10Dq. The nature of the superexchange coupling between 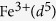 and
and 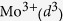 ions is quite complicated because of the orbital degeneracy and two possible hybridization schemes. pdσ hopping favors ferromagnetic superexchange coupling while pdπ hopping favors antiferromagnetic superexchange coupling. The subtle competition between the two determines the magnetic ordering of ground state. Our first-principles calculations show that the ferrimagnetically ordered state is consistently lower in energy than that of the ferromagnetically ordered state in Ni3TeO6-type A2FeMoO6. Thus the polar state with ferrimagnetic ordering can be the favored ground state.
ions is quite complicated because of the orbital degeneracy and two possible hybridization schemes. pdσ hopping favors ferromagnetic superexchange coupling while pdπ hopping favors antiferromagnetic superexchange coupling. The subtle competition between the two determines the magnetic ordering of ground state. Our first-principles calculations show that the ferrimagnetically ordered state is consistently lower in energy than that of the ferromagnetically ordered state in Ni3TeO6-type A2FeMoO6. Thus the polar state with ferrimagnetic ordering can be the favored ground state.
Figure 2. Schematic diagram for the atomic energy levels of Fe-d, Mo-d and O-p orbitals.
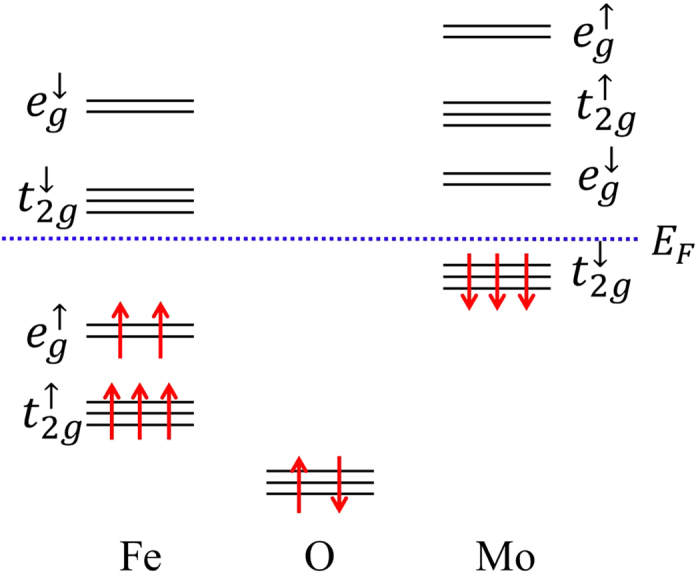
The small arrows denote the spin states while the red large arrows refer to the occupied electron spins. The horizontal dashed line refers to Fermi energy.
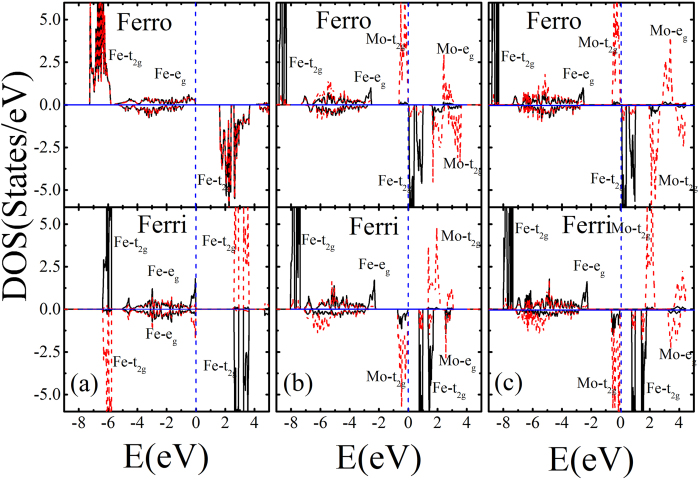
To have an overall picture of the electronic and magnetic properties of A2FeMoO6, the spin-resolved partial densities of states (DOS) are plotted in Fig. 3 for both ferromagnetically and ferrimagnetically ordered structures. To distinguish between the two types of transition-metal ions associated with A(1)O6/FeO6 and A(2)O6/MoO6 octahedral pairs, the DOSs of Fe and Mo are represented by solid (black) and dashed (red) lines, respectively. As shown in Fig. 3, the positions of extended  and localized
and localized 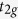 orbitals are in accord with the atomic level scheme in Fig. 2. In agreement with previous studies23,24, the ScFeO3 demonstrates large band gap for both the ferromagnetic
orbitals are in accord with the atomic level scheme in Fig. 2. In agreement with previous studies23,24, the ScFeO3 demonstrates large band gap for both the ferromagnetic 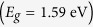 and antiferromagnetic
and antiferromagnetic 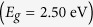 states. For A2FeMoO6 (A = Sc, Lu), the ferromagnetic state shows a vanishingly small band gap while sizeable band gap is present for the ferrimagnetic state. The band gap of ferrimagnetic state is 0.71 and 0.73 eV for Sc2FeMoO6 and Lu2FeMoO6, respectively. The overall electronic spectra are quite similar for the two different compounds regarding the partial densities of states for Fe and Mo d-orbitals. The
states. For A2FeMoO6 (A = Sc, Lu), the ferromagnetic state shows a vanishingly small band gap while sizeable band gap is present for the ferrimagnetic state. The band gap of ferrimagnetic state is 0.71 and 0.73 eV for Sc2FeMoO6 and Lu2FeMoO6, respectively. The overall electronic spectra are quite similar for the two different compounds regarding the partial densities of states for Fe and Mo d-orbitals. The 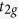 orbitals of Fe and Mo are further reduced to
orbitals of Fe and Mo are further reduced to 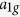 and
and 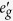 manifolds because of the trigonal crystal-field-splitting energy. Due to the strong hybridization with O 2p states, the eg bands are rather extended. The spin exchange energy is about 2.90 eV for Fe and 1.32 eV for Mo. The total magnetic moment per formula unit is 2 μB in the ferrimagnetically ordered state. For ferromagnetically ordered state, the total magnetic moment per formula unit is 8 μB. The projected magnetic moments on Fe and Mo are 4.06, 2.15 μB and 4.06, 2.20 μB for Sc2FeMoO6 and Lu2FeMoO6, respectively. These values are consistent with the high-spin configuration of Fe3+ and Mo3+. The projected magnetic moment on Fe in ScFeO3 is 4.15 μB, slightly larger than the value 3.71 μB measured experimentally.
manifolds because of the trigonal crystal-field-splitting energy. Due to the strong hybridization with O 2p states, the eg bands are rather extended. The spin exchange energy is about 2.90 eV for Fe and 1.32 eV for Mo. The total magnetic moment per formula unit is 2 μB in the ferrimagnetically ordered state. For ferromagnetically ordered state, the total magnetic moment per formula unit is 8 μB. The projected magnetic moments on Fe and Mo are 4.06, 2.15 μB and 4.06, 2.20 μB for Sc2FeMoO6 and Lu2FeMoO6, respectively. These values are consistent with the high-spin configuration of Fe3+ and Mo3+. The projected magnetic moment on Fe in ScFeO3 is 4.15 μB, slightly larger than the value 3.71 μB measured experimentally.
Figure 3. The spin and atom (Fe, Mo) projected densities of states of ScFeO3 and A2FeMoO6 with 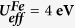 ,
, 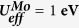 , and
, and 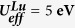 .
.
The DOSs for ferromagnetic and ferrimagnetic states are presented as an upper-half and lower-half of each sub-figure. The spin-up and spin-down DOSs are plotted upwards and downwards respectively. The solid and dashed lines refer to the two different sites of transition metal ions (Fe, Fe for ScFeO3; Fe, Mo for Sc2FeMoO6 and Lu2FeMoO6). The orbital characters are indicated in the spectra. (a) ScFeO3. (b) Sc2FeMoO6. (c) Lu2FeMoO6. The dashed vertical line is the Fermi energy which is set to 0.
The electronic structural patterns can be understood from the level scheme of Fig. 2 together with hybridization processes. In particular, the valence and conduction bands near the Fermi energy is mainly resulted from the 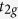 orbitals of Fe and Mo. For the ferromagnetically ordered state, the up-spin
orbitals of Fe and Mo. For the ferromagnetically ordered state, the up-spin 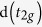 orbitals form the Fe and Mo dominated valence bands while the down-spin
orbitals form the Fe and Mo dominated valence bands while the down-spin 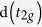 orbitals form the Fe and Mo dominated conduction bands. The hybridization with oxygen orbitals pushes the Mo dominated
orbitals form the Fe and Mo dominated conduction bands. The hybridization with oxygen orbitals pushes the Mo dominated 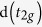 valence band edge upwards and pulls the Fe dominated
valence band edge upwards and pulls the Fe dominated 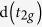 conduction band edge downwards. This makes the ferromagnetic band-gap extremely small. For the ferrimagnetically ordered state, the band structure in the vicinity of the Fermi energy is mainly determined by down-spin
conduction band edge downwards. This makes the ferromagnetic band-gap extremely small. For the ferrimagnetically ordered state, the band structure in the vicinity of the Fermi energy is mainly determined by down-spin 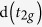 orbitals of Fe and Mo across the Fermi energy. The difference in energy level essentially determines the band-gap between Fe dominated conduction band and Mo dominated valence band. This also explains why the overall features of DOSs for A2FeMoO6 (A = Sc, Lu) look rather similar. In addition, above discussion suggests that ferrimagnetically ordered state mainly involves hybridizing down-spin
orbitals of Fe and Mo across the Fermi energy. The difference in energy level essentially determines the band-gap between Fe dominated conduction band and Mo dominated valence band. This also explains why the overall features of DOSs for A2FeMoO6 (A = Sc, Lu) look rather similar. In addition, above discussion suggests that ferrimagnetically ordered state mainly involves hybridizing down-spin 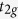 orbitals of Fe and Mo across the Fermi energy. The resulting band splitting, thus, can significantly lower the binding energy. This is also the basic mechanism dictating the ferrimagnetically ordered ground state. The similar scenario also takes place in the double perovskite La2FeCrO6 as proved by the GGA electronic structure calculation32.
orbitals of Fe and Mo across the Fermi energy. The resulting band splitting, thus, can significantly lower the binding energy. This is also the basic mechanism dictating the ferrimagnetically ordered ground state. The similar scenario also takes place in the double perovskite La2FeCrO6 as proved by the GGA electronic structure calculation32.
It is known that the choice of the Coulomb interaction 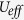 has a notable impact on the electronic structure, and thus affects the relative stability of different magnetically ordered states. To investigate such effect, we have also performed GGA + U simulations for other
has a notable impact on the electronic structure, and thus affects the relative stability of different magnetically ordered states. To investigate such effect, we have also performed GGA + U simulations for other  and
and 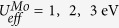 while keeping
while keeping 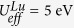 . The choice of parameter values are based on the fact that the Coulomb interaction is typically weaker for spatially more extended 4d electrons than for more localized 3d electrons. The computed energy difference
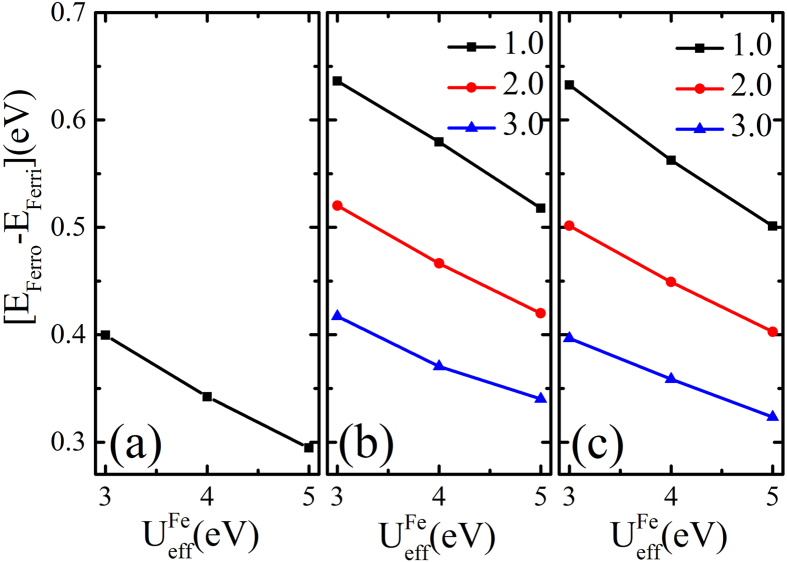
. The choice of parameter values are based on the fact that the Coulomb interaction is typically weaker for spatially more extended 4d electrons than for more localized 3d electrons. The computed energy difference 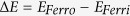 between the ferromagnetically and ferrimagnetically ordered states are shown in Fig. 4 as functions of
between the ferromagnetically and ferrimagnetically ordered states are shown in Fig. 4 as functions of 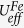 and
and 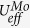 . It has been found that ΔE is a monotonic deceasing function with increasing
. It has been found that ΔE is a monotonic deceasing function with increasing 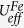 or
or 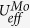 , which varies from 0.65 to 0.3 eV, but the ferrimagnetically ordered state is consistently lower than that of the ferromagnetically ordered state. The monotonic decreasing behavior of energy difference originates from the superexchange interaction,
, which varies from 0.65 to 0.3 eV, but the ferrimagnetically ordered state is consistently lower than that of the ferromagnetically ordered state. The monotonic decreasing behavior of energy difference originates from the superexchange interaction, 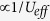 , for ferrimagnetic state since the ferromagnetic state is less sensitive to
, for ferrimagnetic state since the ferromagnetic state is less sensitive to 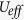 . The energy difference decreases slightly as A’s ionic radius increases, because large A’s ionic radius reduces the effective hopping integral between Fe and Mo ions and so is that of the antiferromagnetic superexchange coupling. However, large A’s ionic radius expands the oxygen octahedra and favors the polar distortion. To estimate the magnetic transition temperature for A2FeMoO6 and ScFeO3, we adopt the single parameter Heisenberg spin model
. The energy difference decreases slightly as A’s ionic radius increases, because large A’s ionic radius reduces the effective hopping integral between Fe and Mo ions and so is that of the antiferromagnetic superexchange coupling. However, large A’s ionic radius expands the oxygen octahedra and favors the polar distortion. To estimate the magnetic transition temperature for A2FeMoO6 and ScFeO3, we adopt the single parameter Heisenberg spin model 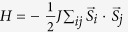 by assuming the same exchange parameter for all the nearest-neighbor couplings. Using S = 5/2 for Fe3+ and S = 3/2 for Mo3+, one can determine the exchange coupling J by matching the energy differences obtained from the Heisenberg model and first-principles calculations. Then magnetic transition temperature
by assuming the same exchange parameter for all the nearest-neighbor couplings. Using S = 5/2 for Fe3+ and S = 3/2 for Mo3+, one can determine the exchange coupling J by matching the energy differences obtained from the Heisenberg model and first-principles calculations. Then magnetic transition temperature 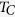 is related to the energy difference ΔE by
is related to the energy difference ΔE by 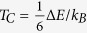 . For
. For 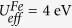 ,
, 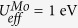 , and
, and 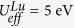 which best reproduced the experimentally observed lattice parameters, TC of ScFeO3 is 661 K. The mean-field estimated
which best reproduced the experimentally observed lattice parameters, TC of ScFeO3 is 661 K. The mean-field estimated 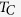 is higher than the measured value 545K26 since the spin fluctuation effect is not accounted for. Similar estimates yield
is higher than the measured value 545K26 since the spin fluctuation effect is not accounted for. Similar estimates yield 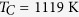 for Sc2FeMoO6 and
for Sc2FeMoO6 and 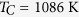 for Lu2FeMoO6, all above room-temperature. More practical estimate of
for Lu2FeMoO6, all above room-temperature. More practical estimate of 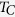 can be made by scaling the energy difference with respect to that of ScFeO3, which gives
can be made by scaling the energy difference with respect to that of ScFeO3, which gives 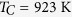 for Sc2FeMoO6 and
for Sc2FeMoO6 and 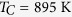 for Lu2FeMoO6. This is consistent with Lu’s results on AlScFeMoO6 (space group: R3)33. Therefore, we have shown that the A2FeMoO6 not only have large magnetization and polarization, but also possess room-temperature magnetic transition temperature
for Lu2FeMoO6. This is consistent with Lu’s results on AlScFeMoO6 (space group: R3)33. Therefore, we have shown that the A2FeMoO6 not only have large magnetization and polarization, but also possess room-temperature magnetic transition temperature 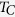 . These encouraging properties make A2FeMoO6 a promising candidate for future multistate memory applications.
. These encouraging properties make A2FeMoO6 a promising candidate for future multistate memory applications.
Figure 4. The energy difference ΔE per unit cell between ferromagnetic and ferrimagnetic states as functions of 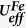 .
.
The lines denoted by solid squares, circles, and triangles refer to 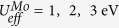 .
. 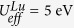 . The unit cell contains two formula units for ScFeO3 and one formula unit for A2FeMoO6. (a) ScFeO3. (b) Sc2FeMoO6. (c) Lu2FeMoO6.
. The unit cell contains two formula units for ScFeO3 and one formula unit for A2FeMoO6. (a) ScFeO3. (b) Sc2FeMoO6. (c) Lu2FeMoO6.
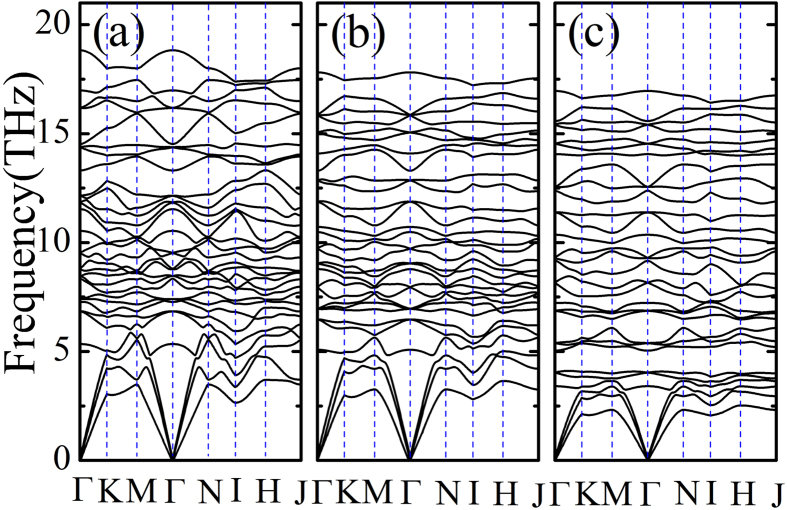
It remains to be verified that the structure of ferrielectric and ferrimagnetic Ni3TeO6-type A2FeMoO6 (A = Sc, Lu) insulators are robust structures and can be prepared by the usual laboratory method. Therefore, the phonon dispersion spectra are calculated using the frozen-phonon method. The calculated phonon dispersions are plotted in Fig. 5 for both the reference compound ScFeO3 and Ni3TeO6-type A2FeMoO6 (A = Sc, Lu). The overall dispersion curves are quite similar for the three compounds except that the phonon frequency scales with the inverse square root of transition metal ion mass. It is clear that the soft-phonon modes are absent in the entire Brillouin Zone, which indicates that the Ni3TeO6-type A2FeMoO6 structure does correspond to stable structures.
Figure 5. Phonon dispersion of Ni3TeO6-type A2FeMoO6 with 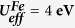 ,
, 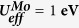 , and
, and 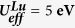 .
.
(a) ScFeO3. (b) Sc2FeMoO6. (c) Lu2FeMoO6. The wave vector takes a path along the high symmetrical points of the Brillouin Zone: Γ (0, 0, 0) → K (1/3, 1/3, 0) → M (1/2, 0, 0) → Γ (0, 0, 0) → N (0, 0, 1/2) → I (1/3, 1/3, 1/2) → H (1/2, 0, 1/2) → J (0, 0, 1/2).
To further check the stability of Ni3TeO6-type A2FeMoO6 (A = Sc, Lu) (R3 structure) against other common structures, we have also considered 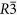 , P21/c, and C2 structures. After the full structural relaxation with respect to the atomic positions and lattice constants, the initial trial C2 structure may converge either to C2/m, C2, C2/c, or Imma structure depending on the material composition. The calculated energies of different structures are summarized in Table 2. Only those of ferrimagnetic (antiferromagnetic) states are shown because they always have lower energy than those of ferromagnetic state. One finds that Ni3TeO6-type A2FeMoO6 (R3 structure) consistently has lower energy than other structures. However, for large ionic radius of Y atom, the stable structure of Y2FeMoO6 takes P21/c space group rather than the R3 space group. This suggests that Ni3TeO6-type A2FeMoO6 is stable with respect to P21/c structure only for small ionic radius of A atoms (see Supplementary Information Table S4). The paraelectric to ferrielectric transition temperature can also be estimated from the energy difference between the structurally connected polar (R3) and nonpolar
, P21/c, and C2 structures. After the full structural relaxation with respect to the atomic positions and lattice constants, the initial trial C2 structure may converge either to C2/m, C2, C2/c, or Imma structure depending on the material composition. The calculated energies of different structures are summarized in Table 2. Only those of ferrimagnetic (antiferromagnetic) states are shown because they always have lower energy than those of ferromagnetic state. One finds that Ni3TeO6-type A2FeMoO6 (R3 structure) consistently has lower energy than other structures. However, for large ionic radius of Y atom, the stable structure of Y2FeMoO6 takes P21/c space group rather than the R3 space group. This suggests that Ni3TeO6-type A2FeMoO6 is stable with respect to P21/c structure only for small ionic radius of A atoms (see Supplementary Information Table S4). The paraelectric to ferrielectric transition temperature can also be estimated from the energy difference between the structurally connected polar (R3) and nonpolar 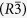 structures. As shown in Table 2, the energy difference is 1.378 eV/2f.u. for ScFeO3, 0.408 and 0.542 eV/f.u. for Sc2FeMoO6 and Lu2FeMoO6, respectively. Scaling the energy with that of ScFeO3 and considering its polar structure being stable above 1400 K1,2 yield a paraelectric-ferrielectric transition temperature
structures. As shown in Table 2, the energy difference is 1.378 eV/2f.u. for ScFeO3, 0.408 and 0.542 eV/f.u. for Sc2FeMoO6 and Lu2FeMoO6, respectively. Scaling the energy with that of ScFeO3 and considering its polar structure being stable above 1400 K1,2 yield a paraelectric-ferrielectric transition temperature 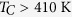 for Sc2FeMoO6 and
for Sc2FeMoO6 and 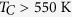 for Lu2FeMoO6. Both of them are well above room-temperature.
for Lu2FeMoO6. Both of them are well above room-temperature.
Table 2. The relative stabilities of various phases of A2FeMoO6 calculated with
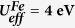 ,
,
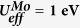 , and
, and
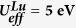 .
.
| R3 | 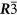 |
P21/c | C2 | |
|---|---|---|---|---|
| Sc2FeMoO6 | 0 | 0.408 | 0.519 | 0.676 (C2/m) |
| Lu2FeMoO6 | 0 | 0.524 | 0.004 | 0.606 (C2) |
| ScFeO3 | 0 (R3c) | 1.378 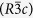
|
0.281 (Pnma) | 1.024 (Imma) |
The energy is given in unit of eV with R3 phase taken as the reference structure.
In the view that ScFeO3, Mn2FeMO6 (M = Nb, Ta, Mo, and W), and Ni3TeO6, all with smaller A-site ions, can be synthesized under the high temperature and high pressure environment34, we expect that the Ni3TeO6-type A2FeMoO6 can also be synthesized under similar conditions. If so, one expects that other room-temperature ferrielectric and ferrimagnetic insulators may also be realized in the corundum-derived transition metal oxides. Through incorporating different magnetic transition metal ions on the cation sites, one can easily tune the superexchange interaction and polar distortion, so that the polarization, magnetization, magnetoelectric coupling as well as critical temperature can be optimized for potential applications.
In summary, comprehensive first-principles calculations have been carried out for the structural, electronic, and magnetic properties of Ni3TeO6-type A2FeMoO6 (A = Sc, Lu). All of them show the ferrielectric and ferrimagnetic insulator properties with large magnetization (2μB/f.u.) and polarization (>7 μCcm−2). The strong antiferromagnetic superexchange interaction between Fe and Mo yields a mean-field critical temperature above room-temperature. Strong intrinsic magnetoelectric coupling is also ensured because the magnetic ions are involved in both the magnetic moment formation and polarization. The Ni3TeO6-type Sc2FeMoO6 and Lu2FeMoO6 are also proved to be stable structures because they have lower energies than other possible structures. Thus, one expects that these materials and other related ones can be synthesized in experiments.
Methods
The study has been carried out using the generalized gradient approximation + U (GGA + U) method35 with Perdew-Becke-Erzenhof exchange-correlation functional36 as implemented in the Vienna ab Initio simulation package (VASP)37,38. To account for the population imbalance on localized transition metal d- and rare earth f-orbitals, the effective on-site Coulomb interactions 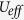 = 4.0, 1.0, and 5.0 eV are adopted for Fe-3d, Mo-4d and Lu-5f electrons, respectively39. The projector augmented wave (PAW) potentials40 explicitly include three valence electrons for Sc (3d14s2), 11 for Y (4s24p64d15s2), and 25 for Lu (5s25p64f145d16s2), 14 for Fe (3p63d64s2), 12 for Mo (4p64d55s1), and six for O (2s22p4) atoms. The same result is also obtained for the PAW potential excluding f electrons for Lu. The wave function is expanded in a plane wave basis with an energy cutoff of 600 eV. The crystal unit cell includes two formula units for ScFeO3, and one formula unit for Sc2FeMoO6 and Lu2FeMoO6. A 7 × 7 × 7 Γ-centered k-points sampling is used for reciprocal space integrations. Each self-consistent electronic calculation is converged to 10−6 eV and the tolerance force is set to 0.005 eV/Å for ionic relaxation. The convergence checks with respect to the k-points sampling have been made for the total energy, densities of states as well as the phonon dispersion curves (see Supplementary Information Figures S1-S3).
= 4.0, 1.0, and 5.0 eV are adopted for Fe-3d, Mo-4d and Lu-5f electrons, respectively39. The projector augmented wave (PAW) potentials40 explicitly include three valence electrons for Sc (3d14s2), 11 for Y (4s24p64d15s2), and 25 for Lu (5s25p64f145d16s2), 14 for Fe (3p63d64s2), 12 for Mo (4p64d55s1), and six for O (2s22p4) atoms. The same result is also obtained for the PAW potential excluding f electrons for Lu. The wave function is expanded in a plane wave basis with an energy cutoff of 600 eV. The crystal unit cell includes two formula units for ScFeO3, and one formula unit for Sc2FeMoO6 and Lu2FeMoO6. A 7 × 7 × 7 Γ-centered k-points sampling is used for reciprocal space integrations. Each self-consistent electronic calculation is converged to 10−6 eV and the tolerance force is set to 0.005 eV/Å for ionic relaxation. The convergence checks with respect to the k-points sampling have been made for the total energy, densities of states as well as the phonon dispersion curves (see Supplementary Information Figures S1-S3).
To calculate the electric polarization of Ni3TeO6-type A2FeMoO6 (A = Sc, Lu) with space group R3, we choose the structure with space group 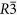 as a reference state41. The
as a reference state41. The 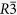 structure displayed in Figure S1 has space inversion symmetry. It is a non-polar insulator and has zero electric polarization (see Supplementary Information). Since the electric polarization is along 3-fold rotational axis, a 30-atom hexagonal unit cell is chosen, so that the in-plane polarization is zero. In calculating the electric polarization, a 7 × 7 × 4 Γ-centered k-points sampling is used for the self-consistent loop and 14 k-points sampling is adopted for parallel direction integration in Berry phase method. As shown in Figure S5, 14 k-points sampling is almost convergent for electric polarization calculation.
structure displayed in Figure S1 has space inversion symmetry. It is a non-polar insulator and has zero electric polarization (see Supplementary Information). Since the electric polarization is along 3-fold rotational axis, a 30-atom hexagonal unit cell is chosen, so that the in-plane polarization is zero. In calculating the electric polarization, a 7 × 7 × 4 Γ-centered k-points sampling is used for the self-consistent loop and 14 k-points sampling is adopted for parallel direction integration in Berry phase method. As shown in Figure S5, 14 k-points sampling is almost convergent for electric polarization calculation.
To calculate the phonon dispersion of Ni3TeO6-type structure of A2FeMoO6 (A = Sc, Lu) and ScFeO3, the structures are firstly atomically relaxed with a higher accuracy using the 8×8×8 Γ-centered k-points sampling and the tolerance force of 0.0001 eV/Å. The phonon dispersion is then calculated using the Phonopy code42 with a 2 × 2 × 2 supercell composed of ten-atom rhombohedral unit cell. The force constants are calculated by VASP using a 4 × 4 × 4 Γ-centered k-points sampling for the supercell.
Additional Information
How to cite this article: Song, G. and Zhang, W. Comparative studies on the room-temperature ferrielectric and ferrimagnetic Ni3TeO6-type A2FeMoO6 compounds (A = Sc, Lu). Sci. Rep. 6, 20133; doi: 10.1038/srep20133 (2016).
Supplementary Material
Acknowledgments
This work was supported in part by the NNSFC under Grant No.11474148. The part of numerical calculations is carried out in the High Performance Computing Center (HPCC) of Nanjing University. The financial support from Outstanding PhD Program B of Nanjing University is also gratefully acknowledged. We thank Sujie Zhang for thoroughly reading the manuscript and polishing the English.
Footnotes
Author Contributions W.Y.Z. supervised the work and G.S. carried out the numerical calculations of this work. G.S. and W.Y.Z. both contributed to the analysis and interpretation of results, and the writing of manuscript.
References
- Eerenstein W., Mathur N. D. & Scott J. F. Multiferroic and magnetoelectric materials. Nature 442, 759–765 (2006). [DOI] [PubMed] [Google Scholar]
- Cheong S.-W. & Mostovoy M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mater. 6, 13–20 (2007). [DOI] [PubMed] [Google Scholar]
- Oh Y. S. et al. Non-hysteretic colossal magnetoelectricity in a collinear antiferromagnet. Nat. Commun. 5, 3201 (2014). [DOI] [PubMed] [Google Scholar]
- Shen S., Chai Y. & Sun Y. Nonvolatile electric-field control of magnetization in a Y-type hexaferrite. Sci. Rep. 5, 8254 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang S.-W. et al. Non-volatile 180° magnetization reversal by an electric field in multiferroic heterostructures. Adv. Mater. 26, 7091–7095 (2014). [DOI] [PubMed] [Google Scholar]
- Heron J. T. et al. Deterministic switching of ferromagnetism at room temperature using an electric field. Nature 516, 370–373 (2014). [DOI] [PubMed] [Google Scholar]
- Zhou Z. et al. Probing electric field control of magnetism using ferromagnetic resonance. Nat. Commun. 6, 6082 (2015). [DOI] [PubMed] [Google Scholar]
- Kimura T. et al. Magnetocapacitance effect in multiferroic BiMnO3. Phys. Rev. B 67, 180401(R) (2003). [Google Scholar]
- Wang J. et al. Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures. Science 299, 1719–1722 (2003). [DOI] [PubMed] [Google Scholar]
- Kimura T. et al. Magnetic control of ferroelectric polarization. Nature 426, 55–58 (2003). [DOI] [PubMed] [Google Scholar]
- Chapon L. C. et al. Structural anomalies and multiferroic behavior in magnetically frustrated TbMn2O5. Phys. Rev. Lett. 93, 177402 (2004). [DOI] [PubMed] [Google Scholar]
- Pimenov A. et al. Possible evidence for electromagnons in multiferroic manganites. Nat. Phys. 2, 97–100 (2006). [Google Scholar]
- Ikeda N. et al. Ferroelectricity from iron valence ordering in the charge-frustrated system LuFe2O4. Nature 436, 1136–1138 (2005). [DOI] [PubMed] [Google Scholar]
- Lafuerza S. et al. Determination of the charge-ordered phases in LuFe2O4. Europhys. Lett. 107, 47002 (2014). [Google Scholar]
- Bristowe N. C. et al. Ferromagnetism induced by entangled charge and orbital orderings in ferroelectric titanate perovskites. Nat. Commun. 6, 6677 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J. H. & Rabe K. M. Epitaxial-strain-induced multiferroicity in SrMnO3 from first principles. Phys. Rev. Lett. 104, 207204 (2010). [DOI] [PubMed] [Google Scholar]
- Lee J. H. et al. A strong ferroelectric ferromagnet created by means of spin-lattice coupling. Nature 466, 954–958 (2010). [DOI] [PubMed] [Google Scholar]
- Windsor Y. W. et al. Multiferroic Properties of o-LuMnO3 Controlled by b-Axis Strain. Phys. Rev. Lett. 113, 167202 (2014). [DOI] [PubMed] [Google Scholar]
- Song G. & Zhang W. First-principles study on the phase diagram and multiferroic properties of (SrCoO3)1/(SrTiO3)1 superlattices. Sci. Rep. 4, 4564 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inaguma Y. et al. High-pressure synthesis, crystal structure, and phase stability relations of a LiNbO3-Type polar titanate ZnTiO3 and its reinforced polarity by the second-order Jahn-Teller effect. J. Am. Chem. Soc. 136, 2748–2756 (2014). [DOI] [PubMed] [Google Scholar]
- Varga T. et al. Coexistence of weak ferromagnetism and ferroelectricity in the high pressure LiNbO3-type phase of FeTiO3. Phys. Rev. Lett. 103, 047601 (2009). [DOI] [PubMed] [Google Scholar]
- Shannon R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 32, 751–767 (1976). [Google Scholar]
- Li M.-R. et al. A polar corundum oxide displaying weak ferromagnetism at room temperature. J. Am. Chem. Soc. 134, 3737–3747 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawamoto T. et al. Room-temperature polar ferromagnet ScFeO3 transformed from a high-pressure orthorhombic perovskite phase. J. Am. Chem. Soc. 136, 15291–15299 (2014). [DOI] [PubMed] [Google Scholar]
- Li M.-R. et al. Polar and magnetic Mn2FeMO6 (M=Nb, Ta) with LiNbO3-type structure: High-pressure synthesis. Angew. Chem. Int. Ed. 52, 8406–8410 (2013). [DOI] [PubMed] [Google Scholar]
- Li M.-R. et al. Magnetic-structure-stabilized polarization in an above-room-temperature ferrimagnet. Angew. Chem. Int. Ed. 53, 10774–10778 (2014). [DOI] [PubMed] [Google Scholar]
- Li M.-R. et al. Mn2FeWO6: A new Ni3TeO6-type polar and magnetic oxide. Adv. Mater. 27, 2177–2181 (2015). [DOI] [PubMed] [Google Scholar]
- Nechache R. et al. Growth, structure, and properties of epitaxial thin films of first-principles predicted multiferroic Bi2FeCrO6. Appl. Phys. Lett. 89, 102902 (2006). [Google Scholar]
- Baettig P., Ederer C. & Spaldin N. A. First principles study of the multiferroics BiFeO3, Bi2FeCrO6, and BiCrO3: Structure, polarization, and magnetic ordering temperature. Phys. Rev. B 72, 214105 (2005). [Google Scholar]
- King-Smith R. D. & Vanderbilt D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654 (1993). [DOI] [PubMed] [Google Scholar]
- Hill N. A. Why are there so few magnetic ferroelectrics? J. Phys. Chem. B 104, 6694–6709 (2000). [Google Scholar]
- Miura K. & Terakura K. Electronic and magnetic properties of La2FeCrO6: Superexchange interaction for a d5-d3 system. Phys. Rev. B 63, 104402 (2001). [Google Scholar]
- Lu X. Z. & Xiang H. J. Designing asymmetric multiferroics with strong magnetoelectric coupling. Phys. Rev. B 90, 104409 (2014). [Google Scholar]
- Belik A. A. & Yi W. High-pressure synthesis, crystal chemistry and physics of perovskites with small cations at the A site. J. Phys.: Condens. Matter 26, 163201 (2014). [DOI] [PubMed] [Google Scholar]
- Loschen C., Carrasco J., Neyman K. M. & Illas F. First-principles LDA + U and GGA + U study of cerium oxides: Dependence on the effective U parameter. Phys. Rev. B 75, 035115 (2007). [Google Scholar]
- Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
- Dudarev S. L. et al. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study. Phys. Rev. B 57, 1505–1509 (1998). [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
- Resta R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 66, 899–915 (1994). [Google Scholar]
- Togo A., Oba F. & Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.