Multicenter Comparison of Machine Learning Methods and Conventional Regression for Predicting Clinical Deterioration on the Wards

Abstract

OBJECTIVE

Machine learning methods are flexible prediction algorithms that may be more accurate than conventional regression. We compared the accuracy of different techniques for detecting clinical deterioration on the wards in a large, multicenter database.

DESIGN

Observational cohort study.

SETTING

Five hospitals, from November 2008 until January 2013.

PATIENTS

Hospitalized ward patients

INTERVENTIONS

None

MEASUREMENTS AND MAIN RESULTS

Demographic variables, laboratory values, and vital signs were utilized in a discrete-time survival analysis framework to predict the combined outcome of cardiac arrest, intensive care unit transfer, or death. Two logistic regression models (one using linear predictor terms and a second utilizing restricted cubic splines) were compared to several different machine learning methods. The models were derived in the first 60% of the data by date and then validated in the next 40%. For model derivation, each event time window was matched to a non-event window. All models were compared to each other and to the Modified Early Warning score (MEWS), a commonly cited early warning score, using the area under the receiver operating characteristic curve (AUC). A total of 269,999 patients were admitted, and 424 cardiac arrests, 13,188 intensive care unit transfers, and 2,840 deaths occurred in the study. In the validation dataset, the random forest model was the most accurate model (AUC 0.80 [95% CI 0.80–0.80]). The logistic regression model with spline predictors was more accurate than the model utilizing linear predictors (AUC 0.77 vs 0.74; p<0.01), and all models were more accurate than the MEWS (AUC 0.70 [95% CI 0.70–0.70]).

CONCLUSIONS

In this multicenter study, we found that several machine learning methods more accurately predicted clinical deterioration than logistic regression. Use of detection algorithms derived from these techniques may result in improved identification of critically ill patients on the wards.

INTRODUCTION

An estimated 2.5 quintillion bytes of data are generated every day, and the volume, velocity, and variety of information has led to the popularization of the term “big data (1).” Companies like Google, Amazon, and Netflix have leveraged big data in concert with complex algorithms to improve predictions of human behavior and events (2). These algorithms, known as machine learning in computer science, are flexible techniques designed to learn and generalize from data. Highly accurate prediction is a valuable asset for companies, as highlighted by the Netflix challenge, which awarded one million U.S. dollars to researchers who improved the accuracy of its algorithm by 10% (3).

Despite their common use in business analytics, the mainstream medical community has lagged behind in terms of studying and implementing machine learning methods for real-time risk prediction. Traditional methods, such as logistic regression, are the standard when developing prediction models even when accuracy, instead of interpretation of the regression coefficients, is the primary goal (4,5). However, previous comparison studies have suggested that machine learning methods can be more accurate than traditional logistic regression across a wide variety of subject areas (6). Thus, when the stakes are high, it is important to consider techniques beyond standard regression to optimize accuracy (7).

The aim of this study was to compare several of the most popular machine learning techniques in a large multicenter dataset of patients on the medical-surgical wards for predicting clinical deterioration. In this area of medicine, small improvements in accuracy can have large benefits given the high mortality associated with clinical deterioration and costs of resource utilization for false alarms. An additional aim of the study was to illustrate how machine learning methods can be visualized in order to provide face validity to clinicians and researchers interested in implementing these techniques.

MATERIALS AND METHODS

Study setting

Details regarding the study population are shown in eTable 1 and have been previously described (8). Briefly, patients with documented ward vital signs from November 2008 to January 2013 at five hospitals, which included a tertiary academic center, two suburban teaching hospitals, and two community hospitals, were included in the study. The University of Chicago Institutional Review Board (IRB #16995A) and NorthShore University HealthSystem (IRB #EH11-258) granted waivers of consent based on general impracticability and minimal harm.

Outcomes

The primary outcome of the study was the composite of ward cardiac arrest, ward to ICU transfer, or death on the wards without attempted resuscitation. Cardiac arrests were manually reviewed for data quality, as previously described (8). ICU transfers were determined using location-stamped vital signs, and death on the wards was confirmed using administrative databases.

Predictor variables

Age, time since ward admission, number of previous ICU stays, vital signs, and routinely collected laboratory values (electrolytes, creatinine, liver function tests, and blood counts) were utilized as predictors (8). These variables were obtained from the electronic health record (EHR) (EPIC; Verona, WI) at the University of Chicago and the Electronic Data Warehouse at the NorthShore hospitals.

Model development

Overview

The dataset was split by date at each hospital into derivation (60%) and validation (40%) cohorts, and all model tuning using ten-fold cross-validation described below was performed in the derivation dataset only. Because previous literature suggested that some machine learning techniques have decreased accuracy in highly unbalanced data (e.g. many more non-event observations than event observations), as was the case in this study, each time window where an event occurred was matched to a randomly selected non-event window for model derivation (9,10). In order to standardize model development in the setting of longitudinal data, a discrete-time survival analysis statistical framework was used (8,11). This involved separating time into discrete eight-hour intervals using the predictor values closest to the beginning of the interval, and the outcome being whether the event occurred within the following interval (see eFigure 1). In the case where data for a variable were missing from a time-block then the value from the prior time block was pulled forward. If no prior value was available then the median value was imputed, similar to other risk score studies (4, 8). Eight-hour intervals were chosen due to the frequency of physiologic data collection and our prior work (8). This methodology transformed the data structure into a binary classification problem, where many of the machine learning methods were developed and are commonly utilized (10,11). A brief overview of the different methods are outlined below, and additional details are provided in the Supplementary Appendix eMethods.

Logistic regression

Two logistic regression models, which utilized all the predictor variables, were compared in this study. The first model was fit with each variable term entering linearly. The second model modeled the predictors using restricted cubic splines with three knots to allow for non-linearity. The number of ICU stays and mental status, which was coded in the alert, responsive to voice, responsive to pain, and unresponsive (AVPU) scale, entered the model linearly due to the small number of possible values.

Tree-based models

Decision trees partition the sample data by splitting the variables at discrete cut-points and are often presented graphically in the form of a tree (10, 12). For this study, the decision tree algorithm determined the best variable and location for each split using the Gini index (10). A cost complexity parameter, which penalizes more complex trees, was used to control the size of the final tree, and the optimal value was determined using ten-fold cross-validation.

Because decision trees often have suboptimal predictive accuracy, several methods were used to combine multiple trees together. First, a bagged tree model was fit. This involved taking random samples of the derivation dataset with replacement and fitting a tree to each sample (10). The final model is then a collection of many trees, the optimal number of which was determined using ten-fold cross-validation. Second, a random forest model was fit. Random forests are modified bagged trees that only allow a random sample of the predictor variables to be considered at each split of each tree (10). The optimal number of trees and predictor variables to be considered at each split were determined using ten-fold cross-validation. Finally, a boosted tree model was fit. This model derived consecutive decision trees using random samples of the training data to predict the residuals of the previous models, thus creating a combination of trees that weight the “difficult to predict” events to a greater degree (10). The optimal number of splits for each individual tree, the total number of trees, and an additional shrinkage factor, which reweights the prediction contribution from each individual tree, were determined using ten-fold cross-validation.

K-nearest neighbors

K-nearest neighbors (KNN) models use local geographic information in the predictor space to predict the outcome of a new sample (10, 12). For example, a KNN model utilizing five neighbors uses the five closest observations in multidimensional space, based on a distance measure, to predict the outcome of a new observation. The optimal number of neighbors is unknown, so ten-fold cross-validation was used to determine the number of neighbors for the final model.

Support vector machines

Support vector machines are unique in that they primarily utilize the data points from each outcome class that are closest to the class boundary or that are misclassified when determining the structure of the boundary (10, 12). The radial basis function, a commonly used flexible kernel function, was used for the support vector machine model in this study. The main tuning parameter is the cost penalty, with higher values penalizing misclassified observations to a greater degree. The optimal value was determined using ten-fold cross-validation and the scale parameter was determined computationally using the method of Caputo et al (10).

Neural networks

Neural networks are non-linear models originally inspired by how the brain works, and involve creating a set of linear combinations of the original predictor variables and then using those as inputs into a hidden layer (or layers) of units, which then create new combinations of these inputs to finally output the probability of the event of interest (10, 12). A feed-forward multi-layer perceptron neural network was fit, and the penalty term, known as weight decay, and the number of hidden units in the model were determined using ten-fold cross-validation.

Model comparisons

Predicted probabilities were calculated for each observation in the validation dataset from each derived model. In order to put the accuracy results in perspective with prior studies, the Modified Early Warning Score (MEWS), a commonly utilized rapid response team activation tool, was also calculated (13). The area under the receiver operating characteristic curve (AUC) was then determined using whether an event occurred within twenty-four hours of each individual observation because this is a standard metric for early warning score comparisons (8,14). A plot of the percentage of observations above a probability threshold versus the percentage of observations detected that were followed by an outcome (i.e. sensitivity), previously described as an “early warning score efficiency curve,” was created for the logistic regression models, MEWS, and the most accurate machine learning method (14). A pre-defined comparison of the percentage of observations in the validation dataset above the 75% sensitivity cut-off for each model was utilized (14). Model calibration, which is the agreement between a model’s predicted probability and the actual probability of an event, was measured in several ways using the discrete-time framework in the validation dataset (15). First, the Hosmer-Lemeshow goodness of fit (H-L) test was calculated for each model, and plots of predicted versus actual risk across risk deciles were created. In addition, the calibration slope and calibration intercept (i.e. Cox calibration) were also calculated. To visualize the contribution of the predictor variables in the most accurate model, a variable importance measure that utilized the change in the Gini index was used (10). The effects of the most accurate predictor variables across different values and 3-D interaction plots were also created for the most accurate model using partial dependence plots (16). All analyses were performed using R version 3.1.1 (The R Foundation for Statistical Computing; Vienna, Austria) and Stata version 13.1 (StataCorps; College Station, Texas). A two-tailed p-value <0.05 denoted statistical significance.

RESULTS

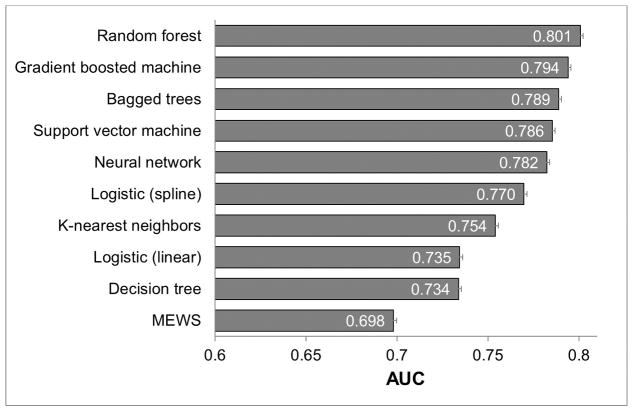
In total, 269,999 patient admissions and 16,452 adverse outcomes (424 cardiac arrests, 2,840 deaths on the ward, and 13,188 ICU transfers) occurred during the study period, with demographic characteristics as previously described elsewhere (8). In the dataset, vital signs had the lowest amount of missing data (<1% except oxygen saturation (10%) and AVPU (19%)). Laboratory data had more missing values than vital signs (complete blood count (7–8%), electrolytes and renal function (11–16%), and liver function (48–50%)). During model derivation, 10,309 time windows with adverse events were randomly matched to 10,309 non-event windows. In the validation dataset, the random forest model was the most accurate (AUC 0.80 [95% CI 0.80–0.80]) followed by the gradient boosted machine (AUC 0.80 [95% CI 0.79–0.80]; Figure 1). The logistic regression model with spline terms was more accurate than the model utilizing linear predictor terms (AUC 0.77 vs 0.74; p<0.01), and all models were more accurate than the MEWS (AUC 0.70 [95% CI 0.70–0.70]). A post-hoc sensitivity analysis using a logistic regression model with four knots for continuous variables had an AUC of 0.69. As shown in e-Figures 2–4, the random forest model was the most accurate model for all three individual outcomes, with an AUC of 0.94 for death, 0.83 for cardiac arrest, and 0.79 for ICU transfer. Of note, the logistic spline model was more accurate than the logistic linear term model for ICU transfer (AUC 0.75 vs 0.71) but was less accurate than the linear term model for detecting cardiac arrest (AUC 0.78 vs 0.81) and death (0.91 vs 0.92). Figure 2 illustrates an “early warning score efficiency curve” for the random forest, logistic regression models, and the MEWS. As shown, at the 75% sensitivity cut-off 31% of the observations in the validation dataset are above the risk threshold associated with this sensitivity for the random forest model compared to 37% for the logistic spline model, and 44% for the logistic linear term model.

Figure 1. Area under the receiver operator characteristic curves of the compared methods for the composite outcome in the validation cohort*.

*Error bars indicate the upper 95% confidence intervals. Abbreviations: MEWS: Modified Early Warning Score, AUC: Area under the receiver operating characteristic curve

Figure 2. Graph illustrating model sensitivity by the percent of observations above a score threshold (i.e. positive screen) for the Modified Early Warning Score, logistic regression models, and random forest model in the validation cohort.

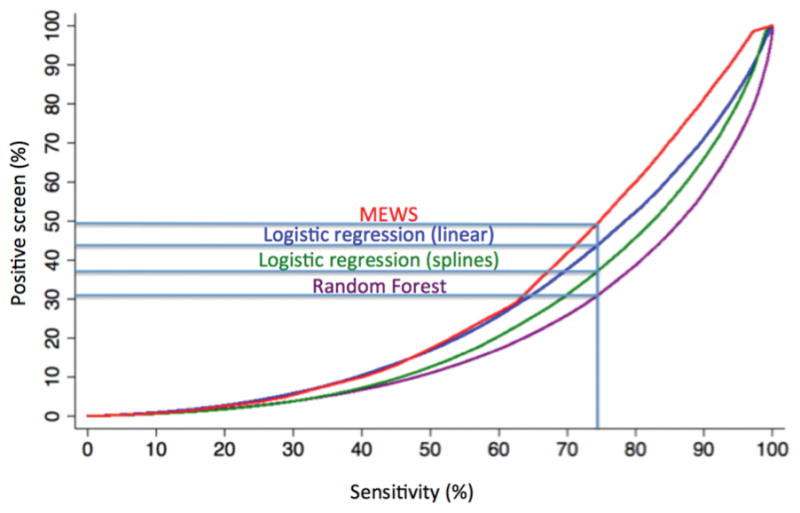
Abbreviations: MEWS: Modified Early Warning Score

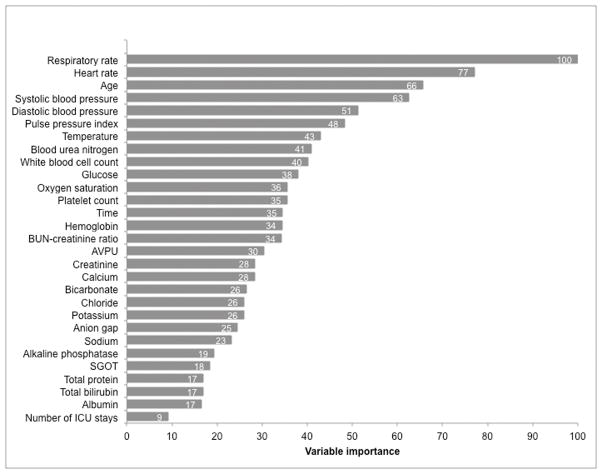
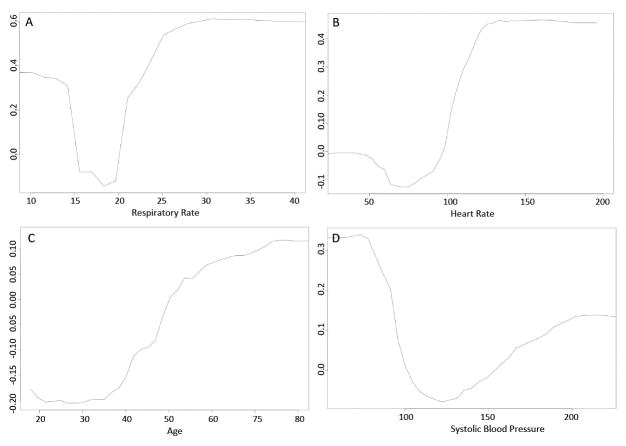
Respiratory rate, heart rate, age, and systolic blood pressure were the most important predictor variables in the random forest model (Figure 3). The partial plots illustrating the effects of these predictors across a range of values in the random forest model are shown in Figure 4. The risk for the outcome was U-shaped for respiratory rate, heart rate, and systolic blood pressure, with increased risk for both high and low values. Risk also increased with increasing age, and an inflection point with more rapidly increasing risk occurred at approximately age 40. Partial plots illustrating two-way interactions between the four most important variables are shown in e-Figures 5–10, with blue indicating lower risk and red indicating higher risk. Some variables, such as heart rate and systolic blood pressure (e-Figure 5), demonstrated little evidence of interaction, with higher risk across both low and high values of each variable across the range of the other variable. Other variables had important qualitative interactions. For example, there was no increased risk for low heart rates when the respiratory rate was 20, while low heart rates had increased risk at other levels of respiratory rate (e-Figure 6). In addition, once the respiratory rate was very high (e.g. >30) the risk of an event was also very high regardless of the heart rate. Model calibration results in the validation dataset are shown in eTable 2 and eFigure 11, with the gradient boosted machine demonstrating the best calibration (H-L p-value 0.68; calibration slope and intercept 0.98 and −0.1, respectively). The calibration of the random forest model was dependent upon the number of variables that were allowed to be considered at each split, even in the derivation dataset (eTable 3).

Figure 3. Importance of the predictor variables in the random forest model, scaled to a maximum of 100.

Abbreviations: BUN: blood urea nitrogen; AVPU: alert, responsive to voice, responsive to pain, unresponsive; SGOT: serum glutamic oxaloacetic transaminase; ICU: intensive care unit

Figure 4.

Partial plot of the effect of respiratory rate (A), heart rate (B), age (C), and systolic blood pressure (D) on the risk of the composite outcome across different values in the random forest model.

DISCUSSION

In this large, multicenter cohort study we found that the random forest algorithm was more accurate than eight other methods for detecting clinical deterioration on the wards. At our pre-defined sensitivity level, the random forest model would need to screen 6% and 13% fewer observations than the logistic spline and logistic linear term models, respectively. In the validation dataset of over 4.6 million observations, this would result in over 500,000 fewer alarms over the study period with the random forest model compared to the logistic model with linear terms. We illustrated how aspects of the random forest model can be visualized, which provides face validity for clinicians hoping to use this flexible algorithm. Finally, for several of the techniques studied, this is the first use of the discrete-time survival analysis framework to model longitudinal data in the medical literature.

Our finding that the random forest algorithm, which was first described by Leo Breiman in 2001, was the most accurate is consistent with prior literature in other areas. For example, Fernandez-Delgado et al. compared over 100 different techniques in 121 datasets, many of which were small and in non-medical fields, and found that the random forest algorithm was the most accurate method (6). This is in stark contrast to the fact that a PubMed search in the core clinical journals for “random forest prediction” resulted in 11 articles compared to over 1400 for “logistic regression prediction” as of January 1, 2015. Random forests automatically investigate interactions and non-linear effects of predictors, which must be pre-specified by the user in logistic regression. This enhanced flexibility can lead to improved accuracy but also increases the chance of overfitting, and studies suggest that large amounts of data are needed to estimate a stable random forest model (17). It is possible that the random forest was most accurate in our data because of the method’s flexibility combined with the large size our derivation dataset. We also found that the gradient boosted machine was the best calibrated model and its AUC was second only to the random forest. The calibration of the random forest was also related to the number of predictors allowed to be utilized at each split in our data. Therefore, in a field where calibration is of high importance it is imperative to investigate this measure in addition to model discrimination.

In the field of predicting in-hospital deterioration, few studies have been performed comparing machine learning techniques to conventional regression. For example, an ICU-based study of 24,508 patients by Pirracchio et al. compared the newly described “Super Learner” algorithm, a combination of multiple machine learning techniques, to previously published severity of illness models and several machine learning algorithms (18). They found that the Super Learner algorithm and the random forest model had greater accuracy (both with AUCs of 0.88) than the established severity of illness scores and other machine learning methods for predicting mortality. In addition, Mao and colleagues developed an early warning score in a single-center study and compared logistic regression models to support vector machine and decision tree models, finding logistic regression to be more accurate (19). Finally, Badriyah et al. developed a decision tree model for ward deterioration and found that its accuracy was similar to the National Early Warning Score (20). Studies in other areas have suggested that logistic regression can be as accurate or more accurate than other machine learning methods (21–23). Thus, as per Wolpert’s “No Free Lunch Theorem,” no one technique will be most accurate across every scenario, and so comparisons of techniques in different research areas and datasets may yield different results (24).

One criticism of machine learning techniques is that they are black boxes and thus may be viewed with suspicion by clinicians. Our study demonstrated that these methods can be much more accurate than a logistic model with easily interpretable linear terms. Therefore, if accuracy is paramount then these methods should strongly be considered. In addition, various ways to visualize variable importance have been developed, as we illustrated in this study (10, 16, 25). Notably, we found that the most important variables in the random forest model have also been shown to be important predictors in prior research in this area (8, 26, 27). In addition, the risk for adverse outcomes across the range of values of the predictors was consistent with clinical intuition and prior work. Finally, because the random forest is inherently an interaction model that can cut variables at points across their entire range, important interactions and threshold values can be discovered that are difficult to find using alternative techniques, such as those between respiratory rate and heart rate in our study.

The proliferation of EHRs across the United States offers a remarkable opportunity to leverage machine learning techniques to improve patient care. Although mainly used only as an electronic chart for reading, recording, and billing purposes, there are examples of using this environment for real-time clinical decision support. For example, Sawyer et al. used EHR data to provide real-time alerting for septic patients on the wards, which resulted in increased early interventions (28). The same group also published a study utilizing electronic alerts with automated pages going to nurses for patients showing signs of clinical deterioration on the wards (29). Similar studies have been published in step-down and ICU patients (30,31), and these real-time alerts may also help bridge the gap between when rapid response teams are typically alerted and when instability events actually occur (32). Our results suggest that utilizing the random forest model has the potential to markedly decrease false alarms compared to logistic regression. These models can be implemented by running the model using a wide range of programming languages or commercially available tools, which can run externally to and interact with the EHR.

Importantly, our utilization of discrete-time survival analysis is the first reported use in the medical literature for several of the machine learning techniques. This method is similar to the approach described by Biganzoli et al. for neural networks, whose study provided examples of its use in cancer datasets (33). Discrete-time decision trees and random forests have been reported by Bou-Hamad et al. using bankruptcy data, but we are unaware of publications in the clinical literature for any of the methods except logistic regression and neural networks (34). Other methods to extend machine learning methods to survival analysis data have been described, but the discrete-time approach provided a standardized approach for model development in this study (35).

There are several limitations of our study. First, our population was from five Illinois hospitals, and our results may not be generalizable to other settings. In addition, because our goal was to compare popular machine learning techniques in a standardized framework, we did not compare all available methods or their variations. There are hundreds of different techniques and variations, and a completely comprehensive study was not feasible.

CONCLUSIONS

In conclusion, we found that several machine learning methods were more accurate than traditional logistic regression for predicting clinical deterioration on the wards. We illustrated how to extend these methods for use with time-varying predictors and how to visualize variable importance and the effect of variables on the risk of the outcome across of range of values. Implementation of the most accurate model, the random forest, may result in considerable resource savings compared to traditional methods.

Abbreviations

AUC

area under the receiver operating characteristic curve

AVPU

alert, responsive to voice, responsive to pain, and unresponsive

CI

confidence interval

EHR

electronic health record

ICU

intensive care unit

KNN

K-nearest neighbors

MEWS

modified early warning score