Near-field Light Scattering Techniques for Measuring Nanoparticle-Surface Interaction Energies and Forces

Abstract

Nanoparticles are quickly becoming commonplace in many commercial and industrial products, ranging from cosmetics to pharmaceuticals to medical diagnostics. Predicting the stability of the engineered nanoparticles within these products a priori remains an important and difficult challenge. Here we describe our techniques for measuring the mechanical interactions between nanoparticles and surfaces using near-field light scattering. Particle-surface interfacial forces are measured by optically “pushing” a particle against a reference surface and observing its motion using scattered near-field light. Unlike atomic force microscopy, this technique is not limited by thermal noise, but instead takes advantage of it. The integrated waveguide and microfluidic architecture allow for high-throughput measurements of about 1000 particles per hour. We characterize the reproducibility of and experimental uncertainty in the measurements made using the NanoTweezer surface instrument. We report surface interaction studies on gold nanoparticles with 50 nm diameters, smaller than previously reported in the literature using similar techniques.

I. Introduction

Nanoparticles represent the largest commercialization of nanotechnology [1-6] with applications in medicine, electronics, batteries and household products, to name a few. Despite the recent manufacturing advances that enable synthesis of a large variety of nanoparticles, there remain significant measurement challenges. In biomedical applications, nanoparticles are often highly reactive, display complicated size-dependent interfacial properties and are applied in complex biological systems with often unclear and ambiguous results [7-10]. Specifically, the vastly increased surface area and high surface energy of nanoparticle dispersions result in performance that is strongly mediated by surface interactions, and there is a pressing demand for improved nanoparticle surface analysis [7, 11-17]. The surface of a nanoparticle is a key determinant of its properties and performance, and the synthesis of nanoparticle dispersions almost always utilizes surface treatment or coating to yield dispersions with both chemical and colloidal stability [11, 18, 19].

In practice, nanoparticle suspensions are incredibly complicated and their behavior is difficult to theoretically predict. Most theoretical approaches begin with the Derjaguin-Landau-Verway-Overbeek (DLVO) theory. The basic premise of the DLVO theory is the summation of effects due to the electrostatic and van der Waals interactions. This theory has been extended to account for many additional effects, typically by adding an additional potential energy term to the summation [20]. While these descriptions have some success in describing simple systems, the theory breaks down in describing more complicated situations [21]. This is particularly true at biological salt concentrations [22].

Due to these shortcomings, predicting the behavior of a realistic engineered suspension from first principles remains a daunting proposition. Yet, evaluating the surface properties and predicting long-term stability is not possible with current commercial techniques [14, 19, 23, 24]. A variety of authors [7, 11-14] and regulatory agencies [25, 26] have specifically cited the need for improved methods to analyze nanoparticle surfaces.

Here we describe our waveguide-based method for making direct measurements of particle-surface interactions. We detail the theoretical background of how the potential energy landscape is determined from measurements of scattered light intensity. We then discuss the waveguide architecture developed by Optofluidics, Inc. which brings this technique into a new regime of high-throughput nanoparticle characterization on samples with diameters as small as 50 nm. We present new data with this high-throughput technique and characterize the reproducibility and uncertainty in measurements made using this method.

II. Background

To gain practical insights into colloidal behavior it is useful to measure the net colloidal forces directly in the native solution. One technique for doing this is Atomic Force Microscopy (AFM) with a colloidal probe. In this technique the colloidal particle of interest is physically attached to a cantilever. As the probe is brought close to a surface, the surface forces cause the device to deflect, which can be calibrated to give the displacement of the cantilever. Independently developed by Butt [27] and Ducker in 1991 [28], colloidal probe AFM has proved useful in the study of many physical phenomena. However, in a colloidal environment thermal noise will actuate the cantilever; deflections will be observed even in the absence of an interacting surface. This fact is commonly used to empirically measure the stiffness of the probe using the equipartition theorem [29]. The implication of this is that AFM is not a suitable technique for studying interactions on the k_BT scale. Considering the stiffness of typical cantilevers used, surface forces smaller than approximately 10-50 pN will cause displacements smaller than the thermal motion of the device. Typical studies with colloidal probe AFM use micrometer scale probes and measure forces in the nN range [30]. Additionally, colloidal AFM suffers from low-throughput.

Another approach to studying particle-surface interactions is to illuminate the surface by guiding light through it. In this configuration, an evanescent field is generated at the interface between the surface and the aqueous suspension. The intensity of light in this evanescent field decays exponentially in the direction normal to the surface. Particles interacting with this evanescent field will scatter light; this scattered light is measured in order to gain information about the particles. The first implementations of this concept involved the use of a dielectric slab, typically a glass microscope slide into which laser light was coupled at an angle beyond the critical angle to generate the evanescent wave. First developed by Prieve [31, 32] and coworkers, this technique is called Total Internal Reflection Microscopy [33] (TIRM).

Briefly, this technique works by noting that the amount of light scattered by a particle depends on its position in the evanescent field, as the optical intensity is a function of distance from the surface. This means that particles scatter more light when they are near the surface than when they are further away. The distribution of the scattered light intensities is related to the distribution of particle positions as it undergoes confined Brownian motion near the surface. Therefore, the probability of finding the particle scattering at a given intensity corresponds to the potential energy associated with that state as described by the Boltzmann statistics. In this way, the potential energy well is mapped. By making statistical measurements that essentially examine the confined Brownian motion of a particle, these light scattering techniques are not limited by thermal noise and are capable of resolving sub-pN forces.

The TIRM technique has given researchers insight into many colloidal phenomena, including polymer and macromolecular mediated depletion interactions [34] and has enabled fundamental studies of the Casimir force [35] and non-equilibrium statistical mechanics [36]. However, the classical TIRM implementation has limitations when applied to smaller particles. Smaller particles scatter much less light, so the signal-to-noise ratio decreases with decreasing size. Smaller particles also diffuse faster, greatly reducing the probability of finding them near a scattering surface for enough time to make a good measurement. In the initial TIRM studies the gravitational settling of the particles was sufficient to balance the electrostatic forces. This quickly becomes insufficient for particles in the single micrometer and smaller regime. One approach for addressing this in the TIRM literature is the use of free space optical tweezers to force particles close to the surface with radiation pressure forces, which improves the ability to measure micrometer scale dielectric particles [37]. Another approach is to introduce a second surface located several hundred nanometers above the scattering surface to physically force particles into the evanescent field. Using this technique, researchers have been able to measure metallic particles such as 100 nm gold spheres [38, 39] and multi-walled carbon nanotubes [40], which interact much more strongly with the evanescent field than dielectrics [41].

Recently we have explored a different strategy, illustrated in Fig. 1, for bringing near-field light scattering techniques to the nanoparticle regime. Unlike the slab approach used in TIRM, which confines light only in one dimension, our technique relies on additional confinement of the light using a waveguide. This has the dual benefits of increasing the local optical intensity at the scattering surface, thereby increasing the signal, and introducing an attractive optical gradient force, which pulls particles close to the surface in a predictable way, increasing confinement. In our previous paper, we introduced the Nanophotonic Force Microscopy (NFM) [42] technique with light confinement in three dimensions using a photonic crystal resonator and demonstrated the ability to measure 100 nm dielectric particles. However, this one particle at a time approach has limited throughput.

Fig. 1.

Nanophotonic force microscopy using a waveguide structure. Nanoparticles are trapped and illuminated by the waveguide's evanescent field. The optical intensity in the evanescent field decays exponentially away from the surface. The particle position fluctuates due to thermal energy about an equilibrium position determined by the optical and surface forces present. The height-dependent scattered intensity allows for mapping of the particle height distribution, from which the potential energy landscape is calculated.

In this paper, we use a waveguide structure which confines light as well as interacting particles in two dimensions, taking advantage of both the increased signal and particle confinement offered by NFM while allowing many particles to be interrogated in rapid succession, greatly increasing throughput. Optical waveguides have previously been used in a variety of sensing and measurement applications including absorbance and Raman spectroscopy for particle identification and chemical sensing [43-45] as well as particle and cell sorting and manipulation [46]. This architecture is well-suited for high-throughput measurements because the optical scattering force propels [47, 48] nanoparticles along the waveguide in the optical propagation direction [49]. This can be expressed as:

$$F_{scat}=\frac{8{\pi }^{3}I{\alpha }^2{\stackrel{`}{\mathrm{o}}}_m}{3c{\lambda }^4}$$ (1)

where I is the optical intensity, α is the polarizability, ε_m is the permittivity of the medium, c is the speed of light, and λ is the optical wavelength. In general there can also be an additional force in this direction due to optical absorption. These forces are balanced by the Stokes drag force:

$$F_{drag}=6\pi \eta Ru$$ (2)

where R is the particle radius, η is the dynamic viscosity of the medium, and the particles travel down the waveguide with velocity u. Rather than waiting to load one particle at a time into a central resonator hot-spot, particles are measured as they continuously move down the waveguide in the direction of optical propagation.

III. Technique Overview

Briefly, our technique works by pushing particles against a waveguide surface, taking advantage of the optical trapping force provided by the light confinement. The particles experience this force as well as the net effect of the surface forces and undergo confined Brownian motion near the surface. The optical intensity in the evanescent field depends exponentially on the distance to the surface, so diffusing particles scatter more light when they sample positions near the surface and less light at times when they are further away. By observing the scattered light from a particle at many times we build up a histogram giving us the probability of finding a particle in a given state, and use the Boltzmann statistics to deduce the potential energy landscape from this probability distribution. Since we know the contribution provided by the optical trap, we can subtract this component, leaving us with the particle-surface interaction, giving insight into the behavior of the system.

Fundamentally, in order to make measurements that are not thermal noise limited one must rely on a technique that accounts for the thermal motion of the particle. In other words, since we are working in liquid environments, the solvent molecules will have thermal energy and will collide with the nanoparticle, transferring some of their energy. This will result in the particle undergoing Brownian motion. A particle near a surface will experience a variety of forces, many of which depend on the particle-surface separation distance. Therefore, this motion will be biased and the particle position will fluctuate about some equilibrium position at which these forces are balanced and the net force on the particle is zero. However, as the particle is pushed away from equilibrium, it will experience a net restoring force due to moving into a region where the forces are not balanced. In the experiments that we present in this paper the dominant forces are a repulsive electrostatic force balanced by an attractive optical gradient force, but the method is generally applicable to the case of other forces.

In energetic terms, as these collisions push a particle away from equilibrium the work done in displacing the particle gives it some potential energy. As the particle moves to a new state, it scatters a different amount of light, which is recorded in the next camera frame. In the limiting case where many observations are made (the question of how many observations are necessary in practice is addressed in Section IV.B) the distribution of intensity states observed corresponds to the probability distribution of finding the particle in a given intensity state. Following the arguments used in the TIRM literature [33, 50], these intensity states follow the Boltzmann distribution [51]:

$$P\left(\text{state 1}\right)\propto e^{\frac{-U\left(\text{state 1}\right)}{k_{B}T}}$$ (3)

where P(state 1) represents the probability of finding the particle in a given state, U(state 1) is the associated energy of that state, k_B is the Boltzmann constant and T is the absolute temperature. Note that this refers to the probability of finding the particle scattering with a given intensity, the quantity that we measure in the experiment. However, we are interested in the probability of finding the particle at a given separation distance from the surface, and in mapping the potential energy landscape as a function of this separation distance. To make this conversion these probability distributions are related by the Jacobian matrix, which in this case this can be stated as

$$P\left(z\right)=P\left(I\left(z\right)\right)\frac{dI\left(z\right)}{dz}$$ (4)

where P(z) is the probability distribution of finding the particle at height z, P(I(z)) is the measured probability distribution of the particle scattering intensity I, and the Jacobian is the derivative of this intensity with respect to the spatial coordinate normal to the surface. We know that the field is evanescent in nature, so we can expect the intensity to decay exponentially:

$$I\left(z\right)=I_0{e}^{-\frac{z}{d}}$$ (5)

where d is the evanescent field penetration depth and I₀ is the surface optical intensity, so combining these equations we get

$$\frac{U\left(z\right)-U\left(z_{eq}\right)}{k_{B}T}=\ln \left[\frac{P\left(I\left(z_{eq}\right)\right)I\left(z_{eq}\right)}{P\left(I\left(z\right)\right)I\left(z\right)}\right]$$ (6)

where z_eq is the equilibrium separation distance. This procedure is known as the Boltzmann inversion- by “inverting” the Boltzmann distribution that we measure, we map out the energy difference between the states. The most probable state is the equilibrium state, so by comparing all other states to the equilibrium we obtain a map of the potential energy, normalized by k_BT, as a function of the distance from equilibrium. The only assumptions made up to this point are that the optical field is exponentially decaying in the direction normal to the scattering surface and that the probability of finding the particle in a given state follows the Boltzmann distribution. For the types of structures used here, finite element simulations indeed verify the exponential dependence of the evanescent field [52]. More generally, previous work in TIRM has established methods of accounting for fields that do not exactly follow this dependence or where multiple scattering events between the particle and the surface need to be accounted for [53].

In practice, our technique works by intentionally generating an attractive optical gradient potential well to pull the particle close to the surface. While this is useful in that it confines the particle close to the surface, the potential energy well that we map includes both the interactions that we are interested in characterizing and a contribution from the optical gradient that we have applied in order to make the measurement. The magnitude of this optical contribution depends on both the polarizability of the particle and the surface optical intensity, which can be adjusted by tuning the input laser power. To account for this we assume that the optical contribution can be completely decoupled from the other interactions. The justification for this assumption is that the optical frequencies used are in the terahertz range, meaning that the timescales of the electromagnetic oscillations are much faster than the timescales associated with ions reforming electrical double layers [54]. We can write out this subtraction symbolically:

$$U_{int}=U_{tot}-U_{opt}$$ (7)

where U_int is the potential energy of the particle-surface interaction, U_tot is the total measured potential energy landscape and U_opt is the optical component. Fortunately, the optical gradient force is well understood and can be computed based on material and system parameters. For particles in the Rayleigh regime, where the particle size is small relative to the wavelength, the Rayleigh gradient force can be integrated giving us [49]:

$$U_{opt}=\frac{2\pi }{c}\alpha I_0{e}^{-\frac{z}{d}}$$ (8)

where c is the speed of light and α is the polarizability. Note that Eq. 8 can be generalized for both metallic and dielectric Rayleigh particles [41]. Theory and experiments have confirmed these models for free-space optical tweezers [55-57], and the applicability of these models to near-field interactions has also been extensively established through theory [58] and simulations [52]. For larger particles where the Rayleigh approximation does not hold, the magnitude of the scattered light will not increase monotonically with size owing to morphology dependent resonances. A full solution to Maxwell's equations is needed, and this is typically accomplished numerically. Even so, the optical gradient itself is unchanged, so the force will still decay exponentially with decay constant determined by the known evanescent field penetration depth. In practice, this means that as long as there are enough data points in the region where the optical effects dominate the surface effects, the optical component can be determined by fitting the data with an exponential function, and this can be subtracted giving the surface force.

We expect the primary component of the particle-surface interaction to be due to the electrostatic repulsion in the overlapping electrical double layers of the particle and the surface. According to the DLVO theory, the component from the screened electrostatic interactions, U_es, has the form of a decaying exponential:

$$U_{es}=Aexp(-z∕{\lambda }_D)$$ (9)

where z is the coordinate normal to the surface, λ_D is the Debye screening length, and A is a coefficient depending on material properties and solution conditions.

IV. Overview of the High-throughput System

A. NanoTweezer Surface

The NanoTweezer Surface instrument consists of opto-fluidic microchips that enable manipulation, as well as visualization and measurements of nanoparticles with an accompanying microscope and CMOS camera. The system is composed of an instrument (~400 mW 1064 nm laser, regulated pneumatic pump for fluid flow, and associated electronics and optics), a microscope mount, and cassettes that house microfluidic chips with photonic waveguide structures (Fig. 2). Laser power, sample flow rate, and imaging acquisition conditions are controlled by a custom software suite.

Fig. 2.

The NanoTweezer Surface commercial system consists of an instrument and microfluidic cassettes. Particles in solution become trapped by an optical waveguide residing on the bottom of a microfluidic channel. Once trapped, particles scatter light and progress down the waveguide in the direction of light propagation.

NanoTweezer chips contain nanostructured Si₃N₄ waveguides with a rectangular cross section of 250 × 600 nm (WxH). Waveguide patterns are defined by e-beam lithography and fabricated using standard nanofabrication techniques. The waveguide is cladded by SiO₂ films (8 μm thickness above and 3 μm below) across the chip with the exception of the experimental window, in which the waveguide is exposed to the fluid sample. The Si₃N₄ waveguide is coated with a 15 nm thick layer of SiO₂, which serves either as a reference surface for studying particles or a platform for surface modification with functional silanes.

Each chip contains three waveguides which are coupled to optical fibers on the edge facet of the chip (Fig. 3). 1064 nm laser light (TE mode polarized) is supplied by the instrument laser, coupled to the waveguides by the pre-aligned optical fibers, and guided to the waveguide outputs where optical power is measured with a photodiode.

Fig. 3.

NanoTweezer chip design. (a) Each chip consists of three waveguides, a microfluidic channel, and an optical fiber assembly for waveguide excitation. The waveguides are cladded by glass across the entire chip with the exception of the experimental window (b), in which a sample delivered to the microfluidic channel interacts with the waveguide. (c) SEM micrograph showing the edge of experimental window. (d) Cross-sectional view of waveguide structure.

A sample is introduced by inserting an aspirator into the solution of interest. The sample is drawn through the system with vacuum pressure and ultimately collected in a waste reservoir. Vacuum pressure is regulated in the range of 0 to 70 mBar, and can be increased to ~300 mBar for rapid sample loading and washing. Precise flow rate control in the range of 0-7 μl/min is achieved by using an in-line flow rate sensor and a PID feedback control loop. Upon introduction of a sample at flow rates below 7 μl/min, particles passing by the waveguide are trapped by the evanescent field and propelled along the waveguide by optical scattering forces. This movement enables continuous imaging of particles as they travel along the waveguide and pass through the imaging region of interest. The intense scattering generated by particles enables high signal to noise imaging at low (<100 μs) exposure times and high frame rates (1500 fps) using a CMOS camera. Images recorded by the camera are analyzed with a custom software package that performs automated particle tracking, intensity measurements, and generation of potential energy wells. Typical throughput of experimental acquisition is ~1000 particles/hour. Image analysis requires an additional 20 minutes for ~1000 particles.

B. Number of Measurements per Particle

The intense scattering of particles in the waveguide's evanescent field enables thousands of measurements to be performed on each trapped particle. Typical residence times of trapped dielectric particles are on the order of 3-10 seconds, depending on the laser power and the particle's size and refractive index, which determine particle velocity. The CMOS camera equipped on the NanoTweezer surface instrument has an upper frame rate limit of 1529 fps, which translates to around 4,500-15,000 measurements per particle.

When too few measurements are made the high energy (low probability) portions of the curve are not sampled enough times for the histogram to accurately represent the probability distribution. As a result, the computed energies of these states fluctuate depending on how many data points are actually used in constructing the distribution. For example, if we only take 1000 measurements in the equilibrium state, the Boltzmann statistics predict that there is a 0.25% probability of observing a particle in a state 6k_BT from equilibrium so the expected value of counts in the corresponding intensity bin is 2.5, but the actual number we observe must be an integer. If we actually sample this state 3 times, we will miscalculate its energy as 5.8k_BT. To quantify this effect, subsets of increasing numbers of measurements were analyzed for 300 nm polystyrene nanoparticles. Fig. 4 shows potential wells constructed from randomly sampled subsets of increasing measurement number from a particle on which a total of 16,000 intensity measurements were collected. For clarity, only five potential wells are displayed in Fig. 4a. Each sub-sampled potential well was compared individually with the potential well constructed from 16,000 measurements by treating the subset potential well as an estimation model and computing the residual sum of squares between the two datasets in the range of ±40 nm (Fig. 4b). An initial increase in the residual sum of squares is observed from 1000-2000 measurements. This is because very few observations are made in the lower probability states near the limits of the range, resulting in high sensitivity to measurement number. After this point, the effect of added measurement number is reduced, and the residual sum of squares decreases significantly for sample sizes above 3000 measurements. While some fluctuation is still observed due to the low probability (i.e. high potential energy) states, now enough observations are made in these states to mitigate these effects. In subsequent data analyses, a minimum measurement number of 3000 is applied to remove particles for which an insufficient number of intensity observations are collected. Raising the required measurement number would reduce uncertainty in potential energy and increase the range of observed displacement values. In practice, however, applying a minimum measurement number can remove a significant portion of the measured particles from the analysis, and a balance between individual particle data quality and inclusion of a sufficient number of particles should be sought.

Fig. 4.

Effect of number of observations on potential well measurement accuracy. (a) Potential energy wells generated from randomly sampled subsets with varying sample size from a 16,000 measurement dataset. (b) Residual sum of squares plotted as a function of subset sample size. Residual sum of squares was computed by comparing the potential well generated from each individual subset to the potential energy well generated from all 16,000 measurements.

C. Throughput

To demonstrate high throughput measurement capability, 300 nm carboxylate modified polystyrene nanoparticles suspended in solutions of varying ionic strength (1.86 - 2.53 mM) were analyzed. Samples were prepared by diluting stock polystyrene bead solutions (Polysciences, Inc) 10,000-fold in varying concentrations of phosphate buffer saline (PBS) solution (Mediatech, Inc). The pH of each solution was measured to be 7.4.

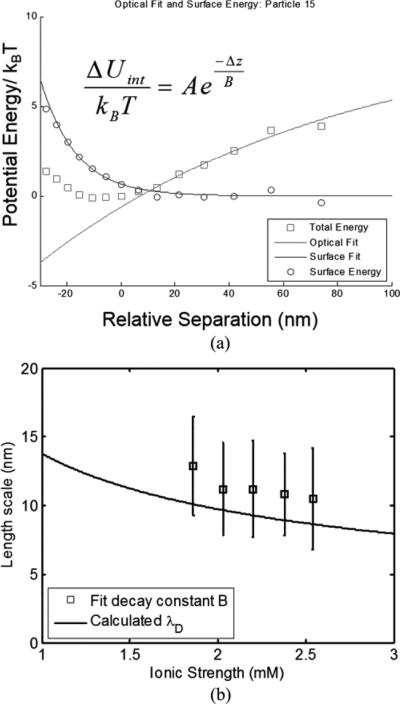
Samples were measured serially on the same chip, at a flow rate of 0.5 μl/min. The measured waveguide output power was held constant at 3 mW for each sample. Although more than 1000 particles were imaged and measured for each solution, after applying a minimum measurement number of 3000 measurements/particle, ~250 particles for each solution were considered for potential well analysis, with an average of 4909±1687 measurements per particle meeting this criterion. The intensity distribution for each particle was processed as described previously to generate a total potential energy curve. The optical energy contribution was estimated by fitting the total potential energy to Eq. 8 in the range of 10-100 nm relative separation, and subtracted from the total energy to yield the surface energy contribution. At typical separation distances, the van der Waals attraction is expected to be negligible and the surface energy profile for the charged particle-surface interaction is expected to follow the form given by Eq. 9 [59]. The surface energy curve for each particle was fit to this form, as shown for an example particle in Fig. 5a. Averages and standard deviations of the measured surface energy magnitudes and decay lengths are summarized in Table 1. As shown in Fig. 5b, the measured decay constant is observed to decrease with increased ionic strength as predicted by the electrostatic model. The fit decay constants agree reasonably well with the calculated solution Debye lengths, consistent with the model used. While within the experimental uncertainty, the cause of the overestimation of the decay constant is unknown. It could result from error in preparation of solutions with known ionic strengths; for example, if the phosphate buffer saline used to prepare the samples of known ionic strength contained a lower salt concentration than reported, this would result in a systematic increase in measured Debye length. Another possible explanation is that the simplified model omits additional contributions, such due to steric effects between the ions [60]. It should also be noted that PBS is not a simple 1:1 electrolyte.

Fig. 5.

(a) Potential energy data of a single particle from a dataset of 1291 particles, showing the measured total energy and optical and surface contributions. (b) Comparison of fit decay constant to solution Debye length over a range of PBS concentrations.

TABLE I.

Summary statistics of high-throughput experiment

Sample	# particles measured	Ionic strength (mM)	calculated λD (nm)	B: Fit decay const./Debye Length (nm)	A: Fit pre-factor
1	166	1.86	10.1	12.9 ± 3.6	0.79 ± 0.3
2	270	2.03	9.7	11.2 ± 3.4	0.78 ± 0.4
3	237	2.20	9.4	11.2 ± 3.5	0.77 ± 0.3
4	300	2.38	9	10.8 ± 3.0	0.74 ± 0.3
5	236	2.54	8.7	10.5 ± 3.7	0.86 ± 0.4

V. Uncertainty Analysis

The measurements made using our technique consist of the integrated scattered light intensity from a particle in a frame captured by our camera. To characterize the uncertainty in these measurements, we measure the intensity of a particle stuck to the waveguide surface over time. As this particle is not actually moving in the z-direction, any observed intensity fluctuations will be due to the noise in the system and can be decoupled from the actual signal we are trying to measure, namely the intensity fluctuations due to particle motion. From this, we determine the uncertainty in I is 3-5% of the measured intensity value.

The next stage of the data processing consists of computing a histogram of the number of counts, N, of observations in a bin with a given intensity range. As each measurement has its own associated uncertainty, the value being placed in a bin is really I ± σ_I where we assume that the errors in I follow the Gaussian distribution and therefore from our observations of the stuck particle we take σ_I/I = 0.05. Integrating the normal distribution between the bounds of each bin gives us the probability of a given value of the intensity falling into each of these bins. Summing these probabilities allows us to determine an expected value for N, and we can also compute the variance in N, σ_N². As the measured potential energy is a function of N, I, N_eq, and I_eq, we can compute the uncertainty in U:

$$\frac{{\sigma }_U}{kT}=\sqrt{{\left(\frac{\partial U}{\partial I}{\sigma }_I\right)}^2+{\left(\frac{\partial U}{\partial I_{eq}}{\sigma }_{I_{eq}}\right)}^2+{\left(\frac{\partial U}{\partial \mathrm{N}}{\sigma }_N\right)}^2+{\left(\frac{\partial U}{\partial N_{eq}}{\sigma }_{N_{eq}}\right)}^2}$$ (10)

where U is the potential energy computed as in Eq. 6, N represents the number of intensity measurements in a bin and N_eq represents the number of measurements in the bin corresponding to equilibrium. These correspond to the probabilities discussed in Eq. 6. For typical experiments, this gives an uncertainty in the energy of each bin of around 0.07-0.08 k_BT. We show error bars computed using this procedure in Fig 6. Propagating this uncertainty to our computation of the force we see that

$$F=-\nabla U\approx -\frac{\nabla U}{\Delta z}$$ (11)

$$\frac{{\delta }_F}{F}\approx \sqrt{{\left(\frac{\delta \Delta U}{\Delta U}\right)}^2+{\left(\frac{\delta \Delta z}{\Delta z}\right)}^2}$$ (12)

Fig. 6.

Experiments on 50 nm diameter gold particles in 0.01× PBS solution. (a) Data from 3 different particles are shown. The black points indicate the experimentally measured potential wells from three independent particles on the same waveguide with the same input optical power. Error bars are computed as described in the text. The blue curves indicate the optical model fits for each particle. The red points show the resulting surface interaction potential energy following optical subtraction. (b) Surface contribution to the energy landscape for a representative data set. Solid line represents fit to the data using Eq. 9. Inset shows the force profile computed from this using Eq. 11.

For typical forces on the order of 1 pN, this means that our uncertainties are on the order of 100 fN. In comparison, the TIRM literature reports force resolutions of about 10 fN and the AFM literature reports resolution of 10-50 pN [37, 61, 62].

The optical force confinement and enhanced signal give us the ability to measure much smaller particles than with conventional TIRM implementations. In general, metallic particles are easier to optically manipulate [41] and scatter far more light than dielectrics of the same size, mainly owing to the fact that metals have much greater polarizability than dielectrics. Taking advantage of this, in Fig. 6a we demonstrate a direct measurement of the interaction of a 50 nm diameter gold nanoparticle (Sigma-Aldrich) with a waveguide. In the figure we show measurements on three independent particles on the same waveguide with the same optical power. As the figure shows, when the optical subtraction is performed the results are remarkably consistent for all three samples. There is sufficient light available for us to make these measurements with 9 μs exposure times. In Fig. 6b we show the surface force computed by taking the derivative of the surface energy for a representative sample, highlighting our ability to make pN scale force measurements. This represents a truly new regime, as these particles are half the size of the smallest gold nanoparticles measured by conventional TIRM implementations [38].

VI. Conclusion

Using near-field light scattering techniques we have demonstrated the capability of making high throughput interaction measurements between nanoparticles and optical waveguide surfaces. The enhanced light confinement and optical gradient structure allow for measurements in the true nanoparticle regime. Here we have shown measurements on particles with diameters as small as 50 nm. However, there are no fundamental lower limits on the size of particles that can be measured as long as a large enough optical force can be applied to confine them in the evanescent field without damaging the particles and the scattered light signal is large enough to be observed. Furthermore, other than the well-known contribution from the optical gradient, no assumptions about the forces involved in the interaction need to be made. This is a key point because biomedically relevant nanoparticle suspensions can be incredibly complex. Going forward, this technique can be useful in characterizing nanoparticle coatings and determining the efficacy of nanoparticle surface modifications and other measures taken to enhance stability. Also, by measuring the same nanoparticles at different post production times in a given solution environment, this can be an important tool in assessing particle shelf-life and quality.