Physicochemical origin of high correlation between thermal stability of a protein and its packing efficiency: a theoretical study for staphylococcal nuclease mutants

Abstract

There is an empirical rule that the thermal stability of a protein is related to the packing efficiency or core volume of the folded state and the protein tends to exhibit higher stability as the backbone and side chains are more closely packed. Previously, the wild type and its nine mutants of staphylococcal nuclease were compared by examining their folded structures. The results obtained were as follows: The stability was not correlated with the number of intramolecular hydrogen bonds, intramolecular electrostatic interaction energy, or degree of burial of the hydrophobic surface; though the empirical rule mentioned above held, it was not the proximate cause of higher stability; and the number of van der Waals contacts N_vdW, or equivalently, the intramolecular van der Waals interaction energy was an important factor governing the stability. Here we revisit the wild type and its nine mutants of staphylococcal nuclease using our statistical-mechanical theory for hydration of a protein. A molecular model is employed for water. We show that the pivotal factor is the magnitude of the water-entropy gain upon folding. The gain originates from an increase in the total volume available to the translational displacement of water molecules coexisting with the protein in the system. The magnitude is highly correlated with the denaturation temperature T_m. Moreover, the apparent correlation between N_vdW and T_m as well as the empirical rule is interpretable (i.e., their physicochemical meanings can be clarified) on the basis of the water-entropy effect.

Elucidating the physicochemical factors governing the thermal stability of a protein is a principal objective of researchers in such fields as biochemistry, biophysics, protein science and engineering, food processing, and pharmaceutics. Primarily through the comparison between structural properties of thermophilic proteins and corresponding mesophilic proteins, it has been suggested that the thermal stability is most influenced by the electrostatic interaction of oppositely charged groups (e.g., hydrogen bonds and salt bridges) within a protein and the packing of its hydrophobic core into the interior (i.e., less exposure of hydrophobic surfaces to water) [1,2]. However, a number of controversial, experimental and theoretical results are found in the literature. For example, the salt bridges act both as stabilizers and as destabilizers [3], the exposed area of the hydrophobic surface is not always correlated with the thermal stability [4], and the polar group burial contributes more to the thermal stability than the nonpolar group burial [5]. On the other hand, it is empirically known that the thermal stability is related to the packing efficiency or core volume of the folded state and the protein tends to exhibit higher stability as the backbone and side chains are more closely packed with smaller cavity volume in the interior [6–10].

The most straightforward way of evaluating the thermal stability is to check the thermal denaturation temperature T_m. One of the methods of changing T_m is the mutation. Comparing the wild type and its mutants in terms of T_m provides a clue to the essential physicochemical factors governing the thermal stability. Chen et al. [11] compared the wild type, four single mutants, and five multiple mutants of staphylococcal nuclease, whose structures were determined by themselves using the X-ray crystallography, by relating T_m with the folded structure. They achieved considerably higher thermal stabilities especially by the multiple mutations, and the denaturation temperatures of the multiple mutants are 12.6 to 19.6 degrees C higher than T_m of the wild type. Their conclusions can be summarized as follows: The thermal stability is correlated with neither the number of protein intramolecular hydrogen bonds nor the intramolecular electrostatic interaction energy; it is not correlated with the degree of burial of the hydrophobic surface; it is considerably correlated with the packing efficiency or core volume; and as the core volume decreases, the cavity volume within the interior becomes smaller and the number of van der Waals contacts becomes larger. According to the remark by Chen et al., higher packing efficiency is not the proximate cause of higher thermal stability. Instead, the number of van der Waals contacts, or equivalently, the intramolecular van der Waals interaction energy is an important factor governing the thermal stability. This view is still a prevailing one though their comparative study was carried out over ten years ago. As for the correlation absence between the thermal stability and the number of intramolecular hydrogen bonds, we have recently obtained the same conclusion for mesophilic and thermophilic cytochromes c [12].

We emphasize that protein folding is the transition from the unfolded state to the folded one in aqueous solution. The protein stability should not be argued with respect to the structural properties of the folded state alone: It is also influenced by those of the unfolded state. The protein stability is closely related to the degree of the free-energy lowering upon folding. An essential point is that the effects of water must fully be taken into account. The folding leads to a gain of intramolecular hydrogen bonds and electrostatic and van der Waals attractive interactions, but it gives rise to serious dehydration penalty, that is, the loss of hydrogen bonds and electrostatic and van der Waals attractive interactions with water molecules accompanying structural reorganization of water molecules near the protein surface. The importance of the loss was first pointed out explicitly by Honig and Nicholls [13]. Our theoretical analysis [14] has also shown that the gain and loss are rather compensating (they are compensating in binding of biomolecules as well) [15]. (The model and theoretical method employed in [14] underestimates the water-entropy gain upon protein folding and also fails to reproduce a positive enthalpy change. The result presented in [15] is more reasonable.) Recently, Terazima and coworkers [16] developed a novel experimental technique which enables us to directly measure the enthalpic change upon protein folding at a prescribed temperature. They showed that apoplastocyanin (apoPC) folding at 25ºC accompanies a large enthalpic increase and thus the loss dominates.

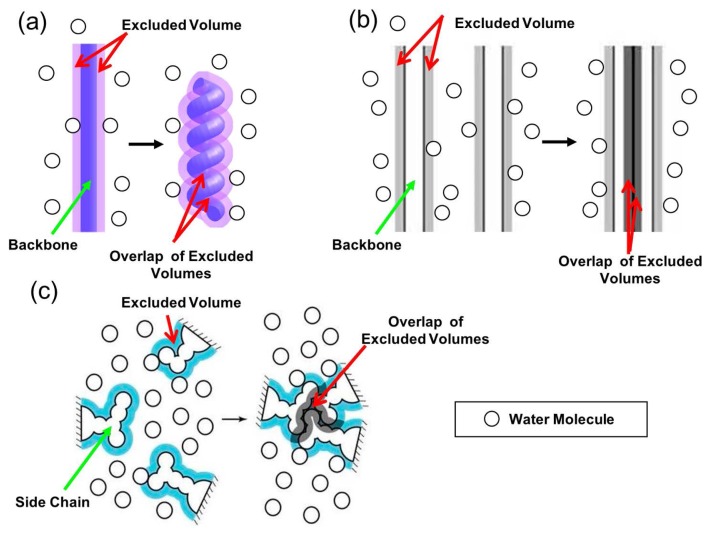
In earlier works [17,18], we showed that protein folding is driven by a large gain of water entropy. The presence of a backbone and side chains generate excluded spaces which the centers of water molecules cannot enter as illustrated in Figure 1. The volume of an excluded space is referred to as “excluded volume” (EV). When the backbone forms α-helix and β-sheet (see Fig. 1a, b), the overlap of the EVs occurs and the total EV decreases by the overlapped volume. This leads to an increase in the total volume available to the translational displacement of water molecules in the system and that in the number of accessible translational configurations of them, accompanying a gain of water entropy. Close packing of side chains (see Fig. 1c), which reduces the total EV, also leads to a water-entropy gain. This entropic EV effect is omnipresent in solvent-solute systems, but it becomes stronger as the molecular size of the solvent decreases and/or the solvent number density increases. Thanks to the hydrogen bonding, water can exist in dense liquid state at ambient temperature and pressure despite its exceptionally small molecular size. The effect is the largest for water among ordinary liquids in nature. Taken together, the water-entropy gain drives a protein to fold. This view is consistent with the experimental observation by Terazima and coworkers referred to above, showing that the water-entropy gain surpasses the sum of enthalpic increase and conformational-entropy loss [16,17] (the conformational entropy is the protein intramolecular entropy).

Figure 1.

(a) Formation of α-helix by a portion of the backbone. (b) Lateral contact of (formation of β-sheet by) portions of the backbone. (c) Close packing of side chains. The total excluded volume decreases by the overlapped volume marked in dark purple or dark gray, leading to a corresponding increase in the total volume available to the translational displacement of solvent molecules in the system.

According to the conventional view, the water adjacent to a nonpolar group is entropically unstable due to the water structuring (i.e., increase in and/or enhancement of water-water hydrogen bonds), and protein folding is driven by the release of such unfavorable water to the bulk through the burial of nonpolar groups [19]. We have recently shown that the entropic gain originating from this factor certainly exists but is too small to elucidate the water-entropy gain manifesting the apoPC-folding data [17]. It is no wonder that the exposed area of the hydrophobic surface is not always correlated with the thermal stability of a protein as mentioned above. Moreover, at low temperatures the water structuring is strengthened, leading to higher stability of the folded state of a protein: Cold denaturation is not explainable [20]. By contrast, cold denaturation can beautifully be elucidated by the entropic EV effect [20].

In the present study, we investigate the significance of the water-entropy effect in the thermal-stability differences among the wild type, four single mutants, and five multiple mutants of staphylococcal nuclease considered by Chen et al. [11] in their study. We employ our recently proposed measure of the thermal stability of a protein [12,21]. The measure ∑ is defined as the water-entropy gain upon protein folding at 25ºC normalized by the number of residues. The gain originates primarily from a decrease in the EV generated by the protein for water molecules. Larger ∑ implies higher T_m. The reliability of ∑ was demonstrated in our earlier works for yeast, bacterial, and human orthologues of frataxins [21] and mesophilic and thermophilic cytochromes c [12]. In the present study, we find that T_m is highly correlated with ∑ for the wild type and mutants of staphylococcal nuclease. We argue that the true physicochemical origin of the thermal stability is the magnitude of the water-entropy gain upon folding. This result is relevant to the observation by Chen et al. that the thermal stability is considerably correlated with the number of van der Waals contacts N_vdW and the packing efficiency or core volume, though they examined only structural properties of the folded state. In particular, N_vdW can be an apparent measure of the thermal stability.

Model and Theory

Physical picture of thermal denaturation of a protein

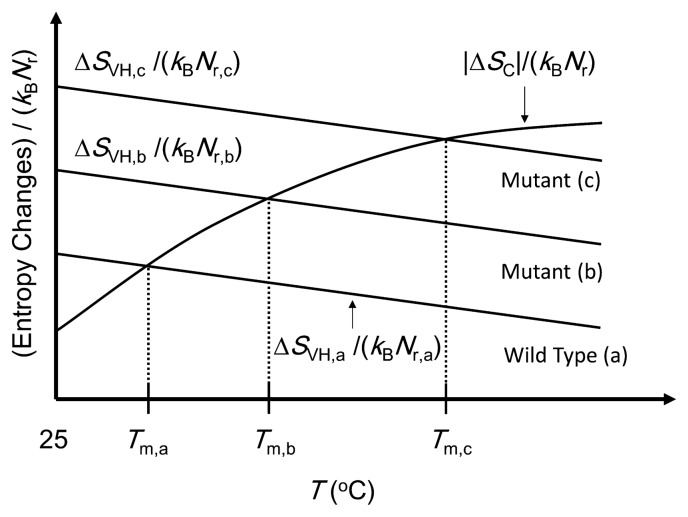
Our physical picture developed for thermal denaturation of proteins [12] is illustrated in Figure 2. T_m denotes the denaturation temperature. A large gain of water entropy occurs upon protein folding. This is because the overall, close packing of the backbone and side chains achieved by the folding leads to a substantial decrease in the total EV. This water-entropy gain ΔS_VH (ΔS_VH> 0) depends on the number density of water ρ and the system temperature T. ΔS_VH is obtained as S_VH of the folded state minus S_VH of the unfolded state. Here, S_VH (S_VH< 0) is the hydration entropy, the water-entropy loss upon solute insertion. If ρ is kept constant, ΔS_VH becomes larger as T increases [22]. If T is kept constant, on the other hand, ΔS_VH becomes smaller as ρ decreases [22]. As a matter of fact, ρ decreases progressively with increasing T above 25ºC, and the effect of ρ dominates: ΔS_VH is a decreasing function of T.

Figure 2.

Simple illustration of our physical picture of thermal denaturation of proteins. The wild type (a) and two mutants, (b) and (c), are considered here. ΔS_VH is the water-entropy gain and ΔS_C is the conformational- entropy loss upon folding. T_m, N_r, and k_B are the denaturation temperature, number of residues, and Boltzmann constant, respectively. The subscripts, “a”, “b”, and “c”, denote the values for the wild type (a) and two mutants, (b) and (c), respectively. ΔS_VH does not necessarily change linearly with the temperature T. The three solid lines of ΔS_VH/(k_BN_r) are not necessarily parallel.

Protein folding is accompanied by a large loss of the protein conformational entropy ΔS_C (ΔS_C< 0). ΔS_C = S_C,F – S_C,U where S_C,F is the conformational entropy of the folded state and S_C,U is that of the unfolded state (the subscripts “F” and “U” denote “folded” and “unfolded”, respectively). S_C,F remains roughly the same against an increase in T due to the constraints arising from the closely packed structure [12]. By contrast, S_C,U is influenced by the allowed ranges of dihedral angles which are dependent on the torsion energy and T. Angles giving high torsion energy are not allowed at low temperatures. As T increases, the allowed range of each angle becomes wider, leading to larger S_C,U. As T increases further, the enlargement of S_C,U is decelerated due to the steric repulsion among atoms in a residue and among atoms in neighboring residues. As a consequence, dS_C,U/dT > 0 and d²S_C,U/dT² < 0 [12], and |ΔS_C| exhibits the same temperature dependence: d|ΔS_C|/dT > 0 and d²|ΔS_C|/dT²< 0. This argument is in good accord with the experimental result reported by Fitter [23].

We treat a wild type and its mutants of a protein. For the conformational entropy, they share almost the same values of S_C,F, S_C,U, and |ΔS_C| as long as the mutations do not include Pro or Gly. For the hydration entropy, however, S_VH,F, S_VH,U, and ΔS_VH are quite sensitive to structural properties and exhibit significantly large changes upon mutation. Since |ΔS_C| and ΔS_VH are in proportion to the number of residues N_r, we consider the dimensionless quantities, |ΔS_C|/(k_BN_r) and ΔS_VH/(k_BN_r), hereafter.

Measure of thermal stability of a protein

In our physical picture illustrated in Figure 2, the thermal stability is described by the competition between |ΔS_C|/(k_BN_r) and ΔS_VH/(k_BN_r) [12]. Below T_m, ΔS_VH/(k_BN_r) is larger than |ΔS_C|/(k_BN_r) and the unfolded state is less stable than the folded state. Above T_m, the inversion occurs, leading to thermal unfolding. The wild type (a) and two mutants, (b) and (c), are considered in Figure 2. We regard ∑ = ΔS_VH,25/(k_BN_r), ΔS_VH/(k_BN_r) at 25ºC, as a measure of the thermal stability of a protein. The larger the measure is, the higher T_m is. The slopes of the three solid lines for (a), (b), and (c) can be different, but the difference is assumed to be not large enough to invert the order of the thermal stability.

There are the mutations which must separately be considered. An example is the mutation from Pro to Gly: Pro→Gly. For a mutant obtained by mutations including Pro→Gly, the unfolded state becomes more extended and flexible than the wild type with the result that S_C,U and |ΔS_C| take larger values (effect I). Hence, the curve of |ΔS_C|/(k_BN_r) exhibits an upward shift. At the same time, the EV of the unfolded state becomes larger due to the more extended structural properties and the decrease in the EV upon folding also becomes larger, which is followed by increased ΔS_VH (effect II). From this argument alone, it is not definite which of the two effects dominates or if T_m becomes higher upon the mutation Pro→Gly. More details are described in “Grouping of mutants”.

We are concerned with the order in terms of the thermal stability of the wild type and its mutants. Incorporating the enthalpic component (i.e., the change in the protein intramolecular energy plus the hydration enthalpy) in the physical picture will shift the value of T_m. However, the order usually remains unchanged, which were verified in our earlier works [12,21].

Water and protein models

We employ a multipolar model for water. In this model, a water molecule is a hard sphere with diameter d_S = 0.28 nm in which a point dipole and a point quadrupole of tetrahedral symmetry are embedded [24,25]. The effect of the molecular polarizability is incorporated using the self-consistent mean field (SCMF) theory [24,25]. At the SCMF level the many-body induced interactions are reduced to pairwise additive potentials involving an effective dipole moment.

The hydration entropy S_VH is determined principally by the entropic EV effect and rather insensitive to the protein-water interaction potentials. Imai et al. [26] have considered the native structures of a total of eight peptides and proteins and calculated S_VH using the three-dimensional reference interaction site model (3D-RISM) theory combined with the all-atom potentials and the SPC/E water model. Even when the protein-water electrostatic potentials are shut off and only the LJ potentials are retained, |S_VH| decreases only by ~5%. Therefore, a protein can be modeled as a set of fused hard spheres.

Integral equation theory for molecular liquids

The integral equation theory (IET) is a powerful tool based on classical statistical mechanics [27]. The water-water potentials and correlations are dependent not only on the distance between centers of water molecules but also on their orientations. The orientation of a water molecule is represented by the three Euler angles. The solute-water potentials and correlations are also angle dependent. Therefore, we employ the angle-dependent IET (ADIET) [22,24,25] for calculating S_VH for a spherical solute. The application to a solute with polyatomic structure is made possible by the combination with the morphometric approach (MA) [28,29].

We calculated the hydration free energy of a hard-sphere solute with diameter 0.28 nm using our water model and the ADIET with the hypernetted-chain (HNC) closure: The value obtained is 3.56 kcal/mol at 27ºC that is in excellent agreement with the values from Monte Carlo simulations for more popular water models: 3.56 kcal/mol at 27ºC for TIP4P and 3.65 kcal/mol at 25ºC for SPC/E [22].

Morphometric approach

The extension of the ADIET [22] to complex solute molecules like proteins is mathematically difficult. This problem can be overcome by combining it with the MA [28,29]. In this approach, a hydration quantity such as S_VH is expressed by the linear combination of only four geometric measures of a solute molecule:

$$S_{\text{VH}}/k_{\text{B}}=C_1{V}_{\text{ex}}+C_{2}A+C_{3}X+C_{4}Y.$$ (1)

Here, k_B is the Boltzmann constant, V_ex is the excluded volume, A is the water-accessible surface area, and X and Y are the integrated mean and Gaussian curvatures of the accessible surface, respectively. Though C₁V_ex is the principal term, the other three terms also influence S_VH. Since the solute shape enters S_VH only via the four geometric measures, the four coefficients (C₁–C₄) can be determined in simple geometries.

The procedure of calculating S_VH of a protein with a prescribed structure comprises the following four steps.

1. S_VH of a hard-sphere solute with diameter d_U is calculated using the ADIET with the HNC closure [22]. The values of S_VH are prepared for sufficiently many different values of d_U.

2. The four coefficients are determined by the least square fitting applied to the following equation for hard-sphere solutes (i.e., Eq. (1) applied to hard-sphere solutes):

   $$\begin{array}{l}{S}_{\text{VH}}/k_{\text{B}}=C_1(4\pi R^3/3)+C_2(4\pi R^2)+C_3(4\pi R)+C_4(4\pi ),\\ R=(d_{\text{U}}+d_{\text{S}})/2.\end{array}$$ (2)

3. The four geometric measures of a protein (V_ex, A, X, and Y) with a prescribed structure are calculated by means of an extension [29] of Connolly’s algorithm [30,31].

4. S_VH of a protein with a prescribed structure is obtained from Eq. (1) where the four coefficients determined in step (2) are used.

The high reliability of the ADIET-MA hybrid method has been demonstrated for such subjects as the quantitative reproduction of the experimentally measured changes in thermodynamic quantities upon apoPC folding [17], elucidation of the mechanisms of cold [20] and pressure [32] denaturating of a protein, and discrimination of the native fold from a number of misfolded decoys [33]. In these studies, the entropic EV effect [17,18] is treated as the key factor.

Materials and Methods

Wild type and mutants of staphylococcal nuclease

We consider the wild type, four single mutants, and five multiple mutants of staphylococcal nuclease whose folded structures are known (see Table 1). For the wild type and T33V, two structural data are available but we employ the data with higher resolution. As Chen et al. [11] themselves have pointed out, the wild type and these mutants are best suited to a detailed study on the physicochemical factors governing the thermal stability, because the measurement of T_m and structure determination have been performed using the same experimental and refinement method at the same laboratory.

Table 1.

Wild type and Mutants of Staphylococcal Nuclease Considered in the Present Study

Mutant Code	Mutationa	Tm (ºC)b	PDB ID	Resolution (Å)	Nmultic	Group
WT (Wild-Type)	- - - - - -	53.3	1EY0	1.6	8	1
WT (Wild-Type)	- - - - - -	53.3	1EYDd	1.7	10	(1)d
T33V	V - - - - -	55.3	1EY5	1.7	9	1
T33V	V - - - - -	55.3	1EZ8d	1.85	3	(1)d
S59A	- - A - - -	56.2	1EY4	1.6	8	1
T41I	- I - - - -	57.2	1EY6	1.75	9	1
S128A	- - - - - A	57.3	1EY7	1.88	5	1
GLA	- - - GLA	65.9	1EY8	1.75	15	2
IGLA	- I - GLA	69.7	1EY9	1.72	9	2
VIGLA	V I - GLA	70.9	1EYA	2.0	5	2
IAGLA	- I AGLA	71.8	1EYC	1.85	4	2
VIAGLA	V I AGLA	72.9	1EZ6	1.9	11	2

^aMutation patterns are represented in a compressed format where mutation points at Thr33, Thr41, Ser59, Pro117, His124, and Ser128 are shown in 6 letters. The residue which is the same as that in the wild type is represented by “-”. The important mutation Pro117→Gly is shown in bold face.

^bThe values of T_m are taken from Table 1 in the article of Chen et al. [11].

^cN_multi is the number of residues which have multiple models in their side chain conformations.

^dThe data points from the PDB structures of lower resolution are omitted in the plots of Figures 3 through 9.

Preparation of folded state

As indicated in Table 1, there are significantly many residues for which multiple side-chain conformation models are registered in the Protein Data Bank (PDB). Instead of generating the conformers arising from all the possible combinations of those side-chain models, we carefully adopt 8 representative conformers. A total of 8 structures are thus obtained for each of the wild type, four single mutants, and five multiple mutants. The N-terminal and C-terminal regions have not been determined in the X-ray crystallography. Since these regions should be flexible in both of the unfolded and folded states (i.e., their structural properties remain unchanged upon folding), they are not specifically modeled. The N-terminal region starts from Lys6 in 1EY0(WT), 1EYD(WT), and 1EY4(S59A) whereas it starts from Leu7 in the others. The coordinates assigned to the atoms of Lys6 are not very reliable because these atoms have relatively larger B-factors. For this reason and to impartially compare the wild type, four single mutants, and five multiple mutants in terms of the thermal stability, we cut Lys6 in the three PDB structures. It follows that we consider 135 residues ranging from Lys7 to Ser141. The proper protonated states of histidines are determined using the procedure “Calculate Protein Ionization and Residue pK” [34] in Accelrys ( BIOVIA) Discovery Studio. This determination is necessitated so that the break of intramolecular hydrogen bonds can be avoided in the energy minimization described below.

The folded structures thus obtained are slightly modified using the energy minimization by CHARMM [35] to remove unrealistic overlaps of some constituent atoms. Since it is important to keep the original X-ray structures as strictly as possible, we put positional restraints in the harmonic form on all the heavy atoms and apply 100 steps of the steepest descent energy minimization followed by the adopted basis Newton-Raphson energy minimization which is continued until the energy change during the minimization cycle becomes smaller than or equal to 1.0×10⁻⁵ kcal/mol or until the number of steps reaches 200. The force constant for the positional restraints is M kcal/(mol·Å²) where M is the mass of each atom (for example, the force constant on a carbon atom is 12 kcal/(mol·Å²)). The minimization is performed by CHARMM [35] with the help of MMSTB Toolkit [36] using the CHARMM22 parameters [37] with the CMAP correction [38] and the GBMV implicit solvent model [39,40]. A quantity (e.g., the measure of the thermal stability ∑ depending on geometric characteristics of the folded and unfolded states) is calculated for the 8 structures and the average of the 8 values is adopted for the folded state.

Preparation of unfolded state

We have recently demonstrated that the measure of the thermal stability ∑ is equally effective when the unfolded state is represented by either a sufficiently large set of random coils or several extended structures [12]. Since the latter representation is much simpler, we employ 5 extended structures whose main-chain dihedral angles (ζ, ψ) range from (−130º, 130º) to (−170º, 170º) with a step of (−10º, 10º). For proline, such dihedral angles are not allowed, and (ζ, ψ) is set to (−60º, 40º). ω is set to 180º. We take the most probable conformer for each side chain from Dunbrack’s backbone-dependent rotamer library [41,42]. All the extended structures are slightly modified using the energy minimization mentioned above. A quantity (e.g., the measure of the thermal stability ∑) is calculated for the 5 structures and the average of the 5 values is adopted for the unfolded state.

Grouping of mutants

The five multiple mutants arise from mutations including Pro→Gly whereas the four single mutants do not. We classify the wild type and four single mutants as group 1 and the five multiple mutants as group 2. When the mutation Pro→Gly is applied, the unfolded state becomes more extended and flexible with the result that the number of accessible conformations becomes larger, leading to increased S_C,U and |ΔS_C| for all T. This effect (effect I) makes the folded state less stable. By contrast, the EV of the unfolded state and the decrease in the EV upon folding become larger, which is followed by increased ΔS_VH for all T. This effect (effect II) makes the folded state more stable. Since the curve of |ΔS_C|/(k_BN_r) for group 1 becomes different from that for group 2 due to effect I, comparing the two groups in a unified manner only with respect to ∑ is not justifiable: For the two groups, we separately evaluate the correlation between two quantities of interest such as ∑ and T_m.

Results and Discussion

Correlation between thermal-stability measure and denaturation temperature

The thermal denaturation temperature T_m is plotted against the measure of the thermal stability ∑ = ΔS_VH,25/(k_BN_r) in Figure 3. ΔS_VH,25 is the water-entropy gain upon protein folding at 25ºC. As expected (see “Measure of thermal stability of a protein” and “Grouping of mutants”), the plot splits into the two groups. The error bars stem from the treatment that 8 different structures are prepared for the folded state. Overall, T_m is highly correlated with ∑: The correlation coefficients are 0.945 and 0.846 for groups 1 and 2 (the average value is 0.896), respectively. As mentioned above, two structural data are available for the wild type and T33V, and the data with higher resolution are adopted in the plot. We have found that the data points for the wild type and T33V deviate more from the line drawn for group 1 when the data with lower resolution are adopted. This result is suggestive that further higher resolution would lead to even higher correlation. ∑ is certainly a good measure of the thermal stability.

Figure 3.

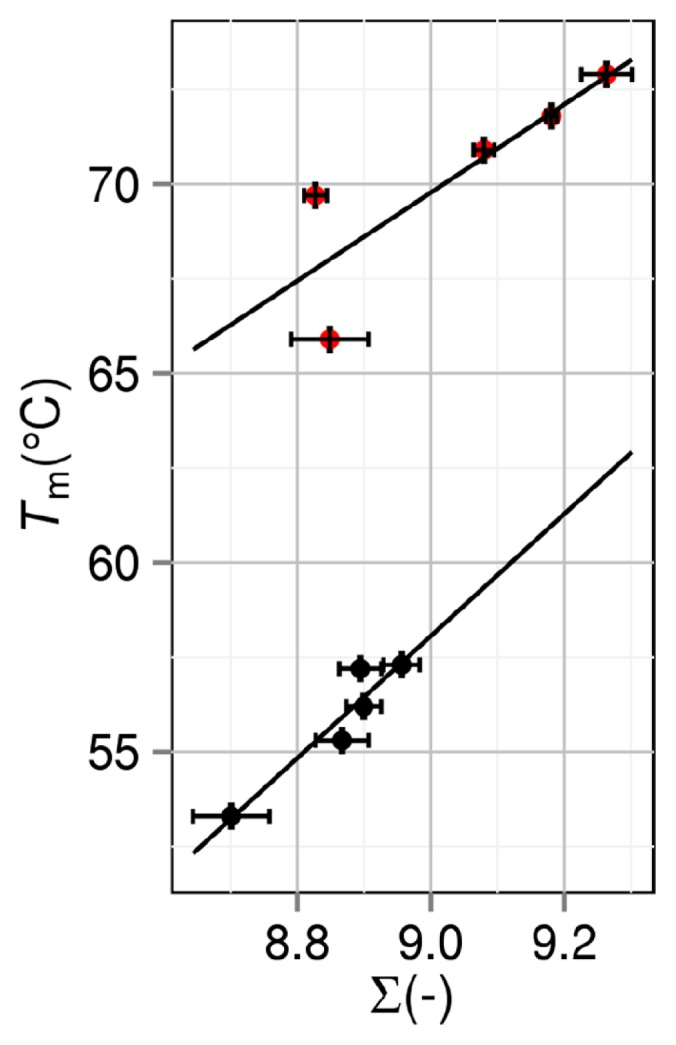
Correlation between thermal-stability measure ∑=ΔS_VH,25 /(k_BN_r) and denaturation temperature T_m. ΔS_VH,25 is the water-entropy gain upon protein folding at 25ºC. N_r and k_B are the number of residues and the Boltzmann constant, respectively. Black closed circles: group 1. Red closed circles: group 2. A mutant in group 2 is obtained by mutations including Pro→Gly.

For the two groups, if the unfolded states are perfectly modeled and ∑ is impartially evaluated, T_m of a mutant in group 2 should be lower than that in group 1 for a given value of ∑. This is because |ΔS_C| for group 2 is larger than that for group 1 for all T. In Figure 3, however, the opposite is true. This result is indicative that the modeling of the unfolded states (see “Preparation of unfolded state”) is not perfect and ∑ for group 2 relative to ∑ for group 1 is under-estimated. In the real system, the unfolded state of a mutant in group 2 is relatively much more extended than that in group 1 due to the mutation Pro→Gly: ∑ of a mutant in group 2 is relatively much larger than that in group 1. In any case, the mutants in each group can be compared impartially just in terms of ∑ calculated in the present manner.

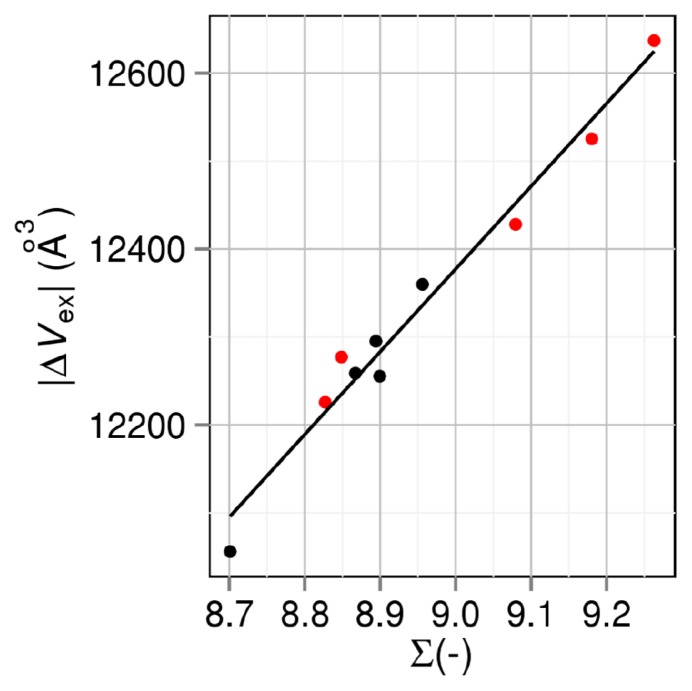
Correlation between thermal-stability measure and excluded-volume change upon folding

ΔS_VH,25 is dependent on the changes in the four geometric measures, ΔV_ex, ΔA, ΔX, and ΔY, upon folding. However, ΔV_ex (ΔV_ex<0) is the pivotal contributor. Figure 4 shows the relation between ∑ and |ΔV_ex|. The correlation coefficient is as high as 0.987. It follows that T_m is highly correlated with |ΔV_ex|. Though |ΔV_ex| is dependent on V_ex of the unfolded state as well as that of the folded state, there is a strong trend that |ΔV_ex| becomes smaller as V_ex of the folded state decreases. Hence, V_ex of the folded state, which is closely related to the packing efficiency or core volume of the folded state, is also correlated with T_m. The observations by Chen et al. [11] can thus be understood.

Figure 4.

Correlation between thermal-stability measure ∑=ΔS_VH,25 /(k_BN_r) and the absolute value of excluded-volume change upon folding |ΔV_ex|. ΔS_VH,25 is the water-entropy gain upon protein folding at 25ºC. N_r and k_B are the number of residues and the Boltzmann constant, respectively. Black closed circles: group 1. Red closed circles: group 2. A mutant in group 2 is obtained by mutations including Pro→Gly.

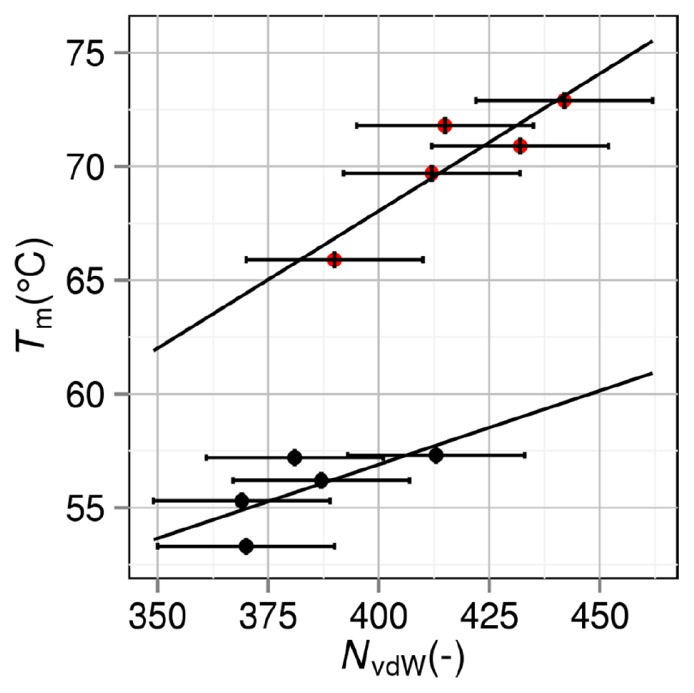
Correlation between number of van der Waals contacts and denaturation temperature

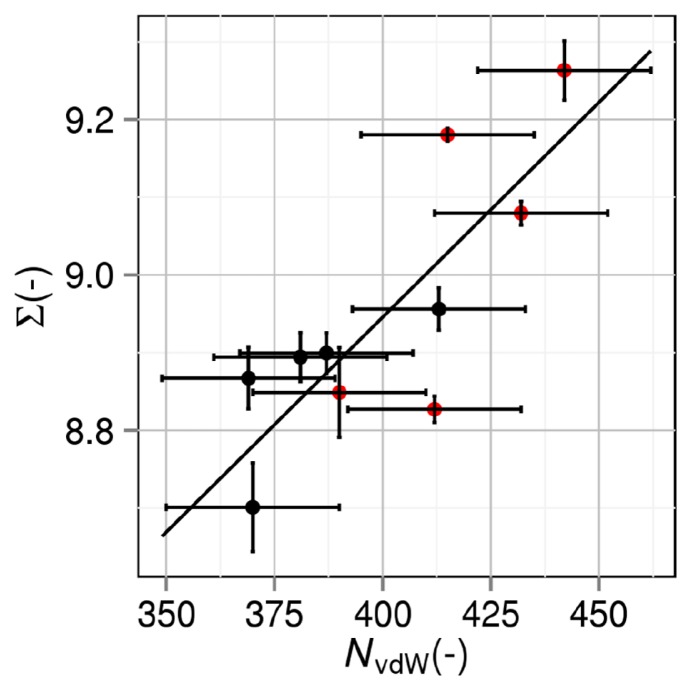
T_m is plotted against the number of van der Waals contacts N_vdW of the folded state in Figure 5. The contact numbers are taken from the values in “Supplemental Material” prepared by Chen et al. [11], where two non-bonded atoms are considered to be in contact with each other the distance between them is less than or equal to the sum of van der Waals radii plus 0.15 Å. Following the choice of Chen et al., we set the horizontal error bars at ±20. It is interesting that the plot splits into the two groups just as in Figure 3. The correlation coefficients are 0.704 and 0.895 for groups 1 and 2 (the average value is 0.800), respectively. Though the average correlation coefficient is smaller than that between T_m and ∑, it can be claimed that T_m is highly correlated with N_vdW of the folded state.

Figure 5.

Correlation between number of van der Waals contacts N_vdW and denaturation temperature T_m. Black closed circles: group 1. Red closed circles: group 2. A mutant in group 2 is obtained by mutations including Pro→Gly.

N_vdW of the folded state should be inversely correlated with V_ex of the folded state. These parameters are independent of the model of the unfolded state. It is observed in Figure 5 that for a given value of N_vdW of the folded state (or equivalently, for a given value of V_ex of the folded state), a mutant in group 2 is more stable than that in group 1. This result suggests that effect II is larger than effect I (see “Grouping of mutants”) for the mutation Pro→Gly in the present case.

Correlation between number of van der Waals contacts and thermal-stability measure

∑ is plotted against N_vdW of the folded state in Figure 6. They are highly correlated with each other and the plot does not split into the two groups. The correlation coefficient reaches 0.814. N_vdW of the folded state can also be an apparent measure of the thermal stability. N_vdW of the folded state should be inversely correlated with V_ex in the folded state. There is a strong trend that |ΔV_ex| becomes larger as V_ex of the folded state decreases. It follows that N_vdW of the folded state represents the magnitude of |ΔV_ex| and ∑. We emphasize “apparent” because it possesses no physical meaning for the following reason: N_vdW of the folded state is closely related to the gain of protein intramolecular van der Waals attractive interaction; however, this is not a driving force of protein folding because it is almost cancelled out by the loss of protein- water van der Waals attractive interaction as shown in our earlier works [14,15]; and the much more powerful driving force is the water-entropy gain.

Figure 6.

Correlation between number of van der Waals contacts N_vdW and thermal-stability measure ∑=ΔS_VH,25/(k_BN_r). ΔS_VH,25 is the water-entropy gain upon protein folding at 25ºC. N_r and k_B are the number of residues and the Boltzmann constant, respectively. Black closed circles: group 1. Red closed circles: group 2. A mutant in group 2 is obtained by mutations including Pro→Gly.

Correlation between number of intramolecular hydrogen bonds, intramolecular electrostatic interaction energy, or area of exposed hydrophobic surface and denaturation temperature

It is worthwhile to know how T_m is correlated with the number of intramolecular hydrogen bonds N_HB, intramolecular electrostatic interaction energy E_ES, or area of exposed hydrophobic surface Ψ. Following the conventional method, N_HB, E_ES, and Ψ are evaluated for the folded state. Ψ is calculated as the sum of accessible surface areas of side-chain atoms in hydrophobic residues (Ala, Val, Leu, Ile, Phe, Pro and Met). Figures 7, 8, and 9 show the N_HB–T_m, E_ES–T_m, and Ψ–T_m correlations, respectively. Though straight lines are drawn by applying the least-squares method to the data in each figure, the correlations are very poor especially for group 2. The slope of the straight line in Figure 7 should be positive, whereas the slopes of the straight lines in Figures 8 and 9 should be negative. This requirement is met for group 1 but the absolute values of the correlation coefficients are only 0.392, 0.523, and 0.140 in Figures 7, 8, and 9, respectively. It is remarkable that for group 2 the use of N_HB, E_ES, or Ψ gives erroneous prediction in terms of the stability change resulting from a mutation.

Figure 7.

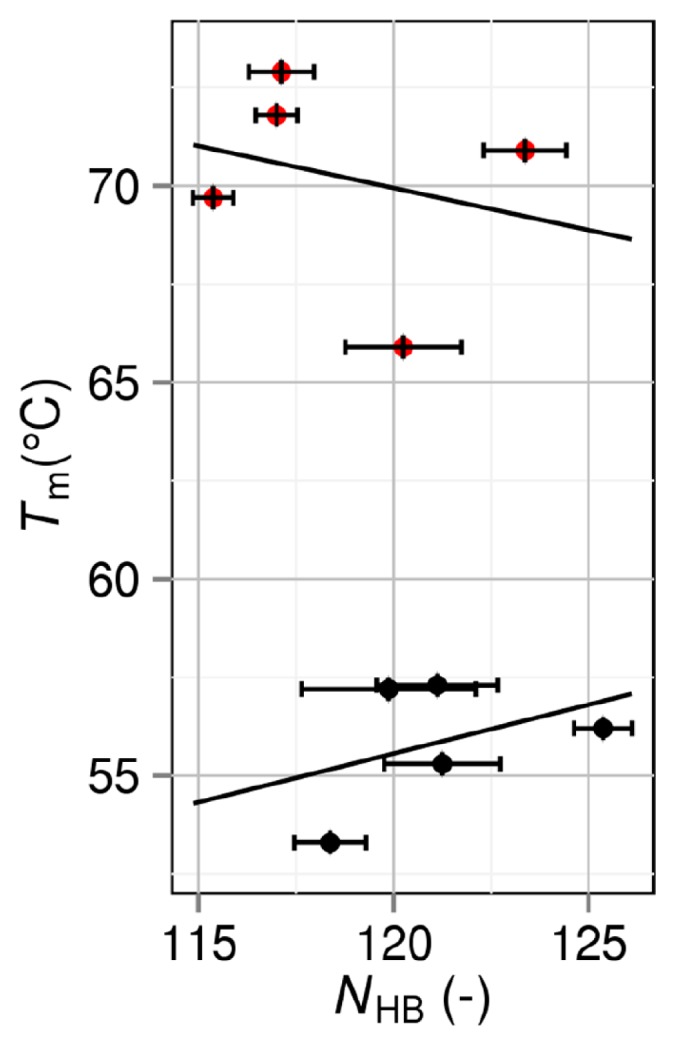
Correlation between number of intramolecular hydrogen bonds N_HB and denaturation temperature T_m. Black closed circles: group 1. Red closed circles: group 2. A mutant in group 2 is obtained by mutations including Pro→Gly.

Figure 8.

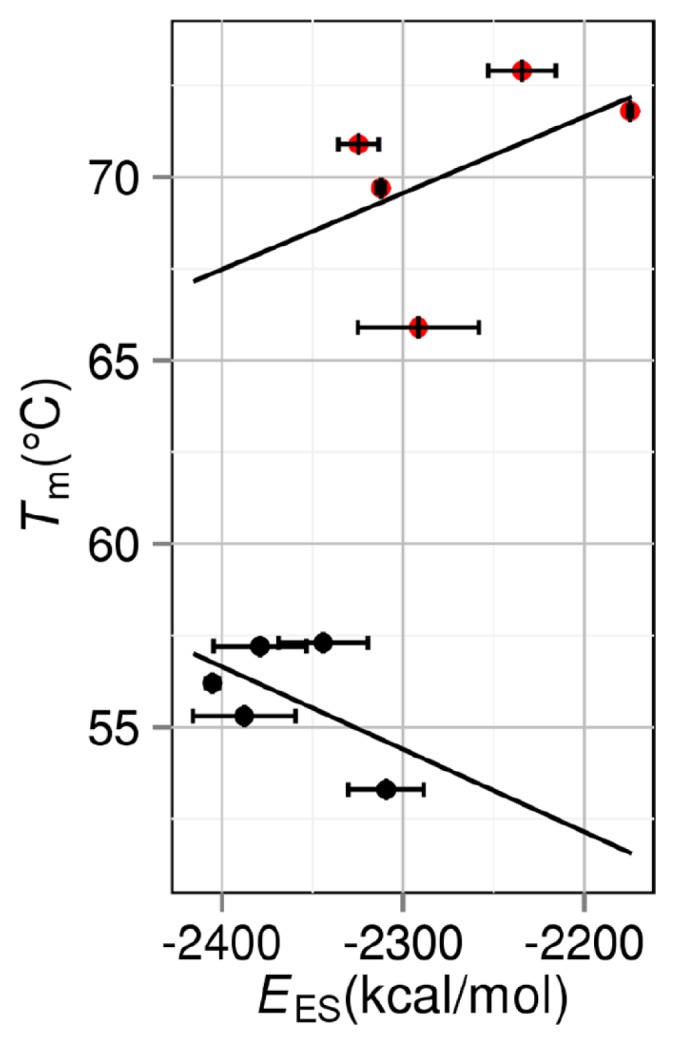
Correlation between intramolecular electrostatic interaction energy E_ES and denaturation temperature T_m. Black closed circles: group 1. Red closed circles: group 2. A mutant in group 2 is obtained by mutations including Pro→Gly.

Figure 9.

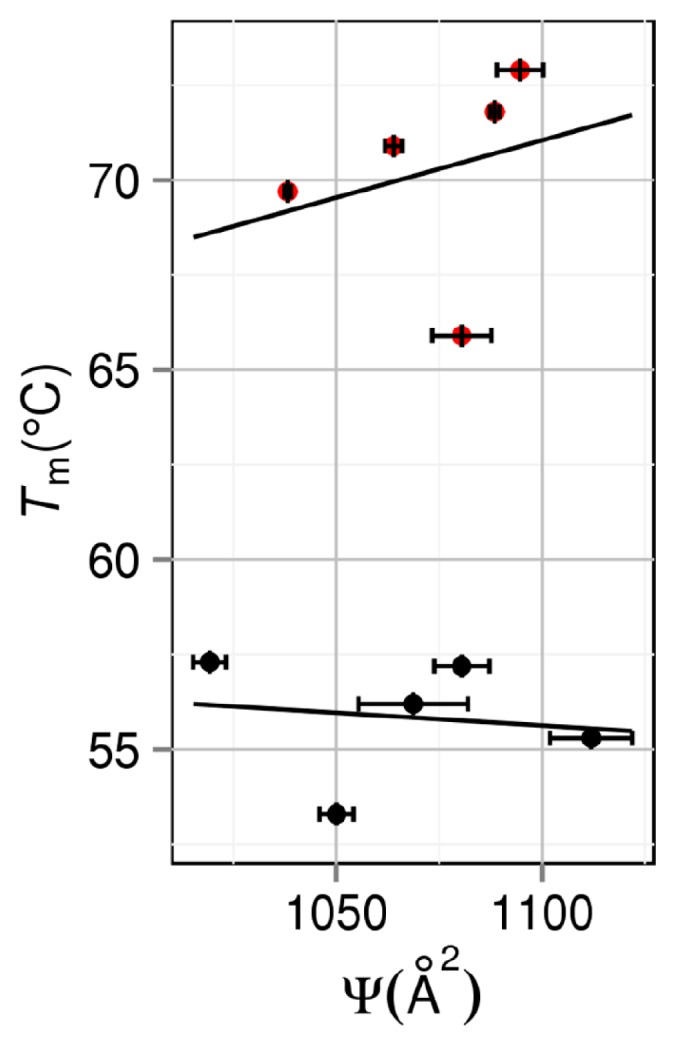
Correlation between area of exposed hydrophobic surface Ψ and denaturation temperature T_m. Black closed circles: group 1. Red closed circles: group 2. A mutant in group 2 is obtained by mutations including Pro→Gly.

Conclusions

Chen et al. [11] considered the wild type, four single mutants, and five multiple mutants of staphylococcal nuclease. In their study, the denaturation temperature was made much higher by any of these multiple mutations. The following empirically known rule [6–10] was verified: The thermal stability of a protein is somewhat related to the packing efficiency or core volume of the folded state; and the protein tends to exhibit higher stability as the backbone and side chains are more closely packed and the cavity volume in the interior is smaller. Interestingly, the thermal stability was not correlated with the number of protein intramolecular hydrogen bonds, intramolecular electrostatic interaction energy, or degree of burial of the hydrophobic surface. Chen et al. pointed out that higher packing efficiency was not the proximate cause of higher stability and the number of van der Waals contacts N_vdW or the intramolecular van der Waals interaction energy defined for the folded state was more reasonable as the cause from a physicochemical viewpoint. It seems that in general the intramolecular energy rather than the water role has caught much attention.

We disagree with the concept that the intramolecular van der Waals interaction energy is an essential factor governing the protein stability against heating. There are two principal reasons for this disagreement. First, the gain of protein intramolecular van der Waals attractive interactions is unavoidably accompanied by the loss of protein-water van der Waals attractive interactions, and the gain and loss are rather compensating [14,15]. Second, the lowering of stability caused by cooling or elevating the pressure should also be explainable by regarding the intramolecular van der Waals interaction energy as the pivotal factor, but this seems to be impossible.

We therefore revisit the study of Chen et al. [11] described above using our recently developed theoretical method [22,29] based on statistical thermodynamics. We note that the protein stability is dependent on not only structural properties of the folded state but also those of the unfolded state. The water-entropy effect, which originates from the translational displacement of water molecules that coexist with the protein in the system, plays the pivotal role. It is essential to employ a molecular model (not a continuum model) for water and suitably account for the geometric characteristics of the protein structure. We argue that the water-entropy gain upon folding at 25ºC is a good measure of the thermal stability.

Some of the important findings are recapitulated as follows. The denaturation temperature T_m is more highly correlated with the measure ∑ than with N_vdW defined for the folded state. ∑ is determined principally by the change in the excluded volume (EV) upon folding, ΔV_ex (ΔV_ex<0). There is a strong trend that |ΔV_ex| becomes larger as the EV of the folded state decreases. Hence, the EV of the folded state, which is closely related to the packing efficiency or core volume of the folded state, is also correlated with T_m. The empirically known rule mentioned above is attributable to the water-entropy effect. Superficially, T_m also exhibits high correlation with N_vdW. However, no firm physical basis can be given to this high correlation. This is because the gain of protein intramolecular van der Waals attractive interaction upon folding is almost cancelled out by the loss of protein-water van der Waals attractive interaction, as shown in our earlier work [14] (the cancellation occurs for binding of biomolecules as well [15]). N_vdW should be inversely correlated with V_ex of the folded state. As mentioned above, |ΔV_ex| tends to become larger as V_ex decreases. It follows that N_vdW approximately represents the magnitude of |ΔV_ex| and ∑, leading to the superficial, high correlation. By contrast, the number of intramolecular hydrogen bonds, intramolecular electrostatic interaction energy, or degree of burial of the hydrophobic surface is not always correlated with V_ex: These factors are not always correlated with the thermal stability. We pointed out the importance of the water entropy for a variety of folding/unfolding processes in earlier works, but its importance in the thermal-stability change upon mutation is shown for the first time in the present study. The cold [20,43,44], pressure [32,43,44], and thermal [43,44] denaturating can be elucidated by our theoretical method focused on the water-entropy effect in a unified manner.

We classify the mutants obtained by mutations including Pro→Gly as group 2 and those to which Pro→Gly is not applied as group 1. When Pro→Gly is included in the mutation, the unfolded state becomes more extended and flexible. As a consequence, the loss of protein conformational entropy upon folding becomes larger (effect I), whereas the gain of water entropy increases (effect II). Effects I and II have conflicting effects, making the folded state less stable and more stable, respectively. The result from our analysis is indicative that effect II dominates in the present case and Pro→Gly leads to considerably higher stability.

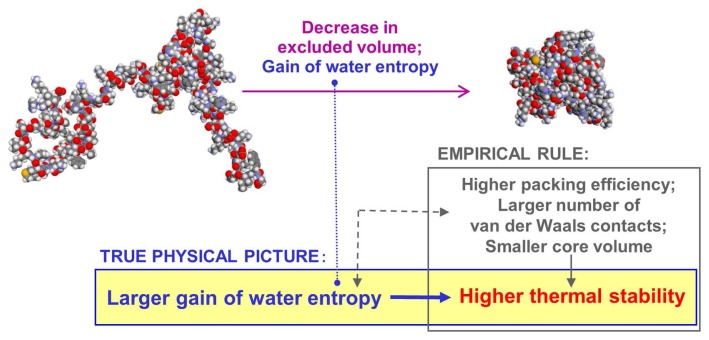
As mentioned above, there is the empirical rule widely known for the thermal stability of a protein. We have given a firm physical meaning to it (the significance of our claim is illustrated in Fig. 10). Tasks for the future are to develop perfect modeling of the unfolded state and to evaluate how the loss of protein conformational entropy upon folding changes due to such mutations as Pro→Gly. We have recently corroborated that the lowering or rising of T_m upon mutation can be predicted with ~75% accuracy by a theoretical method wherein the water-entropy effect is treated as the key factor. We intend to publish the result in a future article.

Figure 10.

Illustration of the significance of our claim.

We emphasize the following. The EV is different from the partial molar volume (PMV). The system-volume change upon protein unfolding is the PMV of the unfolded state minus that of the folded state. The system-volume change is quite small in general [45], but the EV change is far larger. Likewise, even when the system-volume change is not significantly influenced by a mutation [45], the EV change is largely affected. Further, the degree of the EV change should not be judged from its absolute value. It should be judged from the EV change divided by πd_S³/6 (d_S is the molecular diameter of water, 0.28 nm). Even when the EV change appears to be small, the water-entropy change can be remarkable.

We comment on the contribution from the energetic component to protein folding and thermal unfolding. Protein folding is accompanied by a decrease in the protein intramolecular energy (factor 1) and an increase in the hydration energy (factor 2) [14]. Factor 2 is attributed to a loss of protein-water attractive (electrostatic and van der Waals) interactions and a gain of water-water attractive interactions arising from the structural reorganization of water near the protein surface. Let the sum of factors 1 and 2 be ΔΛ. First, factor 1 remains unchanged against an increase in T. According to the experimental results [16], factor 2 dominates (ΔΛ>0) at 298 K and protein folding undergoes an enthalpy increase and factor 2 becomes weaker with increasing T. Thus, the gain of water-water attractive interactions dominates in factor 2, and it is significantly influenced by T. It follows that ΔΛ is a decreasing function of T. Strictly, ΔS_VH/(k_BN_r) in Figure 2 should be replaced by (TΔS_VH– ΔΛ)/(k_BT₀N_r) (T₀= 298 K). The values of T_m for the wild type and two mutants will then exhibit small, upward shifts. However, we assume that the order, T_m,c> T_m,b> T_m,a, remains unchanged and the measure is still effective. The validity of this assumption has been demonstrated in our earlier studies [12,21] as well as in the present study. Nevertheless, we are now examining a new measure “ΔS_VH/(k_BN_r) – ΔΛ/(k_BT₀N_r)” for predicting the thermal-stability changes upon mutations of a protein.

Last, we briefly discuss the relation between the Asakura-Oosawa (AO) theory [46,47] and the concept described in the present article. We have developed statistical-mechanical theories wherein the entropic effect originating from the translational displacement of water molecules in the system is treated as the key factor and applied them to a number of important problems in biophysics [12,15,17,18,20–22,29,32, 33,43,44]. The present article reports part of this development and application. The large bodies immersed in the small particles in the AO theory correspond to biomolecules immersed in water in our approach. Starting from the physical essence of the AO theory, we have made the following progresses: Biomolecules with arbitrary shapes or with polyatomic structures can be considered; a molecular model (not a continuum model) is employed for water; biomolecule-water many-body correlations are also taken into account; and a variety of biological self-assembly processes can now be explicated in a unified manner within the same theoretical framework. We note that the AO theory considers only the excluded-volume term of the pair correlation between a large particle and a small one but the many-body correlations play critical roles in biological systems. Refer to some of our earlier publications [12,15,17,18,20–22,29,32,33,43,44] and references therein for more details.